F=(a импликация b) коньюнкция (c импликация b)
F=(a → b) & (c → b) = (¬a v b) & (¬c v b) – КНФ, но не СКНФ
Сделаем СДНФ:
= (¬a v b) & (¬c v b) =
= (¬a v b v c) & (¬a v b v ¬c) & (a v ¬c v b) & (¬a v ¬c v b) =
= (¬a v b v c) & (¬a v b v ¬c) & (a v b v ¬c) & (¬a v b v ¬c) – это СКНФ
Раскроем скобки и сделаем ДНФ:
= (¬a v b) & (¬c v b) =
= ¬a & ¬c v b & ¬c v ¬a & b v b = ¬a & ¬c v b = – ДНФ, но не СДНФ
= ¬a & b & ¬c v ¬a & ¬b & ¬c v ¬a & b & ¬c v ¬a & b & c v a & b & ¬c v a & b & c – вот теперь СДНФ
Дороро и ПиццаУченик (5)
6 месяцев назад
а не затруднит еще одно задание проверить? “Упростить формулу с помощью равносильных преобразований”, (p дизьюнкция q дизьюнкция r) коньюнкция (p дизьюнкция q дизьюнкция (не) r). У меня вышел такой ответ: p дизьюнкция q. Он правильный?
СДНФ легко строится
по таблице истинности, но если функция
заданна формулой, ее СДНФ можно получить,
преобразуя формулу, без построения
таблицы истинности.
Построение СДНФ
осуществляется в два этапа. Сначала
строится ДНФ. А затем ДНФ превращается
в СДНФ. Чтобы превратить формулу в ДНФ,
нужно выполнить следующие действия.
1. Преобразовать
формулу так, чтобы в ней остались только
операции
![]()
причем
отрицания должны стоять только над
отдельными аргументами. Для этого нужно
воспользоваться законами де Моргана и
равносильностями
![]()
![]()
![]()
,
которые доказываются по таблицам
истинности.
2. Раскрыть скобки
и привести подобные, пользуясь законами
дистрибутивности и другими равносильностями,
а затем упростить формулу. В результате
будет построена ДНФ.
3. Преобразовать
ДНФ в СДНФ. Все ПЭК нужно превратить в
полные ПЭК, для чего поступить так. Если
в ПЭК не входит, например, переменная
y,
нужно домножить эту ПЭК на скобку
![]()
и раскрыть скобки. Повторить операцию
столько раз, сколько нужно, чтобы все
ПЭК стали полными. Если появятся
одинаковые конъюнкции, нужно убрать
повторения, ведь
![]()
.
Пример.
Построить СДНФ формулы
![]()
Сначала построим
таблицу истинности этой формулы (табл.
3), а затем преобразуем формулу в СДНФ
Таблица 3
|
x |
y |
z |
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
Эта функция равна
1 на шести наборах значений переменных,
ее СДНФ содержит шесть слагаемых и
такова
![]()
![]()
.
Преобразуем формулу
![]()
;
![]()
;
![]()
;
![]()
.
Преобразуем ДНФ в СДНФ
![]()
;
![]()
;
![]()
.
2.2.4. Как преобразовать формулу в скнф
СКНФ строится по
таблице истинности, но если таблица
задана формулой, ее СКНФ можно получить,
преобразуя формулу, без построения
таблицы истинности.
Построение СКНФ
осуществляется в два этапа. Сначала
строится КНФ, затем КНФ превращается в
СКНФ.
Чтобы превратить
формулу в КНФ, нужно выполнить следующие
действия.
1. Преобразовать
формулу так, чтобы в ней остались только
операции
причем отрицания должны стоять только
над отдельными аргументами.
2. Воспользоваться
законом дистрибутивности
![]()
и превратить формулу в КНФ.
3. Упростить
получившуюся КНФ.
4. Преобразовать
КНФ в СКНФ.
Все ПЭД нужно
превратить в полные ПЭД, для чего
поступить так. Если в ПЭД не входит,
например, переменная y,
нужно прибавить логически к этой ПЭД
выражение
![]()
и воспользоваться законом дистрибутивности
![]()
.
Повторить операцию столько раз, сколько
нужно, чтобы все ПЭД стали полными. Если
появятся одинаковые ППЭД, нужно убрать
повторения, так как
![]()
.
Пример.
Построим СКНФ формулы из параграфа 2.3.
СКНФ этой формулы такова:
![]()
,
так как функция равна 0 на двух наборах
(0,0,0) и (0,1,1).
Преобразуем
формулу. Как уже было показано
![]()
![]()
.
Тогда
![]()
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое СДНФ
Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).
Определение
СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».
ДНФ выглядит следующим образом:
((A;wedge;overline B;wedge;C);vee;(B;wedge;C))
СДНФ обладает некоторыми определенными свойствами:
- включает различные элементарные конъюнкции;
- все логические слагаемые формулы содержат все переменные, которые входят в функцию F;
- ни в одном логическом слагаемом не содержится переменная и её отрицание.
К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.
Примечание
При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.
Что такое СКНФ
Определение
СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.
КНФ имеет вид:
((A;vee;overline B;vee;C);wedge;(A;vee;C))
Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:
- в ней отсутствуют одинаковые элементарные дизъюнкции;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную нормальную функцию такого типа.
Правила построения по таблице истинности
Дизъюнктивная форма
Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.
Конъюнктивная форма
Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.
Алгоритм приведения к СДНФ и СКНФ
Рассмотрим логическую функцию в виде таблицы истинности.
Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:
- Отметить наборы переменных, значение функции F на которых равно 1.
- Записать для всех отмеченных наборов конъюнкцию всех переменных так: если значение некоторой переменной в этом наборе равняется 1, в конъюнкцию включается сама переменная. В случае противного результата, в конъюнкцию включается ее отрицание.
- Связать полученные конъюнкции операциями дизъюнкции.
Построим совершенную ДНФ:
И как результат получим следующую СДНФ:
(F(x_1,;x_2,;x_3);=;(overline{x_1}wedgeoverline{x_2}wedgeoverline{x_3});vee(overline{x_1};wedge;overline{x_2};wedge;x_3);vee(x_1;wedge;overline{x_2};wedge;overline{x_3});vee;(x_1;wedge;overline{x_2};wedge;x_3);vee;(x_1;wedge;x_2;wedge;x_3))
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:
- Отметить в таблице истинности наборы переменных, значение функции F на которых равно 0.
- Записать для всех отмеченных наборов дизъюнкцию всех переменных — в том случае, когда значение некоторой переменной в этом наборе равняется 0, в дизъюнкцию включается сама переменная, если происходит наоборот, то в дизъюнкцию включается ее отрицание.
- Связать полученные дизъюнкции операциями конъюнкции.
Построим совершенную КНФ:
И как результат получим следующую СКНФ:
(F(x_1,;x_2,;x_3);=;(x_1;vee;overline{x_2};vee;x_3);wedge;(x_1;vee;overline{x_2};vee;overline{x_3});wedge;(overline{x_1};vee;overline{x_2};vee;x_3))
Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.
Доказательство эквивалентности
Эквивалентность — понятие, означающее, что две и более формул представляют одну и ту же функцию. Для обозначения эквивалентности могут использоваться следующие знаки: ( equiv , = , Leftrightarrow .)
Доказать эквивалентность формул можно двумя способами.
- Первый заключается в построении и сравнении таблиц истинности обеих функций. В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
- Второй вариант — метод эквивалентных преобразований. Суть этого метода — построение цепи эквивалентных формул на основе ранее доказанных эквивалентностей.
Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.
Поглощение
(x;vee;xy;=;x)
(x(x;vee;y);=;x;)
Доказательство эквивалентности:
(x;vee;xy;=;x;cdot;l;vee;xy;=;x(l;vee;y);=;x)
(x(x;vee;y);=;xx;vee;xy;=;x;vee;xy;=;x)
Склеивание
(xy;vee;xoverline y;=;x)
Доказательство эквивалентности:
(xy;vee;xoverline y;=;x(y;vee;overline y);=;x;cdot;l;=;x)
Обобщенное склеивание
(xz;vee;yoverline z;vee;xy;=;xz;vee yoverline z)
Доказательство эквивалентности
(xz;vee;yoverline z;vee;xy;=;xz;vee yoverline z;vee;xyz;vee;xyoverline z;=;xz;vee;yoverline z)
Расщепление
(x;vee;overline xy;=;x;vee;y)
Доказательство эквивалентности
(x;vee;overline xy;=;xy;vee;xoverline y;vee;overline xy;=;xy;vee;xoverline y;vee;xy;vee;overline xy;=;x;cdot;l;;vee;y;cdot;l;=;x;vee;y)
Примеры с решением
Задача №1
Приведите к СКНФ (((((Arightarrow B)rightarrowoverline A)rightarrowoverline B)rightarrowoverline C)).
Через применение закона де Моргана и правила( x;rightarrow;y;=;overline x;vee;y) упростим выражения:
(F;=;((((A;rightarrow;B);rightarrow;overline A);rightarrowoverline B);rightarrow;overline C);=;(((overline A;vee;B);rightarrow;overline A);rightarrow;overline B);rightarrowoverline C;);=)
(=;((((overline A;vee;B);rightarrowoverline A);rightarrowoverline B);rightarrow;overline C);=;((overline{((overline A;vee;B)};vee;overline A);rightarrowoverline B);rightarrowoverline C);=)
(=(((overline A;vee;B);vee;overline A);rightarrow;overline B);rightarrow;overline C);=((overline{(overline{(overline Avee B)};vee;overline A;)};vee;overline B);rightarrow;overline C);=)
(=;(overline{(overline{(overline{(overline A;vee;B)};vee;overline A)};vee;overline B)};vee;overline C);=;(((A;vee;B);vee;overline A);vee;overline B);vee;overline C;=)
(=;((overline{(overline A;vee;B)};vee;overline A);wedge;B);vee;overline C;=;(((A;wedge;overline B);vee;overline A);wedge B);vee;overline C;=)
(=((Aoverline B;vee;overline A);vee;overline A);wedge;B);vee;overline C;=(((A;wedge;overline B);vee;overline A);wedge;B);vee;overline C;=)
(=;((Aoverline B;vee;overline A);wedge;B);vee;overline C;=;(Aoverline BB;vee;overline AB);vee;overline C;=;(0;vee;overline AB);vee;overline C;=;overline AB;vee;overline C)
Далее приведем выражение к КНФ:
(F;=;overline AB;vee;overline C;;=;(overline A;vee;overline C);wedge;(B;vee;overline C))
Далее приведем выражение к СКНФ:
(F;=;(overline A;vee;overline C);wedge;(B;vee;overline C);=;(overline A;vee:overline C;vee;Boverline B);wedge;(Aoverline A;vee;B;v;overline C);=)
(=;(overline A;vee;overline C;vee;B);wedge;(A;vee;B;vee;overline C);wedge;(overline A;vee;overline C;vee;overline B);wedge;(overline A;vee;B;;overline C))
Задача №2
Используя эквивалентные преобразования, постройте ДНФ функции (f(widetilde x^n))
(f(widetilde x^3) = (overline{x_1}x_2;oplus;x_3);cdot;(x_1x_3;rightarrow;x_2))
Преобразуем функцию:
(f(widetilde x^3) = (overline{x_1}x_2;oplus;x_3);cdot;(x_1x_3;rightarrow;x_2) = ((overline{x_1}x_2;cdot;overline{x_3};);vee;(overline{overline{x_1}x_2};cdot;x_3));cdot;(overline{x_1x_3};vee;x_2);=)
(=;((overline{x_1}x_2overline{x_3});vee;((overline{overline{x_1}};vee;overline{x_2});x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=;((overline{x_1}x_{2;}overline{x_3});vee;((x_1;vee;overline{x_2});x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=)
(=;(overline{x_1}x_2overline{x_3};vee;x_1x_3;vee;overline{x_2}x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=)
(=(overline{x_1}x_2overline{x_3};cdot(x_1vee x_3vee x_2);vee;x_1x_3;cdot;(overline{x_1};vee;overline{x_3};vee;x_2);vee;overline{x_2}x_3;cdot;(overline{x_1};vee;overline{x_3};vee;x_2));=)
(=;(overline{x_1}x_2overline{x_3};vee;(x_1;x_3overline{x_1};vee;x_1x_3overline{x_3};vee;x_1x_3x_2);vee;(overline{x_2}x_3overline{x_1};vee;overline{x_2}x_3overline{x_3};vee;overline{x_2}x_3x_2);=)
(=;(overline{x_1}x_2overline{x_3};vee;0;vee;0;vee;x_1x_2x_3;vee;overline{x_1}overline{x_2}x_3;vee;0;vee;0);=)
(=;overline{x_1}x_2overline{x_3};vee;x_1x_2x_3;vee;overline{x_1}overline{x_2}x_3)
Для любой логической формулы можно построить бесконечное количество равносильных ей формул. Для этого потребуется произвести некоторое количество тождественных преобразований. Одной из главных задач в алгебре логики является нахождение канонических форм формул. Проще говоря таких, которые построены по одному канону (правилу).
Форма представления какой-либо логической функции будет считаться нормальной, если она выражена через конъюнкцию, дизъюнкцию, а также отрицание переменных. Среди всех нормальных форм можно выделить совершенно нормальные. Это тот случай, когда функция может быть записана только одним единственным способом.
Классы СКНФ и СДНФ
В при решении задач в алгебре логики особая роль отводится классам конъюнктивных и дизъюнктивных совершенно нормальных форм. Они основаны на стандартных понятиях элементарной конъюнкции и дизъюнкции.
Определение 1 — 2
Элементарной конъюнкцией принято называть формулу в том случае, когда она представляет собой конъюнкцию любого количества переменных, которые берутся без отрицания либо с отрицанием. При этом одночленной элементарной конъюнкцией считается только одна единственная переменная либо ее отрицание.
Элементарной дизъюнкцией называют формулу при условии, что она будет являться дизъюнкцией некоторого любого количества переменных и отрицаний, при этом она может быть и одночленной.
СКНФ
Форма любой логической формулы нормального типа не может содержать знаки эквивалентности, импликации, а также отрицания неэлементарных формул. Она может существовать только в двух видах:
- КНФ – конъюнктивная нормальная форма, представляющая собой конъюнкцию нескольких дизъюнкций. К примеру, [(A vee bar{B} vee C) wedge(A vee C)];
- ДНФ – дизъюнктивная нормальная форма, которая является дизъюнкцией нескольких конъюнкций. К примеру, [(A wedge bar{B} wedge C) vee(A wedge C)].
Определение 3
Совершенной конъюнктивной нормальной формой (СКНФ) называют КНФ, удовлетворяющую нескольким условиям:
- В ней не содержится двух и более элементарных дизъюнкций;
- Во всех дизъюнкциях отсутствуют одинаковые переменные;
- Каждая ДНФ содержит в себе все переменные из входящих в нее КНФ.
Любую булеву формулу, не являющуюся тождественной истиной, можно представить в виде СКНФ.
Правила построения СКНФ
В алгебре логики для любого набора переменных, при котором конечное значение функции становится нулевым, можно записать сумму. При этом переменные, имеющие числовые значение больше единицы, должны браться с отрицательным знаком.
Построение должно осуществляться по следующему алгоритму:
- В таблице нужно отметить такие наборы переменных, при которых [f=1].
- Для каждого выбранного набора переменных записываем КНФ, при этом если значение какой-либо из них равно 1, то она включается в неизменном виде, иначе – ее отрицание.
- На последнем этапе все полученные конъюнкции следует связать операциями дизъюнкции.
СНДФ
Определение 4
Совершенной дизъюнктивной нормальной формой (СНДФ) называют удовлетворяющую нескольким условиям ДНФ. Всего должно выполняться три условия:
- В ДНФ не должно содержаться двух и более одинаковых СКНФ.
- Ни в одной из конъюнкций не должно содержаться одинаковых переменных.
- В каждой элементарной КНФ должны содержаться все переменные, входящих в нее ДНФ, при этом их порядок должен полностью совпадать.
Любую булеву формулу в алгебре логики, не являющуюся тождественно ложной, можно представить в виде СНДФ, но только в одном единственном виде.
Правила построения СДНФ
Если существует определённый набор переменных, при котором значение функции равно единице, то можно записать произведения, учитывая, что переменные, значение которых больше нуля, нужно брать с отрицанием.
Алгоритм построения будет следующим:
- В таблице отмечаются все те наборы переменных, при которых [f=0]
- Для каждого отмеченного набора всех переменных записывается ДНФ, при этом если значение какой-либо из них равно нулю, то включается сама переменная, в любом другом случае ее нужно инвертировать.
- В конце все полученные дизъюнкции связываются друг с другом операциями конъюнкции.
Нет времени решать самому?
Наши эксперты помогут!
Примеры нахождения СКНФ и СДНФ
Рассмотрим несколько примеров нахождения СКНФ и СДНФ с помощью данных таблицы истинности.
Примеры 1 — 2
Необходимо по таблице истинности записать логическую функцию.

Решение. Для того чтобы выполнить задачу будем использовать правило построения СДНФ.

Получим СДНФ, которая имеет следующий вид:
[Fleft(x_{1}, x_{2}, x_{3}right)=left(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}}right) veeleft(overline{x_{1}} wedge overline{x_{2}} wedge x_{3}right) veeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}}right) veeleft(x_{1} wedgeright.left.overline{x_{2}} wedge x_{3}right) veeleft(x_{1} wedge x_{2} wedge x_{3}right)]
Далее будем действовать согласно правилу построения СКНФ:

В результате получим:
[Fleft(x_{1}, x_{2}, x_{3}right)=left(x_{1} wedge overline{x_{2}} wedge x_{3}right) wedgeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}}right) wedgeleft(overline{x_{1}} wedge overline{x_{2}} wedge x_{3}right)]
Требуется представить функцию, которая задана в таблице в виде СДНФ и СКНФ.

Решение: Для начала запишем в СНДФ заданную логическую функцию. Чтобы было проще, добавим еще один вспомогательный столбец. Руководствуемся правилом составления СДНФ и учитываем, что требуется ввести знак отрицания, если значение переменной будет нулевым. Это нужно для того, чтобы они не превратили в нули основной функции значение конъюнкции.

Значения, которые получились во вспомогательном столбце соединяем знаком дизъюнкции, в результате чего получаем искомую логическую функцию, которая примет следующий вид:
[Fleft(x_{1}, x_{2}, x_{3}, x_{4}right)=(bar{x} wedge bar{y} wedge z wedge f) veeleft(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right) veeleft(overline{x_{1}} wedge x_{2} wedge x_{3} wedgeright.left.x_{4}right) veeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right)]
После этого потребуется записать логическую функцию в СКНФ. Для этого используем правило ее составления и вводим знаки отрицания для тех переменных, значение которых равно 1. Если пренебречь инвертированием единичных значений, то они могут превратить ДНФ в единицы основных функций.

Все полученные нами значения во вспомогательном столбце соединяем знаком конъюнкции и в итоге получаем логическую функцию в следующем виде.
[Fleft(x_{1}, x_{2}, x_{3}, x_{4}right)=left(x_{1} vee x_{2} vee x_{3} vee x_{4}right) wedgeleft(x_{1} vee x_{2} vee x_{3} vee overline{x_{4}}right) wedgeleft(x_{1} vee x_{2} veeright.\left.overline{x_{3}} vee x_{4}right) wedgeleft(x_{1} vee overline{x_{2}} vee x_{3} vee overline{x_{4}}right) wedgeleft(x_{1} vee overline{x_{2}} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} vee x_{2} vee x_{3} veeright.\left.overline{x_{4}}right) wedgeleft(overline{x_{1}} vee x_{2} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} vee x_{2} vee overline{x_{3}} vee overline{x_{4}}right) wedgeleft(overline{x_{1}} vee overline{x_{2}} vee x_{3} vee x_{4}right) wedge\left(overline{x_{1}} vee overline{x_{2}} vee x_{3} vee overline{x_{4}}right) wedgeleft(overline{x_{1}} vee overline{x_{2}} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right)]
После рассмотрения примеров построения СДНФ и СКНФ с использованием таблицы истинности, стал понятен принцип построения логических функций.
Как решить логическое уравнение без таблицы истинности
Можно выделить различные способы решения систем логических уравнений. Это сведение к одному уравнению, построение таблицы истинности и декомпозиция.
Задача: Решить систему логических уравнений:
Рассмотрим метод сведения к одному уравнению. Данный метод предполагает преобразование логических уравнений, таким образом, чтобы правые их части были равны истинностному значению (то есть 1). Для этого применяют операцию логического отрицания. Затем, если в уравнениях есть сложные логические операции, заменяем их базовыми: «И», «ИЛИ», «НЕ». Следующим шагом объединяем уравнения в одно, равносильное системе, с помощью логической операции «И». После этого, следует сделать преобразования полученного уравнения на основе законов алгебры логики и получить конкретное решение системы.
Решение 1: Применяем инверсию к обеим частям первого уравнения:
Представим импликацию через базовые операции «ИЛИ», «НЕ»:
Поскольку левые части уравнений равны 1, можно объединить их с помощью операции “И” в одно уравнение, равносильное исходной системе:
Раскрываем первую скобку по закону де Моргана и преобразовываем полученный результат:
Полученное уравнение, имеет одно решение: A =0, B=0 и C=1.
Следующий способ – построение таблиц истинности. Поскольку логические величины имеют только два значения, можно просто перебрать все варианты и найти среди них те, при которых выполняется данная система уравнений. То есть, мы строим одну общую таблицу истинности для всех уравнений системы и находим строку с нужными значениями.
Решение 2: Составим таблицу истинности для системы:
Полужирным выделена строчка, для которой выполняются условия задачи. Таким образом, A=0, B=0 и C=1.
Способ декомпозиции. Идея состоит в том, чтобы зафиксировать значение одной из переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения. Затем можно зафиксировать значение второй переменной и т.д.
Решение 3: Пусть A = 0, тогда:
Из первого уравнения получаем B =0, а из второго – С=1. Решение системы: A = 0, B = 0 и C = 1.
В ЕГЭ по информатике очень часто требуется определить количество решений системы логических уравнений, без нахождения самих решений, для этого тоже существуют определенные методы. Основной способ нахождения количества решений системы логических уравнений – замена переменных . Сначала необходимо максимально упростить каждое из уравнений на основе законов алгебры логики, а затем заменить сложные части уравнений новыми переменными и определить количество решений новой системы. Далее вернуться к замене и определить для нее количество решений.
Задача: Сколько решений имеет уравнение ( A → B ) + ( C → D ) = 1? Где A, B, C, D – логические переменные.
Решение: Введем новые переменные: X = A → B и Y = C → D . С учетом новых переменных уравнение запишется в виде: X + Y = 1.
Дизъюнкция верна в трех случаях: (0;1), (1;0) и (1;1), при этом X и Y является импликацией, то есть является истинной в трех случаях и ложной – в одном. Поэтому случай (0;1) будет соответствовать трем возможным сочетаниям параметров. Случай (1;1) – будет соответствовать девяти возможным сочетаниям параметров исходного уравнения. Значит, всего возможных решений данного уравнения 3+9=15.
Следующий способ определения количества решений системы логических уравнений – бинарное дерево. Рассмотрим данный метод на примере.
Задача: Сколько различных решений имеет система логических уравнений:
Приведенная система уравнений равносильна уравнению:
Предположим, что x 1 – истинно, тогда из первого уравнения получаем, что x 2 также истинно, из второго – x 3=1, и так далее до xm = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы. Пусть теперь x 1=0, тогда из первого уравнения имеем x 2 =0 или x 2 =1.
Когда x 2 истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. При x 2=0 получаем, что x 3=0 или x 3=, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных ( m +1 решение, в каждом решении по m значений переменных):
Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m +1.
Урок №6 Решение логических уравнений (10 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Урок 6 Решение логических уравнений.doc
Тема урока: Решение логических уравнений
Образовательная – изучение способов решения логических уравнений, формирование умений и навыков решения логических уравнений и построения логического выражения по таблице истинности;
Развивающая – создать условия для развития познавательного интереса учащихся, способствовать развитию памяти, внимания, логического мышления;
Воспитательная : способствовать воспитанию умения выслушивать мнение других, воспитание воли и настойчивости для достижения конечных результатов.
Тип урока: комбинированный урок
Оборудование: компьютер, мультимедийный проектор, презентация 6.
Повторение и актуализацию опорных знаний. Проверка домашнего задания (10 минут)
На предыдущих уроках мы познакомились с основными законами алгебры логики, научились использовать эти законы для упрощения логических выражений.
Выполним проверку домашнего задания по упрощению логических выражений:
1. Какое из приведенных слов удовлетворяет логическому условию:
(первая буква согласная→вторая буква согласная) ٨ (последняя буква гласная → предпоследняя буква гласная)? Если таких слов несколько, укажите наименьшее из них.
1) АННА 2) МАРИЯ 3) ОЛЕГ 4) СТЕПАН
А – первая буква согласная
В – вторая буква согласная
С – последняя буква гласная
D – предпоследняя буква гласная
Составим выражение: 
2. Укажите, какое логическое выражение равносильно выражению

Упростим запись исходного выражения и предложенных вариантов:

3. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?

Определим значения этих выражений при указанных значениях аргументов:
Ознакомление с темой урока, изложение нового материала (30 минут)
Мы продолжаем изучать основы логики и тема нашего сегодняшнего урока «Решение логических уравнений». Изучив данную тему, вы узнаете основные способы решения логических уравнений, получите навыки решения этих уравнений путем использования языка алгебры логики и умения составления логического выражения по таблице истинности.
1. Решить логическое уравнение
Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
Преобразуем выражение (¬K M) → (¬L M N) 
Выражение ложно, когда оба слагаемые ложны. Второе слагаемое равно 0, если M =0, N =0, L =1. В первом слагаемом K =0, так как М=0, а  .
.
2. Сколько решений имеет уравнение (в ответе укажите только число)?

Решение: преобразуем выражение
A + B =1 и C + D =1
2 способ: составление таблицы истинности
3 способ: построение СДНФ – совершенной дизъюнктивной нормальной формы для функции – дизъюнкции полных правильных элементарных конъюнкций.
Преобразуем исходное выражение, раскроем скобки для того, чтобы получить дизъюнкцию конъюнкций:
Дополним конъюнкции до полных конъюнкций (произведение всех аргументов), раскроем скобки:
 Учтем одинаковые конъюнкции:
Учтем одинаковые конъюнкции:

В итоге получаем СДНФ, содержащую 9 конъюнкций. Следовательно, таблица истинности для данной функции имеет значение 1 на 9 строках из 2 4 =16 наборов значений переменных.
3. Сколько решений имеет уравнение (в ответе укажите только число)?

 ,
,
3 способ: построение СДНФ

Учтем одинаковые конъюнкции:
 1
1
В итоге получаем СДНФ, содержащую 5 конъюнкций. Следовательно таблица истинности для данной функции имеет значение 1 на 5 строках из 2 4 =16 наборов значений переменных.
Построение логического выражения по таблице истинности:
для каждой строки таблицы истинности, содержащей 1 составляем произведение аргументов, причем, переменные, равные 0, входят в произведение с отрицанием, а переменные, равные 1 – без отрицания. Искомое выражение F будет составляется из суммы полученных произведений. Затем, если возможно, это выражение необходимо упростить.
Пример: дана таблица истинности выражения. Построить логическое выражение.

3. Задание на дом (5 минут)

Сколько решений имеет уравнение (в ответе укажите только число)?

По заданной таблице истинности составить логическое выражение и
Выбранный для просмотра документ Урок 6 Решение логических уравнений.ppt
Описание презентации по отдельным слайдам:
Проверка домашнего задания: Какое из приведенных слов удовлетворяет логическому условию: (первая буква согласная→вторая буква согласная) ٨ (последняя буква гласная → предпоследняя буква гласная)? Если таких слов несколько, укажите наименьшее. 1) АННА 2) МАРИЯ 3) ОЛЕГ 4) СТЕПАН 2. Укажите, какое логическое выражение равносильно выражению 3. Дан фрагмент таблицы истинности выражения F: Какое выражение соответствует F? xyzF 0001 0111 1100
Тема урока: Решение логических уравнений
1. Решить логическое уравнение (¬K M) → (¬L M N) =0 Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
3. Сколько решений имеет уравнение (в ответе укажите только число)? 1 способ: рассуждения Ответ: 9 2 способ: составление таблицы истинности ABCD АВСDA+BC+DF
3 способ: построение СДНФ – совершенной дизъюнктивной нормальной формы для функции – дизъюнкции полных конъюнкций. Преобразуем исходное выражение, раскроем скобки для того, чтобы получить дизъюнкцию конъюнкций: (A+B)*(C+D)=A*C+B*C+A*D+B*D= Дополним конъюнкции до полных конъюнкций (произведение всех аргументов), раскроем скобки:
4. Сколько решений имеет уравнение (в ответе укажите только число)?
Построение логического выражения по таблице истинности: для каждой строки таблицы истинности, содержащей 1 составляем произведение аргументов, причем, переменные, равные 0, входят в произведение с отрицанием, а переменные, равные 1 – без отрицания. Искомое выражение F будет составляется из суммы полученных произведений. Затем, если возможно, это выражение необходимо упростить. Пример: дана таблица истинности выражения. Построить логическое выражение. аbcF 0000 0010 0100 0110 1001 1011 1101 1110
Задание на дом: По заданной таблице истинности составить логическое выражение и упростить его. 2. Решить уравнение: 3. Сколько решений имеет уравнение? аbcF 0000 0010 0100 0111 1001 1011 1100 1111
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 949 человек из 80 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Курс добавлен 23.11.2021
- Сейчас обучается 48 человек из 28 регионов
Курс повышения квалификации
Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Курс добавлен 31.01.2022
- Сейчас обучается 33 человека из 19 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 566 504 материала в базе
Материал подходит для УМК
«Информатика (углублённый уровень) (в 2 частях)», Семакин И.Г., Шеина Т.Ю., Шестакова Л.В.
1.6.2. Логические формулы и функции
Другие материалы
- 12.11.2017
- 1996
- 237
- 12.11.2017
- 707
- 1
- 12.11.2017
- 274
- 0
- 12.11.2017
- 977
- 8
- 12.11.2017
- 972
- 0
- 12.11.2017
- 376
- 0
- 12.11.2017
- 705
- 0
- 12.11.2017
- 790
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 12.11.2017 16060
- RAR 112.9 кбайт
- 268 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Егорова Елена Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 4 года и 10 месяцев
- Подписчики: 0
- Всего просмотров: 95670
- Всего материалов: 15
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Забайкалье в 2022 году обеспечат интернетом 83 школы
Время чтения: 1 минута
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
У 76% российских учителей оклад ниже МРОТ
Время чтения: 2 минуты
В Воронеже продлили удаленное обучение для учеников 5-11-х классов
Время чтения: 1 минута
Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.
Время чтения: 2 минуты
Рособрнадзор не планирует переносить досрочный период ЕГЭ
Время чтения: 0 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 18 Алгебра логики
Информатика. 10 класса. Босова Л.Л. Оглавление
§ 18. Алгебра логики
Из курса информатики основной школы вы знаете, что для компьютерных наук большое значение имеет математическая логика, а точнее, её часть, называемая алгеброй логики.
Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.
 Джордж Буль (1815-1864) — английский математик, основоположник алгебры логики. Дж. Буль изучал логику мышления математическими методами и разработал алгебраические методы решения традиционных логических задач. В 1854 году он опубликовал работу, в которой изложил суть алгебры логики, основанной на трёх операциях: and, or, not. Долгое время алгебра логики была известна достаточно узкому классу специалистов. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейноконтактных и электронно-ламповых схем.
Джордж Буль (1815-1864) — английский математик, основоположник алгебры логики. Дж. Буль изучал логику мышления математическими методами и разработал алгебраические методы решения традиционных логических задач. В 1854 году он опубликовал работу, в которой изложил суть алгебры логики, основанной на трёх операциях: and, or, not. Долгое время алгебра логики была известна достаточно узкому классу специалистов. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейноконтактных и электронно-ламповых схем.
18.1. Логические высказывания и переменные
Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно.
Например, высказывание «Джордж Буль — основоположник алгебры логики» истинно, а высказывание «2 + 2 = 5» ложно.
Что вы можете сказать об истинности или ложности предложения «Данное высказывание — ложь»?
Из имеющихся высказываний можно строить новые высказывания. Для этого используются логические связки — слова и словосочетания «не», «и», «или», «если …, то», «тогда и только тогда» и др.
Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым).
Например, из двух простых высказываний «Алгебра логики является основой строения логических схем компьютеров» и «Алгебра логики служит математической основой решения сложных логических задач» можно получить составное высказывание «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач».
Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, В, С). Так, если обозначить элементарное высказывание «Джордж Буль — основоположник алгебры логики» именем А, а элементарное высказывание «2 + 2 = 5» именем В, то составное высказывание «Джордж Буль — основоположник алгебры логики, и 2 + 2 = 5» можно записать как «А и В». Здесь А, В — логические переменные, «и» — логическая связка.
Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь».
Для логических значений «истина» и «ложь» могут использоваться следующие обозначения:

Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).
18.2. Логические операции
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.
Из курса информатики основной школы вам известны логические операции отрицание, конъюнкция и дизъюнкция. Их таблицы истинности представлены ниже.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны, называется конъюнкцией или логическим умножением.
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, называется дизъюнкцией или логическим сложением.
Логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному, называется отрицанием или инверсией.
При построении отрицания простого высказывания:
• используется оборот «неверно, что» или к сказуемому добавляется частица «не»;
• в высказывании, содержащем слово «все», это слово заменяется на «некоторые» и наоборот.
Рассмотрим несколько новых логических операций.
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией или логическим следованием.
Операция импликации обозначается символом ? и задаётся следующей таблицей истинности:

В разговорной речи импликации соответствуют предложения, содержащие связку «если …, то». Эту связку мы используем тогда, когда хотим показать наличие причинно-следственной связи, иначе говоря, зависимость одного события от другого. Например, пусть некоторый человек сказал: «Если завтра будет хорошая погода, то я пойду гулять». Ясно, что человек окажется лжецом лишь в том случае, если погода действительно будет хорошей, а гулять он не пойдёт. Если же погода будет плохой, то, независимо от того, пойдёт он гулять или нет, во лжи его нельзя обвинить: обещание пойти гулять он давал лишь при условии, что погода будет хорошей.
Результат операции импликации, как и других логических операций, определяется истинностью или ложностью логических переменных, а не наличием причинно-следственных связей между высказываниями. Например, абсурдное с житейской точки зрения высказывание «Если 2 > 3, то существуют ведьмы» является истинным с точки зрения алгебры логики.
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией.
Строгая дизъюнкция обозначается символом ? и задаётся следующей таблицей истинности:

В русском языке строгой (разделительной) дизъюнкции соответствует связка «либо». В отличие от обычной дизъюнкции (связка «или») в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдёт только одно событие.
Например, высказывая утверждение «На сегодняшнем матче Петя сидит на трибуне А либо на трибуне Б», мы считаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б, и что сидеть одновременно на двух трибунах Петя не может.
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью.
В логике эквиваленция обозначается символом и задаётся следующей таблицей истинности:

В разговорной речи для выражения взаимной обусловленности используется связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно».
Рассмотрим высказывание «Денис пойдёт в бассейн тогда и только тогда, когда он выучит уроки».
Это высказывание истинно (договорённость соблюдается), если истинны оба элементарных высказывания («Денис пойдёт в бассейн», «Денис выучит уроки»). Высказывание истинно (договорённость не нарушается) и в том случае, если оба элементарных высказывания ложны («Денис не пойдёт в бассейн», «Денис не выучит уроки»). Если же одно из двух высказываний ложно («Денис пойдёт в бассейн, хотя и не выучит уроки», «Денис выучит уроки, но не пойдёт в бассейн»), то договорённость нарушается, и составное высказывание становится ложным.
А сейчас посмотрите внимательно на таблицы истинности строгой дизъюнкции и эквиваленции: если на некотором наборе логических переменных результатом строгой дизъюнкции является истина, то на этом же наборе результатом эквиваленции всегда будет ложь, и наоборот.
Можно сделать выводы:
• операция эквиваленции есть отрицание операции строгой дизъюнкции

• операция строгой дизъюнкции есть отрицание операции эквиваленции

На сегодняшний день в алгебре логики не существует унифицированной символики для обозначения логических операций. В таблице 4.1 представлены логические операции и их наиболее распространённые обозначения, используемые как в алгебре логики, так и в некоторых языках программирования. Здесь же приведены речевые обороты, соответствующие логическим операциям.
Таблица 4.1
Логические операции и их обозначения

Операция отрицания выполняется над одним операндом. Такие операции называются одноместными или унарными. Все остальные логические операции, представленные в таблице 4.1, выполняются над двумя операндами и называются двуместными или бинарными.
18.3. Логические выражения
Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (О, 1), логических переменных, знаков логических операций и скобок.
Для логического выражения справедливо:
1) всякая логическая переменная, а также логические константы (О, 1) есть логическое выражение;
2) если А — логическое выражение, то и 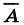 — логическое выражение;
— логическое выражение;
3) если А и В — выражения, то, связанные любой бинарной операцией, они также представляют собой логическое выражение.
При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:
1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.
Операции одного приоритета выполняются в порядке их следования, слева направо. Как и в арифметике, скобки меняют порядок выполнения операций.
Пример 1. Выясним, какие из приведённых слов удовлетворяют логическому условию (первая буква согласная ? вторая буква согласная) & (последняя буква гласная ? предпоследняя буква гласная):
1) ОЗОН;
2) ИГРА;
3) МАФИЯ;
4) ТРЕНАЖ.
Вычислим значение логического выражения для каждого из данных слов:

Итак, заданному условию удовлетворяют первое и четвёртое слова.
Решение логического уравнения — это один или несколько наборов значений логических переменных, при которых логическое уравнение становится истинным выражением.
Пример 2. Решим логическое уравнение

Дизъюнкция ложна в том и только в том случае, когда ложно каждое из образующих её высказываний. Иными словами, наше уравнение соответствует системе уравнений:

Таким образом, значение переменной D уже найдено. Импликация равна нулю в единственном случае — когда из истины следует ложь. Иначе говоря, в нашем случае: А = 1 и С = 0.
Подставим найденные значения переменных в уравнение

Ответ: А = 1, В = 1, С = 0, D = 0.
Логические уравнения могут иметь не одно, а несколько и даже очень много решений. Зачастую требуется, не выписывая все решения уравнения, указать их количество.
Пример 3. Выясним, сколько различных решений имеет логическое уравнение

Дизъюнкция истинна, если истинно хотя бы одно из образующих её высказываний. Решение данного логического уравнения равносильно совокупности, состоящей из двух уравнений:

Первое равенство будет выполняться только при А = 1, В = 1 и С = 0. Поскольку D в этом уравнении не задействовано, оно может принимать любое из двух значений (0 или 1). Таким образом, всего первое уравнение имеет два решения.
Самостоятельно выясните, сколько решений имеет второе уравнение (из совокупности двух уравнений).
Сколько решений имеет исходное уравнение?
Пример 4. Выясним, сколько решений имеет очень простое с виду логическое уравнение х1 & х2 ? х3 & х4 = 1.
Введём замену переменных. Пусть t1 = х1 & х2, t2 = х3 & х4. Тогда исходное уравнение примет вид: t1 ? t2 = 1.
На t1 никаких ограничений нет, эта переменная может принимать значения 0 и 1. Импликация равна 0 только в случае, когда из истины (1) следует ложь (0). Исключим этот вариант. Построим дерево решений, представив на нём значения переменных t1 и t2 при которых t1 ? t2 = 1.

Получаем для t1 и t2 три набора значений: 00, 01, 11. Первая двоичная цифра в каждом из этих трёх наборов — результат выражения х1 & х2, вторая — х3 & х4. Рассмотрим первый набор: существует три набора х1 и х2 таких, что х1 & х2 = 0, другими словами, первый 0 мы можем получить тремя способами. Второй О в этом наборе мы также можем получить тремя способами.
Из курсов информатики и математики основной школы вам известно одно из основных правил комбинаторики — правило умножения. Согласно ему, если элемент А можно выбрать n способами, и при любом выборе А элемент В можно выбрать m способами, то пару (А, В) можно выбрать n • m способами.
Согласно правилу умножения, пару 00 можно получить 3 • 3 = 9 способами.
Что касается пары 01, то первый 0 мы можем получить тремя способами, а для получения 1 существует единственный вариант (х3 & х4 = 1 при х3 = 1 и х4 = 1). Следовательно, есть ещё три набора переменных х1, х2, х3, х4, являющихся решением исходного уравнения.
Самостоятельно доведите решение этой задачи до конца.
18.4. Предикаты и их множества истинности
Равенства, неравенства и другие предложения, содержащие переменные, высказываниями не являются, но они становятся высказываниями при замене переменной каким-нибудь конкретным значением. Например, предложение х 2 + у 2 = 1) — множество точек окружности единичного радиуса с центром в начале координат. Следует отметить, что многие задания, выполняемые вами на уроках математики, прямо связаны с предикатами. Например, стандартное задание «Решить квадратное уравнение x 2 — 3x + 2 = 0» фактически означает требование найти множество истинности предиката Р(х) = (x 2 — 3x + 2 = 0).
Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.
Пусть А и В соответственно являются множествами истинности предикатов А(х) и В(х). Тогда пересечение множеств А и В будет являться множеством истинности для предиката А(х) & В(х), а объединение множеств А и В будет множеством истинности для предиката А(х) ? В(х).
Пример 5. Найдём все целые числа 2, превращающие предикат
P(z) = (z > 5) & (z — 2 5) являются целые числа 6, 7, 8 и т. д. Множеством истинности предиката В(z) = (z — 2 
Множество истинности исходного предиката — пересечение (общие элементы) множеств истинности образующих его предикатов:
Его мощность |Р| = 11.
Пример 6. Рассмотрим предикат (50 2 ) ? (50 > (х + 1) 2 ), определённый на множестве целых чисел. Найдём множество истинности этого предиката.
Зачастую задания такого рода формулируют несколько иначе.
Например, так: «Найдите все целые числа х, для которых истинно высказывание (50 (х + 1)2)».
Проанализируем отдельно каждый из элементарных предикатов (50 2 ) и (50 > (x + 1) 2 ), решив соответствующие неравенства:

Определим значение исходного предиката на каждом из полученных подмножеств, причём отдельно рассмотрим значение х = -8 (оно попадает в два подмножества) и значение х = 7 (оно не попадает ни в одно подмножество):

Итак, множеством истинности исходного предиката являются целые числа, принадлежащие отрезку [-8; 7]. Наименьшим элементом этого множества является число -8, наибольшим — число 7; мощность множества равна 16.
САМОЕ ГЛАВНОЕ
Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно. Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым). Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.
Логические операции имеют следующий приоритет:
1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.
Операции одного приоритета выполняются в порядке их следования, слева направо. Скобки меняют порядок выполнения операций.
Предикат — это утверждение, содержащее одну или несколько переменных. Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.
Вопросы и задания
1. Из данных предложений выберите те, которые являются высказываниями. Обоснуйте свой выбор.
1) Как пройти в библиотеку?
2) Коля спросил: «Который час?»
3) Картины Пикассо слишком абстрактны.
4) Компьютеры могут быть построены только на основе двоичной системы счисления.
2. Из каждых трёх выберите два высказывания, являющихся отрицаниями друг друга:
1) «1999 2000», «1999 ? 2000»;
2) «Петя решил все задания контрольной работы», «Петя не решил все задания контрольной работы», «Петя решил не все задания контрольной работы»;
3) «Луна — спутник Земли», «Неверно, что Луна — спутник Земли», «Неверно, что Луна не является спутником Земли »;
4) «Прямая а не параллельна прямой с», «Прямая а перпендикулярна прямой с», «Прямые а и с не пересекаются» (считаем, что прямые а и с лежат в одной плоскости);
5) «Мишень поражена первым выстрелом», «Мишень поражена не первым выстрелом», «Неверно, что мишень поражена не первым выстрелом».
3. Рассмотрите следующие элементарные высказывания: А = «Река Днепр впадает в Чёрное море», В = «45 — простое число», С = «Вена — столица Австрии», D = «0 — натуральное число».
Определите, какие из них истинные, а какие ложные. Составьте сложные высказывания, применяя каждый раз только одну из пяти логических операций

к высказываниям А, В, С и D. Сколько новых высказываний можно получить с помощью отрицания (инверсии)? Конъюнкции? Дизъюнкции? Импликации? Эквиваленции? Сколько всего новых высказываний можно получить? Сколько среди них будет истинных?
4. Представьте каждую пословицу в виде сложного логического высказывания, построенного на основе простых высказываний. Ответ обоснуйте при помощи таблиц истинности.
1) На вкус и цвет товарищей нет.
2) Если долго мучиться, что-нибудь получится.
3) Не зная броду, не суйся в воду.
4) Тяжело в ученье, легко в бою.
5) То не беда, что во ржи лебеда, то беда, что ни ржи, ни лебеды.
6) Где тонко, там и рвётся.
7) Или грудь в крестах, или голова в кустах.
8) За двумя зайцами погонишься — ни одного не поймаешь.
9) И волки сыты, и овцы целы.
5. Подберите вместо А, В, С, D такие высказывания, чтобы полученные сложные высказывания имели смысл:
1) если (А или В и С), то D;
2) если (не А и не В), то (С или D);
3) (А или В) тогда и только тогда, когда (С и не D).
7. Сколько из приведённых чисел Z удовлетворяют логическому условию: ((Z кратно 4) v (Z кратно 5)) ? (Z кратно 6)?
1) 4; 2) 6; 3) 7; 4) 12.
8. Найдите все целые числа Z, для которых истинно высказывание:

9. Какие из высказываний А, В, С должны быть истинны и ка кие ложны, чтобы были ложны следующие высказывания?

10. Даны три числа в различных системах счисления:
Переведите А, В и С в двоичную систему счисления и вы полните поразрядно логические операции (A v В) & С. Отвеп дайте в десятичной системе счисления.
11. Логическое отрицание восьмиразрядного двоичного числа записанное в десятичной системе счисления, равно 217 Определите исходное число в десятичной системе счисления,
12. Определите логическое произведение и логическую сумм> всех двоичных чисел в диапазоне от 1610 до 2210, включая границы. Ответ запишите в восьмеричной системе счисления.
13. Сколько различных решений имеет логическое уравнение?

14. Сколько решений имеет логическое уравнение х1 & х2 v х3 & x4 = 1?
15. Изобразите в декартовой прямоугольной системе координат множества истинности для следующих предикатов:

16. Предикат ((8x — 6) 65) определён на множестве целых чисел. Найдите его множество истинности. Укажите наибольшее целое число х, при котором предикат превращается в ложное высказывание.
[spoiler title=”источники:”]
http://infourok.ru/urok-reshenie-logicheskih-uravneniy-klass-2278711.html
http://murnik.ru/18-algebra-logiki
[/spoiler]

