Сети Петри[]
Сети Петри — математический аппарат для моделирования динамических дискретных систем. Впервые описаны Карлом Петри в 1962 году.
Пример работы сети Петри
Сеть Петри представляет собой двудольный ориентированный граф, состоящий из вершин двух типов — позиций и переходов, соединённых между собой дугами. Вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры), способные перемещаться по сети.
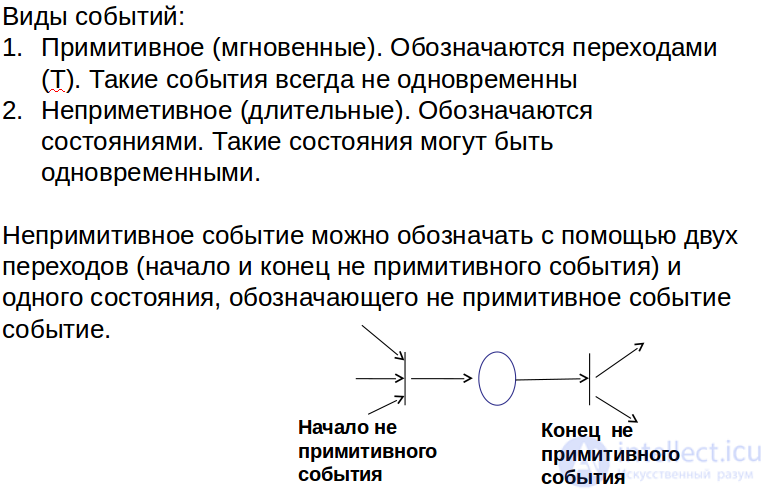
Событием называют срабатывание перехода, при котором метки из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно, либо разновременно, при выполнении некоторых условий.
Как и стандартные UML диаграммы, BPMN и EPC, сети Петри предоставляют возможность графически иллюстрировать процессы включающие выбор, итерации и одновременное выполнение. Но в отличие от данных стандартов, у сетей Петри четкая математическая формулировка и за ними стоит развитая математическая теория.
==Структура сетей Петри==
Сеть Петри состоит из 4-х элементов:
- множество позиций P,
- множество переходов T,
- входная функция I,
- выходная функция O.
Пример сети Петри. Белыми кружками обозначены позиции, полосками — переходы, чёрными кружками — метки.
Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход tj в множество позиций I(tj), называемых входными позициями перехода. Выходная функция O отображает переход pi в множество позиций O(pi), называемых выходными позициями перехода. Структура сети Петри определяется её позициями, переходами, входной и выходной функциями.
Определение
Сеть Петри С является четверкой, C=(P,T,I,O). P={p1, p2, … pi, pn} – конечное множество позиций, n>=0. T={ t1, t2, … tj, tm } – конечное множество переходов, m>=0. Множество позиций и множество переходов не пересекаются, то есть пересечение P и T равно пустому множеству. I: T->P¥ является входной функцией – отображением из переходов в комплекты позиций. O: P¥->T есть выходная функция – отображение из комплектов позиций в переходы.
Произвольный элемент P обозначается символом pi , i=1, …, n, а произвольный элемент T – символом tj, j=1, …, m.
Правила выполнения сетей Петри[]
Выполнением сети Петри управляют количество и распределение фишек в сети. Сеть Петри выполняется посредством запусков переходов. Переход запускается удалением фишек из его входных позиций и образованием новых фишек, помещаемых в его выходные позиции.
Переход запускается, если он разрешен. Переход называется разрешенным, если каждая из его входных позиций имеет число фишек по крайней мере равное числу дуг из позиции в переход. Фишки во входной позиции, которые разрешают переход, называются его разрешающими фишками. Например, если позиции р1 и р2 служат входами для перехода t1, тогда t1 разрешен, если р1 и р2 имеют хотя бы по одной фишке. Для перехода t3 с входным комплектом {p3,p3,p3} позиция р3 должна иметь не менее 3 фишек для разрешения перехода t3.
Определение. Переход 




Переход запускается удалением разрешающих фишек, из всех его входных позиций (количество удаленных фишек для каждой позиции соответствует числу дуг, идущих из этой позиции в переход), с последующим помещением фишек в каждую из его выходных позиций (количество помещаемых фишек в позицию соответствует количеству дуг входящих в данную позицию из перехода).
>Переход t3 I(t3) = {p2} и O(t3) = {p3,p4} разрешен каждый раз, когда в р2 будет хотя бы одна фишка. Переход t3 запускается удалением одной фишки из позиции р2 и помещением одной фишки в позицию р3 и р4 (его выходы). Переход t4, в котором I(t4) = {p4,p5} и O(t4) = {p5,p6,p6} запускается удалением по одной фишке из позиций р4 и р5, при этом одна фишка помещается в р5 и две в р6 (рис. 2).
Рис. 2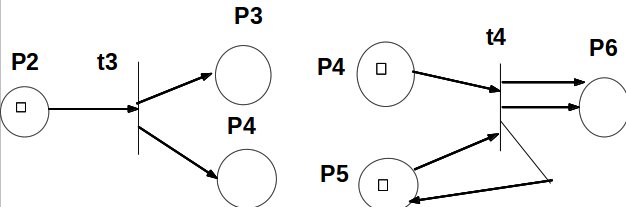
Определение. Переход 



Сразу хочу сказать, что здесь никакой воды про сети петри, и только нужная информация. Для того чтобы лучше понимать что такое
сети петри, е-сети , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.
сети петри – математический аппарат для моделирования динамических дискретных систем. Описаны в диссертационной работе Карла Петри “Kommunikation mit Automaten” на соискание степени доктора наук в 1962 году. Сеть Петри представляет собой двудольный ориентированный граф, состоящий из вершин двух типов – позиций и переходов, соединенных между собой дугами. Вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры), способные перемещаться по сети.

Сети Петри – инструмент моделирования
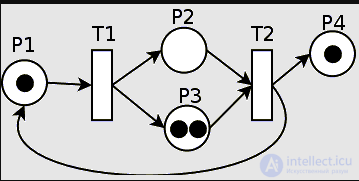
Пример сети Петри. Белыми кружками обозначены позиции, полосками — переходы, черными кружками — метки.
Сеть Петри — это сеть «мест-переходов» N = (Р, Т, F, Н, S), состоящая из следующих объектов: Р и Т — непересекающие- ся множества, на которые разбивается множество всех узлов сети. Узлы из Р называются местами, или позициями, узлы из Г — переходами. Функции F и Н указывают для каждого перехода подмножество мест, связанных с ним дугами: F(t) — множество входных мест перехода t, из которых дуги входят в t; H(t) — множество выходных мест, в которые дуги выходят из t.
Функция S помечает переходы, т. е. S(t) — метка перехода t (разные переходы могут быть помечены одинаково).
Графически сеть Петри (СП) изображается двудольным графом, его элементами являются позиции и переходы, связываемые направленными дугами. Позиция представляется в виде кружка, переход — в виде отрезка прямой [19].
В аналитической форме сеть Петри может быть представлена следующим образом:

где В = {bj} — конечное непустое множество позиций; D — = {d,} — конечное непустое множество переходов; / : В х D —> —» {0, 1} — входная функция (прямая функция инцидентности), которая для каждого перехода задает множество его входных позиций; О: D х В ^ (0, 1} — выходная функция (обратная функция инцидентности), которая для каждого перехода задает множество его выходных позиций; М — функция разметки сети, М: В —> —> (0, 1, 2, …}, ставит каждой позиции в соответствие неотрицательное целое число (равное числу меток в данной позиции).
Для определения интерпретации сети надо ввести понятия состояния сети и срабатывания перехода. Состояние, или раз- метка, М — это функция, которая каждому месту, в простейшем случае, приписывает число 1 или 0, что говорит о наличии или готовности в этом месте объектов для обработки (необходимых для обработки заявок, данных, ресурсов и т. п.) или об их отсутствии соответственно. Графически наличие в позиции объекта представляется точкой, называемой маркером. Согласно классическому определению СП в любой позиции может находиться неограниченное количество маркеров (любое целое положительное число), т. е. «емкость» позиции не ограничена. Поэтому для отображения в классических СП ограниченного ресурса необходимо применять специальные методы.
С учетом введенных обозначений необходимое условие срабатывания перехода d, (для всех входных позиций число находящихся в них меток должно быть не меньше 1) может быть записано следующим образом:
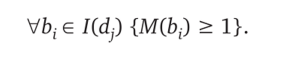
Срабатывание перехода dt изменяет разметку сети М(В) на разметку М'(В) по следующему правилу:
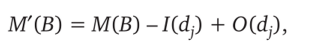
т. е. переход dj изымает по одной метке из каждой своей входной позиции и добавляет по одной метке в каждую из выходных позиций. Смену разметки обозначают так:
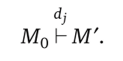
Простое представление системы сетью Петри основано на двух основополагающих понятиях: событиях и условиях. События — это действия, имеющие место в системе. Возникновением события управляет состояние системы. Состояние системы может быть описано множеством условий. Условие — это предикат, или логическое описание состояния системы. Условие может принимать значение либо «ложь», либо «истина».
Так как события являются действиями, то они могут происходить. Для того чтобы событие произошло, необходимо выполнение соответствующих условий. Эти условия называются предусловиями события. Возникновение события может вызвать нарушение предусловий и привести к выполнению других условий — постусловий.
В СП условия моделируются позициями, события — переходами. При этом входы перехода являются предусловиями соответствующего события; выходы — постусловиями. Возникновение события равносильно запуску соответствующего перехода. Выполнение условия представляется маркером(ами) в позиции, соответствующей этому условию. Запуск перехода удаляет разрешающие маркеры, представляющие выполнение предусловий, и образует новые маркеры, которые представляют выполнение постусловий.
Изменение состояния происходит в результате срабатывания какого-нибудь перехода, который становится возможным при готовности всех его входных мест; метка перехода может интерпретироваться как действие, выполняемое при срабатывании перехода.
В зависимости от целей моделирования компоненты настройки могут изменяться.
Приведем минимально необходимые сведения о СП, позволяющие правильно воспринимать излагаемый материал и строить СП для рассматриваемых задач.
1. Однотипные элементы СП не могут между собой связываться дугами непосредственно (рис. 2.1, а).
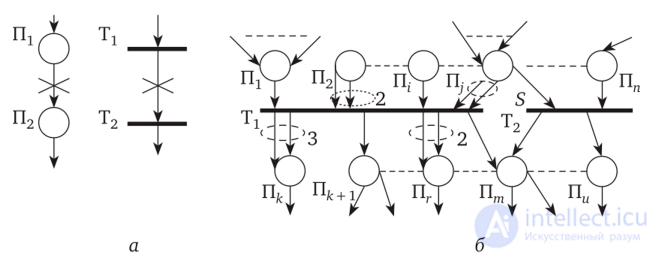
Рис. 2.1
- 2. СП, в которой нет ни одного маркера, называется неразмеченной и не может функционировать.
- 3. Срабатывание перехода в классических СП происходит мгновенно (tcp = 0) в момент выполнения логического условия, разрешающего срабатывание перехода.
- 4. В графическом представлении классических СП любые два (неоднотипных) элемента сети могут быть связаны между собой необходимым количеством дуг. Если число дуг больше единицы, их называют кратными, или дугами кратности К, где К — количество «параллельных» дуг (на рис. 2.1, б кратные дуги показаны пунктирным эллипсом с указанием значения кратности К).
- 5. Логическое условие срабатывания перехода — для срабатывания перехода в каждой позиции, связанной выходящей (ими) дугой(ами) со входом(ами) рассматриваемого перехода, должно находиться количество маркеров (М), не меньшее кратности К (см. рис. 2.1, б).
- 6. При срабатывании перехода из каждой позиции, связанной К выходными дугами со входами сработавшего перехода (К = 1, 2, 3, …), удаляются К маркеров.
- 7. При срабатывании перехода в каждую позицию, связанную входящей (ими) в позицию дугой (ами), выходящей (ими) с выхода(ов) сработавшего перехода, придет количество маркеров, равное количеству связывающих их дуг (т. е. кратности связи).
- 8. Количество маркеров, поступивших на входы перехода при его срабатывании, не связано с количеством маркеров, вышедших при срабатывании этого перехода. На каждой выходящей с перехода дуге появится по одному маркеру.
Событие в сети Петри – это срабатывание перехода в сети, при котором метки из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно, либо разновременно, при выполнении некоторых условий.
Сети Петри разрабатывались для моделирования систем с параллельными взаимодействующими компонентами. Сети Петри впервые предложил Карл Адам Петри. В докторской диссертации “Связь с автоматами” он сформулировал основные понятия теории связи асинхронных компонент вычислительной системы.
1 Понятие сети Петри Сеть Петри представляет собой двудольный ориентированный граф, содержащий вершины двух типов — места (обозначаются кружками) и переходы (обозначаются прямоугольниками). Любая дуга ведет либо от вершины–места в вершину–переход, либо наоборот. Дуги, соединяющие два места или два перехода, запрещены. Места, у которые нет входящих дуг, называются входными. Места, у которых нет исходящих дуг, называются выходными. Каждое место сети Петри может содержать ноль или более меток (маркеров, англ. tokens). Все метки считаются одинаковыми и неотличимыми друг от друга. Распределение меток по местам сети называется ее разметкой. Работа сети начинается с начальной разметки. Метки могут переноситься с одного места на другое. Перенос меток выполняется по следующей схеме.
• Переход является активным, если каждое его входное место содержит по крайней мере одну метку (более точно — по одной метке на каждую входящую в этот переход дугу).
• Активный переход может сработать, при срабатывании переход поглощает по одной метке с каждого своего входного места и размещает по одной метке на каждое свое выходное место (по одной метке на каждую исходящую дугу).
• В каждый момент времени для срабатывания из всех активных переходов недетерминированным образом выбирается один. Если активных переходов нет, то работа сети на этом завершается. Припишем каждому переходу сети Петри некоторый уникальный символ (например, пронумеруем их). Последовательность символов σ, в которой i-ый символ равен символу перехода, сработавшему на i-ом шаге
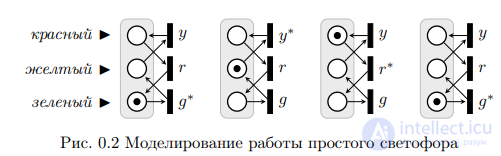
работы сети, называется последовательностью срабатываний сети Петри. Последовательность срабатываний однозначно определяет последовательность разметок µi , где µ0 является начальной разметкой. Тот факт, что после срабатывания t-го перехода разметка µ преобразуется в разметку µ 0 , будем обозначать кратко 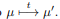 . На рисунке 0.1 показан пример работы сети Петри для последовательности срабатываний σ = [t1, t3]. Активные переходы в каждом случае помечены звездочкой. Заметим, что для той же сети имеется еще только одна возможная последовательность срабатываний σ = [t1, t2].
. На рисунке 0.1 показан пример работы сети Петри для последовательности срабатываний σ = [t1, t3]. Активные переходы в каждом случае помечены звездочкой. Заметим, что для той же сети имеется еще только одна возможная последовательность срабатываний σ = [t1, t2].
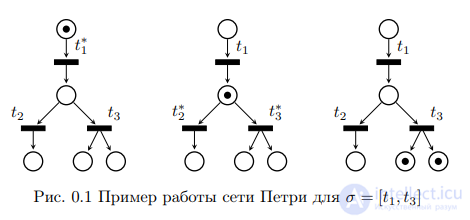
На рисунке 0.2 приведен пример моделирования сетью Петри простого светофора, в котором цвета переключаются в следующем порядке (зеленый, желтый, красный), причем продолжительность каждого сигнала одинакова (и равна одному такту работы сети Петри). Особенностью этой сети является то, что ее работа никогда не завершается.
Формальное определение сеть Петри
Формальным образом сеть Петри определяется как четверка 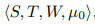 , где
, где

1Символом Z+ будем обозначать множество неотрицательных целых чисел
КЛАССИЧЕСКИЕ СЕТИ ПЕТРИ
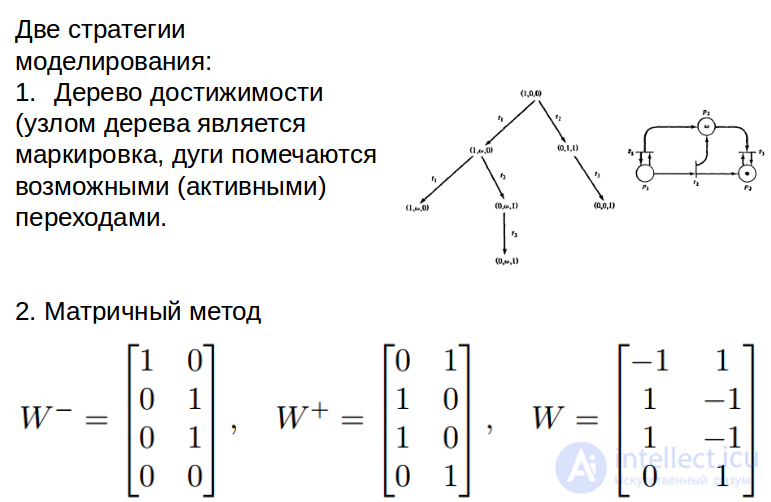
Сеть Петри можно задать и в компактной векторно-матричной форме. В этом случае структура сети Петри (т. е. ее граф) описывается двумя матрицами W+ и W− размера n×m, определяющими наборы дуг, ведущих от мест к переходам (матрица W−) и обратно (W+): 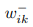 = числу дуг, ведущих из i-го места в k-ый переход;
= числу дуг, ведущих из i-го места в k-ый переход; 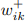 = числу дуг, ведущих в i-ое место из k-го перехода.
= числу дуг, ведущих в i-ое место из k-го перехода.
Из матриц W+ и W− составляется еще одна матрица 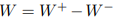 , которая обычно используется для вычисления нового состояния (разметки)
, которая обычно используется для вычисления нового состояния (разметки)
сети после применения к ней заданной последовательности срабатываний.
Начальная разметка сети задается целочисленным вектором µ0 длины n.
Например, для сети, показанной на рисунке 0.3, матрицы W+, W− и W
равны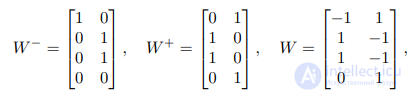
,
а ее разметка (в левой части рисунка) определяется вектором µ = [1, 0, 2, 1]
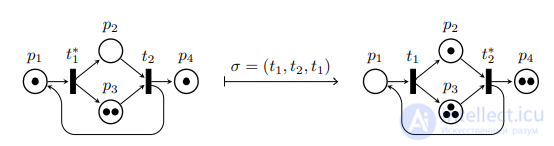
Рис. 0.3 Пример применения последовательности σ к сети Петри
Нетрудно убедиться, что для разметки µ переход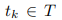 является активным, если выполняется условие
является активным, если выполняется условие
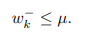
В последней формуле символ 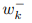 обозначает k-ый столбец матрицы W−, а сравнение двух векторов выполняется поэлементно (т. е. считается, что
обозначает k-ый столбец матрицы W−, а сравнение двух векторов выполняется поэлементно (т. е. считается, что
a ≤ b, если каждый элемент в a меньше или равен соответствующего элемента в b: 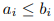 для всех возможных i).
для всех возможных i).
Для сети Петри, показанной в левой части рисунке 0.3, легко проверить, что выполняются следующие неравенства
Значит первый переход в данном случае является активным, а второй — нет.
Пусть для некоторой сети Петри задана корректная последовательность срабатываний σ. Обозначим за v(σ) вектор, k-ый элемент которого равен
числу вхождений символа tk в σ. Например, для сети с двумя переходами (рисунок 0.3) и последовательности σ = (t1, t2, t1) вектор v = [2, 1]. Тогда, легко проверить, что применения последовательности σ к начальной разметке µ приводит к разметке µ0, векторное представление которой вычисляется по следующей формуле:

Например, применение последовательности σ = (t1, t2, t1) к сети, показанной в левой части рисунка 0.3 приведет к разметке, которая может быть
вычислена по формуле (1) следующим образом:
.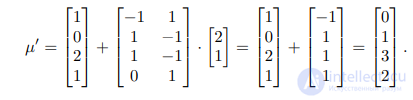
Видно, что результат такого векторно-матричного вычисления полностью
соответствует разметке сети в правой части рисунка 0.3.
Сети Петри – инструмент моделирования
В настоящее время сети Петри применяются, в основном, в моделировании. Во многих областях исследований явление изучается не непосредственно, а косвенно, через модель. Модель – это представление, как правило, в математических терминах того, что считается наиболее характерным в изучаемом объекте или системе. Манипулируя моделью системы, можно получить новые знания о ней, избегая опасности, дороговизну или неудобства анализа самой реальной системы. Обычно модели имеют математическую основу.
Развитие теории сетей Петри проводилось по двум направлениям. Формальная теория сетей Петри занимается разработкой основных средств, методов и понятий, необходимых для применения сетей Петри. Прикладная теория сетей Петри связана главным образом с применением сетей Петри к моделированию систем, их анализу и получающимся в результате этого глубоким проникновением в моделируемые системы.
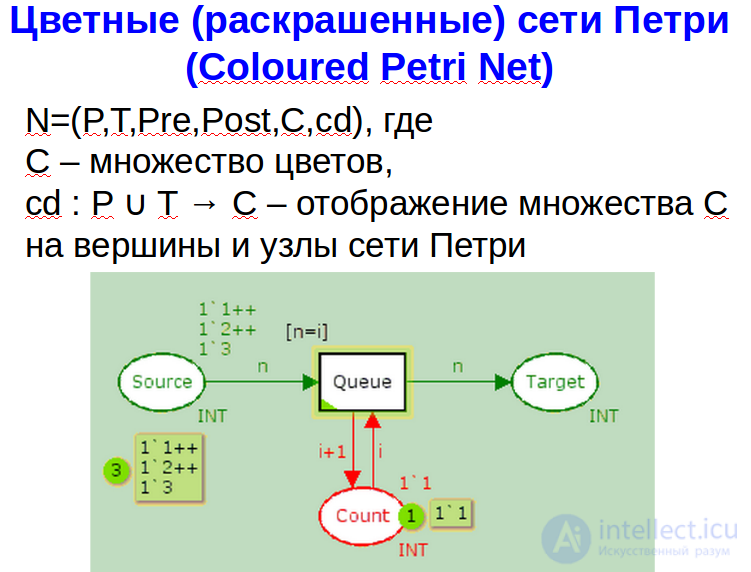
Моделирование в сетях Петри осуществляется на событийном уровне. Определяются, какие действия происходят в системе, какие состояние предшествовали этим действиям и какие состояния примет система после выполнения действия. Выполнения событийной модели в сетях Петри описывает поведение системы. Анализ результатов выполнения может сказать о том, в каких состояниях пребывала или не пребывала система, какие состояния в принципе не достижимы. Однако, такой анализ не дает числовых характеристик, определяющих состояние системы. Развитие теории сетей Петри привело к появлению, так называемых, “цветных” сетей Петри. Понятие цветности в них тесно связано с понятиями переменных, типов данных, условий и других конструкций, более приближенных к языкам программирования. Несмотря на некоторые сходства между цветными сетями Петри и программами, они еще не применялись в качестве языка программирования.
Не смотря на описанные выше достоинства сетей Петри, неудобства применения сетей Петри в качестве языка программирования заключены в процессе их выполнения в вычислительной системе . Об этом говорит сайт https://intellect.icu . В сетях Петри нет строго понятия процесса, который можно было бы выполнять на указанном процессоре. Нет также однозначной последовательности исполнения сети Петри, так как исходная теория представляет нам язык для описания параллельных процессов.
Наилучшими возможностями описания параллельных систем обладают сети Петри. Они не менее мощные, чем MPI, PVM, SDL, UML и другие, но чтобы их выполнять на процессорах необходимо сделать из описания параллельного распределенное.
Сеть Петри первого рода – это цветная сеть Петри, описанная на языке предписаний.
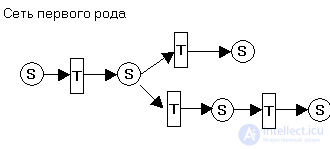
Сеть Петри второго рода – это сеть, представленная в виде иерархической композиции объектов.
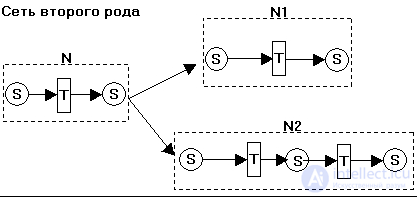
Динамика сети Петри
Процесс функционирования сети Петри может быть наглядно представлен графом достижимых маркировок. Состояние сети однозначно определяется ее маркировкой – распределением фишек по позициям. Вершинами графа являются допустимые маркировки сети Петри, дуги помечены символом срабатывающего перехода. Дуга строится для каждого активированного перехода. Построение прекращается, когда мы получаем маркировки, в которых не активирован ни один переход либо маркировки, содержащиеся в графе.
Отметим, что граф достижимых маркировок – представляет собой автомат.
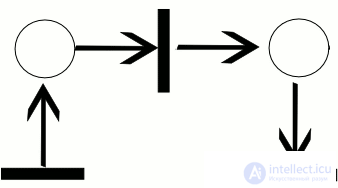
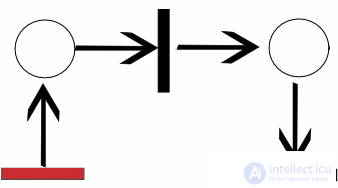
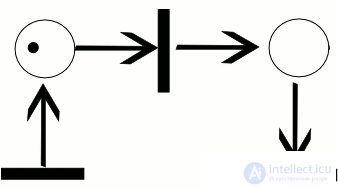
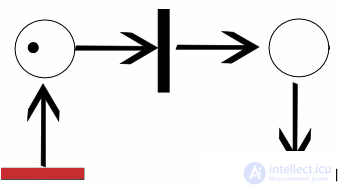
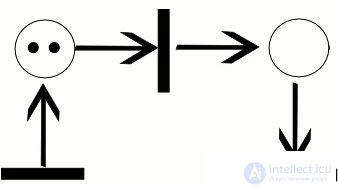
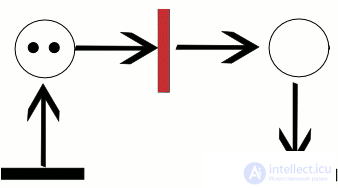
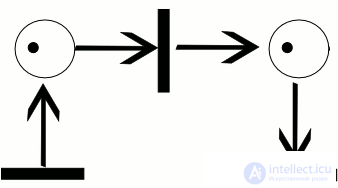
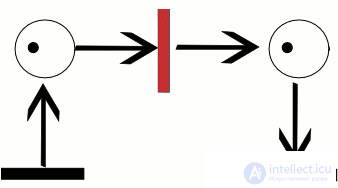
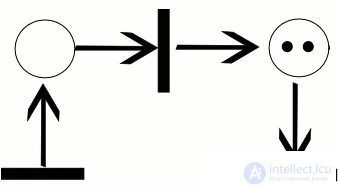
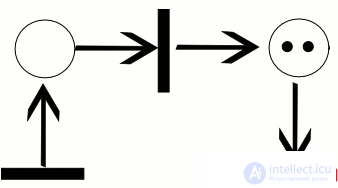
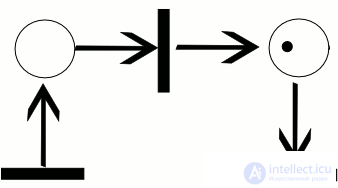
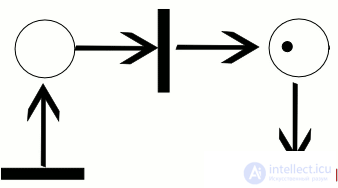
Пример траектории в сети Петри
Виды сетей Петри
Некоторые виды сетей Петри:
Временная сеть Петри – такая сеть, где переходы обладают весом, определяющим продолжительность срабатывания (задержку).
Стохастическая сеть Петри – сеть, в которой задержки являются случайными величинами.
Функциональная сеть Петри – сеть, в которой задержки определяются как функции некоторых аргументов, например, количества меток в каких-либо позициях, состояния некоторых переходов.
Цветная сеть Петри – сеть, в которой метки могут быть различных типов, обозначаемых цветами, тип метки может быть использован как аргумент в функциональных сетях.
Ингибиторная сеть Петри – сеть, в которой возможны ингибиторные, то есть подавляющие, дуги, запрещающие срабатывания перехода, если во входной позиции, связанной с переходом ингибиторной дугой, находится метка.
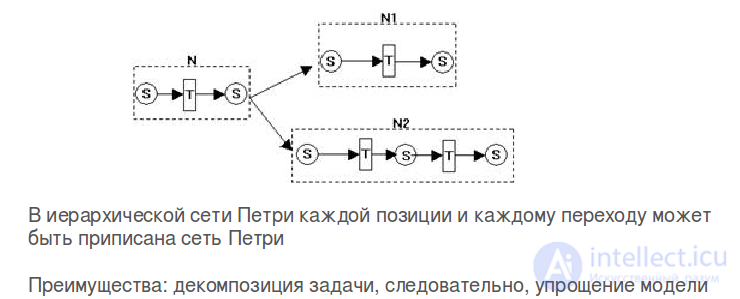
Иерархическая сеть Петри – сеть, содержащая немгновенные переходы, в которые вложены другие, возможно, также иерархические, сети. Срабатывание такого перехода характеризует выполнение полного жизненного цикла вложенной сети.
WF-сети Петри – подкласс сетей Петри, называемый также сетями потоков работ. Формализм WF-сетей введен Вил ван дер Аальстом (англ. Wil van der Aalst) для моделирования потоков работ в workflow-системах.
Сеть Петри PN = (P,T,F) называется сетью потоков работ (WF-сетью), если выполняются следующие условия:
- существует только одна исходная позиция i, такая что отсутствуют переходы входящие в i;
- существует только одна конечная позиция o, такая что отсутствуют переходы выходящие из o;
- каждый узел данной сети расположен на пути от i к о.
WF-сети используются для проверки графов потоков работ на наличие таких структурных конфликтов, как “тупики” (англ. deadlocks) и “недостатки синхронизации” (англ. lack of synchronization). Структурные конфликты отсутствуют, если WF-сеть является бездефектной.
Свойство бездефектности, правильной завершаемости – соответствует следующим требованиям:
- конечная позиция o достижима при любой последовательности переходов от позиции i;
- WF-сеть не содержит лишних позиций (которые никогда не будут выполнены);
- при достижении конечной позиции данной сети не должно оставаться фишек в промежуточных позициях.
Свойство бездефектности соответствует двум хорошо известным свойствам сетей Петри – живости и ограниченности.
е-сети
В отличие от сетей Петри, в Е-сетях :
- — имеются несколько типов вершин-позиций: простые позиции, позиции-очереди, разрешающие позиции;
- — фишки (метки) могут снабжаться набором признаков (атрибутов);
- — с каждым переходом могут быть связаны ненулевая задержка и функция преобразования атрибутов фишек;
- — введены дополнительные виды вершин-переходов;
- — в любую позицию может входить не более одной дуги и выходить также не более одной.
В связи с этим любой переход может быть описан тройкой параметров 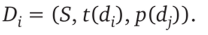
Здесь S — тип перехода, t(d,) — функция задержки, отражающая длительность срабатывания перехода, р(<2;0 — функция преобразования атрибутов меток.
Еще одно важное отличие Е-сетей от сетей Петри состоит в том, что метки интерпретируются как транзакты, перемещающиеся по сети, а вершины-переходы трактуются как устройства, выполняющие ту или иную обработку транзактов. Следствием такого подхода является требование: ни одна вершина-позиция не может содержать более одной метки (т. е. любая Е-сеть изначально является безопасной).
Анализ сетей Петри
Основными свойствами сети Петри являются:
- ограниченность сети Петри – свойство сети, число меток которой в любой позиции сети не может превысить некоторого значения K;
- безопасность сети Петри – есть частный случай ограниченности, K=1;
- сохраняемость сети Петри – есть постоянство загрузки ресурсов, когда ΣA_i N_i постоянна. Где N_i – число маркеров в i-той позиции, A_i – весовой коэффициент;
- достижимость сети Петри – возможность перехода сети из одного заданного состояния (характеризуемого распределением меток) в другое;
- живость сети Петри – возможность срабатывания любого перехода при функционировании моделируемого объекта.
В основе исследования перечисленных свойств лежит анализ достижимости. Методы анализа свойств сетей Петри основаны на использовании графов достижимых (покрывающих) маркировок, решении уравнения состояний сети и вычислении линейных инвариантов позиций и переходов. Применяются также вспомогательные методы редукции, позволяющие уменьшить размер сети Петри с сохранением ее свойств, и декомпозиции, разделяющие исходную сеть на подсети.
Универсальная сеть Петри
В 1974 году Тилак Аджервала показал, что ингибиторная сеть Петри является универсальной алгоритмической системой. В монографии В. Е. Котова приведен набросок доказательства, указывающий правила кодирования ингибиторной сетью программы счетного автомата Минского. Дж. Питерсон приводит примеры других расширенных классов сетей Петри, являющихся универсальной алгоритмической системой: синхронных и приоритетных. Построенная в явном виде универсальная сеть Петри насчитывала несколько тысяч вершин и недавно была уменьшена до 56 вершин.
Бесконечные сети Петри
Бесконечные сети Петри были введены для верификации вычислительных решеток и позволяют определять свойства сетей Петри для регулярных структур (линейная, древовидная, квадратная, треугольная, шестиугольная и гиперкуб) произвольного размера, полученных путем композиции типовых фрагментов.
Теория сетей Петри является хорошо известным и популярным формализмом, предназначенным для работы с параллельными и асинхронными системами. Основанная в начале 60-х годов немецким математиком К. А. Петри, в настоящее время она содержит большое количество моделей, методов и средств анализа, имеющих обширное количество приложений практически во всех отраслях вычислительной техники и даже вне ее.
Свойства сетей Петри
Отдельные элементы сети Петри (места и переходы) могут обладать различными свойствами, на основе которых сначала определяются свойства
самих сетей, а затем строится и их классификация.
Простейшим свойством места является количество меток, которые могут в нем располагаться. Если в любой достижимой разметке число меток
в заданном месте будет не более одной (0 или 1), то такое место называется безопасным. Сеть Петри называется безопасной, если все ее места
безопасны. В безопасных сетях состояние каждого места описывается всего
одним битом, поэтому такие сети могут быть легко реализованы аппаратно,
используя те или иные виды переключателей (триггеров). Кстати, первоначальный вариант определения сети Петри, данный самим Адамом Петри,
как раз подразумевал, что сеть является безопасной.
Однако, для большинства приложений требование безопасности сети
является чересчур строгим. Его можно ослабить, разрешив каждому месту хранить некоторое ограниченное число меток. Более строго, место называется k-ограниченным, если в любой достижимой разметке в данном
месте будет не более k меток. Очевидно, что 1-ограниченное место является безопасным. Место называется ограниченным, если существует такое
k, что это место является k-ограниченным. Наконец, сеть Петри является
k-ограниченной, если любое его место является k-ограниченным, и просто
ограниченной, если все его места ограничены. Ограниченные сети также
допускают эффективную аппаратную реализацию, в которой каждое место
представляется уже счетчиком (например, регистром) некоторой заданной
емкости. Неограниченные сети имеют, как правило, только теоретический
интерес.
Еще одним свойством сетей Петри, основанным на подсчете числа меток,
является свойство консервативности. Сеть называется консервативной, если число меток в любой достижимой разметке сохраняется одним и тем же
(равным числу меток в начальной разметке). Такая модель используется,
например, в тех случаях, когда метки представляют собой некоторые ресурсы системы, которые не уничтожаются и не создаются. Эти ресурсы могут
переходить от одной части системы к другой, но их суммарное количество
в процессе работы системы не изменяется. Нетрудно показать, что любой
переход, который встречается хотя бы в одной достижимой разметке, должен иметь одинаковое число входных и выходных дуг — сколько он выбрал
меток, столько он должен их и поставить.
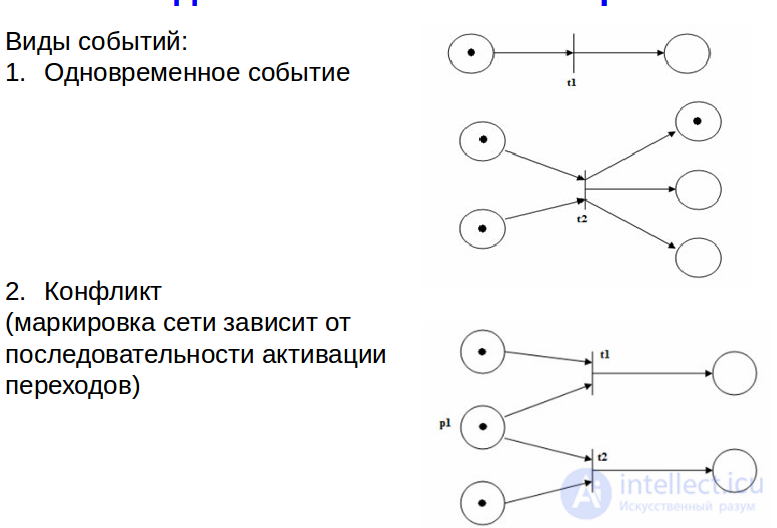
Виды событий в сети Петри
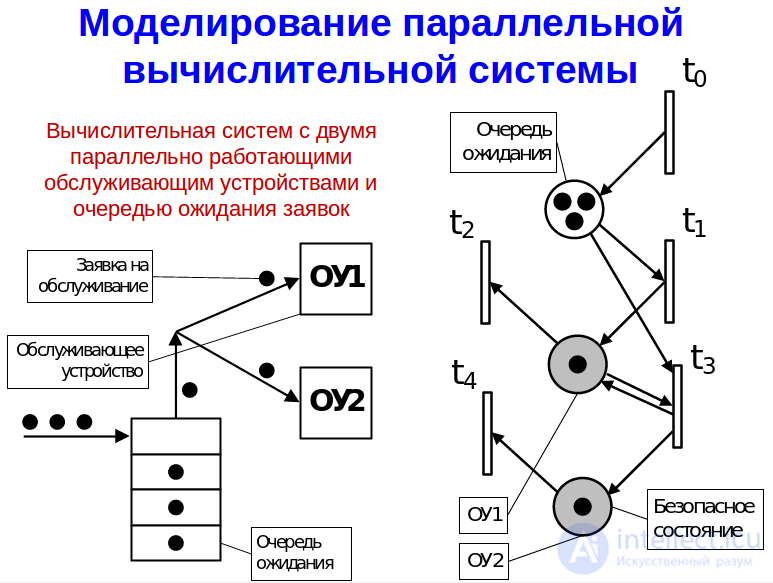
Проверка критериев сети Петри при их моделировании

Стратегии моделирования сетей Петри
Алгоритм построения дерева достижимости
1. Корнем дерева является узел, помеченный начальной маркеровкой. Далее идет построение.
2. Значение m(х)i- = w. Тогда для порожденной вершины z: m (z)i = w.
3.На пути от корневой вершины к вершине х существует вершина у с меньшей маркировкой m (у) < m (х), m (у)i < m (х)i. В этом случае происходит порождение символа бесконечности: m (х) i = w, m (z) i = w. В рассматриваемом примере на след. слайде такой вершиной, например, является вершина с маркировкой (1, 2, 0) -> (1, w, 0).
4. Если существует разрешенная маркировка, то в порождаемой вершине z заносится эта маркировка в соответствии с правилами срабатывания перехода.
Алгоритм завершает свою работу, когда все вершины являются внутренними, терминальными, дублирующими.
Моделирование сети Петри методом дерева достижимости
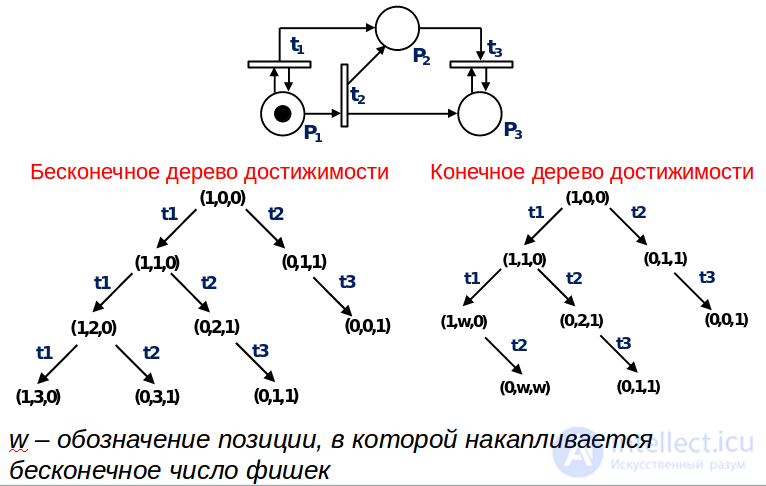
Виды вершин дерева достижимости:
- Граничная: вершина, которая рассматривается на текущем шаге моделирования.
- Терминальная: вершина, из которой нет выходящих дуг (т.е. при данной маркировке нет ни одного разрешенного перехода).
- Внутренняя: вершина, которая уже была рассмотрена при построении дерева достижимости.
- Дублирующая: вершина, которая имеет маркировку, которая уже встречалась в дереве.
Матричный подход к моделированию сети Петри

Моделирование сети Петри, представленной в матричном виде
Изменение маркировки сети Петри описывается с помощью формулы:
µ ‘=µ +W*e
Где v – вектор переходов
µ ‘ – новая маркировка
Физическая интерпретация сеть Петри при моделировании компьютерных сетей
Позиции – место хранения данных;
Метки – передаваемые данные;
Переходы – обработка данных.
Позиции – обработка данных;
Метки – передаваемые данные;
Переходы – место хранения данных.
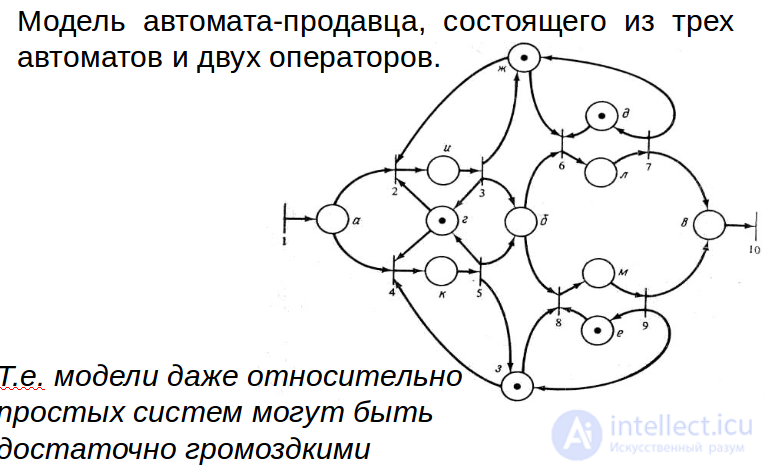
Недостатки сетей Петри
Как отмечает профессор Массачусетского технологического института, США, Карл Хьюит (англ. Carl Hewitt), сетям Петри присущи следующие недостатки:
они моделируют управление потоком, но не сам поток данных;
сложность описания одновременных действий, происходящих во время вычислительного процесса;
физическая интерпретация перехода в сетях Петри весьма сомнительна.
Громоздкость сети Петри для моделирования параллельных процессов
См. также
- конечные автоматы , виды конечных автоматов ,
- сети петри , моделирование автоматных систем сетями петри ,
- диаграмма вариантов использования , use case diagram , диаграмма прецедентов , структурирование прецедентов ,
- диаграмма деятельности , activity diagram ,
- блок-схемы алгоритмов , блок-схема ,
А как ты думаешь, при улучшении сети петри, будет лучше нам? Надеюсь, что теперь ты понял что такое сети петри, е-сети
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Моделирование и Моделирование систем
Сеть
на рисунке 7.1 представляет собой не что
иное, как автоматную сеть Петри (подкласс
сетей Петри) и что позиции можно трактовать
как состояния конечного автомата, а
переходы – как входные символы. Для
полноты соответствия построенной сети
Петри распознающему автомату введем
заключительную позицию Z.
Рисунок
7.1 Исходная сеть Петри
Теперь
следует заметить, что в сети на рисунке
7.1 имеются три идентичных фрагмента,
содержащие позиции A,
B
и C,
каждой из которых инцидентны по два
выходных перехода x2
и x6,
два идентичных фрагмента с позициями
D
и E,
каждой из которых инцидентен выходной
переход x7.
Фрагменты S1,S3;
F1,F4;
F2,F5;
F3,F6,F8
c
выходными переходами x4;
x7;
x0;
x5
соответственно.

Рисунок
7.2. Недетерминированная сеть Петри.
Источником
недетерминированности, очевидно, могут
являться лишь позиции свободного выбора,
исходящие дуги которых являются входящими
дугами переходов, помеченных одинаковыми
терминалами. Способ устранения
недетерминированности виден из рисунка
7.3.

Рисунок
7.3. Детерминированная сеть Петри
Можно
увидеть соответствие графа переходов
минимального автомата и сети Петри,
показав на сети Петри обозначение
состояний минимального автомата(Рисунок
7.4)
 Рисунок
Рисунок
7.4 Сеть Петри с состояниями минимального
автомата.
8
ОПИСАНИЕ ПРОГРАММЫ РЕАЛИЗУЮЩЕЙ
РАСПОЗНАЮЩИЙ АВТОМАТ
Ниже
представлен алгоритм программы.
-
пока
не последняя строка mmo1
делаем: записываем содержимое каждой
строки в переменную str; -
st=1;
-
для
i=первому
символу строки до i
равному последнему символу строки
делаем: -
если
str[i]=x
то:-
увеличиваем
i
и запускаем функцию CheckDigit
определяющую принадлежность символа
содержащегося в str[i]
к множеству {0,1,2,3,4,5,6,7}. Если принадлежит
то переходим в b,
если нет выходим из цикла и показываем
ошибку; -
запускам
функцию NextState
в которую передаётся текущее значение
st
и значение str[i],
функция возвращает следующее значение
st; -
outst=outst+st;
-
возвращаемся
к шагу 3;
-
-
если
str[i]<>x
то выводим ошибку; -
выводим
outst;
9 Описание контрольного примера
Назначение
Контрольный
пример необходим для тестирования
программной реализации автомата –
программы «recognizing».
Исходные
данные
Входная
цепочка символов автомата. Цепочки
символов состоят из символов входного
алфавита автомата: {x0, x1, x2, x3, x4, x5, x6, x7}.
Построим
цепочки символов, для контрольного
примера, исходя из праволинейной
грамматики. Для проверки правильности
работы автомата нужно проверить его с
помощью допустимых цепочек. Что бы
получить допустимую цепочку символов
необходимо взять одно из правил, в левой
части которого стоит начальный символS.
Выписать все терминальные символы из
этого правила и если в конце стоит
нетерминал, то перейти к одному из
правил, в левой части которого стоит
этот нетерминал. Выписать терминальные
символы из этого правила и если в конце
стоит нетерминал, то перейти к новому
правилу и т.д., пока мы не дойдем до
правила, правая часть которого кончается
терминалом.
Для
полной проверки автомата получим
несколько недопустимых цепочек. Их
можно получить, если выписывать терминалы,
не доходя до терминала, который стоит
последним в правиле. Или же если записать
терминал, которого нету в правой части
ни одного из правил, в левой части которых
стоит необходимый нетерминал.
Результаты
испытания программы.
Результаты
испытаний представлены в таблице 9.1
|
Входная |
Результат |
|
x2x4x2x3x0 |
Правильная |
|
x6x0x0x5x5 |
Правильная |
|
x5x3x0 |
Правильная |
|
x2x4x3 |
Незаконченная |
|
x6x3x0 |
Незаконченная |
|
x2x4x5 |
Незаконченная |
Таблица
9.1 Результаты испытаний
Результаты
испытания программы совпали с ожидаемыми,
что говорит о правильности построения
минимального автомата и реализации
программы.
ЗАКЛЮЧЕНИЕ
В
ходе данной работы было выполнено
построение минимального детерминированного
автомата из праволинейной грамматики
двумя различными способами: с помощью
сетей Петри и с помощью таблиц. Автоматы,
полученные двумя способами, идентичны,
что говорит о правильности выполнения
вычислений.
Для
автоматизированной обработки входных
последовательностей была реализована
программа с устанавливаемым автоматом.
Проверка теоретически построенных
допустимых и недопустимых последовательностей
показала, что программа работает верно.
СПИСОК
ЛИТЕРАТУРЫ
Методические
указания к курсовой работе по дисциплине
«Теория языков программирования и
методы трансляции» / Сост. М. А. Сенилов.
– Ижевск:
Изд-во
ИжГТУ, 2008. – 28 с.
ПРИЛОЖЕНИЕ
A
Исходный
код
unit
Unit1;
interface
uses
Windows,
Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs,
StdCtrls;
type
TForm1
= class(TForm)
mmo1:
TMemo;
mmo2:
TMemo;
btn1:
TButton;
procedure
btn1Click(Sender: TObject);
procedure
FormCreate(Sender: TObject);
private
{
Private declarations }
public
{
Public declarations }
end;
var
Form1:
TForm1;
function
CheckDigit(ch:char):boolean;
function
NextState(sym:char; state:string):string;
implementation
{$R
*.dfm}
function
NextState(sym:char; state:string):string;
begin
if
state=’1′ then
case
sym of
‘2’:begin
result:=’2′; exit; end;
‘6’:begin
result:=’7′; exit; end;
‘4’:begin
result:=’4′; exit; end;
else begin result:=’0′; exit; end;
end;
if
state=’2′ then
case
sym of
‘4’:begin
result:=’3′; exit; end;
else
begin result:=’0′; exit; end;
end;
if
state=’3′ then
case
sym of
‘2’:begin
result:=’4′; exit; end;
‘5’:begin
result:=’4′; exit; end;
else begin result:=’0′; exit; end;
end;
if
state=’4′ then
case
sym of
‘3’:begin
result:=’5′; exit; end;
else begin result:=’0′; exit; end;
end;
if
state=’5′ then
case
sym of
‘0’:begin
result:=’11’; exit; end;
‘5’:begin
result:=’1′; exit; end;
else begin result:=’0′; exit; end;
end;
if
state=’6′ then
case
sym of
‘7’:begin
result:=’10’; exit; end;
else begin result:=’0′; exit; end;
end;
if
state=’7′ then
case
sym of
‘6’:begin
result:=’6′; exit; end;
‘0’:begin
result:=’8′; exit; end;
‘3’:begin
result:=’8′; exit; end;
else begin result:=’0′; exit; end;
end;
if
state=’8′ then
case
sym of
‘0’:begin
result:=’9′; exit; end;
else begin result:=’0′; exit; end;
end;
if
state=’9′ then
case
sym of
‘5’:begin
result:=’10’; exit; end;
else begin result:=’0′; exit; end;
end;
if
state=’10’ then
case
sym of
‘5’:begin
result:=’11’; exit; end;
else begin result:=’0′; exit; end;
end;
if
state=’11’ then result:=’0′;
end;
function
CheckDigit(ch:char):boolean;
begin
case
ch of
‘0’:result:=true;
‘1’:result:=true;
‘2’:result:=true;
‘3’:result:=true;
‘4’:result:=true;
‘5’:result:=true;
‘6’:result:=true;
‘7’:result:=true
else
result:=false;
end;
end;
procedure
TForm1.btn1Click(Sender: TObject);
var
i:word;
s,st,outst:string;
symbol:char;
begin
for
i := 0 to Form1.mmo1.Lines.Count-1 do
s:=s+Form1.Mmo1.Lines[i];
i:=1;
st:=’1′;
outst:=’1′;
while
i<=Length(s) do begin
symbol:=s[i];
inc(i);
if
symbol=’x’ then begin
symbol:=s[i];
if
CheckDigit(symbol) then begin
st:=NextState(symbol,st);
outst:=outst+’
‘+st;
end
else
st:=’0′;
end
else
begin
Form1.mmo2.Lines.Add(‘Ошибка
на
символе
‘+ symbol);
break;
end;
inc(i);
if
st=’0′ then begin
Form1.mmo2.Lines.Add(‘Ошибка
на
символе
‘+ symbol);
break;
end;
end;
////
if
st=’11’ then begin
Form1.mmo2.Lines.Add(‘Правильная
строка’);
Form1.mmo2.Lines.Add(‘Состояния:
‘+ outst)
end
else
Form1.mmo2.Lines.Add(‘Незаконченная
строка’)
end;
procedure
TForm1.FormCreate(Sender: TObject);
begin
Form1.mmo1.Lines.Clear;
Form1.mmo2.Lines.Clear;
end;
end.
ПРИЛОЖЕНИЕ
Б
Контрольный
пример
На
рисунке Б.1 изображен пример работы
программы на верных исходных данных.

Рисунок
Б.1
На
рисунке Б.2 изображен пример работы
программы на неверных исходных данных.

Рисунок
Б.2
Соседние файлы в папке Архив1
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Екатерина Андреевна Гапонько
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Сети Петри — это математический объект, который используется, для того чтобы моделировать динамические дискретные системы.
Введение
Сети Петри являются простым и удобным средством, предназначенным для моделирования различных распределенных систем и процессов. Данную модель изобрел немецкий ученый Карл Петри в 1939-ом году, для того чтобы описать различные химические процессы. Однако начало официальной истории сетей Петри относится к 1962-ому году, когда Карл Петри сумел защитить диссертацию «Kommunikation mit Automaten», где он и представил понятие «сети Петри».
Сети Петри
Сеть Петри является двудольным ориентированным графом, содержащим вершины двух типов:
- «места», которые следует обозначать кружками,
- «переходы», которые следует обозначать прямоугольниками.
Каждая дуга может вести или от вершины типа «места» в вершину типа «переход», или же наоборот. Дуги, которые соединяют два «места» или два «перехода», являются запрещенными. Места, которые не имеют входящих дуг, именуются входными. Места, которые не обладают исходящими дугами, именуются выходными.
Любое место сети Петри может иметь нуль или больше меток, которые называются маркерами (tokens). Все метки должны считаться как одинаковые и неотличимые друг от друга. Распределение меток по местам сети именуется ее разметкой. Работа сети должна начинаться с изначальной разметки.
Метки можно переносить с одного места на другое. Перенос меток должен выполняться по следующим правилам:
- Переход может считаться активным, когда любое его входное место имеет по крайней мере одну метку, вернее имеет по одной метке на все, входящие в этот переход дуги.
- Активный переход может срабатывать. Когда переход сработал, то он может поглотить по одной метке с каждого своего входного места и разместить по одной метке на каждое свое выходное место, вернее по одной метке на каждую исходящую дугу.
- В любой момент времени для срабатывания из всего набора активных переходов случайным образом должен быть выбран один. Когда активные переходы отсутствуют, то работа сети считается завершенной.
«Сети Петри» 👇
Присвоим всем переходам сети Петри некоторые уникальные символы, к примеру, их можно пронумеровать. Последовательность символов Ct, в которой i-ый символ равняется символу перехода, который сработал на i-ом шаге работы сети, является последовательностью срабатываний сети Петри.
На рисунке ниже изображен пример работы сети Петри для последовательности срабатываний $C_t = [t_i, t_3]$.

Рисунок 1. Пример работы сети Петри. Автор24 — интернет-биржа студенческих работ
Активные переходы для каждого случая помечены звездочкой. Следует отметить, что для той же сети существует еще лишь одна возможная последовательность срабатываний $Ct = [t1, t2]$.
На рисунке ниже показан пример, где выполнено моделирование при помощи сети Петри обычного светофора, в котором переключение цветов выполняется в следующем порядке:
- Зеленый цвет.
- Желтый цвет.
- Красный цвет.

Рисунок 2. Моделирование работы простого светофора. Автор24 — интернет-биржа студенческих работ
При этом время работы всех цветов является одинаковым и равняется одному такту работы сети Петри. Отличительной чертой данной сети может считаться тот факт, что ее работа никогда не заканчивается.
Формально сети Петри могут быть определены следующими компонентами: S, T,W, µ0, где:
- S является конечным множеством мест (|S| = n).
- T является конечным множеством переходов (|T| = m).
- W : (S х T) U (T х S) → Z+ является мультимножеством дуг.
- µ0 : S → Z+ является начальной разметкой сети.
- Символом Z+ обозначено множество неотрицательных целых чисел.
Сети Петри могут быть заданы и в компактном векторно-матричном формате. В таком варианте, структура сети Петри, то есть ее граф, должна описываться при помощи двух матриц, а именно, W + и W-, имеющих размер nxm. Из матриц W+ и W- может быть составлена еще одна матрица W = W+ – W-, которая, как правило, применяется, для того чтобы вычислить новое состояние (разметку) сети после применения к ней требуемой последовательности срабатываний. Начальная разметка сети должна задаваться целочисленным вектором µ0, имеющим длину n.
Отдельные компоненты сети Петри (места и переходы) способны иметь различные свойства, на базе которых вначале должны определяться свойства самих сетей, а далее выстраивается и их классификация. Самым простым свойством места считается число меток, которые способны в нем располагаться. Когда в каждой достижимой разметке количество меток в определенном месте будет не больше одной, то есть равно нулю или единице, то такое место считается безопасным. Сеть Петри может называться безопасной, когда все ее места являются безопасными. В безопасных сетях состояние всех мест может быть описано всего одним битом, по этой причине подобные сети считаются легко реализуемыми аппаратно, при помощи тех или иных типов переключателей (триггеров). Следует отметить, что изначальный вариант определения сети Петри, который дал сам Адамом Петри, как раз предполагал, что сеть выступает как безопасная.
Тем не менее практически для всех приложений требование безопасности сети считается чрезмерно строгим. Оно может быть ослаблено, если разрешить любому месту сохранять определенное (не бесконечное) количество меток. В более строгом изложении, место является k-ограниченным, когда в любой достижимой разметке в этом месте будет не больше, чем k меток. Естественно, что одно ограниченное место может считаться безопасным.
Место именуется ограниченным, когда известно такое k, что это место выступает как k-ограниченное. Наконец, сеть Петри считается k-ограниченной, когда любое его место выступает как k-ограниченное, и просто ограниченной, когда все его места являются ограниченными. Ограниченные сети также могут допускать эффективную аппаратную реализацию, в которой все места представляются уже счетчиками (к примеру, регистрами) некоторой требуемой емкости. Неограниченные сети обладают, обычно, лишь теоретическим интересом. Помимо этого, сети Петри имеют еще одно свойство, основанное на подсчете количества меток, именуемое свойством консервативности.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

Пример сети Петри. Белыми кружками обозначены позиции, полосками — переходы, чёрными кружками — метки.
Сеть Петри — математический объект, используемый для моделирования динамических дискретных систем, предложенный Карлом Петри в 1962 году.
Определяется как двудольный ориентированный мультиграф, состоящий из вершин двух типов — позиций и переходов, соединённых между собой дугами. Вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры), способные перемещаться по сети. Событием называют срабатывание перехода, при котором метки из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно либо разновременно, при выполнении некоторых условий.
Сеть Петри есть мультиграф, так как он допускает существование кратных дуг от одной вершины графа к другой. Так как дуги являются направленными, то это ориентированный мультиграф. Вершины графа можно разделить на два множества (позиции и переходы) таким образом, что каждая дуга будет направлена от элемента одного множества (позиций или переходов) к элементу другого множества (переходов или позиций); следовательно, такой граф является двудольным ориентированным мультиграфом.
Изначально разрабатывались для моделирования систем с параллельными взаимодействующими компонентами; основные положения теории связи асинхронных компонент вычислительной системы Петри сформулировал в докторской диссертации «Связь автоматов»[1].
Динамика[править | править код]
Процесс функционирования сети Петри может быть наглядно представлен графом достижимых маркировок. Состояние сети однозначно определяется её маркировкой — распределением фишек по позициям. Вершинами графа являются допустимые маркировки сети Петри, дуги помечены символом срабатывающего перехода. Дуга строится для каждого возбуждённого перехода. Построение прекращается, когда мы получаем маркировки, в которых не возбуждён ни один переход, либо маркировки, содержащиеся в графе. Отметим, что граф достижимых маркировок представляет собой автомат.
Виды сетей Петри[править | править код]
Некоторые виды сетей Петри:
- Временна́я сеть Петри — переходы обладают весом, определяющим продолжительность срабатывания (задержку).
- Стохастическая сеть Петри — задержки являются случайными величинами.
- Функциональная сеть Петри — задержки определяются как функции некоторых аргументов, например, количества меток в каких-либо позициях, состояния некоторых переходов.
- Цветная (окрашенная, раскрашенная) сеть Петри — метки могут быть различных типов, обозначаемых цветами, тип метки может быть использован как аргумент в функциональных сетях.
- Ингибиторная сеть Петри — возможны ингибиторные дуги, запрещающие срабатывания перехода, если во входной позиции, связанной с переходом ингибиторной дугой, находится метка.
- Иерархическая сеть — содержит не мгновенные переходы, в которые вложены другие, возможно, также иерархические, сети. Срабатывание такого перехода характеризует выполнение полного жизненного цикла вложенной сети.
- WF-сеть.
- Алгебраическая сеть Петри.
Анализ сетей Петри[править | править код]
Основными свойствами сети Петри являются:

Пример траектории в сети Петри.
В основе исследования перечисленных свойств лежит анализ достижимости. Методы анализа свойств сетей Петри основаны на использовании графов достижимых (покрывающих) маркировок, решении уравнения состояний сети и вычислении линейных инвариантов позиций и переходов. Применяются также вспомогательные методы редукции, позволяющие уменьшить размер сети Петри с сохранением её свойств, и декомпозиции[2], разделяющие исходную сеть на подсети.
Универсальная сеть Петри[править | править код]
В 1974 году Тилак Аджервала показал, что ингибиторная сеть Петри является универсальной алгоритмической системой. В монографии Котова приведён набросок доказательства, указывающий правила кодирования ингибиторной сетью программы счётчикового автомата Минского. Питерсон приводит примеры других расширенных классов сетей Петри, являющихся универсальной алгоритмической системой: синхронных и приоритетных. Построенная в явном виде универсальная сеть Петри[3] насчитывала несколько тысяч вершин и недавно была уменьшена до 56 вершин[4].
Бесконечные сети Петри[править | править код]
Бесконечные сети Петри были введены для верификации вычислительных решеток и позволяют определять свойства сетей Петри для регулярных структур (линейная, древовидная, квадратная, треугольная, шестиугольная и гиперкуб[5]) произвольного размера, полученных путём композиции типовых фрагментов.
См. также[править | править код]
- Системы массового обслуживания
- Имитационное моделирование
- Модель акторов
- Конечный автомат
Примечания[править | править код]
- ↑ Питерсон, 1984, стр. 11 «1.3. Зарождение теории сетей Петри».
- ↑ Зайцев Д. А. Архивная копия от 1 апреля 2022 на Wayback Machine Композиционный анализ сетей Петри // Кибернетика и системный анализ. — 2006, № 1. — С. 143—154.
- ↑ Зайцев Д. А. Архивная копия от 1 апреля 2022 на Wayback Machine Универсальная сеть Петри, Кибернетика и системный анализ, № 4, 2012, с. 24-39.
- ↑ Zaitsev D.A. Архивная копия от 1 апреля 2022 на Wayback Machine Toward the Minimal Universal Petri Net, IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2013, 1- 12.
- ↑ Зайцев Д. А. Архивная копия от 1 апреля 2022 на Wayback Machine, Шмелева Т. Р. Верификация коммуникационных структур гиперкуба параметрическими сетями Петри, Кибернетика и системный анализ, № 1, 2010, С. 119—128.
Литература[править | править код]
- Питерсон Дж. Теория сетей Петри и моделирование систем. — М.: Мир, 1984. — 264 с.
- Котов В. Е. Сети Петри. — М.: Наука, 1984. — 160 с.
- Слепцов А. И., Юрасов А. А. Автоматизация проектирования управляющих систем гибких автоматизированных производств / Б. Н. Малиновский. — Киев: Техніка, 1986. — 160 с.
- Ачасова С. М., Бандман О. Л. Корректность параллельных вычислительных процессов. — Новосибирск: Наука, 1990. — 253 с.
- Мараховский В. Б., Розенблюм Л. Я., Яковлев А. В. Моделирование параллельных процессов. Сети Петри. Курс для системных архитекторов, программистов, системных аналитиков, проектировщиков сложных систем управления. — Санкт-Петербург: Профессиональная литература, АйТи-Подготовка, 2014. — 400 с.
Ссылки[править | править код]
- Учебный курс МГТУ им. Баумана «Основы САПР. Моделирование». Сети Петри. Анализ сетей Петри
- Сети Петри на сайте Института автоматики и процессов управления.
- Исходные тексты примеров программ, реализующих сети Петри и строго иерархические сети.