Сетевой график – это динамическая модель проекта, которая отражает последовательность и зависимость работ, необходимых для успешного завершения проекта. Сетевой график отражает сроки выполнения запланированных работ и ресурсы, необходимые для их выполнения, а также прямые финансовые затраты, возникающие при реализации этих работ.
В английском языке для определения сетевого графика используется термин Project Network — is a graph depicting the sequence in which a project’s terminal elements are to be completed by showing terminal elements and their dependencies.
Основной целью использования сетевого графика является эффективное планирование и управление работами и ресурсами проекта. При этом, под ресурсами в данном контексте понимается как оборудование, производственные мощности или денежные средства, так и трудовые ресурсы, внутренние или внешние для организации, выполняющей проект.
Наибольшая эффективность применения сетевого графика достигается при его использовании для планирования проектов или отдельных взаимосвязанных работ. Сетевой график позволяет довольно точно определить плановые сроки завершения проекта и выявить возможные варианты их сокращения. И, что более важно, сетевой график позволяет на ранней стадии планирования проекта выявить критический путь. Кроме этого сетевой график позволяет осуществлять базовый контроль над ходом работ проекта, их сроками и исполнением бюджета.
Виды сетевых графиков
Сетевой график — это граф, на котором события (состояния работ или объектов в определенный момент времени) представлены в виде вершин, а работы проекта представлены в виде дуг, соединяющих вершины графа. Сетевой график, представленный в таком виде, изначально является частью метода PERT (Program Evaluation and Review Technique).
На практике же чаще используется другой вариант сетевого графика, когда вершинами графа являются работы, а дуги обозначают взаимосвязь между ними. Такой вид сетевого графика является частью метода критического пути (англ., CPM — Critical Path Method).
Рассмотрим второй вариант графика и алгоритм его построения подробнее.
Алгоритм построения сетевого графика
Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.
Шаг 1. Определить основную цель проекта
Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.
Шаг 2. Выявить ограничения
Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.
Шаг 3. Определить состав работ
Определить состав работ, необходимых для достижения цели, поставленной на шаге 1.
Шаг 4. Оценить длительность работ
Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.
Шаг 5. Определить последовательность работ
Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.
Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.
Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.
Шаг 6. Указать связи между работами
Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.
Шаг 7. Определить раннее начало и раннее окончание
Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.
Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.
Шаг 8. Определить поздние начало и окончание
Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
Шаг 9. Определить временной резерв
Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
Шаг 10. Выявить критический путь
Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.
Пример построения сетевого графика
Несмотря на то, что описанный выше алгоритм может показаться сложным, на самом же деле построение сетевого графика задача несложная. Для того, чтобы убедиться в этом рассмотрим построение сетевого графика на простом примере ремонта детской комнаты.
Шаг 1. Определить основную цель проекта
Представьте, что сейчас лето, вашему сыну исполнилось 7 лет и в сентябре он идет в школу. Вы решил обновить его комнату к новому учебному году и сделать ее подходящей для школьника, т.е. должно появиться полноценной рабочее место, зонирование комнаты измениться, и т.д.
В этом случае целью нашего небольшого проекта будет — сделать комнату пригодной и приятной для проживания мальчика, который пойдет в начальную школу.
Шаг 2. Выявить ограничения
Бюджет не более 100,000 руб., ремонтные работы можно вести только в рабочие дни с 10:00 до 18:00 с обязательным перерывом с 12:00 до 14:00. Итого получается — 6 рабочих часов в день.
Шаг 3. Определить состав работ
Немного поразмыслив мы накидали основные работы, которые надо сделать, а именно:
- Нам нужен дизайн-проект новой комнаты;
- Нам надо закупить материалы для ремонта;
- Надо составить смету ремонта;
- Надо выполнить сам ремонт;
- И т.к. мы решили сделать небольшую перепланировку, то надо согласовать ее с ТСЖ.
Отобразим эти работы в виде блоков:
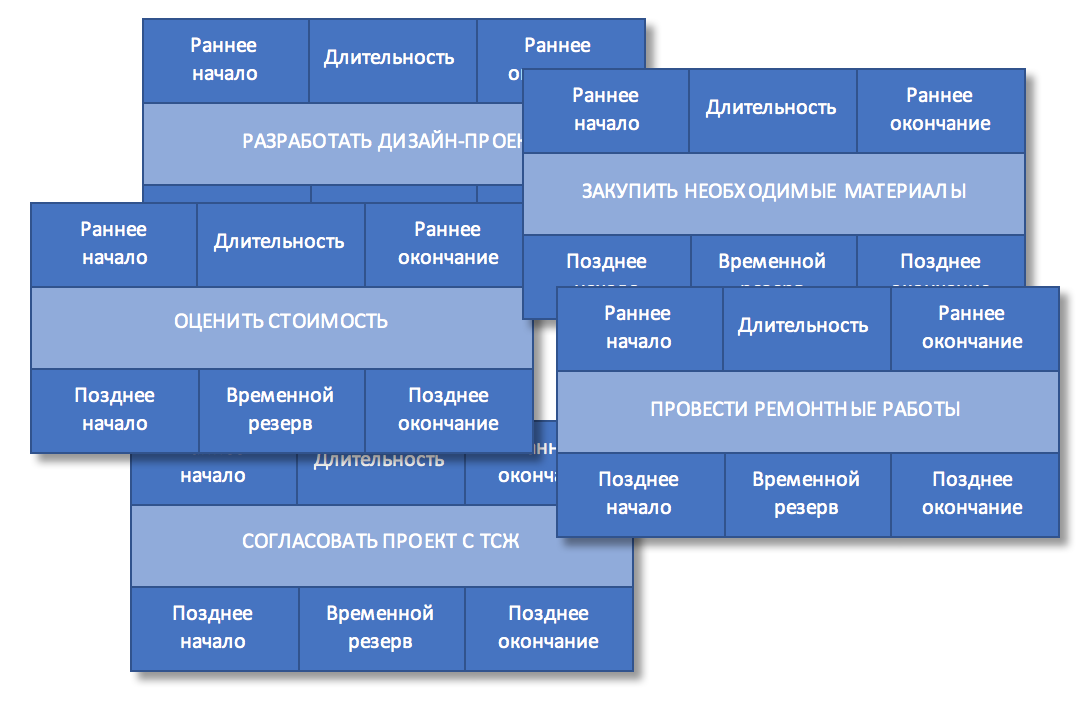
Рисунок 1. Состав работ
Шаг 4. Оценить длительность работ
Мы решили оценивать длительность работ в днях, т.к. до начала учебного года еще достаточно времени, то такая точность планирования нас вполне устраивает.

Рисунок 2. Длительность работ
Шаг 5. Определить последовательность работ
Теперь определим последовательность работ, мы будем использовать схему построения сетевого графика «сверху-вниз». Первая работа, которую необходимо выполнить — это работа «Разработать дизайн-проекта«. Затем мы оценим стоимость проекта, а параллельно начнем согласование с ТСЖ, т.к. эта задача занимает много времени. После того, как мы оценим проект и его согласуем, мы приступим к покупке всех необходимых материалов и уже затем начнем сам ремонт.

Рисунок 3. Последовательность работ
Шаг 6. Указать связи между работами
Укажем стрелками связи между работами.
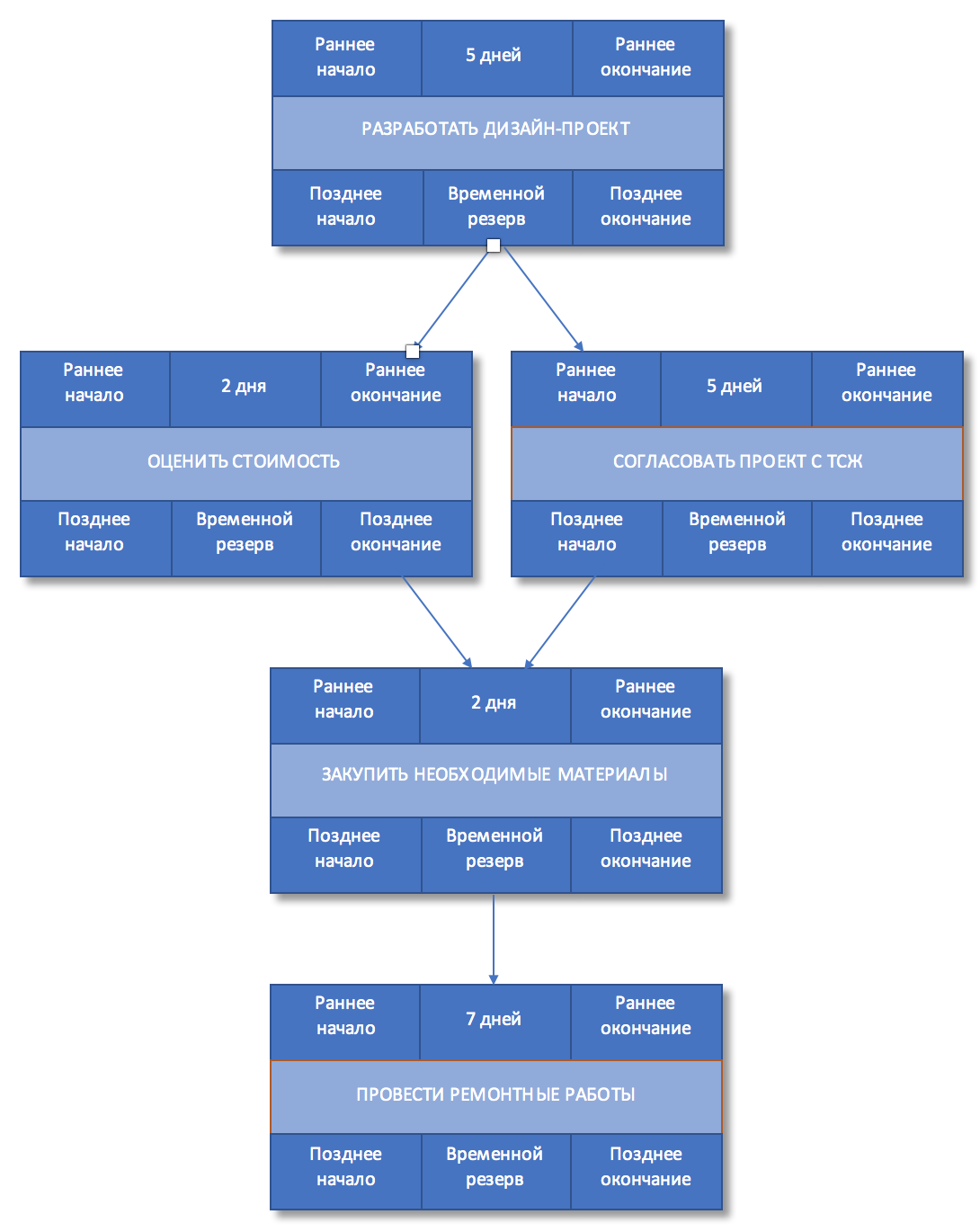
Рисунок 4. Связи между работами
Шаг 7. Определить раннее начало и раннее окончание
Т.к. мы выбрали модель сетевого график «сверху-вниз», то начинаем его и просматривать сверху вниз, начиная с самой верхней работы, и далее по очереди двигаемся к самой нижней работе.
Напомним, что раннее начало последующей работы будет совпадать с ранним завершением предшествующей, а раннее окончание каждой из работ определяется как раннее начало плюс длительность работ Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ.
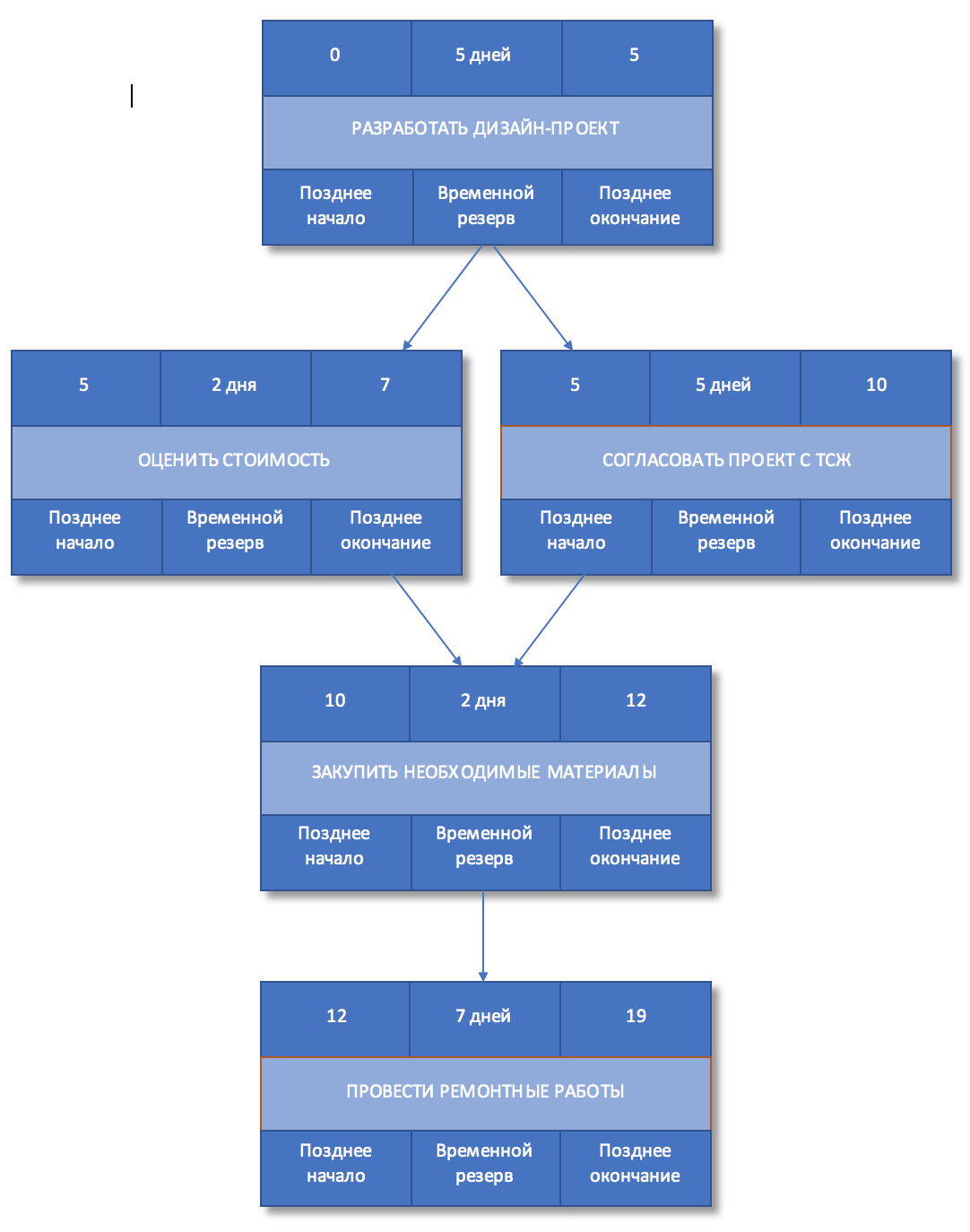
Рисунок 5. Раннее начало и окончание работ
Шаг 8. Определить поздние начало и окончание
Для того, чтобы определить поздние начало и окончание просмотрим сетевой график в обратном направлении — снизу вверх. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
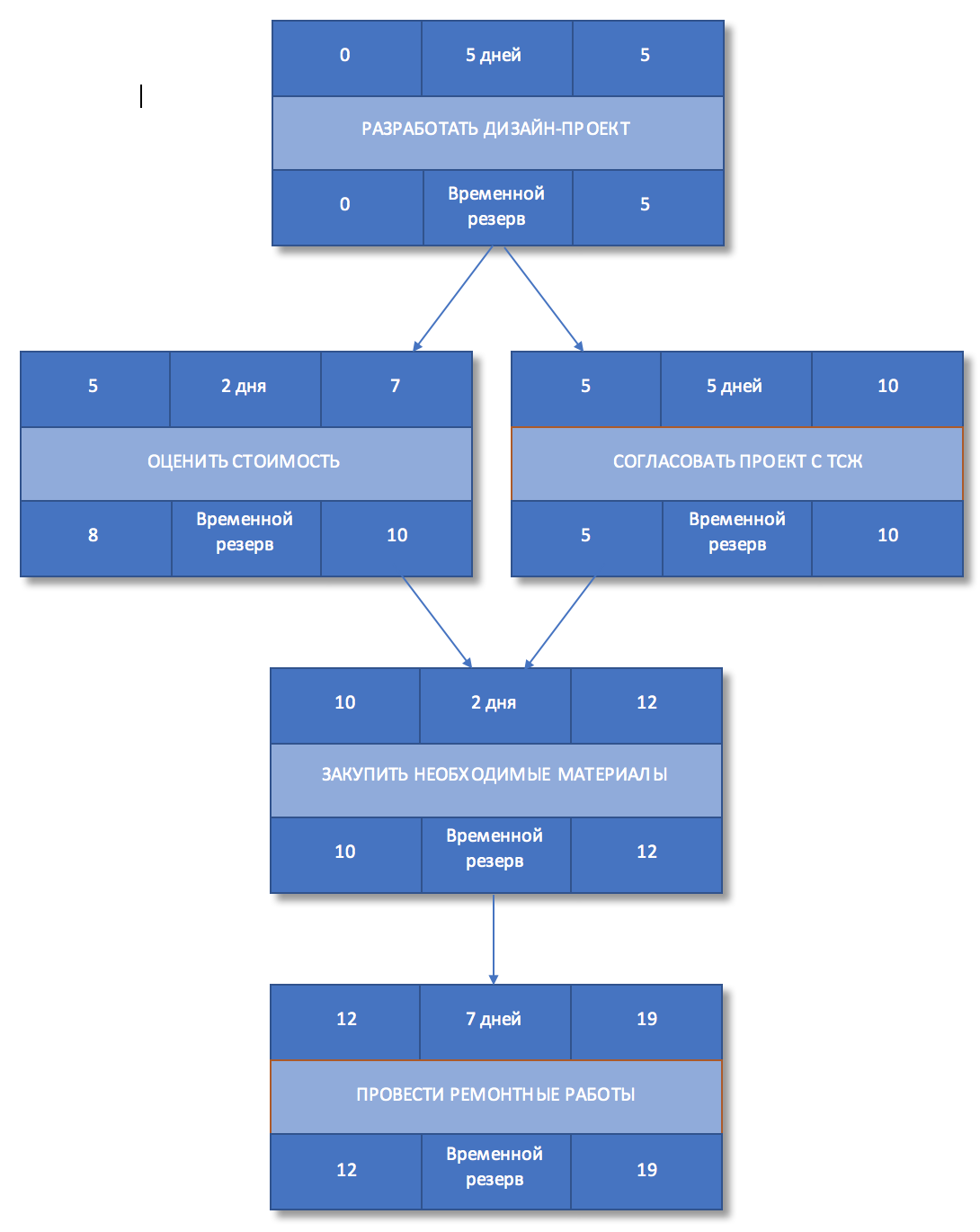
Рисунок 6. Позднее начало и окончание работ
Шаг 9. Определить временной резерв
Вычислим временной резерв для каждой из работ. Он вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
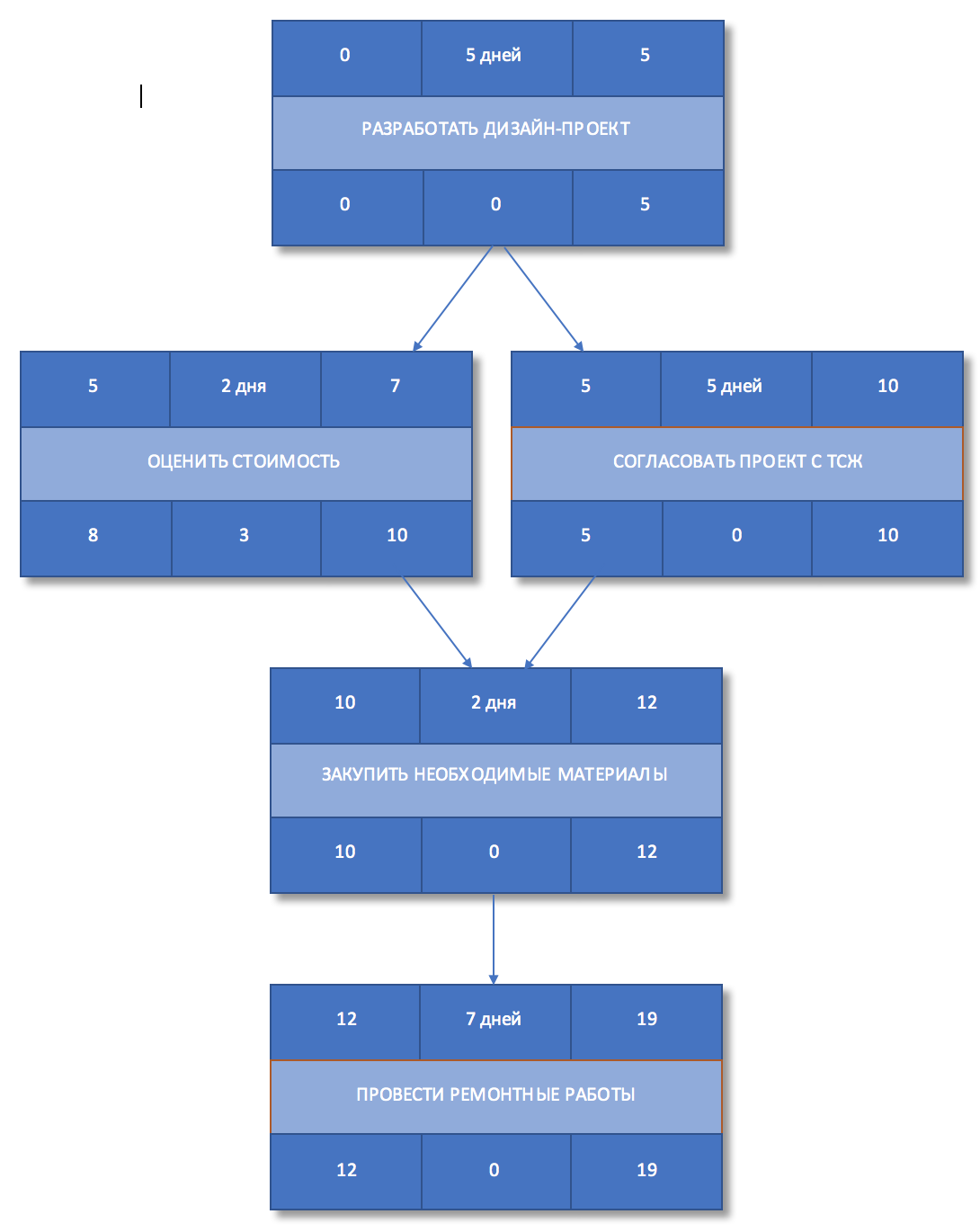
Рисунок 7. Временной резерв
Шаг 10. Выявить критический путь
Как мы уже знаем, критический путь — это цепочка работ, у которых резерв времени равен нулю. Выделим такие задачи на сетевом графике.
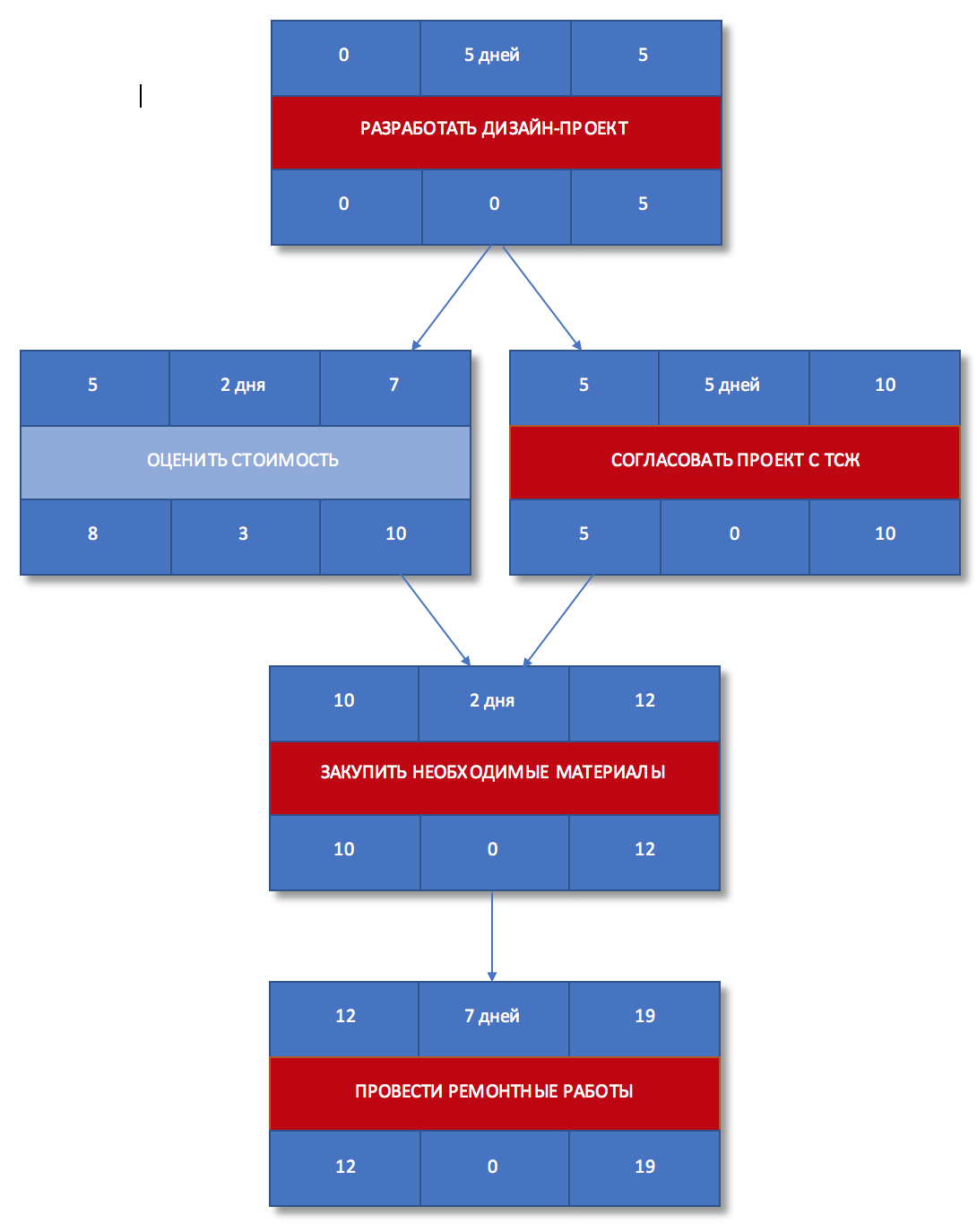
Рисунок 8. Критический путь
Задачи «Разработать дизайн-проект«, «Согласовать проект с ТСЖ» и «Закупить необходимые материалы«, «Провести ремонтные работы» составляю критический путь, а его длина составляет 19 дней. Это означает, что в текущем виде проект не может быть выполнен быстрее, чем за 19 дней. Если мы хотим сократить сроки проекта, то нам необходимо оптимизировать задачи, лежащие на критическом пути.
Например, мы можем начать ремонтные работы раньше получения согласования на перепланировку от ТСЖ, приняв на себя риски того, что согласование может быть не получено.
Просмотры: 136 498
Содержание
- Процедура построения сетевого графика
- Этап 1: построение структуры таблицы
- Этап 2: создание шкалы времени
- Этап 3: заполнение данными
- Этап 4: Условное форматирование
- Вопросы и ответы

Сетевой график – это таблица, предназначенная для составления плана проекта и контроля за его выполнением. Для её профессионального построения существуют специализированные приложения, например MS Project. Но для небольших предприятий и тем более личных хозяйственных нужд нет смысла покупать специализированное программное обеспечение и тратить море времени на обучение тонкостям работы в нем. С построением сетевого графика вполне успешно справляется табличный процессор Excel, который установлен у большинства пользователей. Давайте выясним, как выполнить в этой программе указанную выше задачу.
Читайте также: Как сделать диаграмму Ганта в Экселе
Процедура построения сетевого графика
Построить сетевой график в Экселе можно при помощи диаграммы Ганта. Имея необходимые знания можно составить таблицу любой сложности, начиная от графика дежурства сторожей и заканчивая сложными многоуровневыми проектами. Взглянем на алгоритм выполнения данной задачи, составив простой сетевой график.
Этап 1: построение структуры таблицы
Прежде всего, нужно составить структуру таблицы. Она будет представлять собой каркас сетевого графика. Типичными элементами сетевого графика являются колонки, в которых указывается порядковый номер конкретной задачи, её наименование, ответственный за её реализацию и сроки выполнения. Но кроме этих основных элементов могут быть и дополнительные в виде примечаний и т.п.
- Итак, вписываем наименования столбцов в будущую шапку таблицы. В нашем примере названия колонок будут следующими:
- № п/п;
- Название мероприятия;
- Ответственное лицо;
- Дата начала;
- Продолжительность в днях;
- Примечание.
Если названия не вместятся в ячейку, то раздвигаем её границы.
- Отмечаем элементы шапки и клацаем по области выделения. В списке отмечаем значение «Формат ячеек…».
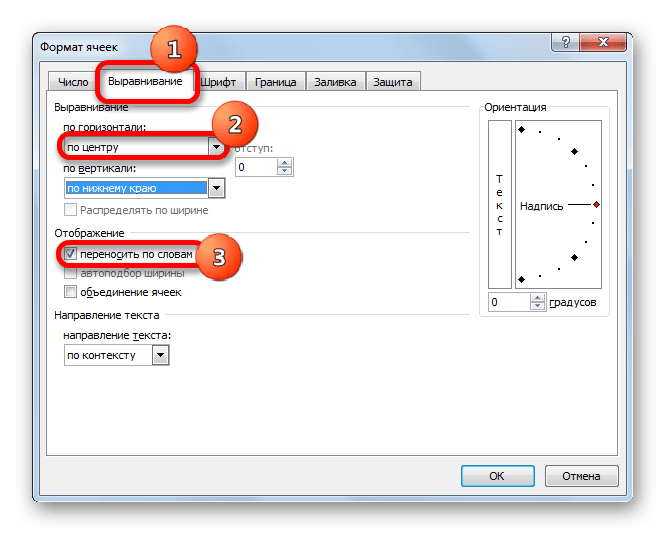
- В новом окне передвигаемся в раздел «Выравнивание». В области «По горизонтали» ставим переключатель в положение «По центру». В группе «Отображение» ставим галочку около пункта «Переносить по словам». Это нам пригодится позже, когда мы будет оптимизировать таблицу в целях экономии места на листе, сдвигая границы его элементов.
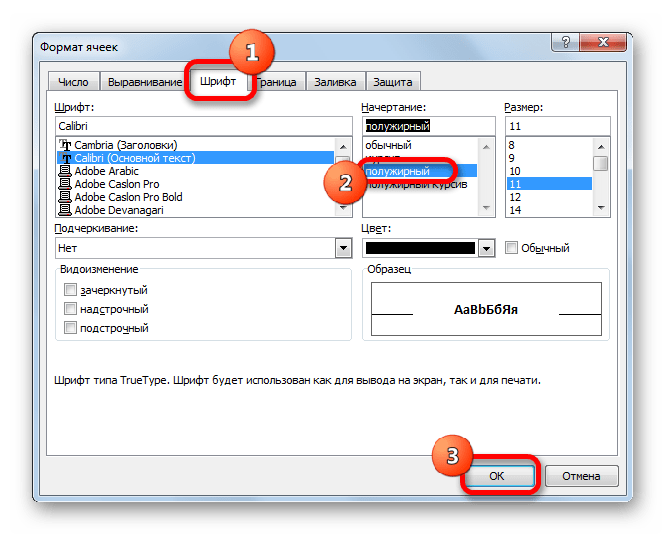
- Перемещаемся во вкладку окна форматирования «Шрифт». В блоке настроек «Начертание» устанавливаем флажок около параметра «Полужирный». Это нужно сделать, чтобы наименования столбцов выделялись среди другой информации. Теперь жмем по кнопке «OK», чтобы сохранить введенные изменения форматирования.
- Следующим шагом станет обозначение границ таблицы. Выделяем ячейки с наименованием столбцов, а также то количество строк ниже их, которое будет равно приблизительному числу запланированных мероприятий в границах данного проекта.
- Расположившись во вкладке «Главная», клацаем по треугольнику справа от пиктограммы «Границы» в блоке «Шрифт» на ленте. Открывается перечень выбора типа границ. Останавливаем свой выбор на позиции «Все границы».
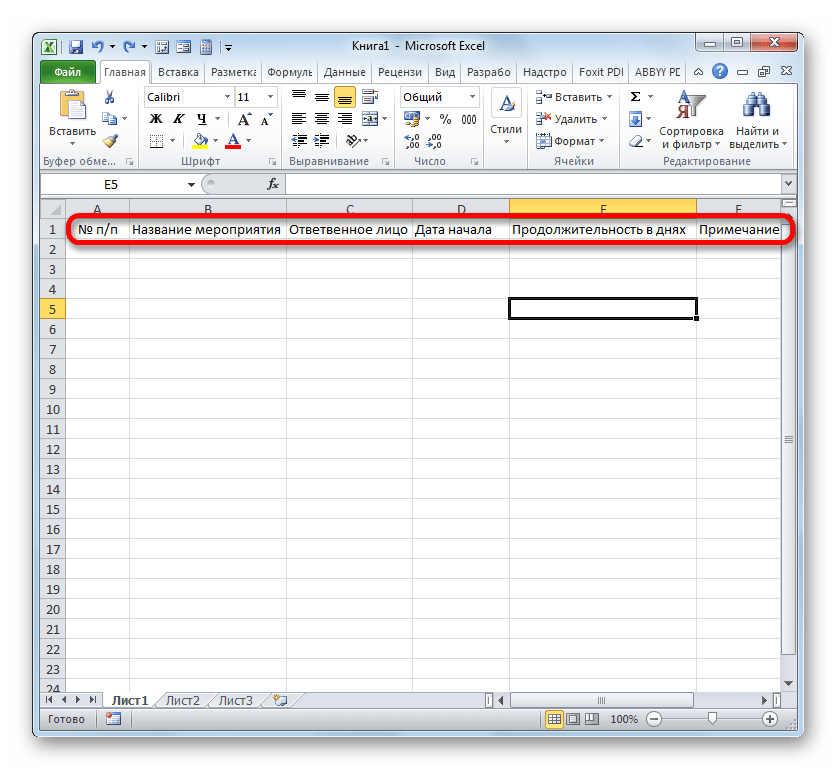
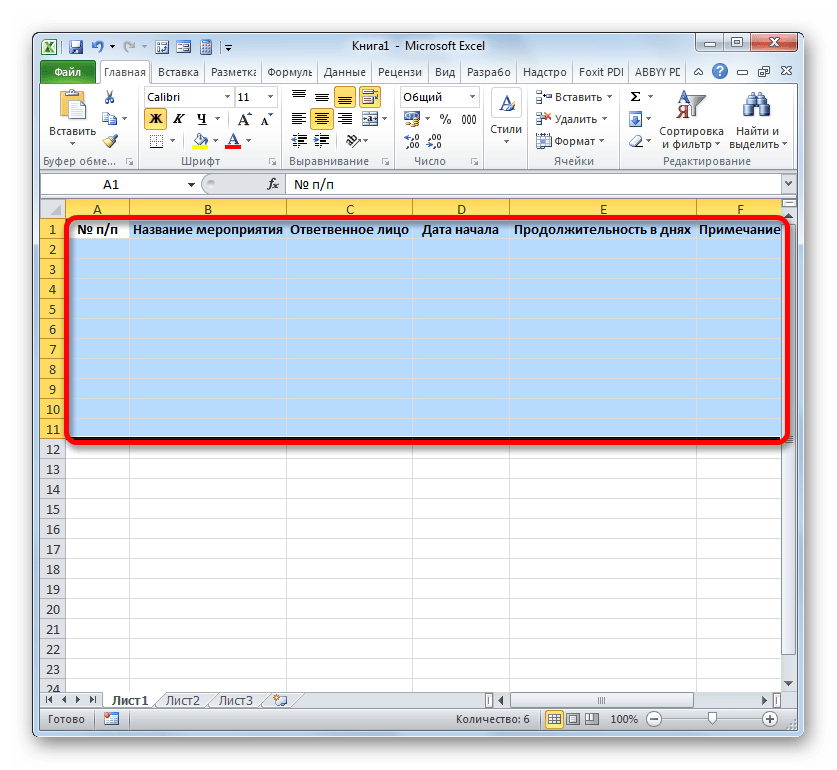
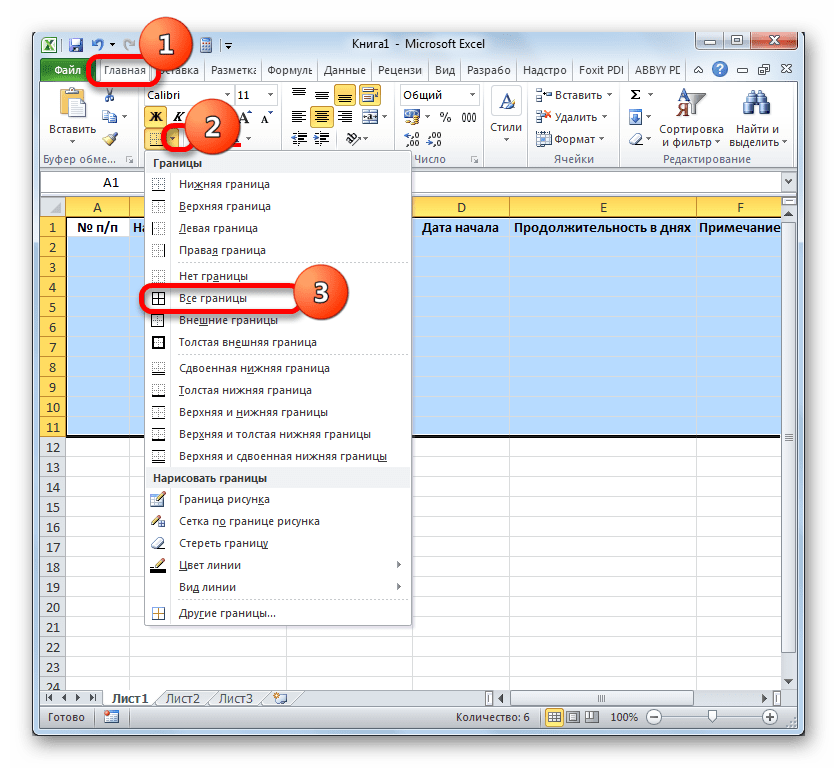
На этом создание заготовки таблицы можно считать оконченным.
Урок: Форматирование таблиц в Экселе
Этап 2: создание шкалы времени
Теперь нужно создать основную часть нашего сетевого графика – шкалу времени. Она будет представлять собой набор столбцов, каждый из которых соответствует одному периоду проекта. Чаще всего один период равен одному дню, но бывают случаи, когда величину периода исчисляют в неделях, месяцах, кварталах и даже годах.

В нашем примере используем вариант, когда один период равен одному дню. Сделаем шкалу времени на 30 дней.
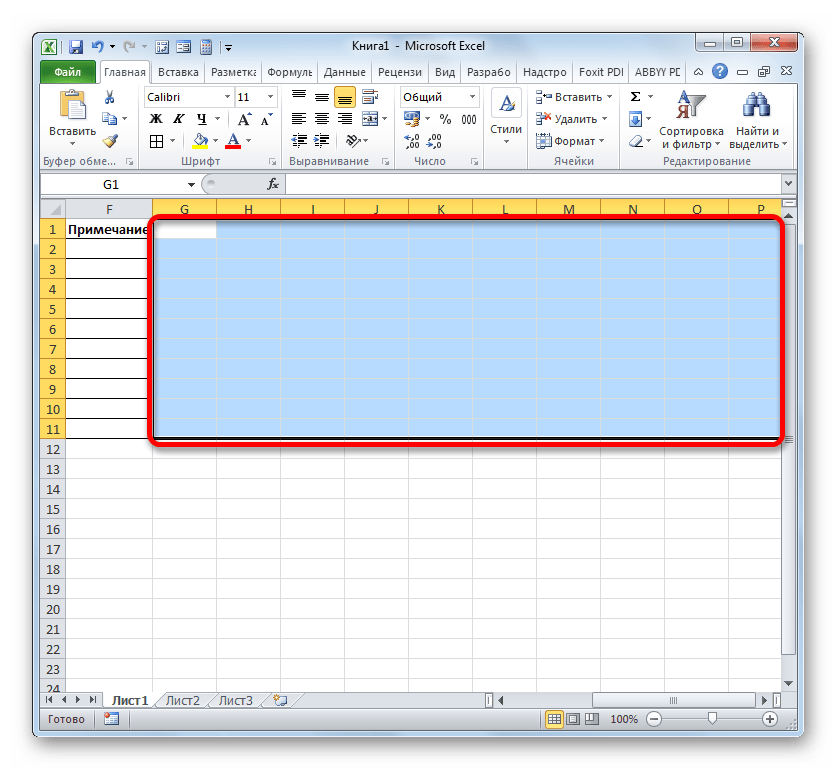
- Переходим к правой границе заготовки нашей таблицы. Начиная от этой границы, выделяем диапазон, насчитывающий 30 столбцов, а количество строк будет равняться числу строчек в заготовке, которую мы создали ранее.
- После этого клацаем по пиктограмме «Граница» в режиме «Все границы».
- Вслед за тем, как границы очерчены, внесем даты в шкалу времени. Допустим, мы будем контролировать проект с периодом действия с 1 по 30 июня 2017 года. В этом случае наименование колонок шкалы времени нужно установить в соответствии с указанным промежутком времени. Конечно, вписывать вручную все даты довольно утомительно, поэтому воспользуемся инструментом автозаполнения, который называется «Прогрессия».
В первый объект шапки шакалы времени вставляем дату «01.06.2017». Передвигаемся во вкладку «Главная» и клацаем по значку «Заполнить». Открывается дополнительное меню, где нужно выбрать пункт «Прогрессия…».
- Происходит активация окна «Прогрессия». В группе «Расположение» должно быть отмечено значение «По строкам», так как мы будем заполнять шапку, представленную в виде строки. В группе «Тип» должен быть отмечен параметр «Даты». В блоке «Единицы» следует поставить переключатель около позиции «День». В области «Шаг» должно находиться цифровое выражение «1». В области «Предельное значение» указываем дату 30.06.2017. Жмем на «OK».
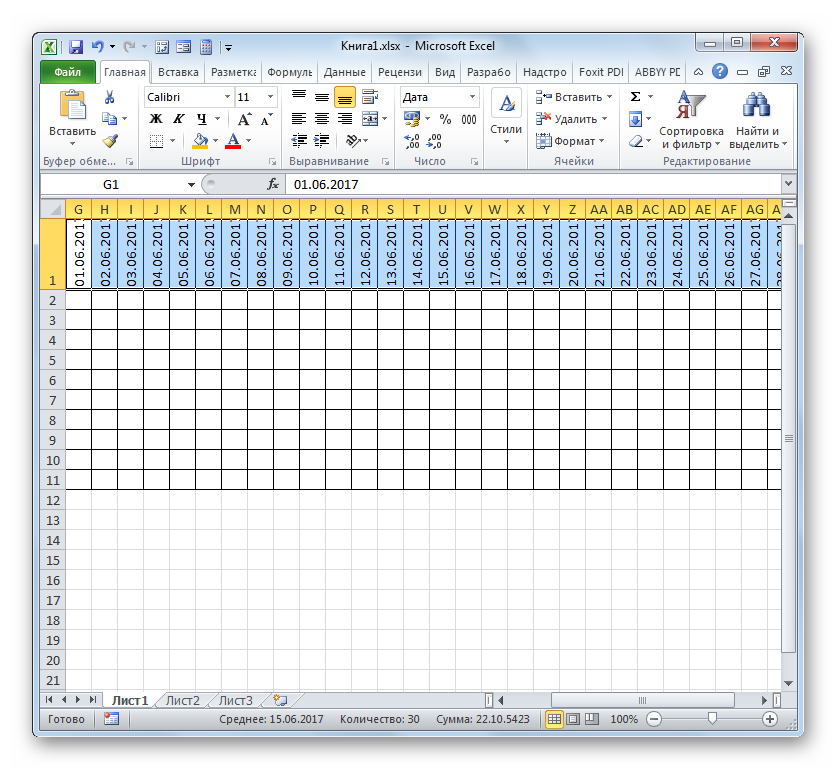
- Массив шапки будет заполнен последовательными датами в пределе от 1 по 30 июня 2017 года. Но для сетевого графика мы имеем слишком широкие ячейки, что негативно влияет на компактность таблицы, а, значит, и на её наглядность. Поэтому проведем ряд манипуляций для оптимизации таблицы.
Выделяем шапку шкалы времени. Клацаем по выделенному фрагменту. В списке останавливаемся на пункте «Формат ячеек». - В открывшемся окне форматирования передвигаемся в раздел «Выравнивание». В области «Ориентация» устанавливаем значение «90 градусов», либо передвигаем курсором элемент «Надпись» вверх. Клацаем по кнопке «OK».
- После этого наименования столбцов в виде дат изменили свою ориентацию с горизонтальной на вертикальную. Но из-за того, что ячейки свой размер не поменяли, названия стали нечитаемыми, так как по вертикали не вписываются в обозначенные элементы листа. Чтобы изменить это положение вещей, опять выделяем содержимое шапки. Клацаем по пиктограмме «Формат», находящейся в блоке «Ячейки». В перечне останавливаемся на варианте «Автоподбор высоты строки».
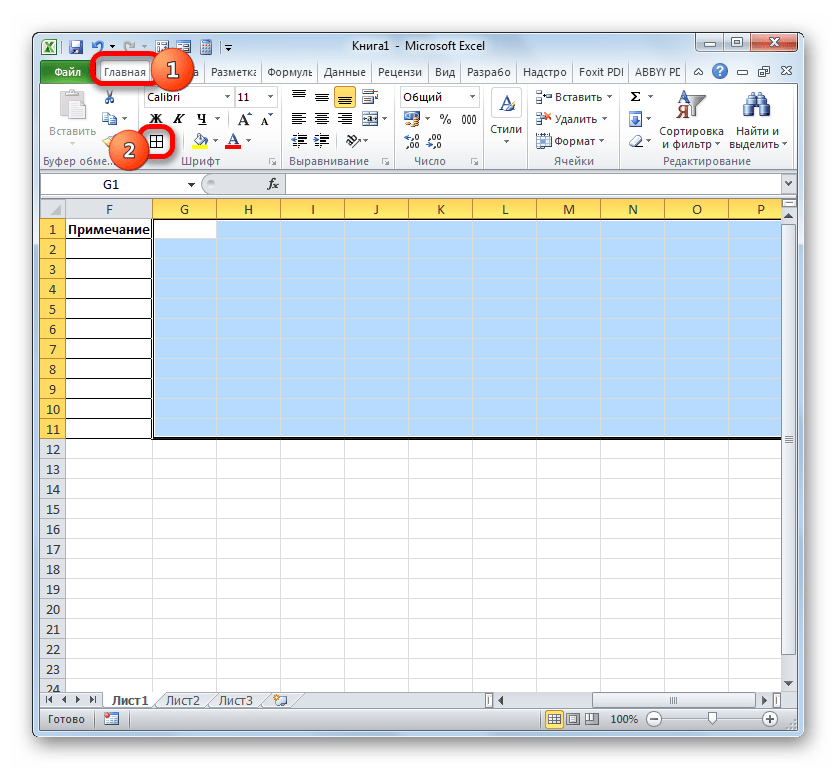
- После описанного действия наименования столбцов по высоте вписываются в границы ячеек, но по ширине ячейки не стали компактнее. Снова выделяем диапазон шапки шкалы времени и клацаем по кнопке «Формат». На этот раз в списке выбираем вариант «Автоподбор ширины столбца».
- Теперь таблица приобрела компактность, а элементы сетки приняли квадратную форму.


Этап 3: заполнение данными
Далее нужно заполнить таблицу данными.
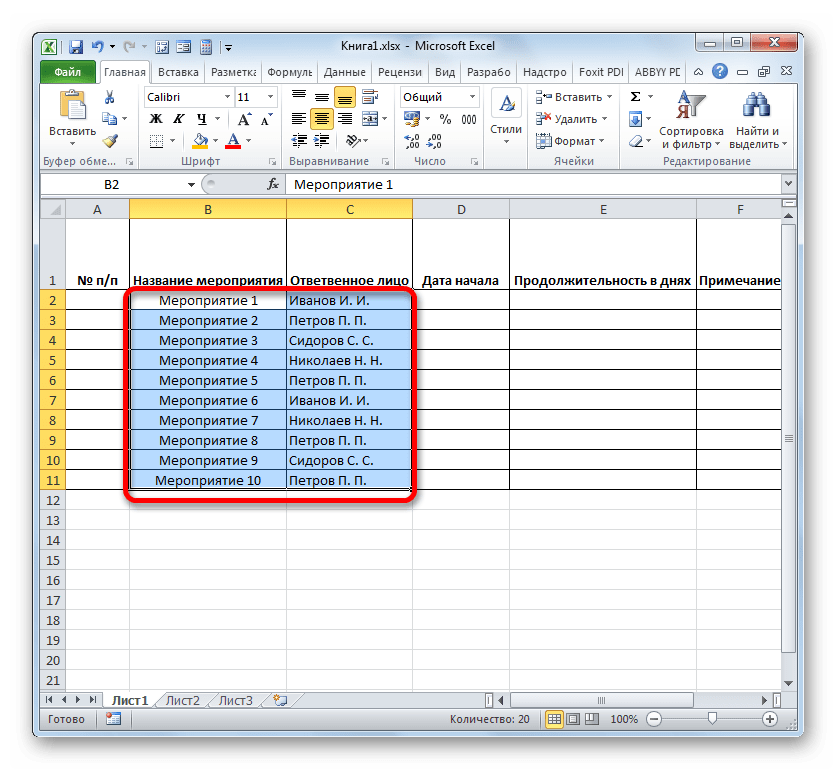
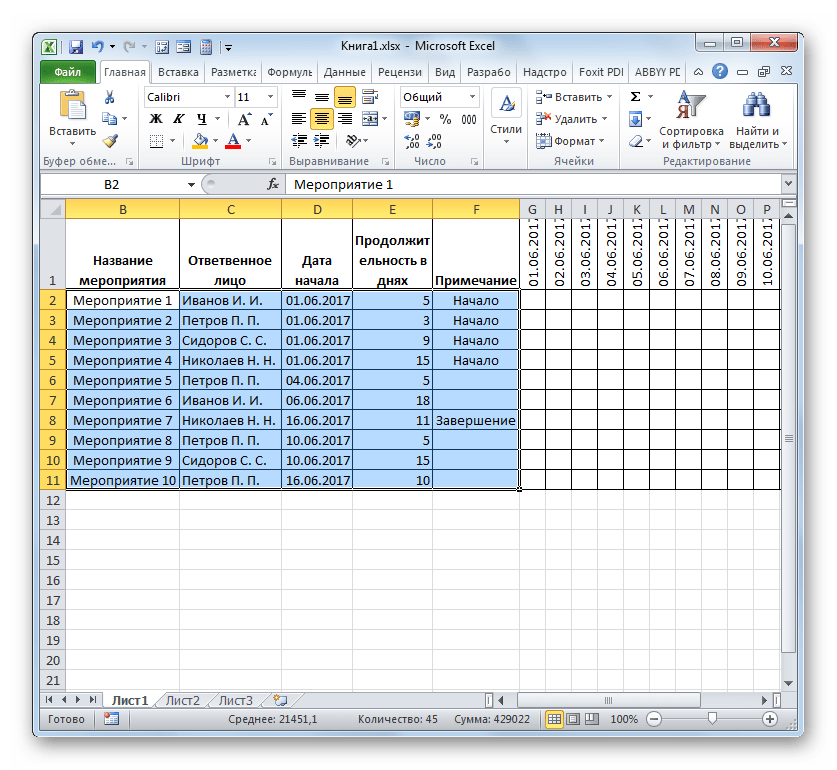
- Возвращаемся к началу таблицы и заполняем колонку «Название мероприятия» наименованиями задач, которые планируется выполнить в ходе реализации проекта. А в следующей колонке вносим фамилии ответственных лиц, которые будут отвечать за выполнение работы по конкретному мероприятию.
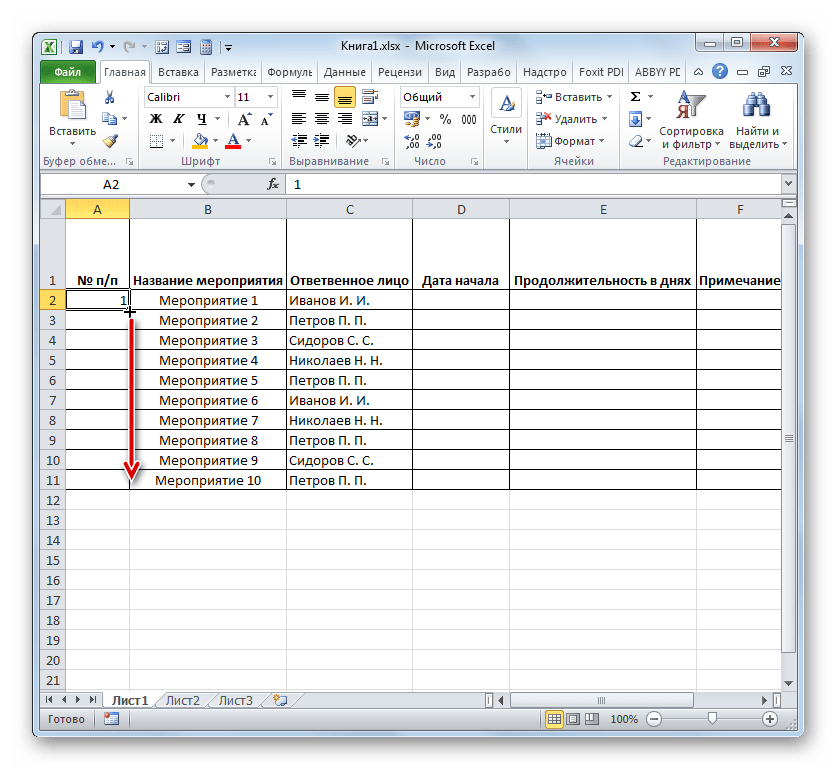
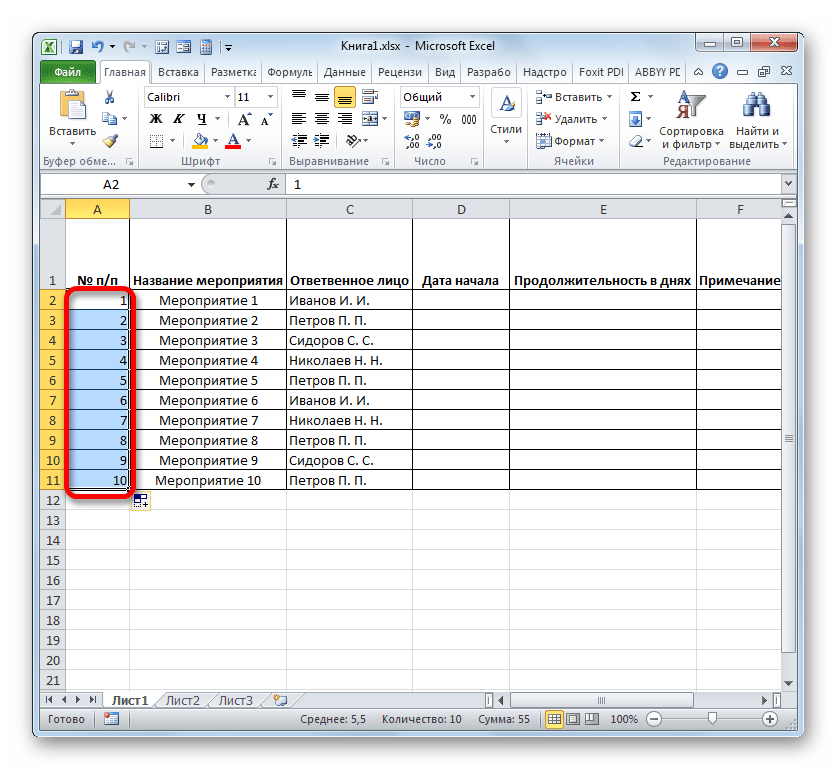
- После этого следует заполнить колонку «№ п/п». Если мероприятий немного, то это можно сделать, вручную вбив числа. Но если планируется выполнение многих задач, то рациональнее будет прибегнуть к автозаполнению. Для этого ставим в первый элемент столбца число «1». Курсор направляем на нижний правый край элемента, дождавшись момента, когда он преобразуется в крестик. Одномоментно зажимаем клавишу Ctrl и левую кнопку мышки, тянем крестик вниз до нижней границы таблицы.
- Весь столбец при этом будет заполнен значениями по порядку.
- Далее переходим к столбцу «Дата начала». Тут следует указать дату начала каждого конкретного мероприятия. Делаем это. В столбце «Продолжительность в днях» указываем количество дней, которое придется потратить для решения указанной задачи.
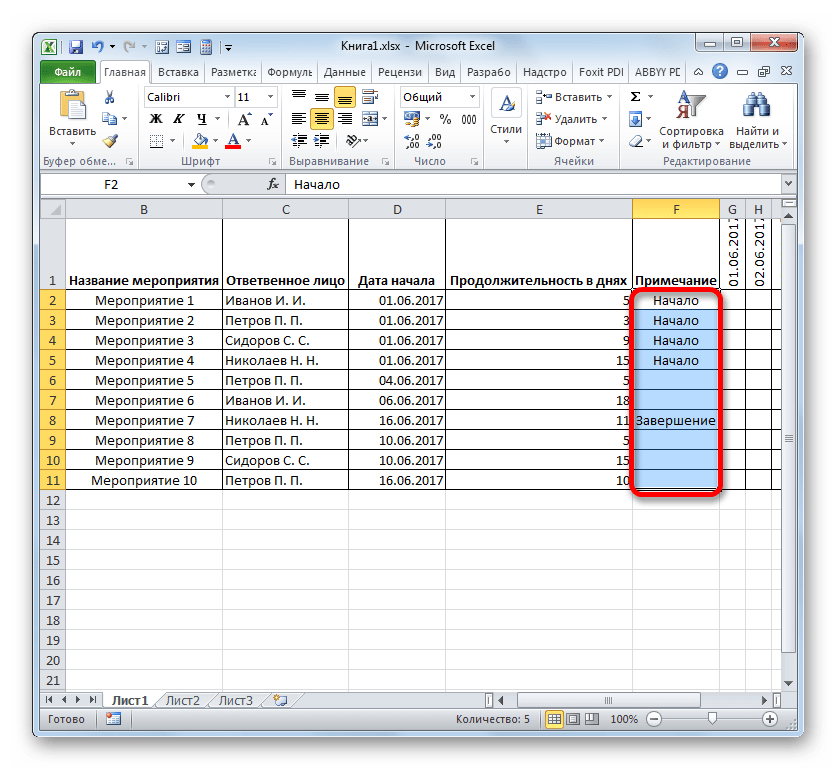
- В колонке «Примечания» можно заполнять данные по мере необходимости, указывая особенности конкретного задания. Внесение информации в этот столбец не является обязательным для всех мероприятий.
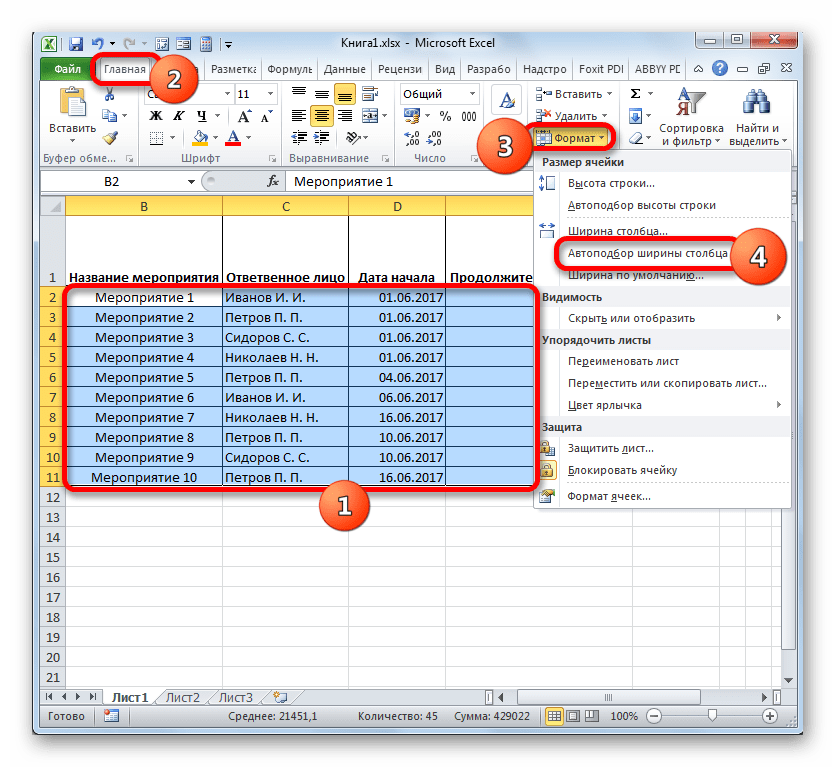
- Затем выделяем все ячейки нашей таблицы, кроме шапки и сетки с датами. Клацаем по иконке «Формат» на ленте, к которой мы уже ранее обращались, жмем в открывшемся списке по позиции «Автоподбор ширины столбца».
- После этого ширина столбцов выделенных элементов сужается до размеров ячейки, в которой длина данных больше всего в сравнении с остальными элементами колонки. Таким образом, экономится место на листе. При этом в шапке таблицы производится перенос наименований по словам в тех элементах листа, в которых они не умещаются в ширину. Это получилось сделать благодаря тому, что мы ранее в формате ячеек шапки поставили галочку около параметра «Переносить по словам».

Этап 4: Условное форматирование
На следующем этапе работы с сетевым графиком нам предстоит залить цветом те ячейки сетки, которые соответствуют промежутку периода выполнения конкретного мероприятия. Сделать это можно будет посредством условного форматирования.
- Отмечаем весь массив пустых ячеек на шкале времени, который представлен в виде сетки элементов квадратной формы.
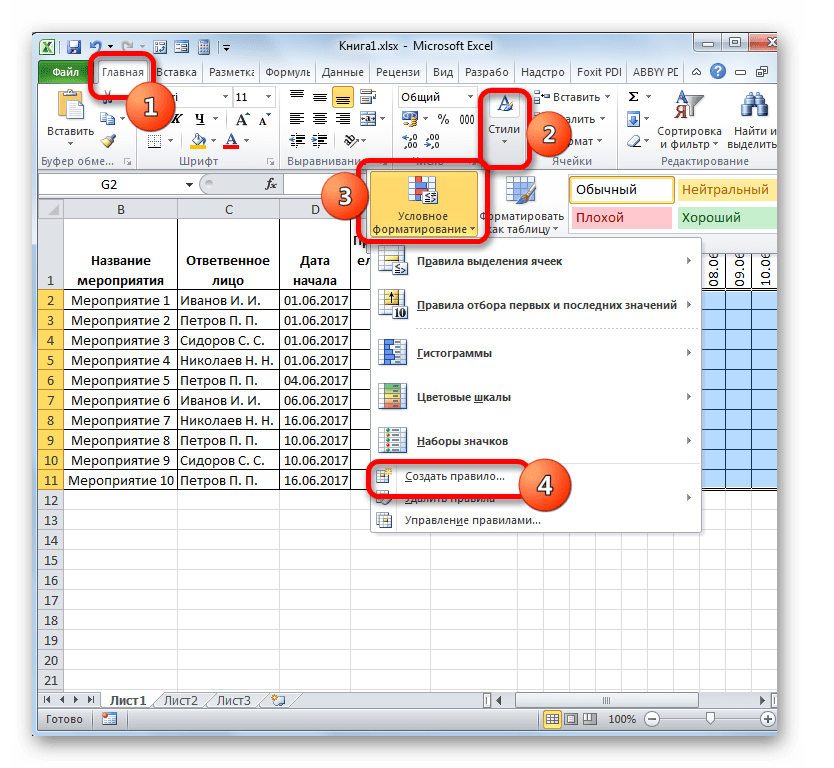
- Щелкаем по значку «Условное форматирование». Он расположен в блоке «Стили» После этого откроется список. В нем следует выбрать вариант «Создать правило».
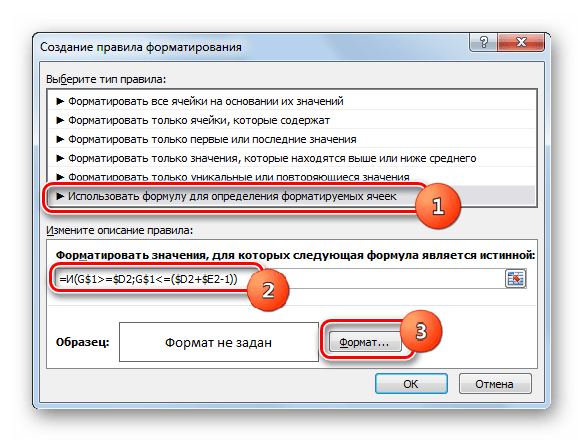
- Происходит запуск окна, в котором требуется сформировать правило. В области выбора типа правила отмечаем пункт, который подразумевает использование формулы для обозначения форматируемых элементов. В поле «Форматировать значения» нам требуется задать правило выделения, представленное в виде формулы. Для конкретно нашего случая она будет иметь следующий вид:
=И(G$1>=$D2;G$1<=($D2+$E2-1))Но для того, чтобы вы могли преобразовать данную формулу и для своего сетевого графика, который вполне возможно, будет иметь другие координаты, нам следует расшифровать записанную формулу.
«И» — это встроенная функция Excel, которая проверяет, все ли значения, внесенные как её аргументы, являются истиной. Синтаксис таков:
=И(логическое_значение1;логическое_значение2;…)Всего в виде аргументов используется до 255 логических значений, но нам требуется всего два.
Первый аргумент записан в виде выражения «G$1>=$D2». Он проверяет, чтобы значение в шкале времени было больше или равно соответствующему значению даты начала определенного мероприятия. Соответственно первая ссылка в данном выражении ссылается на первую ячейку строки на шкале времени, а вторая — на первый элемент столбца даты начала мероприятия. Знак доллара ($) установлен специально, чтобы координаты формулы, у которых стоит данный символ, не изменялись, а оставались абсолютными. И вы для своего случая должны расставить значки доллара в соответствующих местах.
Второй аргумент представлен выражением «G$1<=($D2+$E2-1)». Он проверяет, чтобы показатель на шкале времени (G$1) был меньше или равен дате завершения проекта ($D2+$E2-1). Показатель на шкале времени рассчитывается, как и в предыдущем выражении, а дата завершения проекта вычисляется путем сложения даты начала проекта ($D2) и продолжительности его в днях ($E2). Для того, чтобы в количество дней был включен и первый день проекта, от данной суммы отнимается единица. Знак доллара играет ту же роль, что и в предыдущем выражении.
Если оба аргумента представленной формулы будут истинными, то к ячейкам, будет применено условное форматирование в виде их заливки цветом.
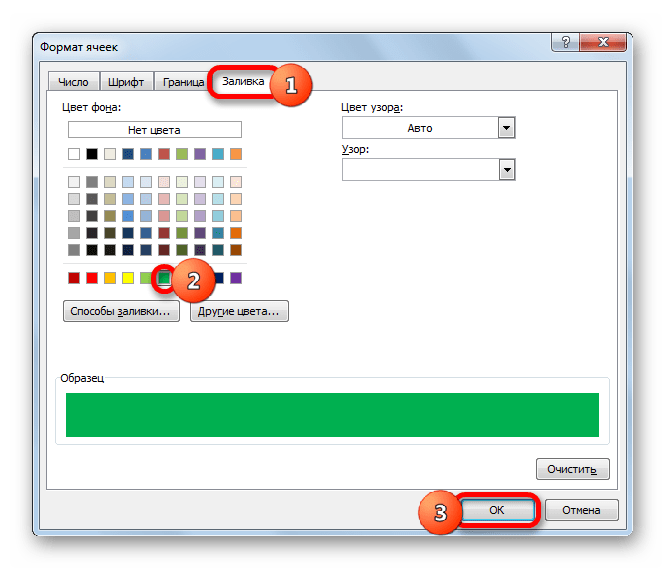
Чтобы выбрать определенный цвет заливки, клацаем по кнопке «Формат…».
- В новом окне передвигаемся в раздел «Заливка». В группе «Цвета фона» представлены различные варианты закраски. Отмечаем тот цвет, которым желаем, чтобы выделялись ячейки дней, соответствующих периоду выполнения конкретной задачи. Например, выберем зеленый цвет. После того, как оттенок отразился в поле «Образец», клацаем по «OK».
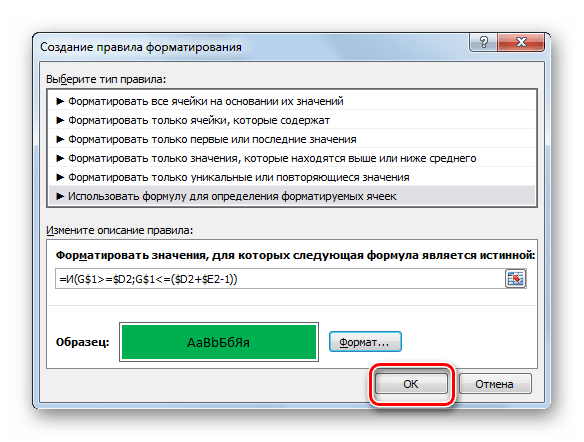
- После возвращения в окно создания правила тоже клацаем по кнопке «OK».
- После выполнения последнего действия, массивы сетки сетевого графика, соответствующие периоду выполнения конкретного мероприятия, были окрашены в зеленый цвет.
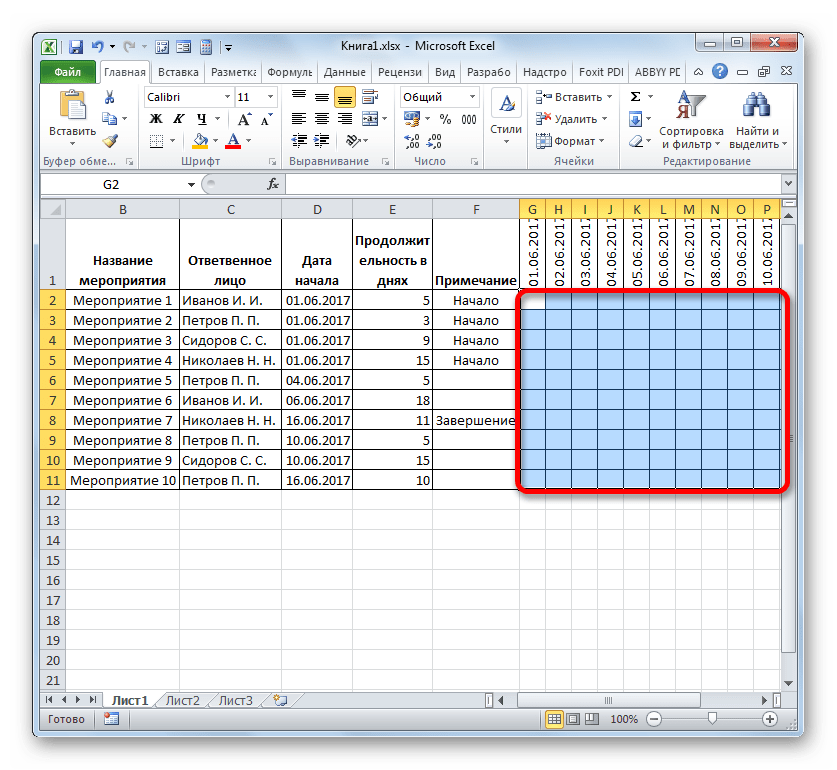
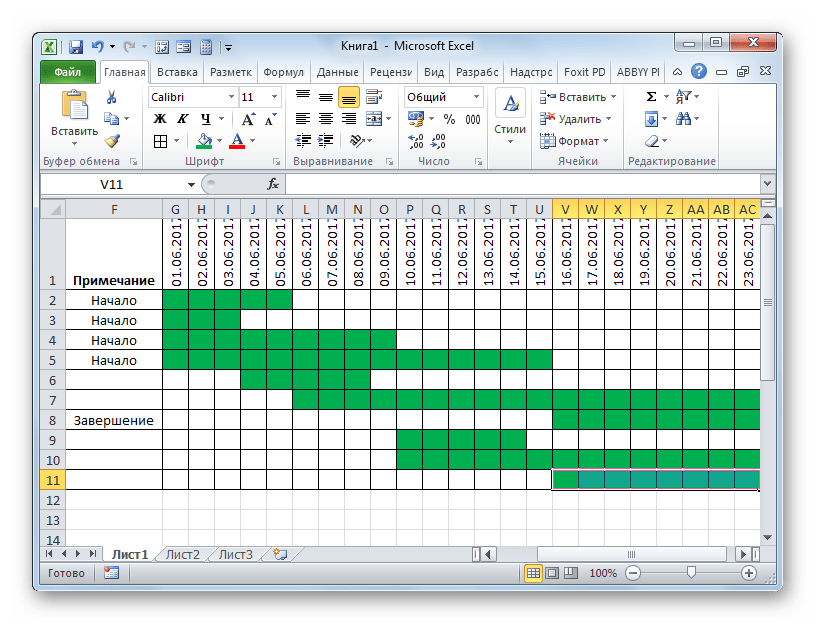
На этом создание сетевого графика можно считать оконченным.
Урок: Условное форматирование в Майкрософт Эксель
В процессе работы мы создали сетевой график. Это не единственный вариант подобной таблицы, который можно создать в Экселе, но основные принципы выполнения данной задачи остаются неизменными. Поэтому при желании каждый пользователь может усовершенствовать таблицу, представленную в примере, под свои конкретные потребности.
Еще статьи по данной теме:
Помогла ли Вам статья?
Порядок и правила построения сетевых графиков
Сетевые графики
составляются на начальном этапе
планирования. Вначале планируемый
процесс разбивается на отдельные работы,
составляется перечень работ и событий,
придумываются их логические связи и
последовательность выполнения, работы
закрепляются за ответственными
исполнителями. С их помощью оценивается
длительность каждой работы. Затем
составляется (сшивается) сетевой график.
После упорядочения сетевого графика
рассчитываются параметры событий и
работ, определяются резервы времени и
критический путь. Проводят анализ и
оптимизация сетевого графика, который
при необходимости вычерчивается заново
с пересчетом параметров событий и работ.
При построении
сетевого графика необходимо соблюдать
ряд правил:
1) все стрелки
сетевого графика имеют общее направление
(слева направо);
2) между парой
событий может быть изображена только
одна работа;
3) используются
возможные варианты следования событий
и работ (табличная запись и пути перехода
приведены на рис. 1);
4) в сетевой модели
не должно быть «тупиковых» событий, то
есть событий, из которых не выходит ни
одна работа, за исключением завершающего
события;
5) в сетевом графике
не должно быть «хвостовых» событий
(кроме исходного), которым не предшествует
хотя бы одна работа;
6) все события,
кроме исходного и завершающего, должны
иметь как входящие, так и выходящие
стрелки;
7) если две работы
начинаются в одно и то же время, в одном
событии и оканчиваются в другом событии,
то вводят фиктивное событие и фиктивную
работу. При этом одна из параллельных
работ замыкается на это фиктивное
событие. Фиктивные работы имеют нулевую
продолжительность и изображаются на
графике пунктирными линиями;
8) в сети не должно
быть замкнутых контуров и петель, то
есть путей, соединяющих некоторые
события с ними же самими.
|
Работа аj |
Опорная работа аi |
Работа аj |
Опорная работа аi |
Работа аj |
Опорная работа аi |
|
а1 |
– |
а1 |
– |
а1 |
– |
|
а2 |
а1 |
а2 |
а1 |
а2 |
– |
|
а3 |
а1 |
а3 |
а1, а2 |
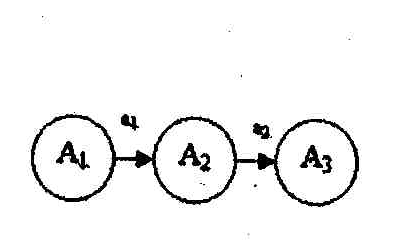
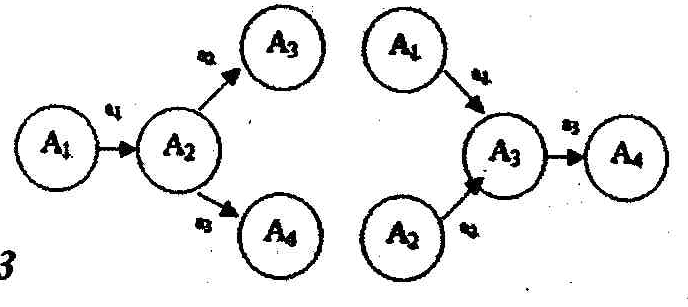
Рисунок 1
Упорядочение сетевого графика. Понятие о пути
Предположим, что
при составлении некоторого проекта
выделено 12 событий – 0,1,2,3,4,5,6,7,8,9,10,11 и
24 связывающие их работы – (0,1), (0,2), (0,3),
(1,2), (1,4), (1,5), (2,3), (2,5), (2,7), (3,6), (3,7), (3,10),
(4,8), (5,8), (5,7), (6,10), (7,6), (7,8), (7,9), (7,10), (8,9),
(9,11), (10,9), (10,11). Необходимо составить и
упорядочить сетевой график.
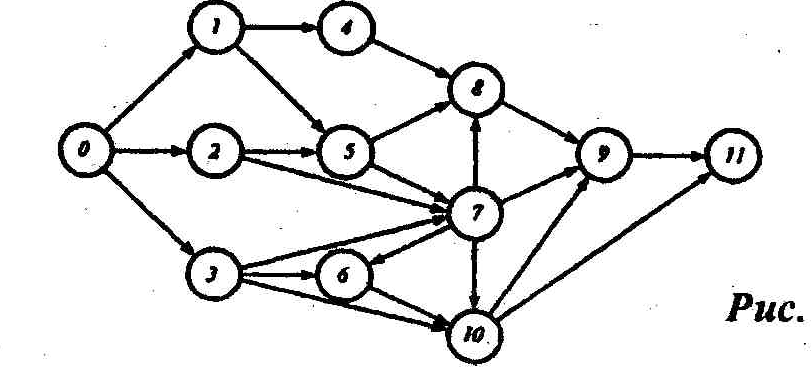
Рисунок 2
Как следует из
перечня работ, исходным событием является
событие 0 (ему не предшествуют никакие
работы), а завершающим – событие 11 (за
ним не следует ни одна работа). Полагая
на сетевых графиках изменении времени
слева направо, поместим событие 0 в левую
часть графика, а событие 11 – в правую
часть, разместив между ними промежуточные
события в некотором порядке, соответствующем
их номерам (рисунок 2). События свяжем
работами-стрелками в соответствии с
перечнем работ.
Упорядочение
сетевого графика заключается
в таком расположении событий и работ,
при котором для любой работы предшествующее
ей событие расположено левее и имеет
меньший номер по сравнению с завершающим
эту работу событием. Другими словами,
в упорядоченном сетевом графике: от
событий с меньшими номерами к событиям
с большими номерами (рисунок 3).
Одно из важнейших
понятий сетевого графика – понятие
пути.
Путь
– любая последовательность работ, в
которой конечное событие каждой работы
совпадает с начальным событием следующей
за ней работы.
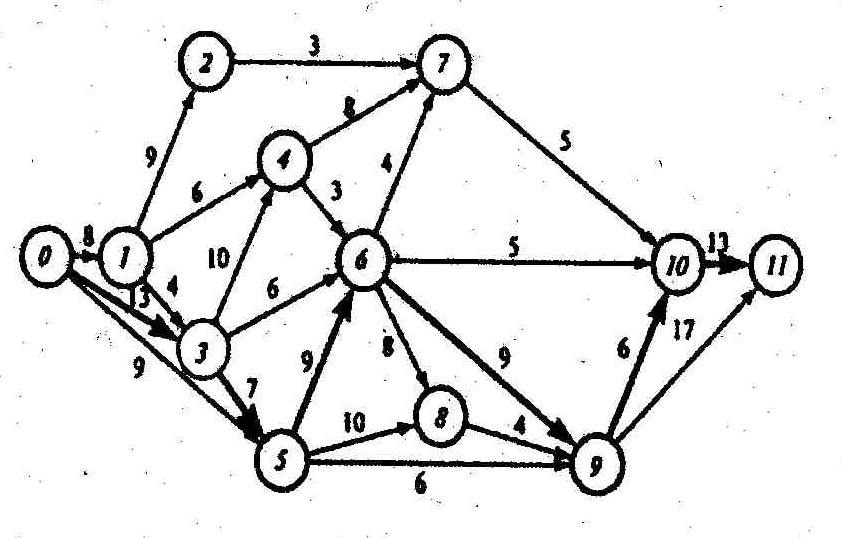
Рисунок 3
Среди различных
путей сетевого графика наибольший
интерес представляет полный
путь L
– любой путь, начало которого совпадает
с исходным событием сети, а конец – с
завершающим.
Наиболее
продолжительный полный путь в сетевом
графике называется критическим.
Критическими называются также работы
и события, расположенные на этом пути.
Например, для
рассматриваемого нами сетевого графика
(рисунок 3) полными путями будут: путь
0→1→2→7→10→11 продолжительностью
8+9+3+5+13=38 суток, путь 0→1→3→4→6→10→11
продолжительностью 8+4+10+3+5+13=43 суток,
путь 0→3→5→6→9→10→11 продолжительностью
13+7+9+13+6+13=61 суток и т.д.
Последний путь
имеет наибольшую продолжительность
(не только среди приведенных четырех
полных путей, но и среди всех полных
путей, которых в данном случае насчитывается
64), поэтому он и является критическом.
Продолжительность критического пути
составляет 61 сутки, то есть для проведения
комплекса работ понадобятся 61 сутки.
Быстрее комплекс выполнить нельзя, так
как для достижения завершающего события
критический путь надо пройти обязательно.
Для достижения
события 11 надо выполнить работу (10,11),
то есть достичь события 10; для достижения
события 10 надо провести работу (9,10), то
есть достичь события 9; для достижения
события 9 надо достичь работу (6,9), то
есть достичь события 6, и т.д.
Определив критический
путь, установили критические события
сети 0,3,5,6,9,10,11 и критические работы
(0,3), (3,5), (5,6), (6,9), (9,10), (10,11).
Критический путь
имеет особое значение в системе СПУ,
так как работы этого пути определяют
общий цикл завершения всего комплекса
работ, планируемых при помощи сетевого
графика. И для сокращения продолжительность
проекта необходимо в первую очередь
сокращать продолжительность работ,
лежащих на критическом пути.
Классический вид
сетевого графика – сеть, вычерченная
без масштаба времени. Поэтому сетевой
график, хотя дает четкое представление
о порядке следования работ, но недостаточно
нагляден для определения тех работ,
которые должны выполняться в каждый
данный момент времени. В связи с этим
небольшой проект после упорядочения
сетевого графика рекомендуется дополнить
линейной
диаграммой проекта.
Такая линейная диаграмма для рассматриваемой
сети показана на рисунке 4.
При построении
линейной диаграммы каждая работа
изображается параллельным оси времени
отрезком, длина которого равна
продолжительности этой работы. При
наличии фиктивной работы нулевой
продолжительности (в рассматриваемой
сети ее нет) она изображается точкой.
События i
и j
, начало и
конец работы (i,
j)
помещают соответственно в начале и
конце отрезка. Отрезки располагают один
над другим, снизу вверх в порядке
возрастания индекса i
, а при одном и том же i
– в порядке возрастания индекса j
(на рисунке
4 вследствие ограниченности места не
показаны работы-отрезки, выходящие из
2-, 3-, 4- и 5-го событий).
По линейной
диаграмме проекта можно определить
коритическое время, критический путь,
а также резервы времени всех работ.
Критическое
время комплекса работ
равно координате на оси времени самого
правого конца всех отрезков диаграммы:
ТКР=t(11)
=61 суток
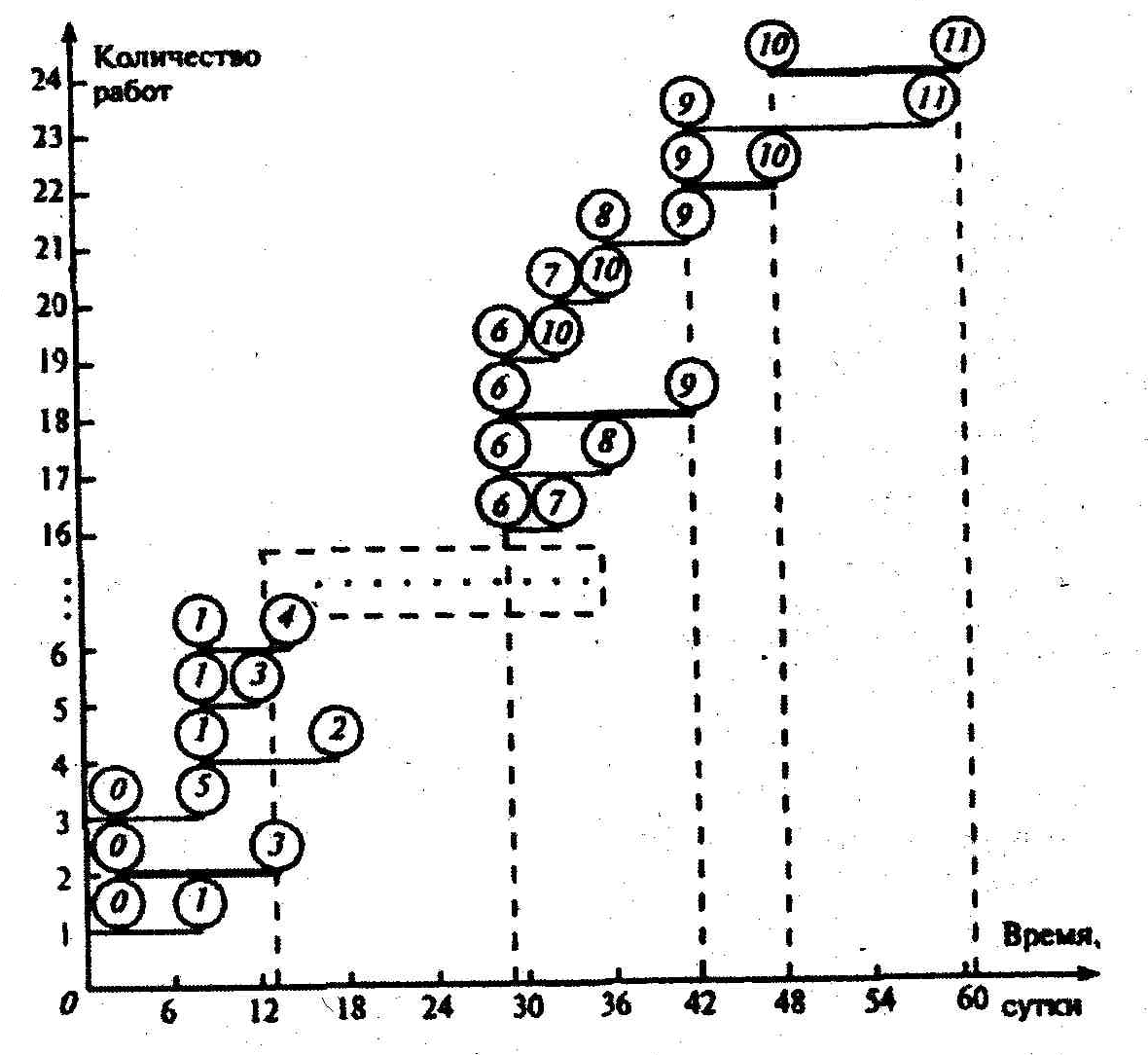
Рисунок 4
Для определения
критического пути рассматриваются
работы-отрезки, конечные события которых
совпадают с завершающим событием сети
(в примере (9,11) и (10,11). Затем находят
отрезок (9,10), правый конец которого лежит
на одной вертикали (10) с левым концом
одного из рассматриваемых ранее отрезков
(10,11). Аналогично определяют и другие
работы-отрезки критического пути:
(6,9),….(0,3) (на рис. 4 они все выделены жирным
шрифтом).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аннотация: От набора работ к сетевому графику. Конструирование сетевого графика проекта, два подхода к разработке сетевых графиков. Основные правила разработки сетевого графика. Принципы построения и анализа сетевых графиков типа “ОУ”. Оценка начала и окончания работ с помощью сетевого графика. Процесс расчета параметров сетевого графика. Прямой анализ – определение ранних сроков начала операций. Обратный анализ — определение поздних сроков завершения операций. Использование результатов прямого и обратного анализа сетевого графика. Ошибки сетевой логики. Приближение к реальности посредством улучшенных методов построения сетевых графиков. Использование задержек (лагов). Отношения типа “от конца к началу”. Отношения “от начала к началу”. Отношения “от конца к концу”. Отношения “от начала к концу”. Комбинация отношений задержки. Операции растяжки
Сетевой график отражает операции проекта, которые необходимо выполнить, логическую последовательность и взаимозависимость этих операций и время начала и окончания самой продолжительной цепочки операций – критический путь.
Сетевой график раскрывает внутренние связи проекта и служит основой для календарного планирования работ и использования оборудования.
Сетевой график дает возможность оценить периоды времени, в течение которых выполнение операций может начинаться и заканчиваться, а также время допустимой задержки их выполнения.
Сетевой график позволяет определить, какие операции являются “критическими” и, следовательно, должны выполняться строго по графику, чтобы проект был завершен в запланированные сроки.
От набора работ к сетевому графику
Сетевой график строится при помощи прямоугольников (блоков) и стрелок.
На рис. 2.1 блок обозначает операцию и стрелка показывает подчиненность операций и направленность хода выполнения проекта.
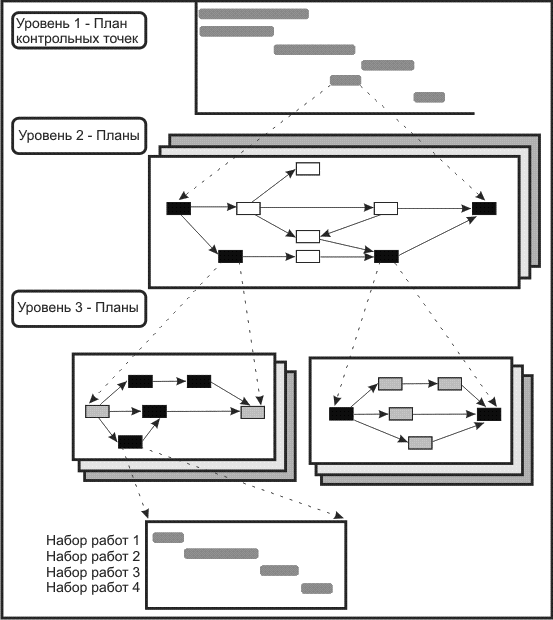
Рис.
2.1.
Развертка сетевых графиков
Операция представляет одну или несколько задач, требующих определенных затрат времени.
Наборы работ используются для разработки детального сетевого графика для руководителей первого уровня (см. уровень 3 “Планы” на рис. 2.1).
Подробные графики двух проектов для руководителей отделов (уровень 2) могут быть объединены в более агрегированную форму и, далее, могут быть сведены к самому общему виду, необходимому для руководителя проекта, высшего руководства и клиента.
Этот верхний уровень обычно представлен в виде графика Ганта и называется планом контрольных точек.Достоверность информации на каждом уровне зависит от точности определения набора работ и операций.
Первое, что нужно сделать для разработки сетевого графика проекта, определить набор работ.
Рис. 2.2 показывает часть структурированного набора работ и как информация используется для разработки сетевого графика.

Рис.
2.2.
Перевод наборов работ в сетевой график
Самый нижний уровень набора работ, подлежащих выполнению на рис. 2.2, называется условно “Печатная плата“.
Счета издержек (на дизайн, на производство, на испытания, на разработку программного обеспечения) обозначают соответствующую проектную работу, отвечающий за нее отдел и бюджет времени, отведенный для ее выполнения. Каждый счет издержек представляет один или несколько наборов работ.
Рис. 2.2 показывает, как наборы работ используются для разработки сетевого графика проекта. Использование наборов работ можно отследить при помощи специальной системы кодирования. Например, в операции А используется рабочий пакет D-1-1 и D-1-2 (спецификация и документация), тогда как операция C использует рабочий пакет S-22-1. Управляющий проектом дает оценку времени выполнения всей операции, исходя из времени на выполнение отдельных работ в наборе. Например, выполнение операции В (прототип 1) потребует 5 недель; операции К (тестирование) -3 недели. После расчета начала и окончания выполнения операций менеджер может определить необходимые ресурсы и составить поэтапный бюджет проекта (с датами).
Конструирование сетевого графика проекта
Терминология
Операция (или работа). Для руководителей проектов операция – это неделимый элемент проекта, требующий затрат времени для своего выполнения.
Обычно выполнение операций связано с затратами времени и трудовых ресурсов.
Иногда это может быть просто время. Примерами этого могут быть операция ожидания подписания контракта или ожидание поступления материалов, одобрения правительства, таможенное оформление грузов и т.д.
Операции обычно состоят из одной или более работ из наборов работ. Как правило, название операциям дается в повелительной форме глагола, например, “разработать спецификацию продукта”.
Операция слияния.Это операция, которая имеет более одной непосредственно предшествующей ей операции.
Параллельные операции.Это операции, которые могут, по желанию менеджера, выполняться одновременно. Однако совсем не обязательно осуществлять параллельные операции одновременно.
Путь.Последовательность связанных, взаимозависимых операций.
Критический путь.Это самый длинный путь во всей системе операций; если выполнение операции на этом отрезке задерживается, выполнение всего проекта задерживается на такое же время.
Событие.Термин используется для обозначения точки времени начала или завершения операции. Событие не требует времени.
Дробящаяся операция.Это операция, за которой сразу следуют несколько операций (от нее исходит более одной стрелки, обозначающей зависимость).
Два подхода к разработке сетевых графиков
Для разработки сетевых графиков могут применяться два подхода:
подход с обозначением операций в узлах (блоках) графика – ОУ ;
подход с обозначением операций на стрелках графика – ОС.
На практике первый метод – ОУ – используется значительно чаще и далее излагается именно этот метод.
Основные правила разработки сетевого графика
При разработке сетевого графика целесообразно придерживаться следующих 8 правил:
- Сетевой график разворачивается слева направо.
- Ни одна операция не может быть начата, пока все предшествующие связанные с ней операции не будут выполнены.
- Стрелки в сетевом графике отображают отношения предшествования и следования. На рисунке стрелки могут пересекаться.
- Каждая операция должна иметь свой собственный номер.
- Номер последующей операции должен быть больше номера любой предшествующей операции.
- Образование петель недопустимо (другими словами, не должно происходить зацикливания хода выполнения установленного набора операций).
- Условные переходы от одной операции к другой не допускаются (имеется в виду определение последовательности хода выполнения операций условиями типа: “Если будет достигнут успех, сделайте то-то…; если нет – ничего не предпринимайте”).
- Опыт показывает, что когда существует несколько исходных операций проекта, то может быть определен общий узел начала всего комплекса работ. Точно так же один узел может быть использован для четкого обозначения окончания проекта.
Моделирование сетевого графика проекта


Свежие публикации автора:
Содержание
- 1 Глоссарий разработки сетевого графика
- 2 Базовый алгоритм и виды связей сетевого графика
- 3 Методы расчета длительности операций
- 4 Методы оптимизации сетевого графика
Менеджер проекта, занимаясь его планированием, должен помнить о проектном треугольнике ограничений: «продолжительность» – «стоимость» – «содержание». Ресурсные и стоимостные ограничения предопределяют качество расписания проекта. Сетевое планирование, хотя и является достаточно рутинным инструментом календарной проработки, тем не менее, позволяет лучшим образом выполнить оптимизацию плана в отношении ресурсов и сроков. Сетевой график, построенный по методу «вершина – работа», предоставляет все возможности применения прикладных методов оптимизации.
Глоссарий разработки сетевого графика
Построение сетевого графика методологически основано на общей концепции СПУ (системы планирования и управления) проектов. Ключевые аспекты данной методологии были рассмотрены в статье на тему сетевого планирования проекта. В настоящем материале мы развиваем начатое осмысление теоретических и прикладных вопросов сетевого моделирования. В первую очередь, нас интересует разработка сетевой диаграммы вида «вершина – работа» в контексте ее составления, оптимизации и корректировки. Логика сетевого планирования достаточно проста, математически метод не сложен.
Тем не менее, на практике применить полноценно эту модель удается не всегда. Возникают затруднения, во многом определяемые психологией участников, не готовых объективно рассчитать сроки исполнения сформулированных задач. Данный метод дает более слабый результат в условиях перегруженности ответственных ресурсов по проектным задачам. Сетевые графики хорошо работают в проектах, где ответственные исполнители заняты только на одном проекте, например, в строительстве. Ниже показана модель процесса календарного планирования, которая служит направляющим ориентиром в работе со средством планирования «сетевой график».

Схема разработки календарного плана проекта
Введем основные понятия, которые понадобятся для составления сетевой модели проекта и ее оптимизации:
- отношение предшествования – это характеристика связи последующей работы в отношении предшествующей;
- путь – это непрерывная последовательность операций (работ) в сетевом графике;
- предшествующий путь – участок полного пути от исходного до рассматриваемого события;
- последующий путь – участок полного пути от рассматриваемого события до любого следующего;
- критический путь – это полный путь, характеризуемый нулевым резервом;
- критическая работа – действие, для которого полный резерв имеет нулевое значение;
- предкритическая работа – операция, для которой менеджер проекта установил число предельного значения полного резерва;
- резерв пути – разница между временной длительностью проекта и длиной пути на графике;
- веха – работа с нулевой продолжительностью, обозначает важное, значимое событие в проекте;
- минимальное время от начала проекта до начала выполнения операции без нарушения отношения предшествования называется ранним сроком начала работы;
- максимальное время с начала проекта до начала выполнения операции, которое позволяет проекту закончиться вовремя без нарушения отношения предшествования, называется поздним сроком начала работы;
- минимальное время, которое требуется для выполнения всех работ без нарушения отношения предшествования, называется ранним окончанием проекта;
- возобновляемый ресурс предполагает ограничение в использовании его на каждом шаге планируемого периода;
- невозобновляемый ресурс предполагает ограничение в использовании его на всем периоде реализации проекта.
Базовый алгоритм и виды связей сетевого графика
Сетевой график позволяет увидеть структуру работ, представить все этапы и взаимосвязи с требуемой степенью детализации. На его основе производится разработка обоснованного плана мероприятий с учетом более эффективного использования ресурсов по заданным критериям. Диаграмма позволяет производить поливариантный анализ альтернативных решений для улучшения календарного плана с использованием компьютерных технологий. Вспомним основные правила построения сетевой модели метода «вершина – работа».
- Элементы сетевого графика включают работы и зависимости (связи) между ними. События на графике не отражаются за исключением вех, представляющих собой основные наиболее важные события, изображаемых в форме «ромбиков», работ с нулевой продолжительностью.
- Работа представляет собой неделимый элемент процесса, требующий времени и других ресурсов для выполнения, изображается в виде прямоугольника, вытянутого по горизонтали. Исходя из этого правила, длина прямоугольника может свидетельствовать о продолжительности операции.
- Разработка графика начинается с размещения на нем исходной работы в крайней левой точке и завершается включением в него конечной операции, закрывающей проект. Календарно начальный момент исходного действия обозначает старт проекта.
- Зависимости (связи) между работами оформляются стрелками, направленными слева направо под разными углами наклона. На основе данного правила связи между операциями определяются одной из форм отношений зависимости.
- Сетевой график имеет только одну работу, в которую входят зависимости, но не выходит ни одна, и одну работу, не имеющей ни одной входящей зависимости.
- Сетевой график не может иметь циклов, т.е. зависимости не должны связывать работы по кругу.

Вид сетевого графика метода «вершина – работа»
Сетевой график строится по следующему алгоритму составления.
- На диаграмме размещается начальная работа проекта, не имеющая предшественников.
- Расположение операции, непосредственно следующей за работой, связанной с ней отношением предшествования, на графике левее предыдущей. Отображение связи предшествования.
- Переход к пункту 2 до тех пор, пока не закончатся работы, имеющие предшественников.
Разработка сетевой диаграммы производится с учетом возможных связей между работами. Основные виды отношений предшествования используются в четырех вариантах связей и в двух дополнительных их разновидностях. Далее на схеме представлены варианты связи следующей по идентификационному номеру работы к предыдущей или, наоборот, последующей. Основные или базовые виды предшествования связаны с перестановками слов «начало» и «окончание»:
- «окончание – начало» (простой вид отношения предшествования);
- «окончание – окончание»;
- «начало – начало»;
- «начало – окончание».
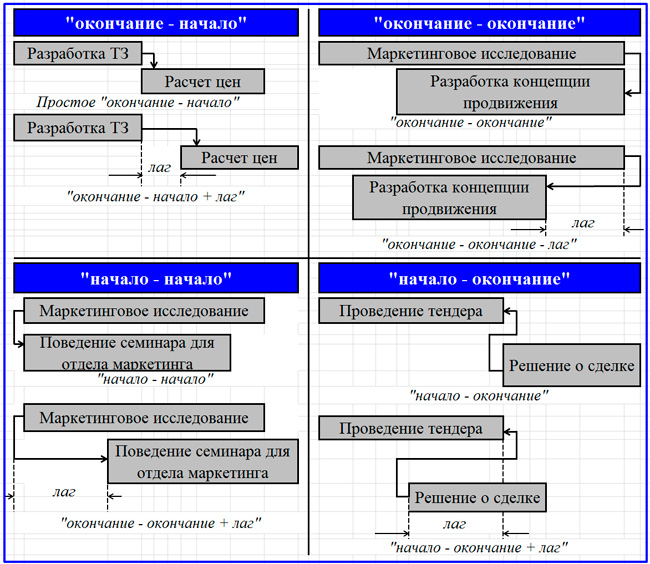
Примеры вариантов отношений предшествования
Методы расчета длительности операций
Для обеспечения построения, анализа и управления расписанием проекта необходимо рассчитать следующие параметры сетевого графика: стоимость, задействованные ресурсы и продолжительность работ. Требуемые ресурсы нужно рассчитать до определения продолжительности операций, так как их длительность во времени, как правило, зависит от состава задействованного ресурсного обеспечения. Кроме того, важно понимать, насколько ресурсы календарно доступны, что, в свою очередь, влияет на сроки работ и их продолжительность. Очевидно, что ключевым параметром выступает именно длительность операций. Для ее оценки используется ряд специальных методов, краткая характеристика которых приведена в табличной форме далее.

Основные методы оценки длительности операций
В случае отсутствия статистических данных по аналогичным операциям и невозможности применить экономико-математические методы расчета часто используют экспертные оценки. У данного метода есть серьезное достоинство – его простота, при условии, что удалось привлечь опытных и объективных экспертов. Но этого достичь бывает нелегко, позиции экспертов по вопросам продолжительности могут оказаться противоположными. Тем не менее, такое положение вещей вполне допустимо при использовании средневзвешенных оценок квалифицированных экспертных мнений.
В разнообразных проектах присутствуют идентичные по природе работы. Например, подготовка устава проекта, разработка ТЗ, проведение тендера по структуре и трудоемкости мало чем отличаются друг от друга. Это свойство используется для оценки длительности по аналогам. В некоторых случаях информацию о параметрах аналогичных работ вполне допустимо использовать для планирования расписания. Для этого схожесть типа и содержания операций должны быть подвергнуты экспертизе.
Параметрическая оценка длительности тесно сопряжена с нормативным подходом. Данный подход задействует такие параметры, в частности, как производительность (объем производства в единицу времени) или выработка. Например, чтобы выполнить монтаж I-го уровня сложности оборудования «А» требуется, допустим, 100 нормо-часов труда специалистов высшей квалификационной категории. Подобного рода мероприятия называют еще работами фиксированного объема, потому что продолжительность их связана с числом выделяемых ресурсов и может быть оценена как объем работ, деленный на количество человеческих ресурсов.
Помимо варианта фиксированного объема отдельно выделяется случай фиксированной продолжительности работы. Примерами таких работ являются действия, связанные с режимом дежурства на объекте, обслуживания оборудования и т.д. Продолжительность в подобных случаях обусловлена длительностью работы обслуживаемого объекта. Для параметрического метода, как мы видим, важно найти параметр, от которого зависит продолжительность операции и причинно-следственные связи, на основе которых возможно определить зависимости параметра от других значений.
Методы оптимизации сетевого графика
Сетевой график проектной реализации связан с содержанием уникальной задачи, параметрами времени и пространства, в которых выполняется проект. Данной деятельности присущи все традиционные функции управления без исключения. С этой точки зрения процесс можно разделить на этапы, в которых весомую долю занимает планирование. Далее вашему вниманию представляется упрощенная блок-схема функциональных этапов управления проектом.
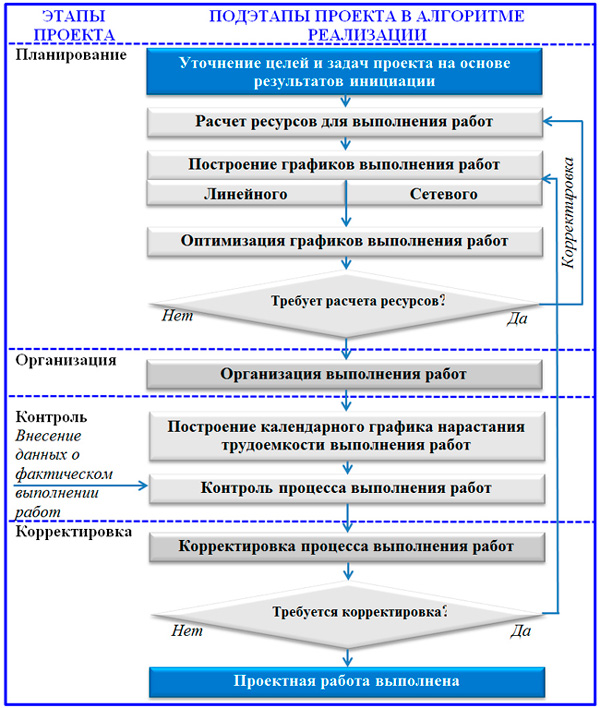
Функционально-процессная блок-схема управления проектом
На текущий момент нас интересует оптимизация сетевого графика как подэтап процесса планирования проектной задачи. Это связано с тем, что после сбора информации о работах и ограничениях разработка визуальной модели в форме сетевой диаграммы подразумевает дальнейшее ее улучшение с использованием методов расчета расписания. Основных методов два: метод критического пути (сокращенно МКП) и анализ расписания по методу PERT.
При использовании МКП производится последовательный расчет наиболее ранних и самых поздних сроков работ по проекту. Далее устанавливается размер полного резерва, при этом критическими работами считаются действия, имеющие нулевой полный резерв. Наконец, рассчитываются временные резервы для выполнения операций, и в качестве самого длинного пути сети выбирается критический путь. Критических путей может быть несколько. Оптимизация сетевого графика методом критического пути применяется для следующих моделей диаграммы:
- для моделей с дискретным и непрерывным временем;
- для моделей с простым отношением предшествования;
- в сетях с обобщенными связями.
Метод оценки и анализа программ (PERT) служит вторым методом, по которому проводится оптимизация сетевого графика. Его основные отличия от МКП основаны на допущении, что длительность работ носит случайный характер, и для целей оценки и анализа сроков следует учитывать неопределенность временного параметра работ проекта. Также делается допущение о независимости всех случайных величин продолжительности критического пути. Для этих целей на основе метода математической статистики и теории вероятности используется β-распределение и оценка параметров распределения с трех экспертных позиций: оптимистичной, пессимистичной и наиболее вероятной.
Корректировка сетевого графика и сокращение общей продолжительности проекта входят в состав ключевых задач проект-менеджера. МКП дает возможность рассчитать оптимальные сроки выполнения проекта, но не позволяет найти инструменты для более действенного сокращения его продолжительности. В этом отношении метод критического пути не обладает достаточной гибкостью. Метод PERT также не лишен недостатков. Во-первых, он нацеливает в основном на оптимистический вариант оценки, во-вторых, PERT в меньшей степени применим к небольшим проектным задачам.
Для эффективной корректировки лучше всего подходят такие современные методы, как метод критической цепи и методы сжатия. Им мы намерены уделить внимание в отдельной статье. Все названные модели и методы являются предметной зоной компетенций PM, владея которыми, менеджеру проще демонстрировать свою эффективность, достигая результата проекта в условиях временных и ресурсных ограничений.
