Каждый менеджер проекта сталкивается с такой типовой для него задачей, как построение сетевого графика. В настоящее время этот процесс полностью автоматизирован и, как правило, у менеджера не возникает больших проблем. Уже давно нет необходимости чертить на бумаге графики, высчитывать ранние и поздние начала или окончания задач, соединять задачи стрелками, вычислять длину критического пути. ИСУП успешно решает все эти задачи.
Однако, без понимания основ и правил построения сетевых графиков менеджеры проектов довольно-таки часто совершают ошибки. Несмотря на то, что современные ИСУП достаточно «умные» и подстраховывают менеджера проекта во многих моментах, связанных с расписанием проекта, тем не менее, остаются «слепые» зоны, которые лежат только в зоне ответственности менеджера проекта.
Для того, чтобы получить настоящую пользу от ИСУП, ей надо уметь грамотно пользоваться, как и любым другим инструментом.
Что такое сетевой график
Сетевой график (англ., Project Network) — это динамическая модель проекта, отражающая зависимость и последовательность выполнения работ проекта, связывающая их завершение во времени с учётом затрат ресурсов и стоимости работ.
Сетевой график может быть построен в двумя способами:
- Вершины графа отображают состояния некоторого объекта (например, строительства), а дуги — работы, ведущиеся на этом объекте.
- Вершины графа отражают работы, а связи между ними — зависимости между работами.
Правила построения сетевого граифка
Прежде всего, построение сетевого графика заключается в правильном соединении между собой событий (на схеме обозначаются кружками) с помощью работ (на схеме обозначаются стрелками). Правильность соединения стрелок заключается в следующем:
- каждая работа в сетевом графике должна выходить из события, которое означает окончание всех работ, результат которых необходим для начала работы;
- событие, обозначающее начало определенной работы не должно включать в себя результаты работ, завершение которых не требуется для начала этой работы;
- сетевой график строится слева направо, и каждое событие с большим порядковым номером должно быть расположено правее предыдущего. Стрелки, изображающие работы, должны также располагаться слева направо.
Исходные работы
Построение графика начинается с изображения работ, не требующих для своего начала результатов выполнения других работ. Такие работы можно назвать исходными, так как все остальные работы комплекса будут выполняться только после их полного выполнения.
В зависимости от специфики планируемого комплекса, исходных работ может быть несколько, а может быть только одна. Размещая исходные работы необходимо учитывать, что на сетевом графике, должно быть только одно исходное событие.
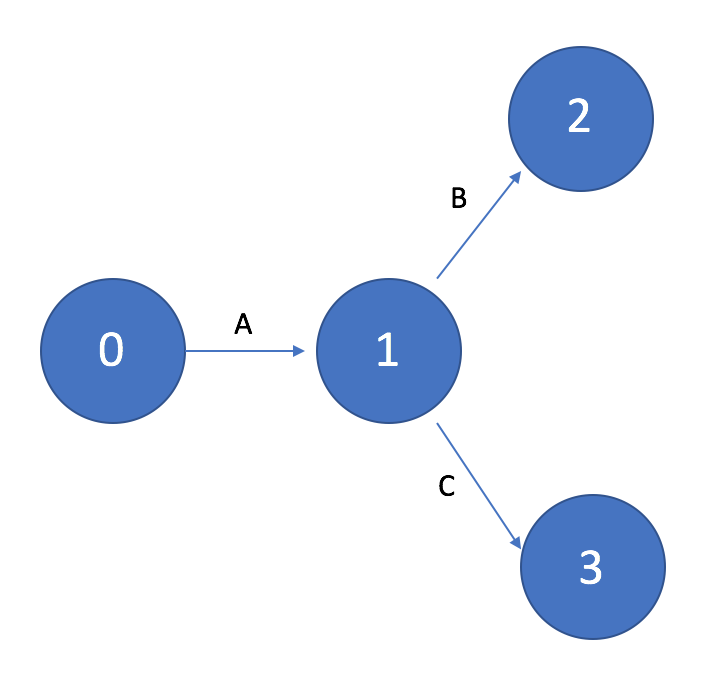
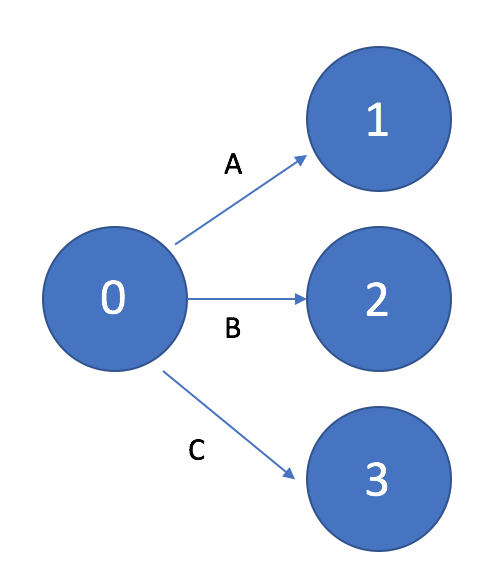
На рисунке 1 показан пример начала сетевого графика с одной исходной работой (работа A), а на рисунке 2 пример начала сетевого графика с тремя исходными работами (работы A, B, C).
Последовательные работы
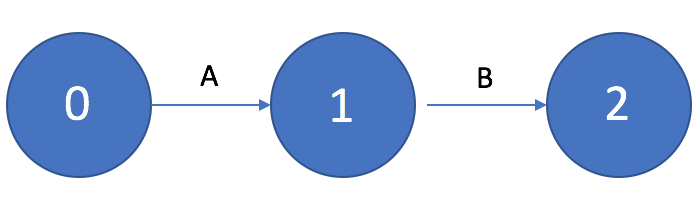
Если работа B должна выполняться только после выполнения работы A, то на графике это изображается в виде последовательной цепочки работ и событий.
Работы, выполняемые после одной и той же работы
Если для выполнения нескольких работ, например, B и C необходим результат одной и той же работы A, то на графике это изображается «параллельными» стрелками, выходящими из события, являющегося результатом выполнения работы А.
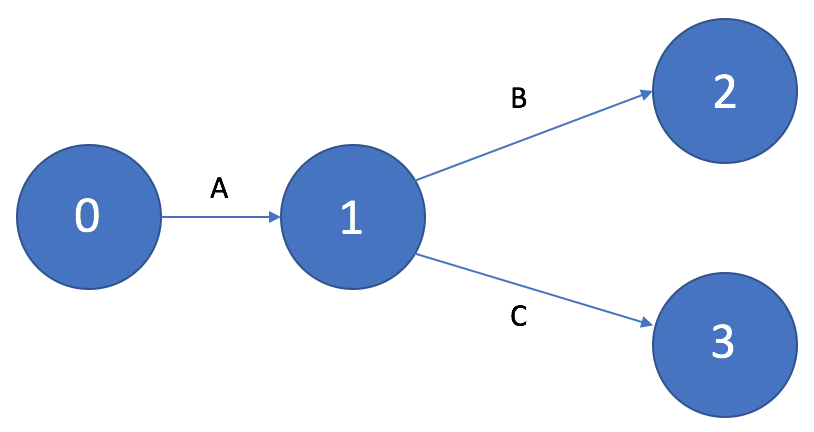
Работа, выполняемая после нескольких работ
Если для выполнения работы C необходим результат работ A и B, то на графике это изображается «параллельными» стрелками, входящими в событие, после достижения которого следует работа C.
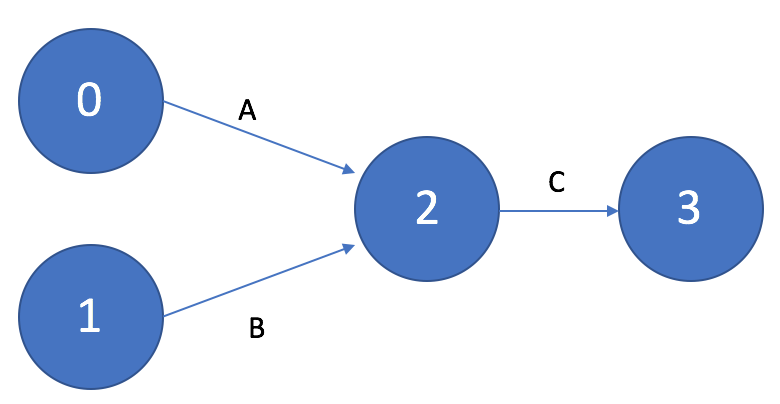
Работы, выполняемые после частичного выполнения других работ
Если для выполнения работ B и C необходим промежуточный результат работы A, то работа A разбивается на подзадачи таким образом, чтобы первая ее подзадача (A1) выполнялась до получения промежуточного результата, необходимого для начала работы B, а вторая подзадача выполнялась до получения промежуточного результата, необходимого для начала работы C, последующая же часть A3, может выполняться параллельно с работами A1 и A2.
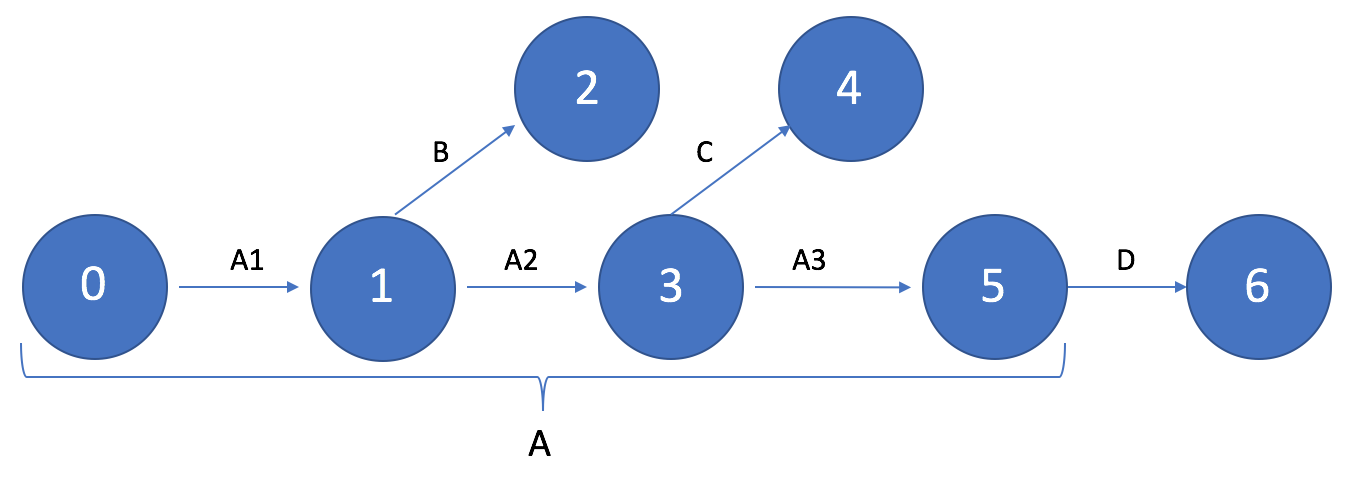
Работы, имеющие общие начальное и конечное события
Два соседних события могут быть объединены одной и только одной работой. Для изображения параллельных работ на сетевом графике вводится так называемое промежуточное событие и фиктивная работа.
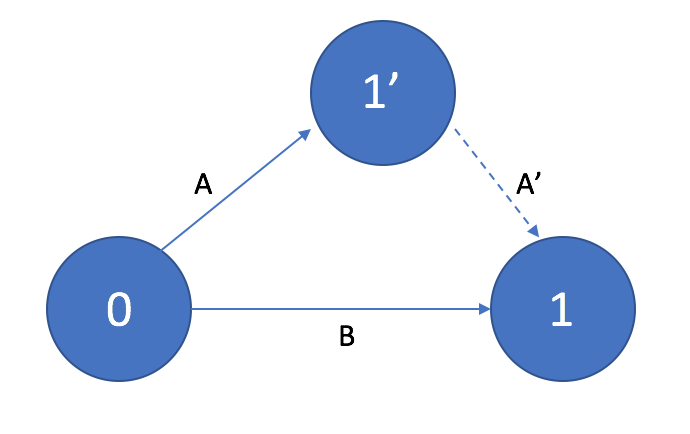
Использование фиктивных работ
Если выполнение работы D возможно только после получения совокупного результата работ A и B, а выполнение работы C – после получения только результата работы А, то в сетевом графике необходимо ввести дополнительное событие и фиктивную работу.
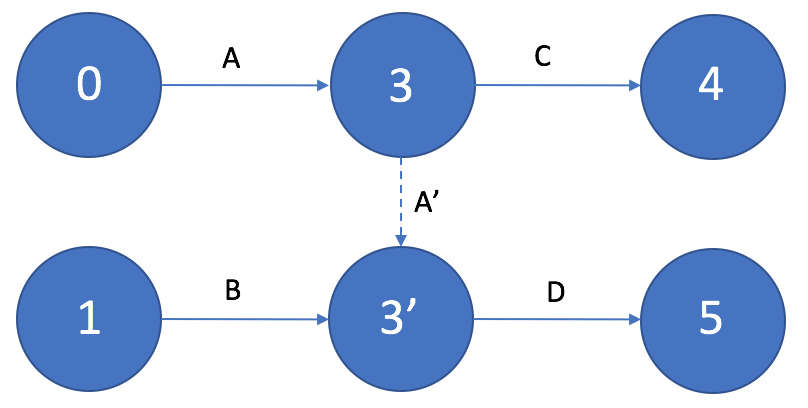
«Хвосты» и «тупики»
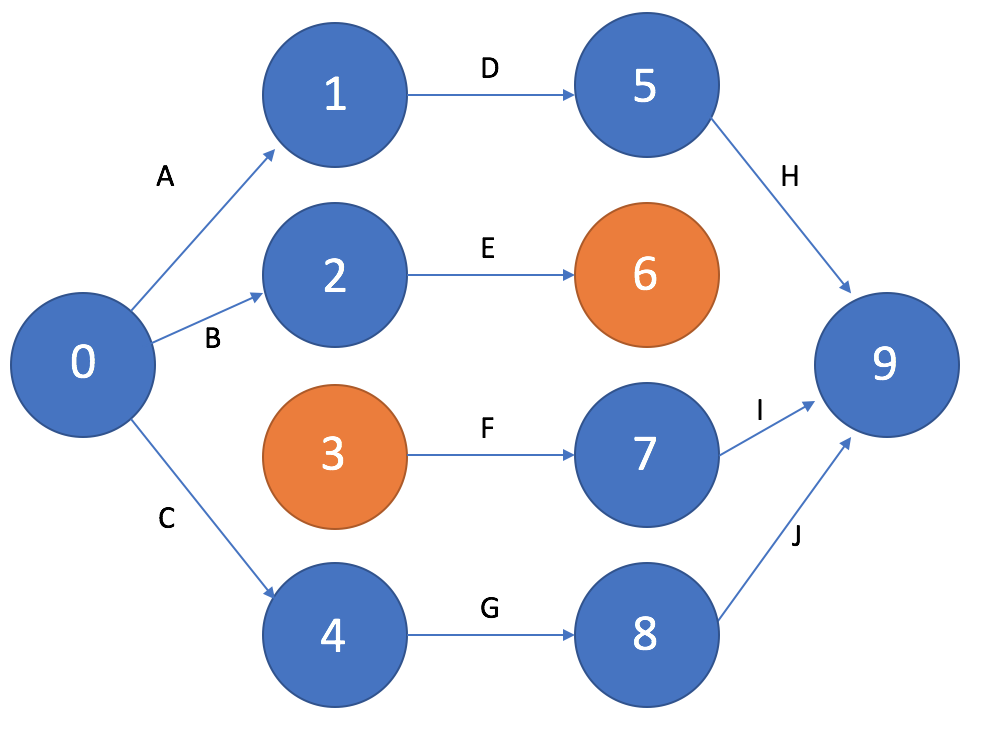
В сети не должно быть «тупиков», т.е. промежуточных событий, из которых не выходит ни одна работа. На рисунке 9 тупиковым событием является событие 6.
Также не должно быть «хвостов», т.е. промежуточных событий, которым не предшествует хотя бы одна работа. На рисунке 9 хвостовым событием является событие 3.
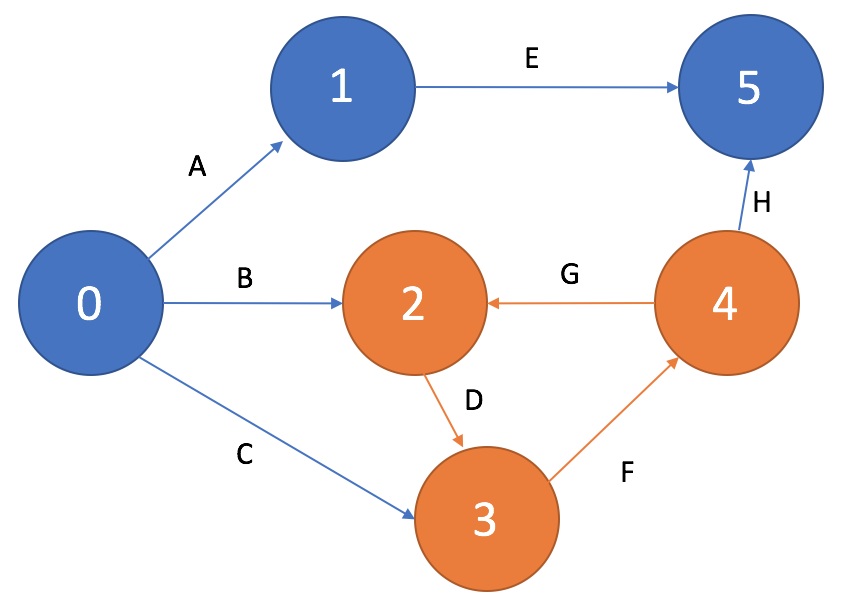
Циклы
На сетевом графике не должно быть циклов, состоящих из взаимосвязанных работ, создающих замкнутую цепь — цепочка работ D->F->G на рисунке 10. Данная ситуация скорее всего свидетельствует об ошибке при составлении перечня работ и определении их взаимосвязей.
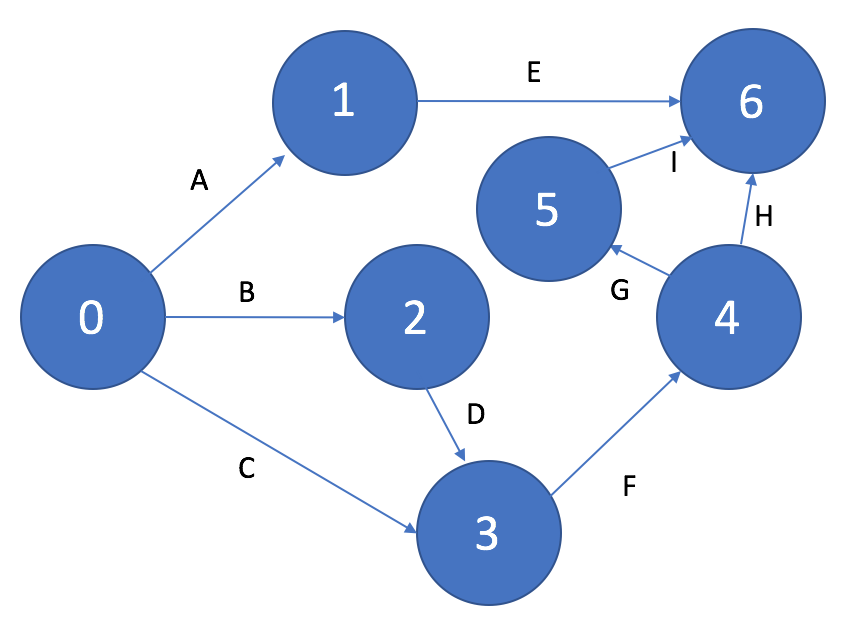
В таком случае необходимо проанализировать исходные данные и в зависимости от сделанных по итогам анализа выводов, либо перенаправить работу создающую цикл в другое событие (если работам, начинающимся в этом событии требуется ее результат, или если она является частью общего результата), либо совсем исключить ее из комплекса (если выявлено, что ее результат не требуется).
На рисунке 11 приведен пример устранения цикла, когда работа G становится частью общего результата.
Именование работ и нумерация событий
Каждая работа в сетевом графике должна определяться однозначно, только ей присущей парой событий, как и не должно быть на графике событий с одинаковыми номерами.
Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 0. Из исходного события вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 1. Затем вычеркивают работы, выходящие из события 1, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 2, и так продолжается до завершающего события.
Просмотры: 72 404
Планирование работы всегда начинается с определения количества задач, ответственных за их исполнение лиц и времени, необходимого для полного завершения. При управлении проектами такие схемы просто необходимы. Во-первых, для того чтобы понимать, какое общее время будет затрачено, во-вторых, чтобы знать, как планировать ресурсы. Именно этим занимаются проектные менеджеры, они в первую очередь осуществляют построение сетевого графика. Пример возможной ситуации рассмотрим далее.

Исходные данные
Руководство рекламного агентства приняло решение о выходе в свет нового рекламного продукта для своих клиентов. Перед сотрудниками фирмы были поставлены такие задачи: рассмотреть идеи рекламных брошюр, привести аргументы в пользу того или иного варианта, создать макет, подготовить проект договора для клиентов и послать всю информацию руководству на рассмотрение. Для информирования клиентов необходимо провести рассылку, расклеить плакаты и обзвонить все фирмы, имеющиеся в базе данных.
Кроме этого, главный руководитель составил детальный план всех необходимых действий, назначил ответственных сотрудников и определил время.
Начнем построение сетевого графика. Пример имеет данные, представленные на следующем рисунке:
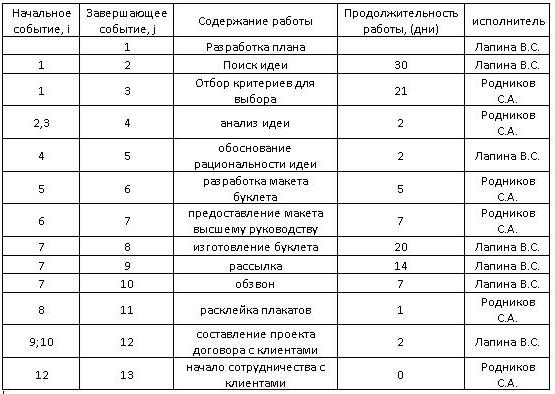
Построение матрицы
Перед тем как сформировать сетевой график, необходимо создать матрицу. Построение графиков начинается с этого этапа. Представим себе систему координат, в которой вертикальные значения соответствуют i (начальное событие), а горизонтальные строки – j (завершающее событие).
Начинаем заполнять матрицу, ориентируясь на данные рисунка 1. Первая работа не имеет времени, поэтому ею можно пренебречь. Рассмотрим детальнее вторую.
Начальное событие стартует с цифры 1 и заканчивается на втором событии. Продолжительность действия равняется 30 дням. Это число заносим в ячейку на пересечении 1 строки и 2 столбца. Аналогичным способом отображаем все данные, что представлено на рисунке ниже.
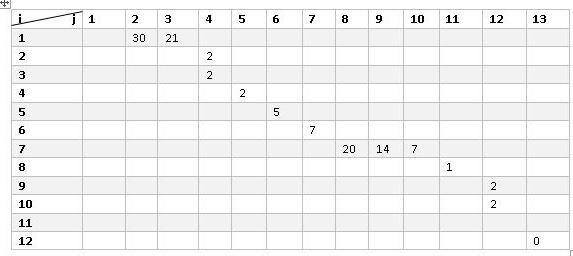
Основные элементы, используемые для сетевого графика
Построение графиков начинается с обозначения теоретических основ. Рассмотрим основные элементы, требующиеся для составления модели:
- Любое событие обозначается кружком, в середине которого находится цифра, соответствующая порядку действий.
- Сама работа – это стрелка, ведущая от одного события к другому. Над стрелкой пишут время, необходимое для ее совершения, а под стрелкой обозначают ответственное лицо.
Работа может выполниться в трех состояниях:
– Действующая – это обыкновенное действие, на совершение которого требуются затраты времени и ресурсов.
– Ожидание – процесс, во время которого ничего не происходит, но он требует затрат времени для перехода от одного события к другому.
– Фиктивная работа – это логическая связь между событиями. Она не требует ни времени, ни ресурсов, но чтобы не прервать сетевой график, ее обозначают пунктирной линией. Например, подготовка зерна и приготовление мешков для него – это два отдельных процесса, они не связаны последовательно, но их связь нужна для следующего события – фасовки. Поэтому выделяют еще один кружочек, который соединяют пунктиром.
Основные принципы построения
Правила построения сетевых графиков заключаются в следующем:
- Все события имеют начало и конец.
- Только к первому событию могут не идти стрелки, и только от последнего они не выходят.
- Все без исключения события должны быть связаны последовательными работами.
- График строится строго слева направо в последовательном порядке.
- Два события может соединять только одна работа. Нельзя ставить две стрелки; если нужно выполнить две работы, то вводят фиктивную с новым событием.
- В сети должны отсутствовать тупики. Нельзя допускать ситуации, указанной на рисунке 3.
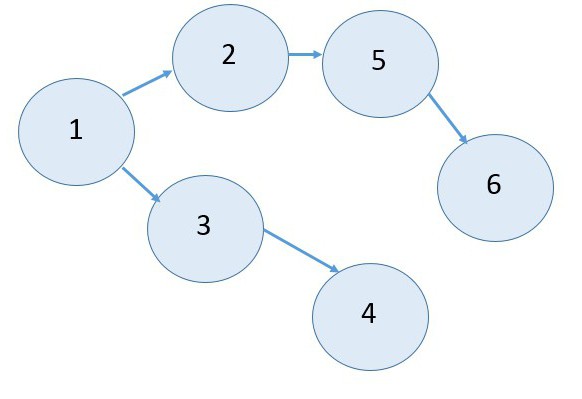
- Нельзя допускать образования циклов и замкнутых контуров.
Построение сетевого графика. Пример
Вернемся к исходному примеру и попробуем начертить сетевой график, используя все данные, указанные ранее.
Начинаем с первого события. Из него выходят два – второе и третье, которые соединяются в четвертом. Далее все идет последовательно до седьмого события. Из него выходят три работы: восьмая, девятая и десятая. Постараемся все отобразить:
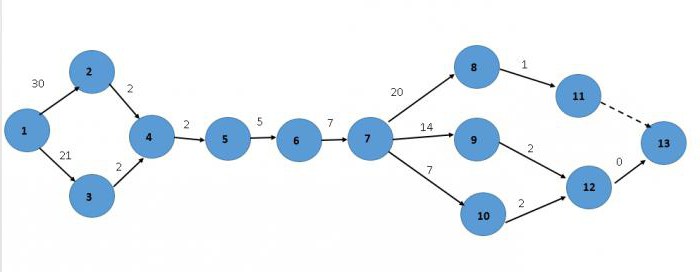
Критические значения
Это еще не все построение сетевого графика. Пример продолжается. Далее нужно рассчитать критические моменты.
Критический путь – это наибольшее время, затраченное на выполнение задания. Для того чтобы его рассчитать, нужно сложить все наибольшие значения последовательных действий. В нашем случае это работы 1-2, 2-4, 4-5, 5-6, 6-7, 7-8, 8-11. Суммируем:
30+2+2+5+7+20+1 = 67 дней
Таким образом, критический путь равен 67 дням.
Если такое время на проект не устраивает руководство, его нужно оптимизировать согласно требованиям.
Автоматизация процесса
На сегодняшний день мало кто из проектных менеджеров вручную рисует схемы. Программа для построения сетевых графиков – это простой и удобный способ быстро рассчитать затраты времени, определить порядок работ и назначить исполнителей.
Кратко рассмотрим самые распространенные программы:
- Microsoft Project 2002 – офисный продукт, в котором очень удобно рисовать схемы. Но проводить расчеты немного неудобно. Для того чтобы совершить даже самое простое действие, нужен немалый багаж знаний. Скачивая программу, позаботьтесь о приобретении инструкции по пользованию к ней.
- SPU v2.2. Очень распространенный бесплатный софт. Вернее, даже не программа, а файл в архиве, для использования которого не нужна установка. Изначально она была разработана для выпускной работы одного студента, но оказалась настолько полезной, что автор выложил ее в сеть.
- NetGraf – еще одна разработка отечественного специалиста из Краснодара. Очень легка, проста в использовании, не требует установки и огромного багажа знаний, как с ней управляться. Плюсом является то, что поддерживает импорт информации из других текстовых редакторов.
- Часто можно встретить вот такой экземпляр – Borghiz. О разработчике мало что известно, как и о том, как пользоваться программой. Но по примитивному методу «тыка» ее можно освоить. Главное, что она работает.
Практика построения сетевого графика


Свежие публикации автора:
Содержание
- 1 Перед стартом моделирования
- 2 Последовательность действий по моделированию
- 2.1 Шаг первый
- 2.2 Шаг второй
- 2.3 Шаг третий
- 2.4 Шаг четвертый
- 3 Дополнительные расчеты модели
- 4 Использование табличного метода
Представим себе ситуацию развития проекта капитального строительства на производственном предприятии. Проект успешно инициирован и полным ходом идут работы по его планированию. Сформирована и утверждена иерархическая структура работ, план по вехам принят. Разработан первичный вариант календарного плана. Поскольку задача оказалась достаточно масштабной, куратор принял решение о разработке еще и сетевой модели. Расчет сетевого графика в прикладном аспекте его исполнения является предметом настоящей статьи.
Перед стартом моделирования
Методологический базис сетевого проектного планирования представлен на нашем сайте несколькими статьями. Я лишь сошлюсь на две из них. Это материалы, посвященные этапу сетевого планирования проекта в целом и непосредственно моделированию сетевого графика проекта. Если в ходе повествования у вас будут возникать вопросы, просмотрите ранее представленные осмысления, основная суть методологии в них изложена. В настоящей статье мы рассмотрим небольшой пример локальной части комплекса строительно-монтажных работ в рамках значительной проектной реализации. Расчеты и моделирование будем выполнять методом «вершина-работа» и классическим табличным способом («вершина-событие») с применением МКР (метода критического пути).
Построение сетевого графика мы начнем на основе первой итерации календарного плана, выполненного в форме диаграммы Ганта. Для целей наглядности предлагаю не учитывать отношения предшествования и максимально упростить последовательность действий. Хотя на практике такое бывает редко, представим в нашем примере, что операции выстроены в последовательность вида «окончание-начало». Ниже вашему вниманию представляются две таблицы: выписка из списка работ проекта (фрагмент из 15-ти операций) и список параметров сетевой модели, необходимый для представления формул.

Пример фрагмента списка операций инвестиционного проекта

Список параметров сетевой модели, подлежащих расчету
Пусть вас не пугает обилие элементов. Построение сетевой модели и расчет параметров достаточно просто выполнить. Важно тщательно подготовиться, иметь под рукой иерархическую структуру работ, линейный график Ганта – в общем, все, что дает возможность определиться с последовательностью и взаимосвязями действий. Еще в первые разы выполнения графика я рекомендую иметь перед собой формулы расчета требуемых значений. Они представлены ниже.

Формулы расчета параметров сетевого графика
Что нам потребуется определить в ходе построения графика?
- Раннее начало текущей работы, в которую входят несколько связей от предыдущих операций. Выбираем максимальное значение из всех ранних окончаний предыдущих операций.
- Позднее окончание текущего действия, из которого выходят несколько связей. Выбираем минимальное значение из всех поздних начал последующих действий.
- Последовательность работ, формирующих критический путь. У этих действий раннее и позднее начала равны, как и раннее и позднее окончание соответственно. Резерв такой операции равен 0.
- Полные и частные резервы.
- Коэффициенты напряженности работ. Логику формул резервов и коэффициента напряженности работы мы рассмотрим в специальном разделе.
Последовательность действий по моделированию
Шаг первый
Построение сетевого графика начинаем путем размещения прямоугольников задач последовательно слева-направо, применяя правила, описанные в предыдущих статьях. При выполнении моделирования методом «вершина-работа» основным элементом диаграммы выступает семисегментный прямоугольник, в составе которого отражены параметры начала, окончания, длительности, резерва времени и наименования или номера операций. Схема представления ее параметров показана далее.

Схема изображения работы на сетевом графике

Результат первого этапа построения сетевого графика
В соответствии с логикой последовательности операций с помощью специализированной программы, MS Visio или любого редактора размещаем образы работ в заданном выше формате. В первую очередь заполняем наименования выполняемых действий, их номера и длительность. Рассчитываем раннее начало и раннее окончание с учетом формулы раннего начала текущего действия в условиях нескольких входящих связей. И так проходим до завершающей фрагмент операции. При этом, в нашем примере проекта тем же графиком Ганта не предусмотрены исходящие связи от операций 11, 12, 13 и 14. «Подвешивать» их на сетевой модели недопустимо, поэтому мы добавляем фиктивные связи к конечной работе фрагмента, выделенные на рисунке синим цветом.
Шаг второй
Находим критический путь. Как известно, это путь, имеющий самую большую продолжительность действий, которые в него входят. Просматривая модель, мы выбираем связи между работами, имеющими максимальные значения раннего окончания действий. Намеченный критический путь выделяем стрелочками красного цвета. Полученный результат представлен на промежуточной схеме далее.

Схема сетевого графика с выделенным критическим путем
Шаг третий
Заполняем значения позднего окончания, позднего начала и полного резерва работ. Для выполнения расчета переходим к конечной работе и берем ее за последнюю операцию критического пути. Это означает, что поздние значения окончания и начала идентичны ранним, и от последней операции фрагмента мы начинаем двигаться в обратную сторону, заполняя нижнюю строку схематического представления действия. Модель выполнения расчета показана ниже на схеме.

Схема расчета поздних начал и окончаний вне критического пути

Итоговый вид сетевого графика
Шаг четвертый
Четвертым шагом алгоритма сетевого моделирования и расчетов выполняется вычисление резервов и коэффициента напряженности. Первым делом имеет смысл обратить внимание на полные резервы путей некритических направлений (R). Они определяются путем вычитания из продолжительности критического пути временной длительности каждого из этих путей, пронумерованных на схеме итогового сетевого графика.
- R пути под номером 1 = 120 – 101 = 19;
- R пути под номером 2 = 120 – 84 = 36;
- R пути под номером 3 = 120 – 104 = 16;
- R пути под номером 4 = 120 – 115 = 5;
- R пути под номером 5 = 120 – 118 = 2;
- R пути под номером 6 = 120 – 115 = 5.
Дополнительные расчеты модели
Выполнение расчета общего резерва текущей операции производится путем вычитания из значения позднего начала раннего начала или из позднего окончания раннего окончания (см. схему расчета выше). Общий (полный) резерв показывает нам возможность начала текущей работы позже или увеличения продолжительности на длительность резерва. Но нужно понимать, что пользоваться полным резервом следует с большой осторожностью, потому что работы, стоящие от текущего события дальше остальных, могут оказаться без запаса времени.
Помимо полных резервов в сетевом моделировании оперируют также и частными или свободными резервами, которые представляют собой разницу между ранним началом последующей работы и ранним окончанием текущей. Частный резерв показывает, есть ли возможность сдвинуть ранее начало операции вперед без ущерба для начала следующей процедуры и всему графику в целом. Следует помнить, что сумма всех частных резервных значений тождественна полному значению резерва для рассматриваемого пути.
Главной задачей выполнения вычислений различных параметров является оптимизация сетевого графика и оценка вероятности выполнения проекта в срок. Одним из таких параметров является коэффициент напряженности, который показывает нам уровень сложности реализовать работу в намеченный срок. Формула коэффициента представлена выше в составе всех расчетных выражений, применяемых для анализа сетевого графика.
Коэффициент напряженности определяется как разница между единицей и частного от деления полного резерва времени работы на разницу длительности критического пути и особого расчетного значения. Это значение включает ряд отрезков критического пути, совпадающих с максимально возможным путем, к которому может быть отнесена текущая операция (i-j). Далее помещен расчет частных резервов и коэффициентов напряженности работ для нашего примера.

Таблица расчета частных резервов и коэффициента напряженности
Коэффициент напряженности варьируется от 0 до 1,0. Значение 1,0 устанавливается для работ, находящихся на критическом пути. Чем ближе значение некритической операции к 1,0, тем труднее удержаться в плановых сроках ее реализации. После того, как значения коэффициента по всем действиям графика посчитаны, операции, в зависимости от уровня этого параметра, могут быть отнесены к категории:
- критической зоны (Кн более 0,8);
- подкретической зоны (Кн более или равно 0,6, но менее или равно 0,8);
- резервной зоны (Кн менее 0,6).
Оптимизация сетевой модели, нацеленная на сокращение общей продолжительности проекта, как правило, обеспечивается следующими мероприятиями.
- Перераспределение ресурсов в пользу наиболее напряженных процедур.
- Снижение трудоемкости операций, расположенных на критическом пути.
- Распараллеливание работ критического пути.
- Переработка структуры сети и состава операций.
Использование табличного метода
Общепризнанные ПП календарного планирования (MS Project, Primavera Suretrack, OpenPlan и т.п.) способны вычислять ключевые параметры сетевой модели проекта. Мы же в настоящем разделе табличным методом выполним настройку подобного расчета обычными средствами MS Excel. Для этого возьмем наш пример фрагмента проектных операций проекта в области СМР. Расположим основные параметры сетевого графика в столбах электронной таблицы.

Модель расчета параметров сетевого графика табличным способом
Преимуществом выполнения расчетов табличным способом является возможность простой автоматизации вычислений и избежание массы ошибок, связанных с человеческим фактором. Красным цветом будем выделять номера операций, располагающихся на критическом пути, а синим цветом отметим расчетные позиции частных резервов, превышающих нулевое значение. Разберем пошагово расчет параметров сетевого графика по основным позициям.
- Ранние начала операций, следующих за текущей работой. Алгоритм расчета настраиваем на выбор максимального значения из раннего времени окончания нескольких альтернативных предыдущих действий. Взять, например, операцию под номером 13. Ей предшествуют работы 6, 7, 8. Из трех ранних окончаний (71, 76, 74 соответственно) нам нужно выбрать максимальное значение – 76 и проставить его в качестве раннего начала операции 13.
- Критический путь. Выполняя процедуру расчета по пункту 1 алгоритма, мы доходим до конца фрагмента, найдя значение продолжительности критического пути, которая в нашем примере составила 120 дней. Значения наибольших ранних окончаний среди альтернативных действий обозначают операции, лежащие на критическом пути. Отмечаем эти операции красным цветом.
- Поздние окончания операций, предшествующих текущей работе. Начиная с концевой работы начинаем движение в обратную сторону от действий с большими номерами к операциям с меньшими. При этом из нескольких альтернатив исходящих работ выбираем наименьшее знание позднего начала. Поздние начала вычисляем как разницу между выбранными значениями поздних окончаний и продолжительности операций.
- Резервы операций. Вычисляем полные (общие) резервы как разницу между поздними началами и ранними началами либо между поздними окончаниями и ранними окончаниями. Значения частных (свободных) резервов получаем в результате вычитания из числа раннего начала следующей операции раннего окончания текущей.
Мы рассмотрели практические механизмы составления сетевого графика и расчета основных параметров временной продолжительности проекта. Таким образом, вплотную приблизились к исследованию возможностей анализа, проводимого с целью оптимизации сетевой модели и формирования непосредственно плана действий по улучшению ее качества. Настоящая тема занимает немного места в комплексе знаний проект-менеджера и не так уж и сложна для восприятия. Во всяком случае, каждый РМ обязан уметь воспроизводить визуализацию графика и выполнять сопутствующие расчеты на хорошем профессиональном уровне.
2.2. Практическое занятие по структурному планированию
Целью занятия является получение навыков составления сетевых графиков, расчета раннего и позднего времени начала работ, нахождения критического пути.
Форма занятия – практическое занятие с использованием рабочей тетради.
Продолжительность – два академических часа.
2.2.1. Пример составления и расчета сетевого графика
Предположим, что мы составляем проект Внедрение бухгалтерской системы для небольшой бухгалтерии, содержащей порядка 10 рабочих мест.
Этап 1. Составление перечня работ
В результате анализа выделяем перечень работ по проекту и оцениваем их длительность в днях. Результаты заносим в табл.2.4.
| № | Название работы | Длительность |
|---|---|---|
| 1 | Начало проекта | – |
| 2 | Выбор системы | 15 |
| 3 | Приобретение программного обеспечения | 7 |
| 4 | Составление проекта сети | 7 |
| 5 | Приобретение компьютеров и сетевого оборудования | 15 |
| 6 | Обучение администратора и программиста | 30 |
| 7 | Монтаж локальной сети | 20 |
| 8 | Установка ПО на компьютеры | 5 |
| 9 | Установка сетевого ПО, настройка сети | 25 |
| 10 | Ввод начальных данных в информационную базу | 40 |
| 11 | Обучение персонала | 30 |
| 12 | Передача в эксплуатацию | 5 |
| 13 | Конец проекта | – |
Этап 2. Определение взаимосвязей между работами
Для каждой работы из табл.2.4 требуется установить номера тех работ, до окончания которых она не может быть начата. Результат заносится в табл.2.5.
| № | Название работы | Предшественники |
|---|---|---|
| 1 | Начало проекта | – |
| 2 | Выбор системы | 1 |
| 3 | Приобретение программного обеспечения | 2 |
| 4 | Составление проекта сети | 2 |
| 5 | Приобретение компьютеров и сетевого оборудования | 2 |
| 6 | Обучение администратора и программиста | 4 |
| 7 | Монтаж локальной сети | 4; 5 |
| 8 | Установка ПО на компьютеры | 3; 5 |
| 9 | Установка сетевого ПО, настройка сети | 6; 7; 8 |
| 10 | Ввод начальных данных в информационную базу | 9 |
| 11 | Обучение персонала | 9 |
| 12 | Передача в эксплуатацию | 10; 11 |
| 13 | Конец проекта | – |
Этап 3. Составление сетевого графика работ
Каждая из работ табл.2.5 на сетевом графике обозначается кружком, в который заносится ее номер. Кружки соединяются стрелками. Стрелка соответствует одному из чисел столбца Предшественники и соединяет работу-предшественник с работой-последователем. Результат изображен на рис.2.9.
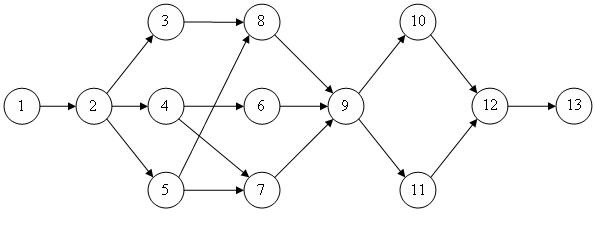
Рис.
2.9.
Сетевой график проекта внедрения бухгалтерской системы
Этап 4. Вычисление раннего времени начала работ
В соответствии со схемой, приведенной на рис.2.2 вычисляем раннее время начала работ с учетом их длительностей из табл.2.4 и связей, задаваемых сетевым графиком на рис.2.9. Вычисления начинаются с первой и заканчиваются последней работой проекта. Последовательность вычислений приведена в табл.2.6. Результат показывает, что длительность проекта равна 122 дня.
| № | Раннее время начала | Длитель-ность | |||
|---|---|---|---|---|---|
| 1 | – | – | – | – | 0 |
| 2 | 1 | 0 | 0 | 0+0 | 0 |
| 3 | 2 | 0 | 15 | 0+15 | 15 |
| 4 | 2 | 0 | 15 | 0+15 | 15 |
| 5 | 2 | 0 | 15 | 0+15 | 15 |
| 6 | 4 | 15 | 7 | 15+7 | 22 |
| 7 |
4 5 |
15 15 |
7 15 |
Max(15 + 7; 15 + 15) |
30 |
| 8 |
3 5 |
15 15 |
7 15 |
Max(15 + 7; 15 + 15) |
30 |
| 9 |
6 7 8 |
22 30 30 |
30 20 5 |
Max(22+30; 30+20; 30+5) |
52 |
| 10 | 9 | 52 | 25 | 52+25 | 77 |
| 11 | 9 | 52 | 25 | 52+25 | 77 |
| 12 |
10 11 |
77 77 |
40 30 |
Max(77+40; 77+30) |
117 |
| 13 | 12 | 117 | 5 | 117+5 | 122 |
Этап 5. Вычисление позднего времени начала работ
Используя длительности работ и сетевой график, вычисляем позднее время начала работ. Вычисления начинаются с последней работы проекта, ведутся в обратном порядке и заканчиваются первой работой. Результаты вычислений приведены в табл.2.7.
| № | Позднее время начала | ||||
|---|---|---|---|---|---|
| 13 | – | – | – | – | 122 |
| 12 | 13 | 122 | 5 | 122-5 | 117 |
| 11 | 12 | 117 | 30 | 117-30 | 87 |
| 10 | 12 | 117 | 40 | 117-40 | 77 |
| 9 |
10 11 |
77 87 |
25 |
Min(77-25; 87-25) |
52 |
| 8 | 9 | 52 | 5 | 52-5 | 47 |
| 7 | 9 | 52 | 20 | 52-20 | 32 |
| 6 | 9 | 52 | 30 | 52-30 | 22 |
| 5 |
7 8 |
32 47 |
15 |
Min(32-15; 47-15) |
17 |
| 4 |
6 7 |
22 32 |
7 |
Min(22-7; 32-7) |
15 |
| 3 | 8 | 47 | 7 | 47-7 | 40 |
| 2 |
3 4 5 |
40 15 17 |
15 |
Min(40-15; 15-15; 17-15 |
0 |
| 1 | 2 | 0 | 0 | 0-0 | 0 |
Этап 6. Вычисление резерва времени работ
Резерв времени равен разнице между поздним и ранним временем начала работ. Занесем в табл.2.8 и значения и разность (резерв).
| Работа № | Раннее время начала | Позднее время начала | Резерв времени |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 |
| 3 | 15 | 40 | 25 |
| 4 | 15 | 15 | 0 |
| 5 | 15 | 17 | 2 |
| 6 | 22 | 22 | 0 |
| 7 | 30 | 32 | 2 |
| 8 | 30 | 47 | 17 |
| 9 | 52 | 52 | 0 |
| 10 | 77 | 77 | 0 |
| 11 | 77 | 87 | 10 |
| 12 | 117 | 122 | 5 |
| 13 | 122 | 122 | 0 |
Этап 7. Нахождение критического пути
Критический путь состоит из работ с нулевым резервом времени. В табл.2.9 они выделены заливкой. Обозначим на сетевом графике критический путь пунктирными стрелками. Результат приведен на pис.2.10.

Рис.
2.10.
Критический путь проекта внедрения информационной системы
2.2.2. Задания для самостоятельного выполнения
Задание 1
Вычислить критический путь по сетевому графику, изображенному на рис.2.9 со значениями длительностей работ, приведенными в табл.2.9.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | – | 60 | 25 | 15 | 30 | 20 | 15 | 70 | 30 | 90 | 20 | 5 | – |
| 2 | – | 30 | 15 | 20 | 25 | 30 | 45 | 45 | 25 | 60 | 40 | 7 | – |
| 3 | – | 44 | 22 | 17 | 34 | 28 | 23 | 64 | 26 | 78 | 32 | 9 | – |
| 4 | – | 24 | 17 | 18 | 26 | 19 | 31 | 69 | 33 | 82 | 15 | 3 | – |
| 5 | – | 36 | 24 | 19 | 25 | 12 | 18 | 55 | 24 | 80 | 22 | 4 | – |
| 6 | – | 57 | 32 | 24 | 18 | 28 | 21 | 59 | 24 | 35 | 27 | 6 | – |
| 7 | – | 29 | 18 | 14 | 37 | 16 | 44 | 38 | 29 | 51 | 22 | 8 | – |
| 8 | – | 37 | 20 | 17 | 18 | 21 | 16 | 40 | 27 | 28 | 30 | 7 | – |
| 9 | – | 18 | 19 | 31 | 30 | 35 | 29 | 38 | 21 | 43 | 19 | 4 | – |
| 10 | – | 21 | 27 | 14 | 34 | 22 | 35 | 30 | 27 | 12 | 40 | 6 | – |
Задание 2
Последовательность работ проекта описывается сетевым графиком, изображенным на рис.2.11. Найти критический путь при условии, что длительности работ заданы одним из вариантов в табл.2.10.
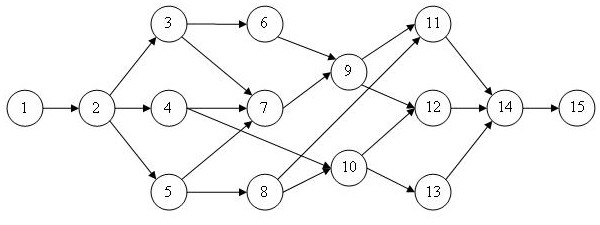
Рис.
2.11.
Сетевой график для задания 2
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | – | 4 | 7 | 8 | 6 | 4 | 6 | 5 | 3 | 7 | 5 | 4 | 3 | 2 | – |
| 2 | – | 7 | 10 | 8 | 9 | 7 | 5 | 6 | 5 | 3 | 4 | 3 | 5 | 5 | – |
| 3 | – | 3 | 6 | 4 | 7 | 5 | 4 | 5 | 4 | 6 | 3 | 6 | 7 | 4 | – |
| 4 | – | 2 | 2 | 3 | 2 | 4 | 4 | 5 | 4 | 3 | 3 | 4 | 5 | 7 | – |
| 5 | – | 7 | 6 | 5 | 4 | 4 | 5 | 6 | 7 | 5 | 5 | 8 | 6 | 3 | – |
| 6 | – | 5 | 7 | 6 | 7 | 8 | 9 | 8 | 9 | 9 | 7 | 6 | 6 | 5 | – |
| 7 | – | 4 | 4 | 5 | 6 | 6 | 5 | 4 | 5 | 5 | 7 | 6 | 8 | 5 | – |
| 8 | – | 7 | 5 | 4 | 3 | 3 | 4 | 5 | 4 | 4 | 2 | 3 | 2 | 2 | – |
| 9 | – | 2 | 3 | 4 | 5 | 7 | 3 | 5 | 6 | 4 | 6 | 8 | 7 | 4 | – |
| 10 | – | 4 | 7 | 3 | 2 | 7 | 5 | 4 | 7 | 2 | 4 | 7 | 10 | 6 | – |
Задание 3
Для проекта Ремонт квартиры выполнить следующие действия:
- самостоятельно составить перечень работ (не менее 15);
- самостоятельно оценить длительность этих работ;
- самостоятельно определить последовательность выполнения работ;
- построить сетевой график;
- выполнить расчет раннего и позднего времени начала работ, найти критический путь.
