В
сетевой модели должна отражаться
технологическая последовательность и
очерёдность отдельных работ. Модель
должна иметь простую форму. Стрелки
должны быть направлены слева направо
от события с меньшим номером к событию
с большим номером, необходимо стремиться
к минимальному пересечению отдельных
работ.
2.1. Основные правила
1.
Правило составных работ – любая работа
а
может быть разбита на составляющие,
если после частичного выполнения её
можно начать следующую работу б.
При этом вводятся логические зависимости
и дополнительные события (рис. 4).
2.
Правило параллельных работ – если между
двумя событиями необходимо показать
две или несколько работ, которые
выполняются параллельно, в модели
вводятся дополнительное событие по
окончании одной из параллельных работ
и логическая зависимость (фиктивная
работа) между ними (рис. 5).
3
Правило зависимых и независимых работ
– если для начала одной работыг
необходимо выполнение всех пред-шествующих
работ a
и б,
а для начала работы в
необходимо выполнение только работы
a,
то вводятся дополнительное событие и
логическая зависимость (рис. 6).
4.
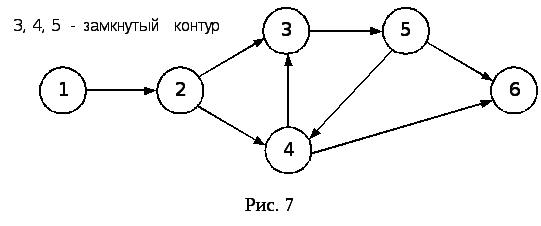
Правило запрещения замкнутых контуров,
т.е. один путь не должен дважды проходить
через одно событие (рис. 7).
5
Правило запрещения тупиковых событий,
т.е. событий, из которых не выходит
ни одна работа, если событие не завершающее
(рис. 8).
6.
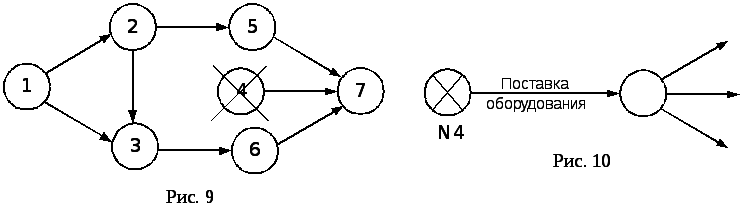
Правило запрещения необеспеченных
событий, т.е. со- бытий, в которые не
входит ни одна работа, если событие не
исходное (рис. 9).
7.
Правило изображения поставки (рис. 10).
2.2. Построение сетей
Для
построения сетевой модели нужно знать
технологию работ и зависимость одних
работ от других. Последовательность
выполнения работ записывается в форме
таблицы, в которой указывается зависимость
данной работы ig
от предшествующей hi.
Пример
1.
По данной зависимости работ построить
сетевую модель.
-
Предшествующая
работа hiДанная
работа
ig–
a
a
б
б
в
б
г
б
д
Решение.
В данном примере работа a
не зависит ни от каких работ, значит,
она является исходной. Работа б
зависит от работы a,
поэтому она начинается после окончания
работы a.
Работы в,
г, д
зависят от работы б,
значит, они начинаются после окончания
работы б.
Больше никаких исходных данных
нет, следовательно, работами в,
г, д
завершается модель и они выполняются
параллельно. Используя правила построения
сетевых моделей, строим модель (рис.
11).
Пример
2 .
По заданной зависимости работ построить
сетевую модель.
|
hi |
ij |
|
– |
а |
|
– |
б |
|
a |
в |
|
a |
г |
|
бв |
д |
Решение.
Работы a
и б
не зависят ни от одной работы, значит,
они выходят из исходного события. Работы
в
и
г
зависят от работы a,
поэтому они начинаются после окончания
работы a,
т.е. выходят из конечного события работы
a.
Работа д
зависит от двух работ б
и в,
значит, работа д
начинается после окончания работ б
и в.
От работ г
и д
по условию не зависит ни одна работа,
следовательно, они завершают сетевую
модель (рис. 12).
Пример
3 .
По заданной зависимости работ построить
сетевую модель.
|
hi |
ij |
|
– |
а |
|
– – |
б в |
|
абв |
г |
|
бв |
д |
|
в |
е |
Решение.
Работы а,
б,
в
не зависят ни от одной работы, значит,
они выходят из исходного события. Работа
г
зависит от трёх работ а,
б,
в,
поэтому она начинается только после их
окончания (рис. 13).

13
Работа
е
начинается после окончания работы в.
Работа
д
зависит
от двух работ б
и в,
поэтому начинается после их окончания
(рис. 14).
От
работ г,
д, е
не зависят никакие работы, следовательно,
они завершают модель (рис. 15).
Соседние файлы в папке методички
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Планирование работы всегда начинается с определения количества задач, ответственных за их исполнение лиц и времени, необходимого для полного завершения. При управлении проектами такие схемы просто необходимы. Во-первых, для того чтобы понимать, какое общее время будет затрачено, во-вторых, чтобы знать, как планировать ресурсы. Именно этим занимаются проектные менеджеры, они в первую очередь осуществляют построение сетевого графика. Пример возможной ситуации рассмотрим далее.
Исходные данные
Руководство рекламного агентства приняло решение о выходе в свет нового рекламного продукта для своих клиентов. Перед сотрудниками фирмы были поставлены такие задачи: рассмотреть идеи рекламных брошюр, привести аргументы в пользу того или иного варианта, создать макет, подготовить проект договора для клиентов и послать всю информацию руководству на рассмотрение. Для информирования клиентов необходимо провести рассылку, расклеить плакаты и обзвонить все фирмы, имеющиеся в базе данных.
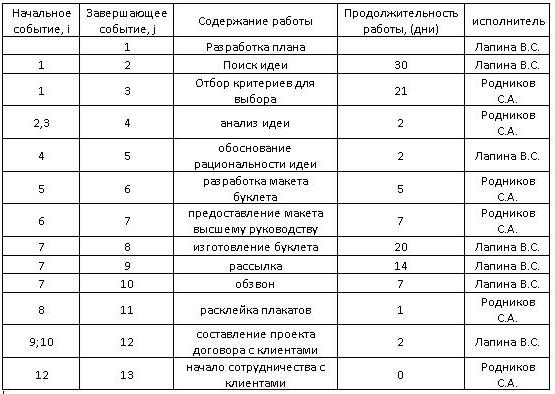
Кроме этого, главный руководитель составил детальный план всех необходимых действий, назначил ответственных сотрудников и определил время.
Начнем построение сетевого графика. Пример имеет данные, представленные на следующем рисунке:
Построение матрицы
Перед тем как сформировать сетевой график, необходимо создать матрицу. Построение графиков начинается с этого этапа. Представим себе систему координат, в которой вертикальные значения соответствуют i (начальное событие), а горизонтальные строки – j (завершающее событие).
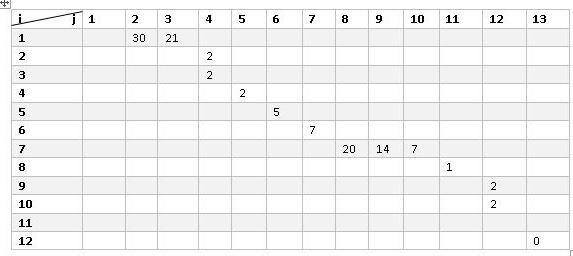
Начинаем заполнять матрицу, ориентируясь на данные рисунка 1. Первая работа не имеет времени, поэтому ею можно пренебречь. Рассмотрим детальнее вторую.
Начальное событие стартует с цифры 1 и заканчивается на втором событии. Продолжительность действия равняется 30 дням. Это число заносим в ячейку на пересечении 1 строки и 2 столбца. Аналогичным способом отображаем все данные, что представлено на рисунке ниже.
Основные элементы, используемые для сетевого графика
Построение графиков начинается с обозначения теоретических основ. Рассмотрим основные элементы, требующиеся для составления модели:
- Любое событие обозначается кружком, в середине которого находится цифра, соответствующая порядку действий.
- Сама работа – это стрелка, ведущая от одного события к другому. Над стрелкой пишут время, необходимое для ее совершения, а под стрелкой обозначают ответственное лицо.
Работа может выполниться в трех состояниях:
– Действующая – это обыкновенное действие, на совершение которого требуются затраты времени и ресурсов.
– Ожидание – процесс, во время которого ничего не происходит, но он требует затрат времени для перехода от одного события к другому.
– Фиктивная работа – это логическая связь между событиями. Она не требует ни времени, ни ресурсов, но чтобы не прервать сетевой график, ее обозначают пунктирной линией. Например, подготовка зерна и приготовление мешков для него – это два отдельных процесса, они не связаны последовательно, но их связь нужна для следующего события – фасовки. Поэтому выделяют еще один кружочек, который соединяют пунктиром.
Основные принципы построения
Правила построения сетевых графиков заключаются в следующем:
- Все события имеют начало и конец.
- Только к первому событию могут не идти стрелки, и только от последнего они не выходят.
- Все без исключения события должны быть связаны последовательными работами.
- График строится строго слева направо в последовательном порядке.
- Два события может соединять только одна работа. Нельзя ставить две стрелки; если нужно выполнить две работы, то вводят фиктивную с новым событием.
- В сети должны отсутствовать тупики. Нельзя допускать ситуации, указанной на рисунке 3.
- Нельзя допускать образования циклов и замкнутых контуров.
Построение сетевого графика. Пример
Вернемся к исходному примеру и попробуем начертить сетевой график, используя все данные, указанные ранее.
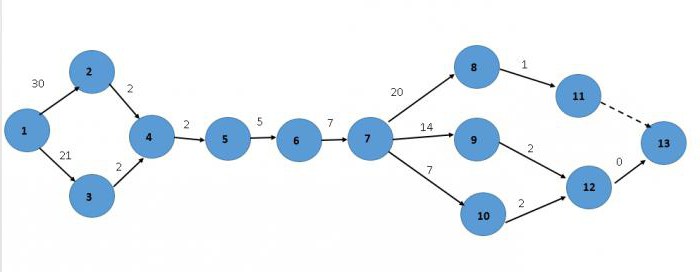
Начинаем с первого события. Из него выходят два – второе и третье, которые соединяются в четвертом. Далее все идет последовательно до седьмого события. Из него выходят три работы: восьмая, девятая и десятая. Постараемся все отобразить:
Критические значения
Это еще не все построение сетевого графика. Пример продолжается. Далее нужно рассчитать критические моменты.
Критический путь – это наибольшее время, затраченное на выполнение задания. Для того чтобы его рассчитать, нужно сложить все наибольшие значения последовательных действий. В нашем случае это работы 1-2, 2-4, 4-5, 5-6, 6-7, 7-8, 8-11. Суммируем:
30+2+2+5+7+20+1 = 67 дней
Таким образом, критический путь равен 67 дням.
Если такое время на проект не устраивает руководство, его нужно оптимизировать согласно требованиям.
Автоматизация процесса
На сегодняшний день мало кто из проектных менеджеров вручную рисует схемы. Программа для построения сетевых графиков – это простой и удобный способ быстро рассчитать затраты времени, определить порядок работ и назначить исполнителей.
Кратко рассмотрим самые распространенные программы:
- Microsoft Project 2002 – офисный продукт, в котором очень удобно рисовать схемы. Но проводить расчеты немного неудобно. Для того чтобы совершить даже самое простое действие, нужен немалый багаж знаний. Скачивая программу, позаботьтесь о приобретении инструкции по пользованию к ней.
- SPU v2.2. Очень распространенный бесплатный софт. Вернее, даже не программа, а файл в архиве, для использования которого не нужна установка. Изначально она была разработана для выпускной работы одного студента, но оказалась настолько полезной, что автор выложил ее в сеть.
- NetGraf – еще одна разработка отечественного специалиста из Краснодара. Очень легка, проста в использовании, не требует установки и огромного багажа знаний, как с ней управляться. Плюсом является то, что поддерживает импорт информации из других текстовых редакторов.
- Часто можно встретить вот такой экземпляр – Borghiz. О разработчике мало что известно, как и о том, как пользоваться программой. Но по примитивному методу «тыка» ее можно освоить. Главное, что она работает.
Содержание
Введение
1. Сетевое планирование
1.1 Понятие сетевого планирования
1.2 Основные понятия сетевого планирования
1.3 Правила построения сетевых моделей
1.4 Направления применения сетевого планирования
2. История сетевого планирования
2.1 Зарубежный опыт
2.2 Сетевое планирование в России
3. Методы сетевого планирования
3.1 Диаграмма Ганта
3.2 Метод критического пути (МКП)
3.3 Метод статистических испытаний (метод Монте-Карло)
3.4 Метод оценки и пересмотра планов (ПЕРТ, PERT)
3.5 Метод графической оценки и анализа (GERT)
3.6 Дополнительные методы расчета сетевого графика
Заключение
Использованная литература и источники
Приложения
Введение
Планирование и управление комплексом работ по проекту представляет собой сложную и, как правило, противоречивую задачу. Оценка временных и стоимостных параметров функционирования системы, осуществляемая в рамках этой задачи, производится различными методами. Среди существующих большое значение имеет метод сетевого планирования.
Сетевое планирование — метод анализа сроков (ранних и поздних) начала и окончания нереализованных частей проекта, позволяет увязать выполнение различных работ и процессов во времени, получив прогноз общей продолжительности реализации всего проекта.
Методы сетевого планирования:
v Детерминированные сетевые методы
· Диаграмма Ганта с дополнительным временным люфтом 10-20 %
· Метод критического пути (МКП)
v Вероятностные сетевые методы
Неальтернативные
· Метод статистических испытаний (метод Монте-Карло)
· Метод оценки и пересмотра планов (ПЕРТ, PERT)
Альтернативные
v Метод графической оценки и анализа (GERT)
Методы сетевого планирования могут широко и успешно применяются для оптимизации планирования и управления сложными разветвленными комплексами работ, которые требуют участия большого числа исполнителей и затрат ограниченных ресурсов.
Следует отметить, что главной целью сетевого планирования является сокращение до минимума продолжительности проекта, таким образом, использование сетевых моделей обусловлено необходимостью грамотного управления крупными народнохозяйственными комплексами и проектами, научными исследованиями, конструкторской и технологической подготовкой производства, новых видов изделий, строительством и реконструкцией, капитальным ремонтом основных фондов и т.п.
С помощью сетевой модели руководитель работ или операции может системно и масштабно представлять весь ход работ или оперативных мероприятий, управлять процессом их осуществления, а также маневрировать ресурсами.
Можно выделить следующие задачи:
1) Рассмотреть понятие сетевого планирования.
2) Выделить основные понятия сетевого планирования.
3) Изучить правила построения сетевых моделей.
4) Определить направления применения сетевого планирования.
5) Изучить история сетевого планирования, как в зарубежных странах, так и в России
6) Разобрать такие методы сетевого планирования, как диаграмма Ганта, метод критического пути, метод Монте-Карло, метод оценки и пересмотра планов (PERT), метод графической оценки и анализа (GERT), а так же дополнительные методы расчета сетевого графика.
1. Сетевое планирование
1.1 Понятие сетевого планирования
Сетевое планирование это метод управления, который основывается на использовании математического аппарата теории графов и системного подхода для отображения и алгоритмизации комплексов взаимосвязанных работ, действий или мероприятий для достижения четко поставленной цели.
Сетевое планирование позволяет определить, во-первых, какие работы или операции из числа многих, составляющих проект, являются “критическими” по своему влиянию на общую календарную продолжительность проекта и, во-вторых, каким образом построить наилучший план проведения всех работ по данному проекту с тем, чтобы выдержать заданные сроки при минимальных затратах.
Сетевое планирование основываются на разработанных практически одновременно и независимо методе критического пути МКП (СРМ — Critical Path Method) и методе оценки и пересмотра планов ПЕРТ (PERT — Program Evaluation and Review Technique).
Методы сетевого планирования применяются для оптимизации планирования и управления сложными разветвленными комплексами работ, требующими участия большого числа исполнителей и затрат ограниченных ресурсов.
Основная цель сетевого планирования – сокращение до минимума продолжительности проекта.
Задача сетевого планирования состоит в том, чтобы графически, наглядно и системно отобразить и оптимизировать последовательность и взаимозависимость работ, действий или мероприятий, обеспечивающих своевременное и планомерное достижение конечных целей. Для отображения и алгоритмизации тех или иных действий или ситуаций используются экономико-математические модели, которые принято называть сетевыми моделями, простейшие из них – сетевые графики. С помощью сетевой модели руководитель работ или операции имеет возможность системно и масштабно представлять весь ход работ или оперативных мероприятий, управлять процессом их осуществления, а также маневрировать ресурсами.
Важная особенность СПУ (сетевого планирования и управления) заключается в системном подходе к вопросам организации управления, согласно которому коллективы исполнителей, принимающие участие в комплексе работ и объединенные общностью поставленных перед ними задач, несмотря на разную ведомственную подчиненность, рассматриваются как звенья единой сложной организационной системы.
Использование методов сетевого планирования способствует сокращению сроков создания новых объектов на 15-20%, обеспечению рационального использования трудовых ресурсов и техники.
В основе сетевого планирования лежит построение сетевых диаграмм. Сетевая диаграмма (сеть, граф сети, PERT-диаграмма) — графическое отображение работ проекта и зависимостей между ними. В СПУ под термином “сеть” понимается полный комплекс работ и вех проекта с установленными между ними зависимостями.
Выделяют два типа сетевых диаграмм – сетевая модель типа “вершина-работа” и “вершина-событие” или “дуги-работы”.
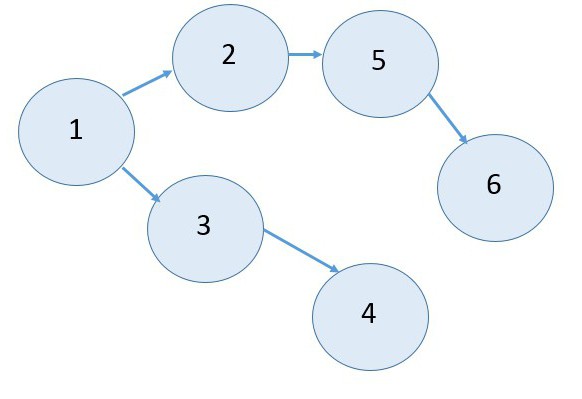
Сетевые диаграммы первого типа отображают сетевую модель в графическом виде как множество вершин, соответствующих работам, связанных линиями, представляющими взаимосвязи между работами. Так же этот тип диаграмм называют диаграммой предшествования—следования. Он является наиболее распространенным представлением сети (рис. 1)
Другой тип сетевой диаграммы — сеть типа “вершина—событие”, на практике используется реже. При данном подходе работа представляется в виде линии между двумя событиями (узлами графа), которые, в свою очередь, отображают начало и конец данной работы. PERT-диаграммы являются примерами этого типа диаграмм (рис. 2).
Можно выделить следующие методы сетевого планирования:
· Детерминированные сетевые методы
o Диаграмма Ганта
o Метод критического пути (МКП)
· Вероятностные сетевые методы
o Неальтернативные
§ Метод имитационного моделирования (метод Монте-Карло)
§ Метод оценки и пересмотра планов (ПЕРТ, PERT)
o Альтернативные
§ Метод графической оценки и анализа (GERT).
1.2 Основные понятия сетевого планирования
Следует выделить следующие понятия, необходимые для сетевого планирования.
Работа – производственный процесс, требующий затрат времени и материальных ресурсов и приводящий к достижению определенных результатов.
По своей физической природе работы можно рассматривать как действие (например, заливка фундамента бетоном, составление заявки на материалы, изучение конъюнктуры рынка), процесс (пример – старение отливок, выдерживание вина, травление плат) и ожидание (процесс, требующий только затраты времени и не потребляющий никаких ресурсов; является технологическим (твердение цементной стяжки) или организационным (ожидание сухой погоды) перерывом между работами, непосредственно выполняемым друг за другом.
По количеству затрачиваемого времени работа может быть:
· действительной, то есть протяжённым во времени процессом, требующим затрат ресурсов;
· фиктивной (или зависимостью), не требующей затрат времени и представляющей связь между какими-либо работами: передача измененных чертежей от конструкторов к технологам, сдача отчета о технико-экономических показателях работы цеха вышестоящему подразделению.
Событие — это факт окончания одной или нескольких работ, необходимых и достаточных для начала следующих работ. События устанавливают технологическую и организационную последовательность работ. События ограничивают рассматриваемую работу и по отношению к ней могут быть начальными и конечными. Начальное событие определяет начало работы и является конечным для предшествующих работ. Исходным считается событие, которое не имеет предшествующих работ в рамках рассматриваемого сетевого графика. Завершающее – событие, которое не имеет последующих работ в рамках рассматриваемого сетевого графика. Граничное событие – событие, являющееся общим для двух или нескольких первичных или частных сетей.
Путь – это любая последовательность работ в сети, в которой конечное событие каждой работы этой последовательности совпадает с начальным событием следующей за ней работы. Путь от исходного до завершающего события называется полным. Путь от исходного до данного промежуточного события называется путем, предшествующим этому событию. Путь, соединяющий какие-либо два события, из которых ни одно не является исходным или завершающим, называется путем между этими событиями.
Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную длину, называют критическим.
Для сетевой модели типа “работы-вершины” используются такие обозначения, как веха – некое ключевое событие, обозначающее окончание одного этапа и начало другого; дуга – связь между работами.
Различают различные типы связей в сетевой модели:
– начальные работы;
– конечные работы;
– последовательные работы;
– работы (операции) дробления;
– работы (операции) слияния;
– параллельные работы.
При составлении сетевых графиков (моделей) используют условные обозначения. (Рис. 3)
1.3 Правила построения сетевых моделей
Процесс разработки сетевой модели включает в себя определение списка работ проекта; оценку параметров работ; определение зависимостей между работами.
При построении сетевого графика необходимо соблюдать ряд правил.
1) Правило последовательности изображения работ: сетевые модели следует строить от начала к окончанию, т.е. слева направо.
2) Правило изображения стрелок. В сетевом графике стрелки, обозначающие работы, ожидания или зависимости, могут иметь различный наклон и длину, но должны идти слева направо, не отклоняясь влево от оси ординат, и всегда направляться от предшествующего события к последующему, т.е. от события с меньшим порядковым номером к событию с большим порядковым номером.
3) Правило пересечения стрелок. При построении сетевого графика следует избегать пересечения стрелок: чем меньше пересечений, тем нагляднее график.
4) Правило обозначения работ. В сетевом графике между обозначениями двух смежных событий может проходить только одна стрелка.
Для правильного изображения работ можно ввести дополнительное событие и зависимость.
5) В сетевой модели не должно быть “тупиковых” событий, то есть событий, из которых не выходит ни одна работа, за исключением завершающего события. Здесь либо работа не нужна и её необходимо аннулировать, либо не замечена необходимость определённой работы, следующей за событием для свершения какого-либо последующего события.
6) Правило расчленения и запараллеливания работ. При построении сетевого графика можно начинать последующую работу, не ожидая полного завершения предшествующей. В этом случае нужно “расчленить” предшествующую работу на две, введя дополнительное событие в том месте предшествующей работы, где может начаться новая.
7) Правило запрещения замкнутых контуров (циклов, петель). В сетевой модели недопустимо строить замкнутые контуры — пути, соединяющие некоторые события с ними же самими, т.е. недопустимо, чтобы один и тот же путь возвращался в то же событие, из которого он вышел.
8) Правило запрещения тупиков. В сетевом графике не должно быть тупиков, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события (в многоцелевых графиках завершающих событий несколько, но это особый случай).
9) Правило запрещения хвостовых событий. В сетевом графике не должно быть хвостовых событий, т.е. событий, в которые не входит ни одна работа, за исключением начального события.
10) Правило изображения дифференцированно-зависимых работ. Если одна группа работ зависит от другой группы, но при этом одна или несколько работ имеют дополнительные зависимости или ограничения, при построении сетевого графика вводят дополнительные события.
11) Правило изображения поставки. В сетевом графике поставки (под поставкой понимается любой результат, который предоставляется “со стороны”, т.е. не является результатом работы непосредственного участника проекта) изображаются двойным кружком либо другим знаком, отличающимся от знака обычного события данного графика. Рядом с кружком поставки дается ссылка на документ (контракт или спецификацию), раскрывающий содержание и условия поставки.
12) Правило учета непосредственных примыканий (зависимостей). В сетевом графике следует учитывать только непосредственное примыкание (зависимость) между работами.
13) Технологическое правило построения сетевых графиков. Для построения сетевого графика необходимо в технологической последовательности установить:
• какие работы должны быть завершены до начала данной работы;
• какие работы должны быть начаты после завершения данной работы;
• какие работы необходимо выполнять одновременно с выполнением данной работы.
14) Правила кодирования событий сетевого графика. Для кодирования сетевых графиков необходимо пользоваться следующими правилами.
1. Все события графика должны иметь свои собственные номера.
2. Кодировать события необходимо числами натурального ряда без пропусков.
3. Номер последующему событию следует присваивать после присвоения номеров предшествующим событиям.
4. Стрелка (работа) должна быть всегда направлена из события с меньшим номером в событие с большим номером.
1.4 Направления применения сетевого планирования
Наиболее распространенными направлениями применения сетевого планирования являются:
· целевые научно-исследовательские и проектно-конструкторские разработки сложных объектов, машин и установок, в создании которых принимают участие многие предприятия и организации;
· планирование и управление основной деятельностью разрабатывающих организаций;
· планирование комплекса работ по подготовке и освоению производства новых видов промышленной продукции;
· строительство и монтаж объектов промышленного, культурно-бытового и жилищного назначения;
· реконструкция и ремонт действующих промышленных и других объектов;
· планирование подготовки и переподготовки кадров, проверка исполнения принятых решений, организация комплексной проверки деятельности предприятий, объединений, строительно-монтажных организаций и учреждений.
Методы сетевого планирования используются при планировании сложных комплексных проектов, например, таких как:
1. Строительство и реконструкция каких-либо объектов;
2. Выполнение научно-исследовательских и конструкторских работ;
3. Подготовка производства к выпуску продукции;
4. Перевооружение армии;
5. Развертывание системы медицинских или профилактических мероприятий.
2. История сетевого планирования
2.1 Зарубежный опыт
Первый этап широкого использования сетевого планирования был связан с появлением диаграмм Ганта, которые появились в начале двадцатого века. Диаграмма Ганга это удобный инструмент для организации, планирования и управления ходом выполнения самых разнообразных процессов.
Второй этап. Методики сетевого планирования были разработаны в конце 50-х годов в США. В 1956 г. М. Уолкер из фирмы “Дюпон”, исследуя возможности более эффективного использования принадлежащей фирме вычислительной машины Univac, объединил свои усилия с Д. Келли из группы планирования капитального строительства фирмы “Ремингтон Рэнд”. Они попытались использовать ЭВМ для составления планов-графиков крупных комплексов работ по модернизации заводов фирмы “Дюпон”. В результате был создан рациональный и простой метод описания проекта с использованием ЭВМ. Первоначально он был назван методом Уолкера-Келли, а позже получил название метода критического пути — МКП (или CPM — Critical Path Method).
Параллельно и независимо в военно-морских силах США был создан метод анализа и оценки программ PERT (Program Evaluation and Review Technique). Данный метод был разработан корпорацией “Локхид” и консалтинговой фирмой “Буз, Аллен энд Гамильтон” для реализации проекта разработки ракетной системы “Поларис”, который объединял около 3800 основных подрядчиков и состоящего из 60 тыс. операций. Использование метода PERT позволило руководству программы точно знать, что требуется делать в каждый момент времени и кто именно должен это делать, а также вероятность своевременного завершения отдельных операций. Проект удалось завершить на два года раньше запланированного срока благодаря успешному руководству программы.
Данный метод управления начал использоваться во всех вооруженных силах США для планирования проектов. Эта методика использовалась при координации работ, выполняемых различными подрядчиками в рамках крупных проектов по разработке новых видов вооружения.
Так же, эта методика управления нашла применение для разработки новых видов продукции и модернизации производства крупными промышленными корпорациями, а так же в строительстве.
Примером успешного применения сетевого планирования проектов можно назвать сооружение гидроэлектростанции на реке Черчилль в Ньюфаундленде (полуостров Лабрадор) с 1967 по 1976 г. В 1974 году ход работ по проекту опережал расписание на 18 месяцев и укладывался в плановую оценку затрат. Заказчиком проекта была корпорация Churchill Falls Labrador Corp., которая для разработки проекта и управления строительством наняла фирму Acress Canadian Betchel. Следует отметить, что значительный выигрыш по времени образовался благодаря применению точных математических методов в управлении сложными комплексами работ, что стало возможным благодаря развитию вычислительной техники. Однако первые ЭВМ были дороги и доступны только крупным организациям. Таким образом, исторически первые проекты представляли собой грандиозные по масштабам работ, количеству исполнителей и капиталовложениям государственные программы.
Третий этапсвязан как с продолжавшимся в конце двадцатого века усовершенствованием прежних методов управления проектами, так и с появлением новых, но на более качественном уровне – с применением современного программного обеспечения и персональных компьютеров. Сначала разработка программного обеспечения велась крупными компаниями с целью поддержки собственных проектов, но вскоре первые системы управления проектами появились и на рынке программного обеспечения. Системы, стоявшие у истоков планирования, разрабатывались для мощных больших компьютеров и сетей мини-ЭВМ.
С появлением персональных компьютеров начался этап наиболее бурного развития систем для управления проектами. Расширился круг пользователей управленческих систем, что привело к необходимости создания систем для управления проектами нового типа. Причем одним из важнейших показателей таких систем являлась простота использования. Поэтому при дальнейших разработках новых версий разработчики старались сохранить внешнюю простоту систем, расширяли их функциональные возможности и мощность, и при этом сохраняли низкие цены, делавшие системы доступными фирмам практически любого уровня.
В настоящее время сложились глубокие традиции использования систем управления проектами во многих областях жизнедеятельности. Увеличение числа пользователей систем проектного менеджмента способствует расширению методов и приемов их использования. Западные отраслевые журналы регулярно публикуют статьи, посвященные системам для управления проектами, включающие советы пользователям таких систем и анализ использования методики сетевого планирования для решения задач в различных сферах управления.
2.2 Сетевое планирование в России
В СССР начало работ по сетевому планированию относят к 1961 году. Тогда методы сетевого планирования нашли применение в строительстве и научных разработках. При создании отечественных подводных ракетоносцев применялся специально разработанный вариант автоматизированной системы программно-целевого управления. В последующие годы сетевое планирование в нашей стране получило широкое применение. Сетевое планирование рассматривалось в широком контексте, в виде развитой системы планирования и управления сложными проектами и программами. Целями сетевого планирования были рациональная организация производственных и иных процессов; выявление временных и материальных ресурсов; управление проектами и программами; предупреждение и устранение возможных отклонений от запланированных результатов; улучшение социально-экономических и других показателей системы; четкое распределение ответственности руководителей и исполнителей различных уровней; повышение эффективности программ и проектов.
Начиная с 90-х годов XX века в нашей стране интерес к сетевому планированию и управлению значительно снизился. Это произошло из-за того, что сетевое планирование ассоциировалось с системой планирования и управления, которая сложилась в административно-командной системе. Существовало множество недостатков этой системы, что обуславливает поиск иных способов управления социально-экономическими процессами, при переходе к рыночным методам хозяйствования. Такой вывод в значительной степени был перенесен на возможности применения сетевого планирования в новых экономических условиях. Кроме того, произошел резкий поворот и переход от централизованных к децентрализованным методам управления экономикой. Установилось и пренебрежительное отношение к методам планирования, которые находили применение при централизованных методах управления. При этом во многом игнорировался тот факт, что многие идеи этих методов были с успехом применены и получили свое развитие в зарубежной практике.
В настоящее время существует сочетание централизованных механизмов регулирования экономики с рыночными подходами Существенную роль в повышении эффективности общественного производства при переходе к рыночным методам выполняет социально-экономическое прогнозирование и планирование. При этом важным средством реализации прогнозов и планов снова является сетевое планирование.
3. Методы сетевого планирования
Существуют разные методы сетевого планирования.
Модели, в которых взаимная последовательность и продолжительности работ заданы однозначно, называются детерминированными сетевыми моделями. К наиболее популярным детерминированным моделям относятся метод построения диаграмм Ганта и метод критического пути (CPM).
Если о продолжительности каких-то работ заранее нельзя задать однозначно или если могут возникнуть ситуации, при которых изменяется запланированная заранее последовательность выполнения задач проекта, например, существует зависимость от погодных условий, ненадежных поставщиков или результатов научных экспериментов, детерминированные модели неприменимы. Чаще всего такие ситуации возникают при планировании строительных, сельскохозяйственных или научно-исследовательских работ. В этом случае используются вероятностные модели, которые делятся на два типа:
· неальтернативные – если зафиксирована последовательность выполнения работ, а продолжительность всех или некоторых работ характеризуется функциями распределения вероятности;
· альтернативные – продолжительности всех или некоторых работ и связи между работами носят вероятностный характер.
К наиболее распространенным методам вероятностного сетевого планирования относятся:
· метод оценки и анализа программ (PERT);
· метод имитационного моделирования или метод Монте-Карло;
· метод графической оценки и анализа программ (GERT).
3.1 Диаграмма Ганта и циклограмма
Одним из наиболее распространенных способов наглядного представления производственного процесса или проекта во времени является линейный или ленточный календарный график – Диаграмма Ганта.
Диаграмма Ганта — горизонтальная линейная диаграмма, на которой задачи проекта представляются протяженными во времени отрезками, характеризующимися датами начала и окончания, задержками и, возможно, другими временными параметрами.
Диаграмма Ганта представляет собой график, в котором процесс представлен в двух видах. В левой частипроект представлен в виде списка задач (работ, операции) проекта в табличном виде с указанием названия задачи и длительности ее выполнения, а часто и работ, предшествующих той или иной задаче. В правой частикаждая задача проекта, а точнее длительность ее выполнения, отображается графически, обычно в виде отрезка определенной длины с учетом логики выполнения задач проекта. (см. Рис. 4)
В верхней, правой части диаграммы Ганта располагается шкала времени. Длина отрезка и его расположение на шкале времени определяют время начала и окончания каждой задачи. Кроме того, взаимное расположение отрезков задач показывает, следуют ли задачи одна за другой или происходит их параллельное выполнение.
Наиболее широко график Ганта использовался в строительстве. В качестве расписания работ график Ганта вполне пригоден, но когда возникает необходимость изменения структуры работ, приходится все работы пересматривать заново, учитывая все многообразие возможных технологических связей между ними. И чем сложнее работы, тем сложнее использовать график Ганта. Тем не менее даже после появления сетевых моделей график Ганта продолжает использоваться как средство представления временных аспектов работ на конечных стадиях календарного планирования, когда продолжительность проекта оптимизирована с помощью сетевых моделей. График Ганта может также использоваться для элементарного контроля работ. Он используется для отражения текущего состояния проекта (статуса проекта) с точки зрения соблюдения сроков.
Циклограмма представляет собой линейную диаграмму продолжительности работ, которая отображает работы в виде наклонной линии в двухмерной системе координат, одна ось которой изображает время, а другая — объемы или структуру выполняемых работ.
Циклограммы активно использовались до 80-х годов XX века в основном в строительной отрасли, особенно при организации поточного строительства. Существуют циклограммы ритмичного и неритмичного потока. Равноритмичным потоком называют такой поток, в котором все составляющие потоки имеют единый ритм, т.е. одинаковую продолжительность выполнения работ на всех захватках. (Рис. 5)
В настоящее время циклограммы практически не используются в управленческой практике как по причине недостатков, указанным ниже, так и по причине неактуальности поточного строительства.
Эти модели просты в исполнении и наглядно показывают ход работы. Однако они не могут отразить сложности моделируемого процесса — форма модели вступает в противоречие с ее содержанием. Основными недостатками являются:
• отсутствие наглядно обозначенных взаимосвязей между отдельными работами (зависимость работ, положенная в основу графика, выявляется только один раз в процессе составления графика (модели) и фиксируется как неизменная; в результате такого подхода заложенные в графике технологические и организационные решения принимаются обычно как постоянные и теряют свое практическое значение после начала их реализации);
• негибкость, жесткость структуры линейного графика, сложность его корректировки при изменении условий (необходимость многократного пересоставления графика, которое, как правило, из-за отсутствия времени не может быть выполнено);
• невозможность четкого разграничения ответственности руководителей различных уровней (информация, поступившая о ходе разработки, содержит в себе на любом уровне слишком много сведений, которые трудно оперативно обработать);
• сложность вариантной проработки и ограниченная возможность прогнозирования хода работ.
3.2 Метод критического пути (МКП)
Метод критического пути позволяет рассчитать возможные календарные графики выполнения комплекса работ на основе описанной логической структуры сети и оценок продолжительности выполнения каждой работы, определить критический путь для проекта в целом.
В основе метода лежит определение наиболее длительной последовательности задач от начала проекта до его окончания с учетом их взаимосвязи. Задачи лежащие на критическом пути (критические задачи) имеют нулевой резерв времени выполнения и в случае изменения их длительности изменяются сроки всего проекта. В связи с этим при выполнении проекта критические задачи требуют более тщательного контроля, в частности, своевременного выявления проблем и рисков, влияющих на сроки их выполнения и, следовательно, на сроки выполнения проекта в целом. В процессе выполнения проекта критический путь проекта может меняться, так как при изменении длительности задач некоторые из них могут оказаться на критическом пути.
Метод критического пути исходит из того, что длительность операций можно оценить с достаточно высокой степенью точности и определенности.
Основным достоинством метода критического пути является возможность манипулирования сроками выполнения задач, не лежащих на критическом пути.
Календарное планирование по МКП требует определенных входных данных. После их ввода производится процедура прямого и обратного прохода по сети и вычисляется выходная информация. (Рис. 6).
Для расчета календарного графика по МКП требуются следующие входные данные:
– набор работ;
– зависимости между работами;
– оценки продолжительности каждой работы;
– календарь рабочего времени проекта (в наиболее общем случае возможно задание собственного календаря для каждой работы);
– календари ресурсов;
– ограничения на сроки начала и окончания отдельных работ или этапов;
– календарная дата начала проекта.
Прямой расчет – определение минимально возможного времени реализации проектаначинается с работ, не имеющих предшественников. В ходе его определяется ES (ранний старт) и EF (ранний финиш). Ранние начала и ранние окончания работ определяются последовательно, слева направо по графику, то есть от исходного события сети к завершающему.
Используются формулы:
ES˳=0
EF=ES+Dur (где Dur – продолжительность)
ESi=EFi-1, при условии что операция (i) не является операцией слияния.
При слиянии: ESi=maxEFi-1
Обратный расчет. Определяются LS (поздний старт), LF (поздний финиш) и R (резерв). Поздние начала и поздние окончания определяются в обратном порядке – от завершающегося события графика к исходящему, то есть справа налево.
EFN=LFN
LSi=LFi-Dur
LFi-1= LSi,
при условии, что (i-1) не является операцией дробления.
При дроблении:
LFi-1= minLSi
При правильных расчетах должно выполняться условие ES˳=LS˳
LF–EF
R=
LS–ES
Таким образом, критический путь – это последовательность операций, не имеющих резерва.
Анализ по методу критического пути представляет собой эффективный метод оценки:
· Задач, которые необходимо решить.
· Возможности параллельного выполнения работ.
· Наименьшего времени выполнения проекта.
· Производственных ресурсов, необходимых для выполнения проекта.
· Последовательности выполнения работ, включая составление графиков и определение продолжительности выполнения работ.
· Очередность решения задач.
· Наиболее эффективного способа сокращения продолжительности выполнения проекта в случае его срочности.
Эффективность анализа по методу критического пути может повлиять на результат проекта, будет он успешным или неудачным. Также анализ может быть очень полезен для оценки важности проблемы, с которой можно столкнуться в ходе внедрения плана.
3.3 Метод имитационного моделирования (метод Монте-Карло)
Метод Монте-Карло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи.
Суть данного метода состоит в том, что результат испытания зависит от значения некоторой случайной величины, распределенной по заданному закону. Поэтому результат каждого отдельного испытания также носит случайный характер. Проведя серию испытаний, получают множество частных значений наблюдаемой характеристики (выборку). Полученные статистические данные обрабатываются и представляются в виде численных оценок интересующих исследователя величин (характеристик системы).
Важной особенностью данного метода является то, что его реализация практически невозможна без использования компьютера.
Метод Монте-Карло имеет две особенности:
1) простая структура вычислительного алгоритма;
2) погрешность вычислений, как правило, пропорциональна D/N, где D – некоторая постоянная, N – число испытаний. Отсюда видно, что для того, чтобы уменьшить погрешность в 10 раз (иначе говоря, чтобы получить в ответе еще один верный десятичный знак), нужно увеличить N (т.е. объем работы) в 100 раз.
Добиться высокой точности таким путем невозможно. Поэтому обычно говорят, что метод Монте-Карло особенно эффективен при решении тех задач, в которых результат нужен с небольшой точностью (5-10%). Способ применения метода Монте-Карло довольно прост. Чтобы получить искусственную случайную выборку из совокупности величин, описываемой некоторой функцией распределения вероятностей:
1) Задаются пределы изменения времени реализации каждой операции.
2) Задается конкретные времена реализации для каждой операции с помощью датчика случайных чисел.
3) Рассчитывается критический путь и время реализации всего проекта.
4) Переход на операцию “2”.
Результатом применения метода Монте-Карло является:
· Гистограмма, которая показывает вероятность времени реализации проекта. (Рис. 7)
· Индекс критичности
3.4 Метод оценки и пересмотра планов (ПЕРТ, PERT)
Метод оценки и пересмотра планов PERT представляет собой разновидность анализа по методу критического пути с более критичной оценкой продолжительности каждого этапа проекта. При использовании этого метода необходимо оценить наименьшую возможную продолжительность выполнения каждой работы, наиболее вероятную продолжительность и наибольшую продолжительность на тот случай, если продолжительность выполнения этой работы будет больше ожидаемой. Метод ПЕРТ допускает неопределенность продолжительности операций и анализирует влияние этой неопределенности на продолжительность работ по проекту в целом.
Этот метод используется, когда для операции сложно задать и определить точную длительность.
Особенность метода PERT заключается в возможности учета вероятностного характера продолжительностей всех или некоторых работ при расчете параметров времени на сетевой модели. Он позволяет определять вероятности окончания проекта в заданные периоды времени и к заданным срокам.
Вместо одной детерминированной величины продолжительности для работ проекта задаются (как правило, экспертным путем) три оценки длительности:
· оптимистическая (работа не может быть выполнена быстрее, чем за tа);
· пессимистическая (работа не может быть выполнена медленнее, чем за tb);
· наиболее вероятная tn
Затем вероятностная сетевая модель превращается в детерминированную путем замены трех оценок продолжительностей каждой из работ одной величиной, называемой ожидаемой продолжительностью tожид и рассчитываемой как средневзвешенное арифметическое трех экспертных оценок длительностей данной работы:
tожид=( tа + tb + tn)/6
Определяется критический путь на основании для каждой tожид операции.
Определяется среднее квадратичное отклонение каждой операции:
Ϭt=( tа + ta) /6
Среднее квадратичное отклонение времени реализации всего проекта:
Ϭпр=√∑ϬtІ
3.5 Метод графической оценки и анализа (GERT)
Метод графической оценки и анализа (метод GERT) применяется в тех случаях организации работ, когда последующие задачи могут начинаться после завершения только некоторого числа из предшествующих задач, причем не все задачи, представленные на сетевой модели, должны быть выполнены для завершения проекта.
Основу применения метода GERT составляет использование альтернативных сетей, называемых в терминах данного метода GERT-cетями.
По существу GERT-сети позволяют более адекватно задавать сложные процессы строительного производства в тех случаях, когда затруднительно или невозможно (по объективным причинам) однозначно определить какие именно работы и в какой последовательности должны быть выполнены для достижения намеченного результата (т.е. существует многовариантность реализации проекта).
Следует отметить, что “ручной” расчет GERT-сетей, моделирующих реальные процессы, чрезвычайно сложен, однако программное обеспечение для вычисления сетевых моделей такого типа в настоящее время, к сожалению, не распространено.
3.6 Дополнительные методы расчета сетевого графика
Расчет сетевого графика методом диагональной таблицы (иногда этот метод называют матричным) ведется с ориентацией на события, а не на работы. В начале вычерчивается квадратная сетка, в которой число строк и число граф равно числу событий графика. (Рис. 8.)Затем слева, сверху вниз, проставляются все номера начальных событий (индекс i), а вверху слева направо — номера конечных событий (индекс j). В ячейках на пересечении начального и конечного событий проставляются значения продолжительности работ (ti–j).
Так жесуществует секторной метод. Он предполагает изображение сетевого графика с увеличенными кружками, разделенными на шесть секторов, которые в дальнейшем могут разбиваться на подсекторы. В верхнем центральном секторе ставится номер события, в нижнем — календарная дата начала работ. В два верхних боковых сектора вносятся ранние начала и окончания работ, а в два боковых нижних — соответственно поздние начала и окончания работ. Слева принято записывать окончания работ, входящих в данное событие, справа — начала работ, выходящих из данного события. (Рис. 9)
Расчет показателей графика ведется двумя проходами: прямым от исходного события до завершающего последовательно по всем путям графика и обратным — от завершающего события до исходного. При прямом проходе определяются ранние начала и окончания работ. При обратном проходе — поздние начала и окончания работ.
Существуют и другие методы расчета сетевого графика, предполагающие расчет аналитических параметров прямо на графике в кружках событий, разделенных на несколько секторов. Один из таких методов — четырехсекторный метод — предполагает разделение кружка события на четыре сектора. Существует несколько модификаций четырехсекторного метода.
Как уже было сказано ранее, в настоящее время происходит расширение методов и приемов использования сетевых методов.
Заключение
Итак, в настоящее время сетевое планирование играет большую роль. Методы сетевого планирования могут широко и успешно применяются для оптимизации планирования и управления сложными разветвленными комплексами работ, которые требуют участия большого числа исполнителей и затрат ограниченных ресурсов.
Следует отметить, что сетевое планирование представляет собой метод управления, основывающийся на использовании математического аппарата теории графов и системного подхода для отображения и алгоритмизации комплексов взаимосвязанных работ, действий или мероприятий для достижения четко поставленной цели; главной целью сетевого планирования является сокращение до минимума продолжительности проекта.
В основе сетевого планирования лежит построение сетевых диаграмм, которые бывают двух типов – типа “вершина-работа” и “вершина-событие” или “дуги-работы”.
При создании сетевого графика в основе построения сети лежат понятия “работа”, “событие” и “путь”.
Методики сетевого планирования были разработаны в конце 50-х годов в США. В СССР начало работ по сетевому планированию относят к 1961 году. Тогда методы сетевого планирования нашли применение в строительстве и научных разработках.
Существуют различные методы сетевого планирования.
Диаграмма Ганта представляет собой горизонтальную линейную диаграмму, на которой задачи проекта представляются протяженными во времени отрезками, характеризующимися датами начала и окончания, задержками и, возможно, другими временными параметрами.
Метод критического путипозволяет рассчитать возможные календарные графики выполнения комплекса работ на основе описанной логической структуры сети и оценок продолжительности выполнения каждой работы, определить критический путь для проекта в целом.
Метод статистических испытаний (иначе называемый методом Монте-Карло) заключается в рассмотрении сети в качестве вероятностной модели, на которой оценки продолжительностей отдельных работ могут принимать любые значения, лежащие в крайних (минимум и максимум) указанных экспертами пределах, и даже выходить за эти пределы в той степени, в которой это допускают законы теории вероятностей.
Метод PERT – метод событийного сетевого анализа, используемый для определения длительности программы при наличии неопределенности в оценке продолжительностей индивидуальных операций. PERT основан на методе критического пути, длительность операций в котором рассчитывается как взвешенная средняя оптимистического, пессимистического и ожидаемого прогнозов. PERT рассчитывает стандартное отклонение даты завершения от длительности критического пути.
Метод графической оценки и анализа (метод GERT) применяется в тех случаях организации работ, когда последующие задачи могут начинаться после завершения только некоторого числа из предшествующих задач, причем не все задачи, представленные на сетевой модели, должны быть выполнены для завершения проекта.
В настоящее время происходит расширение методов и приемов использования сетевых методов.
Сетевая модель позволяет:
· четко представить структуру комплекса работ, выявить с любой степенью детализации их этапы и взаимосвязь;
· составить обоснованный план выполнения комплекса работ, более эффективно по заданному критерию использовать ресурсы;
· проводить многовариантный анализ разных решений с целью улучшения плана;
· использовать для обработки больших массивов информации компьютеры и компьютерные системы.
Источники
1. Алексинская Т.В. Учебное пособие по решению задач по курсу “Экономико-математические методы и модели”. Таганрог: Изд-во ТРТУ, 2002, 153 с.
2. Вентцель Е.С. Исследование операций. М, Советское радио, 1972.
3. Заболотский В.П., Оводенко А.А., Степанов А.Г. Математические модели в управлении: Учеб. пособие/ СПбГУАП. СПб., 2001, 196с.: ил.
4. Ивасенко А.Г. Управление проектами: учебное пособие/А.Г. Ивасенко, Я.И.Никонова, М.В.Каркавин – Ростов н/Дону:Феникс, 2009. – 330 с. – Высшее образование.
5. Кудрявцев Е.М. Microsoft Project. Методы сетевого планирования и управления проектом. – М.: ДМК Пресс, 2005. – 240 с., ил.
6. Мазур И.И., Шапиро В.Д., Ольдерогге Н.Г. Управление проектами: Ученое пособие/ Под общ. ред. И.И.Мазура. – 3-е изд. – М.: Омега-Л, 2004. – с. 664.
7. Тынкевич М.А. Экономико-математические методы (исследование операций). Изд. 2, испр. и доп. – Кемерово, 2000. -177 c. ISBN 5-89070-043-X
8. Управление проектом. Основы проектного управления: ученик/ кол. авт.: под ред. проф. М.Л.Разу. – М.: КНОРУС, 2006. – 768 с.
9. Бюджетирование. http://www.informicus.ru/default.aspx?SECTION=6&id=89&subdivisionid=25
10. Введение в проектный менеджмент. http://www.hr-portal.ru/article/vvedenie-v-proektnyi-menedzhment
11. Вероятностное планирование строительства объектов. http://prosvet.su/articles/menegment/article1/
12. Сетевое планирование. http://www.inventech.ru/lib/glossary/netplan/
13. Метод критического пути. http://ru.wikipedia.org/wiki/Метод_критического_пути
14. Сетевое планирование. http://ru.wikipedia.org/wiki/Сетевое_планирование
15. Ребрин Ю.И.. Основы экономики и управления производством. Сетевое планирование и управление. http://polbu.ru/rebrin_management/ch24_all.html
Приложения
Рис. 1. Фрагмент сети “вершина-работа”
Рис. 2. Фрагмент сети “вершина-событие”
Рис. 3. Условные обозначения в сетевом графике
Рис. 4. Диаграмма Ганта.
Рис. 5. Циклограмма а) равноритмичного и б) неритмичного потока.
Рис. 6. Расчет по методу критического пути
Рис. 7. Гистограмма метода Монте-Карло
Рис. 8. Табличная форма для метода диагональной таблицы
Рис 9. Секторный метод
СЕТЕВОЕ МОДЕЛИРОВАНИЕ СТРОИТЕЛЬНЫХ ПРОЦЕССОВ.pdf