Как составить схему к задаче на проценты

Проценты – традиционно одна из сложных тем школьного курса. При всём многообразии сегодняшних школьных учебников, проценты логичным образом изучаются после изучения правил нахождения части от числа, числа по его части и отношения двух чисел. Ещё бы! Это те же самые три вида задач на проценты: нахождение процента от числа, числа по его проценту и процентное отношение двух чисел. Однако в сознании большинства школьников это абсолютно разные задачи. Причём, вторые гораздо сложнее. Получается, что большинство школьников, даже выпускников, панически боится задач, связанных с понятием “проценты”. Происходит это оттого, что способ решения задач данного типа через определение процента очень громоздок. Как убедительно показать, что 1% – это всего лишь сотая часть числа? Понятно, что в 5–6-ом классе обучение должно быть наглядным. Рисунок, модель, схема и т.п. Русский педагог К.Д. Ушинский указывал, что наглядность отвечает психологическим особенностям детей, мыслящих “формами, звуками, красками, ощущениями”.

Вот естественное задание в начале изучения темы.

Заштрихуйте на рисунке указную часть прямоугольника:

Или, как продолжение, задание посложнее.

Закрасьте на рисунке 20% прямоугольника, затем другим цветом 25% оставшейся части, а третьим цветом 50% нового остатка. Сколько процентов от прямоугольника составляет незакрашенная часть?

В этих заданиях картинка-опора заложена в условии. Так давайте научимся составлять схему по условию задачи, а затем – читать ответ с начерченного рисунка. Начнём со второго – читаем ответ с рисунка.

Какую часть красной полоски составляют остальные полоски?

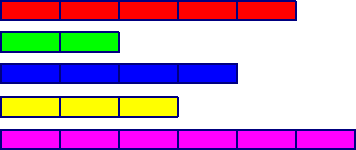
Сколько процентов от красной полоски составляют остальные полоски?

Сколько процентов от синей полоски составляют остальные полоски?

Почему ответы различны при одном и том же рисунке? Запомним это: важно с чем сравниваем, иными словами – что принимаем за целое или 100%.

Нарисуем задачу 1.

Задача 1. Двое работников получали одинаковую зарплату. С нового года первому работнику увеличили зарплату на 25%, второму – на 50%. На сколько процентов зарплата второго работника больше зарплаты первого?

Пусть зарплата каждого была 4 части (в условии упоминается повышение на 25%, то есть на четверть).

Тогда после повышения у первого она стала составлять 5 частей.

А у второго – 6 частей.

Видим, что зарплата второго работника больше зарплаты первого (ведь теперь эту величину принимаем за 100%) на 20%?

Особенно убедительно применение такого изображения при решении задач следующего типа.

Задача 2. Книга дороже альбома на 25%. На сколько процентов альбом дешевле книги?

Большинство не сомневается, что на 25%. Многолетний опыт решения задач подтверждает, что если одна величина больше другой на 25 единиц, то вторая меньше первой тоже на 25 единиц. Будем разрушать сложившийся стереотип.

Изобразим цену альбома отрезком из 4-х частей, тогда цена книги – 5 частей.

Если же принять цену книги за 100%, то видим, что цена альбома составляет 80% цены книги.

Ответ: альбом дешевле книги на 20% её стоимости.

Можно рассмотреть другую задачу, которая не позволяет давать опрометчивый ответ.

Задача 3. На сколько процентов 30 больше, чем 12? На сколько процентов 12 меньше, чем 30?

Наибольшим общим делителем чисел 30 и 12 является число 6. Причём в тридцати шесть содержится 5 раз, а в двенадцати – дважды. Поэтому изобразим 30 отрезком из пяти частей, а 12 – отрезком из двух частей.

Очевидно, что 30 больше 12 на 150%. И очевидно, что сказать: 12 меньше 30 на 150% слишком нелепо. Считываем ответ с рисунка.

Ответ: 12 меньше чем 30 на 60%.

Сложность предыдущих задач в том, что они не содержат именованных величин. Чаще всего в этом случае приходится слышать в качестве решения что-то типа: пусть альбом стоит 100 рублей… Причём рассуждение это вполне годится для получения верного ответа, что требуется, например при решении различных тестов. Но вот известная задача, относимая к задачам повышенной сложности, в которой говорится уже о трёх объектах.

Задача 3. Алик, Боря и Вася собирали грибы. Боря собрал грибов на 20% больше, чем Алик, но на 20% меньше, чем Вася. На сколько процентов больше, чем Алик, собрал грибов Вася?

Первая часть условия легко изображается.

Исходя из второго условия отрезок “Боря” нужно изобразить из четырёх частей, а “Вася” – из пяти.

А теперь совместим изображения. Так как отрезок “Боря” делится и на четыре, и на пять, то длина этого отрезка должна быть 12 частей.

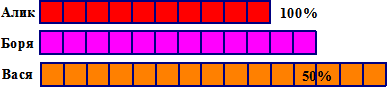
Ответ: Вася собрал грибов на 50% больше, чем Алик.

Сделаем ещё один практичный вывод с помощью рисунка. Для начала заметим, что заштрихованная часть составляет 25% процентов площади прямоугольника.

Как изменилась площадь прямоугольника, если та же часть составляет теперь 50% всей площади?

Итак, фиксированная часть в процентном отношении увеличилась в два раза, площадь прямоугольника при этом уменьшилась в два раза.

Есть тип текстовых задач на проценты, в которых какая-то величина остаётся неизменной: количество сухого вещества, соли, меди и т.д. В таких задачах что-то испаряется, разбавляется, высушивается. Тогда, во сколько раз в процентном соотношении увеличилась (или уменьшилась) неизменяемая величина, во столько раз уменьшилось (увеличилось) целое. Иными словами : процентное содержание неизменяемой по массе величины и масса данного вещества обратно пропорциональны.

Задача 4. Влажность купленного арбуза составила 99%. В результате длительного хранения влажность снизилась до 98%. Как изменилась масса арбуза?

Решение. Свежий арбуз на 99% состоит из жидкости и на 1% – из сухой массы.

В результате усушки количество жидкости уменьшилось и составило 98% от новой, также уменьшившейся массы арбуза. Количество же сухого вещества, оставаясь неизменным, составило 2% от новой массы арбуза. Процентное содержание в арбузе сухого вещества (при неизменной его массе) увеличилось вдвое. Следовательно, масса арбуза в результате усушки уменьшилась вдвое.

Задача 5. В свежих ягодах содержится 90% воды. После сушки ягоды стали легче в 8 раз. Какова влажность сухих ягод?

Решение. Так как масса ягод при неизменном количестве сухого вещества уменьшилась в восемь раз, то процентное содержание сухого вещества увеличилось в 8 раз – с 10% до 80%. Тогда влажность сухих ягод – 20%.

Задача 6. До просушки влажность зерна была равна 23%, а после просушки – 12%. На сколько процентов зерно убыло в весе после просушки?

Решение. Процентное содержание сухого вещества в зерне (при неизменной его массе) изменилось с 77% до 88%, то есть увеличилось в 8/7 раза, тогда масса зерна уменьшилось в 8/7 раза – составила 7/8 от первоначальной массы. 7/8 < 1 на 12,5%.

Задача 7. В колбе имеется раствор поваренной соли. Из колбы в пробирку отливают 1/5 часть раствора и выпаривают до тех пор, пока процентное содержание соли в пробирке не повысится вдвое. После этого выпаренный раствор выливают обратно в колбу. В результате содержание соли в колбе повышается на 3%. Определить исходное процентное содержание соли.

Решение. Процентное содержание соли (при неизменной массе) в пробирке увеличилось вдвое, значит, масса раствора уменьшилась в два раза, то есть составила десятую часть первоначального раствора. После того, как выпаренный раствор вылили обратно в пробирку, его масса уменьшилась в 10/9 раза, а процентное содержание увеличилось соответственно в 10/9 раза. Причём, по условию задачи 1/9 часть соли составляет 3%. Следовательно, вся соль или 10/9части – 30%. А исходное процентное содержание соли – 27%.

Задача 8. Раствор спирта, содержащий 20% примесей, подожгли. Спирт выгорает, а примеси — нет. Смесь перестала гореть, когда содержание спирта стало равняться 40%. В сколько раз уменьшился объем смеси?

Решение. Процентное содержание примесей в спирте увеличилось в три раза: с 20% до 60%. Значит, объём смеси при неизменной массе примесей, уменьшился в три раза.

Задача 9. Вода Тихого Океана содержит 3,5% соли (по весу). Сколько пресной воды надо прибавить к 40 кг такой воды, чтобы со­держание соли в смеси составило 0,5%?

Решение. Процентное содержание в воде соли (при неизменной её массе) уменьшилось в 7 раз: с 3,5% до 0,5%. Следовательно, масса воды увеличилась в 7 раз: с 40 кг до 280 кг. То есть воды надо прибавить 240 кг.

В случае, если именованные величины заданы явно, достаточно просто составить пропорцию.

Задача 10. Влажность свежей травы 75%, влажность сухой – 40%. Необходимо получить 10 кг сухой травы. Сколько свежей травы нужно для этого собрать?

Решение. Так как процентное содержание сухого вещества и масса травы обратно пропорциональны, то имеем пропорцию . Откуда получаем ответ: необходимо собрать 24 кг свежей травы.

Задача 11. Концентрация соли в растворе составляет 5%. На сколько процентов нужно увеличить массу раствора, добавив чистой воды, чтобы концентрация соли составила 1,5%? Решение. Так как концентрация соли в растворе есть отношение массы соли (она постоянна) к массе раствора, то уменьшить концентрацию в 5 : 1,5 = 10/3 раза (при неизменном первом члене отношения) можно, увеличив второй член отношения в 10/3 раза, или на. .

Задачи для самостоятельного решения.

1. В драмкружке число мальчиков составляет 80% от числа девочек. Сколько процентов составляет число девочек от числа мальчиков в этом кружке?
2. Скорость лодки по течению в … раза больше скорости лодки в стоячей воде. Сколько процентов скорости лодки в стоячей воде составляет скорость течения?
3. Брату исполнилось 15 лет, а сестре – 12. “Я на …% старше тебя!” – хвастается брат. “Не очень-то задавайся! – отвечает сестра. – Я только на …% моложе тебя.” Какие числа надо вписать вместо многоточий?
4. Несла Варя ведро воды из колодца. Видит, ребятишки на санках катаются. Оставила ношу и – к ним. Накаталась вдоволь, вспомнила ведре, а оно лопнуло, и лед в нем вместо воды. Дома дед объяснил: “Вода замерзшая увеличивается в объеме на 10%.” Стала Варя соображать: “На сколько процентов уменьшается объем льда при таянии?” Посчитайте и вы.
5. Свежие грибы содержат 98% воды и весят 100 кг. При хранении они усохли и воды оказалось 96%. Найдите массу грибов после высыхания.
6. В траве содержится 60% воды, а в сене 20% воды. Сколько сена получится из тонны травы?
7. Товар подешевел на 20%. На сколько процентов больше можно купить товара за те же деньги?
8. Свежие фрукты содержали 72% воды, а сухие – 20%. Сколько сухих фруктов получится из 20 кг свежих?
9. Кусок сплава меди и олова весом 12 кг содержит 45% меди. Сколько олова надо добавить к этому куску, чтобы в новом сплаве было 40% меди?
10. Сколько чистого спирта надо добавить к 735 г 16%-ного раствора йода в спирте, чтобы получить 10%-ный раствор?
11. Сплав золота и серебра содержит 20% золота. Какую массу сплава и какую массу чистого золота нужно взять для получения 80 кг нового сплава, содержащего 50% золота?
12. Кусок железа с медью массой в 30 кг содержит 45% железа. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 30% железа.
13. Сплав олова и свинца содержит 40% олова. Какую массу сплава и какую массу чистого свинца нужно взять для получения 40 кг нового сплава, содержащего 10% олова?
14. Сколько граммов 25% -го сахарного сиропа нужно добавить к 200 г воды, чтобы концентрация сахара в растворе была 5%.
15. Сколько граммов воды надо добавить к 180 г сиропа, концентрация сахара в котором 25%, чтобы получить сироп с концентрацией сахара 20%?
16. В лесу было 99% дубов. После того как несколько дубов вырубили, их осталось 98%. Какая часть леса осталась?

Доброго времени суток! Только не смейтесь: оказывается, статьи читают и по ночам.

Когда я училась в школе, то совершенно не понимала, как решаются задачи на проценты. И все мамины уверения, что в них нет ничего сложного, до меня не доходили. Мама была сильна в химии, а я – нет. Её решения просто ставили меня в тупик. Страшные слова “концентрация”, “растворы”, “сплавы”, “проценты” никак не укладывались в сознании. И только став преподавателем, я стала с лёгкостью решать такого рода задачи. И в этом мне помогла простая схема, которую я называю “квадратики”.

Но прежде, чем рассказать о ней, я поделюсь некоторыми выводами, сделанными мною. 1) Когда мы читаем фразу “20–процентный водный раствор некоторого вещества”, то что мы должны под этим понимать? Лишь то, что 20% раствора приходится на вещество, а 80% на воду. 2) При смешивании растворов вещество остаётся в воде, его количества, находящиеся в разных растворах, суммируются. 3) Мы будем составлять уравнения либо по количеству вещества в растворах, либо по количеству воды в растворах.

Извините, пожалуйста, если текст задач и их решений покажутся Вам написанными мелкими буквами. Если Вы читаете эту статью с экрана смартфона, просто коснитесь пальцем фотографии, а потом раздвигайте текст так, чтобы он стал крупнее. Приятного прочтения!

Схема “квадратики”

Идея составления схемы очень простая: нужно каждый из растворов (сплавов, фруктов, сухофруктов и т.д.) заменить квадратиком и связать эти квадратики знаками “+”, “-“, “=” так, чтобы отобразилась “технология производства”. А после этого перевести процентное содержание вещества в ту единицу измерения, о которой идёт речь в задаче. Формулу для перевода процентов в “нужную” единицу измерения Вы видите на картинке 1.

Теперь перейдём к решению задач (см. картинки 2, 3, 4, 5, 6, 7).

Следующая задача немного сложнее потому, что решать будем уже не одно линейное уравнение, а систему линейных уравнений (картинка 3).

Остальные задачи ещё проще.

И напоследок задача про грибы. Попробуйте её решить сами. Интересно, какой у Вас получится ответ? Напишите его в комментариях.

Помните, что Вы находитесь на дружелюбном канале.

Ваши комментарии важны и для автора, и для читателей. Делитесь своими мыслями и замечаниями. Истина где-то рядом…

Уважайте себя. С уважением, автор.

Чек-лист «Решение задач на проценты»

1 тип.  Нахождение процента от числа		2 тип.  Нахождение числа по его процентам		3 тип. Нахождение процентного отношения двух чисел (величин).
Чтобы найти процент от числа, необходимо ЧИСЛО разделить на 100 и умножить на количество ПРОЦЕНТОВ.	Чтобы найти число по его процентам, необходимо ЧИСЛО разделить на количество ПРОЦЕНТОВ и умножить на 100.	Чтобы найти процентное отношение двух чисел или величин, необходимо ПЕРВОЕ ЧИСЛО разделить на ВТОРОЕ и  умножить на 100.
Подсказки: –  известно 100 % или всё число (или вся величина); – в тексте задачи: «от», «из них», «от общего количества» (то есть требуется найти % от числа или какой-либо величины); – в краткой записи условия: количество % и число, указанные в условии задачи, записываются на разных строках.	Подсказки: – известно количество ПРОЦЕНТов; – в тексте задачи: «или», «что составляет» (то есть данные об «одном и том же» указаны и в %, и числом); – в краткой записи условия: количество % и число (или величина), указанные в условии задачи, записываются на одной строке.	Подсказки: – известны два ЧИСЛА (или две ВЕЛИЧИНЫ); – в тексте задачи: «какой % …от..»; – число (или величина), о котором необходимо дать ответ в % следует считать ПЕРВЫМ, оно при выполнении действия деления будет являться делимым; – в краткой записи условия: числа (или величины) записываются на разных строках, об одном из них необходимо дать ответ в %;
Пример 1. В книге 60 страниц, Артём прочитал 30 %. Сколько страниц прочитал Артём? Решение: Всего в книге – 60 стр. (100 %) Прочитал – ? стр.,  30 % 30 % = 60 : 100 30 =18 (стр.) Ответ: Артём прочитал 18 страниц.	Пример 2. Денис прочитал 45 % книги. Сколько страниц в книге, если он прочитал 180 страниц? Решение: Прочитал 45 %  или 180 стр. Всего страниц в книге – ? (100 %) 45 % = 180 : 45 100  = 400 (стр.) Ответ: в книге 400 страниц.	Пример 3. Фрекен Бок испекла 250 пирожков, Карлсон съел 10 пирожков. Сколько процентов всех пирожков составляют пирожки, которые съел Карлсон. Решение: Испекла – 250 пирожков Съел – 10 пирожков, ? %. 10 : 250 100  = 4 (%.) Ответ: 4 %.
Алгоритм решения задачи на проценты.   1.            Читаю внимательно задачу. 2.            Записываю кратко условие задачи или составляю схему.                Ориентируюсь на подсказки. 3.            Определяю тип задачи (1, 2 или 3). 4.            Выбираю ход решения задачи. 5.            Записываю решение задачи и ответ.

• Мне нравится 

 

Задачи с процентами часто попадаются в экзаменационных заданиях. Многих они сбивают с толку – как разобраться с условием и как это решить? И совершенно зря, потому что с задачами на проценты каждый часто встречается в обычной жизни.

Пока такие задачки остаются оторванными от реальности строчками в учебнике, их бывает сложно понять и тем более решить. Чтобы стало понятнее, мы вам сейчас покажем примеры из обычной жизни, где вам могут встретиться проценты. А еще просто и доступно объясним, как решать задачи на проценты. И все у вас станет на свои места.

Задачи про проценты вокруг нас

Давайте оглядимся по сторонам: значения в процентах указаны на упаковках с любыми продуктами. Значок процента «%» смотрит на нас с рекламных плакатов скидок и распродаж. В новостях проценты сразу бросаются в глаза, когда речь идет о повышении цен на товары или коммунальные услуги. Разве вы сможете расшифровать все эти послания, если не научитесь решать задачи с процентами? Но вы, конечно, научитесь – мы в вас верим.

А вот такая ситуация: вы купили что-нибудь через интернет и получили извещение от ближайшего почтового отделения. Или сами собираетесь послать подарок другу в другой город. Вам обязательно надо уметь разбираться с процентами, чтобы узнать, сколько денег почта захочет получить за свои услуги по пересылке.

Или возьмем банковские кредиты и ипотеку. Банки в договорах всегда пишут мелкими буквами всякие вещи, которые полезно понимать. Например, какой процент по кредиту придется заплатить банку кроме тех денег, которые вы у него «одолжили» и обязаны вернуть.

А самый близкий школьникам пример связан с ЕГЭ. Каждый год после экзаменов публикуют официальную статистику. В которой немало задействованы и проценты. И эти проценты имеют прямое отношение к будущим выпускникам. Например, процент ребят, сдавших экзамен по математике на «хорошо» и «отлично» косвенно говорит о том, сколько абитуриентов с высокими баллами могли подать документы в вузы на технические специальности. А еще на программирование, прикладную математику и т.п. Чем их больше, тем выше конкурс. Если сравнивать их результаты со своими оценками, можно прикинуть собственные шансы на поступление.

Что такое процент?

Самое очевидное определение: процент – это десятичная дробь. В жизни редко что-то можно сравнивать целиком, чаще приходится сравнивать разные части чего-то целого. Поэтому мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Ну да, все так привыкли к слову «четверть» в школе, что забывают о его формальном значении – «четвертая часть учебного года». Сравнивать сотые доли удобнее всего – так появился процент (1/100): pro centum – «за сто» на латыни.

Все задачи по математике на проценты вертятся вокруг сравнения частей одного целого, определения, какую долю составляет часть от целого, нахождения целого исходя из величины его части и т.п.

Проценты можно записать со знакомым всем значком процента: 1%. Можно представить в виде десятичной дроби (или натурального числа). Для этого нужно разделить на 100: 0,01. Можно наоборот: выразить число в процентах. Тогда его следует умножить на 100%.

Типы задач на проценты

Раз мы уже договорились, что задачи на проценты – это задачи на дроби, такой тактики будем придерживаться и дальше.

Тип 1: Находим процент (дробь) от числа.

• Задача. За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества?
• Решение. Нужно найти 20% от общего количества изготовленных приборов (500). 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло.

Тип 2: Находим число по его проценту (дроби).

• Задача. Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?
• Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 25% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник.

Тип 3: Находим процентное отношение двух чисел (часть от целого числа).

• Задача. В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?
• Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.

Тип 4: Увеличиваем число на процент.

• Задача. На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?
• Решение. Если некое число а увеличено на х%, то оно увеличилось в (1 + х /100) раз. Откуда а * (1 + х /100). Подставим в эту формулу данные нам по условию задачи цифры и получим ответ: 140 * (1 + 15/100) = 161.

Тип 5: Уменьшаем число на процент.

• Задача. Год назад школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
• Решение. Если число а уменьшено на х% и при этом 0 ≤ х ≤ 100, то число уменьшено в (1 – х/100) раз. И нужное нам число находим по формуле а * (1 – х/100). Подставляем цифры из условия задачи и получаем ответ: 100 * (1 – 25/100) = 75.

Тип 6: Задачи на простые проценты.

• Задача. Родители взяли в банке кредит 5000 рублей сроком на год под 15% ежемесячно. Сколько денег они заплатят банку через год?
• Решение. Простые проценты называются так, потому что они начисляются многократно, но всякий раз к исходной сумме. Если обозначить исходную сумму как а, сумму, которая наращивается, как S, процентную ставку как х% и количество периодов начисления процента как у, то формулу можно записать так: S = а * (1 + у * х/100). Теперь подставим сюда цифры из условия задачи и узнаем, сколько денег родители заплатят банку: S = 5000 * (1 + 12 * 15/100) = 14000.

Тип 7: Задачи на сложные проценты.

• Задача. На этот раз сумма кредита 25000 рублей, взятых под те же 15% сроком на 3 месяца. Снова надо узнать, сколько денег придется заплатить банку по истечении срока кредита.
• Решение. Сложные проценты отличаются от простых тем, что процент много раз начисляется не к исходной сумме, а к сумме с уже начисленными раньше процентами. Пускай снова S – наращиваемая сумма, а – исходная, х% – процентная ставка, у – количество периодов начисления процента. В этом случае формула принимает вид: S = а * (1 + х/100)^у. Подставляем цифры из условия: S = 25000 * (1 + 15/100)³ = 38021,875 – искомая сумма.

Кстати, простые задачи на проценты можно очень легко решать с помощью пропорции. Этот метод наглядный и дает такой же результат, так что выбирать можно каждому тот способ решения, который кажется проще. Давайте решим задачу №3 про класс и процент девочек в нем, составив пропорцию.

• Решение. Обозначим искомый процент девочек в классе как х, общее количество учеников примем за 100%. Пропорция выглядит так:

30 – 100%
14 – х%

Перемножим крест накрест левую и правую части пропорции и получим, что 30* х = 14 * 100 («30 относится к х также, как 14 относится к 100»). Откуда найти х уже совсем несложно: х = 14 * 100/30 = 47%.

Задачи на проценты с решением

Давайте решим несколько задач для подготовки к ЕГЭ. Как вы сами видите, решать их совсем несложно. Сейчас просто закрепим материал.

Задача 1. После открытия торгов на бирже в понедельник акции некой компании выросли в цене на неизвестное количество процентов. А во вторник на то же самое количество процентов упали в цене. В итоге они подешевели на 4% по отношению к своей первоначальной стоимости в понедельник. На какой процент акции этой компании поднимались в цене в понедельник?

Решение. Пускай первоначальная стоимость акций это 1. В понедельник акции дорожают на х * 100%. Их стоимость в это время: 1 + х * 1. Во вторник акции дешевеют на х * 100%. Их стоимость после этого: 1 + х – х * (1 + х). После чего они стали дешевле на 4%, т.е. стали стоить 0,96.

Отсюда 1 + х – х * (1 + х) = 0,96 ↔1 – х² = 0,96 ↔ х² = 0,04 ↔ х = 0,2. Т.е. в понедельник акции компании дорожали на 20%.

Задача 2. Четыре пары брюк дешевле одного пальто на 8%. Подсчитайте, на сколько процентов пять пар брюк стоят дороже, чем одно пальто.

Решение. Исходя из условия задачи, стоимость четырех пар брюк – это 92% от стоимости пальто. Легко подсчитать, что стоимость одной пары брюк – это 23% стоимости пальто (92/4 = 23). Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто (23 * 5 = 115). Т.е. пять пар брюк на 15% дороже, чем одно пальто.

Задача 3. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Надо вычислить, какой процент в общий доход семьи приносит заработок жены.

Решение. Из условия следует, что общий доход семьи находится в прямой зависимости от доходов мужа. Не так важно, насколько ему поднимут зарплату. В любом случае общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз эти 67% от общего дохода. Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 – это и есть 4%, на которые уменьшился бы семейных доход. Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии – это 4% дохода, то вся стипендия – это 6%. А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100% – 67%  – 6% = 27%.

Задача 4. В емкости находится 5 литров водного раствора с концентраций вещества, равной 12%. В емкость добавили еще 7 литров воды. Раствор какой концентрации (с каким процентным содержанием вещества) получился после этого?

Решение. Опишем концентрацию вещества в растворе такой формулой: С = Vвещества/ Vраствора * 100%. Изначально в растворе содержится 0,12 * 5 = 0,6 литра вещества. Когда были добавлены 7 литров воды, объем раствора в емкости увеличился. Но концентрация вещества понизилась (его объем остался неизменным). Подставим все известные нам цифры в формулу и получим ответ: 0,6/5 + 7 *100% = 0,6 /12 * 100% = 5%.

Задача 5. В свежих абрикосах 90% влаги, а в кураге, которая из них получается, только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Решение. Исходя из условия, в абрикосах 10% питательного вещества, а в кураге оно содержится в концентрированном виде – 95%. Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества. На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах. Чтобы получить 20 килограммов кураги, нужно взять 19/0,1 = 190 килограммов свежих абрикосов.

Заключение

Сами видите, решать задачи на проценты не так уж сложно. Если усвоить основные правила и подключить воображение, вы сможете щелкать такие задачки как орешки.

Вы даже можете составить задачу на проценты сами по нашим образцам. Кстати, будет очень хорошо, если вы так и поступите. Можете оставить нам свои задачи в комментариях – пускай другие наши читатели решат ваши задачи. А вы сможете решить те, что придумают они. Чтобы задач для подготовки к экзаменам получилось больше, расскажите про эту статью своим друзьям в социальных сетях.

Вот увидите, задачи на проценты вам придется решать еще много раз даже после того, как вы закончите школу. Они встречаются в физике, химии, биологии. Да и в повседневной жизни умение решать их может не раз пригодится. Не бойтесь сложных задач – мы всегда поможем вам найти к ним ключ.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.