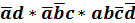В данной статье описывется изучение и построение логических схем на простых логических элементах.
Электронными приборами называются активные вакуумные, газоразрядные и полупроводниковые элементы электрических цепей. Наряду с пассивными элементами (резисторами, катушками индуктивности и конденсаторами) они входят в электрические схемы устройств, в которых происходит преобразование электромагнитной энергии и сигналов. Наиболее простым видом преобразования является выпрямление переменного тока, более сложным — инвертирование постоянного тока в переменный, усиление, генерирование и преобразование сигналов сложной формы. Различают вакуумные и полупроводниковые электронные приборы. В полупроводниковых приборах электрические токи текут в твердом теле — полупроводниках. Поэтому их часто называют твердотельными электронными приборами. К ним относятся полупроводниковые диоды, триоды (транзисторы), тиристоры, светодиоды, фоторезисторы, фототранзисторы. Полупроводниковые электронные приборы наиболее часто используются в современных электронных устройствах.
Логические схемы – физические устройства, реализующие функции математической логики. Логические схемы подразделяются на комбинационные схемы (схемы без памяти) и последовательные схемы (схемы с памятью). Логические схемы являются основой любых систем обработки дискретной информации.
Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию («И», «ИЛИ», «НЕ» и «исключающее ИЛИ»).
В полупроводниковых приборах в качестве уровня используются соответствующие значения напряжения. Например, в ТТЛ схемах при Uпит = 5В низкий уровень составляет 0…1,8В (16% Uпит), высокий – 2…5В.
1. Синтез комбинационной логической схемы
1.1 Составление таблицы истинности
Исходя из задания, было дано следующее условие для построения комбинационной логической схемы:
Y = (1, 2, 3, 5, 7, 12)
Таблица истинности будет выглядеть следующим образом:
Таблица 3.1 – Таблица истинности
|
Состояние входов |
Варианты выходных состояний |
||||
|
a |
b |
c |
d |
y |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
2 |
0 |
0 |
1 |
0 |
1 |
|
3 |
0 |
0 |
1 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
0 |
|
5 |
0 |
1 |
0 |
1 |
1 |
|
6 |
0 |
1 |
1 |
0 |
0 |
|
7 |
0 |
1 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
0 |
|
9 |
1 |
0 |
0 |
1 |
0 |
|
10 |
1 |
0 |
1 |
0 |
0 |
|
11 |
1 |
0 |
1 |
1 |
0 |
|
12 |
1 |
1 |
0 |
0 |
1 |
|
13 |
1 |
1 |
0 |
1 |
0 |
|
14 |
1 |
1 |
1 |
0 |
0 |
|
15 |
1 |
1 |
1 |
1 |
0 |
Алгебраическое выражение ДНФ записывается в виде:
1.2 Минимизация логической функции
Для минимизации логической схемы следует применить метод карт Карно.
Карта Карно — графический способ представления переключательных булевых функций с целью наглядной и удобной их минимизации, обеспечивающий упрощение сложных логических функций многих переменных. Основным методом минимизации логических функций, представленных в виде ДНФ или КНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке.
Применив данный метод к условию, получаем следующую схему:
|
|
|
|
|
|
|
|
||||
|
ab |
1 |
|||
|
|
|
1 |
1 |
|
|
|
|
1 |
1 |
Парные элементы объединены в группы.
Исключив члены, дополняющие друг друга внутри контура, получим минимизированную функцию:
y =
Минимизацию схем целесообразно применять, для уменьшения стоимость конечных устройств, а также их уменьшения. Так как для реализации одной и той же функции требуется, очевидно, гораздо меньше элементов.
1.3 Построение комбинационной логической схемы с использованием элементов «И», «ИЛИ», «НЕ»
«И» – логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.
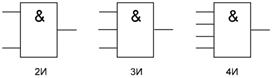
Рисунок 1.1 – графическое обозначение элемента «И»
Условные обозначения логических элементов «И» с разным количеством входов приведены на рисунке. Далее логический элемент «И» с тем или иным числом входов обозначается как «2И», «4И» и т. д. – элемент «И» с двумя входами, с четырьмя входами и т. д.
|
Вход Х1 |
Вход Х1 |
Выход Y |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Таблица 1.1 – таблица истинности для элемента «И»
Таблица истинности для элемента «И» показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе «И» на втором входе. В остальных трех возможных случаях на выходе будет ноль.
Обозначается элемент «И» как прямоугольник с закруглением на выходе или как прямоугольник с символом «1».
«ИЛИ» – логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения. Он так же, как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом.
|
Вход Х1 |
Вход Х1 |
Выход Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Таблица 1.2 – таблица истинности для элемента «ИЛИ»
Таблица истинности для элемента «ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица.
Обозначается элемент «ИЛИ» как закругление на входе и закругление с заострением на выходе или как прямоугольник с символом «1».
«НЕ» – логический элемент, выполняющий над входными данными операцию логического отрицания. Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал.
Таблица 1.3 – таблица истинности для элемента «НЕ»
Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот.
Обозначается элемент «НЕ» в форме треугольника с кружочком на выходе или как прямоугольник с символом «1», с кружком на выходе.
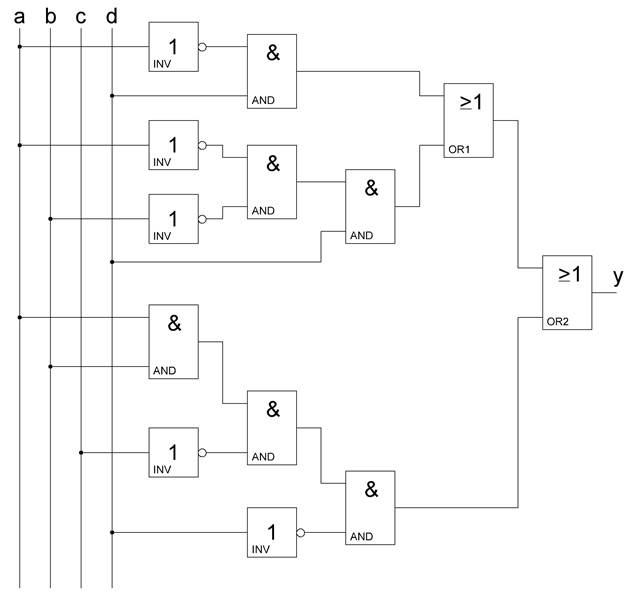
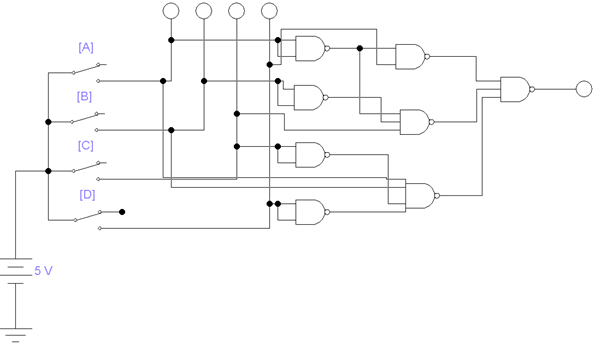
Согласно условию, была получена следующая схема, с использованием логических элементов «И», «ИЛИ», «НЕ», на основе минимизированной функции:
Рисунок 1.2 – Комбинационная логическая схема
с использованием элементов «И», «ИЛИ», «НЕ»
2. Синтез комбинационной логической схемы с использованием логических элементов «И-НЕ», «ИЛИ-НЕ»
2.1 Построение комбинационной логической схемы с использованием элементов «И-НЕ»
«И-НЕ» – логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Другими словами, это элемент «И», дополненный элементом «НЕ».
|
Вход Х1 |
Вход Х1 |
Выход Y |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Таблица 2.1 – таблица истинности для элемента «И-НЕ»
Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И». Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой логической операции в 1913 году. Обозначается как «И», только с кружочком на выходе.
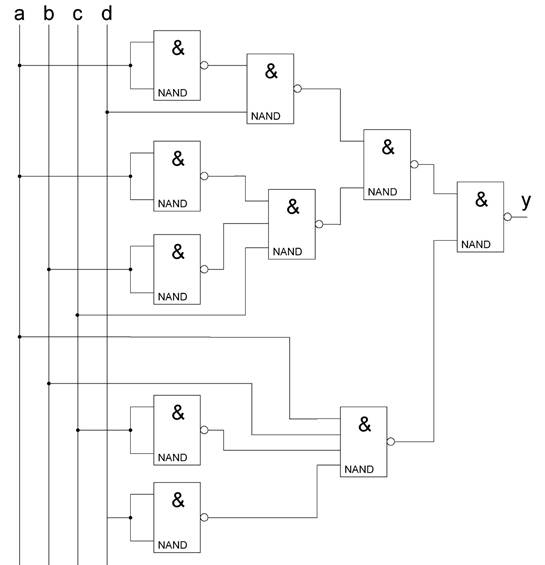
Согласно условию, была получена следующая схема, на основе минимизированной функции:
Рисунок 2.1 – Комбинационная логическая схема
с использованием элементов «И-НЕ»
2.2 Построение комбинационной логической схемы с использованием элементов «ИЛИ-НЕ»
«ИЛИ-НЕ» – логический элемент, выполняющий над входными данными операцию логического сложения, и затем операцию логического отрицания, результат подается на выход. Иначе говоря, это элемент «ИЛИ», дополненный элементом «НЕ» – инвертором. На рисунке приведено условное обозначение логического элемента «2ИЛИ-НЕ».
|
Вход Х1 |
Вход Х1 |
Выход Y |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Таблица 2.2 – таблица истинности для элемента «ИЛИ-НЕ»
Таблица истинности для элемента «ИЛИ-НЕ» противоположна таблице для элемента «ИЛИ». Высокий потенциал на выходе получается лишь в одном случае – на оба входа подаются одновременно низкие потенциалы.
Обозначается как «ИЛИ», только с кружочком на выходе, обозначающим инверсию.
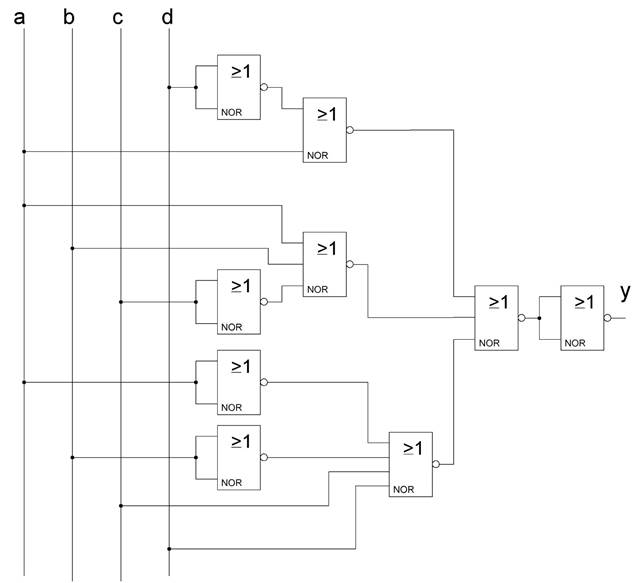
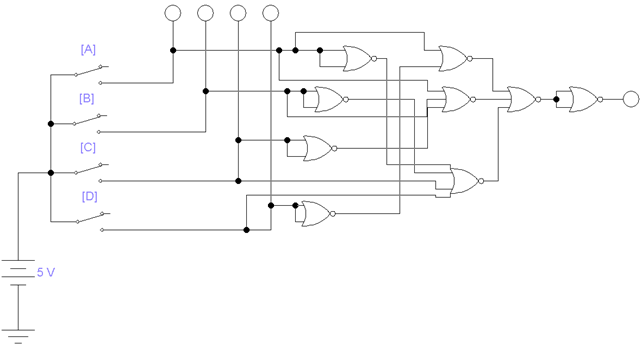
Согласно условию, была получена следующая схема, на основе минимизированной функции:
Рисунок 2.2 – Комбинационная логическая схема
с использованием элементов «ИЛИ-НЕ»
3. Синтез комбинационной логической схемы с использованием логических элементов «И-НЕ», «ИЛИ-НЕ» с использованием мультиплексора
Мультиплексором — называют комбинационное устройство, обеспечивающее передачу в желаемом порядке цифровой информации, поступающей по нескольким входам на один выход. Мультиплексоры обозначают через MUX (от англ. multiplexor), а также через MS (от англ. multiplex or selector).
Схематически мультиплексор можно изобразить в виде коммутатора, обеспечивающего подключение одного из нескольких входов (их называют информационными) к одному выходу устройства.
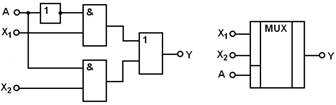
Рисунок 3.1 – Схема и графическое обозначение мультиплексора
Основой данной схемы являются две схемы совпадения на элементах «И», которые при логическом уровне «1» на одном из своих входов повторяют на выходе то, что есть на другом входе.
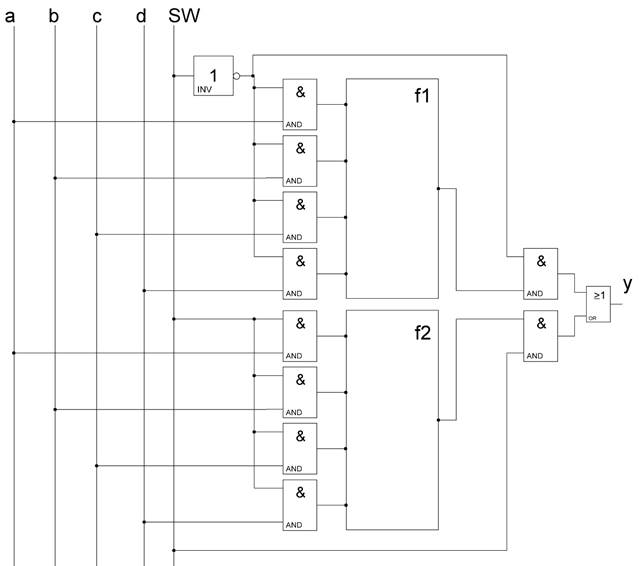
Переключение работы функций осуществляется подачей логического сигнала на шину SW. В зависимости от сигнала «0» или «1» будет включена в работу соответствующая функция. Переключение работы функций осуществляется как по входным сигналам, так и по выходным.
Рисунок 3.2 – Логическая схема мультиплексора
4. Исследование электронных схем методом моделирования в симуляторе
Моделирование всех схем производилось в симуляторе Electronics Workbench.
Electronics Workbench – один из самых известных пакетов схематического моделирования цифровых, аналоговых и аналогово-цифровых электронных схем различной степени сложности.
Данная система схемотехнического моделирования показала достаточно высокую гибкость и точность вычислений, найдя широкое применение, как на предприятиях, так и в высших учебных заведениях. Он включает инструменты для моделирования, редактирования, анализа и тестирования электрических схем. Программа имеет простой интерфейс и идеально подходит для начального обучения электронике. Библиотеки предлагают огромный набор моделей радиоэлектронных устройств от самых известных иностранных производителей с широким диапазоном значений параметров. Кроме этого, есть возможность создания собственных компонентов. Активные элементы могут быть показаны как идеальными, так и реальными моделями. Всевозможные приборы (мультиметры, осциллографы, вольтметры, амперметры, частотные графопостроители, динамики, светодиоды, лампы накаливания, логические анализаторы, сегментные индикаторы) позволяют делать измерения любых величин, строить графики.
Моделирование комбинационной логической схемы с использованием элементов «И», «ИЛИ», «НЕ»:
Рисунок 4.1 – Схема электрическая принципиальная
с использованием элементов «И», «ИЛИ», «НЕ»
Моделирование комбинационной логической схемы с использованием элементов «И-НЕ»:
Рисунок 4.2 – Схема электрическая принципиальная
с использованием элементов «И-НЕ»
Моделирование комбинационной логической схемы с использованием элементов «ИЛИ-НЕ»:
Рисунок 4.3 – Схема электрическая принципиальная
с использованием элементов «ИЛИ-НЕ»
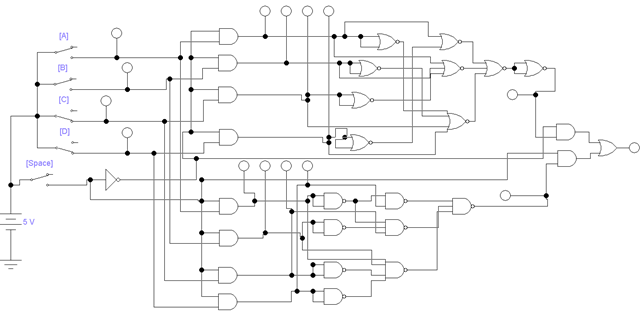
Моделирование комбинационной логической схемы с использованием мультиплексора для переключения схем «И-НЕ» и «ИЛИ-НЕ»:
Рисунок 4.4 – Схема электрическая принципиальная
с использованием мультиплексора
В процессе симулирования, на вход испытуемых схем были поданы все комбинации сигналов из приведенной таблице истинности. На выходе схемы были получены верные сигналы, соответствующие условию задания.
Подача сигналов осуществляется переключением переключателей A, B, C, D, которые позволяют вставить логические сигналы «0» и «1». Контроль за состоянием сигналов можно осуществлять по индикаторным лампам.
На схеме с мультиплексором, для переключения состояния используется клавиша «пробел». Так как обе схемы описывают одну и ту же логику – вне зависимости от переключения мультиплексора, выходной результат будет одинаковый.
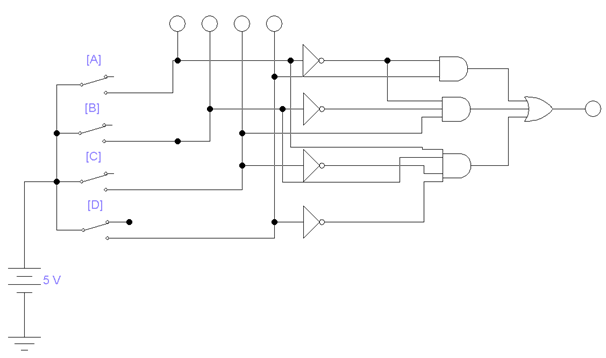
Дополнительно для проверки работоспособности разработанной схемы была построена реальная модель устройства на основе имеющихся в наличии микросхем логики «НЕ», «И-НЕ» серии CD4000B с буферизированным выходом. Схема построена на базе схемы с элементами «И-НЕ».
Полная принципиальная схема устройства приведена ниже. Она состоит из: источника питания напряжением от 8 до 24 вольт; переключателей и индикаторных светодиодов для отображения состояния логических сигналов; микросхем логики; транзистора в качестве ключа включения индикаторного светодиода на выходе логической функции; ограничительных резисторов.
Устройство выполнено на макетной плате. Все элементы соединены дорожками и перемычками в соответствии со схемой.
|
|
|
|
Рисунок 4.5 – лицевая и обратная сторона модели устройства |
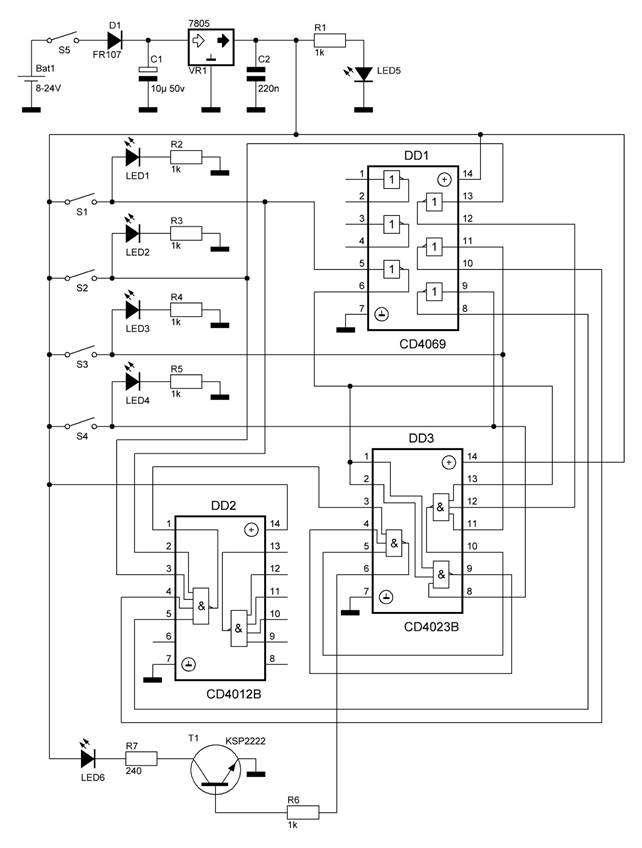
Рисунок 4.6 – принципиальная схема устройства
Для реализации логической функции потребовались 3 комбинированных микросхем.
В качестве инвертора сигналов DD1 применилась микросхема CD4069 (6НЕ), так как была в наличии. Она состоит из 6 независимых логических элемента «НЕ». В этом случае понадобится задействовать только 4 её элемента. В качестве аналога, можно было применить для инвертора микросхему CD4011B (4И-НЕ) с соединенными парами входов у каждого элемента.
Для реализации логики применялись две микросхемы: CD4012B (2И-НЕ) и CD4023B (3И-НЕ). CD4012B представляет собой два элемента И-НЕ с 4 входами, а CD4023B – три элемента «И-НЕ» с 3 входами. Элементы DD1, DD2, DD3 соединены между собой в соответствии с полученной функцией по заданию. Так как микросхемы в своем составе содержат несколько элементов, некоторые из них остались не задействованы.
Параметры у данной серии микросхем следующие: напряжение питания 3-8В; низкий логический уровень 1.5-4В; высокий логический уровень 3.5-11В.
Для индикации логических сигналов применены светодиоды LED1-6 с ограничивающими ток резисторами. По результатам замеров тока светодиодов было выяснено, что для индикаторов (3мм) LED1-5 – A, B, C, D и питания, достаточно тока около 5мА, а для выходного индикатора (5мм) LED6 – 12мА. При напряжении 5В были применены резисторы в 1 кОм и 240 Ом соответственно.
Для управления включением выходного светодиода, в качестве ключа, был применен маломощный биполярный транзистор npn-структуры T1, типа KSP2222A.
Питание построено на базе линейного стабилизатора напряжения VR1 типа LM7805 с фиксированным выходным напряжением 5 вольт. Его характеристики: максимальное входное напряжение 35В; выходное напряжение 5В; максимальный ток нагрузки 1.5А. Для фильтрации возможных импульсов по питанию были применены конденсаторы до и после стабилизатора. Применение стабилизированного напряжения 5В дает возможность напрямую использовать это напряжение для логического «1».
Так как устройство не имеет собственного источника питания, для защиты от переполюсовки применяется последовательно включенный диод D1. Падением напряжения на нем в данном случае можно пренебречь.
Питание схемы осуществляется от батареи типа «КРОНА» напряжением 9В или любого другого источника питания с напряжением от 8 до 24В. Потребляемый ток во время работы составляет около 35мА.
Работает устройство следующим образом. Для включения, необходимо перевести переключатель S5 в положение «ON». Светодиод LED5 зеленого цвета будет говорить о включении устройства. Комбинация входных логических сигналов осуществляется переключателями S1-4, а контроль их положений индицируют красные светодиоды LED1-4. Светодиод желтого цвета LED6 отображает состояние выходного сигнала с данной функции, в зависимости от поданных на нее входных сигналов. Свечение светодиодов означают присутствие логического сигнала «1», а отсутствие свечения – «0».
Для проверки корректности работы был осуществлен тест, в котором на вход схемы были поданы все сигналы из приведенной таблицы истинности, а на выходе схемы были получены те же сигналы, в соответствии с заданием.
Рисунок 4.7 – общий вид устройства
Литература
1. Ширин, И.Я. Схемотехника аналоговых и цифровых устройств: Учебное пособие для ву- зов.- Минск: БНТУ, 2005. – 309 с.
2. Основы электронной техники: Элементы, схемы, системы: [Краткая энциклопедия по электронике] 2-е изд./ К.Ф. Ибрагим; Пер. В.М. Матвеев, Г.Ф. Хохлов и Ф.Г. Хохлов / Под ред. Н.И. Аникушина М.: Мир, 2001. – 397 с.
3. Гусев, В. Г. Электроника / В. Г. Гусев, В. М. Гусев. – М: Высш. шк.,2000.-621 с.
4. Хоровиц, П. Искусство схемотехники. / П. Хоровиц, У. Хилл; пер. с англ. Б. Н. Бронин [и др.]; – М., Мир, 2001. – 704 с.
Логические основы работы компьютера
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Логический элемент «НЕ» (инвертор)
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
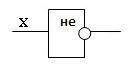
Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «И» (конъюнктор)
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
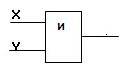
Проверь соответствие логического элемента «И» логическому элементу «И». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «ИЛИ» (дизъюнктор)
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
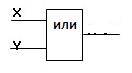
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ». Воспользуйся тренажером Логические элементы.xlsx
Пример 1.
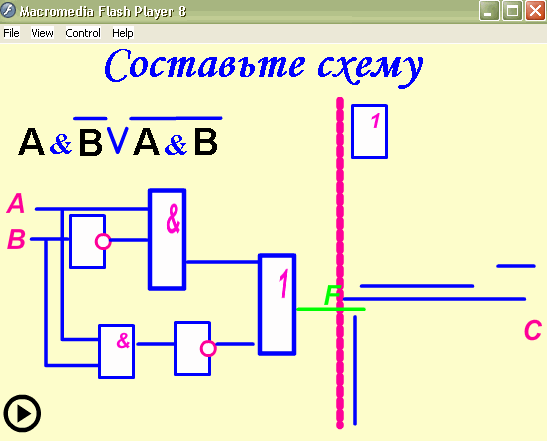
Составьте логическую схему для логического выражения: F=A / B / A.
1. Две переменные – А и В.
2. Две логические операции: 1-/, 2-/.
3. Строим схему:
Пример 2.
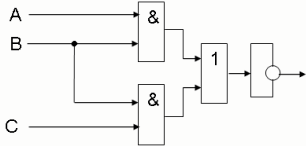
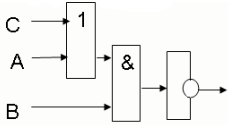
Постройте логическую схему, соответствующую логическому выражению F=А/В/ ¬(В/А). Вычислить значения выражения для А=1,В=0.
1. Переменных две: А и В; 1 4 3 2
2. Логических операций три: / и две /; А/В/ ¬ (В/ А).
3. Схему строим слева направо в соответствии с порядком логических операций:
4. Вычислим значение выражения: F=1 / 0 / ¬(0 / 1)=0
В цифровой технике задача
обычно формулируется в форме таблицы
переключений, которая и называется
таблицей истинности. При составлении
и реализации логических функций
рекомендуется следующий порядок
действий: а) получение
логической функции, соответствующей
таблице истинности; б) преобразование
функции в простейшую форму; в)
реализация полученной функции в виде
соответствующей комбинации базовых
логических схем.
Рассмотрим пример составления
и реализации логической функции, заданной
таблицей истинности (табл. 25).
Первый этап:
1) в таблице истинности
выделяют строки, в которых выходная
переменная Y
имеет значение «логической единицы»;
2) для каждой такой строки
составляют конъюнкцию всех входных
переменных, записывая сомножитель
,
если эта переменная принимает значение
«логическая единица», и,
если – «логический
нуль»;
3) записывают логическую сумму всех
найденных произведений:
.
Т а б л и ц а 25
Таблица истинности логической функции
|
X1 |
X2 |
X3 |
Y |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Второй этап:
используя теоремы алгебры логики,
упрощаем полученное выражение:
.
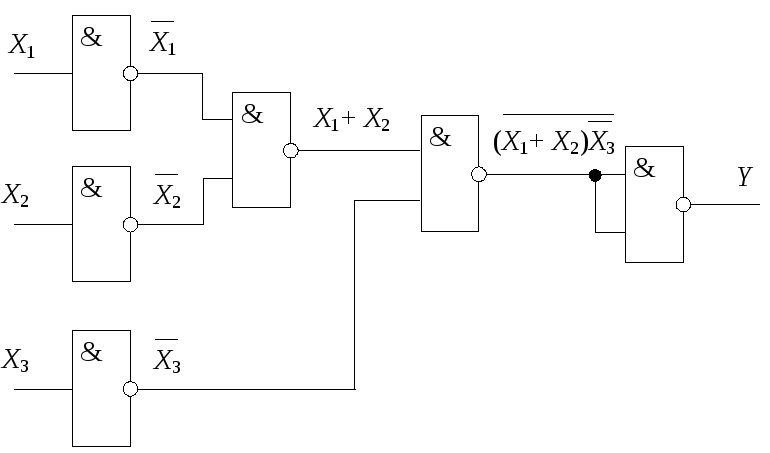
Третий этап:
реализуем полученную
логическую функцию в виде комбинации
логических элементов НЕ, 2И-НЕ (рис. 31).
Рис. 31. Схема, реализующая
функцию Y
8.3. Порядок выполнения работы
1) Собрать схему испытания
логического элемента 2И-НЕ – базового
элемента 155-й серии цифровых микросхем
(рис. 32).
2) Установить режим работы
формирователя логических сигналов в
положение «ШАГ». Изменять с помощью
кнопки «ШАГ» состояние входов элемента
2И-НЕ и убедиться в соответствии работы
данного элемента таблице истинности
(табл. 22).
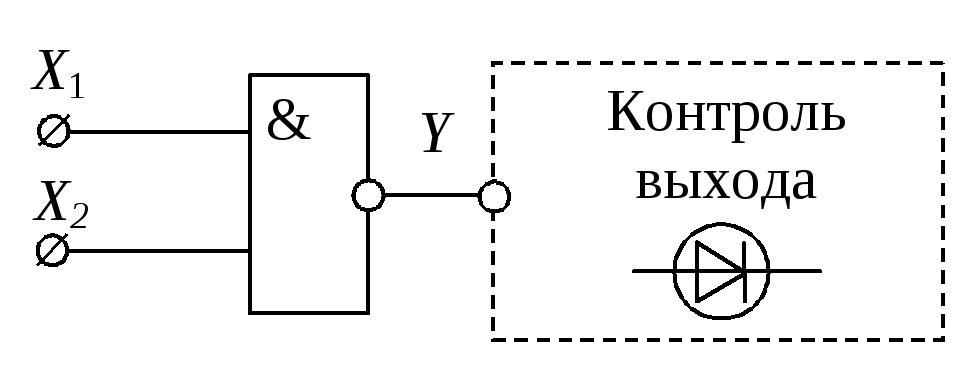
Рис. 32. Схема исследования
элемента 2И-НЕ
3) На основе элемента 2И-НЕ
реализовать основные логические функции
НЕ, И и ИЛИ. Собрать схемы (рис. 30 а, б, в)
на стенде и проверить соответствие их
работы таблицам истинности (табл. 18 –
20). Контроль логического уровня выходного
сигнала осуществить по состоянию
светодиодов «Контроль выхода».
4) По заданной преподавателем
таблице истинности составить логическую
функцию и привести ее к простейшему
виду.
5) Реализовать полученную функцию на
логических элементах стенда: НЕ и 2И-НЕ.
6) Собрать полученную схему на лабораторном
стенде и убедиться в том, что ее работа
соответствует заданной таблице
истинности.
8.4. Контрольные вопросы
1) Перечислите основные логические
функции.
2) Что такое базовый логический элемент?
3) Как реализовать логические
функции И, ИЛИ и НЕ на базе логических
элементов 2ИЛИ-НЕ?
4) Какие методы булевой
алгебры используются для составления
логических функций?
5) Сколько сочетаний имеет таблица
истинности для двух, трех и четырех
аргументов?
Лабораторная работа 9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Редактор схемы логических элементов
Сервис представляет собой ряд калькуляторов: создание схемы из логических элементов, построение таблицы истинности по булевой функции (с помощью него можно будет также упростить эту функцию) и редактор карт Карно.
С помощью первой программы можно онлайн создать схему логических элементов. По построенной схеме находятся СКНФ, СДНФ, полином Жегалкина. Имеется возможность минимизировать булеву функцию.
Если схему необходимо построить по заданной таблице истинности, то используйте этот калькулятор (иногда задается просто строка, например, f=10001011).
- Ввод данных
- Параметры схемы
- Решение
- Видеоинструкция
- Оформление Word
Количество переменных
Стандарт изображений элементов
Инверсные входы
|
INV |
AND |
NAND |
OR |
NOR |
XOR |
MOD |
IF |
Размеры графического полотна
Ширина
Высота
Созданную логическую схему можно сохранить в форматах docx и png (меню Действия).
По логической схеме можно построить СКНФ, СДНФ, полином Жегалкина, карты Вейча-Карно, а также минимизировать булеву функцию.
Здесь будет показано решение
Инструкция к сервису
Для добавления логического элемента необходимо выделить его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле.
Чтобы соединить элементы, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить. Для соединения с переменной xi нажмите на соответствующее ей название.
Построенную схему можно сохранить в формате docx или png.
Булевы функции
С помощью этого калькулятора по булевой функции строится таблица истинности, определяются свойства функции и другие параметры (см. вкладку Параметры решения
). При этом вводится только само логическое выражение без префикса. Например, при f(x,y,z) = x → y!z, ввести необходимо только x → y!z.
Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр Упростить выражение
).
(...) – ввод скобок, x -отрицание (NOT, !, ¬), & – логическое И, AND, ∧, *, v – логическое ИЛИ, OR, ∨, = – эквивалентность, ˜, ≡, ↔, ⊕ – сумма по модулю 2, | – штрих Шеффера, И-НЕ, AND-NOT, ↓ – стрелка Пирса, ИЛИ-НЕ, OR-NOT, ← – обратная импликация.
Для вложенного отрицания необходимо использовать знак !. Например, x v y = !(x v y) или x v y = x v !y
По найденной таблице истинности можно определить логические значения высказываний, например, при x=0, y=0, z=1
Чтобы проверить высказывание на истинность или ложность, функцию необходимо вводить без знака равно
(=). Например, A+B→A&B=1, необходимо ввести A+B→A&B. Если в результате преобразований получится, что f=1, то высказывание истинно, если f=0 – ложно.
Логические (функциональные) элементы {v,&, ¬} являются наиболее распространенными: в силу полноты системы любую булеву функцию (БФ) можно представить в виде суперпозиции дизъюнкции, конъюнкции и отрицания. В качестве функциональных элементов (ФЭ) можно рассматривать любые булевы функции, при этом их можно соединять друг с другом, подавая выходы одних элементов на входы других (суперпозиция БФ).
Область определения БФ E – конечное множество, поэтому БФ можно задать с помощью таблицы истинности, содержащей |E|=2n строк. Столбец значений БФ при этом представляет собой двоичное слово длиной 2n. Поэтому количество различных БФ n переменных равно 22n.
-
Отрицание, ¬
x f
0 1
1 0 -
Конъюнкция, &
x y f
0 0 0
0 1 0
1 0 0
1 1 1 -
Дизъюнкция, v
x y f
0 0 0
0 1 1
1 0 1
1 1 1 -
Сумма по модулю 2, x⊕y
x y f
0 0 0
0 1 1
1 0 1
1 1 0 -
Стрелка Пирса, x↓y
x y f
0 0 1
0 1 0
1 0 0
1 1 0 -
Эквивалентность, x↔y
x y f
0 0 1
0 1 0
1 0 0
1 1 1 -
Импликация, x→y
x y f
0 0 1
0 1 1
1 0 0
1 1 1 -
Штрих Шеффера, x|y
x y f
0 0 1
0 1 1
1 0 1
1 1 0
Другие БФ строятся из элементарных с помощью суперпозиций функций.
Основные равносильности логики высказываний
| Название | Формула |
| Закон исключенного третьего | X v !X ≡ И |
| Закон противоречия | X & !X ≡ Л |
| Закон коммутативности | X & Y ≡ Y & X X v Y ≡ Y v X |
| Закон ассоциативности | (X & Y)&Z ≡ X&(Y&Z) (X v Y) v Z ≡ X v (Y v Z) |
| Закон дистрибутивности | X&(Y v Z) ≡ X&Y v X&Z X v Y&Z ≡ (X v Y)&(X v Z) |
| Закон двойного отрицания | !!X ≡ X |
| Закон идемпотентности | X&X ≡ X, X v X ≡ X |
| Законы де Моргана | !(X v Y) ≡ !X & !Y !(X & Y) ≡ !X v !Y |
| Закон поглощения | X v X&Y ≡ X X&(X v Y) ≡ X |
| Законы склеивания | (X & Y)v(X & !Y) ≡ X (X v Y)&(X v !Y) ≡ X |
| Замена импликации | X → Y ≡ !X v Y |
| Замена эквиваленции | X = Y ≡ X&Y v !X&!Y |
Пример. Упростите выражение: (x˅y˅z)→(x˅y)*(x˅z)
Упростим функцию, используя основные законы логики высказываний.
Замена импликации: A → B = !A v B
Для нашей функции:
(x v y v z)→((x v y) (x v z)) = x v y v z v (x v y) (x v z)
Упростим функцию, используя законы де Моргана: !(A v B) = !A & !B
Для нашей функции:
x v y v z = x y z
По закону дистрибутивности:
(x v y) (x v z) = x v x z v y x v y z
получаем:
f = x y z v x v x z v y x v y z
После элементарных преобразований получаем:
f = x y z v x v x z v y x v y z = x y z v x v y z
f = y z v y z v x
Минимизация булевых функций
В данном сервисе для минимизации булевых функций используются метод Квайна и карт Карно-Вейча. После получения минимальной формы имеется возможность заново построить логическую схему. Если исходная схема понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).
Сократить БФ можно, применяя некоторые равносильности логики высказываний:
- Kx v K ≡ K – тождество поглощения;
- Kx v Kx ≡ K – тождество склеивания;
- Kx v Ky ≡ K(xvy) – дистрибутивный закон,
где K– элементарная конъюнкция. Большинство методов минимизации БФ основываются на первых двух тождествах. А третье – дистрибутивный закон – уменьшает количество букв в формуле, но выводит формулу из класса ДНФ.
При минимизации БФ используют различные термины (и обозначения) для полных элементарных конъюнкций (ПЭК). Наиболее часто используются термины «минтерм» и «конституента единицы». (Для полных элементарных дизъюнкций (ПЭД) используются термины «макстерм» и «конституента нуля»). Слово «конституента» означает «составляющая», а название «минтерм» исходит из определения конъюнкции, как минимального значения ее операндов. При этом используются обозначения mi – для минтерма и Mi – для макстерма. Номер i соответствует двоичной записи той оценки переменных, для которой mi=1.
Метод карт Карно
Склеить можно как целиком всю карту, либо только выделенные единицы (меню Операции).
Количество переменных
Сетка
После минимизации можно получить логическую схему функции и построить таблицу истинности (кнопка Далее)
Этот метод используется для БФ не более, чем с шестью аргументами и основан на тождестве склеивания: Kx v Kx ≡ K – две элементарные конъюнкции (ЭК) склеиваются, если они отличаются только знаком инверсии одного аргумента. Чтобы облегчить нахождение таких пар (четверок, восьмерок,…) склеивающихся ЭК, используют специальное представление БФ в виде таблицы – карты Карно (другое название – диаграмма Вейча). Чтобы заполнить карту Карно необходимо щелкнуть левой кнопкой мышки на соответствующую ячейку.
Карта Карно обладает той особенностью, что две ПЭК, соответствующие соседним клеткам карты, отличаются знаком инверсии только одного аргумента, т.е. их можно склеивать. Причем соседними являются не только клетки, например, с номерами 1 и 3, но и клетки с номерами 12 и 8, 12 и 4, т.е. карту можно «сворачивать» в цилиндр, соединяя горизонтальные (вертикальные) ее границы.
Две единицы «склеиваются» каждый раз, когда они стоят рядом в строке или столбце (карту можно свернуть в цилиндр). В результате склеивания число букв, входящих в ПЭК, уменьшается на единицу.
Минимизая функции через равносильные преобразования
см. таблицу равносильных преобразований
Алгоритм минимизии логической функции
- Замена импликации и эквиваленции.
- Упрощение функции через законы де Моргана.
- Раскрытие скобок, используя законы поглощения, исключенного третьего, противоречия.
- Минимизация через закон дистрибутивности.
Алгоритм Куайна построения сокращенной ДНФ
- Получить СДНФ функции.
- Провести все операции неполного склеивания.
- Провести все операции поглощения.
Построение логической схемы по таблице истинности
По заданной СДНФ (по таблице истинности) определяются существенные и фиктивные переменные, полином Жегалкина и принадлежность классам T0,T1, S, M, L. Также можно создать новую логическую схему (если не выбран пункт Строить новую схему при минимизации булевой функции). Если вычисления происходят по исходной схеме и она понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).
Название переменных можно изменить. Для этого их необходимо выбрать (первая строка таблицы).
Количество переменных
Ввести как вектор значений (в виде строки)
| a | b | c | f |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 |
Для установки параметров решения, необходимо нажать Далее.
Пример. Найдите СДНФ(А) и СКНФ(А) с помощью равносильных преобразований и таблицы истинности, если A = xvyv(x→y)&x
Таблица истинности
| x | y | x | y | xvy | xvy | x→y | (x→y)&x | xvyv(x→y)&x |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
Упростим функцию, используя основные законы логики высказываний.
Замена импликации
A → B = !A v B
Для нашей функции:
x→y = x v y
f = x v y v (x v y) x
Упростим функцию, используя законы де Моргана онлайн.
!(A v B) = !A & !B
!(A & B) = !A v !B
Для нашей функции:
x v y = x y
f = x y v (x v y) x
По закону дистрибутивности:
x x = 0
(x v y) x = y x
x y v (x v y) x = x y v y x
f = x y
Используя равносильные преобразования, найдем СДНФ(А).
СДНФ(А) = x y
Используя равносильные преобразования, найдем СДНФ(А).
1. Для получения элементарных дизъюнкций используем закон дистрибутивности XvYZ=(XvY)(XvZ).
2. Закон исключенного третьего Xv!X=1. При этом элементарную дизъюнкцию можно отбросить (в силу равносильности C & 1 = C).
3. По закону поглощения XvXYZ = X
A = x y
Из КНФ А путем равносильных преобразований получаем СКНФ А, последовательно добиваясь выполнения четырех свойств СКНФ А.
1. Если элементарная дизъюнкция В, входящая в КНФ А, не содержит переменную xi, тогда заменяем В на Bv(xi & !xi) = (B v xi)(B v !xi)
2. Если в некоторую элементарную дизъюнкцию В переменная xi входит дважды, то лишнюю переменную нужно отбросить, так как xi v xi = xi.
3. Если КНФ А содержит две одинаковых элементарных дизъюнкций, то одну можно отбросить, так как B & B = B
4. Если в элементарную дизъюнкцию входит пара xi v !xi, то ее можно отбросить так как xi v !xi=1, а истинное высказывание из конъюнкции можно выбросить (в силу равносильности C & 1 = C).
A = (x v y y) (y v x x) = (x v y) (x v y) (y v x) (y v x)
A = (x v y) (x v y) (y v x) (y v x)
СКНФ(А) = (x v y) (x v y) (x v y)
Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x1,x2,…xn).
2. Все логические слагаемые формулы различны.
3. Ни одно логическое слагаемое не содержит переменную и её отрицание.
4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
F = x y
Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:
1. Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x1,x2,…xn).
2. Все элементарные дизъюнкции различны.
3. Каждая элементарная дизъюнкция содержит переменную один раз.
4. Ни одна элементарная дизъюнкция не содержит переменную и её отрицание
F = (x v y) (x v y) (x v y)
Список литературы
- Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.,1992.
- Бауэр Ф.Л., Гооз Г. Информатика. Вводный курс: Часть 2, М.: Мир, 1990.
- Горбатов В.А. Основы дискретной математики. – М.: Высш. школа, 1986. – 312 с.
Количество входов
Текст
РазмерЦвет
Линия
ТолщинаЦвет
пунктирная – – – –
Размеры в px и фон
wh
Номер входа
Текст
РазмерЦвет
Линия
ТолщинаЦвет
пунктирная – – –
Введите название переменных
Введите название переменных
Количество входов у элемента
Цели урока:
Образовательные:
- закрепить у учащихся представление об
устройствах элементной базы компьютера; - закрепить навыки построения логических схем.
Развивающие:
- формировать развитие алгоритмического
мышления; - развить конструкторские умения;
- продолжать способствовать развитию ИКТ –
компетентности;
Воспитательные:
- продолжить формирование познавательного
интереса к предмету информатика; - воспитывать личностные качества:
- активность,
- самостоятельность,
- аккуратность в работе;
Требования к знаниям и умениям:
Учащиеся должны знать:
- основные базовые элементы логических схем;
- правила составления логических схем.
Учащиеся должны уметь:
- составлять логические схемы.
Тип урока: урок закрепления
изученного материала
Вид урока: комбинированный
Методы организации учебной деятельности:
- фронтальная;
- индивидуальная;
Программно-дидактическое обеспечение:
- ПК, SMART Board, карточки с индивидуальным домашним
заданием.
Урок разработан с помощью программы Macromedia Flash.
Ход урока
I. Постановка целей урока.
Добрый день!
Сегодня мы продолжаем изучение темы
“Построение логических схем”.
Приготовьте раздаточный материал “Логические
основы ЭВМ. Построение логических схем” Приложение 1
Вопрос учителя. Назовите основные
логические элементы. Какой логический элемент
соответствует логической операции И, ИЛИ, НЕ?
Ответ учащихся. Логический элемент
компьютера – это часть электронной логической
схемы, которая реализует элементарную
логическую функцию. Основные логические
элементы конъюнктор (соответствует логическому
умножению), дизъюнктор (соответствует
логическому сложению), инвертор (соответствует
логическому отрицанию).
Вопрос учителя. По каким правилам
логические элементы преобразуют входные
сигналы. Рассмотрим элемент И. В каком случае на
выходе будет ток (сигнал равный 1).
Ответ учащихся. На первом входе есть
ток (1, истина), на втором есть (1, истина), на выходе
ток идет (1, истина).
Вопрос учителя. На первом входе есть
ток, на втором нет, однако на выходе ток идет. На
входах тока нет и на выходе нет. Какую логическую
операцию реализует данный элемент?
Ответ учащихся. Элемент ИЛИ –
дизъюнктор.
Вопрос учителя. Рассмотрим логический
элемент НЕ. В каком случае на выходе не будет тока
(сигнал равный 0)?
Ответ учащихся. На входе есть ток,
сигнал равен 1.
Вопрос учителя. В чем отличие
логической схемы от логического элемента?
Ответ учащихся. Логические схемы
состоят из логических элементов, осуществляющих
логические операции.
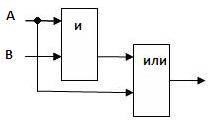
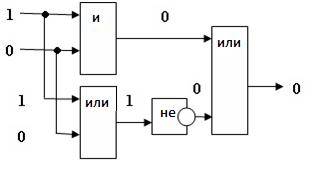
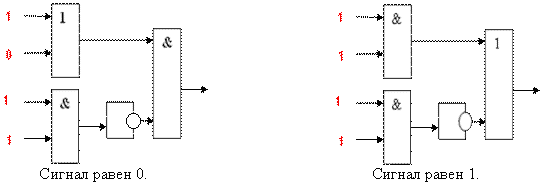
Проанализируем схему и определим сигнал на
выходе.
II. Закрепление изученного материала.
Почему необходимо уметь строить логические
схемы?
Дело в том, что из вентилей составляют более
сложные схемы, которые позволяют выполнять
арифметические операции и хранить информацию.
Причем схему, выполняющую определенные функции,
можно построить из различных по сочетанию и
количеству вентилей. Поэтому значение
формального представления логической схемы
чрезвычайно велико. Оно необходимо для того,
чтобы разработчик имел возможность выбрать
наиболее подходящий ему вариант построения
схемы из вентилей. Процесс разработки общей
логической схемы устройства (в том числе и
компьютера в целом), становится иерархическим,
причем на каждом следующем уровне в качестве
“кирпичиков” используются логические схемы,
созданные на предыдущем этапе.
Дома вам необходимо было построить логические
схемы, соответствующие логическим выражениям.
Вопрос учителя. Каков алгоритм
построение логических схем?
Ответ учащихся. Алгоритм построение
логических схем:
Определить число логических переменных.
Определить количество базовых логических
операций и их порядок.
Изобразить для каждой логической операции
соответствующий ей элемент (вентиль).
Соединить вентили в порядке выполнения
логических операций.
Работа со SMART Board Приложение 2
Проверка домашнего задания Приложение
1. Домашнее задание. Часть 1
Построить логическую схему для логического
выражения: .
- Две переменные – А и В.
- Две логические операции: &,
- Строим схему.
Построить логическую схему для логического
выражения:
Построить логическую схему для логического
выражения:
Построить логическую схему для логического
выражения:
Построить логическую схему для логического
выражения:
Построить логическую схему для логического
выражения:
Построить логическую схему для логического
выражения:
Вычислить значение данного выражения для А=1,
В=0.
Ответ F=1
III. Пропедевтика (законы логики)
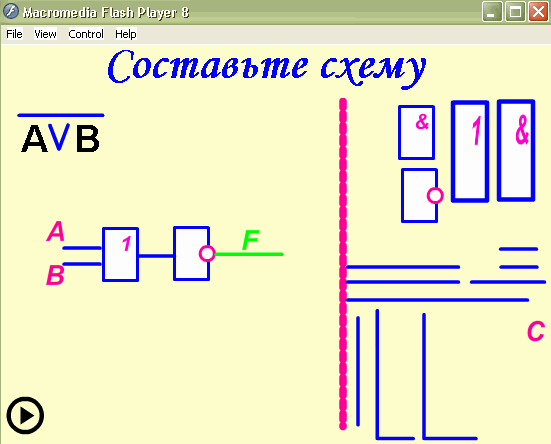
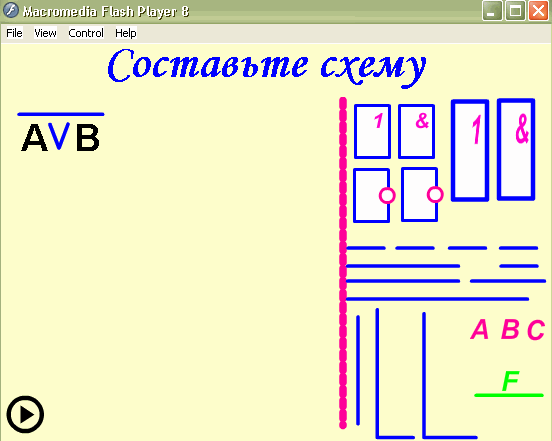
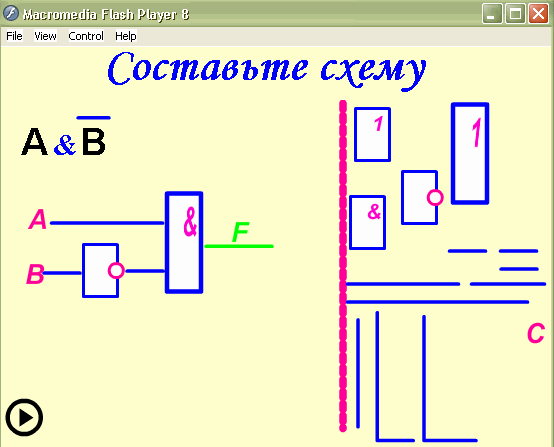
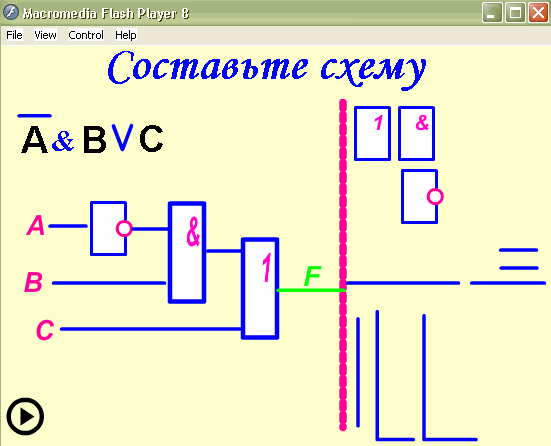
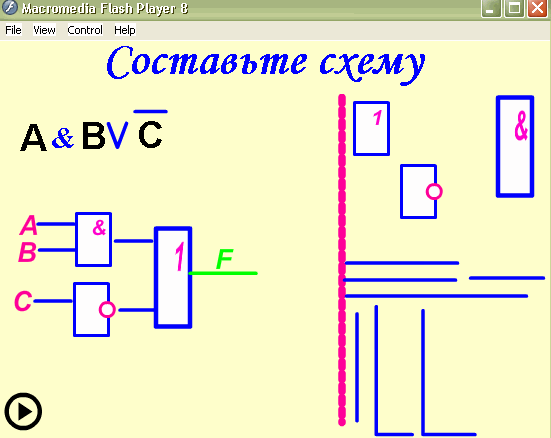
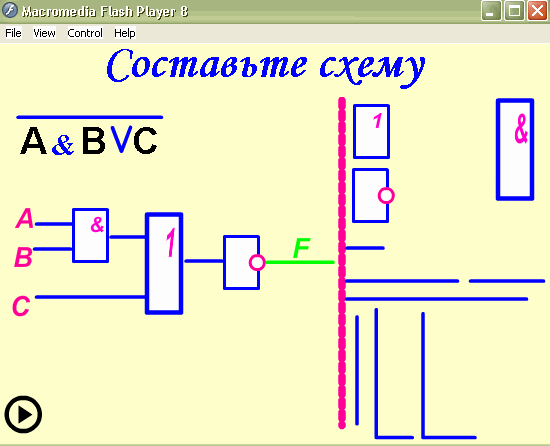
Выполним задачу обратную данной. Составим
логическое выражение по заданной логической
схеме:
Данное логическое выражение можно упростить.
Операция И – логическое умножение, ИЛИ –
сложение. Запишем выражение, заменяя знаки & и U
на * и + соответственно.
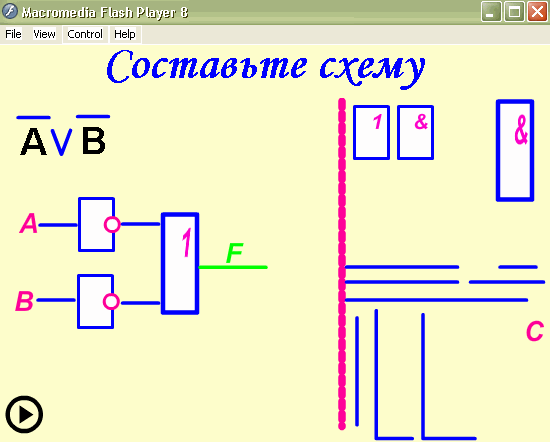
F= (A*B+B*С) Упростим F=
(B*(А+С)), затем запишем
и тогда
логическая схема примет вид:
Вывод: Логические схемы, содержащие
минимальное количество элементов, обеспечивают
большую скорость работы и увеличивают
надёжность устройства.
Алгебра логики дала конструкторам мощное
средство разработки, анализа и
совершенствования логических схем. Проще, и
быстрее изучать свойства и доказывать
правильность работы схемы с помощью выражающей
её формулы, чем создавать реальное техническое
устройство.
Таким образом, цель нашего следующего урока –
изучить законы алгебры логики.
IV. Домашнее задание. Часть 2
V. Практическая работа.
Программа – тренажер “Построение логических
схем”
www.Kpolyakov.narod.ru Программа “Logic”,
Спасибо за урок!
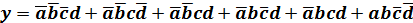
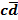
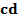
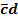
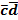
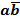
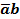

 1
1