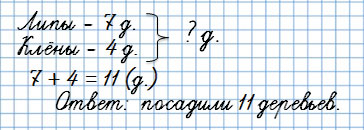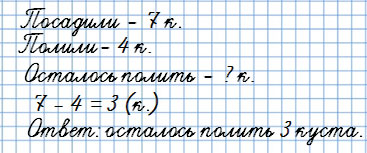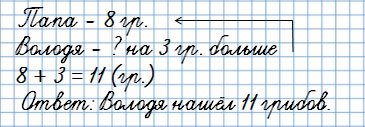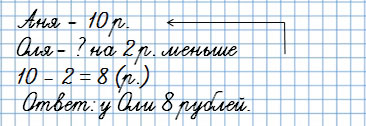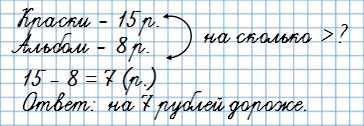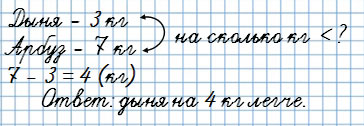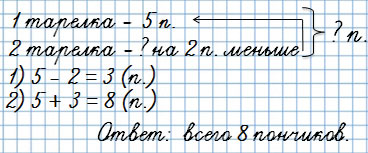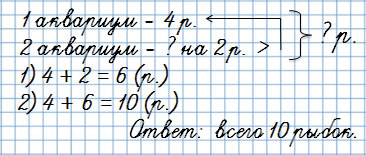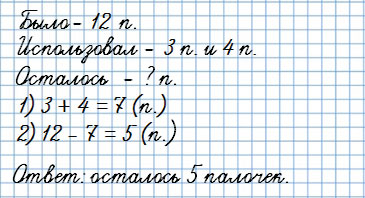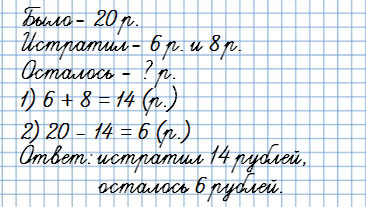- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Образцы оформления задачи
В разделе “Задачи” мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
1. Задачи на нахождение суммы
В вопросе задач такого типа всегда есть “Сколько всего?”
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
В вопросе “Сколько … осталось?”
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
3. Задачи на увеличение или уменьшение числа на несколько единиц
В условии “на … больше”
Папа с Володей собирали грибы. Папа нашёл 8 грибов, а Володя на 3 гриба больше.
Сколько грибов нашёл Володя?
В условии “на … меньше”
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
В вопросе “На сколько больше…?”
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
“На сколько меньше…?”
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии “Было…Стало…”
В вопросе “Сколько добавили?”
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии “Было… Осталось…”
В вопросе “Сколько уехало?”
“Сколько человек вышло?”
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии “Убрали… Осталось…”
В вопросе “Сколько было сначала?”
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Первый вид
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Второй вид
В классе два маленьких аквариума. В первом аквариуме 4 рыбки, а во втором – на 2 рыбки больше.
Сколько рыбок в двух аквариумах?
Третий вид
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
Четвёртый вид
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
или
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
II тип:
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
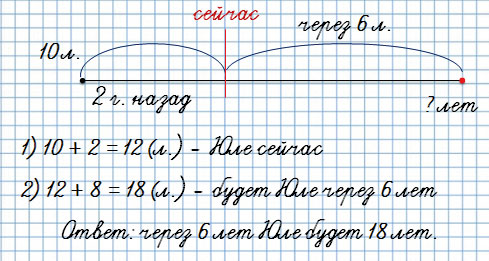
Задачи с составлением рисунка по условию:
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Советуем посмотреть:
Обратные задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 15,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 23,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 24,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 28,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 30,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 35,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 44,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 5,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
2 класс
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 63. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 26,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 55,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 57,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 51,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 69,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 34. ПР 3. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 86,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 108,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 41,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 45,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 36,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 114,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 79,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Номер 80,
Мерзляк, Полонский, Якир, Учебник
Номер 81,
Мерзляк, Полонский, Якир, Учебник
Номер 106,
Мерзляк, Полонский, Якир, Учебник
Номер 293,
Мерзляк, Полонский, Якир, Учебник
Номер 383,
Мерзляк, Полонский, Якир, Учебник
Номер 484,
Мерзляк, Полонский, Якир, Учебник
Номер 496,
Мерзляк, Полонский, Якир, Учебник
Номер 505,
Мерзляк, Полонский, Якир, Учебник
Номер 506,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 362,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 363,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 383,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 393,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 405,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 419,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 420,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 421,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 429,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 443,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
ГДЗ и ответы к учебнику математики за 4 класс (Часть 1 — 2) Моро, Бантова, Волкова.
Часть 1
Страницы учебника
Часть 2
Страницы учебника
Если вам понравился сайт, поделитесь страничкой в соцсетях, чтобы не потерять его:
Составь по схеме и реши задачу, дополнив ее условие ответом, полученным при решении задачи 4.
Как называются задачи 4 и 5? Попробуй составить еще две подобные задачи.
reshalka.com
ГДЗ учебник по математике 4 класс Дорофеев. Часть 2 страница 73. Номер №5
Решение
Задача.
От одной станции одновременно в противоположных направлениях выехали два автобуса. Через 3 часа расстояние между ними было 291 км. Скорость первого автобуса 55 км/ч. Найди скорость второго автобуса?
Решение:
1) 291 : 3 = 97 (км/ч) − скорость удаления автобусов;
2) 97 − 55 = 42 (км/ч) − скорость второго автобуса.
Ответ: 42 км/ч
Задачи 4 и 5 называют обратными.
Обратная задача 1.
От одной станции одновременно в противоположных направлениях выехали два автобуса. Через 3 часа расстояние между ними было 291 км. Скорость первого автобуса 42 км/ч. Найди скорость второго автобуса?
Решение:
1) 291 : 3 = 97 (км/ч) − скорость удаления автобусов;
2) 97 − 42 = 55 (км/ч) − скорость первого автобуса.
Ответ: 55 км/ч
Обратная задача 2.
От одной станции одновременно в противоположных направлениях выехали два автобуса. Скорость первого автобуса 42 км/ч, а скорость второго − 55 км/ч. Через сколько часов расстояние между автобусами будет 291 км?
Решение:
1) 42 + 55 = 97 (км/ч) − скорость удаления автобусов;
2) 291 : 97 = 3 (ч) − время, через которое расстояние между автобусами будет 291 км.
Ответ: 291 км

Если с самого первого класса правильно научить ребенка решать задачи, действуя по алгоритму, то к четвертому он будет это делать с необыкновенной легкостью. Если же не получилось научиться и требуется готовое решение, мы к вашим услугам.
Решебник проверен учителем начальных классов.
Если затрудняетесь в краткой записи условия задачи, смотрите, как она правильно оформляется в статье по ссылке >>
Если что-то не понятно, задавайте вопросы в комментариях.
Задачи из раздела Числа, которые больше 1000, страницы 3-85
Страница 4. Умножение и деление на однозначное число
Страница 4, задача 1. Мама заготовила 18 л сока. У нее получилось 5 одинаковых банок яблочного сока и и 4 такие банки вишневого сока. Сколько литров сока в одной банке? Сколько литров яблочного и вишневого сока заготовила мама?
Решение: 1) 5+4=9 банок сока всего, 2) 18:2=2 л в одной банке; 3) 2*5=10 л яблочного сока, 4) 2*4=8 л вишневого сока.
Записываем:
1) 5 + 4 = 9 (б.) – всего фруктового сока
2) 18 : 9 = 2 (л) – сока в одной банке
3) 2 • 5 = 10 (л) – яблочного сока
4) 2 • 4 = 8 (л) – вишнёвого сока
Ответ: 2 л сока в одной банке, 10 л яблочного сока и 8 л вишнёвого.
Задача 4. Площадь квадрата 36 см2. 1) Какой длины в сантиметрах (целых) могут быть стороны прямоугольников с такой же площадью, как у квадрата? Найди периметр каждого из них. 2) Найди длину стороны равностороннего треугольника, периметр которого равен периметру одного из этих прямоугольников.
Решение: Любое произведение двух целых чисел которые будет давать в результате 36 можно представить как две стороны таких прямоугольников. Начнем с 1. 1 вопрос 1) 1*36=36 см2 36*2+1*2=74 см 2) 2*18=36 см2 18*2+2*2=40 см 3) 3*12=36 см2 12*2+3*2=30 см 4) 4*9=36 см2 9*2+4*2=26 см 5) не получается с целыми числами; 2 вопрос Скажем возьмем треугольник с периметром 30. Если взять другие значения, из возможных, то стороны будут не в целых сантиметрах. 30:3=10 см каждая сторона треугольника
Страницы 5-11. ГДЗ к теме Скорость, время, расстояние
Страница 5, задача 8. Аист может лететь со скоростью 600 м/ мин. Какое расстояние он пролетит за 1 сек? Запиши скорость полета аиста в разных единицах.
Решение: Если аист летит 600 м в минуту, то в секунду он пролетит в 60 раз меньше, так как секунд в минуте 60. То есть… 600:60=10 метров в секунду. Если представить в км в час, то надо разделить на 1000, так как именно столько метров в км и умножить на 3600 так как в часе столько секунд. 10*3600:1000=36 км/ч скорость аиста То есть 36 км/ч=600 м /мин = 10 м/с.
Записываем:
600 : 60 = 10 (м) – пролетит аист за 1 с
Ответ: 10 м.
600 м/мин = 10 м/с = 36 км/ч
Страница 7, задача 22. Теплоход проходит за 4 ч такое же расстояние, как и моторная лодка за 9 ч. Узнай скорость моторной лодки, если известно, что скорость теплохода 36 км/ч.
Решение: 36*4=144 км пройдет теплоход за 4 часа; 144:9=16 км/ч скорость моторной лодки.
Записываем решение и ответ:
1) 36 * 4 = 144 (км) − расстояние, которое проходит и теплоход и моторная лодка
2) 144 : 9 = 16 (км/ч) − скорость моторной лодки
Ответ: 16 км/ч.
Задача 23. На решение двух задач Васе потребовалось 24 мин, а на решение трёх примеров на деление — 18 мин. Во сколько раз больше занимало у Васи решение задачи, чем решение примера?
1) 24 : 2 = 12 (мин) − занимало решение одной задачи
2) 18 : 3 = 6 (мин) − занимало решение одного примера
3) 12 : 6 = в 2 (раза) − больше занимало у Васи решение задачи, чем решение примера
Ответ: в 2 раза больше.
Страница 11, задача 4. Одновременно на встречу друг другу вышли два поезда: из Москвы – товарный, а из Санкт Петербурга – пассажирский. Скорость пассажирского поезда была в два раза больше, чем товарного. На каком расстоянии от Москвы встретятся поезда, если считать, если расстояние этими городами 660 км?
Решение: За одно и тоже время пассажирский поезд будет проезжать в 2 раза большее расстояние по сравнению с товарным. То есть если разделить все расстояние, то 2/3 проедет пассажирский и 1/3 проедет товарный, до того как они встретятся, то есть преодолеют весь путь между городами. В итоге… 1) 660*1/3=220 км это расстояние пройдет товарный поезд и на этом расстоянии от Москвы встретятся поезда.
Пусть товарный поезд до встречи прошел одну часть пути
1) 1 * 2 = 2 (части) − пути прошел пассажирский поезд
2) 1 + 2 = 3 (части) − пути всего
3) 660 : 3 = 220 (км) − от Москвы встретились поезда
Ответ: 220 км.
Страницы 12-24. Ответы к теме Умножение на числа, оканчивающиеся нулями
Страница 12, задача 37. В хозяйстве от каждой коровы получали в среднем по 14 л молока в сутки. Сколько литров молока получат в этом хозяйстве от 10 коров за 7 суток? Реши задачу разными способами.
Способ 1:
1) 14 * 10 = 140 (л) – молока получат от 10 коров за 1 сутки
2) 140 * 7 = 980 (л) – молока получат от 10 коров за 7 суток
Ответ: 980 л.Cnoco6 2:
1) 14 * 7 = 98 (л) – молока получат от одной коровы за 7 суток
2) 98 * 10 = 980 (л) – молока получат от 10 коров за 7 суток
Ответ: 980 л.
Задача 38. С поля вывозили овощи на 10 машинах. Каждая из этих машин делала по 8 рейсов в день и вывозила по 5 т овощей за один рейс. Сколько тонн овощей вывезли эти машины за 6 дней?
Решение: 10*8*5*6=2400 (т) вывезли за 6 дней.
Запишем:
1) 5 * 8 = 40 (т) − овощей вывозила одна машина за день
2) 40 * 6 = 240 (т) − овощей вывозила одна машина за 6 дней
3) 240 * 10 = 2400 (т) − овощей вывезли все машины за 6 дней
Ответ: 2400 т овощей.
Страница 13, задача 41. На пасеке 30 ульев дали за лето по 36 кг мёда и 20 ульев — по 42 кг. Сколько всего килограммов мёда получили с этих ульев за лето?
1080 840
30 * 36 + 20 * 42 = 1920 (кг)
Ответ: 1920 кг меда получили со всех ульев.
Задача 42. В магазин поступили цветные карандаши и фломастеры, всего 560 штук. Карандаши были в 40 коробках, по 12 штук в каждой, а фломастеры — в 10 коробках, поровну в каждой. Сколько фломастеров было в каждой коробке?
1) 12 * 40 = 480 (шт.) – карандашей
2) 560 – 480 = 80 (шт.) – фломастеров
3) 80 : 10 = 8 (шт.) – фломастеров в 1 коробке
Ответ: 8 фломастеров.
Страница 14, задача 48. Овощеводы получили в одной теплице по 32 кг овощей с каждого квадратного метра на площади 400 м2, а в другой — по 28 кг овощей на площади 300 м2. Сколько килограммов овощей получили в двух теплицах?
32 * 400 + 28 * 300 = 12800 + 8400 = 21200 (кг)
Ответ: 21200 кг овощей получили в двух теплицах.
Задача 49. Во вторник в ателье сшили 11 одинаковых курток, а в среду – 13 таких же курток. Всего на них израсходовали 72 м ткани. Сколько метров ткани израсходовали в каждый из этих дней?
Решение: 1) 11+13=24 (к) всего сшили; 2) 72:24=3 м ушло на каждую куртку; 3) 3*11=33 м ткани потратили во вторник; 4) 3*13=39 м ткани потратили в среду.
1) 11 + 13 = 24 (к.) – сшили за 2 дня
2) 72 : 24 = 3 (м) – ткани уходит на 1 куртку
3) 11 * 3 = 33 (м) – ткани израсходовали во вторник
4) 13 * 3 = 39 (м) – ткани израсходовали в среду
Ответ: 33 м, 39 м.
Задача 51. 1) Два велосипедиста выехали навстречу друг другу в 9 ч утра и встретились в 11 ч утра. Сколько времени был в пути до встречи каждый велосипедист?
2) Из двух посёлков выехали одновременно навстречу друг другу велосипедист и мотоциклист. Они встретились через 40 мин. Сколько времени был в пути до встречи каждый из них?
1) 11 — 9 = 2 (ч)
Ответ: 2 часа ч был в пути каждый велосипедист2) Каждый из них был в пути 40 мин.
Страница 15, задача 56. От двух пристаней отправились навстречу друг другу два теплохода. Один из них шел до встречи 4 ч со скоростью 36 км/ч. Другой теплоход прошел до встречи третью часть пути, пройденного первым. Поставь вопрос и реши задачу.
Решение: Сколько км прошел каждый из теплоходов до встречи? Какое расстояние прошли 2 теплохода? 1) 36:3=12 км/ч скорость второго теплохода; 2) 36*4=144 км прошел первый теплоход; 3) 12*4=48 км прошел второй теплоход 4) 48+144=192 км прошли два теплохода.
Записываем:
Какое расстояние прошел до встречи второй теплоход?
1) 36 * 4 = 144 (км) – прошел первый теплоход
2) 144 : 3 = 48 (км) – прошел второй теплоход
Ответ: 48 км.Какое расстояние между пристанями?
144 + 48 = 192 (км)
Ответ: 192 км расстояние между пристанями.
Задача 58. Бабушке вместе с внучкой Олей 63 года, а вместе с внучкой Машей 65 лет. Всем им вместе 73 года. Сколько лет каждой из них?
1) 73 – 63 = 10 (лет) – Маше
2) 73 – 65 = 8 (лет) – Оле
3) 73 – 10 – 8 = 55 (лет) бабушке.
Ответ: бабушке 55 лет, Оле 8 лет, Маше 10 лет.
Страница 16, задача 61. Реши задачи, сравни решения.
1) Два лыжника вышли одновременно навстречу друг другу из двух посёлков и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч, а второй — со скоростью 14 км/ч. Найди расстояние между посёлками.
2) Из двух посёлков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шёл со скоростью 12 км/ч, а второй — со скоростью 14 км/ч. Через сколько часов лыжники встретились?
3) Из двух посёлков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч. С какой скоростью шёл второй лыжник?
1. 1) 12 * 3 = 36 (км) − прошел первый лыжник
2) 14 * 3 = 42 (км) − прошел второй лыжник
3) 36 + 42 = 78 (км) − расстояние между поселками
Ответ: 78 км.2. 1) 12 + 14 = 26 (км/ч) − скорость сближения лыжников
2) 78 : 26 = 3 (ч) − время лыжников в пути до встречи
Ответ: 3 часа.3. 1) 78 : 3 = 26 (км/ч) − скорость сближения лыжников
2) 26 − 14 = 14 (км/ч) − скорость второго лыжника
Ответ: 14 км/ч.Сравнение задач.
В первом случае мы искали расстояние между поселками, умножив скорости лыжников на время в пути до встречи и сложив результаты;
во втором время лыжников до встречи, сложив скорости лыжников и разделив расстояние между поселками на этот результат, а в третьем скорость второго лыжника, разделив расстояние между городами на время в пути и отняв от этого результат скорость первого лыжника.
Задача 62. Составь и реши три похожие задачи про пешеходов, которые шли навстречу друг другу со скоростями 4 км/ч и 5 км/ч и встретились через 2 ч.
1. Два пешехода вышли одновременно навстречу друг другу из двух поселков и встретились через 2 ч. Первый пешеход шел со скоростью 4 км/ч, а второй − со скоростью 5 км/ч. Найди расстояние между поселками.
Решение:
1) 4 * 2 = 8 (км) − прошел первый пешеход
2) 5 * 2 = 10 (км) − прошел второй пешеход
3) 8 + 10 = 18 (км) − расстояние между поселками
Ответ: 18 км.2. Из двух поселков, расстояние между которыми 18 км, вышли одновременно навстречу друг другу два пешехода. Первый из них шел со скоростью 4 км/ч, а второй со скоростью 5 км/ч. Через сколько часов пешеходы встретились?
Решение:
1) 4 + 5 = 9 (км/ч) − скорость сближения пешеходов
2) 18 : 9 = 2 (ч) − время пешеходов в пути до встречи
Ответ: 2 часа.3. Из двух поселков, находящихся на расстоянии 18 км, вышли одновременно навстречу друг другу два пешехода и встретились через 2 ч. Первый пешеход шел со скоростью 4 км/ч. С какой скоростью шел второй пешеход?
Решение:
1) 18 : 2 = 9 (км/ч) − скорость сближения пешеходов
2) 9 − 4 = 5 (км/ч) − скорость второго пешехода
Ответ: 5 км/ч.
Страница 17, задача 67. Из двух городов, расстояние между которыми 520 км, одновременно вышли навстречу друг другу два поезда и встретились через 4 ч. Один поезд шёл со скоростью 60 км/ч. С какой скоростью шёл другой поезд?
1) 60 * 4 = 240 (км) – прошел первый поезд
2) 520 — 240 = 280 (км) – прошел другой поезд
3) 280 : 4 = 70 (км/ч) – скорость другого поезда
Ответ: 70 км/ч.2 способ
1) 520 : 4 = 130 (км/ч) − скорость сближения поездов
2) 130 − 60 = 70 (км/ч) − скорость второго поезда
Ответ: 70 км/ч.
Задача 68. От двух пристаней, расстояние между которыми 120 км, одновременно отошли навстречу друг другу два теплохода. Один из них шел со скоростью 22 км/ч, другой со скоростью 18 км/ч. Через сколько часов теплоходы встретились? Какое расстояние прошел до встречи каждый теплоход?
Решение: 1) 22+18=40 км проходили 2 теплохода каждый час; 2) 120:40=3 ч понадобилось теплоходам чтобы встретиться: 3) 22*3=66 км прошел один теплоход; 4) 18*3=54 км прошел второй теплоход.
Запишем решение и ответ:
1) 22 + 18 = 40 (км/ч) – скорость сближения теплоходов
2) 120 : 40 = 3 (ч) – время, через которое встретились теплоходы
3) 22 * 3 = 66 (км) – прошел первый теплоход
4) 18 * 3 = 54 (км) – прошел второй теплоход
Ответ: 3 ч, 66 км, 54 км.
Страница 18, задача 1. Витя ждал гостей на день рождения. Вокруг стола поставили несколько табуретов и несколько стульев. У каждого табурета было по 3 ножки, а у каждого стула — по 4. Ребята заняли все стулья и табуреты, и оказалось, что всех ножек — у стульев, табуретов и ребят — 49. Сколько всего ребят было за столом?
У каждого гостя 2 ноги, у каждого стула 4 ножки, а у каждого табурета − 3, значит, каждый гость и его место составляют:
1) 2 + 4 = 6 (ног) − если гость сидит на табурете или
2) 2 + 3 = 5 (ног) − если гость сидит на стуле.
3) 6 + 5 = 11 (ног) − имеет каждая пара гостей, сидящих на табурете и на стуле.
4) 49 : 11 = 4 (ост. 5) − это 4 пары гостей это 4 * 2 = 8 гостей, из них 4 на табуретках и 4 на стульях; остается еще 5 ног − это один гость, сидящий на табурете.
Значит, на стульях сидели 4 гостя, а на табуретах 4 + 1 = 5 гостей.
5) 4 + 5 = 9 (ребят) − было всего за столом.
Ответ: 9 ребят.
Страница 19, задача 5. Для отделки платья ленту длиной 1 м 50 см надо разрезать на несколько частей по 25 см, на несколько частей по 16 см и ещё одну часть длиной 2 см так, чтобы не было обрезков. Догадайся, как это сделать, и запиши, сколько будет частей по 25 см и сколько будет частей по 16 см.
1 м 50 см = 150 см
1) 150 − 2 = 148 (см) − составят части по 16 см и 25 см;
2) 25 + 16 = 41 (см) − составляет длина одной пары 16 см и 25 см;
3) 148 : 41 = 3 (ост. 25) − 3 пары частей − это 3 части по 16 см и 3 части по 25 см; остается еще 25 см − это одна часть, без пары.
Значит, будет 3 части по 16 см и 1 + 3 = 4 части по 25 см.
Ответ: 1 часть длиной 2 см, 3 части по 16 см и 4 части по 25 см.
Задача 6. Сергей живёт в посёлке и в школу ездит на велосипеде. Занятия в школе начинаются в 9 ч. В 8 ч 40 мин Сергей всегда уже проезжает половину пути от дома до школы. В школу Сергей приезжает за 10 мин до начала занятий. Сколько минут занимает путь Сергея до школы?
1) 9 ч – 10 мин = 8 ч 50 (мин) – время приезда Сергея в школу
2) 8 ч 50 мин – 8 ч 40 мин = 10 (мин) – время, затраченное на половину пути
3) 2 * 10 = 20 (мин) – занимает путь Сергея до школы
Ответ: 20 мин.
Страница 20, задача 4. Для ремонта квартиры купили 8 рулонов обоев длиной по 10 м 50 см. После ремонта осталась одна четвёртая часть купленных обоев. Сколько метров обоев осталось? Реши задачу разными способами.
1 способ:
1) 10 м 50 см * 8 = 84 (м) – обоев было куплено
2) 84 : 4 = 21 (м) – обоев осталось
Ответ: 21 м.2 способ:
1) 8 : 4 = 2 (р.) – обоев осталось после ремонта
2) 2 * 10 м 50 см = 21 м обоев осталось
Ответ: 21 м.
Страница 21, задача 12. Два мальчика одновременно пробежали навстречу друг другу по спортивной дорожке, длина которой 100 м. Они встретились через 10 с. Первый мальчик бежал со скорость 4 м/с с какой скоростью бежал второй мальчик?
Решение: 1) 100:10=10 м/с пробегали оба мальчика; 2) 10-4=6 м/с бежал второй мальчик.
Записываем:
1) 10 * 4 = 40 (м) – пробежал до встречи первый мальчик
2) 100 – 40 = 60 (м) – пробежал до встречи второй мальчик
3) 60 : 10 = 6 (м/с) – скорость второго мальчика
Ответ: 6 м/с.
Задача 13. Товарный поезд прошёл 315 км. Он был в пути до остановки 3 ч и после остановки 4 ч. Сколько километров прошёл поезд до остановки и сколько после, если он шёл с одинаковой скоростью?
1) 3 + 4 = 7 (ч) – был поезд в пути
2) 315 : 7 = 45 (км/ч) – скорость поезда
3) 3 * 45 = 135 (км) – прошел поезд до остановки
4) 4 * 45 = 180 (км) – прошел поезд после остановки
Ответ: 135 км, 180 км.
Страница 22, задача 20. У хозяйки 3 корзины с яблоками. Всего в них 60 кг яблок. В первой и второй корзинах вместе 38 кг яблок, а во второй и третьей вместе 40 кг. Сколько килограммов яблок в каждой корзине?
1) 60 − 38 = 22 (кг) − яблок в третьей корзине
2) 40 − 22 = 18 (кг) − яблок во второй корзине
3) 38 − 18 = 20 (кг) − яблок в первой корзине
Ответ: 20 кг, 18 кг, 22 кг.
Задача 24. В новом студенческом общежитии 20 трёхкомнатных квартир, 40 двухкомнатных и 4 однокомнатные. Сколько студентов в общежитии, если у каждого из них отдельная комната?
20 * 3 + 40 * 2 + 4 = 60 + 80 + 4 = 144 (ст.) в общежитии.
Ответ: 144 студентов.
Задача 25. Директор предприятия часто ведёт международные переговоры по телефону. Одна минута разговора с Белоруссией стоит а р., с Францией — а * 3 р., с Китаем — а * 5 р. Состоялось 6 разговоров с Белоруссией, 4 разговора с Францией и 2 разговора с Китаем. Продолжительность каждого разговора 5 мин. Составь различные выражения по этому условию и поясни, что они означают.
1) 5 * a (р.) − стоит пятиминутный разговор с Белоруссией;
2) 5 * (a * 3) = 15 * a (р.) − стоит пятиминутный разговор с Францией;
3) 5 * (a * 5) = 25 * a (р.) − стоит пятиминутный разговор с Китаем;
4) 5 * a * 6 = 30 * a (р.) − стоят все разговоры с Белоруссией;
5) 5 * (a * 3) * 4 = 60 * a (р.) − стоят все разговоры с Францией;
7) 5 * (a * 5) * 2 = 50 * a (р.) − стоят все разговоры с Китаем;
8) 5 * a * 6 + 5 * (a * 3) * 4 + 5 * (a * 5) * 2 = 5 * (a * 6 + a * 3 + a * 5) (р.) − стоимость всех переговоров.
Задача 26. За 6 табуреток заплатили а р., а за 4 стула — b р.
1) Поставь к этому условию два разных вопроса, чтобы задача решалась так: b : 4 — a : 6; (b : 4): (а : 6).
2) Найди значение каждого выражения при a = 1200 р. и b = 3200 p.
1)
b : 4 — a : 6 — на сколько дороже стул табуретки?
(b : 4): (а : 6) — во сколько раз больше стоит стул, чем табуретка?2)
b : 4 — a : 6 = 3200 : 4 — 1200 : 6 = 800 — 200 = на 600 (р.)
(b : 4) : (a : 6) = (3200 : 4) : (1200 : 6) = 800 : 200 = в 4 (раза)
Задача 27. Журнал объявил конкурс детских рисунков, в котором приняла участие одна девятая часть его подписчиков. Сколько подписчиков у журнала, если редакция получила рисунки от 10000 детей?
10000 * 9 = 90000 (п.) у журнала.
Ответ: 90000 подписчиков.
Страница 23, задача 31. На выставке представлены 1370 книг. Из них учебников для младших школьников – 156, это в 3 раза меньше, чем учебников для старших школьников, а учебников для студентов столько, сколько учебников для младших и старших школьников вместе. Остальные книги для учителей. Сколько книг для учителей представлено на выставке?
Решение: 1) 156*3=468 учебников для старших школьников; 2) 156+468=624 учебников для студентов; 3) 1370-624-468-156=122 книги для учителей.
Записываем:
1) 156 * 3 = 468 (к.) – для старших школьников
2) 156 + 468 = 624 (к.) – для студентов
3) 156 + 468 + 624 = 1248 (к.) – всего для школьников и студентов
4) 1370 – 1248 = 122 (к.) – для учителей на выставке
Ответ: 122 книги.
Страница 25-41. ГДЗ по теме Деление на числа, оканчивающиеся нулями
Страница 25, задача 75. Из 1т молока получается 83 кг сыра или 45 кг масла. На сколько килограммов больше сыра, чем масла, получится из 20 т молока? Реши задачу разными способами.
Решение: 1 способ 1) (83-45)*20=760 (кг) на столько кг больше получится сыра из 20 т молока; 2 способ 1) 20*83-20*45=760 (кг) на столько кг больше получится сыра из 20 т молока;
Записываем:
1 способ
1) (83-45)*20=760 (кг)
Ответ: на 760 кг больше получится сыра из 20 т молока.2 способ
1) 20*83-20*45=760 (кг)
Ответ: на 760 кг больше получится сыра из 20 т молока.
Страница 26, задача 82. Из двух городов, расстояние между которыми 846 км, вышли одновременно навстречу друг другу два поезда. Один шел со скоростью 85 км/ч, другой со скоростью 60 км/ч. Какое расстояние будет между поездами через 3 часа?
Решение: 1) 85+60=145 км проходили поезда каждый час; 2) 145*3=435 км прошли за 3 часа; 3) 846-435=411 км останется между поездами через 3 часа.
Страница 27, задача 90. В мастерской в первый день сшили 19 одинаковых рюкзаков, во второй – 23 таких рюкзака. На все рюкзаки пошло 84 м ткани. Сколько метров ткани расходовали каждый день?
Решение: 1) 19+23=42 рюкзака сшили за 2 дня; 2) 84:42=2 м ткани пошло на каждый рюкзак; 3) 19*2=38 м израсходовали в первый день; 4) 23*2=46 м израсходовали во второй день.
Страница 28, задача 95. Из 2 м полотна получается 3 наволочки. Сколько таких наволочек получится из 42 м полотна?
Решение: 1) 42:2=21 раз по 2 метра в 42 метрах; 2) 21*3=63 наволочки получится из 42 метров.
Страница 29, задача 107. Длина реки Волги 3690 км. Туристы прошли на лодках третью часть ее длины. Сколько дней они плыли, если двигались со скоростью 6 км/ч и ежеденевно находились в плавании по 5 часов.
Решение: 1) 5*6=30 км проплывали туристы каждый день; 2) 3690:3=1230 3 часть реки; 3) 1230:30=41 день плыли.
Страница 30, задача 112. На завод отправлено 3600 т угля в вагонах, по 60т в каждом, и столько же угля в вагонах, по 90 т в каждом. Каких вагонов потребовалось больше и на сколько больше?
Решение: 1) 3600:60=60 вагонов по 60 т; 2) 3600:90=40 вагонов по 90 т. 3) 60-40=20 на вагонов потребовалось больше с массой загрузки в 60 т
Страница 33, задача 127. В киоске продавали тетради: школьные по цене а рублей за тетрадь, общие по цене с рублей за тетрадь. Сколько стоят вместе 5 школьных тетрадей и 5 общих? Запиши выражения, которые показывают, как можно решить эту задачу двумя способами.
Решение: 1 способ 5*а+5*с 2 способ 5* (а+с)
Страница 34, задача 134. Из двух поселков выехали одновременно навстречу друг другу два всадника. Первый ехал со скоростью 200 м/мин, а второй проезжал в минуту на 20 м меньше. Всадники встретились через 50 минут. Найди расстояние между поселками.
Решение: 1) 200-20=180 м/мин ехал второй всадник. 2) 200+180=380 м проезжали всадники каждую минуту; 3) 380*50=19000 метров расстояние между поселками.
Страница 36, задача 18. Во время разлива ширина реки увеличилась на 800 м и достигла 1 км. Во сколько раз увеличилась ширина реки во время разлива?
Решение: 1) 1000-800=200 метров была ширина реки; 2) 1000:200=5 в 5 раз увеличилась ширина реки.
Страница 37, задача 24. Грузовая машина прошла 1500 км. Сколько горючего было израсходовано, если на каждые 50 км пути требуется 16 л горючего?
Решение: 1) 1500:50=30 раз по 50 км в 1500 км; 2) 30*16= 480 литров было израсходовано.
Страницы 42-56. Решебник к теме Умножение на двузначное и трехзначное число
Страница 42, задача 144. Чтобы получить 3 кг подсолнечного масла, надо взять 16 кг семян подсолнечника. Сколько килограммов семян потребуется, чтобы получить 15 кг подсолнечного масла?
Решение: 1) 15:3=5 раз 3 кг в 15 кг; 2) 5*16=80 кг семян потребуется.
Страница 43, задача 150. В рыбном хозяйстве в одном пруду вырастили по 7 кг на 1 м2 площади пруда и получили 67200 кг рыбы, а в другом пруду по – 8 кг карпа на 1 м2 площади и получили 61600 рыбы. На сколько квадратных метров площадь одного пруда больше площади другого?
Решение: 1) 67200:7=9600 м2 площадь первого пруда; 2) 61600:8=7700 м2 площадь второго пруда; 3) 9600-7700=1900 м2 один пруд больше другого.
Страница 44, задача 158. Два самолета вылетели в одно и тоже время с аэродрома в противоположных направлениях. Через 10 минут после вылета расстояние между ними было 270 км. первый самолет летел со скоростью 15 км/мин. С какой скоростью летел второй самолет?
Решение: 1) 10*15=150 км пролетел первый самолет за 10 минут; 2) 270-150=120 км пролетел второй самолет за 10 мин; 3) 120:10-12 км/мин летел второй самолет.
Страница 45, задача 162. При экономном раскрое сберегли на каждом пальто по 12 см ткани, а на каждом костюме по 13 см ткани. Сколько сэкономят ткани при раскрое 96 пальто и 96 костюмов? Сколько детских пальто можно сшить из сэкономленной ткани, если на одно пальто идет 2 м ткани?
Решение: 1) 12*96=1152 см сэкономили на пальто; 2) 13*96=1248 см сэкономили на костюмах; 3) 1152+1248=2400 см или 24 метра сэкономили всего; 4) 24:2=12 пальто можно сшить из сэкономленной ткани.
Страница 47, задача 175. Два самолета летели с одинаковой скоростью. Первый самолет был в воздухе 4 ч, второй – 6 ч. Первый пролетел на 1400 км меньше второго. Какое расстояние пролетел каждый самолет?
Решение: 1) 6-4=2 часов в воздухе был больше второй самолет за которые он пролетел 1400 км; 2) 4:2=2 раза в 4 часах по 2 часа; 3) 2*1400=2800 км пролетел первый самолет; 4) 6:2=3 раза в 6 часах по 2 часа; 5) 3*1400=4200 км пролетел второй самолет.
Остается только добавить, что в четвертом классе все еще могут снизить оценку за неаккуратность, даже по математике, поэтому домашнее задание старайтесь написать красивым почерком. Если есть какие-то вопросы по ГДЗ решебника, задавайте в комментариях.
Страница 48, задача 184. Длина цветника прямоугольной формы равна 20 м, а ширина – 5 м. Его площадь составляет десятую часть площади огорода. Найди площадь огорода.
Решение: 1) 20*5=100 м2 площадь цветника; 2) 100*10=1000 м2 площадь огорода.
Страница 49, задача 187. Двум классам поручено расчистить школьный каток, длина которого 20 м, а ширина 10 м. В одном классе 26 учеников, а в другом 24. Сколько квадратных метров должен расчистить каждый класс, если распределить работу по числу учеников.
Решение: 1) 20*10=200 м2 площадь катка; 2) 26+24=50 уч всего учеников в двух классах; 3) 200:50=4 м2 должен расчистить каждый ученик; 4) 4*26=104 м2 должен расчистить класс где 26 учеников; 5) 4*24=96 м2 должен расчистить класс где 24 ученика.
Записываем:
1) 20*10=200 (м2 ) – площадь катка
2) 26+24=50 (уч.) – в двух классах
3) 200:50=4 (м2 ) – должен расчистить каждый ученик
4) 4*26=104 (м2 ) – должен расчистить класс, где 26 учеников
5) 4*24=96 (м2 ) – должен расчистить класс, в котором 24 ученика
Ответ: 104 м2 и 96 м2 .
Страница 57-85. Деление на двузначное и трехзначное число
…
Со страницы 86 и до конца второй части учебника идет итоговое повторение всего изученного и материал для расширения и углубления знаний, что пригодится ученику в подготовке к итоговому тестированию
Решебник и ГДЗ по Математике 4 класс
- Видеорешения
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Французский язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- Технология
- Испанский язык
- Казахский язык
- 1
- 2
- 3
Математика 4 класс Богданович. Решебник. ГДЗ. Скорость, время, расстояние.
Сложение и вычитание многозначных чисел.
Категория: —>> Математика 4 класс Богданович
Задание: —>> 381 — 400 401 — 418
наверх
Задание 381.
Рассмотри решение задачи и прочитай объяснение.
Задача. За 2ч автобус проехал 120 км, проезжая за каждый час одинаковое расстояние. Сколько километров автобус проезжал за 1 ч?
Решение: 120 : 2 = 60 (км). Ответ: за 1 ч автобус проезжал 60 км.
Объяснение. Если за каждый час автобус проезжает 60 км, то говорят, что он движется со скоростью 60. км в час.
Это записывают так: 60 км/ч.
Чтобы найти скорость, надо расстояние поделить на время.
Задание 382.
По данным таблицы вычисли скорость движения велосипедиста, пассажирского самолёта, ласточки.
Решение:
- Скорость велосипедиста: 28 км : 2 ч = 14 км/ч.
- Скорость ласточки: 180 км : 2 ч = 90 км/ч.
- Скорость самолета: 1500 км : 3 ч = 500 км/ч.
Задание 383.
Велосипедист был в пути 6 ч, а мотоциклист 2 ч. Велосипедист проехал 72 км, а мотоциклист 100 км. На сколько скорость мотоциклиста больше скорости велосипедиста?
План решения
- 1) Какова скорость велосипедиста?
- 2) Какова скорость мотоциклиста?
- 3) На сколько скорость мотоциклиста больше скорости велосипедиста?
Решение:
- 1) 72 : 6 = 12 (км/ч) скорость велосипедиста;
- 2) 100 : 2 = 50 (км) скорость мотоциклиста;
- 3) 50 — 12 = 38 (км/ч).
- Ответ: скорость мотоциклиста на 38 км/ч больше, чем скорость велосипедиста.
Задание 384.
Расстояние 400 м мальчик пробежал туда и обратно за 4 мин. С какой скоростью бежал мальчик?
Решение:
- 1) 400 : 4 = 100 (м/мин).
- Ответ: скорость мальчика 100 м/мин.
Задание 385.
Расстояние между условными пунктами K и M на орбите искусственного спутника Земли составляет 320 км. Четвёртую часть этого расстояния спутник пролетел за 10 с. С какой скоростью он летел?
Решение:
- 1) 320 : 4 = 80 (км) четвертая часть расстояния;
- 2) 80 : 10 = 8 (км/с).
- Ответ: скорсть спутника 8 км/с.
Задание 386.
Решение:
1)
| 8000 + 7000 = 15000 | 90000 + 7000 = 97000 | 1500 − 300 = 1200 | 1210 − 300 = 910 |
| 600 + 7000 = 7600 | 23000 + 7000 = 30000 | 2000 − 300 = 1700 | 5200 − 300 = 4900 |
| 60 + 7000 = 7060 | 45000 + 7000 = 52000 | 900 − 300 = 600 | 11000 − 300 = 10700 |
- 2)
- 20 грн 08 к − 59 к = 2008 к − 59 к = 949 к = 9 грн 49 к .
- 12 грн 70 к − 8 грн 07 к = 4 грн 63 к .
3) 3 грн 60 к : 3 = 360 : 3 = 120 к = 1грн 20 к .
Задание 387.
Расстояние между двумя пристанями 320 км. Половину этого расстояния моторная лодка прошла за 4 ч. С какой скоростью шла лодка?
Решение:
- 1) 320 : 2 = 160 (км) половина расстояния;
- 2) 160 : 4 = 40 (км/ч).
- Отвтет: скорость лодки 40 км/ч.
Задание 388.
Расстояние 20 км всадник проехал туда и обратно за 4 ч. С какой скоростью ехал всадник?
Решение:
- 1) 20 + 20 = 40 (км) расстояние туда и обратно;
- 2) 40 : 4 = 10 (км/ч).
- Ответ: скорость всадника 10 км/ч.
Задание 389.
Прочитай задачу и рассмотри её решение.
- Задача. Лыжник был в пути 3 ч, двигаясь со скоростью 12 км/ч. Какое расстояние прошёл лыжник?
- Решение: 12 — 3 = 36 (км).
- Ответ: за 3 ч лыжник прошёл 36 км.
Чтобы найти расстояние, надо скорость умножить на время
Задание 390.
Пассажирский катер шёл 4 ч, а буксирный 7 ч. Какой из них прошёл большее расстояние и на сколько километров, если скорость пассажирского катера 24 км/ч, а буксирного 14 км/ч?
Решение:
- 1) 24 * 4 = 96 (км) прошел пассажирский катер;
- 2) 14 * 7 = 98 (км) прошел буксирный катер;
- 3) 98 — 96 = 2 (км).
- Ответ: буксирный катер прошел на 2 км больше.
Задание 391.
По данным таблицы найди расстояния.
Решение:
- Пешеход: 5км/ч * 4ч = 20 км .
- Такси: 70 км/ч * 2 ч = 140 км .
- Электропоезд: 120 км/ч * 3 ч = 360 км .
Задание 392.
В течение дня туристы шли пешком 2 ч, на автобусе ехали 3 ч. Пешком они двигались со скоростью 4 км/ч, на автобусе ехали со скоростью 45 км/ч. Какой путь преодолели туристы за день?
Решение:
- 1) 2 * 4 = 8 (км) преодолели туристы пешком;
- 2) 3 * 45 = 135 (км) преодолели турсты на автобусе;
- 3) 8 + 135 = 143 (км).
- Ответ: за день туристы преодолели 143 км.
Задание 393.
Решение:
- 54408 + 351875 + 973 = 406283 + 973 = 407256
- 10 ц 3 кг − 4 ц 12 кг = 5 ц 91 кг
- 48350 − 9405 + 598 = 38945 + 598 = 39543
- 8365 − (2120 + 1080) = 8365 − 3200 = 5165
Задание 394.
На птичьем дворе было 16 цыплят, а утят — в 4 раза больше.
- По условию задачи можно поставить такие вопросы:
- 1) Сколько утят было на птичьем дворе?
- 2) Сколько было цыплят и утят вместе?
- 3) На сколько больше было утят, чем цыплят? Выполни устно вычисления и запиши ответы.
Решение:
- 1) 16 * 4 = 64 Утят — 64;
- 2) 16 + 64 = 80 — цыплят и утят.
- 3) 64 — 16 = 48 — Утят на 48 больше, чем цыплят.
Задание 395.
В течение двух дней велосипедист был в дороге 12 ч и за это время проехал 180 км. Сколько километров проедет мотоциклист за 20 ч, если его скорость на 36 км/ч больше скорости велосипедиста?
Решение:
- 1) 180 : 12 = 15 (км/ч) скорость велосипедиста;
- 2) 15 + 36 = 51 (км/ч) скрость мотоциклиста;
- 3) 51 * 20 = 1020 (км).
- Ответ: мотоциклист проедет 1020 км.
Задание 396.
Решение:
- 1) 10 ц 08 кг − 4 ц 12 кг = 5 ц 96 кг
- 2) 12 км 750 м + 4 км 75 м = 16 км 825 м
- 3) 47650 − 875 − 6588 = 46775 − 6588 = 40187
- 4) 3358 − (12 + 778) = 3358 − 790 = 2568
Задание 397.
Автомобиль ехал 2 ч со скоростью 66 км/ч. После этого ему осталось проехать расстояние в 3 раза большее, чем он уже проехал. Какое расстояние должен был проехать автомобиль?
Решение:
- 1) 2 * 66 = 132 (км) проехал автомобиль;
- 2) 132 * 3 = 396 (км) осталось проехать автомобилю;
- 3) 396 + 132 = 528 (км).
- Ответ: автомобиль должен был проехать 528 км.
Задание 398.
Прочитай задачу и рассмотри ее решение.
- Задача. Пассажир проехал на автобусе 180 км. Скорость автобуса 60 км/ч. Сколько времени ехал пассажир на автобусе?
- Решение: 180 : 60 = 3 (ч).
- Ответ: пассажир ехал на автобусе 3 ч.
Чтобы найти время, надо расстояние поделить на скорость.
Задание399.
По данным таблицы найди время движения.
Решение:
- Лыжник: 26 км : 13 км/ч = 2 ч.
- Поезд: 240 км : 60 км/ч = 4 ч.
- Легковой автомобиль: 240 км : 80 км/ч = 3 ч.
Задание 400.
По асфальтированной дороге автомобиль проехал расстояние 210 км со скоростью 70 км/ч, а по грунтовой — 90 км со скоростью 45 км/ч. За какое время автомобиль проехал всё расстояние?
Решение:
- 1) 210 : 70 = 3 (ч) ехал автомобиль по асфальтированной дорогое4;
- 2) 90 : 45 = 2 (ч) ехал автомобиль по грунтовой дороге;
- 3) 3 + 2 = 5 (ч).
- Ответ: автомобиль проехал все расстояние за 5 ч.
Задание: —>> 381 — 400 401 — 418
Логические задачи для 4 класса
Задача 1
Брату и сестре 2 года назад вместе было 15 лет. Сейчас сестре 13 лет.
Сколько должно пройти лет, чтобы брату исполнилось 9 лет?
Ответ: 3 года
Задача 2
Запиши число 7 при помощи четырех троек и знаков действий.
Найди несколько решений.
Ответ: (7 = 3 : 3 + 3 + 3, 7 = 3 + 3 + 3 : 3, 7 = 3 + 3 : 3 + 3)
Задача 3
Речь пойдёт про единицы времени. Что можно узнать, данным произведением 60 х 60 х 24 х 7?
Ответ: Количество секунд в неделю
Задача 4
На пароме помещается или 6 грузовиков, или 10 легковушек.
В четверг паром, полностью загруженный, 5 раз пересек реку и переправил 42 машины.
Сколько было среди них грузовиков?
Ответ: 12
Задача 5
В гости к Игорю пришли друзья.
Сколько их было, если каждый из них сложил из даты своего рождения число и номер месяца и получил 35? Причём даты рождения у всех гостей разные.
Ответ: 8
Задача 6
Ребята измеряли шагами длину игровой площадки.
У Лизы получилось 25 шагов, у Полины – 27, у Максима – 22, а у Юры – 24.
У кого из ребят самый короткий шаг?
Ответ: У Полины
Задача 7
У сороконожки 90 ножек. Она купила 13 пар сапожек. Но при этом 16 ног остались босыми.
Сколько пар старых сапожек было на сороконожке до покупки новых сапожек?
Ответ: 24
Задача 8
Из 64 маленьких кубиков составили большой куб. Синей краской покрасили пять граней большого куба.
Назови количество маленьких кубиков с тремя синими гранями.
Ответ: 4 – по углам
Задача 9
Расставь скобки так, чтобы получилось верное равенство 211 – 126 – 74 · 8 = 88
Ответ: (211 – 126 – 74) · 8 = 88
Задача 10
Если самое большое трехзначное число уменьшить на самое большое двузначное число, полученный результат разделить на 4, а затем вычесть 25, то получится возраст мудреца-звездочета.
Сколько лет звездочету?
Решение:
1. 999 — 99 = 900
2. 900 : 4 = 225
3. 225 — 25 = 200
Ответ: 200 лет
Задача 11
Длина прямоугольного бассейна в 5 раз больше его ширины, причем ширина на 20 м меньше. Найдите площадь дна бассейна.
Решение:
1. 20 : 4 = 5 (м) составляет 1 часть, и является шириной бассейна
2. 5 * 5 = 25 (м) длина бассейна
3. 25 * 5 = 125 (м2) площадь дна бассейна
Ответ: площадь бассейна равна 125 м2
Задача 12
Степа Смекалкин задумал число. Потом он уменьшил это число на 19 и к произведению прибавил 19. В ответе у него тоже получилось 19. Какое число задумал Степа?
Ответ: 0
Дальше: Задачи на логику 4 класс с решением
Стратегии и ресурсы для учителей начальной школы
Решение математических задач KS2 имеет решающее значение для успеха в национальных оценках. Если ваши ученики Key Stage 2 все еще не могут рассуждать и решать задачи по математике, вот несколько стратегий решения проблем, которые можно попробовать на своих классах; все они соответствуют предложенным Офстедом стратегиям обучения в начальной школе.
Рассуждения и решение задач широко считаются одними из самых важных занятий школьной математики.Еще в 1982 году в The Cockcroft Report говорилось:
«Способность решать задачи лежит в основе математики. Математика «полезна» только в той степени, в которой ее можно применить к конкретной ситуации, и это способность применять математику к множеству ситуаций, которые мы называем «решением проблем». […] На каждом этапе […] учитель должен помочь ученикам понять, как применять изучаемые концепции и навыки и как использовать их для решения задач.Эти задачи должны относиться как к применению математики к повседневным ситуациям в рамках опыта учеников, так и к ситуациям, которые незнакомы ».
Тридцать с лишним лет спустя решение задач по-прежнему является сердцевиной учебной программы по математике и — наряду с беглость и рассуждение — завершают триаду целей Новой национальной учебной программы 2014 года.
Взгляд Офстеда на решение задач в учебной программе математики
Несмотря на центральную роль, Офстед сообщает, что «решению проблем в учебной программе математики уделяется недостаточно внимания».Неудивительно, что решению проблем не учат так хорошо, потому что учителям может не хватать уверенности или они склонны полагаться на меньший набор проверенных и проверенных стратегий, которые им удобны, но которые не всегда могут «сработать». Если вы хотите оказать дополнительную поддержку тем ученикам, которые еще не освоили решение проблем, вам, вероятно, понадобится ряд различных стратегий, в зависимости от решаемой задачи и способностей ученика.
Поэтому мы создали бесплатный ресурс KS2, предназначенный для координаторов математики и учителей KS2, который научит вас, когда и как использовать 9 основных методов решения проблем: Полное руководство по методам решения проблем
Контекст решения проблем KS2
Согласно Джейн Джонс, бывшему специалисту по HMI и ведущему специалисту по математике в стране, в ее презентации на Jurassic Maths Hub:
- Проблемы не нужно ставить в контексте реальной жизни, остерегайтесь псевдоконтекстов.
- Набор головоломок и других задач помогает ученикам стратегически подходить к задачам, последовательно разворачивать решения и использовать записи, чтобы помочь им обдумывать следующие шаги.
- Особенно важно, чтобы учителя и преподаватели делали упор на рассуждениях, а не просто проверяли правильность окончательного ответа.
- Ученики любого уровня подготовки должны научиться решать проблемы, а не только самые успешные или быстрые работники.
Полное руководство по методам решения проблем
9 готовых к работе техник решения проблем с сопутствующими задачами, чтобы получить независимое рассуждение KS2
Как подойти к задачам KS2 по математике
Итак, что мы делаем? В советах Well Ofsted довольно четко указано, что делать при обучении решению проблем.Джейн Джонс говорит, что мы должны:
- Ставить задачи в рамках обучения по всем темам для всех учеников.
- Измените способы, которыми вы создаете проблемы.
- Старайтесь не побуждать учеников слишком рано и сосредотачиваться на получении «ответа» — ученикам необходимо укрепить свою уверенность, навыки и стойкость в решении проблем, чтобы они могли применять их естественным образом в других ситуациях.
- Обязательно обсудите с учениками альтернативные подходы, чтобы помочь им развить рассуждения.
- Обеспечьте, чтобы задачи для тех, кто достиг высоких результатов, требовали навыков рассуждения и решения проблем, а не только сложных цифр.
Пожалуй, больше, чем большинство тем по математике, обучение решению задач всех учеников требует систематического подхода. Ученики могут столкнуться с любым количеством многоступенчатых задач со словами во время своего экзамена SAT, и они будут решать их без нашей помощи. Чтобы по-настоящему дать ученикам инструменты, необходимые для решения задач по математике, мы должны усвоить методы решения задач, приближающихся к .
Имея это в виду, ниже приведены некоторые методы и приемы, которые вы должны учитывать при обучении решению проблем на уроках математики KS2. Для получения более подробной информации о том, как обучать этим методам, загрузите полное руководство по методам решения проблем
Модели для подхода к решению проблем KS2
Стать уверенным в себе и способным решать проблемы — это сложный бизнес, требующий ряда навыков и опыт. Детям нужно за чем следить. Они не могут просто составить план атаки из воздуха, поэтому модели решения проблем важны, особенно когда они запоминаются.Они помогают установить в учениках такую закономерность, чтобы, когда они видят проблему, они чувствовали себя уверенно, предпринимая шаги для ее решения.
Узнайте, как мы обучаем учеников самостоятельно решать задачи, в нашем блоге: 20 математических стратегий KS2, которые гарантируют прогресс для всех учеников.
Наиболее часто используемой моделью является модель Джорджа Поля (1973), который предложил 4 этапа решения проблем, а именно:
- Понять проблему
- Разработать стратегию для ее решения
- Осуществить стратегию
- Проверить результат
Многие модели следовали модели Polya и использовали аббревиатуры для обозначения этапов.Какую модель вы используете, может зависеть от возраста детей, которых вы обучаете, а иногда и от типов словесных задач, которые они пытаются решить. Ниже приведены несколько примеров сокращений моделей Polya:
КУБИКИ
C — Обведите вопросительные слова
U — Подчеркните ключевые слова
B — Поместите в рамку любые ключевые числа
E — Оцените (какие шаги мне предпринять?)
S — Решить и проверьте (имеет ли мой ответ смысл и как я могу дважды проверить?)
RIDE
R — Прочтите задачу правильно.
I — Укажите соответствующую информацию.
D — Определите операцию и единицу выражения ответа.
E — Введите правильные числа и вычислите
IDEAL
I — Определите проблему
D — Определите проблему
E — Изучите варианты
A — Действуйте по плану
L — Посмотрите на последствия
RICE
R — Прочтите и запишите задачу
I — Проиллюстрируйте свое мышление с помощью картинок, моделей, числовых линий и т. Д.
C — Вычислите, вычислите и проверьте
E — Объясните свое мышление
RUCSAC
R — Прочтите вопрос и подчеркните важные моменты
U — Поймите: подумайте, что делать, и напишите числовые предложения, которые вам понадобятся
C — Выберите, как вы это сделаете
S — Решите проблему
A — Ответьте
C — Проверьте
QUACK
Q — Вопрос — внимательно прочтите
U — Поймите — подчеркните или обведите ключевые элементы
A — Приблизительно — подумайте о размере своего ответа
C — Вычислите
K — Определите, разумен ли ответ
TEAR
T — Подумайте о проблеме и обдумайте
E — Изучите и найдите корень проблемы
A — Действуйте, выбрав стратегию
R — Повторно проанализируйте и оцените эффективность метода
Идея, лежащая в основе этих моделей решения проблем, заключается в следующем. то же самое: дать детям структуру и построить внутренний монитор, чтобы у них был деловой способ работы с проблемой.
Модель, которую вы выбираете, менее важна, чем знание того, что ученики могут опираться на модель, которой нужно следовать, чтобы они подходили к задачам систематически и осмысленно. Намного более простая модель — которую мы используем в Ultimate Guide to KS2 Problem Solving Техники — это УЦР: понять проблему, общаться и размышлять.
Что включено в руководство?
После прочтения полного руководства по методам решения проблем KS2, мы гарантируем, что у вас будет новый метод решения проблем, который вы сможете опробовать завтра в классе.В нем представлены подсказки для вопросов и упражнения, которые можно попробовать, а также показаны пошаговые инструкции по обучению этим 9 техникам
Когнитивная активация: получение учеников KS2 в зоне лампочки
Если вам нужно больше убеждения, ученики, которые используют стратегии, которые их вдохновляют Подумайте о математике более глубоко. Проблемы связаны с более высокими достижениями по математике. В 2015 году Национальный фонд исследований в области образования (NFER) опубликовал документ «PISA на практике: когнитивная активация в математике». Этот проницательный отчет в значительной степени ускользнул от внимания математиков, но он предлагает значительную пищу для размышлений о том, что мы, как учителя, можем сделать, чтобы повысить математическую грамотность и повысить математические достижения.
В когнитивной активации нет ничего загадочного; просто обучение стратегиям решения проблем, о которых ученики могут думать и использовать, когда сталкиваются с математической проблемой, которую они пытаются решить. Познавательный Он побуждает нас, учителей, разрабатывать проблемы, которые могут быть решены более чем одним способом и «могут потребовать разных решений в разных контекстах». Чтобы это сработало, ключевым моментом является знакомство детей со сложным контентом и поощрение культуры исследовательской беседы. Как есть:
- Давать ученикам задачи по математике, требующие от них длительного размышления.
- Просить учеников использовать свои собственные процедуры для решения сложных задач.
- Создание учебного сообщества, в котором учащиеся могут ошибаться.
- Попросить учеников объяснить, как они решили задачу и почему они выбрали этот метод.
- Представьте ученикам проблемы в разных контекстах и попросите их применить то, что они узнали, в новых контекстах.
- Ставить ученикам задачи без очевидного метода решения или нескольких решений.
- Поощрение учеников к размышлению над проблемами.
Искра когнитивной активации — это то же самое, что разжечь огонь — после того, как он загорелся, он может гореть самостоятельно. Однако это требует времени, структуры и использования нескольких методов для приближения к решению проблем. Такие приемы, как открытое решение проблем, обычно изучаются на примерах, поэтому мы советуем вам создать несколько моделей для изучения учениками, а также контрольные вопросы для самостоятельной работы. Существует множество примеров, и мы рекомендуем вам изучить их больше (например, анализировать и исследовать, создавать древовидную диаграмму и использовать более простые числа).
Прочтите это: Как развить математические рассуждения у учеников KS2
Это время, усилия и планирование, однако, будут потрачены не зря. Оснащение учеников инструментами для решения задач, с которыми они никогда раньше не сталкивались, больше похоже на обучение на всю жизнь, чем на обучение математике. Навыки, которые они приобретут в результате успешного обучения решению проблем, будут навыками, которые они будут использовать и оттачивать всю оставшуюся жизнь, а не только для сдачи экзаменов SAT.
Чтобы узнать о различных методах решения проблем с объяснениями, контекстным использованием, примерами задач и контрольными вопросами, не забудьте загрузить наше бесплатное полное руководство по решению проблем и методам рассуждений KS2 здесь.
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Каждую неделю репетиторы-специалисты по математике Third Space Learning поддерживают тысячи учеников в сотнях школ, проводя еженедельные индивидуальные онлайн-уроки и занятия по математике, призванные восполнить пробелы и ускорить успеваемость.
С 2013 года мы помогли более 60 000 учеников начальных школ стать более уверенными и способными математиками. Узнайте больше или запросите индивидуальное предложение для вашей школы, чтобы рассказать нам о потребностях вашей школы и о том, как мы можем помочь.
Решение математических задач
-
Тематический каталог
-
Гуманитарные и социальные науки
-
Антропология
-
Изобразительное искусство
-
Каталог коммуникаций, кино и театра
-
Массовые коммуникации / Связи с общественностью / Фильм
-
Речевое общение
-
Театр
-
английский
-
Сочинение
-
Развивающий английский
-
Литература и творческое письмо
-
Техническая коммуникация
-
История
-
Междисциплинарные исследования
-
Семейные исследования и человеческое развитие
-
Гуманитарные науки
-
Расовые и этнические исследования
-
Социальная наука
-
Женские и гендерные исследования
-
Музыка
-
Философия
-
Политическая наука
-
Психология
-
Религия
-
Социальная работа / семейная терапия / социальные услуги
-
Социология
-
Мировые языки
-
китайский язык
-
французский язык
-
Немецкий
-
Итальянский
-
Японский
-
Языковые методы
-
латинский
-
португальский
-
русский
-
испанский язык
-
Математика и наука
-
Анатомия и физиология
-
Биология и микробиология
-
Специальности Биология / Биология высшего уровня
-
Микробиология
-
Неосновная биология
-
Химия
-
Наука об окружающей среде
-
География и атмосферные науки
-
Геология и океанография
-
Здоровье и кинезиология
-
Математика
-
Продвинутая математика
-
Исчисление
-
Развивающая математика
-
Конечная математика и прикладное исчисление
-
Гуманитарные науки Математика / Математика для учителей
-
Математика для карьеры
-
Математика
-
Математика Precalculus
-
Техническая математика
-
Питание
-
Физика и астрономия
-
Статистика
-
Вводная статистика
-
Статистика верхнего уровня
-
Профессиональная карьера
-
Бизнес
-
Бухгалтерский учет и налогообложение
-
Деловые коммуникации
-
Бизнес Закон
-
Бизнес-математика
-
Деловые навыки
-
Наука принятия решений
-
Финансы
-
Страхование
-
Введение в бизнес
-
MIS
-
Управление
-
Маркетинг
-
Офисные технологии
-
Деловая статистика
-
Коммуникационные науки и расстройства
-
Компьютерная наука
-
Консультации
-
Уголовное правосудие
-
Кулинария, гостиничный бизнес, путешествия и туризм
-
Кулинарное искусство
-
Наука о еде
-
Гостеприимство
-
Путешествия и туризм
-
Исследования глухих и образование глухих
-
Экономика
-
Образование
-
Учебный план и инструкция
-
ELL
-
Дошкольное образование
-
Ed Psych / Тесты и измерения
-
Образовательное администрирование и лидерство
-
Образовательные исследования
-
Основы / Введение в обучение
-
Учебные технологии
-
Подготовка лицензии
-
Чтение и грамотность
-
Специальное образование
-
EMS и пожарная наука (BRADY)
-
Скорая медицинская помощь (BRADY)
-
Наука о пожаре (BRADY)
-
Инженерное дело
-
Биоинженерия
-
Химическая инженерия
-
Гражданская и экологическая инженерия
-
Электротехника и вычислительная техника
-
Общая инженерия
-
Промышленная инженерия
-
Машиностроение и аэрокосмическая техника
-
Техническая математика / Техническая физика
-
Мода и дизайн интерьера
-
Потребительская наука
-
Мода
-
Дизайн интерьера
-
Медицинские профессии
-
Базовые курсы здоровья
-
Клиническая лабораторная наука
-
Стоматологическая помощь
-
Гигиена полости рта
-
Управление медицинской информацией
-
Массажная терапия
-
Медицинская помощь
-
Кодирование медицинского страхования
-
Медицинская терминология
-
Медицинская транскрипция
-
Помошник медсестры
-
Трудотерапия
-
Аптечный служащий
-
Флеботомия
-
Физиотерапия
-
Хирургическая техника
-
Респираторная терапия
-
Информационные технологии
-
СНГ: вычислительные концепции
-
СНГ: офисные приложения
-
Компьютерная графика / Искусство
-
Разработка игр
-
Безопасность
-
Обучение и сертификация
-
Юридические исследования и помощник юриста
-
Уход
-
LPN / LVN
-
RN
-
Успех студентов и развитие карьеры
-
Торговля и технологии
-
сельское хозяйство
-
Автомобильная техника
-
Строительные и технические работы
-
CAD / Инженерная графика / Черчение
-
Управление строительством и гражданские технологии
-
Электроника и электроэнергетика
-
Инженерные технологии и промышленный менеджмент
-
Экологические технологии
-
Технические сделки: NCCER / Contren
-
Изучающие английский язык
-
Войдите, чтобы загрузить ресурсы инструктора
-
Скачивание и использование инструкторских ресурсов
-
Продукты и услуги для обучения
-
Цифровая среда обучения
-
Веселье
-
MyLab
-
Освоение
-
Учебная программа по концепциям медсестер
-
Льготы
-
Начать
-
Отзывы
-
Обучение и поддержка
-
Редакторы и авторы
-
Район 3.0
-
Содержание курса
-
Учебники и электронные тексты
-
Электронный текст Пирсона
-
Системные Требования
-
Мобильное приложение Pearson eText
-
Коллекции Пирсона
-
Решения для дистанционного обучения
-
Системы обучения действиям
-
CourseConnect
-
Служба поддержки
-
Педагоги, начните
-
Студенты, начните
-
FAQs
-
Системные Требования
-
NCCERconnect
-
Особенности
-
Доступные названия
-
Служба поддержки
-
Поддержка преподавателей
-
Студенческая поддержка
-
Системные Требования
-
Pearson Workforce Education
-
Проперо
-
Для студентов
-
Как работает Проперо
-
Опыт курса
-
Получение кредита колледжа
-
Homeschool / Учащиеся до 12 лет
-
Военнослужащие
-
Работающие профессионалы
-
Для преподавателей и учебных заведений
-
Как работает Проперо
-
Академическое качество
-
Академические руководители
-
Факультет
-
Студенто-ориентированное обучение
-
Корпоративное обучение
-
Партнеры
-
Курсы
-
Истории успеха
-
Отзывы студентов
-
Отзывы преподавателей
-
Служба поддержки
-
Системные Требования
-
Техподдержка
-
Запросить дополнительную информацию
-
Виртуальная академия EMS
-
Инструменты обучения и взаимодействия
-
Приложение для обучения Aida Calculus
-
Обучение каталитике
-
Особенности
-
Истории пользователей
-
Развитие навыков критического мышления
-
Вовлечение студентов в активное обучение
-
Использование командного подхода к обучению
-
Гуманитарные и социальные науки
- Антропология
- Изобразительное искусство
-
Каталог коммуникаций, кино и театра
- Массовые коммуникации / Связи с общественностью / Фильм
-
Речевое общение
- Театр
-
английский
- Сочинение
- Развивающий английский
- Литература и творческое письмо
- Техническая коммуникация
- История
-
Междисциплинарные исследования
- Семейные исследования и человеческое развитие
- Гуманитарные науки
- Расовые и этнические исследования
- Социальная наука
- Женские и гендерные исследования
- Музыка
- Философия
- Политическая наука
- Психология
- Религия
- Социальная работа / семейная терапия / социальные услуги
- Социология
-
Мировые языки
- китайский язык
- французский язык
- Немецкий
- Итальянский
- Японский
- Языковые методы
- латинский
- португальский
- русский
- испанский язык
-
Математика и наука
- Анатомия и физиология
-
Биология и микробиология
- Специальности Биология / Биология высшего уровня
- Микробиология
- Неосновная биология
- Химия
- Наука об окружающей среде
- География и атмосферные науки
- Геология и океанография
- Здоровье и кинезиология
-
Математика
- Продвинутая математика
- Исчисление
- Развивающая математика
- Конечная математика и прикладное исчисление
- Гуманитарные науки Математика / Математика для учителей
- Математика для карьеры
- Математика
- Математика Precalculus
- Техническая математика
- Питание
- Физика и астрономия
-
Статистика
- Вводная статистика
- Статистика верхнего уровня
-
Профессиональная карьера
-
Бизнес
- Бухгалтерский учет и налогообложение
- Деловые коммуникации
- Бизнес Закон
- Бизнес-математика
- Деловые навыки
- Наука принятия решений
- Финансы
- Страхование
- Введение в бизнес
- MIS
- Управление
- Маркетинг
- Офисные технологии
- Деловая статистика
- Коммуникационные науки и расстройства
- Компьютерная наука
- Консультации
- Уголовное правосудие
-
Кулинария, гостиничный бизнес, путешествия и туризм
- Кулинарное искусство
- Наука о еде
- Гостеприимство
- Путешествия и туризм
- Исследования глухих и образование глухих
- Экономика
-
Образование
- Учебный план и инструкция
- ELL
- Дошкольное образование
- Ed Psych / Тесты и измерения
- Образовательное администрирование и лидерство
- Образовательные исследования
- Основы / Введение в обучение
- Учебные технологии
- Подготовка лицензии
- Чтение и грамотность
- Специальное образование
-
EMS и пожарная наука (BRADY)
- Скорая медицинская помощь (BRADY)
- Наука о пожаре (BRADY)
-
Инженерное дело
- Биоинженерия
- Химическая инженерия
- Гражданская и экологическая инженерия
- Электротехника и вычислительная техника
- Общая инженерия
- Промышленная инженерия
- Машиностроение и аэрокосмическая техника
- Техническая математика / Техническая физика
-
Мода и дизайн интерьера
- Потребительская наука
- Мода
- Дизайн интерьера
-
Медицинские профессии
- Базовые курсы здоровья
- Клиническая лабораторная наука
- Стоматологическая помощь
- Гигиена полости рта
- Управление медицинской информацией
- Массажная терапия
- Медицинская помощь
- Кодирование медицинского страхования
- Медицинская терминология
- Медицинская транскрипция
- Помошник медсестры
- Трудотерапия
- Аптечный служащий
- Флеботомия
- Физиотерапия
- Хирургическая техника
- Респираторная терапия
-
Информационные технологии
- СНГ: вычислительные концепции
- СНГ: офисные приложения
- Компьютерная графика / Искусство
- Разработка игр
- Безопасность
- Обучение и сертификация
- Юридические исследования и помощник юриста
-
Уход
- LPN / LVN
- RN
- Успех студентов и развитие карьеры
-
Торговля и технологии
- сельское хозяйство
- Автомобильная техника
- Строительные и технические работы
- CAD / Инженерная графика / Черчение
- Управление строительством и гражданские технологии
- Электроника и электроэнергетика
- Инженерные технологии и промышленный менеджмент
- Экологические технологии
- Технические сделки: NCCER / Contren
-
Бизнес
- Изучающие английский язык
-
Войдите, чтобы загрузить ресурсы инструктора
- Скачивание и использование инструкторских ресурсов
-
Цифровая среда обучения
- Веселье
- MyLab
- Освоение
-
Учебная программа по концепциям медсестер
- Льготы
- Начать
- Отзывы
- Обучение и поддержка
- Редакторы и авторы
- Район 3.0
-
Содержание курса
-
Учебники и электронные тексты
-
Электронный текст Пирсона
- Системные Требования
- Мобильное приложение Pearson eText
-
Электронный текст Пирсона
- Коллекции Пирсона
-
Учебники и электронные тексты
-
Решения для дистанционного обучения
- Системы обучения действиям
-
CourseConnect
-
Служба поддержки
- Педагоги, начните
- Студенты, начните
- FAQs
- Системные Требования
-
Служба поддержки
-
NCCERconnect
- Особенности
- Доступные названия
-
Служба поддержки
- Поддержка преподавателей
- Студенческая поддержка
- Системные Требования
- Pearson Workforce Education
-
Проперо
-
Для студентов
- Как работает Проперо
- Опыт курса
- Получение кредита колледжа
- Homeschool / Учащиеся до 12 лет
- Военнослужащие
- Работающие профессионалы
-
Для преподавателей и учебных заведений
- Как работает Проперо
- Академическое качество
- Академические руководители
- Факультет
- Студенто-ориентированное обучение
- Корпоративное обучение
- Партнеры
- Курсы
-
Истории успеха
- Отзывы студентов
- Отзывы преподавателей
-
Служба поддержки
- Системные Требования
- Техподдержка
- Запросить дополнительную информацию
-
Для студентов
- Виртуальная академия EMS
-
Инструменты обучения и взаимодействия
- Приложение для обучения Aida Calculus
-
Обучение каталитике
- Особенности
-
Истории пользователей
- Развитие навыков критического мышления
- Вовлечение студентов в активное обучение
- Использование командного подхода к обучению
Решение проблем: найти шаблон (2–8 классы)
Решение проблем: найти шаблон
Что это?
«Поиск закономерностей» — это стратегия, при которой учащиеся ищут закономерности в данных для решения проблемы.Учащиеся ищут повторяющиеся элементы или числа или серию повторяющихся событий. Следующая проблема может быть решена путем поиска шаблона:
В средней школе 1000 шкафчиков, где учится 1000 учеников. Первый ученик открывает все 1000 шкафчиков; затем второй ученик закрывает шкафчики 2, 4, 6, 8, 10 и так далее до шкафчика 1000; третий ученик меняет состояние (открывает закрытые шкафчики, закрывает открытые шкафчики) шкафчиков 3, 6, 9, 12, 15 и т. д .; четвертый ученик меняет состояние шкафчиков 4, 8, 12, 16 и так далее.Это продолжается до тех пор, пока у каждого ученика не будет очереди. Сколько шкафчиков будет открыто в конце?
Чтобы получить ответ, перейдите по адресу: Ask Dr. Math, 1000 Lockers
Почему это важно?
Шаблоны часто представляются учащимся без контекста задачи со словами, как в следующем примере: «Найдите шаблон в этой последовательности, объясните, как он работает, и используйте этот шаблон для предсказания следующих четырех чисел. 7, 10, 13 , 16, 19, __, __, __, __. »
Младшие школьники часто открывают для себя и продолжают использовать узоры, в которых используются геометрические формы.Например, желтый круг, красный квадрат, зеленый треугольник, желтый круг, красный квадрат, зеленый треугольник и т. Д.
Обнаружение закономерностей может помочь учащимся усвоить факты умножения, когда они замечают, что 4 x 7 — это то же самое, что 7 x 4, и что все числа в столбце 10 заканчиваются нулем.
Стратегия «Найти шаблон» может использоваться для решения многих математических задач и может использоваться в сочетании со многими другими стратегиями, включая создание таблицы, составление списка или упрощение задачи.
Как это сделать?
Предложите ученикам задачу, которая требует от них найти образец для решения проблемы.Например:
Если вы построите четырехгранную пирамиду из баскетбольных мячей и не учитываете дно как сторону, сколько мячей будет в пирамиде, состоящей из шести слоев?
Использование совместных учебных групп для поиска решений проблем помогает учащимся выразить свои мысли, провести мозговой штурм, обсудить варианты и обосновать свою позицию. Найдя решение, каждая группа может представить его классу, объясняя, как они пришли к своему решению и почему они считают его правильным.Или студенты могут объяснять свои решения в письменной форме, а учитель может отображать решения. Затем студенты могут перемещаться по комнате, чтобы прочитать решение каждой группы.
-
Понять проблему
Продемонстрируйте, что первым шагом к решению проблемы является ее понимание. Это включает в себя определение ключевой информации, необходимой для поиска ответа. Это может потребовать от студентов прочитать задачу несколько раз или изложить ее своими словами.
Иногда вы можете решить проблему, просто распознав шаблон, но чаще вам нужно расширить шаблон, чтобы найти решение. Составление числовой таблицы поможет вам более четко увидеть закономерности.
В этой задаче учащиеся понимают:
На верхнем уровне будет один баскетбольный мяч. Мне нужно найти, сколько шаров будет в каждом слое пирамиды, с первого по шестой. Мне нужно найти, сколько баскетбольных мячей будет во всей пирамиде.
-
Выберите стратегию
Чтобы успешно использовать эту стратегию, вы должны быть уверены, что модель действительно будет продолжаться.Попросите учащихся назвать причины, по которым они думают, что эта закономерность предсказуема, а не основана на вероятности. Проблемы, которые легче всего решить, найдя шаблон, включают те, которые просят учащихся расширить последовательность чисел или сделать прогноз на основе данных. В этой задаче учащиеся также могут составить таблицу или нарисовать картинку, чтобы организовать и представить свое мышление.
Поиск шаблона — подходящая стратегия для решения проблемы. Это модель, которая предсказуема и будет продолжаться.
-
Решение проблемы
Начните с верхнего слоя или одного баскетбольного мяча. Определите, сколько шаров должно быть под этим шаром, чтобы образовался следующий слой пирамиды. При необходимости используйте манипуляторы. Студенты могут использовать любые манипуляторы, от монет до кубиков и мячей для гольфа. Учащиеся также могут рисовать картинки, чтобы помочь им решить проблему.
Вы можете попросить группы использовать разные манипуляторы, а затем сравнить их решения, чтобы определить, повлиял ли тип манипулятивного действия на решение.Если учащиеся моложе, начните с трех уровней и обсудите их ответы на эту более простую задачу. Затем переходите к другим уровням, по мере того как учащиеся понимают, как решить проблему.
907 1 907 = 4) 907 (16 + 9 = 25)
Слой Шаров добавлено Шаров в этом слое 1 (вверху) 1 1 907 907 1 3 5 9 (4 + 5 = 9) 4 7 16 (9 + 7 = 16) 5 25 6 11 36 (25 + 11 = 36) Если это помогает визуализировать пирамиду, используйте манипуляторы для создания третьего слоя.Запишите номер и ищите выкройку. Второй слой добавляет 3 баскетбольных мяча, а следующий — 5 баскетбольных мячей. Каждый раз, когда вы добавляете новый слой, количество баскетбольных мячей, необходимых для создания этого слоя, увеличивается на 2.
- 1
- 1 + 3 = 4
- 4 + 5 = 9
- 9 + 7 = 16
- 16 + 9 = 25
- 25 + 11 = 36
Продолжайте, пока не будут записаны шесть слоев. После того, как шаблон будет найден, учащимся может не понадобиться использовать манипуляторы.
Затем добавьте баскетбольные мячи, использованные для создания всех шести слоев.Ответ — 91 мяч. Посмотрите в списке, нет ли другого шаблона. Количество шаров, используемых на каждом уровне, равно квадрату номера слоя. Итак, 10-й слой будет иметь 10 x 10 = 100 шаров.
-
Проверить
Прочтите проблему еще раз, чтобы убедиться, что на вопрос дан ответ.
Да, я нашел общее количество баскетбольных мячей в шестислойной пирамиде.
Проверьте математику, чтобы убедиться, что она верна.
1 + 4 + 9 + 16 + 25 + 36 = 91
Определите, была ли выбрана лучшая стратегия для этой проблемы или существовал другой способ решения проблемы.
Поиск шаблона был хорошим способом решить эту проблему, потому что шаблон был предсказуем.
-
Объясните
Учащиеся должны объяснить свой ответ и процесс, который они прошли, чтобы его найти. Студентам важно рассказать или написать о своем мышлении. Продемонстрируйте, как написать абзац, описывающий шаги, которые предприняли учащиеся, и то, как они принимали решения на протяжении всего процесса.
Сначала я начал с первого слоя.Я использовал блоки для создания пирамиды и составил список из количества блоков, которые я использовал. Затем я создал таблицу для записи количества шаров в каждом слое.
907 1 907 = 4) 907 (16 + 9 = 25)
Слой Шаров добавлено Шаров в этом слое 1 (вверху) 1 1 907 907 1 3 5 9 (4 + 5 = 9) 4 7 16 (9 + 7 = 16) 5 25 6 11 36 (25 + 11 = 36) Я сделал четыре слоя, а затем увидел узор.Я видел, что для каждого слоя количество использованных шаров было числом слоя, умноженным на себя. Я закончил выкройку без блоков, умножив количество шариков в слоях 5 и 6.
Затем я сложил все шарики в каждом слое.
1 + 4 + 9 + 16 + 25 + 36 = 91Я получил 91 мяч.
-
Практика с инструкциями
Попросите учащихся решить следующую задачу, используя стратегию «Найти шаблон».
Женщина пытается сократить количество банок газировки, которые она пьет каждую неделю. Она составляет план, что через несколько недель она будет пить только одну банку газировки. Если она начнет с 25 банок в первую неделю, 21 банку во вторую неделю, 17 банок в третью неделю, 13 банок в четвертую неделю и продолжит эту схему, сколько недель ей потребуется, чтобы достичь своей цели?
Попросите учащихся поработать в парах, группах или индивидуально, чтобы решить эту задачу. Они должны уметь рассказать или написать о том, как они нашли ответ, и обосновать свои рассуждения.
Как можно расширить эту стратегию?
Математические задачи могут быть простыми, с несколькими критериями, необходимыми для их решения, или они могут быть многомерными, требующими диаграмм или таблиц для организации мышления учащихся и записи шаблонов. При использовании шаблонов ученикам важно выяснить, будет ли шаблон предсказуемо сохраняться. Попросите учащихся определить, есть ли причина для продолжения шаблона, и убедитесь, что учащиеся используют логику при поиске шаблонов для решения проблем.
-
Например, если идет дождь в воскресенье, снег в понедельник, дождь во вторник и снег в среду, будет ли дождь в четверг?
-
Другой пример: если Лорен выиграла первую и третью партию в шахматы, а Уолтер выиграл вторую и четвертую партию, кто выиграет пятую партию?
-
Другой пример: если растение выросло на 13 сантиметров за первую неделю и 10 сантиметров за вторую неделю, на сколько сантиметров оно вырастет за третью неделю?
Поскольку это вопросы вероятности или природы, убедитесь, что учащиеся понимают, почему шаблоны нельзя использовать для поиска ответов.
No related posts.