Как составить шкалу отношений

Шкала отношений

Шкалой
отношений (подобия)
называется
шкала, если множество допустимых
преобразований состоит
из преобразований подобия

где
а>0
–
действительные
числа.
Нетрудно убедиться, что в шкалах отношений
остаются неизменными отношения численных
оценок объектов. Действительно, пусть
в одной шкале объектам
исоответствуют шкальные
значения

и
,
а
в другой
и.
Тогда имеем:

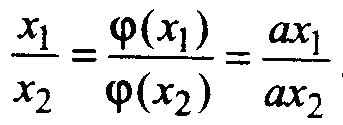
Данное
соотношение объясняет название шкал
отношений. Примерами
измерений в шкалах отношений являются
измерения массы и длины объектов.
Известно, что при установлении массы
используется
большое разнообразие численных оценок.
Так, производя
измерение в килограммах, получаем одно
численное значение, при измерении в
фунтах – другое и т.д. Однако можно
заметить,
что в какой бы системе единиц ни
производилось измерение массы, отношение
масс любых объектов одинаково и при
переходе
от одной числовой системы к другой,
эквивалентной, не
меняется. Этим же свойством обладает и
измерение расстояний
и длин предметов.

Как
видно из рассмотренных примеров,
шкалы
отношений отражают
отношения свойств объектов, т.е. во
сколько раз свойство
одного объекта превосходит это же
свойство другого объекта.

Шкалы
отношений образуют подмножество шкал
интервалов фиксированием
нулевого значения параметра b
: b
= 0. Такая
фиксация
означает задание нулевой точки начала
отсчета шкальных значений для всех шкал
отношений. Переход от одной шкалы
отношений к другой, эквивалентной ей
шкале осуществляется с
помощью преобразований подобия
(растяжения), т.е. изменением
масштаба измерений. Шкалы отношений,
являясь частным случаем
шкал интервалов, при выборе нулевой
точки отсчета сохраняют
не только отношения свойств объектов,
но и отношения расстояний между парами
объектов.

Шкала разностей

Шкалы
разностей
определяются
как шкалы, единственные с точностью
до преобразований сдвига

,

b –
действительные
числа. Это означает, что при переходе
от одной числовой системы
к другой меняется лишь начало отсчета.
Шкалы разностей
применяются в тех случаях, когда
необходимо измерить, насколько один
объект превосходит по определенному
свойству другой объект. В шкалах разностей
неизменными
остаются разности численных оценок
свойств.
Действительно,
если

и

– оценки
объектов

и

в
одной шкале, а
и
– в
другой шкале, то имеем:

Примерами
измерений в шкалах разностей могут
служить измерения
прироста продукции предприятий (в
абсолютных единицах)
в текущем году по сравнению с прошлым,
увеличение численности
учреждений, количество приобретенной
техники за год и
т.д.

Другим
примером измерения в шкале разностей
является летоисчисление
(в годах). Переход от одного летоисчисления
к другому
осуществляется изменением начала
отсчета.

Как
и шкалы отношений, шкалы разностей
являются частным
случаем шкал интервалов, получаемых
фиксированием параметра а
(а= 1),
т.е. выбором единицы масштаба измерений.
Точка
отсчета в шкалах разностей может быть
произвольной Шкалы
разностей, как и шкалы интервалов,
сохраняют отношения
интервалов между оценками пар объектов,
но, в отличие от шкалы отношений, не
сохраняют отношения оценок свойств
объектов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

То шкала отношений Это шкала, которая используется для измерения количественных переменных и имеет абсолютный нуль, то есть этот ноль подразумевает отсутствие того, что измеряется.

Например: Заработную плату можно измерить с помощью шкалы отношений, поскольку она является количественной величиной, то есть выражается цифрами. которые представляют количества, и потому что можно установить абсолютный нуль, то есть этот ноль представляет собой отсутствие зарплата.

Шкалы используются в статистике (дисциплина, в которой информация о репрезентативная выборка) для измерения и сравнения переменных, которые отражаются в данных (значения, которые каждый Переменная).

На основе данных составляются графики, таблицы или диаграммы, которые позволяют изучать, описывать и классифицировать явления, предметы или людей, делать прогнозы или устанавливать тенденции.

Имеется четыре шкалы: номинальная, порядковая, интервальная и относительная. Они различаются в зависимости от того, на что похож ноль, в зависимости от типа переменной, которую они позволяют анализировать, в соответствии с вычислениями, которые можно произвести с их значениями, и в соответствии с их свойствами.

Характеристики шкалы отношений

Примеры шкалы отношений

1. Высота. Высота измеряется с помощью шкалы отношений, поскольку значения переменных представлены положительными действительными числами (например, здание может достигать 30,5 метров), и его можно складывать, вычитать, умножать и делить, а также потому, что ноль указывает на отсутствие высота. Кроме того, можно установить соотношение и пропорциональность величин (например, одно здание может быть вдвое выше другого), тождество (например, два здания могут иметь одинаковую или разную высоту) и величину (например, высота одного здания может быть больше, меньше или равна высоте другого) и интервал всегда постоянный.
2. Деньги. Деньги, которые есть у человека, компании или учреждения, измеряются по шкале отношений, потому что значения переменных представлены числами. положительные реалы (например, у человека может быть 40 000,7 долларов), и их можно складывать, вычитать, умножать и делить, а поскольку ноль указывает на отсутствие Деньги. Кроме того, можно проводить операции соотношения и пропорциональности (например, у одной компании денег может быть на 40% больше, чем у другой), тождества (для например, у двух людей может быть одинаковая сумма денег) и величины (например, у одного человека может быть больше денег, чем у другого), а интервал всегда равен постоянный.
3. Масса. Вес тела измеряется по шкале отношений, так как значения переменных представлены положительными действительными числами (для например, мяч может весить 0,45 кг) и его можно складывать, вычитать, умножать и делить, а поскольку ноль означает отсутствие масса. Кроме того, можно проводить операции соотношения и пропорциональности (например, мяч может весить 50% от того, что весит другой), тождества (например, два мячи могут иметь разный вес) и величину (например, вес одного мяча может быть меньше, больше или равен весу другого) и интервал всегда постоянный.
4. Объем. Объем тела измеряется по шкале отношений, так как значения переменных представлены положительными действительными числами (для например, объем шара может быть 30 м³) и его можно складывать, вычитать, умножать и делить, а ведь ноль означает отсутствие объем. Кроме того, можно проводить операции отношения и пропорциональности (например, объем одной сферы может быть вдвое меньше объема другой), тождества (для например, объем двух сфер может быть одинаковым) и по величине (например, объем одной сферы может быть больше объема другой) и интервал всегда постоянный.
5. Количество свойств. Количество имущества, принадлежащего кому-либо, можно измерить с помощью шкалы отношений, поскольку значения переменных представлены целыми числами. положительное (например, у человека 5 свойств) и его можно складывать, вычитать, умножать и делить, а так как ноль указывает на отсутствие количества характеристики. Кроме того, можно проводить операции отношения и пропорциональности (например, один человек может иметь в три раза больше свойств, чем другой), тождества (например, два люди могут иметь одинаковое количество свойств) и величины (например, один человек может иметь большее количество свойств, чем другой) и интервал всегда постоянный.
6. Время. Время измеряется по шкале отношений, потому что значения переменных представлены положительными действительными числами (например, фильм может длиться два с половиной часа) и их можно складывать, вычитать, умножать и делить и потому что ноль означает отсутствие Погода. Кроме того, можно проводить операции соотношения и пропорциональности (например, один фильм может длиться в два раза дольше другого), тождества (например, два фильмы могут различаться по длине) и величине (например, длина одного фильма может быть больше, чем длина другого), а интервал всегда постоянный.
7. масса. Масса измеряется по шкале отношений, потому что значения переменных представлены положительными действительными числами (для например, масса тела может быть 4,5 кг) и ее можно складывать, вычитать, умножать и делить, а ведь ноль означает отсутствие масса. Кроме того, можно проводить операции отношения и пропорциональности (например, масса одного тела может быть вдвое больше массы другого), тождества (например, два объекта могут иметь разные массы) и величину (например, масса одного тела может быть меньше, больше или равна массе другого), а интервал всегда постоянный.
8. Расстояние. Расстояние измеряется по шкале отношений, поскольку значения переменных представлены положительными действительными числами (например, расстояние между двумя местами может быть 5,3 км) и их можно складывать, вычитать, умножать и делить, а поскольку ноль указывает на отсутствие расстояние. Кроме того, можно проводить операции отношения и пропорциональности (например, расстояние может быть половиной другого), тождества (для например, два расстояния могут быть равны) и величины (например, одно расстояние может быть больше другого), а интервал всегда постоянный.
9. Высота. Высота измеряется с помощью шкалы отношений, поскольку значения переменных представлены положительными действительными числами (например, рост человека может быть 1,56 м) и его можно складывать, вычитать, умножать и делить, а так как ноль означает отсутствие высота. Кроме того, можно проводить операции соотношения и пропорциональности (например, рост одного человека может составлять 70% роста другого), тождества (например, например, два человека могут иметь разный рост) и величину (например, рост одного человека может быть меньше роста другого) и интервал всегда постоянный.
10. Доход. Доход человека, правительства, компании или учреждения измеряется по шкале отношений, поскольку значения переменных представлены положительными действительными числами. (например, ежемесячный доход правительства может составлять 567 398 097,37 долларов США), и его можно складывать, вычитать, умножать и делить, а поскольку ноль означает отсутствие доход. Кроме того, можно проводить операции соотношения и пропорциональности (например, июньский доход правительства может составлять 90% майского дохода), тождества (например, правительство может иметь разный доход в два разных месяца) и величину (например, августовский доход может быть больше, чем сентябрьский), а интервал всегда равен постоянный.
11. расходы. Затраты компании, учреждения или государства измеряются по шкале отношений, поскольку значения переменных представлены действительными числами. положительный (например, затраты компании могут составлять 45 000,49 долл. США), и их можно складывать, вычитать, умножать и делить, а поскольку ноль означает отсутствие расходы. Кроме того, можно проводить операции соотношения и пропорциональности (например, затраты на одно сырье могут в четыре раза превышать затраты на другое), тождества (например, затраты на два сырья могут быть одинаковыми) и величины (например, затраты на одно сырье могут быть больше затрат на другое), а интервал всегда постоянный.
12. Возраст. Возраст измеряется с помощью шкалы отношений, поскольку значения переменных представлены целыми положительными числами (для например, человеку 47 лет) и его можно складывать, вычитать, умножать и делить, а также потому, что ноль означает отсутствие возраста. Кроме того, можно проводить операции соотношения и пропорциональности (например, возраст одного человека может быть ⅓ от возраста другого), тождества (например, двух люди могут быть одного возраста) и величины (например, возраст одного человека может быть меньше, равен или больше возраста другого), а интервал всегда постоянный.
13. Продажи. Продажи компании или магазина измеряются по шкале отношений, поскольку значения переменных представлены целыми числами. положительный (например, объем продаж может быть равен 984), и его можно складывать, вычитать, умножать или делить, а поскольку ноль означает, что не было продажа. Кроме того, можно проводить операции соотношения и пропорциональности (например, продажи одного магазина могут быть в два раза больше продаж другого), тождества (например, продажи одного магазина могут отличаться от продаж другого) и величины (например, продажи одного магазина могут быть меньше продаж другого) и интервал всегда постоянный.
14. Скорость. Скорость объекта измеряется по шкале отношений, потому что значения переменных представлены положительными действительными числами (для например, скорость самолета может быть 93,4 км/ч) и ее можно складывать, вычитать, умножать и делить, а поскольку ноль означает, что нет скорость. Кроме того, можно выполнять операции отношения и пропорциональности (например, скорость одного самолета может быть в три раза больше скорости другого), идентичности (например, две скорости могут быть одинаковыми) и величины (например, 100 км/ч больше, чем 90 км/ч), а интервал всегда постоянный.
15. Энергия. Энергия измеряется по шкале отношений, потому что значения переменных представлены положительными действительными числами (например, энергия электроэнергии, потребляемой компьютером, может составлять 200 Втч) и ее можно складывать, вычитать, умножать и делить, а ведь ноль подразумевает отсутствие Энергия. Кроме того, можно выполнять операции соотношения и пропорциональности (например, лампа мощностью 40 Вт потребляет в два раза больше электроэнергии, чем лампа мощностью 20 Вт), идентичность (например, энергия, потребляемая бритвой, равна энергии, потребляемой зарядным устройством для сотового телефона) и величина (например, энергия, потребляемая кондиционером [1613 Вт·ч], больше энергии, потребляемой холодильником [75 Вт·ч]), и интервал всегда равен постоянный.

Он может служить вам:

Онлайн-доступ к журналу: http://izvestia_psy.isu.ru/ru/index.html

2016. Т. 18. С. 90-101

Серия «Психология»

Иркутского государственного университета

И 3 В Е С Т И Я

УДК 159.9.07

Построение шкалы отношений в психологических измерениях

Е. А. Фальтермайер, А. И. Худяков

Российский государственный педагогический университет им. А. И. Герцена, г. Санкт-Петербург

Аннотация. Предлагаются подходы к решению проблемы психологического измерения на основе объединения результатов теоретических и экспериментальных исследований. В продолжение разговора о корректности применения математических моделей в психологических измерениях при построении шкал интервалов предлагается рассмотреть пример построения шкалы отношений при психологическом измерении. По результатам прямых методов психологического измерения стимулов, не имеющих физической метрики, можно построить метрические шкалы – интервалов и отношений. Структура этих шкал снимает вопрос о конкретной единице измерения, так как соответствующие допустимые преобразования позволяют работать с условными единицами. Математическая модель любого процесса будет действенной, если имеется априорное представление о сути процесса. Когда мы используем вероятность, мы не решаем проблему, а просто обходим ее острые углы.

Ключевые слова: психологическое измерение, психофизическое шкалирование, шкалы отношений, эмпирические процедуры, вероятностные модели, метод парных сравнений, непосредственная оценка отношений, непосредственная количественная оценка, непосредственная количественная оценка субъективных интервалов.

В психологии до сих пор право построения шкал отношений на основе результатов прямых методов измерений традиционно оставляется психофизике-2 Стивенса, несмотря на то что Г. Экман еще в 50-е гг. прошлого века использовал методы непосредственной оценки отношений, в которых испытуемый не имел возможности изменять «интенсивность» стимула, как в методе бисекции Стивенса [5; 6]. К сожалению, в отечественной литературе практически не встречаются ссылки на работы Экмана и его последователей, хотя эти методы используются сегодня в таких прикладных задачах, как, например, психологическое измерение восприятия физического напряжения [4]. Возможно, это следствие ослабления интереса к проблемам психологии измерений и к проблемам экспериментальной психологии вообще.

В этой статье мы постараемся показать способность человека адекватно манипулировать образами стимулов в структуре «обобщенного образа» на уровне оценки отношений, т. е. доказать возможность построения психологической шкалы отношений на основе данных прямых методов оценки.

Теоретическая модель построения шкалы отношений

В основе построения искомой шкалы лежит экспериментально полученная матрица парных сравнений, в которой каждый элемент представляет оценку отношения степени выраженности указанного критерия в двух сравниваемых стимулах. То есть испытуемый должен указать, во сколько раз один стимул в паре больше отвечает предложенному критерию оценки по сравнению с другим:

a1} = Si / Sj, (1)

где aij – элемент матрицы парных сравнений, представляющий оценку отношения между соответствующими стимулами (i – номер столбца матрицы, j – номер строки); Si, Sj – числовые представления стимулов в субъективном пространстве, т. е. искомые шкальные значения.

В результате проведения эмпирической процедуры измерения (эксперимента) мы получаем неполную матрицу парных сравнений отношений. В этой матрице номер столбца каждой заполненной клеточки соответствует номеру стимула, который был в паре оценен выше, следовательно, число, стоящее в этой ячейке, больше 1. Диагональные элементы матрицы представлены 1, так как они отвечают случаю сравнения стимула с самим собой. Поэтому на первом шаге обработки экспериментальная неполная матрица преобразовывается в полную, т. е. в симметричную незаполненную ячейку помещается величина, обратная величине в соответствующей заполненной ячейке: aiJ- = 1/aji.

Проведем суммирование равенства (1) по индексу i: Xiaij = (XiSi)1/<SJ, т. е. суммирование элементов матрице в j-й строке. Из этого равенства следует

Sj = YjSi / YJaj. (2)

YJiSi – для данного набора стимулов и конкретного испытуемого является константой. Обозначим ее к1, XiSi = k1. Шкала отношений, по определению, задается с точностью до произвольной константы а, определяющей масштаб или единицу измерения шкалы: y = ax – допустимое преобразование. Так как мы предполагаем построение шкалы отношений, то здесь и далее нам вполне достаточно получить шкальные значения с точностью до некоторой произвольной константы, значение которой мы можем считать равным 1.

Таким образом, мы получаем искомое шкальное значение для j-ro стимула. Проведем суммирование равенства (1) по индексу j, т. е. суммирование в i-м столбце YJay = S, • X j(1/Sj).

XJ(1/Sj) – величина постоянная для данного набора стимулов и данного испытуемого, следовательно, X J(1/Sj) = к2. Таким образом, мы получаем искомое шкальное значение для i-ro стимула:

Si = к2 • X Jaj. (3)

Рассмотрим случай i = J = y: Sj = Si = Sy = к1 / X iaiy = к2 • XJayj, из этого следует (Sy • Sy) = (к • к2) • ( X Jayj / Xiaty).

С точностью до константы (к1 • к2) мы получили третье выражение для искомого шкального значения

^ = / £1а1у). (4)

Кроме этого, из приведенных рассуждений следует наличие еще одной константы, значение которой может быть оценено в эксперименте, а именно -из равенства к1 / £}а[у = к2 • £ следует

£га,у • £]ау! = к1/к2, (5)

т. е. для данного набора стимулов и данного испытуемого (для конкретной экспериментально полученной полной матрицы парных сравнений отношений) должно быть постоянным произведение сумм элементов матрицы по строкам и по столбцам, в случае выполнения наших предположений. А предположение, положенное в основу приведенных рассуждений, было одно: испытуемый в состоянии адекватно оценивать отношение субъективных значений пары стимулов.

Найденные шкальные значения представляют индивидуальную шкалу отношений конкретного испытуемого. Если эта шкала действительно обладает свойствами шкалы отношений, то шкальное значение индивидуальной шкалы Б связано с «истинным» значением Д линейным соотношением Ь •

Б, = ЛЯг, следовательно, £ Б, = Ь£Яг, отсюда Ь = £Бг / £ Я

Я = «г / £«, (6)

так как значение суммы £ является постоянным для данного стимульного набора, точнее для представления данного стимульного набора в совокупном обобщенном образе, и можно принять ее равной 1.

«Совокупный обобщенный образ» – рабочее название обобщенного образа группы испытуемых, однородной по реакции на предложенный стимульный набор.

В концепции обобщенного образа подчеркивается его индивидуальность. Но постулирование абсолютной «индивидуальности» приводит к абсурду. Абсолютно индивидуальные, т. е. абсолютно непохожие, абсолютно различные, системы в принципе не могут взаимодействовать – любой вид взаимодействия систем предполагает наличие у них каких-то общих свойств. Мы же – люди -взаимодействуем достаточно успешно, более того, взаимодействие друг с другом представляет основу нашего существования. Поэтому рабочее понятие «индивидуальности обобщенного образа» в психологическом эксперименте подразумевает необходимость и возможность выделения в группе испытуемых подгрупп с более или менее аналогичными реакциями. Критерий этого выделения определяется конкретной задачей эксперимента.

Правильность вышеприведенных выводов и предлагаемого алгоритма построения шкалы отношений проверяется экспериментально.

Доказательством возможности построения шкалы отношений прямыми методами оценки может служить два факта:

1) выполнение равенства (5) £}а{у • £]ау= к для полученной в эксперименте матрицы;

2) три построенные на этой матрице шкалы – $ = к / Ха, $ = к2 • Х/ву, $у = ^(Х ]ау) / Ца^, – должны быть эквивалентны с точностью до постоянного множителя, т. е. связаны соотношением у = а • х.

Для проверки выдвинутых предположений был проведен эксперимент.

Описание эксперимента

Стимульный набор. Стимульный набор состоял из 20 фотографий, сделанных фотохудожником. В наборе представлено четыре различных сюжета -один человек или группа людей в бытовой обстановке. Каждому сюжету соответствует пять фотоизображений, которые отличаются степенью контраста. Отличия степени контраста фотоизображений в пределах каждого сюжета одинаковы для всех четырех сюжетов.

Испытуемые. В эксперименте приняли участие 43 человека – студенты третьего курса факультета психологии СПбГУ.

Процедура. Испытуемым в случайном порядке предъявлялись пары стимулов из набора. В качестве критерия оценки был выбран интегральный критерий «простое предпочтение».

Предлагалась инструкция: «Вам будут предъявляться пары фотографий. Ваша задача выбрать ту фотографию в паре, которая кажется Вам более предпочтительной в предложенной паре. Кроме того, оцените, пожалуйста, во сколько раз вам показалась предпочтительней выбранная Вами фотография по отношению ко второй фотографии в паре».

Ответы испытуемых заносились в матрицу парных сравнений. Далее метод непосредственной оценки отношений будем называть НОО.

После завершения процедуры метода парных сравнений (МПС) испытуемым предлагалось оценить 20 стимулов-фотографий по критерию «простое предпочтение» методом непосредственного качественного оценивания (НКО) в шкале размахом от 0 до 100.

В результате проведенного эксперимента мы получили от каждого испытуемого наборы «сырых» оценок для методов НКО, МПС и НОО. Для дальнейшей обработки были допущены результаты, полученные по методу НКО от всех 43 испытуемых, по методам МПС и НОО результаты 41 испытуемого.

На основе полученных «сырых» оценок методами НКО и МПС строились шкалы интервалов по описанному ранее алгоритму [1]. По данным метода НОО строились предполагаемые шкалы отношений по описанным в уравнениях (2), (3) и (4) алгоритмам с нормированием на сумму шкальных оценок согласно уравнению (6). Кроме того, вычислялось значение константы, предлагаемое уравнением (5).

Полученные шкальные значения представляют оценки некоторого «истинного» значения Ri, сделанные каждым испытуемым в общей для всех шкале (к общей шкале мы привели индивидуальные шкалы испытуемых путем нормирования согласно уравнению (6)). Следовательно, если наши предположения верны, вычисление группового шкального значения для предполагаемой шкалы отношений в принципе не отличается от построения группового значения шкал интервалов. Как правило, для этой цели чаще всего используется значение среднего арифметического, если нет для этого явных противопоказаний –

выраженной асимметричности или полимодальности распределения индивидуальных оценок.

«Средняя геометрическая совершенно необходима для определения среднего значения признака, если он характеризует темп роста, темп увеличения численности популяции. Средняя геометрическая удобна особенно в тех случаях, если признак выражен в долях единиц или в процентах и изменяется во времени и по периодам» [3, с. 184]. Помимо этого, среднее геометрическое используют при сильно выраженной асимметричности распределения, когда пытаются уменьшить асимметричность путем логарифмирования, например, надеясь получить логнормальное распределение.

В нашем случае вышеприведенные причины для отказа от использования среднего арифметического отсутствуют. Поэтому мы не считаем целесообразным использовать в качестве меры центральной тенденции для интериндивидуальных оценок шкалы отношений значение среднего геометрического, которое рекомендует Экман.

В таблице 1 приведены шкальные значения полученных в эксперименте шкал, построенных по результатам работы всей выборки испытуемых.

Таблица 1

Шкальные значения, построенные по данным всей выборки испытуемых

НКО МПС НОО-1 НОО-2 НОО-3 НОО-4

К < К < К < К < К а К а

1 3,5 3,1 7,73 3,96 61,1 32,2 4,3 1,3 4,2 1,2 4,3 1,2

2 5,4 3,3 10,7 5,61 61,0 31,8 5,3 1,9 5,1 1,9 5,2 1,8

3 3,6 2,7 6,49 3,5 60,8 28,1 4,0 1,0 3,8 0,97 3,9 0,97

4 2,9 2,4 5,24 3,1 57,8 24,8 3,8 1,1 3,7 1,0 3,8 1,0

5 2,1 2,5 4,12 3,04 57,2 25,9 3,4 1,1 3,4 0,99 3,4 1,0

6 6,4 3,0 12,7 3,56 59,6 30,1 6,2 1,4 6,1 1,7 6,1 1,5

7 6,9 3,0 13,3 4,21 56,5 17,9 6,5 1,7 6,9 4,0 6,7 2,6

8 6,2 2,9 12,1 3,5 57,9 22,3 5,8 1,2 5,8 1,9 5,8 1,5

9 5,0 3,1 9,54 3,78 59,2 27,9 4,9 1,3 4,9 1,5 4,9 1,4

10 3,7 3,0 7,44 5,23 55,2 17,4 4,4 1,4 4,5 1,9 4,4 1,6

11 4,1 3,0 10,2 4,11 57,9 26,7 5,1 1,4 5,1 1,7 5,1 1,6

12 5,8 3,1 12,1 5,0 57,3 30,2 6,1 2,0 6,3 2,6 6,2 2,3

13 3,7 2,6 9,12 3,7 58,7 32,1 4,9 1,5 4,9 1,7 4,9 1,5

14 3,4 2,6 8,15 3,97 55,6 21,0 4,5 1,5 4,6 1,6 4,6 1,5

15 3,4 2,8 7,66 4,49 56,8 24,4 4,5 1,8 4,6 1,9 4,5 1,8

16 5,3 3,3 10,7 4,4 57,2 19,6 5,3 1,6 5,3 1,8 5,3 1,7

17 5,5 3,5 10,7 4,8 59,8 31,3 5,5 2,2 5,3 1,9 5,4 2,0

18 5,7 3,3 11,2 4,5 58,4 30,7 5,3 1,8 5,3 2,0 5,3 1,8

19 5,2 3,2 9,88 4,55 58,9 29,9 5,0 1,8 5,0 2,1 5,0 1,9

20 3,9 3,7 7,24 5,8 57,0 30,8 4,3 2,1 4,5 2,9 4,4 2,5

Примечание: НКО, МПС, НОО – методы измерения. НОО-1 значение константы уравнения (5), НОО-2 – шкала, построенная суммированием по строкам, НОО-3 – шкала, построенная суммированием по столбцам, НОО-4 – шкала, построенная согласно уравнению (4). К – шкальные значения, а – среднеквадратичные отклонения, № – номер стимула.

Анализ результатов

Первым шагом проверки выдвинутых предположений был анализ вида связи шкальных значений, построенных на основе данных различных эмпирических процедур. То, что методы МПС и НКО дают возможность построения шкал интервалов, было показано в [1]. В таблице 2 приведены характеристики связи между построенными шкалами. Во-первых, линейность связи шкал данных МПС и НКО еще раз подтверждает доказанное выше положение о том, что они являются шкалами интервалов. Во-вторых, данные таблицы не дают никаких оснований отклонить гипотезу о линейной связи между шкалами интервалов (МПС и НКО) и шкалами, построенными по предложенным алгоритмам (НОО-2, НОО-3, НОО-4). Это говорит о том, что построенные шкалы по крайней мере обладают свойствами шкал не ниже уровня шкал интервалов.

Таблица 2

Оценка линейности связи между шкалами, построенными на основе результатов методов МПС, НКО, НОО-2, НОО-3, НОО-4

Параметры HKO МПС

HOO-2 HOO-3 HOO-4 HOO-2 HOO-3 HOO-4 НКО/МПС

Fi 0,029 0,031 0,031 0,008 0,015 0,011 0,017

F2 1,21 1,27 1,27 0,33 0,615 0,45 0,73

Fs 143,0 95,1 121,6 546,6 216,1 367,8 182,6

r 0,942 0,917 0,933 0,984 0,961 0,976 0,954

a 0,61 0,61 0,6 0,32 0,33 0,32 0,49

b 2,25 2,17 2,21 2,02 1,92 1,97 0,04

Примечание: – статистики Фишера для оценки адекватности линейной модели; Е3 – статистика Фишера для оценки корректности линейной модели; г – значение коэффициента корреляции; а, Ь – параметры линейной связи у = ах + Ь.

На втором шаге проверки рассмотрим, насколько в полученных экспериментальных данных выполняется равенство (5). Оценки соотношения (5) представлены в столбце НОО-1 табл. 1. Распределение этих оценок имеет следующие характеристики: среднее значение 58,25, среднеквадратичное отклонение 1,7, размах max – min = (61,1 – 55,2) = 5,9. Можно сделать вывод, что соотношение (5) вполне выполняется, а флуктуации этой «константы» вызываются погрешностями измерения.

На третьем шаге проверялась гипотеза о линейном характере связи между шкалами, построенными согласно уравнениям (2)-(4), т. е. НОО-2, НОО-3, НОО-4. Значения соответствующих статистик, приведенные в табл. 3, не дают оснований отклонить гипотезу о линейной связи между построенными шкалами. Более того, введение в каждую шкалу общей нулевой точки увеличивает линейность зависимости и уменьшает отклонение аппроксимирующей прямой от 0 (значения параметра b).

Таким образом, анализ экспериментальных данных подтверждает выдвинутые предположения, положенные в основу построения шкал отношений: постоянство произведения сумм по строкам и по столбцам, эквивалентность трех построенных шкал. Кроме того, обнаружена линейная связь со шкалами интервалов. Из этого следует вывод о том, что построенные шкалы действительно являются шкалами отношений, что испытуемый в состоянии адекватно оценивать отношения между образами стимулов.

Таблица 3

Оценка линейности связи между шкалами, построенными на основе результатов методов НОО-2, НОО-3, НОО-4

Параметры Без нулевой точки С нулевой точкой

2/3 2/4 3/4 2/3 2/4 3/4

Р: 0,007 0,002 0,001 0,008 0,002 0,002

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

0,29 0,08 0,04 0,33 0,074 0,062

Рз 650,5 2726 2505 1791 7747 6600

Г 0,987 0,997 0,996 0,995 0,999 0,999

а 0,93 0,97 1,03 0,98 0,99 1,01

Ь 0,33 0,13 -0,15 0,12 0,04 -0,05

Примечание: Рь F’l – статистики Фишера для оценки адекватности линейной модели; Р3 – статистика Фишера для оценки корректности линейной модели; г – значение коэффициента корреляции; а, Ь параметры линейной связи у = ах + Ь.

В дальнейшем мы будем использовать шкалу отношений, построенную согласно равенству (3), так как при этом способе построения шкалы отношений манипуляции с числами минимальны.

При построении шкалы согласно равенству (2) к операции суммирования добавляется арифметическая операция деления, а для построения шкалы согласно равенству (4) требуется, кроме деления, еще и извлечение квадратного корня. Очевидно, что увеличение количества арифметических операций с результатами измерений увеличивает ошибку вычислений, т. е. в конечном итоге ошибку измерения.

Формирование субъективного «эталона» оценки

В стимульном наборе обсуждаемого эксперимента изменяются две объективные характеристики – степень контраста и сюжет фотоизображения. Очевидно, что эти два параметра «физически» независимы. Считается, что параметр «сюжет» более «субъективен», т. е. отношение к сюжетам со стороны испытуемых более дифференцировано по сравнению с параметром «контраст». Поэтому мы рассмотрели индивидуальные оценки испытуемыми сюжетов предъявляемых изображений. Оценкой сюжета считалась максимальная оценка из оценок 5 фотографий, представляющих данный сюжет. В результате в первоначальной выборке испытуемых выделились две подвыборки. В каждую выделенную группу вошли испытуемые, у которых распределения оценок по четырем сюжетам не отличались между собой на 5%-ном уровне значимости. В таблице 4 приведены шкальные значения, построенные по результатам каждой группы. В таблице 5 приведены результаты выполнения предположений о возможности построения шкал интервалов в группах. Эти результаты не дают оснований сомневаться в правильности выдвинутых предположений.

Таким образом, на первом шаге анализа структуры «субъективного эталона» мы выявили наличие интериндивидуальных различий как первый «объективный» фактор, формирующий «субъективный эталон» оценки.

В случае данного эксперимента-измерения существуют еще два объективных фактора-параметра, а именно сюжет и степень контраста. Рассмотрим их взаимодействие в процессе оценки.

Таблица 4

Шкальные значения шкал интервалов (МПС), отношений НОО и значения контрольной константы (НОО-1) в двух выделенных группах испытуемых

№ Группа 1 (п = 24) Группа 2 (п = 15)

МПС НОО-1 НОО МПС НОО-1 НОО

К а К а К а К а К а К а

1 7,17 4,2 55,5 27,8 4,2 1,3 7,5 3,1 76,6 46,0 4,3 1,1

2 11,0 5,5 57,6 27,6 5,5 1,7 11,0 5,1 74,8 46,2 5,5 2,0

3 6,21 3,5 55,2 22,3 3,9 1,1 7,4 3,5 73,3 38,3 4,1 1,2

4 4,83 3,2 53,2 21,1 3,7 1,0 5,7 3,0 69,8 35,1 3,7 1,2

5 3,54 2,5 51,8 17,9 3,3 0,98 4,4 3,0 70,1 37,4 3,6 1,2

6 13,3 3,0 58,7 36,7 6,4 1,3 13,0 3,5 71,4 44,5 6,1 1,5

7 14,6 3,6 52,6 16,0 6,9 1,7 13,0 4,5 62,2 18,3 7,0 2,3

8 12,4 3,0 56,3 26,3 5,8 1,0 12,0 3,2 67,6 31,6 5,7 1,5

9 9,62 3,7 57,6 34,3 4,9 1,3 10,0 3,7 69,8 41,1 4,9 1,6

10 6,92 5,1 52,5 18,5 4,2 1,3 8,0 6,0 57,5 13,7 4,4 1,9

11 8,21 3,3 56,2 30,5 4,4 1,0 12,0 4,1 69,1 40,1 5,8 1,6

12 10,9 5,3 58,1 36,7 5,6 2,0 14,0 3,7 69,2 46,2 7,2 1,9

13 7,83 3,2 57,4 38,4 4,3 1,0 10,0 3,6 72,2 49,0 5,7 1,7

14 7,12 3,0 52,5 19,1 3,9 0,98 9,6 4,1 66,1 31,0 5,2 1,7

15 5,75 2,8 52,9 18,2 3,7 0,94 9,4 5,4 65,8 34,7 5,4 2,4

16 12,1 3,2 53,9 19,4 5,8 1,3 8,1 5,3 63,6 22,6 4,5 1,9

17 12,5 4,1 59,4 38,2 6,4 1,9 8,9 5,9 67,5 42,6 5,0 3,1

18 12,7 3,3 57,4 34,2 5,8 1,3 8,4 4,8 70,2 46,3 4,3 2,0

19 10,9 3,9 55,0 31,7 5,4 1,7 6,5 3,8 74,2 44,4 3,9 1,5

20 8,8 6,2 54,3 35,7 5,0 2,3 3,6 2,7 71,4 47,2 2,9 1,2

Примечание: п – количество испытуемых в группе.

Таблица 5

Оценка линейности связи между шкалами, построенными на основе результатов методов НОО и МПС для двух групп испытуемых

Параметры Группа 1 (п = 24) Группа 2 (п = 15)

Р, 0,018 0,02

Р2 0,432 0,3

Рз 537 301

Г 0,984 0,971

X 55,5 69,2

а 2,4 4,6

Примечание: п – количество испытуемых в группе; Р,, Р2 – статистики Фишера для оценки адекватности линейной модели; Р3 – статистика Фишера для оценки корректности линейной модели; г – значение коэффициента корреляции; X – среднее значения контрольной константы (НОО-1); а – среднеквадратичное отклонение.

В таблице 6 приведены шкалы, построенные по результатам оценок стимулов, у которых в процессе оценки изменялась только степень контраста, при сохранении сюжета и шкалы оценок, сделанных при одновременном изменении и степени контраста, и сюжета.

Таблица 6

Шкальные значения шкал отношений НОО оценки стимулов с изменением сюжета и контраста 5″, с изменением только контраста К, в двух выделенных группах испытуемых

Группа 1 (п = 24)

№ 51 82

К 5 К 8

X d X d X d X d

0 0 0 0 0 0 0 0

1 5,1 0,71 4,2 1,3 5,7 1,6 6,5 1,3

2 6,9 0,21 5,5 1,7 6,0 2,1 6,9 1,7

3 4,6 0,65 3,9 1,1 5,3 0,88 5,8 1,0

4 4,4 0,75 3,7 1,0 4,1 1,0 4,9 1,3

5 4,0 0,98 3,3 0,98 3,9 1,5 4,3 1,3

№ 83 84

К 8 К 8

X d X d X d X d

0 0 0 0 0 0 0 0

1 4,9 0,88 4,4 1,0 5,2 0,73 5,9 1,33

2 6,4 2,1 5,7 2,0 5,7 2,1 6,4 1,99

3 4,9 1,3 4,4 1,0 5,0 0,83 5,9 1,38

4 4,6 0,7 3,9 0,98 4,7 1,0 5,5 1,71

5 4,3 1,2 3,8 0,94 4,6 1,7 5,1 2,34

Группа 2 (п = 15)

№ 81 82

К 8 К 8

X d X d X d X d

0 0 0 0 0 0 0 0

1 5,1 1,0 4,4 1,1 5,2 1,4 6,2 1,5

2 6,6 2,3 5,6 2,0 6,1 2,7 7,0 2,3

3 4,9 1,4 4,2 1,2 5,1 0,9 5,7 1,5

4 4,1 0,8 3,7 1,2 4,5 1,9 4,9 1,6

5 4,3 1,6 3,6 1,2 4,3 1,7 4,4 1,9

№ 83 84

К 8 К 8

X d X d X d X d

0 0 0 0 0 0 0 0

1 5,2 1,2 5,8 1,6 5,8 1,7 4,5 1,9

2 6,5 2,4 7,3 1,9 5,8 2,5 5,0 3,1

3 4,7 1,0 5,7 1,7 5,1 1,3 4,3 2,0

4 4,5 1,0 5,2 1,7 4,8 1,6 4,0 1,5

5 4,2 1,3 5,4 2,4 3,6 1,2 3,0 1,2

Примечание: 8Ь 82, 83, 84 – номера сюжетов; № – номер стимула; X – шкальное значение; d -среднеквадратичное отклонение.

Данные, приведенные в табл. 7, показывают линейность связи между шкалами, построенными при оценке стимулов с одним изменяющимся параметром, и шкалами с двумя переменными параметрами. Причем значение коэффициента a в уравнении линейной связи y = ax + b для двух из четырех сюжетов каждой группы больше 1 (S2 / K2, S4 / K4 в группе 1; S2 / K2, S3 / K3 в группе 2), соответственно, для остальных меньше.

Таблица 7

Оценка линейности связи между шкалами отношений, построенными на основе оценок стимулов с изменением только контраста и оценок стимулов с одновременным изменение контраста и сюжета S/K

Параметры Si / K S2 / K2 S3 / K3 S4 / K4 S1 / K1 S2 / K2 S3 / K3 S4 / K4

Fi 0,009 0,02 0,005 0,008 0,009 0,027 0,03 0,009

F2 0,22 0,48 0,12 0,19 0,135 0,41 0,45 0,135

F3 1413 761 2470 1312 1179 417 303 492

r 0,999 0,997 0,999 0,999 0,998 0,995 0,994 0,996

a 0,8 1,12 0,88 1,16 0,84 1,16 1,16 0,84

b 0,07 0,00 0,00 0,00 0,05 -0,1 0,16 0,01

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Примечание: Рь – статистики Фишера для оценки адекватности линейной модели; Р3 – статистика Фишера для оценки корректности линейной модели; г – значение коэффициента корреляции; а, Ь – параметры линейной связи у = ах + Ь.

Величина углового коэффициента линейной зависимости соответствует оценке сюжета как такового, более высоко оцененные сюжеты демонстрируют более крутой подъем прямых линий. Параметр сюжета играет роль постоянного «ускорения» в зависимости от роста общего «предпочтения» фотоизображения от увеличения «предпочтения» простого контраста. Причем разный наклон психометрических прямых определяется в данном случае не контекстом измерения и не эффектом стимульного ряда [2; 3], а взаимодействием постоянной составляющей образа стимула – сюжета – с «субъективным эталоном» в системе обобщенного образа.

Следует подчеркнуть, что эти зависимости (рис. 1 и 2) представляют скорее психометрические прямые, нежели привычные психофизические функции. По обеим осям отложены «субъективные» шкалы. Таким образом, как и в статье [1], посвященной построению шкал интервалов, мы имеем дело с функциональными зависимостями «субъективного» от «субъективного».

Таким образом, анализ экспериментальных данных подтверждает выдвинутые предположения, положенные в основу построения шкал отношений: постоянство произведения сумм по строкам и по столбцам, эквивалентность трех построенных шкал. Это подкрепляется линейностью связи со шкалой, построенной по данным МПС. Следовательно, можно сделать вывод, что построенные шкалы действительно являются шкалами отношений, что испытуемый в состоянии адекватно непосредственно оценивать отношения между образами стимулов.

Связь между шкалами НОО-2 и НОО-3

40 т

35

НОО-2

Рис. 1. Связь между шкалами НОО-2 и НОО-3

Рис. 2. Связь между шкалами, построенными по данным методов НОО-2 и МПС

Список литературы

1. Худяков А. И. О возможности построения шкалы интервалов в психологических измерениях / А. П. Худяков // Изв. Пркут. гос. ун-та. Сер. Психология. – 2016. -Т. 15. – С. 31-49.

2. Худяков А. П. Психофизика обобщенного образа / А. П. Худяков // Palmarium Academic Publishing. LAP LAMBERT Academic Publishing GmbH & Co. KG. Saarbrücken. – Germany, 2012. – 247 p.

3. Худяков А. П. Психология измерений /А. П. Худяков. – СПб. : Копи-Р Групп, 2013. – 220 с.

4. Худяков А. П. Экспериментальная психология / А. П. Худяков. – X. : Гуманит. центр, 2016. – 408 с.

5. Ekman P. Constants across cultures in the face and emotions / P. Ekman, W. V. Frisen // Journal of Personality and Social Psychology. – 1971. – N 17. – P. 124-129.

6. Sydow H. Mathematische Psychologie / H. Sydow, P. Petzold. – Berlin : Springer, 1981. – 323 p.

Attitude Scale Building in Psychological Measurements

E. A. Faltermeier, A. I. Khudiakov

Herzen State Pedagogical University of Russia, Saint-Petersburg

Abstract. Ways to cope with the problem of psychological measurements through combining results of theoretical and practical research are presented. The example of attitude scale building with regard to psychological measurements is considered in the context of soundness of mathematical models application to psychological measurements when building interval scales. Using the results of direct methods of psychological measurement of stimuli having no physical metric it is possible to build metric scales of intervals and attitudes. The structure of the scale makes it possible not to use particular unit of measure as permissible transformations enable using conditional units. Mathematical model of any process will be valid if there is a preconceived idea of the process nature. When using probability, the problem is not solved but its contentious issues are skirted.

Keywords: psychological measurement, psychophysical scaling, attitude scale, empirical procedures, chance models, method of paired comparisons, direct estimation of attitudes, direct quantitative estimation, direct quantitative estimation of subjective intervals.

Фальтермайер Екатерина Андреевна аспирант, кафедра психологии профессиональной деятельности Российский государственный педагогический университет им. А. И. Герцена 191186, г. Санкт-Петербург, Набережная реки Мойки, 48 e-mail: khudjakova. kat@gmail. com

Худяков Андрей Иванович доктор психологических наук, профессор, кафедра психологии профессиональной деятельности

Российский государственный педагогический университет им. А. И. Герцена 191186, г. Санкт-Петербург, Набережная реки Мойки, 48 e-mail: haipsy@yandex.ru

Faltermeier Ekaterina Andreevna Postgraduate, Department of Psychology of Professional Activity Herzen State Pedagogical University of Russia

48, Moika Embankment, Saint-Petersburg, 191186

e-mail: khudjakova. kat@gmail. com

Khudiakov Andrey Ivanovich Doctor of Sciences (Psychology), Professor, Department of Vocational Psychology Herzen State Pedagogical University of Russia

48, Moika Embankment, Saint-Petersburg, 191186

e-mail: haipsy@yandex.ru