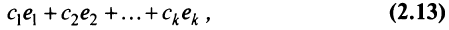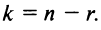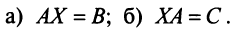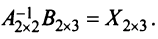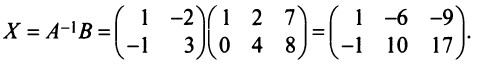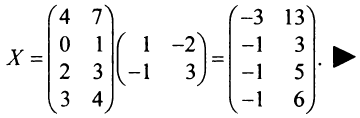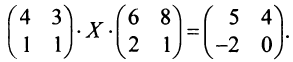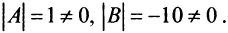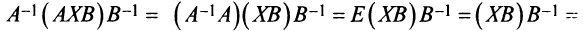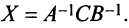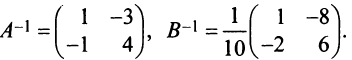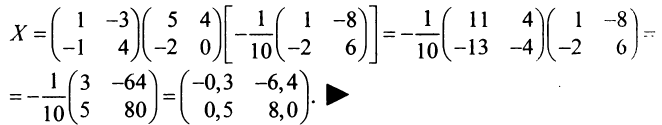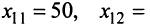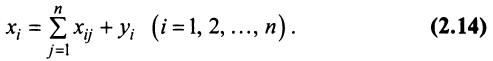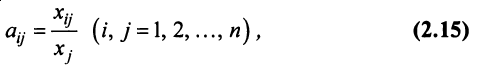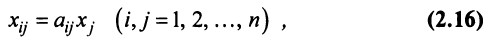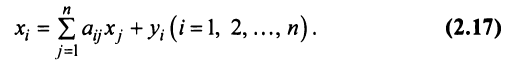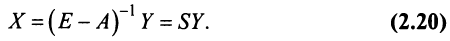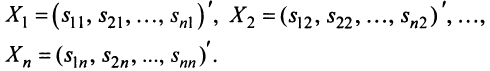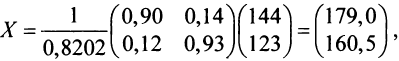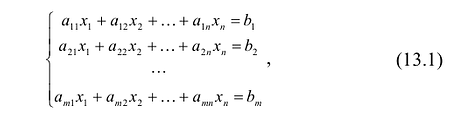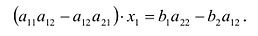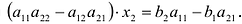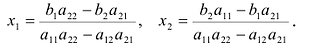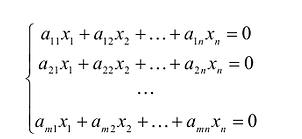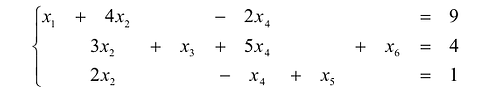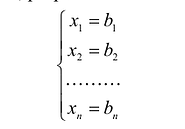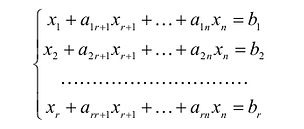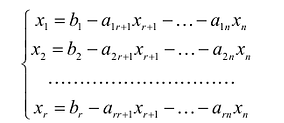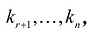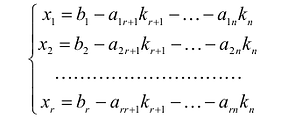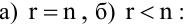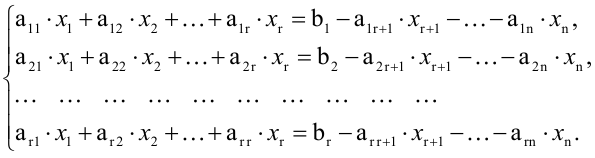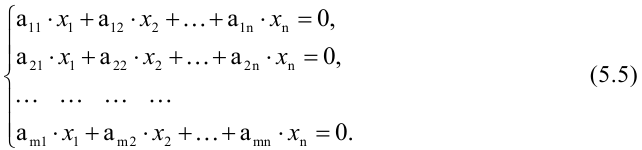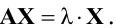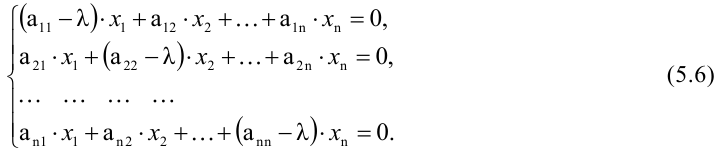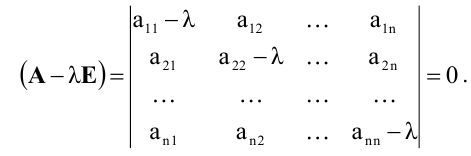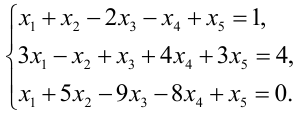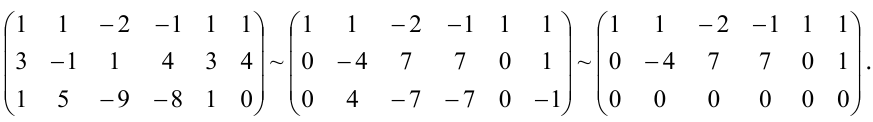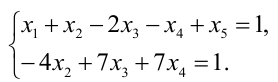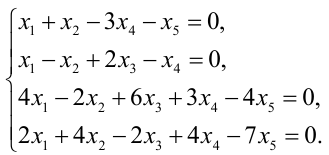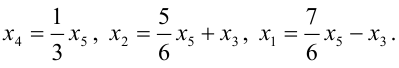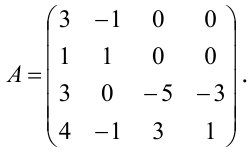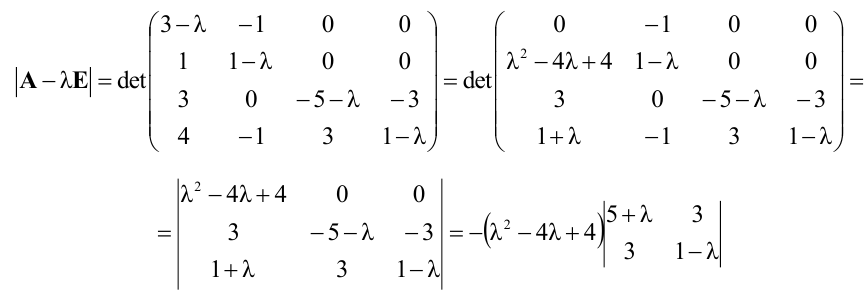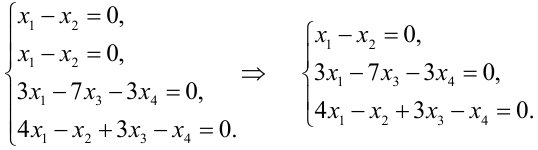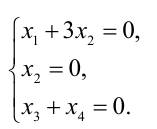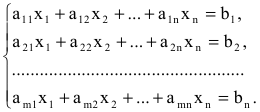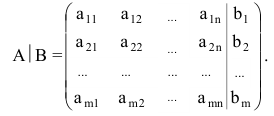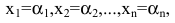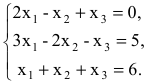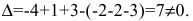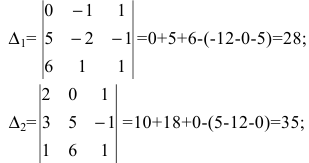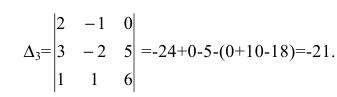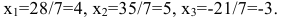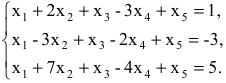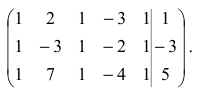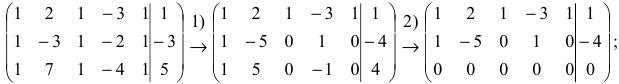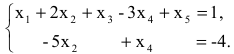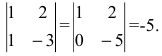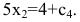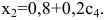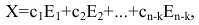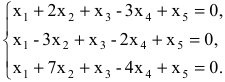Полная система для лото 3 даёт стопроцентную гарантию выигрыша при совпадении трёх номеров. Как создать свою собственную полную систему игры в лото 3 из любого количества (до 99) номеров.
Полная система комбинаций номеров гарантирует выпадение одной тройки при совпадении трёх номеров.
Система ограничена вводом 14 номеров.
Это моя программа – при использовании давайте ссылку на страницу.
.
Форма для выбора номеров
Выбрано номеров:
#полнаясистема #лото3 #3номера
Видео канал сайта
Новости сайта
На страницах сайта можно найти последние результаты популярных лотерей, а также закономерность выпадения номеров по тиражам, системы номеров, варианты анализа номеров, статистика тиражей.
Советы и предложения по ведению сайта и новости по лотерейной тематике публикуйте в группе соцсетей или направляйте на мою страничку.
Новости
Cайт igravloto.ru
Сайт “Системы игры в числовые лотереи” сайт не является игровым сайтом, не относится к сайтам азартной тематики.
Он не является официальным сайтом Государственных лотерей “Столото” и любых других числовых лото.
Здесь собраны результаты тиражей и проведен их статический анализ. Cайт собирает статистику тиражей популярных числовых лотереи.
О сайте
Лотерейный билет
На сайте не организуются азартные игры и не продаются лотерейные билеты.
Претензии по лотерейным билетам, помощь в получении выигрышей, свои предложения направляйте на официальные сайты организаторов лотерей.
Сайт не консультирует посетителей по организационным вопросам проведения тиражей.
Помощь
Реклама на сайте
Рекламные блоки от рекламных компаний, размещенные на сайте, могут содержать рекламу лотерейных сайтов (или азартных игр) от своих проверенных рекламодателей.
Для размещения Вашей рекламы на сайте igravloto.ru внесите соответствующие изменения в настройках рекламных объявлений.
Контакты
Афоризмы о игре
Зачем мне играть в выдуманные игры, когда на свете так много настоящей игры.
Карта сайта
Социальные сети
Присоединяйтесь к группам сайта в социальных сетях. Сохраняйте ссылки в своих профилях.
Социальные сети
.
Как решать систему уравнений
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
Система линейных уравнений с тремя переменными
Линейное уравнение с тремя переменными и его решение
Уравнение вида ax+by+cz = d , где a, b, c, d – данные числа, называется линейным уравнением с тремя переменными x, y и z.
Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; frac<1> <2>x-8y-5z = 7$
Уравнение с тремя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x,y и z.
Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$
Решением уравнения с тремя переменными называется упорядоченная тройка значений переменных (x,y,z), обращающая это уравнение в тождество.
О тождествах – см. §3 данного справочника
Например: для уравнения 2x+5y+z=8 решениями являются тройки x = -2, y = 1, z = 7; x = -1, y = 1, 6 , z = 2; x = -3, y = 2, 4, z = 2 и т.д. Уравнение имеет бесконечное множество решений.
Геометрическим представлением линейного уравнения с тремя переменными является плоскость в трёхмерном координатном пространстве .
Решение системы линейных уравнений с тремя переменными методом подстановки
Алгоритм метода подстановки для системы уравнений с тремя переменными аналогичен алгоритму для двух переменных (см.§45 данного справочника)
Например: решить систему
$$ <left< begin 3x+2y-z = 8 \ x-y+z = -2 \ 2x-3y-5z = 1 end right.> Rightarrow <left< begin 3(y-z-2)+2y-z = 8 \ x = y-z-2 \ 2(y-z-2)-3y-5z = 1 end right.> Rightarrow $$
$$ Rightarrow <left< begin x = y-z-2 \ 5y-4z = 14 \ -y-7z = 5 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ 5(-7z-5)-4z = 14 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ -39z = 39 end right.> Rightarrow $$
$$ Rightarrow <left< begin x = 2-(-1)-2 = 1 \ y = -7cdot(-1)-5 = 2 \ z = -1 end right.> Rightarrow <left< begin x = 1 \ y = 2 \ z = -1 end right.> $$
Решение системы линейных уравнений с тремя переменными методом Крамера
Для системы с 3-мя переменными действуем по аналогии.
Дана система 3-х линейных уравнений с 3-мя переменными:
$$ <left< begin a_1 x+b_1 y+c_1 z = d_1 \ a_2 x+b_2 y+c_2 z = d_2 \ a_3 x+b_3 y+c_3 z = d_3 end right.> $$
Определим главный определитель системы:
$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end $$
и вспомогательные определители :
$$ Delta_x = begin d_1 & b_1 & c_1 \ d_2 & b_2 & c_2 \ d_3 & b_3 & c_3 end, Delta_y = begin a_1 & d_1 & c_1 \ a_2 & d_2 & c_2 \ a_3 & d_3 & c_3 end, Delta_z = begin a_1 & b_1 & d_1 \ a_2 & b_2 & d_2 \ a_3 & b_3 & d_3 end $$
Тогда решение системы:
Соотношение значений определителей, расположения плоскостей и количества решений:
Три плоскости пересекаются в одной точке
Три плоскости параллельны
Две или три плоскости совпадают или пересекаются по прямой
Бесконечное множество решений
Осталось определить правило вычисления определителя 3-го порядка.
Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):
$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end = a_1 = begin b_2 & c_2 \ b_3 & c_3 end – b_1 = begin a_2 & c_2 \ a_3 & c_3 end + c_1 = begin a_2 & b_2 \ a_3 & b_3 end = $$
$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$
Примеры
Пример 1. Найдите решение системы уравнений методом подстановки:
$$<left< begin z = 3x+2y-13 \ 2x-y+3(3x+2y-13) = -2 \ x+2y-(3x+2y-13) = 9 end right.> Rightarrow <left< begin z = 3x+2y-13 \ 11x+5y = 37 \ -2x = -4 end right.> Rightarrow $$
$$Rightarrow <left< begin z = 3cdot2+2cdot3-13 = -1 \ y = frac<37-11cdot2> <5>= 3 \ x = 2 end right.> Rightarrow <left< begin x = 2 \ y = 3 \ z = -1 end right.> $$
$$ <left< begin x = -y-3z+6 \ 2(-y-3z+6)-5y-z = 5\ (-y-3z+6)+2y-5z = -11 end right.> Rightarrow <left< begin x = -y-3z+6 \ -7y-7z = -7 |:(-7) \ y-8z = -17 end right.> Rightarrow $$
$$ Rightarrow <left< begin x = -y-3z+6 \ y+z = 1 \ y-8z = -17 end right.> Rightarrow <left< begin x = -y-3z+6 \ 9z = 18 \ y = 1-z end right.> Rightarrow <left< begin x = 1-6+6 = 1 \ z = 2 \ y = 1-2 = -1 end right.> Rightarrow$$
Пример 2. Найдите решение системы уравнений методом Крамера:
$$ Delta = begin 3 & 2 & -1 \ 2 & -1 & 3\ 1 & 2 & -1 end = 3 = begin -1 & 3 \ 2 & -1 \ end – 2 = begin 2 & 3 \ 1 & -1 \ end – 1 = begin 2 & -1 \ 1 & 2 \ end = $$
$$ Delta_x = begin 13 & 2 & -1 \ -2 & -1 & 3 \ 9 & 2 & -1 \ end = 13 = begin -1 & 3 \ 2 & -1 \ end – 2 = begin -2 & 3 \ 9 & -1 \ end – 1 = begin -2 & -1 \ 9 & 2 \ end = $$
$$ Delta_y = begin 3 & 13 & -1 \ 2 & -2 & 3 \ 1 & 9 & -1 \ end = 3 = begin -2 & 3 \ 9 & -1 \ end – 13 = begin 2 & 3 \ 1 & -1 \ end – 1 = begin 2 & -2 \ 1 & 9 \ end = $$
$$ Delta_z = begin 3 & 2 & 13 \ 2 & -1 & -2 \ 1 & 2 & 9 \ end = 3 = begin -1 & -2 \ 2 & 9 \ end – 2 = begin 2 & -2 \ 1 & 9 \ end + 13 = begin 2 & -1 \ 1 & 2 \ end = $$
$$ Delta = begin 1 & 1 & 3 \ 2 & -5 & -1\ 1 & 2 & -5 end = 1 = begin -5 & -1 \ 2 & -5 \ end – 1 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & -5 \ 1 & 2 \ end = $$
$$ Delta_x = begin 6 & 1 & 3 \ 5 & -5 & -1 \ -11 & 2 & -5 \ end = 6 = begin -5 & -1 \ 2 & -5 \ end – 1 = begin 5 & -1 \ -11 & -5 \ end + 3 = begin 5 & -5 \ -11 & 2 \ end = $$
$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$
$$ Delta_y = begin 1 & 16 & 3 \ 2 & 5 & -1 \ 1 & -11 & -5 \ end = 1 = begin 5 & -1 \ -11 & -5 \ end – 6 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & 5 \ 1 & -11 \ end = $$
$$ Delta_z = begin 1 & 1 & 6 \ 2 & -5 & 5 \ 1 & 2 & -11 \ end = 1 = begin -5 & 5 \ 2 & -11 \ end – 1 = begin 2 & 5 \ 1 & -11 \ end + 6 = begin 2 & -5 \ 1 & 2 \ end = $$
Пример 3*. Решите систему уравнений относительно x,y,и z:
$$ a neq b, b neq c, a neq c $$
Решаем методом замены:
$$ <left< begin z = -(a^3+a^2 x+ay)\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 end right.> Rightarrow <left< beginz = -(a^3+a^2 x+ay)\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \ (c^2-a^2 )x+(c-a)y = a^3-c^3 end right.> $$
Т.к. $ a neq b$ второе уравнение можно сократить на $(a-b) neq 0$
Т.к.$ a neq c$ третье уравнение можно сократить на $(a-с) neq 0 $. В третьем уравнении после сокращения поменяем знаки:
Из второго уравнения получаем:
Т.к. $b neq c$ можно сократить на $(b-c) neq 0$:
$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$
$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$
Алгебраические системы с тремя неизвестными с примерами решения
Алгебраические системы с тремя неизвестными
Для систем с тремя неизвестными определения понятий равносильности и следствия, а также свойства преобразований систем формулируются аналогично тому, как это было сделано для систем с двумя неизвестными.
Будем рассматривать системы вида
где 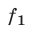
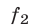
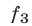
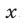
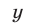
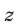
Сформулируем для систем уравнений с тремя неизвестными следующие утверждения, которые могут оказаться полезными при решении систем.
1° Если 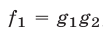
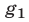
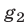
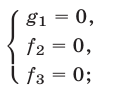
и поэтому множество решений системы (1) в этом случае есть объединение множеств решений систем (2) и (3).
2°. Если уравнение
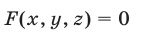
есть следствие системы (1), то система
равносильна системе (1), т. е. при добавлении к системе (1) еще одного уравнения (4), являющегося следствием этой системы, получается система, равносильная системе (1).
3°. Если уравнение (4) — следствие системы (1), причем 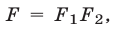
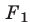
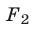
4°. Система (1) равносильна каждой из следующих систем:
5°. Если уравнение 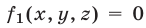
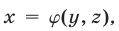
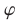
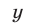
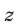
Это утверждение лежит в основе метода исключения неизвестных: система (1) сводится к системе (5), (6) с двумя неизвестными.
Прежде чем переходить к примерам алгебраических систем с тремя неизвестными, отметим, что нет общих рецептов для нахождения решений систем. Каждый раз нужно учитывать конкретные особенности рассматриваемой системы. Можно дать только общий совет: решайте побольше задач.
Рассмотрим сначала системы с тремя неизвестными, которые сводятся к кубическим уравнениям.
К таким системам относятся системы симметрических алгебраических уравнений, т.е. системы вида (1), где 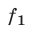
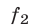
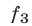
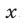
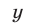
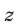
В этом случае удобно ввести следующие переменные:
Простейший пример системы рассматриваемого вида — система
Система (7) и кубическое уравнение
связаны следующим образом.
Если 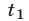
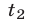
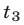
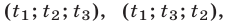
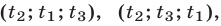
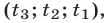
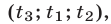
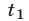
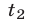
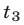
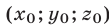
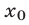
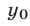
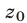
Доказательство этого утверждения основано на использовании формул Виета для корней уравнения (8):
Для сведения к системам (7) систем симметрических уравнений вида
можно использовать следующие тождества:
Примеры с решениями
Пример №186.
Решить систему уравнений
Решение:
Используя уравнения (12), (13) и тождество (9), получаем
Применяя формулу (11) и учитывая равенства (13)-(15), находим
Следовательно, исходная система равносильна системе вида (7), в которой 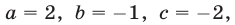
Корни этого уравнения — числа 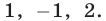
Ответ.
Обратимся теперь к системам с тремя неизвестными, которые не являются симметрическими.
Пример №187.
Решить систему уравнений
Решение:
Так как правые части уравнений отличны от нуля, то 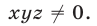
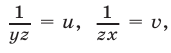
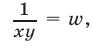
Сложив уравнения системы (16), находим
Из (16) и (17) получаем 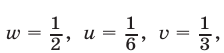
Перемножив почленно уравнения системы (18), которая равносильна исходной, имеем 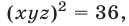
Следовательно, исходная система равносильна совокупности систем (18), (19) и (18), (20), которые имеют решения 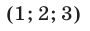
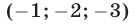
Ответ.
Пример №188.
Решить систему уравнений
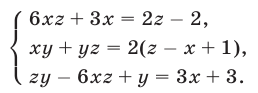
Решение:
Будем решать систему методом исключения неизвестных и сведением, в конечном счете, к одному уравнению с одним неизвестным. Складывая почленно уравнения (21) и (23), получаем
Так как 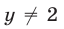
Запишем далее уравнение (22) в виде
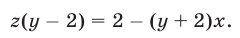
Исключив 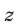
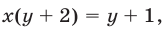
Заметим, что система (27), (25), (21) равносильна системе (21)— (23). Подставляя выражения для 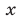
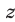
или 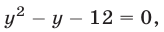
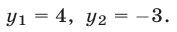
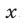
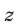
Ответ.
Пример №189.
Решить систему уравнений
Решение:
Перемножив уравнения системы (28), получаем
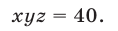
Уравнение (29) является следствием системы (28), которая равносильна системе
Уравнения (30), (31), (32) имеют решения 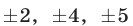
Ответ.
Пример №190.
Найти решения системы уравнений
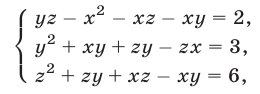
Решение:
Вычитая из уравнения (34) уравнение (33), получаем
Далее, вычитая из уравнения (35) уравнение (33), находим
Наконец, складывая уравнения (34) и (35), получаем
Система (37)-(39) равносильна системе (33)-(35), а при условии (36) — системе линейных уравнений
имеющей единственное решение
Ответ.
Пример №191.
Решить систему уравнений
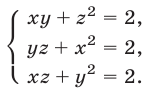
Решение:
Вычтем из уравнения (41) уравнение (40) и преобразуем полученное уравнение к виду
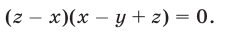
Выполнив ту же операцию с уравнениями (42) и (41), имеем
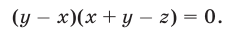
Система (43), (44), (42), равносильная системе (40)-(42), распадается на следующие четыре системы:
Полученные системы легко решаются методом исключения неизвестных. Объединив решения этих систем, найдем все решения исходной системы.
Ответ.
Пример №192.
Решить систему уравнений
Решение:
Решим эту систему как линейную относительно 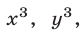
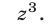
Перемножив уравнения системы (46) и полагая 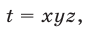
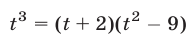
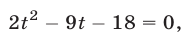
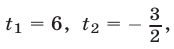
Система (45) в силу утверждения 3° равносильна совокупности систем (46), (47) и (46), (48), каждая из которых имеет единственное решение.
Ответ.
Пример №193.
Решить систему уравнений
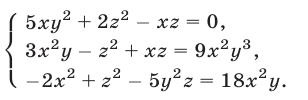
Решение:
Если 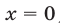
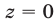
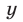
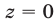
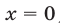
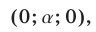

Будем искать решения системы (49) такие, что 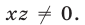
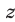
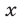
Прибавив к уравнению (51) второе уравнение системы (49), умноженное на 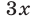
Каждое из уравнений (51), (52) является следствием системы (49).
Так как 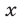
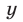
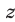
Исключая 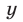
Уравнения (53) и (54) являются следствиями системы (49), а уравнение (54) равносильно совокупности уравнений
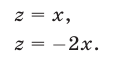
Из (55) и (53) следует, что 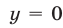
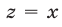
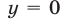
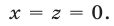
Из (56) и (53) следует, что 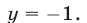
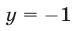
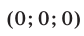
Ответ. 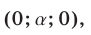
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
[spoiler title=”источники:”]
http://reshator.com/sprav/algebra/7-klass/sistema-linejnyh-uravnenij-s-tremya-peremennymi/
http://lfirmal.com/algebraicheskie-sistemyi-s-tremya-neizvestnyimi-s-primerami-resheniya/
[/spoiler]
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
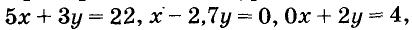
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 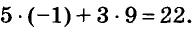
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 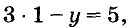
Уравнение 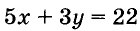
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 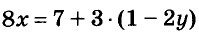
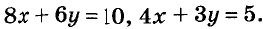
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 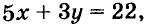
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решите уравнение:
Решение:
а) При любых значениях х и у значения выражения 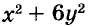
б) Значение выражения 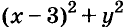
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 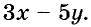
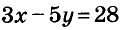
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 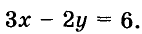
Если на координатной плоскости обозначить соответствующие этим парам точки, то окажется, что все они размещены на одной прямой (рис. 89). Эту прямую (рис. 90) называют графиком данного уравнения.
Выразим из уравнения 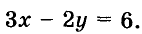
Это функция, график которой изображён на рисунке 90. Вообще, если 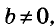
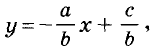
График каждого уравнения первой степени с двумя переменными — прямая. И каждая прямая координатной плоскости — график некоторого линейного уравнения с двумя переменными.
Каждая точка графика уравнения имеет координаты, удовлетворяющие данное уравнение. Например, точка М графика уравнения 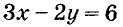
График линейной функции одновременно является графиком некоторого линейного уравнения с двумя переменными. Например, уравнения 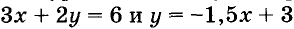
Чтобы построить график уравнения первой степени о ‘ 1 двумя переменными, достаточно найти два его решения, обозначить на координатной плоскости соответствующие им точки и провести через них прямую.
Такое уравнение удовлетворяет любая пара чисел. Его графиком является вся координатная плоскость.
•Если 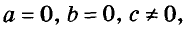
Такое уравнение не имеет ни одного решения.
Известно, что две прямые на плоскости могут пересекаться, быть параллельными или совпадать. Так же могут располагаться на координатной плоскости и графики двух уравнений первой степени с двумя переменными (рис. 91).
Взаимное расположение графиков уравнений
Пример:
Постройте график уравнения:
Решение:
Уравнению а) удовлетворяет каждая пара чисел (c ; 4), где с — произвольное число. График этого уравнений — прямая, параллельная оси х, проходящая через точку A(0 ; 4) (рис. 92).
Бесконечно много решений уравнения б) — множество пар (2 ; p), где p — произвольное число. График этого уравнения — прямая параллельная оси у (рис. 93).
Уравнение в) удовлетворяет каждая пара чисел, график этого уравнения — вся координатная плоскость.
Уравнение г) не имеет ни одного решения, его график — пустое множество.
Определение и вычисление систем уравнений
Пример:
4 кг конфет и 3 кг пряников стоят 26 руб., а 6 кг конфет и 2 кг пряников — 34 руб. Сколько стоит 1 кг конфет и 1 кг пряников?
Эту задачу можно решить, составив уравнение с одной переменной, а можно воспользоваться другим способом.
Пусть 1 кг конфет стоит х руб., а 1 кг пряников — у руб.
Тогда
Имеем два уравнения с двумя переменными. Надо найти такие значения переменных х и у, которые удовлетворяют одновременно и первое, и второе уравнения, то есть обращающие каждое из уравнений в верное равенство. Другими словами: надо найти общее решение обоих уравнений, или решить систему данных уравнений.
Если требуется найти общие решение двух или нескольких уравнений, говорят, что эти уравнения образуют систему. Записывают систему уравнений, объединяя их фигурной скобкой:
Решением системы уравнений называют общее решение всех её уравнений.
Например, пара чисел (3; 2) является решением системы
то есть:
Решить систему уравнений —это означает найти множество всех её решений .
Решать системы уравнений можно графическим способом. Решим, например, систему (*). Для этого построим на одной координатной плоскости графики обоих её уравнений (рис. 95). Координаты каждой точки графика уравнения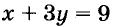
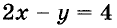
Графическим способом обычно находят приближённые решения. А подставив значения 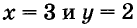
Каждая ли система двух уравнений имеет только одно решение? Нет. Например, система уравнений
имеет бесконечно много решений. Ведь графики обоих этих уравнений — одна и та же прямая (убедитесь в этом самостоятельно). Следовательно, координаты каждой точки этой прямой, например(-2; -6), (-1; -4,5), (0; -3), (1; -1,5), (2; 0),… — решения данной системы уравнений.
Есть системы уравнений, которые не имеют ни одного решения. Графики таких уравнений — параллельные прямые (см. рис. 91).
Вы уже знаете, что уравнение и функции — удобные математические модели многих задач. Системы уравнений также используют как математические модели. Иногда, исходя из условия задачи, систему уравнений с двумя переменными легче составить, чем одно уравнение. И решать её бывает легче, чем уравнение с одной переменной, соответствующее условию той же задачи.
Пример:
Сколько решений имеет система уравнений
Решение:
Так как 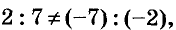
Пример:
Решите графически систему уравнений
Решение:
Найдём координаты точек пересечения графиков уравнений системы с осями координат.
Построим графики данных уравнений (рис. 96). Эти графики — параллельные прямые, не имеющие общих точек. Ответ. Система уравнений решений не имеет.
Способ подстановки
Графический способ решения систем уравнений громоздок и даёт, как правило, приближённые решения. Поэтому чаще системы решают другими способами, в частности способом подстановки.
Пусть, например, надо решить систему
Выразим из второго её уравнения переменную х через у:
Так как первое уравнение системы должны удовлетворять те же значения переменных, что и второе, подставим найденное выражение 9-3у вместо х в первое уравнение. Получим уравнение с одной переменной:
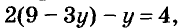
Подставим значение у = 2 в уравнение х = 9 – Зу и найдём соответствующее значение переменной х:
Следовательно, решением системы является пара чисел (3; 2).
Чтобы решить систему уравнений способом подстановки, надо:
- выразить из какого-нибудь её уравнения одну переменную через другую;
- подставить в другое уравнение системы вместо этой л временной полученное выражение;
- решить получившееся уравнение с одной переменной;
- найти соответствующее значение второй переменной.
Этим способом можно решать любую систему линейных уравнений с двумя переменными. Однако удобнее, если коэффициент при какой-либо переменной в уравнении равен 1.
Пример №1
Решите систему уравнений
Решение:
Заменим данные уравнения линейными, получим систему:
Иногда можно подставлять из одного уравнения системы во второе не значение отдельной переменной, а значение целого выражения.
Например, решая систему уравнений
можно значение выражения 2х-4у из второго уравнения подставить в первое:
Тогда
Ответ. х = 3, у = -2.
Проверка.
2 • 3 – 4(-2) = 6 + 8 = 14. Найденная пара чисел (3; -2) удовлетворяет данную систему уравнений.
Пример №2
Решите систему уравнений:
Решение:
Выразим из второго уравнения значение Дроби 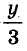
Тогда
Ответ. (8; 6).
Способ сложения
Дана система уравнений:
Сначала решим её способом подстановки. Выразим из первого уравнения переменную у через х и подставим полученное выражение вместо у во второе уравнение:
Дальше уже несложно закончить решение системы.
А можно ли уравнение 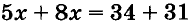
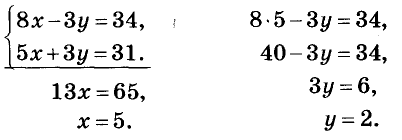
Таким образом решают системы, в которых коэффициенты при какой-либо переменной — противоположные числа. А к такому виду можно свести любую систему линейных уравнений с двумя переменными. Пусть, например, дана система
Умножим обе части её первого уравнения на 2, а второго — на -3; получим систему, в которой коэффициенты при переменной х — противоположные числа. Уравнения полученной системы равносильны уравнениям данной. Следовательно, она имеет такие же решения, что и данная.
Оформлять решение можно таким образом: 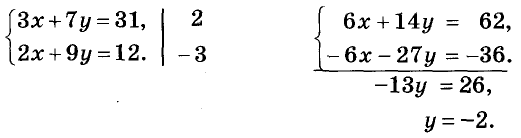
Решение. (15; -2).
Способом сложения можно решить не только системы линейных уравнений, а и многих нелинейных.
Пример №3
Решите систему уравнений
Решение:
Выполнив сложение левых и правых частей данных уравнений, получим:
Значит, 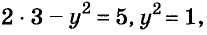
Проверка показывает, что найденные пары чисел (3; 1) и (3; -1) удовлетворяют данную систему уравнений.
Ответ. Система уравнений имеет два решения: (3; 1) и (3; -1).
Пример №4
Решите систему уравнений
Решение:
Умножим все члены первого уравнения на 3, а второго — на 5. Упростим полученные уравнения:
Чтобы воспользоваться способом сложения, ещё раз умножим все члены первого уравнения на 3, а второго — на 5 и почленно сложим их:
Ответ. (4; 1).
Решение задач составлением системы уравнений
Многие задачи, особенно такие, в которых надо найти значения двух величин, удобно решать с помощью систем уравнений.
Пример:
За 5 блокнотов и 6 тетрадей заплатили 6,9 руб. Сколько стоит один блокнот и одна тетрадь, если 4 блокнота дороже 3 тетрадей на 2,4 руб.?
Решение:
Допустим, что блокнот стоит х руб., а тетрадь — у руб. За 5 блокнотов заплатили 5х руб., а за б тетрадей — 6у руб. Вместе за них заплатили 6,9 руб., следовательно,
Так как 4 блокнота дороже 3 тетрадей на 2,4 руб., имеем ещё одно уравнение:
Переменные х и у в обоих уравнениях обозначают одни и те же цены. Значит, надо решить систему этих двух уравнений:
Ответ. Блокнот стоит 90 к., тетрадь — 40 к.
Эту задачу можно решить также составлением уравнения с одной переменной. Любую задачу, которая решается составлением системы линейных уравнений, можно решить и с помощью уравнения с одной переменной. Только систему уравнений чаще составить легче, чем уравнение с одной переменной.
Существует немало задач, которые удобно решать с помощью системы трёх уравнений с тремя переменными. Решим одну из них.
Пример:
Капитал в 10 000 руб. поделите на три части так, чтобы первая была на 2 000 руб. больше второй и на 3 000 руб. — третьей.
Решение:
Обозначим искомые части капитала буквами х,у и z. По условию задачи
Искомые значения переменных должны удовлетворять системе трёх уравнений с тремя переменными:
Сложив почленно левые и правые части этих уравнений, будем иметь Зх = 15 000, отсюда х = 5 000. Тогда из второго уравнения получим:
5000 -у = 2000, y = 3000, а из третьего вычислим:
5 000 -z = 3 000, z = 2 000. Ответ. 5000 руб., 3000 руб. и 2000 руб.
Обобщим задачу 1:
Пример:
За 5 блокнотов и 6 тетрадей заплатили m руб. Сколько стоит один блокнот и одна тетрадь, если 4 блокнота дороже 3 тетрадей на n руб.?
Здесь m и n – параметры, то есть буквы, считающиеся в условиях задачи данными, неизменными. Задачи с параметрами так же можно решать с помощью уравнений или системы уравнений, только ответами к ним будут не конкретные числа, а выражения, содержащие параметры.
Решим сформулированную задачу.
Решение:
Ответ. Один блокнот и одна тетрадь стоят соответственно
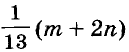
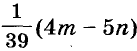
Пример:
Поделите капитал 8 100 руб. на две части так, чтобы меньшая часть составляла 80 % от большей.
Решение:
Пусть большая часть равна х руб., тогда меньшая — 80 % от х, то еть 0,8х. Имеем систему двух уравнений:
Ответ: 4500 руб. и 3600 руб.
Пример:
Найдите два числа, сумма которых равна 15, а разность их квадратов на 60 больше.
Решение:
Если искомые числа равны х и у, то
Так как 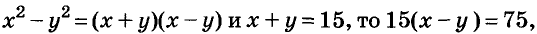
Её решение х = 10, у = 5 является решением и данной иидачи.
Ответ. 10 и 5.
История систем уравнений
Задачи, сводящиеся к системе уравнений с двумя переменными, учёные Вавилона умели решать ещё более 4 тысяч лет тому назад.
Китайские математики более 2 тысяч лeт тому назад разработали общий метод решения систем линейных уравнений с тремя и более неизвестными и описали его в трактате «Математика в девяти книгах».
Древнегреческий математик Диофант (III в.) находил натуральные решения и таких, например, задач: «Найдите два числа с данной разностью и таких, чтобы разность их квадратов была больше их разности на заданное число». Если искомые числа обозначить через х и у, а данные — через а и b, то задаче соответствует такая система уравнений:
Графический способ решения уравнений одним из первых предложил выдающийся французский философ, математик, физик, физиолог Р. Декарт. Он ввёл понятие переменной величины и удобную математическую Рене Декарт символику. (1596-1650)
В 1637 г. Р. Декарт опубликовал работу «Размышления о методе», в которой описал метод координат, связывающий алгебру с геометрией. Пользуясь этим методом, геометрические задачи можно решать алгебраическими методами, а алгебраические — геометрическим.
Р. Декарт — основатель очень известного ранее философского учения картезианство. Это название произошло от латинизированного имени Декарта – Картезий.
Напомню:
Уравнение вида ах + by = с, где а,b,c — данные числа, называют линейным уравнением с двумя переменными хну. Если 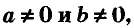
Пару чисел, удовлетворяющую уравнение с двумя переменными, называют решением этого уравнения. Например, пара чисел (3; -2) — решение уравнения 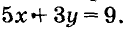
Два уравнения с двумя переменными называют равносильными, если они имеют те же решения. Равносильные уравнения с двумя переменными имеют одинаковые графики.
Если нужно найти общие решения двух или нескольких уравнений, говорят, что эти уравнения образуют систему уравнений.
Решением системы уравнений называют общее решение всех её уравнений. Пример системы двух линейных уравнений с переменными х и у:
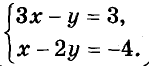
Системе двух уравнений первой степени с двумя переменными в декартовой системе координат соответствует пара прямых. Поскольку две прямые на плоскости могут пересекаться , совпадать или быть параллельными, то и соответствующая им система уравнений может иметь одно решение, бесконечно много или не иметь ни одного решения.
Решать системы уравнений с двумя переменными можно разными способами — подстановки, сложения или графическим способом.
Системы линейных уравнений
К системам линейных уравнений приводит множество прикладных, в том числе и экономических задач.
Основные понятия и определения
Система 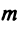
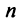
где 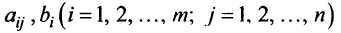
В более краткой записи с помощью знаков суммирования систему можно записать в виде:
Решением системы (2.1) называется такая совокупность 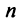
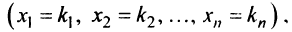
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Например, система уравнений
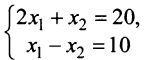
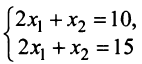
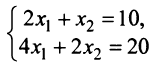
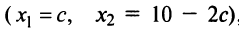
Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений. С помощью элементарных преобразований системы уравнений, рассмотренных в гл.1 применительно к матрицам (например, умножение обеих частей уравнений на числа, не равные нулю; сложение уравнений системы), получается система (2.1), равносильная данной.
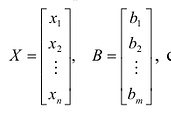
Запишем систему (2.1) в матричной форме. Обозначим:
где 
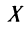
Так как число столбцов матрицы 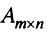
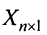
есть матрица-столбец. Элементами полученной матрицы являются левые части системы (2.1). На основании определения равенства матриц систему (2.1) можно записать в виде:
Система n линейных уравнений с n переменными.
Метод обратной матрицы и формулы Крамера
Пусть число уравнений системы (2.1) равно числу переменных, т.е. 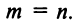
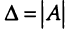
Рассмотрим решение системы двух уравнений с двумя переменными:
в которой хотя бы один из коэффициентов при переменных отличен от нуля.
Для решения этой системы исключим переменную 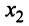
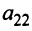
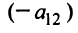
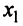
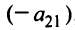
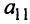
Выражение в скобках есть определитель системы
Обозначив 
Из полученной системы следует, что если определитель системы 
Если 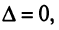
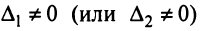
Если 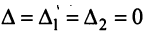
Для получения решения системы (2.1) при 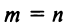
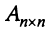
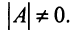
Умножая слева обе части матричного равенства (2.3) на матрицу 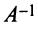
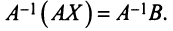
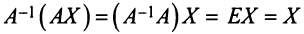
Теорема Крамера. Пусть 
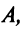
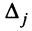
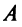
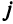
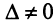
Формулы (2.8) получили название формул Крамера.

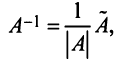
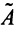
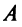
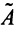
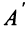
Учитывая, что 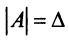
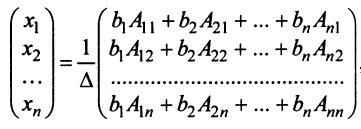
На основании свойства 9 определителей (см. § 1.4) 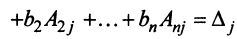
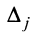
Заметим, что фактически формулы Крамера были получены нами в частном случае при решении системы (2.4) 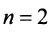
Пример №5
Решить систему уравнений
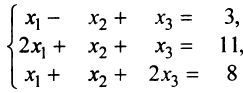
Решение:
Тогда в матричной форме данная система имеет вид: 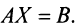
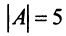
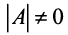
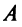
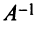
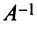
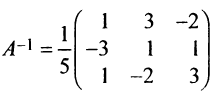
т.е. решение системы (4; 2; 1).
б) Найдем определитель системы 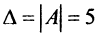
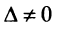
Вычислим определители матриц 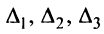
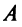
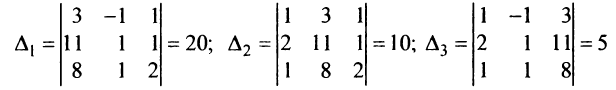
Теперь по формулам Крамера (2.8)
т.е. решение системы (4; 2; 1).
В конце решения системы (любым способом) рекомендуем сделать проверку, подставив найденные значения в уравнения системы, и убедиться в том, что они обращаются в верные равенства. ►
Существенным недостатком решения систем 
Метод Гаусса
Рассмотрим решение системы (2.1) т линейных уравнений с 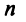
Метод Гаусса — метод последовательного исключения переменных — заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Предположим, что в системе (2.1) коэффициент при переменной 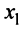
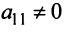
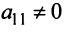
Шаг 1. Умножая первое уравнение на подходящие числа (а именно на 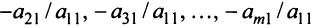
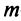
где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после первого шага.
Шаг 2. Предположим, что 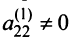
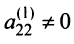
Умножая второе уравнение на подходящие числа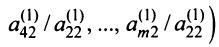
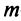
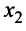
Продолжая процесс последовательного исключения переменных 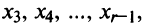
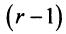
Число нуль в последних 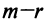
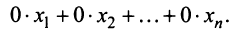
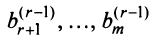
Таким образом, для любой совместной системы числа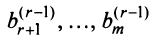
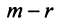
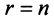
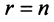
Переход системы (2.1) к равносильной ей системе (2.10) называется прямым ходом метода Гаусса, а нахождение переменных из системы (2.10) — обратным ходом.
Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Рассмотрим матрицу
называемую расширенной матрицей системы (2.1), ибо в нее, кроме матрицы системы 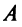
Пример №6
Решить систему уравнений:
Решение:
Расширенная матрица системы имеет вид: 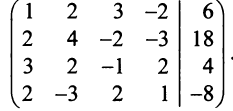
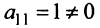
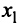
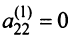
Шаг 2. Так как теперь 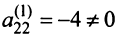
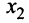
Шаг 3. Учитывая, что 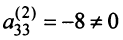
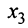
Получим (см. последнюю матрицу) систему уравнений
откуда, используя обратный ход метода Гаусса, найдем из четвертого уравнения 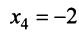
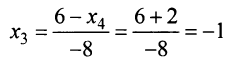
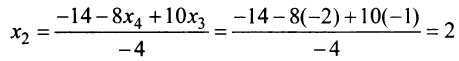
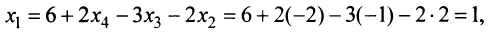
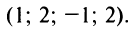
Пример №7
Методом Гаусса решить систему уравнений:
Решение:
Преобразуем расширенную матрицу системы
Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво — оно привелось к неверному равенству 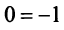
Система  линейных уравнений с
линейных уравнений с  переменными
переменными
Ранее было установлено, что ранг матрицы равен максимальному числу ее линейно независимых строк (см. § 1.6). Поэтому, если строки расширенной матрицы 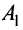
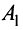
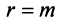
Вопрос о разрешимости системы (2.1) в общем виде рассматривается в следующей теореме.
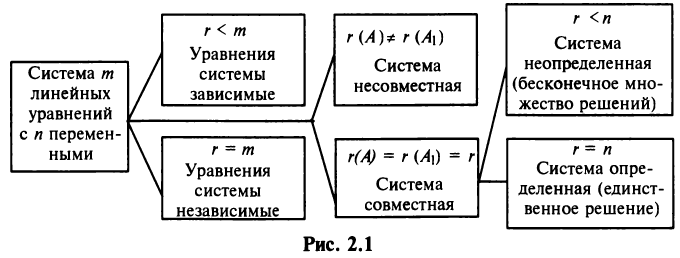
Теорема Кронекера—Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

равны нулю. В этом случае, как нетрудно проверить, ранг матрицы и ранг расширенной матрицы системы (2.10), так же как и данной системы (2.1), совпадают (оба равны 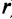
Для совместных систем линейных уравнений верны следующие теоремы.
- Если ранг матрицы совместной системы равен числу переменных, т.е.
, то система (2.1) имеет единственное решение.
- Если ранг матрицы совместной системы меньше числа переменных, т.е.
, то система (2.1) неопределенная и имеет бесконечное множество решений.
Результаты исследования системы (2.1) приведем в виде схемы (рис. 2.1):
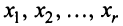
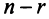
Решение системы (2.1), в котором все 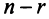
Так как каждому разбиению переменных на основные и неосновные соответствует одно базисное решение, а число способов разбиения не превосходит числа сочетаний 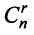
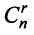
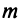
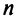
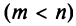
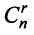
Приведенная на рис. 2.1 схема не означает, что для решения системы (2.1) в общем случае необходимо вычислять отдельно, а затем сравнивать ранги матрицы системы 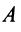
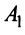
Достоинства метода Гаусса по сравнению с другими:
- значительно менее трудоемкий;
- позволяет однозначно установить, совместна система или нет, а в случае совместности найти ее решения (единственное или бесконечное множество);
- дает возможность найти максимальное число линейно независимых уравнений — ранг матрицы системы.
Пример №8
Методом Гаусса решить систему
Решение:
Преобразуем расширенную матрицу системы (для удобства вычислений берем в качестве первой строки коэффициенты второго уравнения, у которого коэффициент при 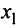
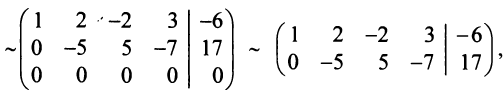
Оставляем в левой части переменные 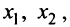
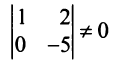
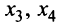
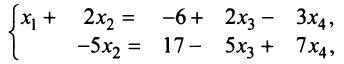
Задавая неосновным переменным произвольные значения 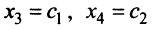
Пример №9
Найти все базисные решения системы, приведенной в примере 2.4.
Решение:
Ранг матрицы системы 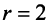
Общее число групп основных переменных не более чем 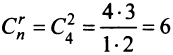
Выясним, могут ли переменные 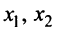
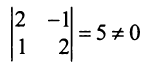
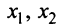
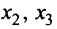
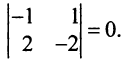
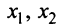
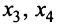
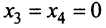
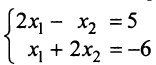
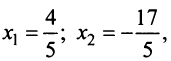
Если взять за основные переменные 
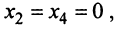
Системы линейных однородных уравнений
Фундаментальная система решений
Система 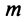
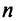
Система линейных однородных уравнений всегда совместна, так как она всегда имеет, по крайней мере, нулевое (или тривиальное) решение (0, 0, …, 0).
Если в системе (2.12)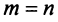
Иначе: система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при
Обозначим решение системы (2.12) 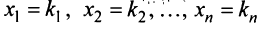
Решения системы линейных однородных уравнений обладают следующими свойствами:
- Если строка
— решение системы (2.12), то и строка
— также решение этой системы.
- Если строки
и
— решения системы (2.12), то при любых
их линейная комбинация
— также решение данной системы.
Убедиться в справедливости указанных свойств решений системы линейных однородных уравнений можно непосредственной подстановкой их в уравнения системы.
Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы. Поэтому представляет интерес найти такие линейно независимые решения системы (2.12), через которые линейно выражались бы все остальные ее решения.
Определение. Система линейно независимых решений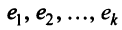
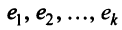
Теорема. Если ранг 
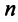
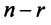
Поэтому общее решение системы (2.12) линейных однородных уравнений имеет вид:
где 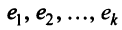
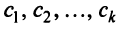
Можно показать, что общее решение системы т линейных уравнений с п переменными (2.1) равно сумме общего решения соответствующей ей системы однородных линейных уравнений (2.12) и произвольного частного решения этой системы (2.1).
Пример №10
Даны матрицы 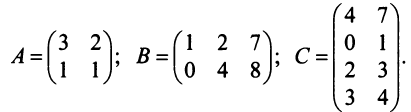
Решение:
а) Для невырожденной матрицы 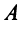
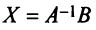
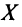
Найдем обратную матрицу 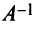
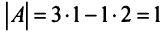
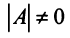
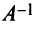
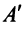
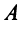
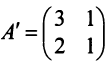
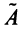
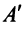
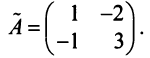
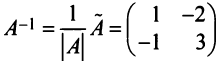
б) Полагая матрицу 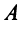
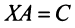
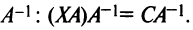
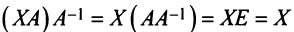
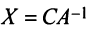
матрицы переменных (4 x 2), так как 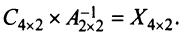
Пример №11
Решить уравнение
Решение:
Обозначив 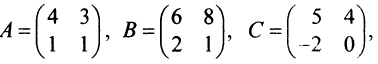
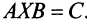
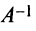
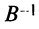
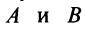
Получим 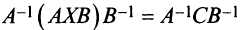
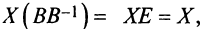
Теперь найдем
Поэтому
Пример №12
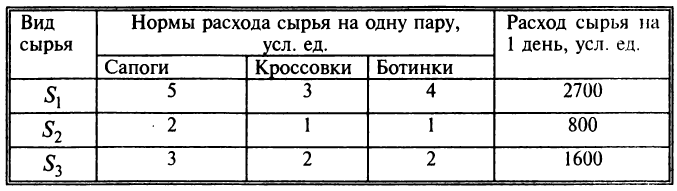
Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок; при этом используется сырье трех типов: 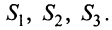
Найти ежедневный объем выпуска каждого вида обуви.
Решение:
Пусть ежедневно фабрика выпускает 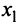
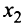
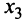
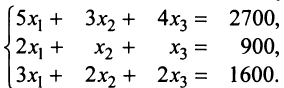
Пример №13
С двух заводов поставляются автомобили длядвух автохозяйств, потребности которых соответственно 200 и 300 машин. Первый завод выпустил 350 машин, а второй — 150 машин. Известны затраты на перевозку машин с завода в каждое автохозяйство (см. таблицу).
Минимальные затраты на перевозку равны 7950 ден. ед. Найти оптимальный план перевозок машин.
Решение:
Пусть 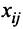
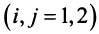
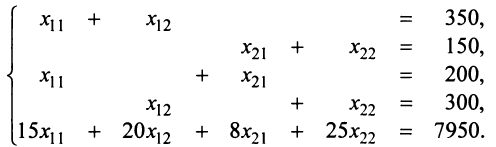
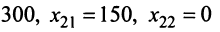
Модель Леонтьева многоотраслевой экономики (балансовый анализ)
Цель балансового анализа — ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из я отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой — как потребитель продукции и своей, и произведенной другими отраслями.
Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В. Леонтьевым.
Предположим, что рассматривается 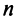
Рассмотрим процесс производства за некоторый период времени (например, год).
Введем следующие обозначения: 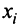
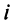
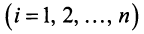
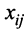
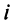
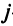
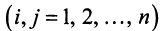
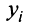
Так как валовой объем продукции любой 
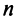
Уравнения (2.14) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в (2.14), имеют стоимостное выражение.
Введем коэффициенты прямых затрат
показывающие затраты продукции 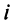
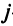
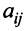
вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной. Теперь соотношения баланса (2.14) примут вид:
Обозначим
где 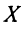
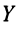
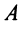
Тогда систему (2.14) можно записать в матричном виде:
Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска 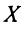
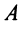
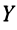
Перепишем уравнение (2.18) в виде:
Если матрица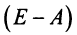
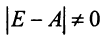
Матрица 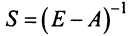
Чтобы выяснить экономический смысл элементов матрицы 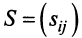
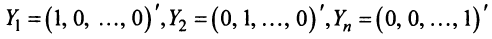
Следовательно, каждый элемент 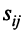
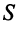
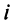
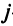
В соответствии с экономическим смыслом задачи значения 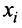
Матрица 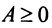
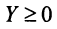
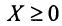
Существует несколько критериев продуктивности матрицы 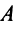
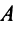
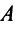
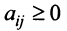
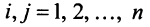
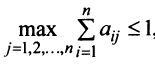
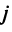
Пример №14
В таблице приведены данные об исполнении баланса за отчетный период, усл. ден. ед.:
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроительной сохранится на прежнем уровне.
Решение:
Имеем
По формуле (2.15) находим коэффициенты прямых затрат:
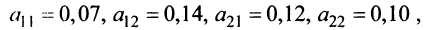
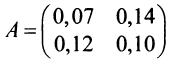
Поэтому для любого вектора конечного продукта 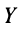
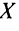
Найдем матрицу полных затрат 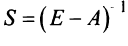
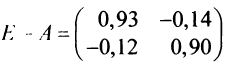
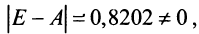
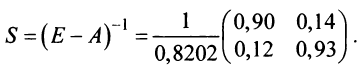
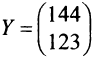
т.е. валовой выпуск в энергетической отрасли надо увеличить до 179,0 усл. ед., а в машиностроительной — до 160,5 усл. ед.
Системы линейных уравнений в линейной алгебре
Для исследования процессов функционирования экономики, при построении математических моделей конкретных задач, возникающих перед менеджером в процессе его деятельности, в ряде случаев используются системы линейных уравнений. Так, например, при межотраслевом анализе – изменение объема выпуска отрасли при фиксированном коэффициенте прямых затрат в случае изменения спроса необходимо искать путем решения системы линейных уравнений, которая является моделью изучаемого процесса.
Нахождение решений системы линейных уравнений может быть осуществлено различными методами. Выбор метода зависит от рассматриваемой задачи и соответствующей математической модели. В ряде случаев необходимо лишь знать – существует ли решение рассматриваемой системы.
Цель данного раздела – исследовать совместность системы линейных уравнений и дать некоторые методы их решения. Эти методы позволяют найти точное решение системы. Кроме этого, существуют методы, позволяющие находить приближенные решения, например, метод Якоби, метод Гаусса-Зейделя, метод пошагового агрегирования. В этом разделе они не рассматриваются.
Рассмотрим совокупность уравнений:
где 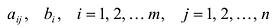
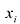
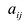
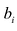
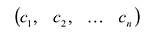
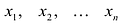
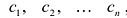
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет ни одного решения.
Система называется определенной, если она имеет единственное решение, и неопределенной, если у нее есть, по крайней мере, два различных решения.
Две системы с п неизвестными называются эквивалентными, если множества их решений совпадают. Матрица 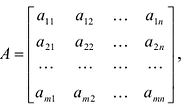


При исследовании системы (13.1) ищут ответ на следующие три вопроса:
- когда система совместна;
- если система совместна, то определена ли она;
- как отыскать ее решения.
Критерий совместности системы линейных уравнений
Ответ на первый вопрос дает теорема Кронекера-Капелли – критерий совместности системы линейных уравнений.
Теорема. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.
Правило Крамера решения систем линейных уравнений
Рассмотрим невырожденные системы линейных уравнений, т.е. системы, у которых m= n и определитель матрицы системы отличен от нуля. Определитель матрицы называется определителем системы. Следующая теорема, называемая правилом Крамера, отвечает на второй вопрос.
Пусть дана система двух линейных уравнений с двумя неизвестными:
Коэффициенты этой системы составляют квадратную матрицу второго порядка:
Решим систему (13.3). Для этого умножим первое уравнение системы на 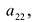
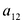
Аналогично, исключая 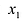
Если 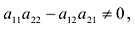
Общий знаменатель значений неизвестных 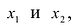
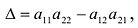
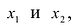
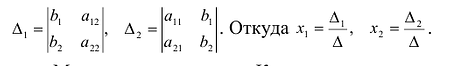
Правило Крамера. Если определитель 
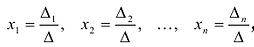
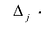

Невырожденную систему линейных уравнений АХ = В можно решить и иным способом.
Поскольку матрица А – невырожденная, то для нее существует единственная обратная матрица 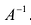
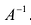
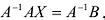
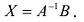
Мы ответили на три вопроса относительно систем линейных уравнений. Однако применение теоремы Крамера, которая позволила дать этот ответ, приводит к слишком громоздким вычислениям.
Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса.
- Заказать решение задач по высшей математике
Метод Гаусса
Метод Гаусса основан на теореме: если к некоторому уравнению системы прибавить другое уравнение этой системы, умноженное на любое действительное число, или умножить любое уравнение системы на отличное от нуля действительное число, то полученная система будет эквивалентна исходной.
Метод Гаусса называют также методом последовательного исключения неизвестных, осуществляя его за несколько итераций. На каждой итерации выбирается разрешающее уравнение и базисное неизвестное. В качестве разрешающего уравнения можно взять любое уравнение системы, которое ранее не было выбрано разрешающим и не все коэффициенты которого равны нулю. За базисное неизвестное выбирают неизвестное, коэффициент при котором в разрешающем уравнении, называемый разрешающим коэффициентом, не равен нулю.
Алгоритм метода следующий:
- Выбирают разрешающее уравнение и базисное неизвестное.
- Делят обе части разрешающего уравнения на разрешающий коэффициент и исключают базисное неизвестное из всех уравнений системы, кроме разрешающего. Отбрасывают, если они появились, уравнения, все коэффициенты и свободный член в котором равны нулю. Если получилось уравнение, в котором коэффициенты нулевые, а свободный член не нуль, то система несовместна, конец. Если таких уравнений нет, то шаг 1. Если все уравнения были использованы в качестве разрешающих, то шаг 3.
- Если нет, то шаг 1.
- Базисные неизвестные оставляют слева, а небазисные (назовем их свободными, так как они могут принимать любые значения) переносят вправо. Тем самым получено общее решение системы. Конец.
Однородные системы уравнений
Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:
Очевидно, что всякая однородная система совместна и имеет нулевое (тривиальное) решение. Поэтому применительно к однородным системам линейных уравнений часто приходится искать ответ на вопрос о существовании ненулевых решений. Ответ на этот вопрос можно сформулировать в виде следующей теоремы.
Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.
Доказательство: Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что г не превосходит п. В случае у = п система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при r < n.
Следствие. Однородная система уравнений в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Доказательство: Если у системы уравнений m
выполняется условие r < n и, значит, система имеет ненулевое решение.
Следствие: Однородная система n уравнений с n неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.
Доказательство: Допустим, система и линейных однородных уравнений, матрица которой 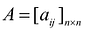
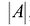
Разрешенные системы линейных уравнений
Переменная 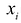
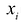
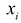
Например, система уравнений:
содержит разрешенные переменные 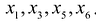
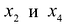
Если каждое уравнение содержит разрешенную переменную, то такую систему называют разрешенной. Очевидно, что приведенная в качестве примера система уравнений является разрешенной.
Выбрав из каждого уравнения разрешенной системы по одной разрешенной переменной, можно сформировать набор попарно различных переменных, который называется набором разрешенных переменных данной системы. В общем случае набор разрешенных переменных определен неоднозначно. Например, у рассмотренной выше системы можно выбрать два набора разрешенных переменных:
Переменные системы, которые не входят в данный набор разрешенных неизвестных, называются свободными. Если в системе фиксирован набор разрешенных переменных 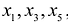
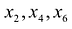
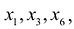
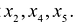
Допустим, что разрешенная система уравнений содержит переменные 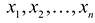
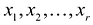
В первом случае, когда r = n, все переменные системы образуют набор разрешенных переменных системы 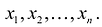
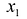
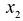
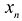
Очевидно, что такая система уравнений имеет только одно решение 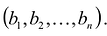
Во втором случае, когда r < n разрешенная система состоит из г уравнений вида:
Переменные 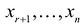
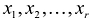
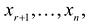
Теорема (свойство свободных переменных). Если свободным переменным системы придать 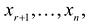
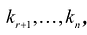
- можно построить решение К системы уравнений, у которого значения свободных переменных будут равны соответственно
- если у решений К и L системы уравнений значения свободных переменных совпадают, то и сами решения совпадают.
Доказательство: Если значения свободных переменных 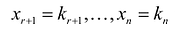
То есть 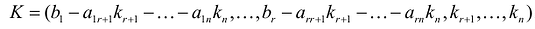
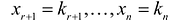
Следствие. Все решения системы получаются так же, как и решение К.
Значения для свободных переменных можно выбирать бесконечным числом различных способов, поэтому система уравнений является неопределенной.
Разрешенная система уравнений совместна всегда. Она будет определенной, если число уравнений равно числу неизвестных, и неопределенной, если число уравнений меньше числа неизвестных.
Системы линейных уравнений общего вида
Если система (5.1) оказалась совместной, т. е. матрицы 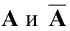
Перенесем лишние неизвестные 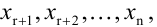
Ее можно решить относительно 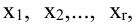
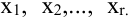
Система (5.1) называется однородной, если все 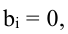
Из теоремы Кронекера-Капелли следует, что она всегда совместна, так как добавление столбца из нулей не может повысить ранга матрицы. Это, впрочем, видно и непосредственно -система (5.5) заведомо обладает нулевым, или тривиальным, решением 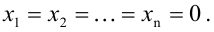
Если r = n, то нулевое решение будет единственным решением системы (5.5); при r < n система обладает решениями, отличными от нулевого, и для их разыскания применяют тот же прием, как и в случае произвольной системы уравнений.
Всякий ненулевой вектор – столбец 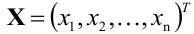
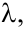
Число 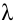
В математической экономике большую роль играют так называемые продуктивные матрицы. Доказано, что матрица А является продуктивной тогда и только тогда, когда все собственные значения матрицы А по модулю меньше единицы.
Для нахождения собственных значений матрицы А перепишем равенство 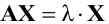
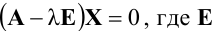
Получили систему линейных однородных уравнений, которая имеет ненулевые решения тогда и только тогда, когда определитель этой системы равен нулю, т.е.
Получили уравнение n-ой степени относительно неизвестной 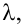
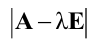
Для нахождения собственных векторов матрицы А в векторное уравнение 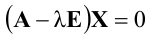
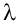
Пример №15
Исследовать систему уравнений и решить ее, если она совместна.
Решение:
Будем находить ранги матриц 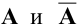
Очевидно, что 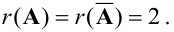
Поскольку определитель при неизвестных 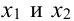
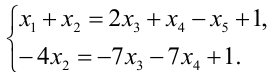
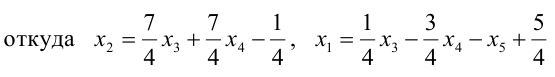
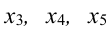
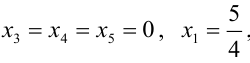
Вектор 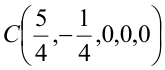
Пример №16
Исследовать систему уравнений и найти общее решение в зависимости от значения параметра а.
Решение:
Данной системе соответствует матрица 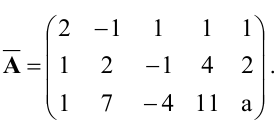
следовательно, исходная система равносильна такой:
Отсюда видно, что система совместна только при а=5. Общее решение в этом случае имеет вид:
Пример №17
Выяснить, будет ли линейно зависимой система векторов:
Решение:
Система векторов является линейно зависимой, если найдутся такие числа 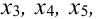
В координатной записи оно равносильно системе уравнений:
Итак, получили систему линейных однородных уравнений. Решаем ее методом исключения неизвестных:
Система приведена к ступенчатому виду, ранг матрицы равен 3, значит, однородная система уравнений имеет решения, отличные от нулевого г < n. Определитель при неизвестных 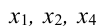
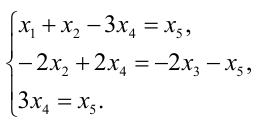
Система имеет бесчисленное множество решений; если свободные неизвестные 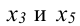
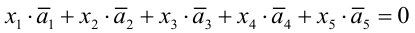
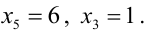
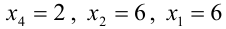
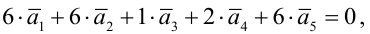
Пример №18
Найти собственные значения и собственные векторы матрицы
Решение:
Вычислим определитель матрицы А
Итак, 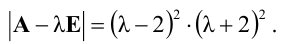
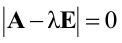
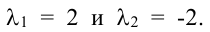
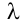
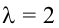
Следовательно, собственному значению 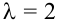
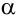
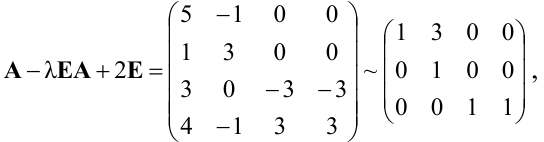
Поэтому собственному значению 
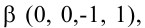
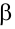
Системы линейных уравнений в высшей математике
Линейной системой m уравнений с n неизвестными 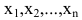
Числа 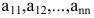
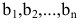
Линейную систему удобно записывать в матричной форме:
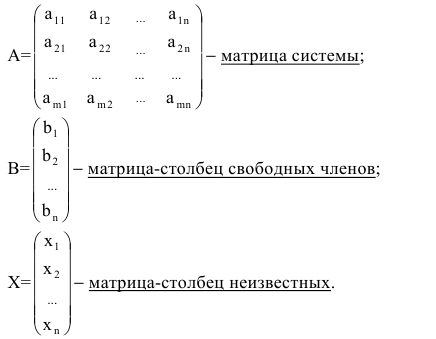
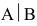
Система линейных уравнений называется однородной, если все свободные члены равны нулю. В противном случае она называется неоднородной.
Решением системы m уравнений с n неизвестными называется совокупность значений неизвестных
при подстановке которых все уравнения системы обращаются в тождества.
Система называется совместной, если она имеет хотя бы одно решение. В
противном случае она называется несовместной.
Замечание. Однородная система линейных уравнений всегда совместна,
т.к. имеет нулевое решение.
Решить систему – значит найти все ее решения.
Решение невырожденных систем линейных уравнений
Система n линейных уравнений с n неизвестными называется невырожденной, если матрица системы невырожденная.
Правило Крамера:
Невырожденная система имеет единственное решение, которое можно найти по формулам
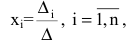
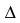
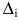
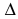
Пример №19
Решить систему уравнений по формулам Крамера.
Решение:
Выпишем матрицу системы: 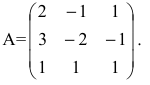
Следовательно, матрица А невырожденная и система имеет единственное решение, которое может быть найдено по формулам Крамера. Найдем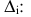
Тогда
Решение произвольных систем линейных уравнений
Теорема Кронекера-Капелли:
Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы системы.
Не ограничивая общности, можно считать, что базисный минор располагается в первых k строках и k столбцах матрицы системы. Отбросив m-k последних уравнений искомой системы, записывают укороченную систему:
Неизвестные 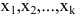
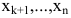
Придавая свободным неизвестным произвольные числовые значения, решают укороченную систему относительно базисных неизвестных. Решение укороченной (а следовательно, и исходной) системы будет являться функцией от n-k свободных неизвестных и называться общим решением системы.
Вывод. Если ранг расширенной системы не равен рангу основной матрицы, то система несовместна. Если ранг системы равен рангу расширенной системы и равен количеству неизвестных, то система имеет единственное решение. Если же ранг системы равен рангу расширенной системы и меньше числа неизвестных, то система имеет бесчисленное множество решений.
В общем случае для решения систем линейных уравнений применяют метод Жордана-Гаусса. Согласно ему расширенную матрицу системы с помощью элементарных преобразований над строками приводят к трапециевидной форме. Такой матрице соответствует система, которую легко решить, начиная с последнего уравнения.
Пример №20
Исследовать систему уравнений и в случае совместимости решить ее:
Решение:
Выпишем расширенную матрицу системы:
Найдем ранг матрицы методом Гаусса. Путем элементарных преобразований над строками приведем данную матрицу к трапециевидной форме:
- первую строку умножили на -1 и прибавили ко второй, первую строку умножили на -1 и прибавили к третьей;
- вторую строку прибавили к третьей.
Отсюда rank A=rank 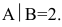
Очевидно, если мы проделаем над уравнениями системы любое из приведенных выше преобразований, то получим систему, равносильную исходной. Из коэффициентов преобразованной матрицы составим систему:
Выберем в качестве базисного минора стоящий в первых двух строках и столбцах:
Тогда неизвестные 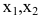
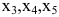
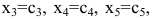
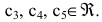
Следовательно,
Тогда 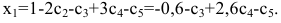
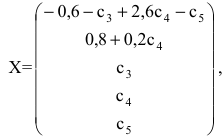
Для существования нетривиального решения однородной системы линейных уравнений необходимо и достаточно, чтобы ранг системы k был меньше числа неизвестных n. Тогда общее решение однородной системы может быть записано в виде
где 
Пример №21
Найти фундаментальную систему решений:
Решение:
На основании предыдущего примера выпишем общее решение системы:
где 
образуют фундаментальную систему решений.
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R”
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
- Многочлен – виды, определение с примерами
- Квадратичные формы – определение и понятие
Сумма 3 чисел равна 16. Сумма первого и третьего 11, асумма третьего и второго 8. Найдите это числа.
Если сумма всех трех чисел равна 16, а сумма первого и третьего равна 11, то из этого легко найти значение второго числа. Достаточно из суммы всех трех вычесть сумму только указанных двух. Получим 16 – 11 = 5.
Значит, второе число – пятерка.
А нам еще известна, вот же удача, сумму второго и третьего, которая равна 8. Из этого значения вычитаем известное нам второе и получаем, что третье равно трем (8 – 5).
Ну, а дальше совсем просто. Даже вычислять сумму второго и третьего не придется – нам она уже и так известна. Вычитаем её из общей суммы и находим, что первое число равно восьми (16 – 8).
Ответ: 8, 5, 3
автор вопроса выбрал этот ответ лучшим
Кареля Топин
[182K]
2 года назад
Такая математическая задача решается путём решения системы из трёх уравнений.
Обозначим первое число как “x”, второе – “y”, третье “z” составим и решим систему из трёх уравнений.
x + y + z = 16 (1)
x + z = 11 (2)
y + z = 8 (3)
Из (3) уравнения найдём y = 8 – z, из (2) уравнения найдём x = 11 – z и подставим эти значения в (1) уравнение. В результате получаем:
11 – z + 8 – z + z = 16;
19 + z = 16, отсюда z = 3. Подставляем значение “z” во (2) уравнение и получаем x = 8. Подставляем значение “z” в (3) уравнение и получаем y = 5.
Ответ: Первое число x = 8, второе число y = 5 и третье число z = 3.
Проверка: 8 + 5 + 3 = 16.
SolomiyMon
[93.1K]
2 года назад
По условиям задачи сумма трех чисел равна – 16.
Обозначим неизвестные числа буквами “а”, “в” и “с” и запишем их в виде суммы:
a + в + с = 16
a + с = 11, находим, чему равна “а”:
а = 11 – с
в + c = 8, соответственно находим “в”:
в = 8 – с
Составляем уравнение, подставляя вместо “а” и “в” полученные выражения с неизвестной “с”.
(11 – с) + (8 – с) + с = 16
Убирая скобки, получаем такое уравнение:
11 – с + 8 – с + с = 16
19 – с = 16
с = 19 – 16
с = 3
Ищем остальные неизвестные:
а = 11 – с
а = 11 – 3
а = 8
в = 8 – с
в = 8 – 3
в = 5
Проверка: а + в + с = 8 + 5 + 3 = 16
Ответ: первое число – 8, второе – 5, третье – 3.
larisatiurina1500
[14.9K]
2 года назад
По условию задачи сумма трех чисел равна 16. Обозначим их, как А; В; С
А+В+С=16.
А+С=11 от сюда выходит В=16-11=5
В+С=8 от сюда выходит, что
А=16-8=8 С=8-5=3
Проверяем 8+5+3=16
Евгений трохов
[56.5K]
2 года назад
Сумма трех чисел равна 16.
А вот если к этой сумме прибавить еще раз третье число, то будет :
11+8=19,отсюда:
Третье число равно 19-16=3
Тогда первое число равно:
11-3=8.
А второе число равно:
8-3=5.
Проверка :
8+5+3=16
Ответ:это числа 8,5, 3.
Мудрый Датч
[75.5K]
2 года назад
Известно, что по условию задачи сумма первого и третьего равна 11, а сумма третьего и второго равна 8. Складываем значение этих сумм: 11+8=19. Получается, что данная сумма превосходит сумму всех трех на величину третьего, поэтому равно третье число 3, так как 16 равна сумма трёх чисел. Теперь легко найти второе число, оно равно 5: 8-3=5, а первое число равно 8: 11-3=8. Верный ответ: 8,5,3.
КорнетОболенский
[162K]
2 года назад
Задача взята видимо из какой-то олимпиады для средней школы. На первый взгляд, решается несходу.
Приходится прибегать к системе уравнений:
- a+m+n = 16
- a+n = 11
- m+n=8
Из 1) и 3) следует, что а = 16 – (m+n) = 16 – 8 = 8
Теперь, зная, что а = 8 из 2) получаем, что n=11-8=3
И, окончательно, из 1) m= 16 – 8 – 3 =5
Получаем ответ: это числа 8,5,3.
Имеем исходные соотношения:
(1) a1 + a2 + a3 = 16,
(2) a1 + a3 = 11,
(3) a2 + a3 = 8,
Высчитываем новое соотношение (1) – (2):
(3) a1 = 8,
Высчитываем новое соотношение (2) – (3):
(4) a3 = 3,
Высчитываем новое соотношение (3) – (4):
(5) a2 = 5.
Знаете ответ?
Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений
с двумя неизвестными.
Запомните!
Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют
«x» и «y»),
которые объединены в общую систему фигурной скобкой.
Например, система уравнений может быть задана следующим образом.
Чтобы решить систему уравнений, нужно найти и «x», и «y».
Как решить систему уравнений
Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.
Способ подстановки
или
«железобетонный» метод
Первый способ решения системы уравнений называют способом подстановки или «железобетонным».
Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно
решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений,
всегда пробуйте решить её методом подстановки.
Разберем способ подстановки на примере.
Выразим из первого уравнения «x + 5y = 7»
неизвестное «x».
Важно!
Чтобы выразить неизвестное, нужно выполнить два условия:
- перенести неизвестное, которое хотим выразить, в левую часть уравнения;
- разделить и левую и правую часть уравнения на нужное число так,
чтобы коэффициент при неизвестном стал равным единице.
Перенесём в первом уравнении «x + 5 y = 7» всё что
содержит «x» в левую часть,
а остальное в правую часть по
правилу переносу.
При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение
на число не требуется.
Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.
| x = 7 − 5y | |
| 3(7 − 5y) − 2y = 4 |
Подставив вместо «x» выражение «(7 − 5y)»
во второе уравнение,
мы получили обычное линейное уравнение с одним неизвестным «y».
Решим его по правилам
решения линейных уравнений.
Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение
«3(7 − 5y) − 2y = 4» отдельно.
Вынесем его решение отдельно с помощью
обозначения звездочка (*).
| x = 7 − 5y | |
| 3(7 − 5y) − 2y = 4 (*) |
(*) 3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
− 17y = − 17 | :(−17)
y = 1
Мы нашли, что «y = 1».
Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.
Ответ: x = 2; y = 1
Способ сложения
Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения.
Вернемся к нашей системе уравнений еще раз.
По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.
Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.
Запомните!
При сложения уравнений системы
левая часть первого уравнения полностью складывается
с левой частью второго уравнения,
а правая часть полностью складывается с
правой частью.
| x + 5y = 7 | (x + 5y) + (3x − 2y) = 7 + 4 | ||
| + => |
x + 5y + 3x − 2y = 11 |
||
| 3x − 2y = 4 | 4x + 3y = 11 |
При сложении уравнений мы получили уравнение «4x + 3y = 11».
По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.
Вернемся снова к исходной системе уравнений.
Чтобы при сложении неизвестное «x» взаимноуничтожилось,
нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент
«−3».
Для этого умножим первое уравнение на «−3».
Важно!
При умножении уравнения на число, на это число умножается каждый член уравнения.
| x + 5y = 7 | ·(−3) | |
| 3x − 2y = 4 |
| x ·(−3) + 5y · (−3) = 7 · (−3) |
|
| 3x − 2y = 4 |
| −3x −15y = −21 | |
| 3x − 2y = 4 |
Теперь сложим уравнения.
| −3x −15y = −21 | (−3x −15y ) + (3x − 2y) = −21 + 4 | ||
| + => |
−3x −15y + 3x − 2y = −21 + 4 |
||
| 3x − 2y = 4 | −17y = −17 |:(−17) | ||
| y = 1 |
Мы нашли «y = 1».
Вернемся к первому уравнению и подставим вместо «y» полученное числовое
значение и найдем «x».
Ответ: x = 2; y = 1
Пример решения системы уравнения
способом подстановки
Выразим из первого уравнения «x».
Подставим вместо «x» во второе уравнение полученное выражение.
| x = 17 + 3y | |
| (17 + 3y) − 2y = −13 (*) |
(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
17 + y = −13
y = −13 − 17
y = −30
Подставим в первое уравнение полученное числовое значение «y = −30» и
найдем «x».
| x = 17 + 3 · (−30) | |
| y = −30 |
Ответ: x = −73; y = −30
Пример решения системы уравнения
способом сложения
Рассмотрим систему уравнений.
| 3(x − y) + 5x = 2(3x − 2) | |
| 4x − 2(x + y) = 4 − 3y |
Раскроем скобки и упростим выражения в обоих уравнениях.
| 3x − 3y + 5x = 6x − 4 | |
| 4x − 2x − 2y = 4 − 3y |
| 8x − 3y = 6x − 4 | |
| 2x −2y = 4 − 3y |
| 8x − 3y − 6x = −4 | |
| 2x −2y + 3y = 4 |
Мы видим, что в обоих уравнениях есть «2x».
Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в
полученном уравнении осталось только «y».
Для этого достаточно умножить первое уравнение на «−1».
| 2x − 3y = −4 |·(−1) | |
| 2x + y = 4 |
|
2x · (−1) − 3y · (−1) = −4 · (−1) |
|
| 2x + y = 4 |
Теперь при сложении уравнений у нас останется только «y» в уравнении.
| −2x + 3y = 4 | (−2x + 3y ) + (2x + y) = 4 + 4 | ||
| + => |
−2x + 3y + 2x + y = 4 + 4 |
||
| 2x + y = 4 | 4y = 8 | :4 | ||
| y = 2 |
Подставим в первое уравнение полученное числовое значение «y = 2» и
найдем «x».
Ответ: x = 1; y = 2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
8 мая 2020 в 16:20
Алина Козлова
Профиль
Благодарили: 0
Сообщений: 1
Алина Козлова
Профиль
Благодарили: 0
Сообщений: 1
у-2х=-3
х+у=3
0
Спасибо
Ответить
9 мая 2020 в 21:50
Ответ для Алина Козлова
Evgeny Bayron
Профиль
Благодарили: 0
Сообщений: 1
Evgeny Bayron
Профиль
Благодарили: 0
Сообщений: 1
y=3-x
3-x-2x=-3
x=2
y-2*2=-3
y=1
0
Спасибо
Ответить
15 мая 2019 в 13:21
Марина Чернявская
Профиль
Благодарили: 0
Сообщений: 1
Марина Чернявская
Профиль
Благодарили: 0
Сообщений: 1
Решительно систему уравнений.
4x+3y =22.
-x+7y =10.
a)графическим способом.
б)способом подстановки
в)способом сложения
0
Спасибо
Ответить
15 мая 2019 в 22:31
Ответ для Марина Чернявская
Лёха Чешуйка
Профиль
Благодарили: 0
Сообщений: 2
Лёха Чешуйка
Профиль
Благодарили: 0
Сообщений: 2
в): Домножаем первое на 1, второе на 4:
4x+3y=22
-4x+28y=40
Складываем:
4x+(-4x)+3y+28y=22+40
31y=62
y=62/31
y=2
Подставляем y в первое:
4x+3 · 2=22
4x=22-6
4x=16
x=4
0
Спасибо
Ответить
15 мая 2019 в 22:41
Ответ для Марина Чернявская
Лёха Чешуйка
Профиль
Благодарили: 0
Сообщений: 2
Лёха Чешуйка
Профиль
Благодарили: 0
Сообщений: 2
б): Выражаем из второго x:
-x=10-7y
x=7y-10
Подставляем x в первое:
4(7y-10)+3y=22
28y-40+3y=22
31y=22+40
31y=62
y=2
Подставляем y в первое:
4x+3 · 2=22
4x=22-6
4x=16
x=4
0
Спасибо
Ответить
20 октября 2015 в 13:24
Елена Тутуликова
Профиль
Благодарили: 0
Сообщений: 1
Елена Тутуликова
Профиль
Благодарили: 0
Сообщений: 1
Помогите, пожалуйста, решить систему уравнений.{y + sinx = 5; {4y + 2 sinx = 19
Спасибо!
0
Спасибо
Ответить
23 октября 2015 в 21:25
Ответ для Елена Тутуликова
Елизавета Яременко
Профиль
Благодарили: 0
Сообщений: 5
Елизавета Яременко
Профиль
Благодарили: 0
Сообщений: 5
Я думаю{y + sinx =5; {4y + 2 sinx =19
0
Спасибо
Ответить
9 июня 2016 в 14:19
Ответ для Елена Тутуликова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
sinx = 1/2
y = 9/2
0
Спасибо
Ответить



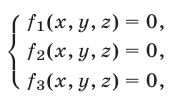
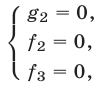
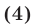
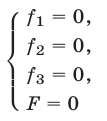
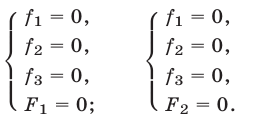
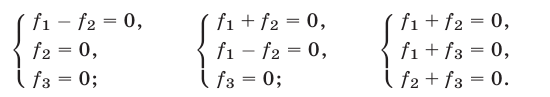
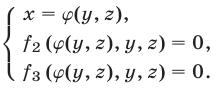
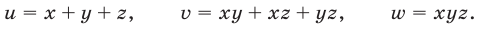
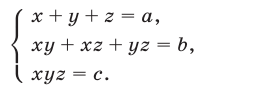

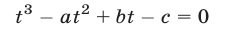
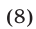
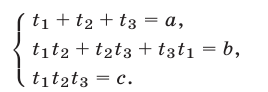
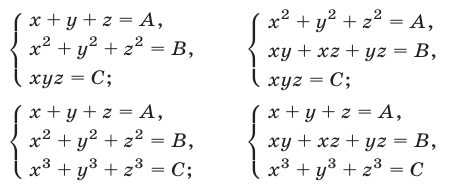
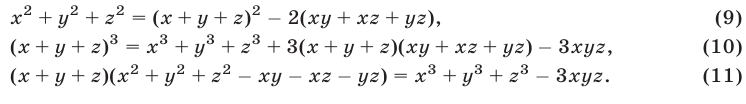
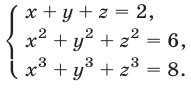
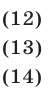
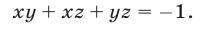
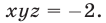
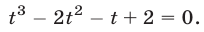
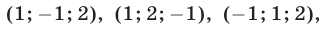
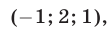
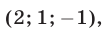
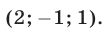
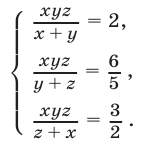
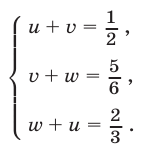
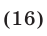
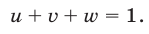
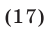
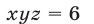
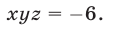
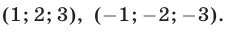
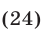
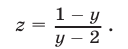
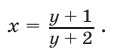
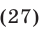
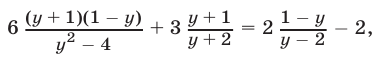
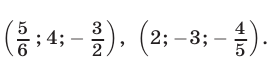

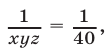
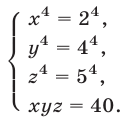
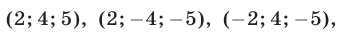
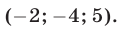
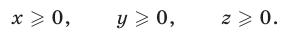
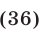
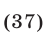
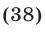
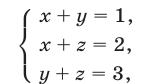
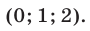
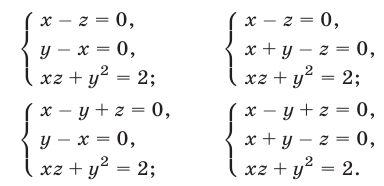
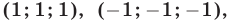
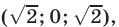
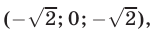
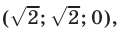
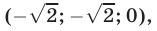
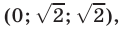
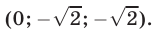
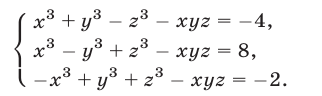
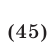
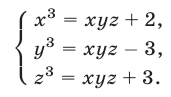

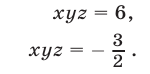

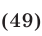
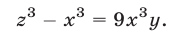
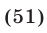
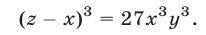
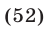
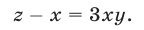
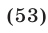
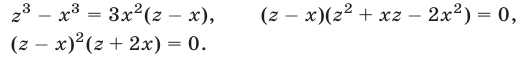

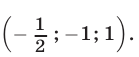
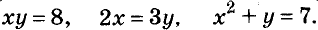
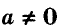
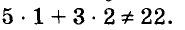
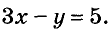
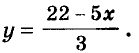
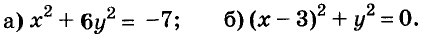
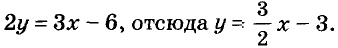
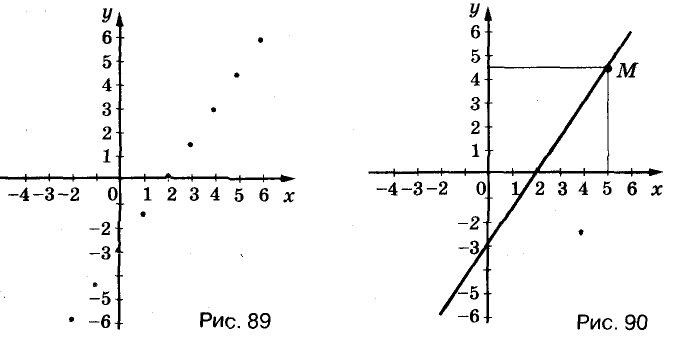
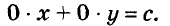
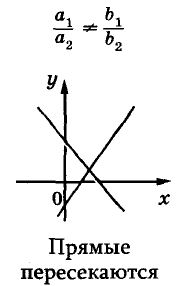
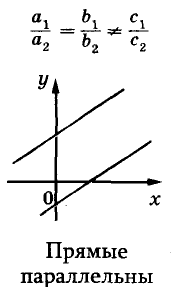
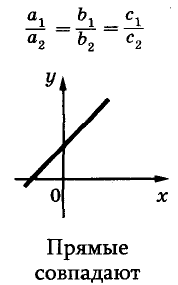
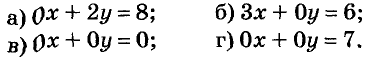
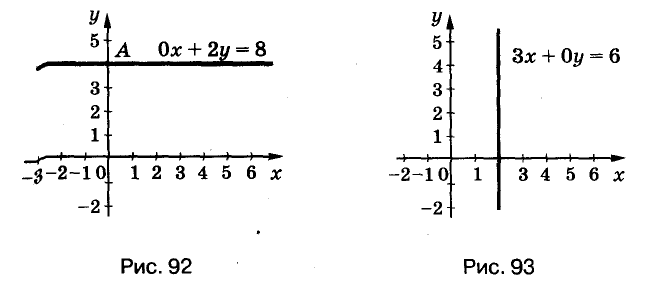
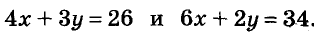
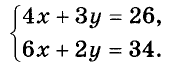
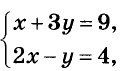
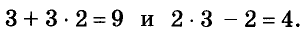
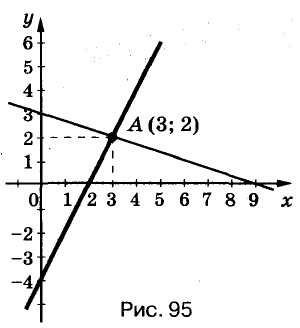
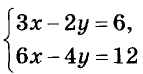
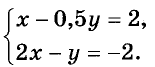
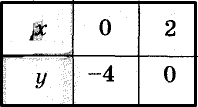

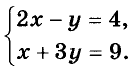
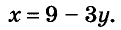
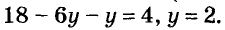
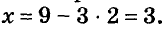
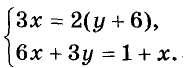
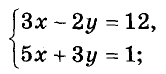
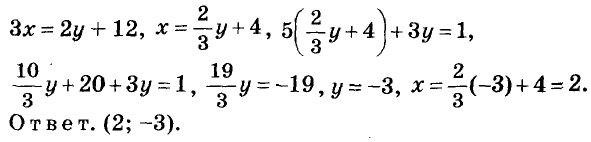
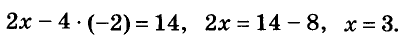
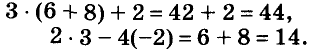
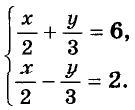
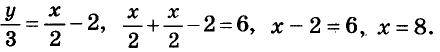
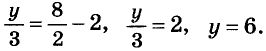
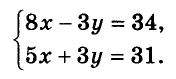
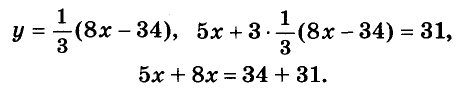
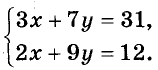
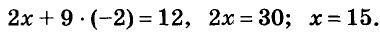
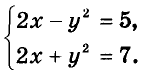
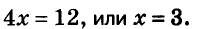
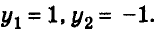
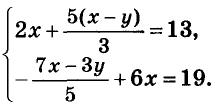
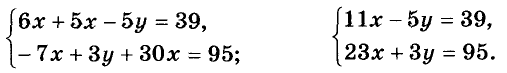

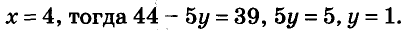
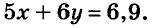
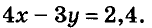
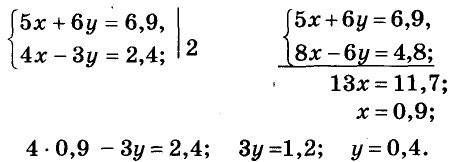
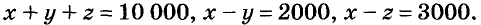
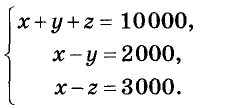
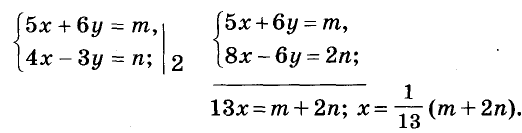
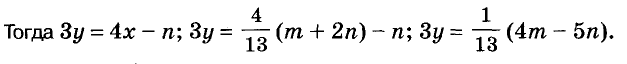
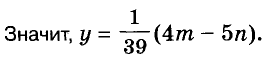
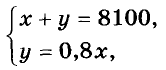
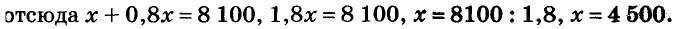
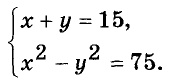
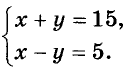
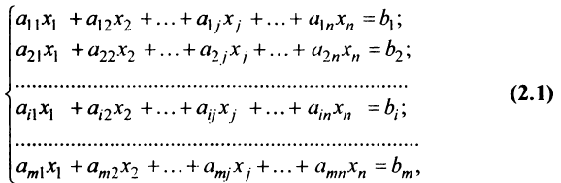
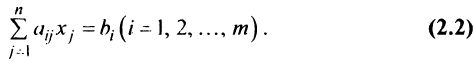
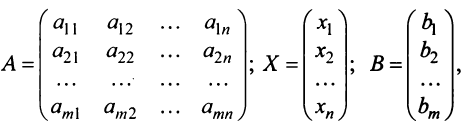
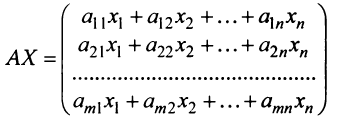
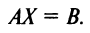

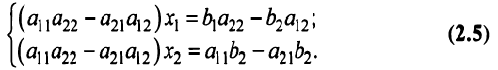
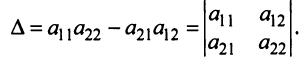

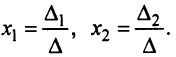
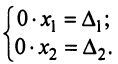

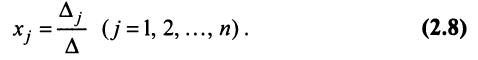

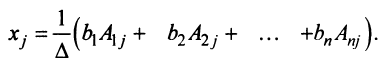
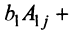
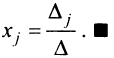
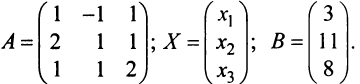
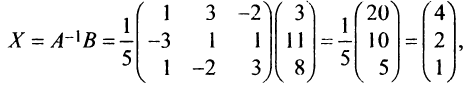
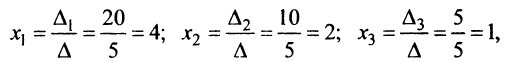
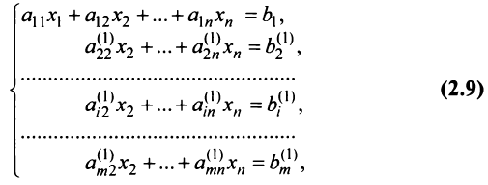
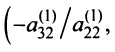
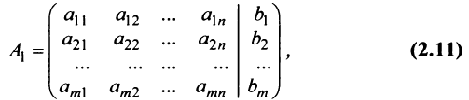
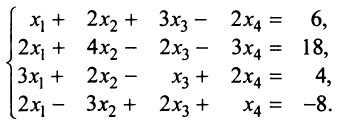
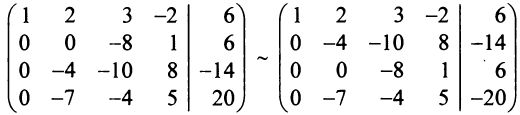
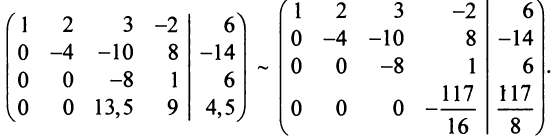
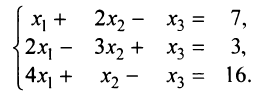
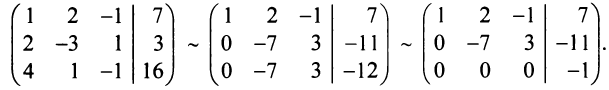
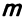 линейных уравнений с
линейных уравнений с 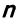 переменными
переменными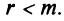
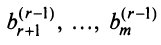

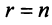 , то система (2.1) имеет единственное решение.
, то система (2.1) имеет единственное решение.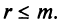
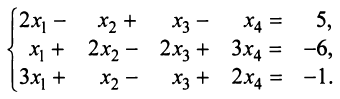
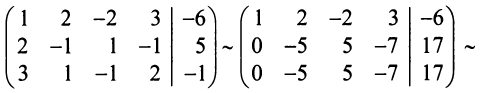
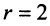
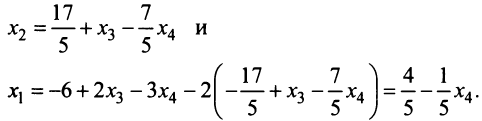
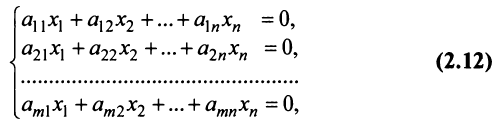
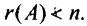
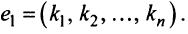
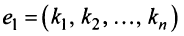 — решение системы (2.12), то и строка
— решение системы (2.12), то и строка 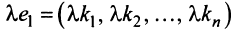 — также решение этой системы.
— также решение этой системы.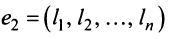 — решения системы (2.12), то при любых
— решения системы (2.12), то при любых 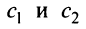 их линейная комбинация
их линейная комбинация 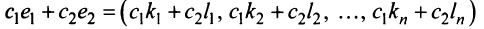 — также решение данной системы.
— также решение данной системы.