Метод контурных токов.Решение задач
Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m – количество ветвей, а n – количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.
Основные понятия
Контурный ток – это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I11, I22 и тд.
Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.
Контурная ЭДС – это сумма всех ЭДС входящих в этот контур.
Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.
Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.
Общий план составления уравнений
1 – Выбор направления действительных токов.
2 – Выбор независимых контуров и направления контурных токов в них.
3 – Определение собственных и общих сопротивлений контуров
4 – Составление уравнений и нахождение контурных токов
5 – Нахождение действительных токов
Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

Выполняем все поэтапно.
1. Произвольно выбираем направления действительных токов I1-I6.
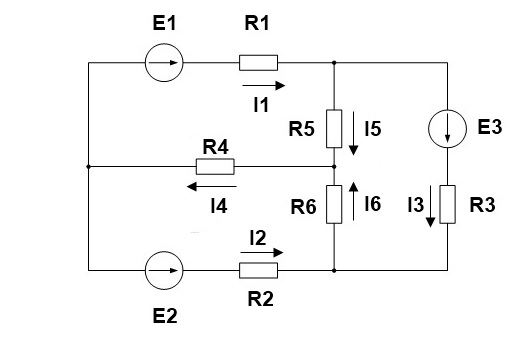
2. Выделяем три контура, а затем указываем направление контурных токов I11,I22,I33. Мы выберем направление по часовой стрелке.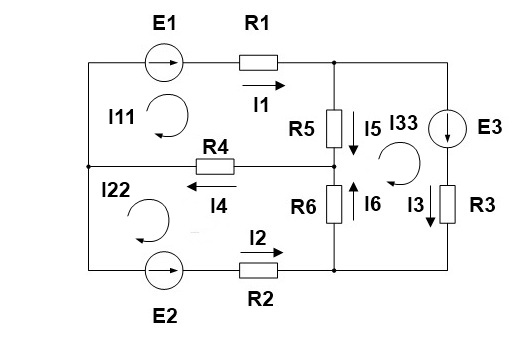
3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.
R11=R1+R4+R5=10+25+30= 65 Ом
R22=R2+R4+R6=15+25+35 = 75 Ом
R33=R3+R5+R6=20+30+35= 85 Ом
Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R4 принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.
R12=R21=R4=25 Ом
R23=R32=R6=35 Ом
R31=R13=R5=30 Ом
4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.
Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:
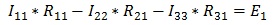
Ток первого контура I11, умножаем на собственное сопротивление R11 этого же контура, а затем вычитаем ток I22, помноженный на общее сопротивление первого и второго контуров R21 и ток I33, помноженный на общее сопротивление первого и третьего контура R31. Данное выражение будет равняться ЭДС E1 этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.
Те же действия проделываем с двумя другими контурами и в итоге получаем систему:

В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.
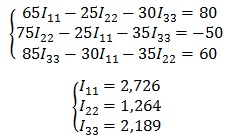
5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.
Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.

Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.
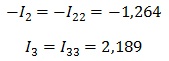
Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.
Например, через резистор R4 протекает ток I4, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть
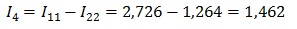
А для остальных
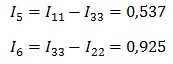
Так решаются задачи методом контурных токов. Надеемся что вам пригодится данный материал, удачи!
Рекомендуем – Метод двух узлов
Содержание:
Метод контурных токов:
Контурным током называют условный ток, протекающий внутри независимого контура.
Напомним, что контуры называются независимыми (подробнее см. разд. 2.1), если они отличаются друг от друга хотя бы одним элементом (ветвью). Направление отсчёта контурного тока выбирается произвольно и независимо от выбора направлений отсчётов контурных токов в других контурах. В отличие от метода токов ветвей, рассмотренного в лекции 4, данный метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной числу 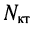
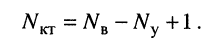
Предварительно покажем, что при известных контурных токах можно найти токи всех ветвей, а потому и напряжения на всех элементах цепи. Действительно, ток в любом элементе (ветви) определяется по первому закону Кирхгофа (ЗТК) как алгебраическая сумма контурных токов, протекающих в этом элементе. Например, при выбранных в удлинителе (рис. 5.3) направлениях отсчётов токов элементов и контурных токов имеем:
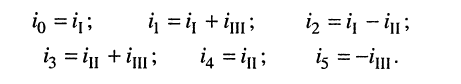
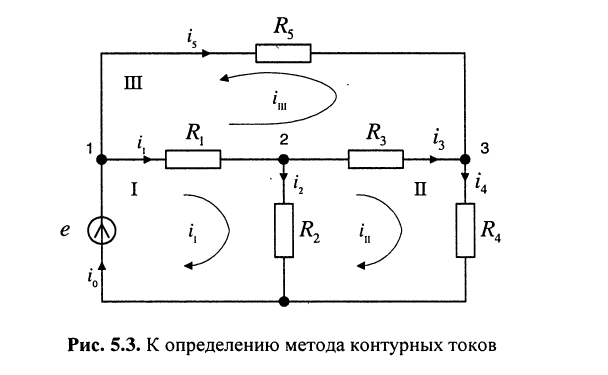
Зная токи, протекающие в элементах, можно по закону Ома определить напряжения на каждом из них.
Определение:
Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются контурные токи, называется методом контурных токов.
Составление контурных уравнений
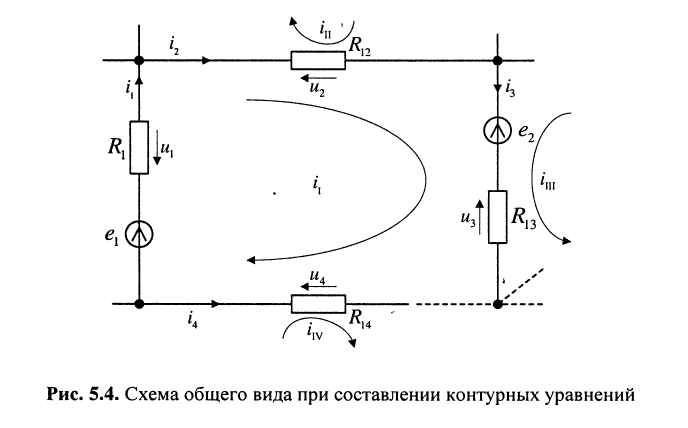
При составлении системы контурных уравнений воспользуемся вторым законом Кирхгофа и будем полагать, что (рис. 5.4):
При этих условиях, выбранных независимых контурах и заданных направлениях отсчётов контурных токов запишем уравнение для первого контура (см. рис. 5.4) согласно второму закону Кирхгофа:
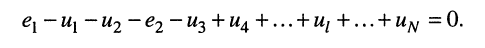 (5.5)
(5.5)
Выразим напряжения на элементах 1-го контура через токи ветвей по закону Ома:
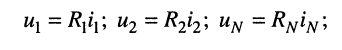
или в общем виде:
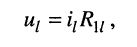 (5.6)
(5.6)
Подставим (5.6) в (5.5)
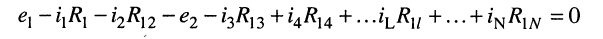 (5.7)
(5.7)
и выразим токи ветвей через контурные токи, нумерация которых осуществляется римскими цифрами и прямыми латинскими буквами. Из рис. 5.4 видно, что:
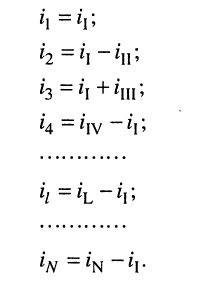
Произведём замену токов ветвей в выражении (5.7) через соотношения (5.8):
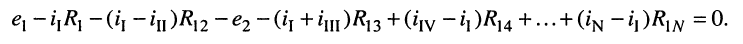
Умножим полученное уравнение на-1, раскроем скобки, приведём подобные члены и перенесём в правую часть известные значения напряжений источников; после выполнения этих действий контурное уравнение принимает вид
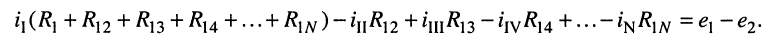
Подобное уравнение можно было бы составить и для любого другого контура, поэтому полученный результат позволяет сделать обобщающие выводы:
Аналогично записываются узловые уравнения для всех других контуров цепи, в результате чего образуется система контурных уравнений вида:
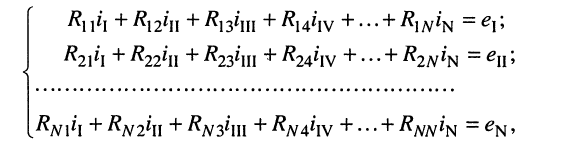 (5.9)
(5.9)
где:
Система контурных уравнений (5.9) составлена относительно неизвестных контурных токов и записана в канонической форме, а именно:
- контурные ЭДС, как свободные члены, записываются в правых частях уравнений;
- неизвестные контурные токи записываются в левых частях уравнений с последовательно возрастающими индексами;
- уравнения располагаются в соответствии с порядковыми номерами контуров.
Пример 5.2.
Записать систему контурных уравнений для удлинителя (рис. 5.3).
Решение. Предварительно найдём собственные и взаимные сопротивления трёх контуров:
I контура:
• собственное сопротивление 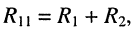
• взаимные сопротивления: со вторым контуром 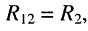 с третьим контуром
с третьим контуром 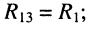
II контура:
• собственное сопротивление 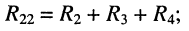
• взаимные сопротивления: с первым контуром 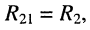 с третьим контуром
с третьим контуром 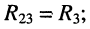
III контура:
• собственное сопротивление 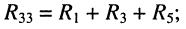
• взаимные сопротивления: с первым контуром 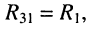 с третьим контуром
с третьим контуром 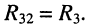
Заметим, что:
Теперь можно записать систему контурных уравнений, руководствуясь указанными ранее правилами:
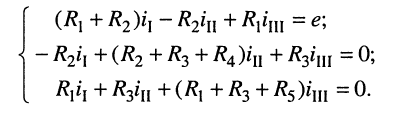
Особенности составления контурных уравнений
Рассмотренные ранее цепи не содержали независимых источников тока, поэтому количество контурных уравнений согласно (5.4) равно количеству независимых контуров. Однако цепь может иметь несколько источников токов. В этом случае следует выбрать такое дерево цепи, при котором источники токов входили бы в число соединительных элементов. Тогда через каждый источник тока будет проходить ток только одного контура, который равен задающему току источника. Поэтому уменьшается как число неизвестных контурных токов, так и число контурных уравнений. Следовательно, если цепь содержит 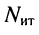 источников тока, то известно
источников тока, то известно 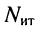 контурных токов, а число контурных уравнений оказывается равным
контурных токов, а число контурных уравнений оказывается равным
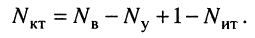 (5.10)
(5.10)
Пример 5.3.
Записать систему контурных уравнений для цепи, схема которой изображена на рис. 5.5.
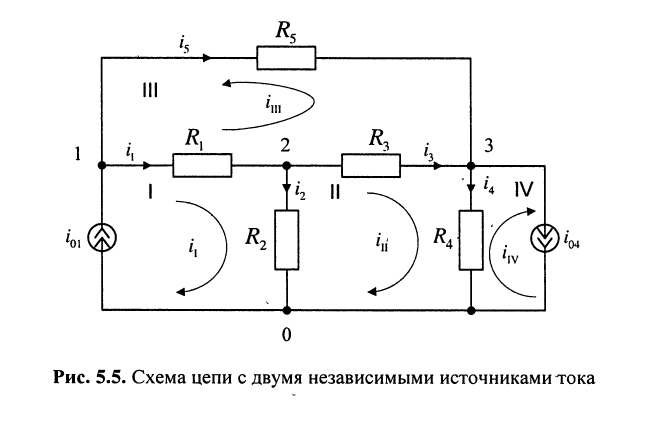
Решение. Цепь содержит два источника тока: в первом и четвёртом контурах, где контурные токи совпадают с токами источников:
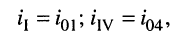
поэтому достаточно записать только два контурных уравнения — для второго и третьего контуров.
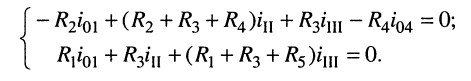
В уравнении для третьего контура отсутствует слагаемое, содержащее ток 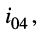 поскольку взаимное сопротивление этого контура с четвёртым равно нулю, т. е. между этими контурами нет никакой связи.
поскольку взаимное сопротивление этого контура с четвёртым равно нулю, т. е. между этими контурами нет никакой связи.
Важно:
метод контурных токов применяют в тех случаях, когда число контурных уравнений меньше числа узловых уравнений, а также при анализе колебаний в линейных электрических цепях произвольной конфигурации, содержащих все виды элементов.
Решение системы контурных (узловых) уравнений
Решение системы контурных (узловых) уравнений состоит в нахождении неизвестных контурных токов (узловых напряжений) для последующего вычислением токов и напряжений на элементах цепи. Если параметры цепи (сопротивления, проводимости, токи источников токов, ЭДС источников напряжений) заданы численно, то решение систем осуществляется с помощью специальных пакетов программ математического моделирования, например, Matlab или Matcad.
Основные понятия теории определителей
При теоретическом анализе удобнее использовать методы теории определителей, позволяющие записать решения в компактной форме. Прежде чем обращаться к этим методам, дадим основные понятия теории определителей.
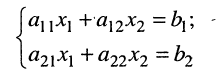 (5.11)
(5.11)
с неизвестными 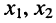 и свободными членами
и свободными членами 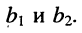 Решая эту систему, получаем:
Решая эту систему, получаем:
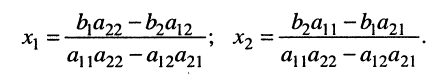 (5.12)
(5.12)
Стоящее в знаменателях полученных дробей выражение 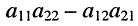 называется определителем (детерминантом) второго порядка и записывается в виде
называется определителем (детерминантом) второго порядка и записывается в виде
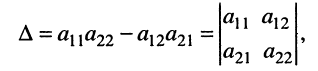 (5.13)
(5.13)
где вертикальные чёрточки являются знаком определителя. С помощью этого обозначения формулы (5.13) можно записать в виде
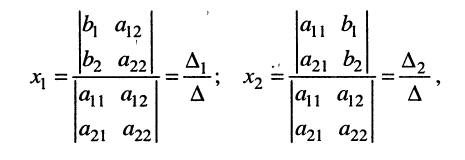 (5.14)
(5.14)
где 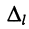 — определитель, полученный из определителя системы заменой столбца коэффициентов при
— определитель, полученный из определителя системы заменой столбца коэффициентов при 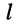 -ой неизвестной столбцом свободных членов.
-ой неизвестной столбцом свободных членов.
Из соотношений (5.14) следует: каждая из неизвестных 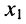 и
и 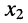 равна дроби, у которой в знаменателе стоит определитель системы
равна дроби, у которой в знаменателе стоит определитель системы 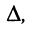 а в числителе — определитель
а в числителе — определитель 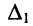 и
и 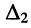 соответственно, полученный из определителя системы подстановкой столбца свободных членов вместо столбца коэффициентов при данной неизвестной.
соответственно, полученный из определителя системы подстановкой столбца свободных членов вместо столбца коэффициентов при данной неизвестной.
Подобным образом решается система уравнений любого порядка. Остаётся выяснить, как вычислять определители, если их порядок больше двух.
Рассмотрим вычисление определителя на примере системы третьего порядка:
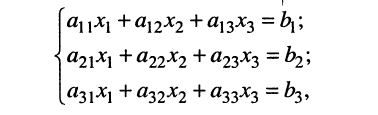
решение которой приводит к дробям вида (5.12), где в знаменателе оказывается выражение
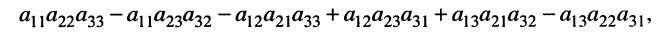 (5.15)
(5.15)
называемое определителем третьего порядка и обозначаемое
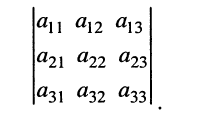 (5.16)
(5.16)
Применяя к (5.16) выражение (5.15), запишем определитель (5.16) в более удобной и наглядной форме:
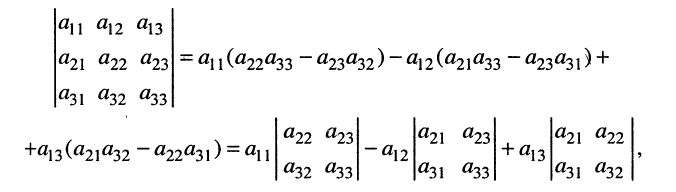 (5.17)
(5.17)
по которой можно вычислять значение определителя третьего порядка. Нетрудно видеть, что правая часть равенства состоит из суммы произведений коэффициентов (элементов) первой строки и определителей второго порядка с нужными знаками. Эти определители называются минорами и получаются из исходного определителя вычёркиванием первой строки и соответствующего данному элементу столбца. Например, минор относительно элемента 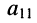 получается вычёркиванием первой строки и первого столбца (рис. 5.6, а), минор относительно элемента
получается вычёркиванием первой строки и первого столбца (рис. 5.6, а), минор относительно элемента 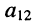 получается вычёркиванием первой строки и первого столбца (рис. 5.6, б). Таким образом, получено разложение определителя третьего порядка по элементам первой строки.
получается вычёркиванием первой строки и первого столбца (рис. 5.6, б). Таким образом, получено разложение определителя третьего порядка по элементам первой строки.
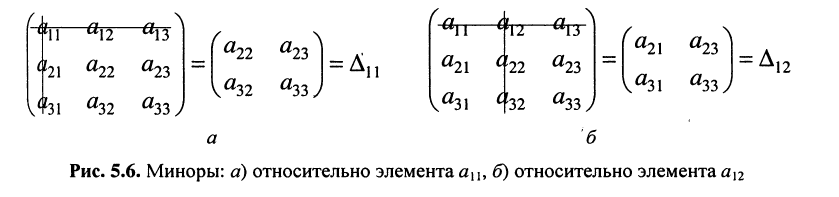
Подобные разложения можно произвести относительно элементов любой строки, предварительно записав соответствующие миноры.
Определение:
Минором 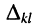 относительно
относительно 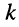 -ой строки и
-ой строки и 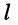 -ro столбца (относительно элемента аи) называется определитель, получаемый из исходного определителя, если в последнем вычеркнуть
-ro столбца (относительно элемента аи) называется определитель, получаемый из исходного определителя, если в последнем вычеркнуть 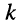 -ю строку и
-ю строку и 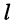 -ый столбец.
-ый столбец.
Знак минора определяется по формуле 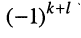 или же по мнемоническому правилу: для левого верхнего элемента всегда берётся “+”, а для других элементов — в шахматном порядке по схеме, представленной на рис. 5.7.
или же по мнемоническому правилу: для левого верхнего элемента всегда берётся “+”, а для других элементов — в шахматном порядке по схеме, представленной на рис. 5.7.
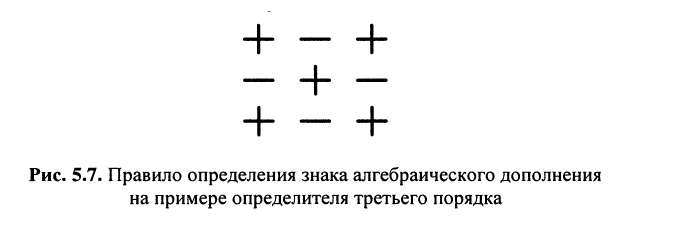
Определение:
Алгебраическим дополнением 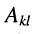 относительно к-ой строки и 1-го столбца (относительно элемента
относительно к-ой строки и 1-го столбца (относительно элемента 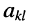 ) называется минор, взятый с нужным знаком по правилу
) называется минор, взятый с нужным знаком по правилу 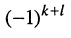 , т. е.
, т. е.
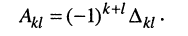 (5.18)
(5.18)
Из сказанного следует: определитель равен сумме произведений элементов какого-нибудь из рядов (строки или столбца) на алгебраические дополнения этих элементов.
При вычислении определителей больших порядков их предварительно разлагают на алгебраические дополнения. Отметим также, что подобно (5.14) для любой системы, у которой 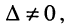 имеет место формула для вычисления
имеет место формула для вычисления 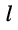 -ой неизвестной (формула, или правило Крамера
-ой неизвестной (формула, или правило Крамера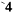 )
)
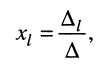 (5.19)
(5.19)
т. е. каждая 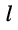 -ая неизвестная равна дроби, у которой в знаменателе стоит определитель системы, а в числителе — определитель, полученный из определителя системы подстановкой столбца свободных членов вместо столбца коэффициентов при
-ая неизвестная равна дроби, у которой в знаменателе стоит определитель системы, а в числителе — определитель, полученный из определителя системы подстановкой столбца свободных членов вместо столбца коэффициентов при 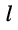 -ой неизвестной.
-ой неизвестной.
 Габриэль Крамер (1704—1752) — швейцарский математик, заложивший в 1750 г. основы теории определителей.
Габриэль Крамер (1704—1752) — швейцарский математик, заложивший в 1750 г. основы теории определителей.
Применение теории определителей для решения контурных (узловых) уравнений
Применяя методы теории определителей к системе контурных уравнений (5.9), по формуле Крамера находим решение для первого контурного тока
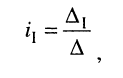
где
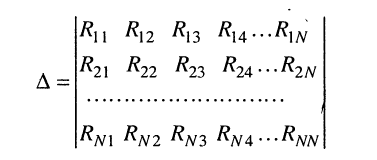 (5.20)
(5.20)
представляет собой определитель системы контурных уравнений (5.9), а
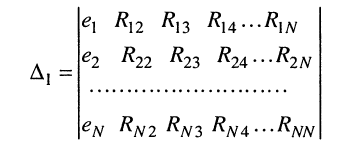
находится из определителя (5.20) при замене в нём первого столбца свободными членами. Заметим, что определитель (5.20) является симметричным относительно главной диагонали, поскольку 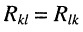 при
при 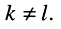
Разлагая определитель 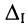 на алгебраические дополнения по элементам первого столбца, получаем выражение для первого контурного тока
на алгебраические дополнения по элементам первого столбца, получаем выражение для первого контурного тока
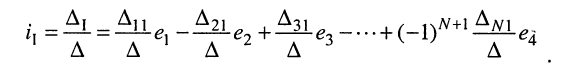 (5.21)
(5.21)
Аналогичное решение можно найти и для L-го контурного тока, разлагая определитель 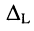 на алгебраические дополнения по элементам 1-го столбца:
на алгебраические дополнения по элементам 1-го столбца:
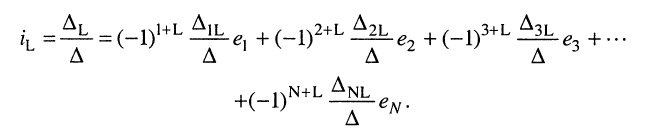 (5.22)
(5.22)
Полученное общее решение (5.22) системы контурных уравнений (5.9) показывает, что реакция в виде токов в электрической цепи представляет собой сумму реакций, вызываемых каждым из воздействий 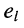 в отдельности в предположении, что все другие источники отсутствуют. Этот факт является следствием линейности электрической цепи, описываемой системой линейных уравнений, и составляет содержание принципа наложения.
в отдельности в предположении, что все другие источники отсутствуют. Этот факт является следствием линейности электрической цепи, описываемой системой линейных уравнений, и составляет содержание принципа наложения.
Аналогичным образом рассчитывается система узловых уравнений (5.2).
Примеры использования теории определителей
Задача 5.1.
Цепь имеет единственный источник напряжения 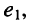 по отношению к которому сама цепь представляет собой пассивный резистивный двухполюсник (рис. 5.8). Требуется найти входное сопротивление двухполюсника.
по отношению к которому сама цепь представляет собой пассивный резистивный двухполюсник (рис. 5.8). Требуется найти входное сопротивление двухполюсника.
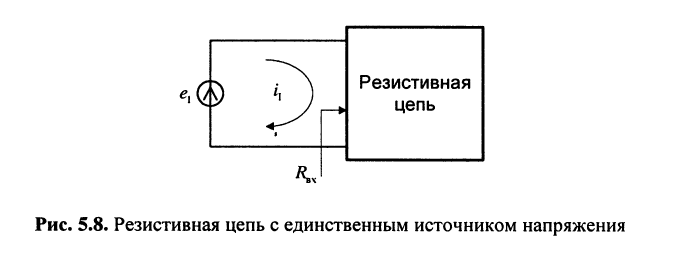
Решение. Для удобства назовём контур, замыкающийся через источник, первым. Тогда из (5.21) следует
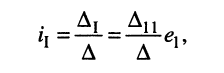 (5.23)
(5.23)
и согласно закону Ома имеем
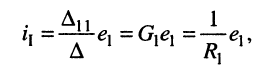
откуда получаем соотношение
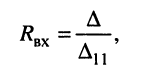 (5.24)
(5.24)
называемое входным сопротивлением двухполюсника. Оно представляет собой эквивалентное сопротивление пассивного резистивного двухполюсника.
Заметим, что в резистивном двухполюснике электрическая энергия может только рассеиваться, поэтому при выбранных на рис. 5.8 направлениях отсчёта тока и напряжения коэффициент 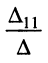 в (5.23) представляет собой вещественное положительное число, что справедливо и для (5.24). Следовательно, любой резистивный двухполюсник ведёт себя подобно резистивному элементу, сопротивление которого равно входному сопротивлению двухполюсника.
в (5.23) представляет собой вещественное положительное число, что справедливо и для (5.24). Следовательно, любой резистивный двухполюсник ведёт себя подобно резистивному элементу, сопротивление которого равно входному сопротивлению двухполюсника.
Задача 5.2.
Найти ток в заданной ветви резистивной цепи (рис. 5.9), имеющей единственный источник напряжения в 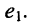
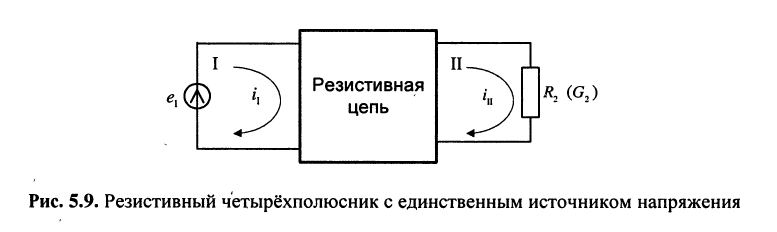
Решение. Такую цепь можно рассматривать как резистивный четырёхполюсник, в котором вновь для удобства обозначим контур, содержащий источник напряжения, первым (I), а контур, содержащий интересующую нас ветвь, вторым (II).
При выбранных направлениях отсчёта ЭДС источника 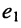 и тока второго контура
и тока второго контура 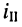 согласно (5.22) при
согласно (5.22) при 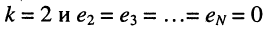 получаем:
получаем:
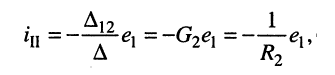 (5.25)
(5.25)
где
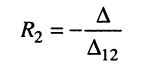
представляет собой собственное сопротивление второго контура и потому эквивалентное сопротивление четырёхполюсника.
Метод контурных токов
При расчете сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа) необходимо решать систему из большого количества уравнений, что значительно затрудняет вычисления.
Так, для схемы рис. 4.13 необходимо составить и рассчитать систему из 7-ми уравнений
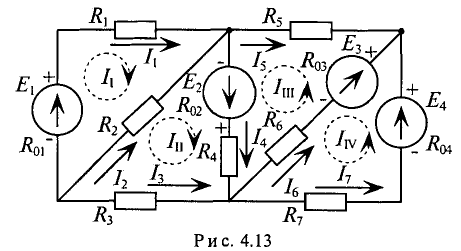
Ту же задачу можно решить, записав только 4 уравнения по второму закону Кирхгофа, если воспользоваться методом контурных токов.
Суть метода состоит в том, что в схеме выделяют т независимых контуров, в каждом из которых произвольно направлены (см. пунктирные стрелки) контурные токи 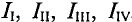 . Контурный ток — это расчетная величина, измерить которую невозможно.
. Контурный ток — это расчетная величина, измерить которую невозможно.
Как видно из рис. 4.13, отдельные ветви схемы входят в два смежных контура. Действительный ток в такой ветви определяется алгебраической суммой контурных токов смежных контуров.
Таким образом
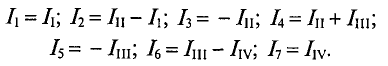
Для определения контурных токов составляют т уравнений по второму закону Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в данный контур (по одну сторону от знака равенства), и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров (по другую сторону знака равенства).
Для данной схемы (рис. 4.13) необходимо составить 4 уравнений. Со знаком «плюс» записываются ЭДС и падения напряжено разные стороны знака равенства), действующие в направлении контурного тока, со знаком «минус» — направленные проконтурного тока.
Система уравнений для схемы (рис. 4.13):
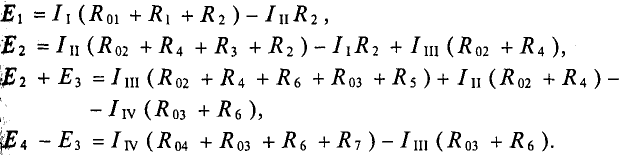
Решением системы уравнений вычисляются значения контур-токов, которые и определяют действительные токи в каждой и схемы (рис. 4.13).
Пример 4.11
Определить токи во всех участках сложной цепи (рис. 4.14), если: 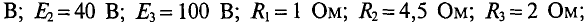
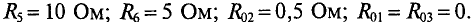
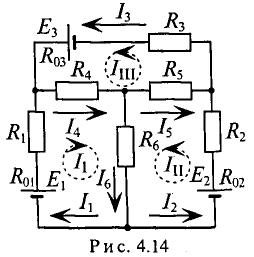
Решение
Необходимо составить 3 уравнения по второму закону для определения контурных токов 1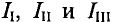 (направление урных токов выбрано произвольно указано пунктирными линиями).
(направление урных токов выбрано произвольно указано пунктирными линиями).
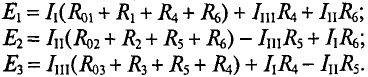
Подставляются числовые значения величин
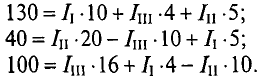
Из уравнения (2) определяется ток 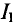
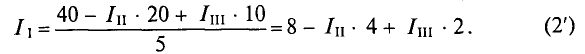
Значение тока 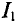 (выражение (2′)) подставляется в уравнение (1):
(выражение (2′)) подставляется в уравнение (1):
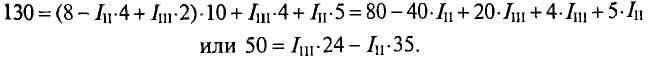
То же значение тока 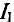 подставляется в уравнение (3):
подставляется в уравнение (3):
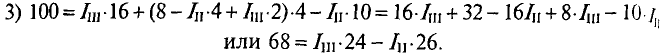
Из полученного уравнения (3) вычитается полученное уравнение (1). В результате получим
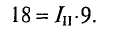
Откуда контурный ток 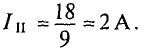
Из уравнения (3) определяется контурный ток 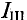
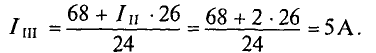
Из уравнения (2′) определяется ток 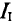
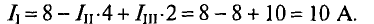
Вычисляются реальные токи в заданной цепи:
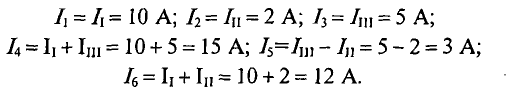
Проверяется правильность решения для 1 -го контура (рис. 4.14).
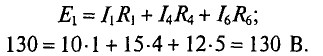
Решение правильное.
Такую же проверку можно произвести и для других контуров (2-го и 3-го):
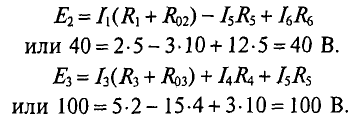
Проверка показала правильность решения.
Определение метода контурных токов
Данный метод является фундаментальным и применим для расчета любых электрических цепей. Он базируется на уравнениях, составленных по второму закону Кирхгофа. В схеме выделяются независимые контуры, в каждом из них произвольно выбираются направления контурных токов и составляются уравнения по второму закону Кирхгофа. Для цепи по рис. 3.1 имеем:
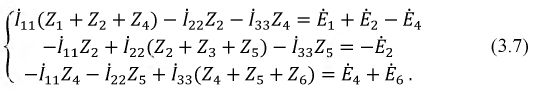
Введем в полученную систему уравнений обобщенные параметры:
собственное сопротивление контура – сумма сопротивлений, входящих в состав контура, например, для первого контура:
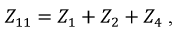
смежные сопротивления – сопротивления на границах контуров, например, 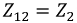 сопротивление на границе первого и второго контуров, суммарная ЭДС, например, для первого контура:
сопротивление на границе первого и второго контуров, суммарная ЭДС, например, для первого контура:
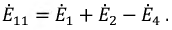
Тогда система уравнений примет вид:
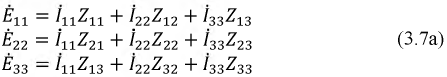
Используя матричный метод расчета, можем записать:
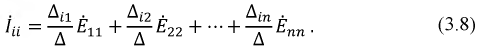
В уравнении (3.8)  – главный определитель системы (3.7a), a
– главный определитель системы (3.7a), a 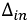 – алгебраическое дополнение для соответствующей контурной ЭДС. В ветвях, которые не граничат с другими контурами, реальные токи будут:
– алгебраическое дополнение для соответствующей контурной ЭДС. В ветвях, которые не граничат с другими контурами, реальные токи будут:
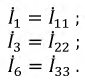
Токи ветвей, находящихся на границах контуров:
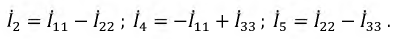
Справочный материал по методу контурных токов
Метод контурных токов является одним из основных методов расчета сложных электрических цепей, которым широко пользуются на практике. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурное токи, замыкающиеся в контурах.
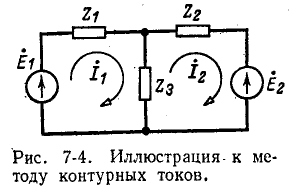
На рис. 7-4 в виде примера показана двухконтурная электрическая цепь, в которой 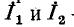 — контурные токи. Токи в сопротивлениях
— контурные токи. Токи в сопротивлениях 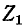 и
и 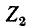 равны соответствующим контурным токам; ток в сопротивлении
равны соответствующим контурным токам; ток в сопротивлении 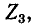 являющемся общим для обоих контуров, равен разности контурных токов
являющемся общим для обоих контуров, равен разности контурных токов 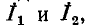 так как эти токи направлены в ветви
так как эти токи направлены в ветви 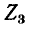 встречно*. При этом если положительное направление искомого тока в ветви
встречно*. При этом если положительное направление искомого тока в ветви 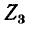 принять совпадающим с направлением контурного тока
принять совпадающим с направлением контурного тока 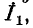 то ток в ветви будет равен
то ток в ветви будет равен 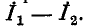 В противном случае он будет равен
В противном случае он будет равен 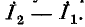
Число уравнений, записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, т. е. для электрической схемы с числом узлов q и числом ветвей р задача нахождения контурных токов сведется к решению системы р — q + I уравнений. Так, в схеме рис. 7-4 q = 2, р = 3; следовательно, число уравнений равно 3 — 2+1=2 (число независимых контуров).
 Следует отметить, что если положительное направление одного из контурных токов
Следует отметить, что если положительное направление одного из контурных токов 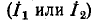 изменить на обратное, то ток в ветви
изменить на обратное, то ток в ветви 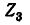 будет равен сумме этих токов.
будет равен сумме этих токов.
Условимся сумму комплексных сопротивлений, входящих в контур, называть собственным сопротивлением контура, а комплексное сопротивление, принадлежащее одновременно двум или нескольким контурам, — общим сопротивлением этих контуров.
Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от данного контурного тока в собственном сопротивлении контура берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис. 7-4, где направление обоих контурных токов выбрано по ходу часовой стрелки.
Для заданной электрической схемы с двумя независимыми контурами (рис. 7-4) могут быть записаны два уравнения по второму закону Кирхгофа, а именно:,
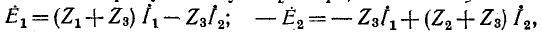
где 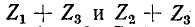 — собственные сопротивления контуров 1 и 2;
— собственные сопротивления контуров 1 и 2; 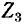 — общее сопротивление контуров 1 и 2 (знак минус в уравнениях обусловлен выбором положительных направлений контурных токов).
— общее сопротивление контуров 1 и 2 (знак минус в уравнениях обусловлен выбором положительных направлений контурных токов).
Если заданная электрическая схема содержит п независимых контуров, то на основании второго закона Кирхгофа получается система из п уравнений:
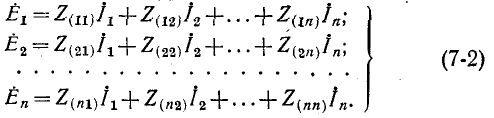
Здесь 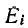 — контурная э. д. с. в контуре
— контурная э. д. с. в контуре 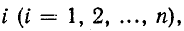 т. е. алгебраическая сумма э. д. с., действующих в данном контуре; э. д. с., совпадающие по направлению с направлением обхода, берутся со знаком плюс, а направленные встречно — со знаком минус;
т. е. алгебраическая сумма э. д. с., действующих в данном контуре; э. д. с., совпадающие по направлению с направлением обхода, берутся со знаком плюс, а направленные встречно — со знаком минус;
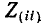 — собственное сопротивление контура i;
— собственное сопротивление контура i;
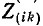 — общее сопротивление контуров
— общее сопротивление контуров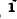 i и k.
i и k.
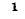 Индексы собственных и общих сопротивлений контуров заключены в скобки для отличия их от входных и передаточных сопротивлений, приводимых в последующих разделах книги.
Индексы собственных и общих сопротивлений контуров заключены в скобки для отличия их от входных и передаточных сопротивлений, приводимых в последующих разделах книги.
В соответствии со сказанным ранее собственные сопротивления 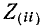 войдут со знаком плюс, поскольку обход, контура принимается совпадающим с положительным направлением контурного тока
войдут со знаком плюс, поскольку обход, контура принимается совпадающим с положительным направлением контурного тока 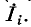 Общие сопротивления
Общие сопротивления 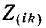 войдут со знаком минус, когда токи
войдут со знаком минус, когда токи 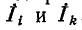 направлены в них встречно.
направлены в них встречно.
Решение уравнений (7-2) относительно искомых контурных токов может быть найдено с помощью определителей:
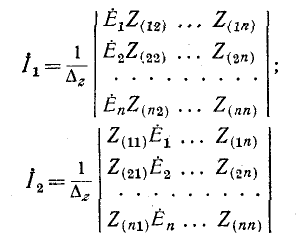
ит. д., где определитель системы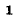
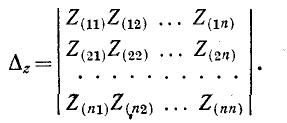
Согласно правилу разложения определителя по элементам столбца определитель равен сумме произведений элементов столбца на их алгебраические дополнения. Поэтому решение уравнений запишется в виде 
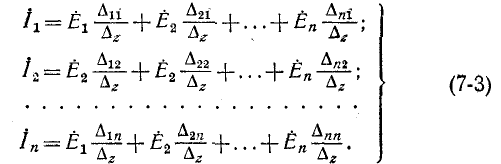
 Определитель снабжен индексом z, так как его элементами являются комплексные сопротивления.
Определитель снабжен индексом z, так как его элементами являются комплексные сопротивления.
 На практике во многих случаях решение системы уравнений (7-2) может быть выполнено более просто последовательным исключением неизвестных,
На практике во многих случаях решение системы уравнений (7-2) может быть выполнено более просто последовательным исключением неизвестных,
Здесь Дitl — алгебраическое дополнение элемента Z{lk) определителя системы, т. е. умноженный на (—1)‘+* минор элемента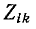 (минор образуется из определителя системы исключением из него i-й строки и
(минор образуется из определителя системы исключением из него i-й строки и 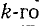 столбца).
столбца).
Сокращенно система уравнений (7-3) записывается в виде:
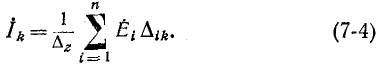
Первый индекс алгебраического дополнения i, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру контура, контурная э. д. с. которого умножается на данное алгебраическое дополнение. Второй индекс 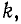 обозначающий номер столбца, вычеркиваемого в определителе системы, соответствует номеру контура, для которого вычисляется контурный ток.
обозначающий номер столбца, вычеркиваемого в определителе системы, соответствует номеру контура, для которого вычисляется контурный ток.
Уравнения (7-2), выражающие второй закон Кирхгофа, записаны в предположении, что источниками электрической энергии служат источники э. д. с. При наличии в электрической схеме источников тока они могут быть заменены эквивалентными источниками э. д. с.
Если проводимости источников тока равны нулю, то целесообразно выбрать заданные токи в качестве контурных; тогда число неизвестных контурных токов и соответственно число уравнений сократятся на число заданных токов.
Если в заданной электрической схеме имеются параллельные ветви, то замена их эквивалентным комплексным сопротивлением сокращает число контуров (за счет тех, которые образованы параллельными ветвями).
Электрические цепи могут быть планарными или непланарными.
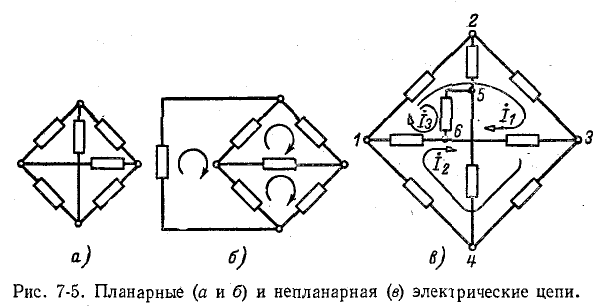
Планарная, или плоская, электрическая цепь может быть вычерчена на плоскости в виде схемы с непере-крещивающимися ветвями. В некоторых случаях пересечение ветвей в электрической схеме, являющееся результатом Принятого способа начертания схемы, устраняется при другом способе изображения данной планарной электрической цепи, как это, например, представлено на рис. 7-5.
Электрическая цепь, приведенная на рис. 7-5, а, планарна, так как имеющееся пересечение ветвей устранимо в соответствии с рис. 7-5, б.
Не планарная электрическая цепь не может быть вычерчена на плоскости в виде схемы с неперекрещиваю-щимися ветвями. Примером такой электрической цепи служит приведенная на рис. 7-5, в непланарная цепь, пересечение ветвей в которой не может быть устранено.
Если направление контурных токов во всех контурах планарной электрической цепи одинаково, например совпадает с ходом часовой стрелки, то общие сопротивления смежных контуров входят в систему уравнений (7-2) со знаком минус, так как контурные токи смежных контуров
направлены в общих ветвях встречно. Направление контурных токов по ходу часовой стрелки принимается во всех контурах, кроме внешнего, охватывающего всю схему. В последнем контурный ток направляется против часовой стрелки'(см. пример 7-2). Это правило, однако, не является обязательным.
В случае непланарной электрической цепи не представляется возможным иметь в общих ветвях только разности контурных токов, как это, например, видно из схемы рис. 7-5, в.
Пример 7-2.
Пользуясь методом контурных токов, определить ток в диагонали бюстовой схемы рис. 7-6.
Выбранные положительные направления контурных токов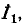
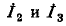 указаны на схеме стрелками. Число уравнений, записываемых по второму закону Кирхгофа, равно трем (по числу независимых контуров):
указаны на схеме стрелками. Число уравнений, записываемых по второму закону Кирхгофа, равно трем (по числу независимых контуров):
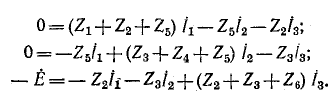
Решение полученной системы уравнений относительно контурных токов 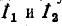 дает:
дает:
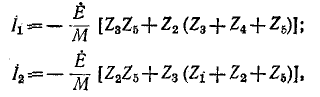
где М имеет то же значение, что и в примере 7-1.
Искомый ток в диагонали мостовой схемы равен разности контурных токов:
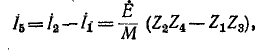
что совпадает с полученным в примере 7-1 ответом.
Следует заметить, что если в заданной схеме контуры выбрать так, чтобы через ветвь 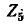 проходил только один контурный ток, то искомый ток в ветви
проходил только один контурный ток, то искомый ток в ветви 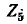 будет равен именно Рис. 7-6. Пример 7-2. этому контурному току, т, е.
будет равен именно Рис. 7-6. Пример 7-2. этому контурному току, т, е.
задача сведется к нахождению только одного контурного тока (вместо двух).
- Метод свертывания электрической цепи
- Метод преобразования схем электрических цепей
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений
- Метод узловых потенциалов
- Принцип и метод наложения
- Входные и взаимные проводимости
- Преобразование треугольника сопротивлений в эквивалентную звезду
Изучаем метод контурных токов с примерами
Электрические схемы могут быть очень сложными. Чтобы рассчитать действующие в них токи, пользуются первым и вторым правилами Кирхгофа. В этом случае составляют систему уравнений, на основании которых можно узнать, какова сила электротока в каждом контуре. Метод контурных токов позволяет сократить объем проводимой работы. Решать уравнения можно самостоятельно или же используя онлайн калькулятор.
Суть метода
В составе любой электрической цепи имеются контуры и ветви. Действующие в них электротоки определяют при помощи правил Кирхгофа. При этом количество уравнений будет совпадать с количеством неизвестных величин.

Существуют способы упростить расчет цепей, сокращая количество необходимых для решения задачи уравнений. Один из наиболее известных основывается на таком понятии, как контурный ток. С его помощью процедура расчёта становится более эффективной, что особенно выгодно при рассмотрении наиболее сложных электрических цепей.
Иногда возникает вопрос, являются ли контурные токи реальными токами ветвей. В отдельных случаях это может быть так, но не всегда. Действительный ток равен контурному, если он протекает лишь в одном контуре.
При проведении расчётов онлайн или офлайн применяются особые, искусственно смоделированные электротоки. Одна из особенностей смоделированных электротоков заключается в том, что каждый проходит внутри элементарного контура. При этом рассматриваются только те из них, которые по сравнению друг с другом имеют новые ветви.
Расчет по методу контурных токов предполагает, что не все токи в рассматриваемой схеме являются независимыми. Поэтому этот способ позволяет сократить количество нужных для расчета уравнений. С его помощью можно определить действительные токи на каждом участке схемы.
Практическое применение
Чтобы лучше понять, как можно определить токи в ветвях цепи методом контурных токов, предлагаем рассмотреть такую схему.

Анализ схемы показывает, что есть и контурные, и реально протекающие электротоки. Первые имеют индекс из одной цифры, вторые — из двух. Нужно заметить, что каждая сторона треугольника является отдельным контуром. В каждом из них задано направление обхода. Оно выбирается произвольно, но определяет знаки токов проходящих в ветвях. В качестве нагрузки используются резисторы, но могут рассматриваться и более сложные элементы. Учитывая направление токов, составляем систему уравнений:

Чтобы рассчитать составленную систему, воспользуемся правилами Кирхгофа:

Расчет цепей методом контурных электротоков можно выполнить также с помощью специальных онлайн сервисов. Приведенная выше формула может быть представлена следующим равенством:

В этом выражении использованы следующие обозначения:
- Равные индексы, относящиеся к сопротивлению, представляют собой суммарную величину для k-го контура электрической цепи.
- Если для сопротивления использованы индексы k и m, то речь идёт об общем сопротивлении, которое входит одновременно в 2 контура с такими номерами.
- Нужно обратить внимание, что в последней формуле присутствуют контурные токи в k-м контуре.
- С правой стороны знака равенства указана суммарная электродвижущая сила для k-го контура.
При определении неизвестной величины слагаемое берётся с плюсом в тех ситуациях, когда направления электротоков в соседних контурах совпадают, и с минусом, когда они противоположные. ЭДС контура может быть положительной или отрицательной. Первый вариант применяется в тех случаях, когда направления электродвижущей силы и контурного электротока совпадают. В противном случае ЭДС берётся с минусом.
Уравнение составляется не для всех контуров. Исключением являются те, в которых присутствует источник электротока. В такой ситуации контурный ток совпадает с реальным. Количество уравнений в полученной системе равно количеству контуров, являющихся независимыми, то есть тех, у которых имеется хотя бы одна ветвь, отличающая их от всех других. Решение полученной системы уравнений позволит вычислить электротоки на каждом участке схемы.
Примеры решения задач
Необходимо решить задачу с исходными данными, представленными на рисунке ниже.

Исходя из заданной схемы, можно выделить три контура. Затем следует указать направление контурных и действительных электротоков.

Теперь следует рассчитать собственные сопротивления каждого контура.

Составляем систему уравнений для определения контурных токов. Поскольку есть три контура, то уравнений также будет три. При этом следует учитывать направление электротоков и ЭДС.

После подстановки известных значений сопротивлений в полученные уравнения находим величину интересующих нас токов.

На последнем этапе определяем значения действительных токов.

Так решаются задачи с помощью метода контурных электротоков. Главное преимущество данного метода заключается в сокращенном числе уравнений. Оно уменьшается до m – n + 1, где m — это количество ветвей, а n — узлов в электроцепи.
Видео по теме
Метод контурных токов.
Метод контурных токов – один из основных
и широко применяемых на практике методов.
Он заключается в определении по второму
закону Кирхгофа контурных токов. Для
каждого контура цепи задают ток, который
остается неизменным. В цепи протекает
столько контурных токов, сколько
независимых контуров в ней содержится.
Направление контурного тока выбирают
произвольно.
Контурные токи, проходя через узел,
остаются непрерывными. Следовательно,
первый закон Кирхгофа выполняется
автоматически. Уравнения с контурными
токами записываются только для второго
закона Кирхгофа. Число уравнений,
составленных по методу контурных токов,
меньше чем по методу законов Кирхгофа.
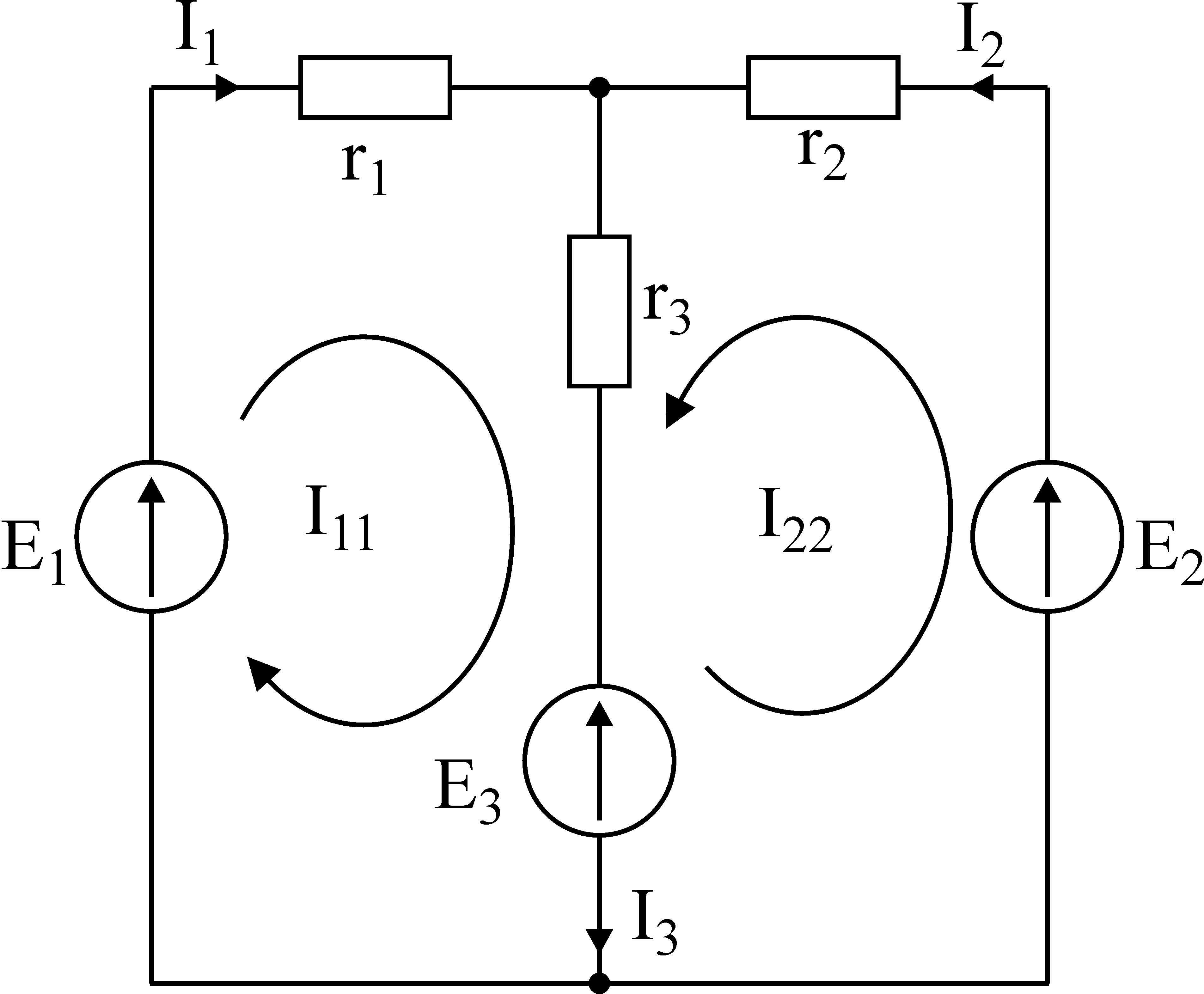
Рис.28. Иллюстрация к методу контурных
токов.
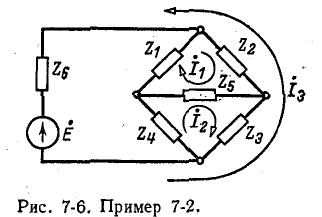
На рис.28 показана цепь с двумя независимыми
контурами, следовательно, и с двумя
контурными токами I11иI22.
Токи в ветвях I1иI2равны контурным
токам:
I1=I11,
I2=I22
Ток I3равен сумме
этих двух контурных токов:
I3=I11+I22
По второму закону Кирхгофа для первого
контура цепи:
I1r1+I3r3=E1-E3
Или: I11r1+(I11+I22)r3=E1-E3;
I11
(r1+r2)+I22r3=E1-E3
Обозначим r1+r2=r11
r3=r12;
E1-E3
Тогда: I11r11+I2r12=E11
r11– сумма всех
сопротивлений, входящих в контурI,
называетсясобственным сопротивлением
контура.
r12– сопротивление
ветви, общей для контураIиII;
E11=E1-E2– алгебраическая сумма всех э.д.с.,
содержащихся в первом контуре; со знаком
«-» берется э.д.с., действующая навстречу
контурному току рассматриваемого
контура.
E11называетсяконтурной э.д.с.
Аналогично для второго контура рис.28.
I11r21+I22r22=E22,
где r21=r3;r22=r2+r3;
E22=E2-E3
Уравнения, составленные по методу
контурных токов, всегда записывают в
виде системы. Для схемы рис.28:
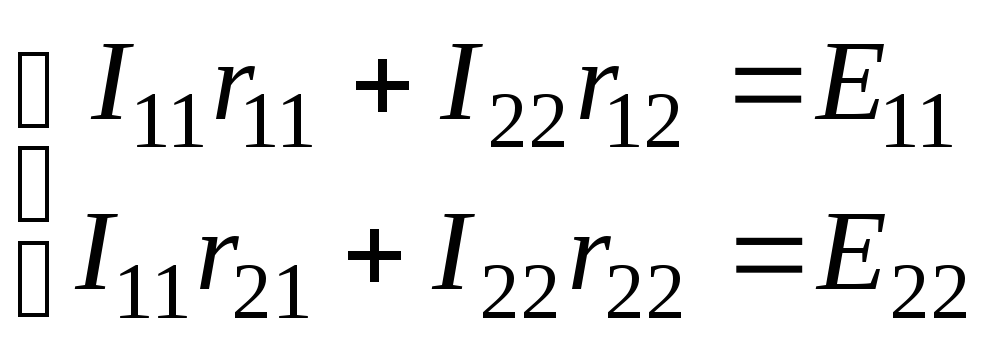
В результате решения системы находят
контурные токи, а затем токи ветвей.
Если заданная электрическая цепь
содержит nнезависимых
контуров, то на основании второго закона
Кирхгофа получаетсяnконтурных уравнений:
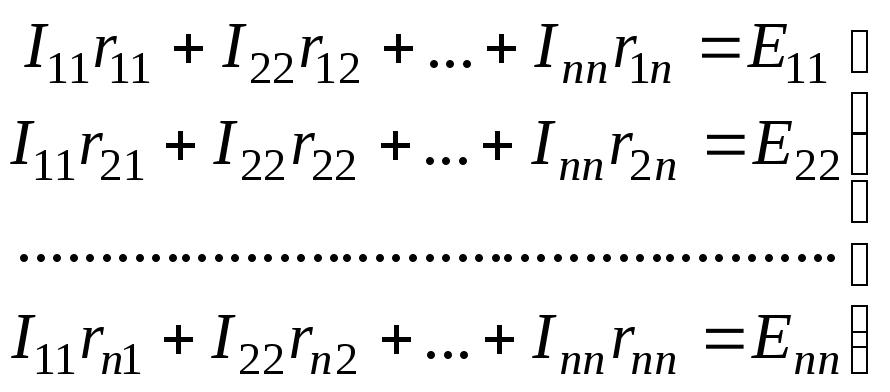 (29)
(29)
Собственные сопротивления riiвходят в уравнения (29) со знаком «+»,
поскольку обход контура принимается
совпадающим с положительным направлением
контурного токаIii.
Общие сопротивленияrikвойдут в уравнения со знаком «-», когда
токиIiиIkнаправлены в них встречно.
Число уравнений, составляемых по методу
контурных токов, определяется по формуле:
Nур=Nb-Ny+1-Nи.т.
где Nb– число ветвей электрической цепи;
Ny–
число узлов;
Nи.т.– число идеальных
источников тока.
Е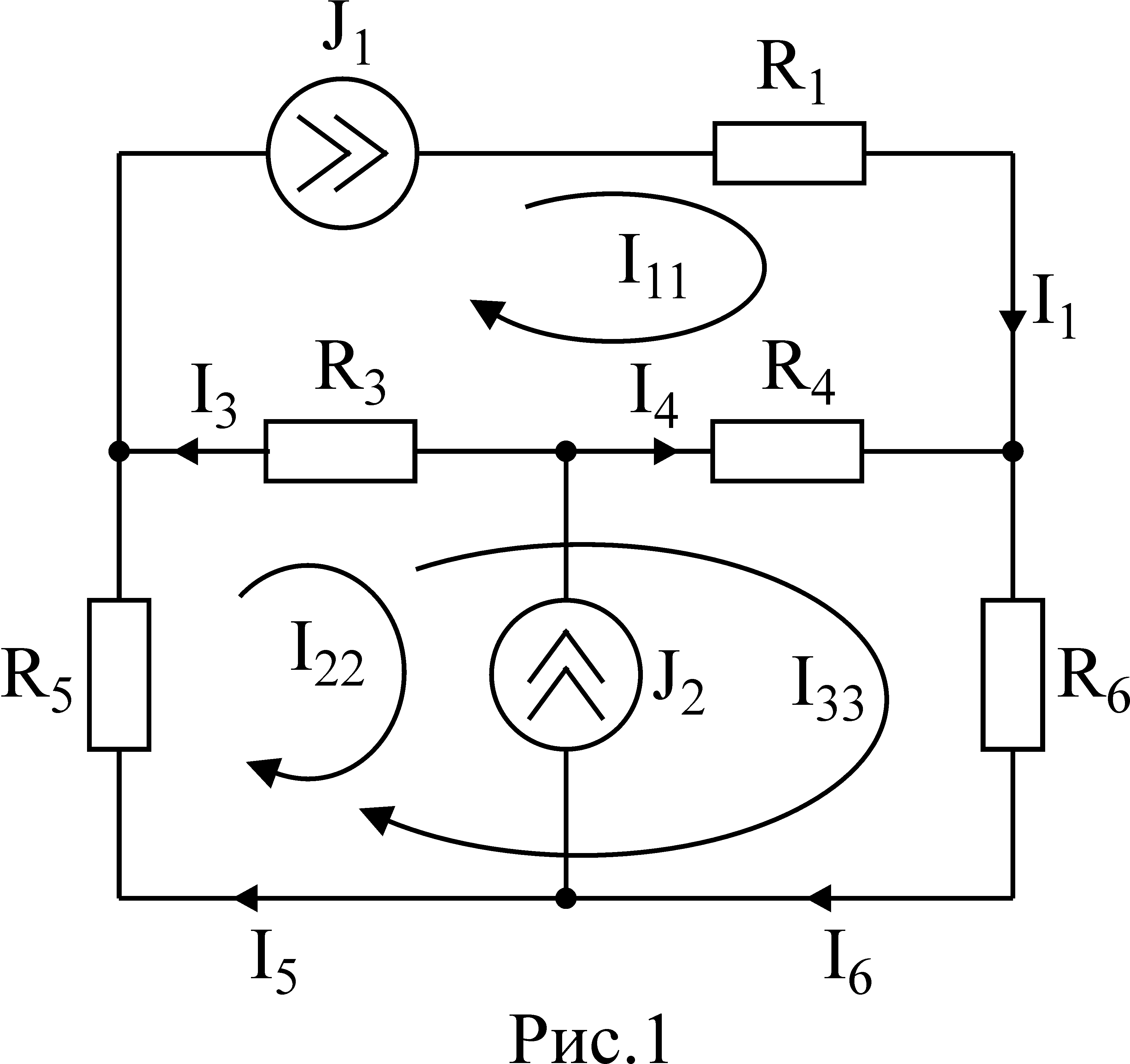 сли
сли
в цепи отсутствуют источники тока, число
уравнений равно числу контурных токов
и, соответственно, числу независимых
контуров рассматриваемой электрической
цепи.
Пример.
Решим пример 2 параграфа 11, используя
метод контурных токов.
Цепь содержит три контура, через которые
протекают контурные токи.
При наличии источников тока надо так
направлять контурные токи, чтобы они
протекали через данные источники. Но
через один источник тока не может
протекать два контурных тока.
На рис.1 обозначены положительные
направления контурных токов. Очевидно,
что I11=J1;I22=-J2
Контурный ток I33–
неизвестен, для него составляем
уравнение:
I33
(R3+R4+R5+R6)-I11
(R3+R4)+I22
(R5+R3)=0
В правой части уравнения стоит «0», т.к.
отсутствует контурная э.д.с.
В результате решения определяем I33=16,25
мА
Итак: I1=I11=20мА;
I3=I11-I22-I33=20-(-10)-16,25=13,75мА.
I4=-I11+I33=-20+16,25=-3,75мА;
I5=I22+I33=-10+16,25=6,25мА;
I6=I33=16,25мА.
Соседние файлы в папке Конспект 2
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ме́тод ко́нтурных то́ков — метод сокращения размерности системы уравнений, описывающей электрическую цепь. Это метод расчёта электрических цепей, при котором за неизвестные принимаются токи в контурах, образованных некоторым условным делением электрической цепи.
Основные принципы[править | править код]
Любая электрическая цепь, состоящая из Р рёбер (ветвей, участков, звеньев) и У узлов, может быть описана системой уравнений в соответствии с 1-м и 2-м правилами Кирхгофа. Число уравнений в такой системе равно Р, из них У–1 уравнений составляется по 1-му правилу Кирхгофа для всех узлов, кроме одного; а остальные Р–У+1 уравнений – по 2-му правилу Кирхгофа для всех независимых контуров. Поскольку независимыми переменными в цепи считаются токи рёбер, число независимых переменных равно числу уравнений, и система разрешима.
Существует несколько методов сократить число уравнений в системе. Одним из таких методов является метод контурных токов.
Метод использует тот факт, что не все токи в рёбрах цепи являются независимыми. Наличие в системе У–1 уравнений для узлов означает, что зависимы У–1 токов. Если выделить в цепи Р–У+1 независимых токов, то систему можно сократить до Р–У+1 уравнений. Метод контурных токов основан на очень простом и удобном способе выделения в цепи Р–У+1 независимых токов.
Метод контурных токов основан на допущении, что в каждом из Р–У+1 независимых контуров схемы циркулирует некоторый виртуальный контурный ток. Если некоторое ребро принадлежит только одному контуру, реальный ток в нём равен контурному. Если же ребро принадлежит нескольким контурам, ток в нём равен сумме соответствующих контурных токов (с учётом направления обхода контуров). Поскольку независимые контура покрывают собой всю схему (т.е. любое ребро принадлежит хотя бы одному контуру), то ток в любом ребре можно выразить через контурные токи, и контурные токи составляют полную систему токов.
Построение системы контуров[править | править код]
Использование плоских графов[править | править код]

Выделение независимых контуров на плоском графе электрической схемы.
Наиболее простым и наглядным методом построения системы независимых контуров является построение плоского графа схемы, то есть размещение ветвей и узлов цепи на плоскости без взаимных пересечений рёбер. Плоский граф разбивает плоскость на К ограниченных областей. Можно показать, что замкнутые цепочки рёбер, ограничивающие эти области, являются системой независимых контуров для рассматриваемой схемы.
Метод плоского графа предпочтителен при ручном расчёте схем. В случае, если схему невозможно изобразить в виде плоского графа, а также в случае компьютерного построения системы контуров применение этого метода может оказаться невозможным.
Метод выделения максимального дерева[править | править код]
Дерево представляет собой подмножество звеньев цепи, представляющее собой односвязный (то есть состоящий из одной части) граф, в котором нет замкнутых контуров. Дерево получается из цепи путём исключения из него некоторых звеньев. Максимальное дерево – это дерево, для которого добавление к нему любого исключённого звена приводит к образованию контура.
Метод выделения максимального дерева основан на последовательном исключении из цепи определённых звеньев согласно следующим правилам:
- На каждом шагу из цепи в произвольном порядке исключается одно звено;
- Если исключение звена приводит к нарушению односвязности графа (то есть граф разбивается на две изолированных части, либо появляются «висящие» узлы), то звено возвращается в цепь;
- Если при исключении звена граф не теряет односвязности, звено остаётся исключённым;
- Переходим к следующему шагу.
В конце работы алгоритма число исключённых из цепи звеньев оказывается точно равно числу независимых контуров схемы. Каждый независимый контур получается присоединением к цепи соответствующего исключённого звена.
Пример выделения максимального дерева
-

Удаление звена R1
-

Удаление звеньев R2 и R3
-

Удаление звена R4 приводит к появлению «висячего» узла
-
Присоединение к дереву удалённого звена образует контур
Построение системы уравнений[править | править код]
Для построения системы уравнений необходимо выделить в цепи P – У + 1 независимых контуров. По каждому из этих контуров будет составлено одно уравнение по 2-му правилу Кирхгофа. В каждом контуре необходимо выбрать направление обхода (например, по часовой стрелке).
Выделение независимых контуров можно осуществить одним из перечисленных выше методов. Следует отметить, что система независимых контуров, как правило, не единственна, как не единственно и максимальное дерево цепи. Однако системы уравнений, составленные по различным системам контуров, математически эквивалентны, поэтому возможен специальный подбор системы контуров, дающей наиболее простую систему уравнений.
Отметим также, что при любом выборе системы контуров в любом контуре обязательно найдётся ребро, которое входит только в этот контур и ни в какой другой. Таким образом, контурный ток всегда совпадает с током в одном из рёбер этого контура. Например, для схемы, изображённой на рисунке, звено 4 входит только в левый контур, поэтому контурный ток обозначен как I4. То же самое относится к двум другим контурам, токи в которых обозначены как I5 и I6. В литературе встречаются и другие обозначения для контурных токов, например, римскими цифрами (II, III, IIII …), латинскими буквами (IA, IB, IC …) и т.д.
Принцип построения системы уравнений следующий.
- Все токи в звеньях выражаем через контурные токи. В данном случае необходимо выразить только те токи, которые не совпадают с одним из контурных токов:
- Для каждого контура записываем уравнение по второму закону Кирхгофа:
- В левой части каждого уравнения записываем сумму токов в звеньях, входящих в контур, умноженных на сопротивление соответствующего звена. Суммирование происходит с учётом знака: если ток в звене совпадает с направлением обхода контура, слагаемое записывается со знаком «плюс», в противном случае — со знаком «минус».
- В правой части каждого уравнения записываем сумму ЭДС источников, а также сумму произведений токов источников на сопротивление соответствующего звена. Суммирование также происходит с учётом знака, в зависимости от совпадения или несовпадения направления источника с направлением контурного тока:

Рис. 1. Пример электрической схемы
Для первого контура (I4):
Для второго контура (I5):
Для третьего контура (I6):
Окончательно получаем систему уравнений

Оптимизированная процедура составления системы[править | править код]
Как видно из вышесказанного, процедуру составления системы можно упростить следующим образом:
- В левой части К-го уравнения записываем произведение контурного тока на сумму сопротивлений всех звеньев, входящих в контур:
где 

- От левой части уравнения отнимаем остальные контурные токи, умноженные на суммы сопротивлений звеньев, по которым контур К пересекается с этими контурами:
где 

- В правой части уравнения записываем сумму источников ЭДС с учётом знаков («плюс» — если направления ЭДС и обхода контура совпадают, «минус» — в противном случае):
- К правой части уравнения прибавляем величины источников тока, умноженные на сопротивление соответствующего звена с учётом знаков («плюс» — если направления источника тока и обхода контура совпадают, «минус» — в противном случае):
Составив уравнения для всех независимых контуров, получаем совместную систему P–У+1 уравнений относительно P–У+1 неизвестных контурных токов.
Пример[править | править код]

Рис. 2. Метод контурных токов
Предположим, что в левом контуре по часовой стрелке течет контурный ток I11, а в правом (также по часовой стрелке) — контурный ток I22. Для каждого из контуров составим уравнения по второму закону Кирхгофа. При этом учтем, что по смежной ветви (с сопротивлением R5) течет сверху вниз ток I11–I22. Направления обхода контуров примем также по часовой стрелке.
Перепишем эти уравнения следующим образом:
где
— полное сопротивление первого контура;
— полное сопротивление второго контура;
— сопротивления смежной ветви между первым и вторым контурами, взятые со знаком минус;
— контурная ЭДС первого контура;
— контурная ЭДС второго контура.
Формальный подход[править | править код]
В матричном виде система уравнений для метода контурных токов выглядит следующим образом[1]:
где

- 0, если ребро j не входит в контур i;
- 1, если ребро входит в контур, и направление ребра соответствует направлению обхода контура;
- –1, если ребро входит в контур, и направление ребра противоположно направлению обхода контура.
Для каждого ребра задаётся направление, которое обычно ассоциируется с направлением тока в этом ребре;





Пример системы уравнений[править | править код]
Для схемы, представленной в предыдущем разделе (см. “Построение системы уравнений”, рис. 1), матрицы имеют вид:


Перемножаем матрицы в соответствии с матричным уравнением:




Раскрывая матричную запись, получаем следующую систему уравнений:

Примечания[править | править код]
- ↑
Нейман Л. Р., Демирчян К. С. Теоретические основы электротехники: в 2-х т. Учебник для вузов. Том I. — 3-е изд., перераб. и доп. — Л.: Энергоиздат. Ленингр. отд-ние, 1981. — 536 с., ил.
См. также[править | править код]
- Правила Кирхгофа
- Эквивалентная схема
- Источник напряжения
- Источник тока
Литература[править | править код]
- Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Гардарики, 2002. — 638 с. — ISBN 5-8297-0026-3.

















