Как составить систему уравнений не имеющую решений

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные
числа, а x₁,…,x_n – неизвестные. В обозначении
коэффициентов a_ij первый индекс iобозначает номер уравнения,
а второй j – номер неизвестного, при
котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей
системы.

Числа, стоящие в
правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение
системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих
неизвестных x₁,…,x_n.

Наша задача
будет заключаться в нахождении решений системы. При этом могут возникнуть три
ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся
   знаком.
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных
уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений,
то она называется несовместной.

Рассмотрим
способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность
кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений
с тремя неизвестными:

Рассмотрим
матрицу системы и матрицы столбцы
неизвестных и свободных членов

Найдем произведение

т.е. в результате
произведения мы получаем левые части уравнений данной системы. Тогда пользуясь
определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно
найти, т.к. её элементы являются решением данной системы. Это уравнение
называют матричным уравнением.

Пусть
определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом.
Умножим обе части уравнения слева на матрицу A^-1, обратную матрице A: . Поскольку A^-1A = E и E∙X = X, то получаем решение
матричного уравнения в виде X = A^-1B.

Заметим, что
поскольку обратную матрицу можно найти только для квадратных матриц, то
матричным методом можно решать только те системы, в которых число уравнений
совпадает с числом неизвестных. Однако, матричная запись системы возможна и
в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому
нельзя найти решение системы в виде X = A^-1B.

Примеры. Решить системы уравнений.

1. 

   Найдем матрицу
   обратную матрице A.

   ,

   Таким образом, x = 3, y = – 1.

2. 

   Итак, х₁=4,х₂=3,х₃=5.

3. Решите матричное уравнение: XA+B=C, где

   Выразим искомую
   матрицу X из заданного уравнения.

   

   Найдем матрицу А^-1.

   

   Проверка:

   

4. Решите матричное уравнение AX+B=C, где

   Из уравнения
   получаем .

   

   Следовательно,

ПРАВИЛО КРАМЕРА

Рассмотрим
систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е.
составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно
1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ
≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак,
рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение
системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁
и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о
разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ
≠ 0, то система имеет единственное решение и обратно. Если же
определитель системы равен нулю, то система либо имеет бесконечное множество
решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему
уравнений

1. 

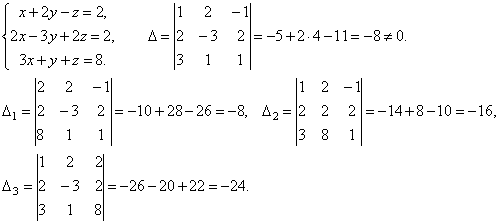
   Итак, х=1, у=2, z=3.
2. Решите систему уравнений
   при различных значениях параметра p:

   Система имеет единственное решение, если Δ
   ≠ 0.

   . Поэтому .

   

   1. При
   2. При p = 30 получаем систему уравнений которая не имеет решений.
   3. При p = –30 система принимает вид и, следовательно,
      имеет бесконечное множество решений x=y, yÎR.

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем,
в которых число уравнений совпадает с числом неизвестных, причём определитель
системы должен быть отличен от нуля. Метод Гаусса является более универсальным
и пригоден для систем с любым числом уравнений. Он заключается в
последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим
слагаемые, содержащие x₁. Для этого второе
уравнение разделим на а₂₁ и умножим на –а₁₁, а
затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате
исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым.
Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃,
затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять
местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются
тем, что выписывают расширенную матрицу системы:

и затем
приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям
матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы
уравнений методом Гаусса.

1. 

   Вернувшись к системе уравнений, будем иметь

   
2. 

   Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

   

   Вернувшись к системе уравнений, несложно заметить, что третье уравнения
   системы будет ложным, а значит, система решений не имеет.

3. 

   Разделим вторую строку матрицы на 2 и поменяем местами первый и третий
   столбики. Тогда первый столбец будет соответствовать коэффициентам при
   неизвестной z, а третий – при x.

   

   Вернемся к системе уравнений.

   Из третьего уравнения выразим одну неизвестную через другую и подставим в
   первое.

   

Таким образом, система имеет бесконечное множество решений.

Системы линейных алгебраических уравнений

Общие
понятия.
Линейным (относительно неизвестных
)
называют алгебраическое уравнение
первой степени, т.е. уравнение вида,
где– числа. Системалинейных уравнений снеизвестными имеет вид

(6)

В
общем случае число уравнений в системе
не обязательно совпадает с числом
неизвестных:
может быть меньше, равно или больше
числа.

Числа
(вещественные или комплексные) называются
коэффициентами системы
(6);
–свободными
членами;
–неизвестными.

Систему (6) можно
записать в матричной форме:

,
(7)

где
,,.

Если
,
то система называетсяоднородной,
в противном случае она называется
неоднородной.
Матрицу
называютматрицей
системы (6).
Расширенной
матрицей системы
(6) линейных уравнений называют матрицу
,
к которой добавлен (справа) столбец
свободных членов.
Такую матрицу будем обозначать в
дальнейшем символом.

Определение.
Совокупность
чиселназываетсярешением
системы (6),
если после замены неизвестных
числамисоответственно каждое из уравнений
системы превращается в верное равенство.

Пример
11.
Рассмотрим систему линейных уравнений

Эта
система 2-х уравнений с тремя неизвестными
решений не имеет, так как любая тройка
чисел, удовлетворяющая первому уравнению,
не может удовлетворять второму.

Пример
12.
Система

имеет
единственное решение
,.

Пример
13. Рассмотрим
систему линейных уравнений

Пара
чисел
есть одно из решений этой системы трех
уравнений с двумя неизвестными,– другое решение. Эта система имеет
бесконечно много решений: значения,при любом действительном значенииудовлетворяют данной системе.

Рассмотренные
примеры систем линейных уравнений
показывают, что, вообще говоря, система
может либо вовсе не иметь решений, либо
иметь единственное решение, либо иметь
их несколько (в последнем случае,
оказывается, система всегда имеет
бесконечное множество решений).

Определение.
Система линейных уравнений, не имеющая
ни одного решения, называется несовместной.
Система, обладающая хотя бы одним
решением, называется совместной.

Относительно
каждой системы линейных уравнений могут
быть поставлены следующие вопросы:

1. Совместна заданная
   система или нет?

2. В
   случае, если система совместна, как
   определить, сколько она имеет решений
   – одно или несколько?

3. Как найти все
   решения системы?

Ответ на все эти
вопросы дает теория систем линейных
уравнений.

Правило
Крамера.
Ограничимся сначала рассмотрением
систем, у которых число уравнений равно
числу неизвестных (такие системы называют
квадратными).

Пусть
дана система
линейных уравнений снеизвестными:

(8)

Определитель

,

составленный
из коэффициентов при неизвестных,
называется определителем
системы (8).

Теорема.
Если
определитель
квадратной системы (6) отличен от нуля,
то эта система имеет единственное
решение. Это решение может быть найдено
по формулам

,

где
– определитель, получаемый из определителязаменой-го
столбца на столбец свободных членов.

(Без доказательства)

Формулы
для неизвестных носят название формул
Крамера.

Пример
14.
Решить
систему линейных уравнений методом
Крамера:

Вычислим определитель
матрицы системы:

Значит, система
имеет единственное решение. Вычислим
определители

Определитель
получается из определителязаменой 1-го столбца столбцом свободных
членов.

Определитель
получается из определителязаменой 2-го столбца столбцом свободных
членов.

Заменим
в определителе
3-ий столбец столбцом свободных членов
и вычислим

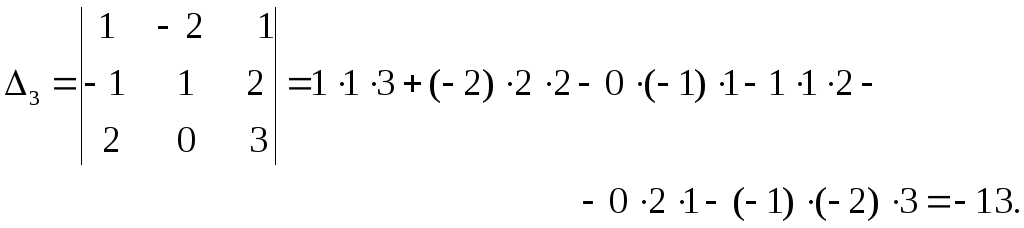
Решение системы
находим по формулам:

Ответ. (2; 1;1)

Метод
Гаусса (метод последовательного
исключения неизвестных) решения систем
линейных уравнений.
Под элементарными преобразованиями
системы линейных уравнений понимаются
следующие операции:

1. умножение
   какого-либо уравнения системы на число,
   отличное от нуля;

2. прибавление к
   одному уравнению другого уравнения;

3. перемена местами
   уравнений в системе.

Комбинируя
элементарные преобразования первого
и второго типов, мы можем к любому
уравнению прибавить другое уравнение,
умноженное на произвольное число.

Производя
элементарные преобразования в системе,
мы получаем новую систему. Очевидно,
что каждому элементарному преобразованию
системы соответствуют аналогичные
преобразования над строками расширенной
матрицы этой системы и, наоборот, каждому
элементарному преобразованию строк
расширенной матрицы соответствует
некоторое элементарное преобразование
в системе. Таким образом, элементарные
преобразования в системе сводятся к
соответствующим преобразованиям над
строками ее расширенной матрицы.

Определение.
Две системы линейных уравнений от одних
и тех же неизвестных называются
равносильными,
если каждое решение одной из них является
решением другой, и наоборот (или если
обе системы несовместны).

Заметим,
что число уравнений в равносильных
системах может быть различным.

Теорема.
При элементарных
преобразованиях система линейных
уравнений переходит в равносильную
систему.

(Без доказательства)

Сущность метода
Гаусса заключается в том, что с помощью
элементарных преобразований система
уравнений приводится к такому виду,
чтобы матрица системы оказалась
треугольной. Для упрощения изложения
мы будем иметь дело не с самой системой
(6), а с расширенной матрицей этой системы
(производя при этом элементарные
преобразования только над строками
матрицы).

Пример
15. Решить
систему уравнений методом Гаусса

Запишем расширенную
матрицу системы.

.

Нашей
целью является приведение матрицы к
треугольному виду. Для этого будем
выполнять элементарные преобразования
над строками матрицы. Первую строку
выбираем в качестве ведущей (у нее
элемент
).
К элементам первой строки прибавим
соответствующие элементы второй строки,
а от третьей строки отнимем первую,
умноженную на 2. Получим систему,
равносильную данной:

Вычтем
из третьей строки вторую, умноженную
на 9:

Получили
систему треугольного вида. Из последней
строки матрицы получаем уравнение
из которого находим

Второй
строке матрицы соответствует уравнение:
Подставляя найденное значениев это уравнение, получаемПодставляя в первое уравнение системызначенияполучаем

Ответ: (−2; 1; 3).

Критерий
совместности системы линейных уравнений.
Рассмотрим снова произвольную систему
линейных уравнений снеизвестными, которую запишем, как и
раньше, в матричной форме (7).

Очевидно,
что ранги матриц
исвязаны неравенством.

Вопрос
о совместности системы (7) полностью
решается следующей теоремой.

Теорема
Кронекера-Капелли.
Для того
чтобы система линейных уравнений была
совместна, необходимо и достаточно,
чтобы ранг матрицы этой системы был
равен рангу ее расширенной матрицы,
т.е. чтобы
.

(Без доказательства)

Если
совместность системы линейных уравнений
установлена, то возникает вопрос о том,
сколько она имеет решений. Ответ о числе
решений системы линейных уравнений
дает следующая теорема

Теорема
(о числе решений).
Пусть для
системы
линейных уравнений снеизвестными выполнено условие
совместности, т.е. рангматрицы системы равен рангу ее расширенной
матрицы. Тогда, если ранг матрицы системы
равен числу неизвестных (),
то система имеет единственное решение.
Если же ранг матрицы системы меньше
числа неизвестных (),
то система имеет бесконечное множество
решений, а именно: некоторымнеизвестным можно придавать произвольные
значения, тогда оставшиесянеизвестных определятся уже единственным
образом.

(Без доказательства)

Пример
16. Решить
систему уравнений методом Гаусса,
предварительно исследовав ее на
совместность:

Запишем
систему уравнений в виде расширенной
матрицы:

Поменяем
местами первую и вторую строки матрицы:

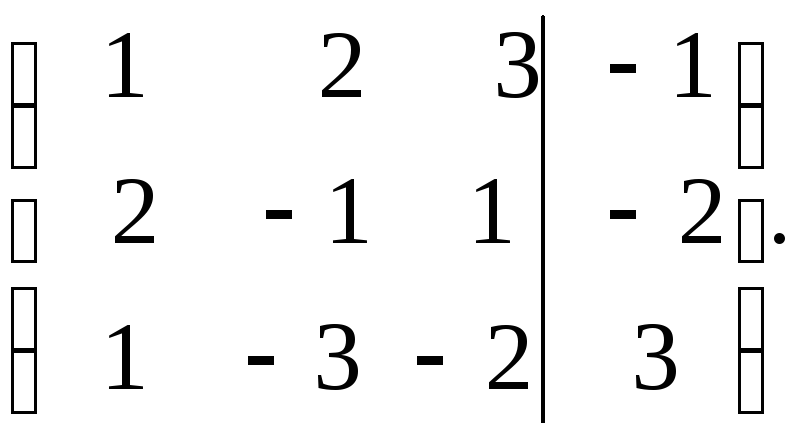
Первую
строку матрицы будем считать ведущей
(первый элемент строки равен 1), она не
будет меняться при преобразованиях.
Будем стремиться привести матрицу к
треугольному виду. Для того чтобы в
первом столбце матрицы получить нули,
выполним следующие преобразования: из
второй строки вычтем первую, умноженную
на 2, а от третьей вычтем первую. Получим
матрицу, равносильную данной:

Чтобы получить
матрицу треугольного вида, необходимо
вычесть из третьей строки вторую.
Окончательно получаем:

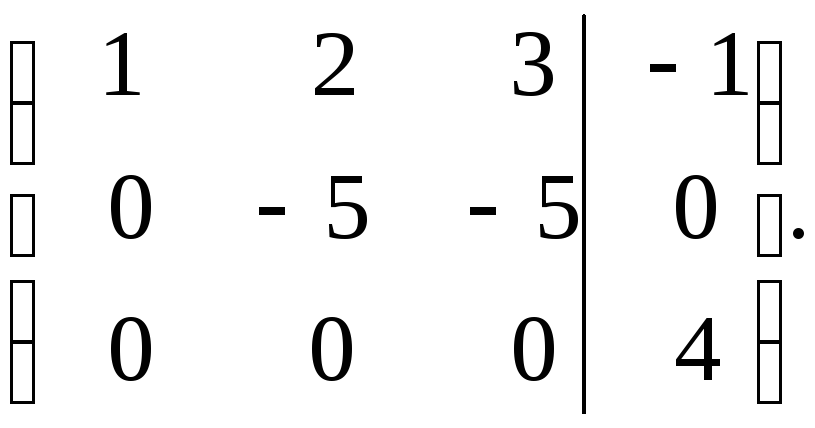
Ранг
расширенной матрицы системы равен 3,
ранг основной матрицы системы равен 2,
т.е.
,
следовательно, система несовместна.

Пример
17. Решить
систему уравнений методом Гаусса,
предварительно исследовав ее на
совместность:

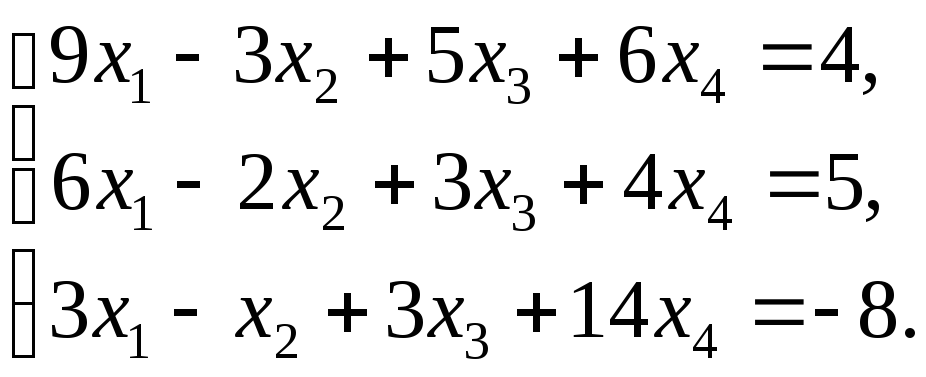
Запишем
систему уравнений в виде расширенной
матрицы:

Поменяем
местами первую и третью строки матрицы:

Будем
приводить матрицу к треугольному виду,
для этого выполним следующие преобразования:
первая строка будет ведущей, а от второй
строки вычтем первую, умноженную на 2,
а из третьей вычтем первую, умноженную
на 3. Получим равносильную систему:

Умножим
вторую строку на
,
третью наПри этом получим матрицу

Вычтем
из третьей строки вторую и получим
матрицу треугольного вида.

Ранг
расширенной матрицы системы равен рангу
матрицы системы, т.е.
Сравним ранг матрицы с числом неизвестных
системы:.
Согласно теореме о числе решений система
имеет бесконечное множество решений.
Найдем их.

Из
последней строки матрицы треугольного
вида имеем
,
третьей строке соответствует уравнение.
Зная,
получаемПервой строке матрицы соответствует
уравнение:Подставляя в это уравнение,получим уравнениеПусть,
тогда.

Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

§ 2. Системы линейных уравнений

Решение многих задач сводится к решению систем линейных уравнений.

Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение в верное числовое равенство.

Например, пара чисел `(2;3)` является решением системы уравнений

$$ left{begin{array}{l}2x+3y=13,\ x+5y=17,end{array}right.$$

а пара чисел `(1;1)` не является решением системы, т. к. эта пара не является решением каждого из уравнений системы.

Обозначим множество решений первого уравнения буквой `A`, а множество решений второго уравнения – `B`. Множество решений системы этих уравнений составляет пересечение множеств `A` и `B` (рис. 9). При этом возможны случаи, когда пересечение двух множеств является пустым (рис. 10) или совпадает с каждым из множеств `A` и `B` (рис. 11).

Графиком линейного уравнения `ax+by=c`, где `a^2+b^2>0`, является прямая. Следовательно, решение системы линейных уравнений с двумя неизвестными для указанного случая сводится к нахождению на координатной плоскости общих точек двух прямых линий. А две прямые на плоскости могут:

1) пересекаться, т. е. иметь единственную общую точку;

2) быть параллельными, т. е. не иметь общих точек;

3) совпадать, т. е. иметь бесконечно много общих точек.

Значит, система двух линейных уравнений с двумя неизвестными может либо иметь единственное решение, либо вообще не иметь решения, либо иметь бесконечное множество решений.

При решении систем применяют метод подстановки, метод сложения и метод введения новых переменных.

Покажем на конкретном примере, как применяется метод подстановки.

Теперь приведём пример, где применяется метод сложения.

Метод введения новых переменных позволяет упростить вид системы.

Покажем на конкретном примере, как применяется метод введения новых переменных.

Мы рассмотрели системы двух уравнений с двумя неизвестными, теперь рассмотрим систему из трёх уравнений с тремя неизвестными.

С помощью способа сложения сводим систему трёх уравнений с тремя неизвестными к системе двух уравнений с двумя неизвестными. Покажем это на примере.

При решении задач могут получаться системы уравнений с большим количеством неизвестных, их решение осуществляется аналогичным образом.

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений
с двумя неизвестными.

Например, система уравнений может быть задана следующим образом.

Чтобы решить систему уравнений, нужно найти и «x», и «y».

Как решить систему уравнений

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки
или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно
решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений,
всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

Выразим из первого уравнения «x + 5y = 7»
неизвестное «x».

Перенесём в первом уравнении «x + 5 y = 7» всё что
содержит «x» в левую часть,
а остальное в правую часть по
правилу переносу.

При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение
на число не требуется.

Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.

	x = 7 − 5y
3(7 − 5y) − 2y = 4

Подставив вместо «x» выражение «(7 − 5y)»
во второе уравнение,
мы получили обычное линейное уравнение с одним неизвестным «y».
Решим его по правилам
решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение
«3(7 − 5y) − 2y = 4» отдельно.
Вынесем его решение отдельно с помощью
обозначения звездочка (*).

	x = 7 − 5y
3(7 − 5y) − 2y = 4  (*)

(*)   3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
                 − 17y = − 17     | :(−17)
y = 1

Мы нашли, что «y = 1».
Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения.
Вернемся к нашей системе уравнений еще раз.

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

	x + 5y = 7		(x + 5y) + (3x − 2y) = 7 + 4
	+          =>	x + 5y + 3x − 2y = 11
3x − 2y = 4		4x + 3y = 11

При сложении уравнений мы получили уравнение «4x + 3y = 11».
По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

Чтобы при сложении неизвестное «x» взаимноуничтожилось,
нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент
«−3».

Для этого умножим первое уравнение на «−3».

	x + 5y = 7 | ·(−3)
3x − 2y = 4

	x ·(−3) + 5y · (−3) = 7 · (−3)
3x − 2y = 4

	−3x −15y = −21
3x − 2y = 4

Теперь сложим уравнения.

	−3x −15y = −21		(−3x −15y ) + (3x − 2y) = −21 + 4
	+          =>	−3x −15y + 3x − 2y = −21 + 4
3x − 2y = 4		−17y = −17 |:(−17)
		y = 1

Мы нашли «y = 1».
Вернемся к первому уравнению и подставим вместо «y» полученное числовое
значение и найдем «x».

Ответ: x = 2; y = 1

Пример решения системы уравнения
способом подстановки

Выразим из первого уравнения «x».

Подставим вместо «x» во второе уравнение полученное выражение.

	x = 17 + 3y
(17 + 3y) − 2y = −13 (*)

(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
17 + y = −13
y = −13 − 17
y = −30

Подставим в первое уравнение полученное числовое значение «y = −30» и
найдем «x».

	x = 17 + 3 · (−30)
y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения
способом сложения

Рассмотрим систему уравнений.

	3(x − y) + 5x = 2(3x − 2)
4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

	3x − 3y + 5x = 6x − 4
4x − 2x − 2y = 4 − 3y

	8x − 3y = 6x − 4
2x −2y = 4 − 3y

	8x − 3y − 6x = −4
2x −2y + 3y = 4

Мы видим, что в обоих уравнениях есть «2x».
Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в
полученном уравнении осталось только «y».

Для этого достаточно умножить первое уравнение на «−1».

	2x − 3y = −4      |·(−1)
2x + y = 4

	2x · (−1) − 3y · (−1) = −4 · (−1)
2x + y = 4

Теперь при сложении уравнений у нас останется только «y» в уравнении.

	−2x + 3y = 4		(−2x + 3y ) + (2x + y) = 4 + 4
	+          =>	−2x + 3y + 2x + y = 4 + 4
2x + y = 4		4y = 8         | :4
		y = 2

Подставим в первое уравнение полученное числовое значение «y = 2» и
найдем «x».

Ответ: x = 1; y = 2

---

Ваши комментарии

Оставить комментарий:

---