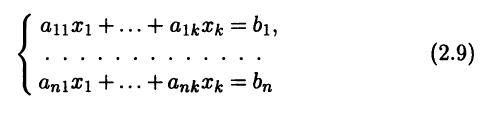Как составить систему уравнений определяющую линейную оболочку

Способы описания подпространств линейного пространства

Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.

Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству . Чтобы установить изоморфизм , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства .

Первый (внутренний) способ. Пусть в пространстве заданы столбцы . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.

Рассматривая линейную оболочку столбцов как линейное подпространство , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства .

Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:

1) составить из данных столбцов матрицу размеров ;

2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;

3) определить размерность и базис подпространства

– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,

– столбцы матрицы , содержащие единичные элементы (в начале каждой «ступеньки»), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.

Таким образом, если подпространство задано своими образующими , то его размерность равна рангу системы столбцов , т.е. , а базисом служит максимальная линейно независимая подсистема образующих.

Второй (внешний) способ. Пусть подпространство задано как множество решений однородной системы уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств , где — множество решений i-го уравнения системы . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства , а базисом служит фундаментальная система решений однородной системы . Способы нахождения фундаментальной системы решений рассмотрены ранее.

Переход от одного способа описания подпространств к другому

Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов . Требуется составить такую однородную систему уравнений, множество решений которой совпадает с , т.е. . Для этого нужно выполнить следующие действия.

1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.

2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .

3. Из последних строк матрицы составить матрицу .

4. Записать искомую систему уравнений .

Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа , чтобы выполнялось равенство . Другими словами, при каких неоднородная система ( уравнений с неизвестными ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.

Пример 8.8. Подпространство задано линейной оболочкой столбцов . Составить систему уравнений, определяющую подпространство .

Решение. 1. Составляем матрицу и блочную матрицу:

2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):

Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу

3. Из последних строк матрицы составляем матрицу искомой системы.

4. Записываем систему уравнений Заданные в условии примера столбцы являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .

Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: . Требуется найти размерность и базис этого подпространства, т.е. представить его в виде линейной оболочки . Для этого нужно выполнить следующие действия.

1. Найти фундаментальную систему решений однородной системы . Искомая размерность .

2. Представить заданное пространство как линейную оболочку .

Первый пункт алгоритма удобно выполнять следующим образом:

– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;

– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу к виду , где — простейший вид матрицы ;

– из последних столбцов матрицы составить фундаментальную матрицу .

Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.

Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.

Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений

Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6

Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .

2. Столбцы являются искомым базисом, так как они линейно независимы и .

Источник

Способы описания подпространств линейного пространства

Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:

1) составить из данных столбцов матрицу размеров ;

2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;

3) определить размерность и базис подпространства

– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,

– столбцы матрицы , содержащие единичные элементы (в начале каждой “ступеньки”), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.

Переход от одного способа описания подпространств к другому

3. Из последних строк матрицы составить матрицу .

4. Записать искомую систему уравнений .

Решение. 1. Составляем матрицу и блочную матрицу:

3. Из последних строк матрицы составляем матрицу искомой системы.

1. Найти фундаментальную систему решений однородной системы . Искомая размерность .

2. Представить заданное пространство как линейную оболочку .

Первый пункт алгоритма удобно выполнять следующим образом:

– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;

– из последних столбцов матрицы составить фундаментальную матрицу .

Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.

Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений

Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6

Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .

2. Столбцы являются искомым базисом, так как они линейно независимы и .

Учебное пособие: Методические указания для студентов 1 курса Одесса 2008

Одесский национальный университет им. И. И. Мечникова

Институт математики, экономики и механики

( решение типовых задач)

Методические указания для студентов 1 курса

Составители: д-р ф-м н., проф. Варбанец П.Д.,

к-т ф-м н., доц. Савастру О.В.

Рецензенты: д-р ф-м н., проф. Евтухов В.М.,

к-т ф-м н., доц. Белозеров Г.С.

Рекомендовано к печати

Ученым советом ИМЭМ Одесского национального университета им. И. И. Мечникова

протокол № 1 от 5 февраля 2008 г.

1. Линейные пространства …………………………………. 5

1.1. Линейные пространства и подпространства………….5

1.2. Базис пространства, его размерность…………………6

1.3. Координаты вектора в данном базисе…………….…11

1.4. Сумма и пересечение подпространств………………12

2. Евклидовы и унитарные пространства ………….…. 17

2.1. Процесс ортогонализации Шмидта………………….17

2.3. Ортогональная проекция и перпендикуляр на подпространство……………………………………………………..20

3. Операторы в линейных пространствах……………. 23

3.1. Образ, ядро линейного оператора……………………28

3.2. Матрица линейного оператора в данных базисах…..29

3.3. Собственные векторы и собственные значения..…. 31

3.4. Канонический корневой базис и жорданова нормальная форма…………………………………………………….34

4. Операторы в евклидовых и унитарных пространствах..40

5. Приведение двух квадратичных форм к каноническому виду…………………………………………………………. 45

Линейные пространства и линейные операторы представляют собой начало абстрактной части математики, с которой студенту в дальнейшем неоднократно придется иметь дело.

Эти методические указания по самостоятельной работе студентов предполагают использование следующего задачника:

И.В.Проскуряков. Сборник задач по линейной алгебре. М., Наука, 1974.

В дальнейшем мы будем придерживаться следующих обозначений (если в тексте нет специальной оговорки):

¾ – произвольные пространства над некоторым полем ;

¾ – пространство – мерных строк (столбцов) с элементами из поля над полем (арифметическое пространство).

¾ – действительное – мерное арифметическое пространство;

¾ – комплексное – мерное арифметическое пространство;

¾ – пространства геометрических векторов (прямой, плоскости, пространства);

¾ – евклидовы пространства (с указанием размерности или без него);

¾ – подпространства данного пространства (- индекс, не связанный с размерностью);

¾ векторы рассматриваемого пространства; – нулевой вектор;

¾ скаляры из данного поля, – нуль этого поля;

¾ линейные операторы, в отдельных случаях – матрицы;

¾ матрицы линейных операторов в базисах соответственно ;

¾ размерности пространств ;

¾ ранги операторов (матриц) ;

¾ скалярное произведение в данном пространстве;

¾ векторное произведение в данном пространстве .

Основными типами задач этого параграфа являются следующие:

А) выяснение вопроса, будет ли данное множество с указанными операциями линейным пространством, подпространством;

В) выделение базиса пространства, определение его размерности;

С) вычисление координат вектора в данном базисе;

D) нахождение суммы, пересечения подпространств, их размерностей и базисов.

1.1. Линейные пространства и подпространства.

Для решения задач первой группы необходимо знание аксиом линейного пространства (вообще, не следует приниматься за решение задач любого раздела, не ознакомившись предварительно с основными понятиями и теоремами данного раздела). Заметим, что в группе аксиом линейного пространства содержатся требования неограниченной применимости, однозначности и замкнутости линейных операций, которые не выделены под отдельными номерами. Распространенная ошибка: забывают проверить выполнение этих условий.

В тех условиях, когда данное множество состоит из векторов некоторого известного пространства, полезной является следующая теорема (критерий подпространства):

Теорема. Подмножество векторов пространства над полем является подпространством тогда и только тогда, когда

1. замкнуто относительно сложения, т.е. ,

2. замкнуто относительно умножения векторов на любые скаляры из основного поля : .

Некоторые из задач требуют хорошего знания других разделов курса (элементарной теории матриц, квадратичных форм, систем линейных уравнений). Ниже мы подробнее остановимся на одной из этих задач.

1.2. Базис пространства, его размерность.

Построение базиса пространства, подпространства несколько упрощается, если мы располагаем некоторыми представлениями о размерности пространства, подпространства. Одним из наводящих соображений здесь может быть следующее. Подмножество векторов пространства выделяется из с помощью дополнительных условий, накладываемых на векторы. При этом, чем больше таких условий, тем меньшей, вообще говоря, будет размерность подпространства . Если , а выделено с помощью условий специального вида, то есть основания ожидать, что .

Задача 1.1. (№1297[4]) Доказать, что множество п -мерных векторов, у которых первая и последняя координаты равны между собой, образует линейное подпространство пространства .

Решение. Множество образует линейное подпространство пространства , так как удовлетворяет критерию подпространства. Действительно, выделяется из с помощью одного условия , поэтому

Кроме того, нетрудно показать, что . Для этого рассмотрим векторы стандартного базиса . Векторы не принадлежат . Но построение базиса подпространства в ряде случаев удобно выполнить, исходя из стандартного базиса самого пространства, изменяя его векторы так, чтобы они «попали» в подпространство. Поэтому преобразуем векторы так, чтобы у них первая и последняя координаты были равны. Например, пусть . Рассмотрим систему векторов . Она образует базис , так как нетрудно проверить, что она является линейно независимой и каждый вектор из подпространства линейно выражается через вектора этой системы. А так как количество векторов системы равно , то и . Итак, наше предположение оказалось верным.

Линейные подпространства, размерности которых на 1 меньше размерности самого пространства называются гиперплоскостями .

В следующей задаче условий больше.

Задача 1.2. (№1298[4]) Доказать, что множество п -мерных векторов, у которых координаты с четными номерами равны нулю, образует линейное подпространство пространства .

Решение. Для доказательства того, что является подпространством, нужно также воспользоваться критерием подпространства. Так как поэтому следует ожидать, что , где – наибольшее четное число, не превышающее (, если – четное, и , если – нечетное). Базисом является подсистема стандартного базиса пространства , содержащая векторы только с нечетными номерами.

Задача 1.3. Проверить, является ли множество многочленов степени 3 с вещественными коэффициентами подпространством пространства многочленов степени ().

Решение. Воспользуемся критерием подпространства. Проверим условие .

Пусть , тогда

так как степень суммы этих двух многочленов равна двум. Итак, множество не является подпространством.

Задача 1.4. (№№1291, 1308[4]) Найти какой-нибудь базис и размерность линейного подпространства пространства , если составляют все векторы из , у которых сумма координат .

Решение. Очевидно векторы стандартного базиса

(1 на – ой позиции ) множеству не принадлежат ни при каком . Однако, замена на векторах последнего нуля числом (-1) дает нам векторы из . Таким образом мы получаем систему векторов

из , которая линейно независима (почему?) и обязана быть базисом , ибо из условия задачи явно следует, что из и, следовательно, .

Попутно решен вопрос (и подтвердилась гипотеза) о размерности ( выделено из одним условием).

Задача 1.4. (№1306[4]) Пусть – неотрицательная квадратичная форма от неизвестных ранга . Доказать, что все решения уравнения =0 образуют мерное линейное подпространство пространства .

Поиск решения. Вспоминаем основные понятия теории квадратичных форм (матрица формы, ранг формы, определение формы). Очевидно, что более подробные записи данного уравнения в виде

, никак не указывают на способ решения задачи.

В процессе дальнейших размышлений начинаем понимать, что мы должны исходить из неотрицательной определенности формы . Нормальный вид такой формы

(1)

а множество решений уравнения =0 в этом случае состоит из векторов вида

, (2)

Где – произвольные числа из . Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть ()-мерное подпространство пространства . Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга невырожденным линейным преобразованием приводится к виду (1). Создается план решения: преобразовать форму к виду (1) , найти решения (2) уравнения =0 для преобразованной формы, а затем с помощью обратного преобразования построить решения уравнения =0 для данной формы .

Решение. По теореме о приведении квадратичной формы к нормальному виду существует невырожденное линейное преобразование

, приводящее форму к виду

Множество решений уравнения состоит из векторов где , то есть из векторов

Обозначим (1 на – ой позиции) и докажем, что множество решений уравнения =0 есть линейная оболочка системы векторов

Пусть . Тогда

Очевидно и другое:

Кроме того, система линейно независима (проверяется непосредственно). Составляем линейную комбинацию . Получаем . Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица является невырожденной.

Отсюда . Тем самым мы показали, что система является линейно независимой. Следовательно, – линейное пространство (по построению) и его размерность

1.3. Координаты вектора в данном базисе.

Решение вопроса о ранге системы векторов, заданных координатами в некотором базисе, выделение из системы ее максимальной линейно независимой подсистемы, выражение остальных векторов в виде линейных комбинаций векторов этой подсистемы сводится к решению этих же задач для системы строк (столбцов) координатной матрицы, которые подробно обсуждались в соответствующем параграфе первой части.

1.4.Сумма и пересечение подпространств.

Пусть – данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств и . находится по формуле

. (3)

Несколько сложнее обстоит дело с поиском базиса пересечения . В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй – с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).

Задача 1.6. Найти базис суммы и пересечения подпространств, натянутых на системы векторов

Решение. Обозначим , . Будем считать, что координаты векторов заданы в единичном базисе .

1 способ. Как известно, базисом суммы служит любая база системы векторов , . Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.

Итак, . Базис составляют .

. Базис составляют .

Базис составляют . По формуле (3) получаем . Базис пересечения будем искать из условия . Значит, представим в виде и . Приравниваем правые части . Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда будет образовывать базис пересечения.

Решив систему, строим ФСР.

Вектор образует базис .

2 способ. 1) Составим таблицу Штифеля для объединенной системы векторов , и перебрасываем наверх сначала векторы , пока это возможно (квадратиками выделены разрешающие элементы). Векторы , переходящие налево, не пишем и их координаты не вычисляем.

[spoiler title=”источники:”]

http://www.bestreferat.ru/referat-405168.html

[/spoiler]

Название: Методические указания для студентов 1 курса Одесса 2008
Раздел: Остальные рефераты
Тип: учебное пособие Добавлен 17:40:19 17 сентября 2011 Похожие работы
Просмотров: 2273 Комментариев: 8 Оценило: 1 человек Средний балл: 2 Оценка: неизвестно Скачать

Источник

Пусть L – n-мерное линейное пространство, в котором фиксирован некоторый базис е = (e₁ … е_n) и выбраны векторы a₁, …, a_k, b. Запишем разложение выбранных векторов по базису е:

a_j = ea_j, j = 1,k, b = eb,

где a_j = (a_1j … a_nj)^T , j = 1,k, b = (b₁ … b_n)^T – столбцы координат соответствующих векторов
. Пусть А – матрица типа n × k, составленная из координатных столбцов векторов a₁, …, а_k, а (A|b) – матрица, полученная из матрицы А добавлением справа еще одного столбца b.

Для вектора b возможны два случая:

1) вектор b принадлежит линейной оболочке span{a₁,…, a_k};

2) вектор b не принадлежит span{a₁,…,a_k}.

В первом случае добавление к системе векторов a₁, …, a_k вектора b не приводит к расширению линейной оболочки системы и, следовательно,

dimspan{a₁,… ,а_k} = dimspan{a₁,… ,а_k,b}.

По теореме 2.6 заключаем, что RgA = Rg(A|b).

Во втором случае, наоборот, добавление вектора b к системе векторов a₁, …, а_k приводит к расширению линейной оболочки, причем по теореме 2.5

dimspan{a₁,… ,а_k,b} = dimspan{a₁,… ,а_k} + 1,

так как

span{a₁,…, a_k, b} = span{a₁,…, a_k} ⊕ span{b}.

Следовательно, Rg(A|b) = RgA + 1.

Выясним теперь, что означают эти два случая “на координатном уровне”. В первом случае условие b ∈ span{a₁,… ,a_k} означает существование разложения

х₁а₁ +… + x_ka_k = b (2.8)

с некоторыми действительными коэффициентами x₁, …, x_k.
Записывая это векторное равенство в координатной форме, получаем систему линейных алгебраических уравнений (СЛАУ)

относительно переменных х = (х₁ … x_k)^T, которая в матричной форме имеет вид Ах = b. Существование разложения (2.8) означает, что полученная система имеет решение. Во втором случае представление (2.8) невозможно, т.е. система (2.9) не имеет решений.

Итак, следующие четыре утверждения эквивалентны между собой:

– b ∈ span{a₁,…,a_k};

– dimspan{a₁,… ,а_k,b} = dimspan{a₁,…,а_k};

– Rg(A|b) = RgA;

– система Ах = b из n линейных алгебраических уравнений относительно k неизвестных совместна.

Эквивалентность последних двух утверждений составляет содержание теоремы Кронекера – Капелли [III], которая верна для произвольных СЛАУ. Отметим, что любая система из п ли-нейных алгебраических уравнений относительно к неизвестных может быть получена как результат проведенных рассуждений. Для этого достаточно в качестве векторов a₁, …, a_k рассмотреть столбцы коэффициентов при неизвестных, а в качестве вектора b – столбец свободных членов. Все эти столбцы могут рассматриваться как n-мерные векторы в линейном арифметическом пространстве Rⁿ.

Таким образом, теорему Кронекера – Капелли можно переформулировать следующим образом: для того чтобы линейная оболочка системы векторов a₁, …, а_k совпадала с линейной оболочкой расширенной системы a₁, …, а_k, b, необходимо и достаточно, чтобы были равны размерности этих линейных оболочек.

Предположим, что квадратная СЛАУ Ах = b имеет решение при любом столбце b правых частей. Рассматривая столбцы матрицы А и столбец b как элементы a₁, …, a_n, b n-мерного линейного арифметического пространства и записывая СЛАУ в векторной форме

x₁a₁ + x₂a₂ + … + x_na_n = b,

заключаем, что линейная оболочка системы векторов a₁, …, а_n совпадает со всем линейным пространством Rⁿ. Из этого следует, что ранг этой системы векторов равен размерности линейного пространства n, а так как в системе ровно n векторов, то она, согласно теореме 2.6, линейно независима. Другими словами, столбцы матрицы А линейно независимы, а матрица А является невырожденной (см. теорему о базисном миноре [III]).

Таким образом, если квадратная СЛАУ Ах = b имеет решение при любой правой части, то матрица А системы невырождег на, а решение системы при любой правой части единственно.

Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ

Источник

Вообщем надо составить систему уравнений, определяющую линейную оболочку данной системы векторов
(4;4;8;12),(1;2;3;4),(5;1;6;11),(8;5;13;21)
Я нашел теорию, который полностью отвечает на поставленный вопрос(ну так авторам кажется, мне нет.)
Во общем привел к ступенчатому виду. Ранг получился 2.

Потом выдали это:
Матрица

1	-1	1	-1	1
0	2	-1	1	2

Поэтому произвольный вектор x₂ <v1; v2> имеет вид x = a₁v₁ + a₂v₂. Пусть (x₁; x₂; x₃; x₄; x₅)
— его координаты в стандартном базисе; тогда, приравнивая соответствующие координаты,
имеем:

x₁ = a₁ + a₂; x₂ = a₂ – a₁; x₃ = a₁; x₄= – a₁; x₅ =a₁ + 3a₂;

Теперь, исключая неизвестные a₁ и a₂, получаем искомую линейную систему на координаты
произвольного вектора x из <v₁; v₂>:

x₁ = 2x₃ + x₂
x₄ = -x₃
x₅ = x₃ + 3x₂ + 3x₃

————-
Вопрос:
Откуда мы получили Имеем?
PDF книга , 14 Пример.
Там еще два способа, но их я трогать не хочу, вроде этот как то ближе.

Источник

Способы описания подпространств линейного пространства

Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству $mathbb{R}^n$ . Чтобы установить изоморфизм $Vleftrightarrow mathbb{R}^n$ , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства $mathbb{R}^n$ .

Первый (внутренний) способ. Пусть в пространстве $mathbb{R}^n$ заданы столбцы a_1,a_2,ldots,a_k . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.

Рассматривая линейную оболочку $L=operatorname{Lin}(a_1,a_2,ldots,a_k)$ столбцов как линейное подпространство $mathbb{R}^n$ , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства $dim{L}=operatorname{rg} (a_1,a_2,ldots,a_k)$ .

Поэтому для нахождения размерности и базиса подпространства $L=operatorname{Lin} (a_1,a_2,ldots,a_k)$ нужно выполнить следующие действия:

1) составить из данных столбцов матрицу $A=begin{pmatrix} a_1&cdots&a_k end{pmatrix}$ размеров ntimes k ;

2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;

3) определить размерность и базис подпространства $L=operatorname{Lin} (a_1,a_2,ldots,a_k):$

– количество ненулевых строк в матрице равняется размерности подпространства, т.е. $dim{L}= operatorname{rg}A= operatorname{rg}(a_1,a_2,ldots,a_k)= operatorname{rg}A'$ ,

Таким образом, если подпространство $Ltriangleleft mathbb{R}^n$ задано своими образующими a_1,a_2,ldots,a_k: $L=operatorname{Lin} (a_1,a_2,ldots,a_k)$ , то его размерность равна рангу системы столбцов , т.е. $dim{L}= operatorname{Lin} (a_1,a_2,ldots,a_k)$ , а базисом служит максимальная линейно независимая подсистема образующих.

Второй (внешний) способ. Пусть подпространство $Ltriangleleft mathbb{R}^n$ задано как множество L={Ax=o} решений однородной системы Ax=o уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств $textstyle{L_1capldotscap L_m=bigcuplimits_{i=1}^{m}L_i}$ , где L_i — множество решений i-го уравнения системы (i=1,ldots,m) . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства dim{L}=n-operatorname{rg}A , а базисом служит фундаментальная система решений однородной системы Ax=o . Способы нахождения фундаментальной системы решений рассмотрены ранее.

Переход от одного способа описания подпространств к другому

Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов $a_1,a_2,ldots,a_{k}:$ $L=operatorname{Lin} (a_1,a_2,ldots,a_{k})$ . Требуется составить такую однородную систему Psi x=o уравнений, множество решений которой совпадает с , т.е. L={Psi x=o} . Для этого нужно выполнить следующие действия.

1. Из данных столбцов составить матрицу $A=begin{pmatrix}a_1&cdots&a_k end{pmatrix}$ размеров ntimes k , а затем блочную матрицу (Amid E) , приписав к матрице единичную матрицу n-го порядка.

2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу (Amid E) к виду (Lambdamid S) , где Lambda — простейший вид матрицы $Lambda=begin{pmatrix} E_r!!&vline!!&O\hline O!!&vline!!&O end{pmatrix}$ .

3. Из последних (n-r) строк матрицы составить матрицу $Psi=(Omid E_{n-r})S$ .

4. Записать искомую систему уравнений Psi x=o .

Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид x=beta_1a_1+ldots+ beta_ka_k . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа beta_1,ldots,beta_k , чтобы выполнялось равенство x=beta_1a_1+ldots+beta_ka_k . Другими словами, при каких неоднородная система Abeta=x ( уравнений с неизвестными $beta=begin{pmatrix} beta_1&cdots&beta_k end{pmatrix}^T$ ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство Psi x=o . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.

Пример 8.8. Подпространство $Ltriangleleft mathbb{R}^n$ задано линейной оболочкой столбцов $a_1=begin{pmatrix}1&1&1&1end{pmatrix}^T,$ $a_2=begin{pmatrix}1&2&1&3end{pmatrix}^T,$ $a_3=begin{pmatrix} 3&4&3&5 end{pmatrix}^T$ . Составить систему уравнений, определяющую подпространство .

Решение. 1. Составляем матрицу $A=begin{pmatrix} a_1&a_2&a_3 end{pmatrix}$ и блочную матрицу:

$(Amid E_4)= begin{pmatrix}1&1&3!!&vline!!&1&0&0&0\ 1&2&4!!&vline!!&0&1&0&0\ 1&1&3!!&vline!!&0&0&1&0\ 1&3&5!!&vline!!&0&0&0&1 end{pmatrix}!.$

$(Amid E_4)sim begin{pmatrix}1&1&3!!&vline!!&1&0&0&0\ 0&1&1!!&vline!!&-1&1&0&0\ 0&0&0!!&vline!!&-1&0&1&0\ 0&2&2!!&vline!!&-1&0&0&1 end{pmatrix}sim begin{pmatrix}1&1&3!!&vline!!&1&0&0&0\ 0&1&1!!&vline!!&-1&1&0&0\ 0&0&0!!& vline!!&-1&0&1&0\ 0&0&0!!&vline!!&1&-2&0&1 end{pmatrix}!.$

$Asim begin{pmatrix}1&1&3\ 0&1&1\ 0&0&0\ 0&0&0 end{pmatrix}sim begin{pmatrix}1&0!!&vline!!&0\ 0&1!!&vline!!&0\hline 0&0!!&vline!!&0\ 0&0!!& vline!!&0 end{pmatrix}= Lambda;quad S=begin{pmatrix}1&0&0&0\ -1&1&0&0\ -1&0&1&0\ 1&-2&0&1 end{pmatrix}!;quad r=operatorname{rg}A=2.$

3. Из последних n-r=4-2=2 строк матрицы составляем матрицу $Psi=begin{pmatrix}-1&0&1&0\ 1&-2&0&1 end{pmatrix}$ искомой системы.

4. Записываем систему уравнений $Psi x=ocolon begin{cases}-x_1+x_3=0,\ x_1-2x_2+x_4=0.end{cases}$ Заданные в условии примера столбцы a_1,,a_2,,a_3 являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .

Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: L={Ax=o} . Требуется найти размерность и базис varphi_1,ldots,varphi_k этого подпространства, т.е. представить его в виде линейной оболочки $L=operatorname{Lin}(varphi_1,ldots,varphi_k)$ . Для этого нужно выполнить следующие действия.

1. Найти фундаментальную систему $varphi_1,ldots,varphi_{n-r}$ решений однородной системы Ax=o (r=operatorname{rg}A) . Искомая размерность k=n-r .

2. Представить заданное пространство как линейную оболочку $L=operatorname{Lin} (varphi_1,ldots,varphi_{n-r})$ .

Первый пункт алгоритма удобно выполнять следующим образом:

– составить блочную матрицу $begin{pmatrix}dfrac{A}{E}end{pmatrix}$ , приписав к матрице единичную матрицу n-го порядка;

– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу $begin{pmatrix}dfrac{A}{E}end{pmatrix}$ к виду $begin{pmatrix}dfrac{Lambda}{T}end{pmatrix}$ , где Lambda — простейший вид матрицы $Acolon, Lambda=begin{pmatrix}E_r!!&vline!!&O\hline O!!& vline!!&Oend{pmatrix}$ ;

– из последних (n-r) столбцов матрицы составить фундаментальную матрицу $Phi=Tcdot! begin{pmatrix}dfrac{O}{E_{n-r}}end{pmatrix}$ .

Столбцы фундаментальной матрицы $Phi=begin{pmatrix} varphi_1&cdots& varphi_{n-r} end{pmatrix}$ составляют искомую фундаментальную систему решений.

Пример 8.9. Найти размерность и базис подпространства $Ltriangleleft mathbb{R}^4$ , заданного системой уравнений

$begin{cases} x_1+x_2+2x_3+x_4=0,\[2pt] 2x_1+3x_2+x_4=0,\[2pt] 3x_1+4x_2+2x_3+2x_4=0. end{cases}$

Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6 (m=3,,n=4,,r=operatorname{rg}A=2)colon

$Phi=begin{pmatrix}varphi_1&varphi_2 end{pmatrix}= begin{pmatrix} -6&-2\ 4&1\ 1&0\ 0&1end{pmatrix}!.$

Ее столбцы varphi_1,,varphi_2 образуют фундаментальную систему решений. Размерность подпространства равна k=n-r=2 , dim{L}=2 .

2. Столбцы varphi_1,,varphi_2 являются искомым базисом, так как они линейно независимы (operatorname{rg}Phi=2) и $L=operatorname{Lin} (varphi_1, varphi_2)$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Способы описания подпространств линейного пространства

Переход от одного способа описания подпространств к другому

Способы описания подпространств линейного пространства

Переход от одного способа описания подпространств к другому

Учебное пособие: Методические указания для студентов 1 курса Одесса 2008

Линейные операции над векторами

Базис. Cкалярное произведение

Векторное и смешанное произведения векторов

Декартова система координат. прямая на плоскости

Плоскость в пространстве

Прямая в пространстве

Кривые второго порядка — I

Кривые второго порядка — II

Поверхности второго порядка

Матрицы и операции с ними

Обратная матрица

Ранг матрицы

Системы линейных алгебраических уравнений

Свойства решений однородных и неоднородных СЛАУ

Способы описания подпространств линейного пространства

Переход от одного способа описания подпространств к другому

Вам также может понравиться

Как найти зону в майнкрафт

Как найти мью в физике формулы

Код ошибки 80246005 при обновлении windows 7 как исправить

Добавить комментарий Отменить ответ