Решение системы линейных уравнений графическим способом
ВИДЕО С ТЕОРИЕЙ:
Видео YouTube
ВИДЕО С РАЗБОРОМ ЗАДАНИЙ:
Видео YouTube
Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться, такую группу уравнений мы называем системой.
Объединяем уравнения в систему с помощью фигурной скобки:
Графический метод
Недаром ответ записывается так же, как координаты какой-нибудь точки.
Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.
Например, построим графики уравнений из предыдущего примера.
Пример 1
Для этого сперва выразим yyy в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно xxx):
⎧
⎪⎪⎪
⎪
Для того чтобы графически решить систему уравнений с двумя переменными нужно:
1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);
Разберем это задание на примере.
Решить графически систему линейных уравнений.
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Пример 2
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:
а) иметь единственное решение;
б) не иметь решений;
в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Пример 3
Графическое решение системы 
Пример 4
Решить графическим способом систему уравнений.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Ответ: (4; 5).
Пример 5
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
Ответ: (-2; 5).
ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.
Видео YouTube
ДОМАШНЯЯ РАБОТА: ВЫПОЛНЯТЬ ВСЕ ШАГИ ПОСТРОЕНИЯ, КАК ПОКАЗАНО В ВИДЕО РАЗБОРАХ И ПРИМЕРАХ. В УЧЕБНИКЕ ТЕОРИЯ НА СТРАНИЦАХ СТР 195-199. ВСЕ ИЗУЧИТЬ, ТЕМА ОЧЕНЬ ВАЖНАЯ.
Как составить систему уравнений с двумя переменными по графику
Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться , такую группу уравнений мы называем системой.
Объединяем уравнения в систему с помощью фигурной скобки:
Графический метод
Недаром ответ записывается так же, как координаты какой-нибудь точки.
Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.
Например, построим графики уравнений из предыдущего примера.
Пример 1
Для этого сперва выразим y y y в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно x x x ):
Для того чтобы графически решить систему уравнений с двумя переменными нужно:
1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);
Разберем это задание на примере.
Решить графически систему линейных уравнений.
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Пример 2
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:
а) иметь единственное решение;
б) не иметь решений;
в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Пример 3
Графическое решение системы
Пример 4
Решить графическим способом систему уравнений.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Пример 5
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.
Видео YouTube
Системы уравнений с двумя переменными
п.1. Понятие системы уравнений с двумя переменными и её решения
п.2. Графический метод решения системы уравнений с двумя переменными
Поскольку каждое из уравнений с двумя переменными можно изобразить в виде графика на плоскости, графический метод решения систем таких уравнений достаточно удобен.
п.3. Примеры
Пример 1. Решите графическим способом систему уравнений:
а) ( left< begin < l >mathrm & \ mathrm <4x+3y=0>& endright. )
( mathrm ) – окружность с центром в начале координат
( mathrm <4x+3y=0>) – прямая ( mathrm )
Система имеет два решения (–3; 4) и (3; –4)
Ответ: <(–3; 4) ; (3; –4)>.
б) ( left< begin < l >mathrm & \ mathrm & endright. )
( mathrm ) – гипербола ( mathrm )
y – x = 4 – прямая y = x + 4
Система имеет два решения (–5; –1) и (1; 5)
Ответ: <(–5; –1) ; (1; 5)>.
в) ( left< begin < l >mathrm & \ mathrm & endright. )
x 2 + y = 1 – парабола y = –x 2 + 1
x 2 – y = 7 – парабола y = x 2 – 7
Система имеет два решения (–2; –3) и (2; –3)
Ответ: <(–2; –3) ; (2; –3)>.
г) ( left< begin < l >mathrm & \ mathrm & endright. )
xy = 1 – гипербола ( mathrm )
x 2 + y 2 = 2 – окружность с центром в начале координат, радиусом ( mathrm<sqrt<2>> )
Система имеет два решения (–1; –1) и (1; 1)
Ответ: <(–1; –1) ; (1; 1)>.
Пример 2*. Решите графическим способом систему уравнений
a) ( left< begin < l >mathrm & \ mathrm <frac1x-y=1>& endright. )
x 3 – y = 1 – кубическая парабола y = x 3 – 1, смещённая на 1 вниз.
( mathrm <frac1x-y=1>) – гипербола ( mathrm ), смещённая на 1 вниз
Система имеет два решения (–1; –2) и (1; 0)
Ответ: <(–1; –2) ; (1; 0)>.
б) ( left< begin < l >mathrm <|x|+|y|=2>& \ mathrm & endright. )
|x| + |y| = 2 – квадрат с диагоналями 4, лежащими на осях
x 2 + y 2 = 4 – окружность с центром в начале координат, радиусом 2
Система имеет четыре решения (2; 0), (0; 2) , (–2; 0) и (0; –2)
Ответ: <(2; 0) ; (0; 2) ; (–2; 0) ; (0; –2)>.
в) ( left< begin < l >mathrm & \ mathrm & endright. )
y – x 2 = 4x + 6 – парабола y = (x 2 + 4x + 4) + 2 = (x + 2) 2 + 2, ветками вверх, смещённая на 2 влево и на 2 вверх
y + |x| = 6 – ломаная, y = –|x| + 6. Для x > 0, y = –x + 6, для x 0, y = x, для x
Графический метод решения системы уравнений
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы будем рассматривать решение систем двух уравнений с двумя переменными. Вначале рассмотрим графическое решение системы двух линейных уравнений, специфику совокупности их графиков. Далее решим несколько систем графическим методом.
[spoiler title=”источники:”]
http://reshator.com/sprav/algebra/9-klass/sistemy-uravnenij-s-dvumya-peremennymi/
http://interneturok.ru/lesson/algebra/9-klass/sistemy-uravneniy/graficheskiy-metod-resheniya-sistemy-uravneniy
[/spoiler]
Как записать систему уравнений по графику
Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться , такую группу уравнений мы называем системой.
Объединяем уравнения в систему с помощью фигурной скобки:
Графический метод
Недаром ответ записывается так же, как координаты какой-нибудь точки.
Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.
Например, построим графики уравнений из предыдущего примера.
Пример 1
Для этого сперва выразим y y y в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно x x x ):
Для того чтобы графически решить систему уравнений с двумя переменными нужно:
1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);
Разберем это задание на примере.
Решить графически систему линейных уравнений.
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Пример 2
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:
а) иметь единственное решение;
б) не иметь решений;
в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Пример 3
Графическое решение системы
Пример 4
Решить графическим способом систему уравнений.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Пример 5
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.
Видео YouTube
Алгоритм определения формулы линейной функции по графику
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Выполнила учительница математики МБОУ Башкирский лицей № 1 муниципального района Учалинский район Республики Башкортостан Хидиятова Залифа Даутовна
Алгоритм определения формулы линейной функции по графику»
На рисунке представлен график функции у = kx +b.
Записать формулу линейной функции, соответствующей данному графику.
1) Так как ордината точки пересечения графика функции с осью Оy равна 1, следовательно, b=1.
Значит, у = kx+ 1
2) Выбираем на графике произвольную точку, например, А (2;2) и определяем её координаты: если x = 2, то у = 2. Подставим в нашу формулу вместо Х и У и получим уравнение относительно k.
2 = 2k+1
2k=1
k = 0.5 Записываем формулу линейной функции: у = 0,5х + 1.
Написать ФОРМУЛУ линейной функции У= КХ+В, график которой изображен на рисунке :
Это ВПР задание 8) это ответ:
ВНИМАНИЕ : задание на сегодня 16 апреля
Внимание : вот эти следующие задания пока НЕ РЕШАТЬ.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 924 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 686 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 309 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 578 849 материалов в базе
Материал подходит для УМК
«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
16. Линейная функция и её график
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Другие материалы
- 16.09.2020
- 199
- 11
- 31.03.2020
- 1166
- 30
- 16.03.2020
- 227
- 1
- 16.03.2020
- 191
- 1
- 08.03.2020
- 282
- 6
- 20.02.2020
- 1246
- 71
- 21.01.2020
- 180
- 0
- 09.12.2019
- 418
- 13
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 30.09.2020 16028
- DOCX 549.2 кбайт
- 155 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 38659
- Всего материалов: 37
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Объявлен конкурс дизайн-проектов для школьных пространств
Время чтения: 2 минуты
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Профессия педагога на третьем месте по популярности среди абитуриентов
Время чтения: 1 минута
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Графический метод решения системы уравнений
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы будем рассматривать решение систем двух уравнений с двумя переменными. Вначале рассмотрим графическое решение системы двух линейных уравнений, специфику совокупности их графиков. Далее решим несколько систем графическим методом.
источники:
http://infourok.ru/algoritm-opredeleniya-formuly-linejnoj-funkcii-po-grafiku-4463697.html
http://interneturok.ru/lesson/algebra/9-klass/sistemy-uravneniy/graficheskiy-metod-resheniya-sistemy-uravneniy
Время чтения: 7 минут.
Сегодня мы разберем, что такое система уравнений и какие существуют методы ее решения: быстро, кратко, понятно🧠
То есть, по итогу решения системы у нас будет пара значений x и y, которые мы можем подставить в два уравнения и получить верное равенство.
Способы решения систем уравнения:
- Графический метод 📈
- Способ подстановки 📝
- Способ сложения ➕
Ниже разберем каждый метод подробнее.
1. Графический метод решения
Чтобы решить систему графически, нам нужно:
- Выразить из каждого уравнения переменную y;
- Построить таблицы значений для каждого уравнения (см. картинку ниже);
- Построить графики по полученным в таблице точкам;
- Найти точку пересечения графиков – это и будет решение
Таким образом, решением данного уравнения будет являться точка (3;2), то есть x=3, y=2.
Памятка для системы уравнений графическим методом
По коэффициентам при х сразу можно понять, будет ли система иметь решения.
2. Способ подстановки
Способ подстановки говорит сам за себя – что-то берем и подставляем вместо другого. Ниже представлен алгоритм действий👇
Давай рассмотрим решение на конкретном примере.
То есть, мы выразили y из первого уравнения, подставили его во второе и нашли значение х. После чего нашли значение y. Все просто!💁♀️
3. Способ сложения
Напоминаю для тех, кто забыл:
- коэффициенты – это числа перед x и y;
- x и y – это переменные.
Получается, наша задача – это избавиться от одной из переменных, чтобы дальше решать обыкновенное уравнение с одной переменной.
Звучит не очень то и сложно. Давай разберем на примере!
В примере мы умножили первое уравнение на -2, чтобы при х вместо 5 стал коэффициент -10.
А затем сложили первое и второе уравнение: -10x + 10x = 0. Вот мы и избавились от х😏Дальше решение очень напоминает предыдущий способ.
На этом все! Ниже будет несколько примеров для тренировки. Если хочешь закрепить полученные знания, то обязательно реши их.
Остались вопросы? Можешь написать о них в комментариях!
#образование #математика #ОГЭ #егэ #впр
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Системы линейных уравнений с двумя переменными
- Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными
Рассмотрим задачу:
Разность двух чисел равна 4, а их произведение 12. Найдите эти числа.
Решение:
Обозначим первое число буквой 
, а второе буквой 
. По условию задачи разность чисел равна 4, т.е. – = 4.
Так как произведение чисел равно 12, то = 12.
Мы составили два уравнения с двумя переменными. Чтобы ответить на вопрос задачи, надо найти такие значения переменных, которые обращают в верное равенство каждое из уравнений – = 4 и = 12, т.е. найти общие решения этих уравнений. В таких случаях говорят, что требуется решить систему уравнений.
Систему уравнений записывают с помощью фигурной скобки. Поэтому, составленную нами систему уравнений, можно записать так:
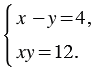
Пара значений переменных = 6, = 2 является решением каждого уравнения системы, т.к. оба равенства 6 – 2 = 4 и 6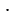
2 = 12 являются верными. Такую пару называют решением системы.
Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение в верное равенство.
Решить систему уравнений – это значит найти все ее решения или убедиться, что их нет.
Для того чтобы решить систему линейных уравнений с двумя переменными, можно использовать использовать графики уравнений.
Решим систему уравнений:
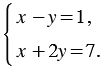
Выразив из уравнения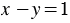 
переменную через переменную , получим линейную функцию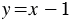 
. Построим в координатной плоскости график этой функции.
Для этого составим таблицу значений функции для некоторых значений аргумента .
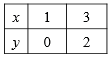
Отметим на координатной плоскости точки с координатами (1; 0) и (3; 2) и проведем через них прямую, которая является графиком линейной функции .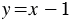
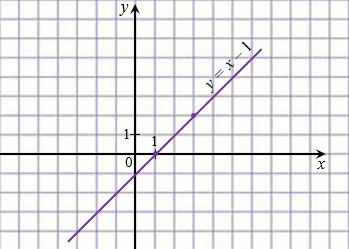
Выразив из уравнения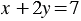 
переменную через переменную (для этого перенесем переменную из левой части уравнения в правую, изменив ее знак, и разделим обе части уравнения на 2), получим линейную функцию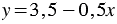 
. Построим в той же координатной плоскости график этой функции.
Для этого составим таблицу значений функции для некоторых значений аргумента .
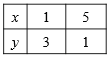
Отметим на имеющейся координатной плоскости точки с координатами (1; 3) и (5; 1) и проведем через них прямую, которая является графиком линейной функции .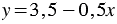
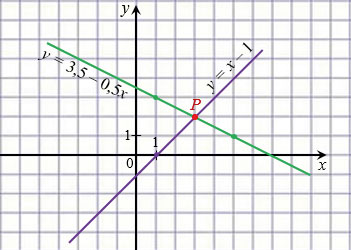
Мы получили, что прямые, которые соответствуют уравнениям 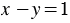и 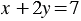, пересекаются в точке Р(3; 2), координаты этой точки удовлетворяют как первому уравнению системы, так и второму, т.е. являются решением системы. Значит, рассматриваемая система имеет единственное решение: = 3, = 2.
Описанный выше метод решения системы уравнений называют графическим.
Суть графического метода решения системы уравнений с двумя переменными:
1) построить на одной координатной плоскости графики уравнений, входящих в систему;
2) найти координаты всех точек пересечения построенных графиков;
3) полученные пары чисел и будут искомыми решениями.
Заметим, что графический способ обычно позволяет находить решения лишь приближенно. Поэтому графический метод эффективен в тех случаях, когда требуется определить количество решений системы.
Определим, сколько решений может иметь система двух линейных уравнений с двумя переменными.
1) Если одно из уравнений системы не имеет решения, то и вся система решений не имеет.
2) Если графиком одного из уравнений системы является вся плоскость, то система имеет бесконечно много решений.
3) Если графиками уравнений, входящих в систему линейных уравнений, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:
- если прямые пересекаются, то система имеет единственное решение.
Рассмотренная нами выше система
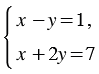
имеет единственное решение = 3, = 2.
- если прямые совпадают, то система имеет бесконечно много решений.
Рассмотрим систему
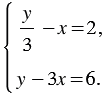
Если умножить обе части первого уравнения этой системы на 3, то решения этого уравнения, а значит, и всей системы не изменятся. Получим:
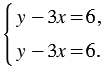
В полученной системе первое и второе уравнения одинаковые, значит, решения этой системы совпадают с решениями уравнения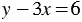 
. Но это уравнение имеет бесконечно много решений, а следовательно, и рассматриваемая система имеет бесконечно много решений.
- если прямые параллельны, то система решений не имеет.
Рассмотрим систему
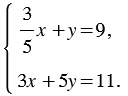
Если умножить обе части первого уравнения этой системы на 5, то решения этого уравнения, а значит, и всей системы не изменятся. Получим:
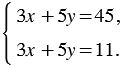
Очевидно, что не существует такой пары значений и , при которых выражение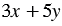 
одновременно принимает значения и 45, и 11. Следовательно, рассматриваемая система не имеет решений.
Советуем посмотреть:
Уравнения с двумя переменными
Линейное уравнение с двумя переменными и его график
Решение систем линейных уравнений методом подстановки
Решение систем линейных уравнений методом сложения
Решение задач с помощью систем линейных уравнений
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 1008,
Мерзляк, Полонский, Якир, Учебник
Номер 1012,
Мерзляк, Полонский, Якир, Учебник
Номер 1036,
Мерзляк, Полонский, Якир, Учебник
Номер 1066,
Мерзляк, Полонский, Якир, Учебник
Номер 1087,
Мерзляк, Полонский, Якир, Учебник
Номер 1122,
Мерзляк, Полонский, Якир, Учебник
Номер 1223,
Мерзляк, Полонский, Якир, Учебник
Номер 1229,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 7,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 310,
Мерзляк, Полонский, Якир, Учебник
Номер 333,
Мерзляк, Полонский, Якир, Учебник
Номер 334,
Мерзляк, Полонский, Якир, Учебник
Номер 335,
Мерзляк, Полонский, Якир, Учебник
Номер 336,
Мерзляк, Полонский, Якир, Учебник
Номер 338,
Мерзляк, Полонский, Якир, Учебник
Номер 348,
Мерзляк, Полонский, Якир, Учебник
Номер 355,
Мерзляк, Полонский, Якир, Учебник
Номер 356,
Мерзляк, Полонский, Якир, Учебник
Номер 435,
Мерзляк, Полонский, Якир, Учебник
