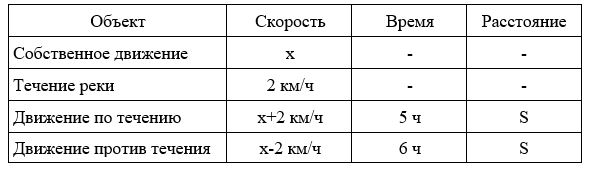
Зная различные методы решения систем линейных уравнений, вы овладеваете прекрасным инструментом, который помогает решать различные виды текстовых задач. И сегодня я хотел бы вам показать, как решается при помощи систем линейных уравнений задачи на движение, рассмотрим на одном примере все этапы. Вспомним основные формулы и понятия:
Пример: Велосипедист ехал 2ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его по шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе и с какой по лесной дороге?
Решение:
1. Пусть х км/ч – скорость велосипедиста в лесу, тогда у км/ч – скорость велосипедиста при движении по шоссе.
2. Следовательно, за два часа езды по лесной дороге велосипедист прошел расстояние 2х км, а за 1 час езды по шоссе он прошел расстояние у км.
3. Тогда поусловию задачи получаем:
2х + у = 40 км.
4. Читаем дальше задачу: ” Скорость его на шоссе была на 4 км/ч больше, чем скорость на лесной дороге” . Получаем:
у = х + 4 км/ч.
5. Составим систему уравнений:
Перенесем х в правую сторону с противоположным знаком,получим:
Теперь домножим второе уравнение системы на (-1):
Тогда получаем:
Теперь давайте применим “метод сложения” для решения данной системы. Сложим первое и второе уравнения системы:
В результате получили, что х= 12 км/ч , то есть мы нашли скорость велосипедиста в лесу.
Теперь найдем у, подставив наш х во второе уравнение системы и получим:
Окончательно получаем следующие ответы: велосипедист ехал по лесной дороге со скоростью 12 км/ч, а по шоссе со скоростью 16 км/ч.
Ответ: 12 км/ч; 16 км/ч.
Всем спасибо за внимание!)
Классная работа
Решение задач с помощью систем линейных уравнений.
Задачи на движение.
Гуськова
Елена Евгеньевна,
учитель математики
МОУ «Лицей № 86»
? км/ч
? км/ч
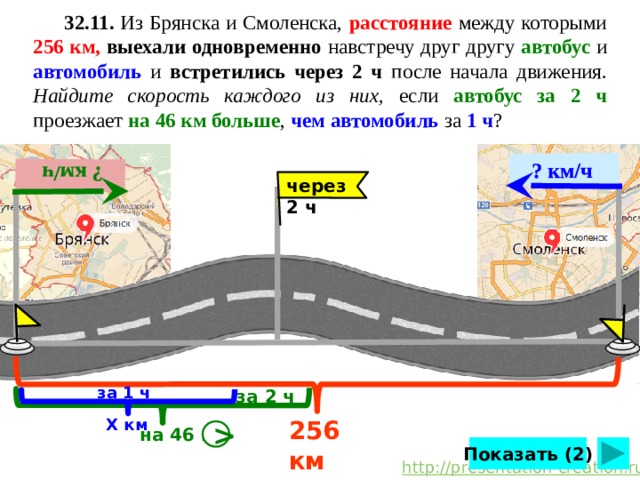
32.11. Из Брянска и Смоленска, расстояние между которыми 256 км, выехали одновременно навстречу друг другу автобус и автомобиль и встретились через 2 ч после начала движения. Найдите скорость каждого из них, если автобус за 2 ч проезжает на 46 км больше , чем автомобиль за 1 ч ?
через 2 ч
А.Г.Мерзляк, В.М.Поляков 7 класс. №32.11 стр.225. Сделайте клик по кнопке «Показать» ( 2 раза)
а+(52,4-38,7)
за 1 ч
за 2 ч
Х км
256 км
на 46 км
Показать (2)
2
Из Брянска и Смоленска, расстояние между которыми 256 км , выехали одновременно навстречу друг другу автобус и автомобиль и встретились через 2 ч после начала движения. Найдите скорость каждого из них, если автобус за 2 ч проезжает на 46 км больше , чем автомобиль за 1 ч ?
Первый этап . Составляем математическую модель задачи
Скорость, км/ч
Автобус
Автомобиль
Время, ч
?
? км/ч
Расстояние, км
2 ч
2 ч
х км/ч
2х
у
2у
Обозначим скорость автобуса – х км/ч, а скорость автомобиля – у км/ч. Автобус проезжает за 2 часа на 46 км больше, чем автомобиль за 1 час..
Составим и решим систему уравнений:
Из Брянска и Смоленска, расстояние между которыми 256 км , выехали одновременно навстречу друг другу автобус и автомобиль и встретились через 2 ч после начала движения. Найдите скорость каждого из них, если автобус за 2 ч проезжает на 46 км больше , чем автомобиль за 1 ч ?
Второй этап . Решаем систему линейных уравнений
+
6х = 348
х=58
Значит, скорость автобуса 58 км/ч, скорость автомобиля 70 км/ч.
Ответ: скорость автобуса 58 км/ч, скорость автомобиля 70 км/ч.
? км/ч
? км/ч
32.12. С двух станций, расстояние между которыми 300 км , одновременно навстречу друг другу отправились пассажирский и товарный поезда, которые встретились через 3 ч после начала движения. Если бы пассажирский поезд вышел на 1 ч раньше , чем товарный, то они встретились бы через 2,4 ч после выхода товарного поезда . Найдите скорость каждого поезда.
через 3 ч
через 2,4 ч
на 1 ч
раньше
если на 1 ч
раньше
А.Г.Мерзляк, В.М.Поляков 7 класс. №32.12 стр.225. Сделайте клик по кнопке «Показать» (3 раза)
а+(52,4-38,7)
300 км
Показать (3)
5
С двух станций, расстояние между которыми 300 км , одновременно навстречу друг другу отправились пассажирский и товарный поезда, которые встретились через 3 ч после начала движения. Если бы пассажирский поезд вышел на 1 ч раньше , чем товарный, то они встретились бы через 2,4 ч после выхода товарного поезда . Найдите скорость каждого поезда.
V 1 , км/ч
Пассажирский
Товарный
х
t 1 , ч
S 1 , км
у
3
V 2 , км/ч
х+у
3x
3
3у
t 2 , ч
х
3
2,4 +1
у
S 2 , км
300
2,4
3,4х
х+у
–
2,4у
300
Составим и решим систему уравнений:
С двух станций, расстояние между которыми 300 км , одновременно навстречу друг другу отправились пассажирский и товарный поезда, которые встретились через 3 ч после начала движения. Если бы пассажирский поезд вышел на 1 ч раньше , чем товарный, то они встретились бы через 2,4 ч после выхода товарного поезда . Найдите скорость каждого поезда.
Значит, скорость пассажирского поезда 60 км/ч, скорость товарного – 40 км/ч.
Ответ: скорость пассажирского поезда 60 км/ч, скорость товарного – 40 км/ч.
? км/ч
? км/ч
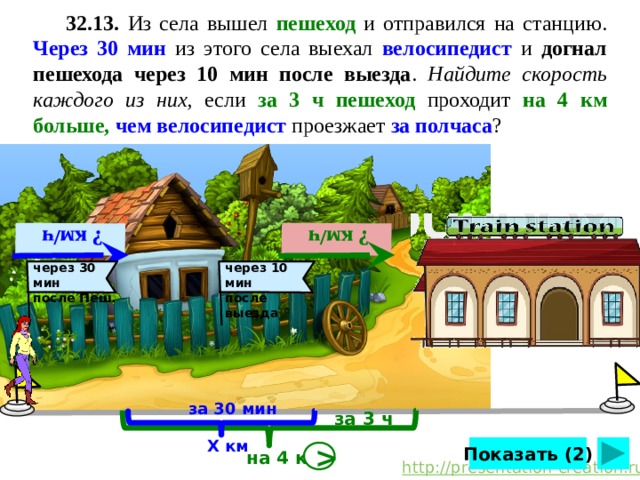
32.13. Из села вышел пешеход и отправился на станцию. Через 30 мин из этого села выехал велосипедист и догнал пешехода через 10 мин после выезда . Найдите скорость каждого из них, если за 3 ч пешеход проходит на 4 км больше, чем велосипедист проезжает за полчаса ?
через 10 мин
через 30 мин
после выезда
после Пеш.
А.Г.Мерзляк, В.М.Поляков 7 класс. №32.13 стр.226. Сделайте клик по кнопке «Показать» ( 2 раза)
а+(52,4-38,7)
за 30 мин
за 3 ч
Х км
Показать (2)
на 4 км
8
Из села вышел пешеход и отправился на станцию. Через 30 мин из этого села выехал велосипедист и догнал пешехода через 10 мин после выезда . Найдите скорость каждого из них, если за 3 ч пешеход проходит на 4 км больше , чем велосипедист проезжает за полчаса ?
V 1 , км/ч
V 1 , км/ч
Пешеход
Пешеход
t 1 , ч
х
t 1 , ч
х
Велосипедист
Велосипедист
у
S 1 , км
S 1 , км
у
3
3
0,5
V 2 , км/ч
0,5
–
–
3x
3x
V 2 , км/ч
0,5у
t 2 , ч
t 2 , ч
0,5у
х
–
х
–
На 4 км больше
S 2 , км
у
S 2 , км
у
На 4 км больше
х-у
х-у
х
у
–
–
одинаковое
одинаковое
Составим и решим систему уравнений:
Из села вышел пешеход и отправился на станцию. Через 30 мин из этого села выехал велосипедист и догнал пешехода через 10 мин после выезда . Найдите скорость каждого из них, если за 3 ч пешеход проходит на 4 км больше , чем велосипедист проезжает за полчаса ?
Значит, скорость пешехода 6 км/ч, скорость велосипедиста – 16 км/ч.
Ответ: скорость пешехода 6 км/ч, скорость велосипедиста 16 км/ч.
.
? км/ч
? км/ч
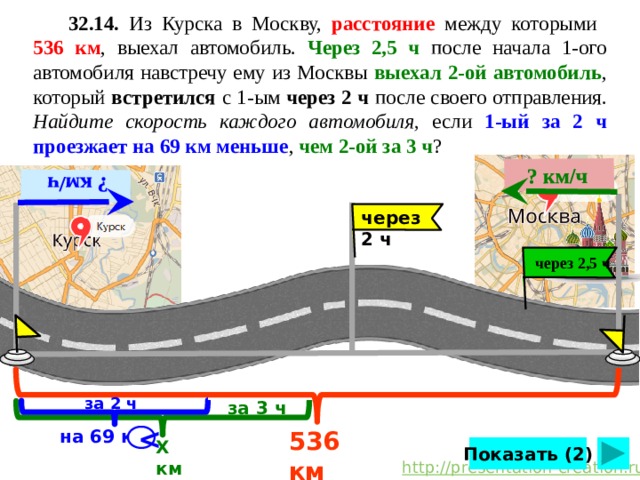
32.14. Из Курска в Москву, расстояние между которыми 536 км , выехал автомобиль. Через 2,5 ч после начала 1-ого автомобиля навстречу ему из Москвы выехал 2-ой автомобиль , который встретился с 1-ым через 2 ч после своего отправления. Найдите скорость каждого автомобиля, если 1-ый за 2 ч проезжает на 69 км меньше , чем 2-ой за 3 ч ?
через 2 ч
через 2,5 ч
А.Г.Мерзляк, В.М.Поляков 7 класс. №32.14 стр.226. Сделайте клик по кнопке «Показать» ( 2 раза)
а+(52,4-38,7)
за 2 ч
за 3 ч
на 69 км
536 км
Х км
Показать (2)
11
Из Курска в Москву, расстояние между которыми 536 км , выехал автомобиль. Через 2,5 ч после начала 1-ого автомобиля навстречу ему из Москвы выехал 2-ой автомобиль , который встретился с 1-ым через 2 ч после своего отправления. Найдите скорость каждого автомобиля, если 1-ый за 2 ч проезжает на 69 км меньше , чем 2-ой за 3 ч ?
V 1 , км/ч
V 1 , км/ч
1 автомобиль
1 автомобиль
2 автомобиль
t 1 , ч
2 автомобиль
х
t 1 , ч
х
S 1 , км
у
у
S 1 , км
2+2,5
2+2,5
2
–
4,5x
–
2
4,5x
V 2 , км/ч
V 2 , км/ч
2у
t 2 , ч
2у
t 2 , ч
х
х
–
–
у
S 2 , км
S 2 , км
у
536 км
536 км
х-у
х-у
–
–
на 69 км меньше
на 69 км меньше
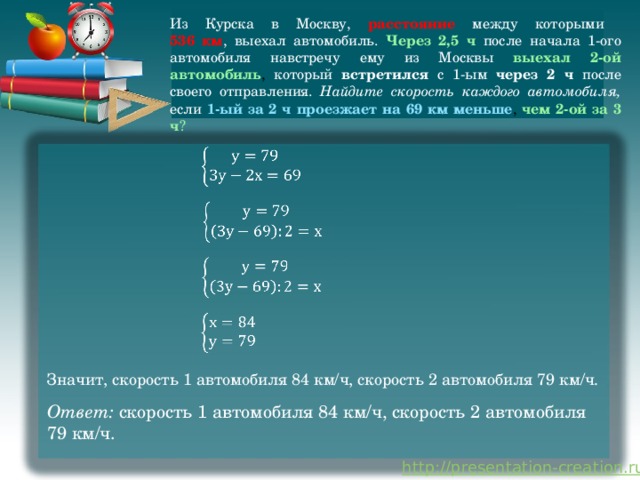
Составим и решим систему уравнений:
35у = 2765
у=79
Из Курска в Москву, расстояние между которыми 536 км , выехал автомобиль. Через 2,5 ч после начала 1-ого автомобиля навстречу ему из Москвы выехал 2-ой автомобиль , который встретился с 1-ым через 2 ч после своего отправления. Найдите скорость каждого автомобиля, если 1-ый за 2 ч проезжает на 69 км меньше , чем 2-ой за 3 ч ?
Значит, скорость 1 автомобиля 84 км/ч, скорость 2 автомобиля 79 км/ч.
Ответ: скорость 1 автомобиля 84 км/ч, скорость 2 автомобиля 79 км/ч.
Ресурсы
Особая благодарность учителю информатики лицея № 86 г.Ярославля Ирине Сергеевне Смирновой за визуализацию задач на движение к учебнику «Алгебра 7» под ред. А.Г.Мерзляк, В.М.Поляков.
Основной фон презентации – https://presentation-creation.ru /
Пример №1
Допустим, из точки ( displaystyle A) и из точки ( displaystyle B) навстречу друг другу выехали две машины. Скорость одной машины – ( displaystyle 60) км/ч, а скорость ( displaystyle 2) машины – ( displaystyle 40) км/ч. Они встретились через ( displaystyle 1,2) часа.
Какое расстояние между пунктами ( displaystyle A) и ( displaystyle B)?
1 вариант решения
Можно рассуждать так: машины встретились, значит расстояние между городами – это сумма расстояния, которая прошла первая машина, и расстояния, которое прошла вторая.
( displaystyle 60cdot 1,2text{ }=text{ }72) (км) – путь, который проехала первая машина
( displaystyle 40cdot 1,2text{ }=text{ }48) (км) – путь, который проехала вторая машина
( displaystyle 72 + 48 = 120) (км) – расстояние, которое проехали обе машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).
2 вариант решения (более рациональный)
А можно просто воспользоваться очень логичной формулой о сложении скоростей.
Проверим, работает ли она:
( displaystyle 60 + 40 = 100) (км/ч) – скорость сближения машин
( displaystyle 100cdot 1,2text{ }=text{ }120) (км) – расстояние, которые проехали машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).
Оба решения являются верными. Второе просто более рациональное.
Пример №3
Итак, задача:
Из пункта ( displaystyle A) и пункта ( displaystyle B) машины движутся навстречу друг другу со скоростями ( displaystyle 50) км/ч и ( displaystyle 80) км/ч. Расстояние между пунктами – ( displaystyle 195) км.
Через сколько времени машины встретятся?
1 вариант решения
Пусть ( displaystyle x) – время, которое едут машины, тогда путь первой машины – ( displaystyle 50x), а путь второй машины – ( displaystyle 80x).
Их сумма и будет равна расстоянию между пунктами ( A) и ( B) – ( displaystyle 50x+80x=195).
Решим уравнение:
( displaystyle 50x+80x=195)
( displaystyle 130x=195)
( displaystyle x=1,5) (ч) – время, через которое встретились машины.
2 вариант решения (более рациональный)
( displaystyle 50 + 80 = 130) (км/ч) – скорость сближения машин;
( displaystyle 195:130 = 1,5) (ч) – время, которое машины были в пути.
Задача решена.
Пример №4
Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями ( displaystyle 60) км/ч и ( displaystyle 40) км/ч. Через сколько минут они встретятся. Если расстояние между пунктами ( displaystyle 100) км?
2 способа решения:
I способ
Относительная скорость автомобилей ( displaystyle 60+40=100) км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью ( displaystyle 100) км/ч. Так как между автомобилями изначально расстояние ( displaystyle 100) км, время, через которое второй автомобиль проедет мимо первого:
( displaystyle t=frac{100}{100}=1 час=60 минут).
II способ
Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его ( displaystyle t). Тогда первый автомобиль проехал путь ( displaystyle 60t), а второй – ( displaystyle 40t).
В сумме они проехали все ( displaystyle 100) км. Значит,
( displaystyle 60t+40t=100Rightarrow t=1 час=60 минут).
Из пункта ( displaystyle A) в пункт ( displaystyle B), расстояние между которыми ( displaystyle 30) км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на ( displaystyle 65) км больше, чем велосипедист.
Определите скорость велосипедиста, если известно, что он прибыл в пункт ( displaystyle B) на ( displaystyle 156) минут позже, чем мотоциклист.
Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать – прямая, пункт ( displaystyle A), пункт ( displaystyle B), две стрелочки…
В общем рисуй, и сейчас сравним, что у тебя получилось.
Пустовато как-то, правда? Рисуем таблицу.
Как ты помнишь, все задачи на движения состоят из ( displaystyle 3) компонентов: скорость, время и путь. Именно из этих граф и будет состоять любая таблица в подобных задачах.
Правда, мы добавим еще один столбец – имя, про кого мы пишем информацию – мотоциклист и велосипедист.
Так же в шапке укажи размерность, в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?
У тебя получилась вот такая таблица?
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | |||
| мотоциклист |
Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.
Первое, что мы имеем – это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен ( displaystyle 30) км. Вносим!
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | ( displaystyle 30) | ||
| мотоциклист | ( displaystyle 30) |
Рассуждаем дальше. Мы знаем, что мотоциклист проезжает на ( displaystyle 65) км/ч больше, чем велосипедист, да и в задаче нужно найти скорость велосипедиста…
Возьмем скорость велосипедиста за ( displaystyle x), тогда скорость мотоциклиста будет ( displaystyle x+65)…
Если с такой переменной решение задачи не пойдет – ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | ( displaystyle x) | ( displaystyle 30) | |
| мотоциклист | ( displaystyle x+65) | ( displaystyle 30) |
Таблица преобразилась. У нас осталась не заполнена только одна графа – время. Как найти время, когда есть путь и скорость?
Правильно, разделить путь на скорость. Вноси это в таблицу.
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | ( displaystyle x) | ( displaystyle frac{30}{x}) | ( displaystyle 30) |
| мотоциклист | ( displaystyle x+65) | ( displaystyle frac{30}{65+x}) | ( displaystyle 30) |
Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.
Что мы можем на нем отразить?
Молодец. Скорость передвижения мотоциклиста и велосипедиста.
Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.
Какие данные не отражены ни в таблице, ни на рисунке?
Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени – ( displaystyle 156) минут.
Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.
( displaystyle 156) минут / ( displaystyle 60) минут = ( displaystyle 2,6) часа.
И что дальше, спросишь ты? А дальше числовая магия!
Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?
Правильно. Мы можем составить уравнение, основываясь на разнице во времени!
( displaystyle frac{30}{x}-frac{30}{65+x}=2,6)
Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.
Это уравнение – рациональное. Если не знаешь, что это такое, прочти тему «Рациональные уравнения».
Приводим слагаемые к общему знаменателю:
( displaystyle frac{30cdot left( 65+x right)}{xcdot left( 65+x right)}-frac{30x}{xcdot left( 65+x right)}=2,6)
Раскроем скобки и приведем подобные слагаемые: Уф! Усвоил? Попробуй свои силы на следующей задаче.
( displaystyle frac{1950}{xcdot left( 65+x right)}=2,6)
Из этого уравнения мы получаем следующее:
( displaystyle 2,6cdot xcdot left( 65+x right)=1950)
( displaystyle xcdot left( 65+x right)=frac{1950}{2,6})
( displaystyle xcdot left( 65+x right)=750)
Раскроем скобки и перенесем все в левую часть уравнения:
( displaystyle {{x}^{2}}+65{x}-750=0)
Вуаля! У нас простое квадратное уравнение. Решаем!
( displaystyle {{x}^{2}}+65{x}-750=0)
( displaystyle D={{b}^{2}}-4ac)
( displaystyle D={{65}^{2}}-4cdot 1cdot left( -750 right)=4225+3000=7225)
( displaystyle sqrt{D}=sqrt{7225}=85)
( displaystyle {{x}_{1,2}}=frac{-bpm sqrt{D}}{2a})
( displaystyle {{x}_{1}}=frac{-65+85}{2}=10)
( displaystyle {{x}_{2}}=frac{-65-85}{2}=-75)
Мы получили два варианта ответа. Смотрим, что мы взяли за ( displaystyle x)? Правильно, скорость велосипедиста.
Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь, о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ – ( displaystyle 10) км/ч.
Пример №9
Два велосипедиста одновременно отправились в ( displaystyle 165)-километровый пробег. Первый ехал со скоростью, на ( displaystyle 5) км/ч большей, чем скорость второго, и прибыл к финишу на ( displaystyle 5,5) часов раньше второго.
Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Напоминаю:
- Прочитай задачу пару раз – усвой все-все детали. Усвоил?
- Начинай рисовать рисунок – в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
- Проверь, все ли величины у тебя одинаковой размерности, и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь, какие там графы?).
- Пока все это пишешь, думай, что взять за ( displaystyle x)? Выбрал? Записывай в таблицу!
- Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок – помни о «3Р»!
Все сделал? Молодец! У меня получилось, что скорость велосипедиста – ( displaystyle 10) км/ч.
Пример №10
Из пункта ( displaystyle A) круговой трассы выехал велосипедист. Через ( displaystyle 40) минут он еще не вернулся в пункт ( displaystyle A) и из пункта ( displaystyle A) следом за ним отправился мотоциклист.
Через ( displaystyle 20) минут после отправления он догнал велосипедиста в первый раз, а еще через ( displaystyle 40) минут после этого догнал его во второй раз.
Найдите скорость велосипедиста, если длина трассы равна ( displaystyle 50) км. Ответ дайте в км/ч.
Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:
Пусть скорость велосипедиста будет ( displaystyle x), а мотоциклиста – ( displaystyle y). До момента первой встречи велосипедист был в пути ( displaystyle 60) минут, а мотоциклист – ( displaystyle 20).
При этом они проехали равные расстояния:
( displaystyle 60x=20y (1))
Между встречами велосипедист проехал расстояние ( displaystyle 40x), а мотоциклист – ( displaystyle 40y).
Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:
(Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили – спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.)
Значит,
( displaystyle 40x+50=40y (2))
Полученные уравнения решаем в системе:
( displaystyle left{ begin{array}{l}60x=20y\40x+50=40yend{array} right.Leftrightarrow left{ begin{array}{l}y=3x\4x+5=4yend{array} right.Rightarrow text{4}x+5=12xRightarrow )
( displaystyle Rightarrow x=frac{5}{8}=0,625frac{text{км}}{мин}=0,625cdot 60frac{text{км}}{text{ч}}=37,5frac{text{км}}{text{ч}})
Ответ: ( displaystyle 37,5).
Разобрался? Попробуй решить самостоятельно следующие задачи:
Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, – это стоячая вода.
Скорость течения в озере равна ( displaystyle 0).
Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь – налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести.
Это понятно? Логично же.
А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…
Это происходит потому что у реки есть скорость течения, которая относит твой плот по направлению течения.
Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) – он движется со скоростью течения.
Разобрался? Тогда ответь вот на какой вопрос – «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?
Здесь возможно два случая:
1 случай – ты плывешь по течению, и тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.
2 случай – ты плывешь против течения. Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы ( displaystyle 100) метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость – скорость течения.
Методика
решения задач «на движение»
Уравнения, которые
составляются на основании условий задач на движение, обычно содержат такие
величины, как расстояние, скорости движущихся объектов, время, а также скорость
течения воды (при движении по реке). При решении этих задач принимают следующие
допущения:
1.
Если нет специальных оговорок,
то движение считается равномерным.
2.
Повороты движущихся тел,
переходы на новый режим движения считаются происходящими мгновенно.
3.
Если тело с собственной
скоростью х движется по реке, скорость течения которой равна у,
то скорость движения тела по течению считается равной (х+у), а против
течения – (х-у).
При решении задач на
движение рекомендуется сделать рисунок, отображающий все условия задачи. При
этом решающий задачу должен выбрать схему решения: какого вида уравнения
составлять, то есть что сравнивать: время, затраченное на движение на отдельных
участках пути, или пройденный каждым объектом путь.
При решении задач такого
типа часто необходимо узнать время встречи двух объектов, начинающих движение
одновременно из двух точек с разными скоростями и движущихся навстречу друг
другу либо в случае, когда один объект догоняет другой.
1.2.1 Задачи на встречное
движение
Пусть расстояние между
точками А и В равно S.
Два тела начинают движение
одновременно, но имеют разные скорости v1 и v2.
Пусть С – точка встречи, а t – время движения тел до встречи. В случае
движения навстречу друг другу имеем АС=v1t, BC=v2t.
Сложим эти два равенства:
АС+СВ=v1t+v2t=(v1+v2)t
Þ AB=S=(v1+v2)t Þ .
Задание
13 № 99592. Из
городов A и B навстречу друг другу выехали
мотоциклист и велосипедист. Мотоциклист приехал в B на
3 часа раньше, чем велосипедист приехал в A, а встретились они
через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Решение.
Примем расстояние между
городами 1. Пусть время движения велосипедиста равно x ч, тогда время
движения мотоциклиста равно =3 ч,x . К моменту встречи они
находились в пути 48 минут и в сумме преодолели всё расстояние между городами, поэтому
Таким образом,
велосипедист находился в пути 4 часа.
Ответ: 4.
Задача 2. Расстояние между городами А и В равно 60 км. Два поезда выходят
одновременно: один из А в В, другой из В в А. Пройдя 20 км, поезд, идущий из А
в В, останавливается на полчаса, затем, пройдя 4 минуты, встречает поезд,
идущий из В. Оба поезда прибывают к месту назначения одновременно. Найдите
скорости поездов.
Решение:
Отобразим все условия
задачи на рисунке.
Заметим, что если время в
условии задачи выражено как в часах, так и в минутах, то минуты надо перевести
в часы. В нашем случае 4 мин=4/10 часа=1/15 часа.
Так как в задаче надо
определить две величины, введем две переменные и составим два уравнения.
Пусть х км/ч –
скорость поезда, вышедшего из пункта А;
у км/ч – скорость поезда, вышедшего из пункта В.
Так как в задаче известно
расстояние, выразим время через скорость и расстояние: – время, за которое
поезд из А прошел 20 км, – время, затраченное поездом из А до встречи в пункте
D.
– расстояние, которое
прошел поезд из А за 4 минуты после остановки.
Тогда поезд из А до
встречи в пункте D прошел км.
км – расстояние,
пройденное поездом из В до встречи.
– время, пройденное
поездом из В до встречи в пункте D.
Так как по условию в
пункте D поезда встретились, они затратили на путь до встречи одинаковое время,
поэтому получаем первое уравнение.
С другой стороны, выразим
время движения поездов после встречи в пункте D.
Так как , то – время
движения поезда из В после встречи.
Так как , то – время
движения поезда из А после встречи.
По условию .
Таким образом, мы
составили систему двух уравнений с двумя переменными.
Решим систему, для чего
из первого уравнения выразим у и подставим это выражение вместо у
во второе уравнение.
Решим полученное
уравнение х1=60; х2=–600.
Так как х –
скорость, то х2 не подходит по смыслу задачи. Подставим
полученное значение х в выражение для у
Ответ: vA=60 км/ч, vB=40
км/ч.
Задача 3.
Из городов А и В, расстояние между которыми равно 180 км,
отправлены одновременно навстречу друг другу 2 поезда. После их встречи поезд,
вышедший из города А, прибыл в город В через 2 часа, а
другой прибыл в город А через 4 часа 30 минут. Найти
скорость каждого поезда.
Решение.
При решении этой задачи
удобным представляется принять за неизвестное один из участков пути до момента
встречи. Пусть, например, путь первого поезда до встречи равен , тогда путь
второго поезда – .
После встречи I поезд
прошел, наоборот, расстояние , причем за 2 часа, значит, его скорость
равна . Второй поезд прошел после встречи путь за 4.5 часа, значит, его
скорость – .
Выразим теперь время
движения каждого из поездов до встречи (по условию оно одинаково).
Время I поезда до встречи
равно , а второго – .
Получим уравнение: ,
откуда
Ответ. и .
1.2.2 Задачи на движение
в одном направлении
Если одно тело догоняет
другое, то теперь получаем АС=v1t, BC=v2t.
Вычтем эти равенства:
АС–ВС=(v1–v2)t.
Так как АС–ВС=AB=S,
то время, через которое первое тело догонит второе, определяется равенством.
№ 99611. По
двум параллельным железнодорожным путям в одном направлении следуют
пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и
30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского
поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте.
Ответ дайте в метрах.
Решение.
Скорость сближения
поездов равна 60 км/ч или 1 км/мин. Следовательно, за 1 минуту пассажирский
поезд сместится относительно товарного на 1 км. При этом он преодолеет
расстояние, равное сумме длин поездов. Поэтому длина пассажирского поезда равна
1000 − 600 = 400 м.
Приведём другое решение.
Скорость сближения
поездов равна
Пусть длина пассажирского
поезда равна х метров. За 60 секунд один поезд проходит мимо
другого, то есть преодолевает расстояние х + 400. Тогда:
Поэтому длина
пассажирского поезда 400 м.
Ответ: 400.
Задача 2. Из пункта А
по одному и тому же маршруту одновременно выехали грузовик и легковой
автомобиль. Скорость автомобиля постоянна и составляет скорости грузовика.
Через 30 минут за ними из того же пункта выехал мотоциклист со скоростью
. Найти скорость легкового автомобиля, если известно, что мотоциклист догнал
грузовик на час раньше, чем легковой автомобиль.
Решение. Пусть – скорость грузовика, тогда – скорость легкового
автомобиля. Обозначим за – время, через которое мотоциклист догнал грузовик (с
момента выезда мотоциклиста), тогда грузовик до этого момента находился в пути
. При этом их пройденные пути оказались равными, значит
(1)
Мотоциклист догнал
легковой автомобиль через час после грузовика, значит, с начала движения он был
в пути , а легковой автомобиль . Так как их пройденные пути в этот момент
совпадают, то
(2)
Получим систему из
уравнений (1) и (2), решив которую найдем, что – скорость грузовика, значит,
скорость легкового автомобиля будет . Ответ. .
1.2.3 Задачи на движение
в противоположных направлениях
№ 503316. Велосипедист
выехал с постоянной скоростью из города А в город В,
расстояние между которыми равно 128 км. На следующий день он отправился обратно
в А со скоростью на 8 км/ч больше прежней. По дороге он сделал
остановку на 8 часов. В результате велосипедист затратил на обратный путь
столько же времени, сколько на путь из А в В.
Найдите скорость велосипедиста на пути из В в А.
Ответ дайте в км/ч.
Решение.
Пусть велосипедист ехал
из А в В со скоростью км/час, тогда обратно он ехал со
скоростью км/час.
Разность времен на пути туда и обратно составляет 8 часов, откуда имеем:
Искомая скорость
велосипедиста на обратном пути на 8 км/час больше, поэтому она равна 16
км/час.
Ответ: 16.
1.2.4 Задачи на движение
по воде
Задача 1. Пароход прошел
4 км против течения реки, а затем прошел еще 33 км по течению, затратив на весь
путь один час. Найдите собственную скорость парохода, если скорость течения
реки равна 6,5 км/ч.
Решение:
Пусть х км/ч –
собственная скорость парохода.
Тогда (х+6,5) км/ч – скорость
парохода по течению.
(х–6,5) км/ч – скорость
парохода против течения.
Так как против течения
пароход прошел 4 км со скоростью (х–6,5) км/ч, то
ч. – время движения
парохода против течения.
Так как по течению
пароход прошел 33 км со скоростью (х+6,5) км/ч, то
ч. – время движения
парохода по течению.
По условию
решим полученное
уравнение
Откуда получаем
квадратное уравнение
х2–37х+146,25=0 х1=4,5
км/ч и х2=32,5 км/ч.
Осуществим отбор
полученных решений.
Через х мы обозначили
собственную скорость парохода, при этом скорость течения реки 6,5 км/ч, поэтому
х1=4,5 км/ч не подходит по смыслу задачи (при такой скорости пароход не выплыл
бы против течения).
Поэтому, собственная
скорость парохода равна 32,5 км/ч.
Ответ: v=32,5 км/ч.
Задача 2. Теплоход
проходит по течению реки до пункта назначения 459 км и после стоянки
возвращается в пункт отправления. Найдите скорость течения, если скорость
теплохода в неподвижной воде равна 22 км/ч, стоянка длится 10 часов, а в пункт
отправления теплоход возвращается через 54 часов после отплытия из него. Ответ
дайте в км/ч.
Скорость течения реки
как искомую величину принимаем за x (км/ч).
Тогда скорость движения
теплохода по течению равна 22 + х (км/ч), а его скорость против
течения 22 – х.
Расстояние
в ту, и в другую сторону одинаковое и равно 459 км.
Всего теплоход
затрачивает 54 часов (на весь путь: туда, 10 часов стоянки, обратно). То есть:
54 = (ПО
ТЕЧЕНИЮ)+(СТОЯНКА)+( ПРОТИВ ТЕЧЕНИЯ)
Расстояние
и в ту, и в другую сторону одинаково и равно
459 км.
Занесем скорость
и расстояние в таблицу. Заполняем графу «время».
Время, затраченное на
путь до пункта назначения 459/(22+х),
Время, затраченное на
путь обратно (против течения) 459/(22–х).
Подставляем
данные и получаем уравнение:
Мы не будем подробно
останавливаться на технике решения уравнения. Всё
понятно — раскрываем скобки, складываем
подобные члены.
Получаем квадратное
уравнение: х2 = 25.
Его решением являются
корни –5 и 5.
Поскольку скорость
течения положительна, значит она равна 5 (км/ч).
Ответ: 5
1.2.5 Задачи на движение
по замкнутой трассе
В этом параграфе показаны
общие пути решения задач на движение по окружности. Выделим основные понятия и
сделаем некоторые замечания.
1. Пусть дана окружность длиной l, и по ней движется точка,
совершающая полный оборот за время t.
Тогда отношение будет
выражать длину дуги, описываемую точкой за единицу времени (или, с точки зрения
физики, это линейная скорость точки).
2. Часто полезно бывает работать с угловой скоростью точки,
т. е. углом, описываемым точкой за единицу времени.
При этом .
3. Пусть две точки А и В находятся в начальный момент
времени на окружности, и дуга АВ содержала . Известно, что через t единиц
времени точка А догонит точку В.
Точка В за t единиц
времени опишет угол , а точка А – , и разность этих углов составит , т.
е. будет справедливо равенство .
4. Пусть две точки А и В стартовали с одного
положения. Скорость точки А – , больше скорости В – . Известно,
что через время t точка А догонит точку В.
Из рисунка видно, что к
моменту, когда А догонит точку В, она опишет окружность и пройдет
путь точки В, т. е. , или .
Аналогично, при тех же
условиях, работая с угловыми скоростями, получим уравнение .
Опираясь на выше
изложенные наблюдения, решим несколько задач, придерживаясь следующего
алгоритма:
1.
Обозначить за неизвестные
время полного оборота каждой точки
2.
Выразить линейные или угловые
скорости
3.
Составить уравнение или
систему уравнений по условию задачи
4.
Решить полученное уравнение
(систему)
5.
Ответить на вопрос задачи
Замечание. Пункты 1 и 2 можно поменять местами.
Задача №1. Два спортсмена бегают по одной замкнутой дорожке стадиона. Скорость
каждого постоянна, но на пробег всей дорожки первый тратит на 10 сек
меньше, чем второй. Если они начнут пробег с общего старта, то еще раз сойдутся
через 720 сек. Какую часть длины всей дорожки пробегает в секунду каждый
бегун?
Решение. Примем длину окружности за единицу. Пусть – время пробега полного
круга первым бегуном, тогда – потребуется второму бегуну; – такую часть
окружности пробегает первый бегун за 1 с; – пробегает второй бегун за 1 с.
За 720 с первый бегун обежит частей окружности, а второй частей, и
разность этих величин равна 1.
Получим уравнение . Решим
это уравнение:
, (не удовлетворяет
условию задачи).
Тогда и части дорожек
пробегают второй и первый бегун соответственно за 1 секунду.
Ответ: и части дорожки.
Примечание. Задачу можно решить аналогично, используя понятие «угловой
скорости».
Задача №3. По двум концентрическим окружностям равномерно вращаются сразу
две точки. Полный оборот одна из них совершает на 5 секунд быстрее, чем
другая, и поэтому успевает сделать в одну минуту на 2 оборота больше.
Пусть в начале движения лучи, направленные от центров окружностей к этим
точкам, сливались. Вычислить, какова величина угла между лучами будет через 1 с.
Решение. Пусть начальное положение точек соответствует точкам А и В.
Тогда через 1 с точка А займет положение А’, точка В
– B’. Из рисунка видно, что искомый угол равен разности углов поворота
точки А и точки В за 1 с.
Пусть – время полного
оборота точки А, тогда – время полного оборота точки В.
За 1 мин, т. е. 60
сек, точка А пройдет угол , а точка В – , причем точка А
совершит на 2 оборота больше, т. е. опишет угол на больший.
Получим уравнение .
Разделив почленно
уравнение на , получим
– не подходит по условию
задачи.
Итак, за 1 с точка
А совершит оборот на , точка В – . Искомый угол будет равен . Ответ:
Еще раз подчеркнем, что
цель этого параграфа – показать общий метод решения задач, и он не исключает
наличие других, более изящных, путей решения. В частности, решение этой задачи
можно провести в одну строчку, рассуждая так: поскольку за 1 мин, т. е.
за 60 секунд, между точками возникает разрыв в радиан, то за одну
секунду этот разрыв будет выражаться числом . При этом одно из условий
задачи оказалось лишним.
2 Решение задач
графическим способом
Задача 1. По городскому
скверу, длина которого 500 м, одновременно начали прогуливаться два пожилых
человека. Один прогуливается со скоростью 50 м/м, а другой доходит до конца
аллеи за 6 мин и с той же скоростью возвращается назад. Определить, сколько раз
эти два пожилых человека встретятся в течение 25 минут?
500
0 6 10 12 18 20 24 30
Так как скорость первого
50 м /мин, то до конца сквера он доходит за 10 минут. Можно построить графики
движения этих пожилых людей. По чертежу сразу видно, что графики пересекутся в
трёх точках, значит пожилые люди встретятся 3 раза.
Ответ: 3 раза.
Задача 2.Расстояние между
городами Новокузнецк и Киселёвска составляет примерно 60 км. Одновременно из
этих городов, навстречу друг другу, выехали два автобуса. Первый автобус
затратил на свой путь 1 час и 30 мин, а второй 1 час и 12 мин. На каком
расстоянии от Киселёвска и через какое время с момента начала движения,
автобусы встретятся.
Изобразим на чертеже
графики движения автобусов между двумя городами. Так как автобусы выходят
одновременно, но из различных точек, то и графики движения автобусов также
будут выходить из различных точек, одна – из начала координат, другая – из
точки, соответствующей 60 км на оси ОS. По оси ot отложим время движения этих
автобусов.
s Нов.60
28
40 72 90 t
Графики движения
автобусов пересеклись в одной точке, координаты этой точки соответствуют
времени движения автобусов до встречи и расстоянию, которое автобусы проехали
до места встречи.
Ответ: Расстояние от Киселёвска до места встречи автобусов равно 28 км;
Автобусы встретились через 40 минут после начала движения.
Задача № 4.
Эта задача взята из
сборника заданий для подготовки к ГИА за 2012 год. Из пунктов А и В,
расстояние между которыми 15 км, одновременно навстречу друг другу выехали два
велосипедиста. После их встречи велосипедист, выехавший из А, прибыл в В через
20 мин, а велосипедист, выехавший из В, прибыл в А через 45 мин. На каком расстоянии
от В велосипедисты встретились?
Эту задачу можно решить
алгебраическим способом, но для этого надо составить систему двух уравнений с
двумя неизвестными. Попробуем решить эту задачу графическим способом. Построим
графики движения этих велосипедистов. Так как они выехали из разных пунктов
навстречу друг другу, то и графики движения выходят из разных точек навстречу
друг другу.
s
45
15 В
?
у
А
0 х 20 t
Графики пересекутся в
момент встречи. По чертежу можно увидеть пару подобных треугольников. Обозначим
за х – время движения велосипедистов до момента их встречи, а за у – расстояние
от А до места встречи. Составим пропорции:
у: х = 15: (х+20) – из
первой пары треугольников
у: 45 = 15: (х + 45) – из
второй пары треугольников.
Выразим переменную у
через х в той и другой пропорции и приравняем их. Получим уравнение с одним
неизвестным, которое решим уже с помощью алгебраических преобразований.
у = 15х : (х+20) из 1
уравнения
у = 45×15 : (х+45) из 2
уравнения
15х : (х+20) = 45×15 :
(х+45);
15х × (х+45) =
(х+20)×675;
15х2 + 675х=
675х +13500;
15х2 = 13500;
х2 = 900;
х = ±30.
Выбираем только х = 30 и
находим у = 15х 30 : (30 + 20) = 9.
Расстояние от А до места
встречи составляет 9 км, тогда расстояние от В до места встречи составляет 15 –
9 = 6 (км).
Ответ: Расстояние от пункта А до места встречи 6 км.
Заключение.
Математика, давно став
языком науки и техники, в настоящее время всё шире проникает в повседневную
жизнь. Основной задачей обучения математике в школе является обеспечение
прочного и сознательного овладения учащимися системой математических знаний и
умений, необходимых в повседневной жизни и трудовой деятельности каждому члену
современного общества, достаточных для изучения смежных дисциплин и продолжения
образования, а также в профессиональной деятельности, требующей достаточно
высокой математической культуры. Для жизни в современном обществе важным
является формирование математического стиля мышления, проявляющего в
определённых умственных навыках.
Решая задачи, учащиеся
приобретают новые математические знания, готовятся к практической деятельности.
Решая задачи, ребёнок активизирует мыслительную деятельность, развивая
логическое мышление.
За время обучения в школе
учащийся решает огромное число однотипных задач, приобретая общие умения
решения задач, а встретившись с малоизвестными задачами, теряются и не решают
их. Можно ли научить решать любую задачу? Нет, так как изобразить методику
обучения решению задач, подходящую для всех детей невозможно, но помочь
расширить круг решаемых задач можно.
В данной работе обобщен и
систематизирован учебный материал по задачам «на движение», который необходим
для успешного их решения. При решении каждой задачи данного типа учитывались её
особенности, применялись разнообразные приёмы их решения. Использование
алгоритмов, таблиц, рисунков, общих приемов дает возможность ликвидировать у
большей части учащихся страх перед текстовой задачей, научить распознавать типы
задач и правильно выбирать прием решения.
«Решайте задачи проще» –
совет, которому необходимо следовать каждому выпускнику.
Список использованной
литературы
1.Открытый банк заданий
по математике (http//mathege.ru)
2. Петухова Л.И. О
решении текстовых задач по математике // Фестиваль педагогических идей
«Открытый урок». – М.: Первое сентября, 2004. – 540 с.
3.Решу ЕГЭ
(http://reshuege.ru/ )
4. Шевкин
А.В. Текстовые задачи : 7 – 11 классы: Учебное пособие по математике / А.
В. Шевкин. – М. : ТИД «Русское слово – РС», 2003. – 184 с.
5. Фридман Л.М., Турецкий
Е.Н. Как научиться решать задачи. – М.: Просвещение, 1984. – 250 с.
Приложение
Примеры задач из текстов
ГИА и ЕГЭ
Задачи систематизированы
по типам:
1.
Связь основных характеристик
движения: S; V; t
2.
Средняя скорость
3.
Движение навстречу
4.
Движение в противоположных
направлениях
5.
Движение в одном направлении
6.
Движение по окружности
(замкнутой трассе)
7.
Движение по воде
8.
Движение протяжённых тел
9.
Движение в гору и с горы
1.
Связь основных характеристик
движения: S; V; t
1.
(ГИА 6 баллов) Один автомобиль
проходит в минуту на 200м больше, чем другой, поэтому затрачивает на
прохождение одного километра на 10сек меньше. Сколько километров в час проходит
каждый автомобиль?
2.
(ГИА 4 балла) Турист, находящийся
в спортивном лагере, должен успеть к поезду на железнодорожную станцию. Если он
поедет на велосипеде со скоростью 15км/час, то опоздает на 30мин , а если
поедет на мопеде со скоростью 40км/час, то приедет за 2час до отхода поезда.
Чему равно расстояние от лагеря до станции?
3.
(ГИА 2 балла) Скорость
велосипедиста от посёлка до станции была на 1км/час больше, чем на обратном
пути. На обратный путь он затратил на 2 мин. Больше. Расстояние между пунктами
7км. Найдите первоначальную скорость велосипедиста.
4.
(ЕГЭ) Велосипедист выехал с
постоянной скоростью из города А в город В, расстояние между которыми равно 98
км. На следующий день он отправился обратно со скоростью на 7 км/ч больше
прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на
обратный путь столько же времени, сколько на путь из А в В. Найдите скорость
велосипедиста на пути из А в В. Ответ дайте в км/ч.
5.
(ЕГЭ) Товарный поезд каждую
минуту проезжает на 900 метров меньше, чем скорый, и на путь в 180 км тратит
времени на 3 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ
дайте в км/ч.
2. Средняя скорость
1.
(ЕГЭ) Половину времени,
затраченного на дорогу, автомобиль ехал со скоростью 66 км/ч, а вторую половину
времени — со скоростью 82 км/ч. Найдите среднюю скорость автомобиля на
протяжении всего пути. Ответ дайте в км/ч.
2.
(ЕГЭ) Путешественник переплыл
море на яхте со средней скоростью 24 км/ч. Обратно он летел на спортивном
самолете со скоростью 456 км/ч. Найдите среднюю скорость путешественника на
протяжении всего пути. Ответ дайте в км/ч.
3.
(ЕГЭ) Первую треть трассы
автомобиль ехал со скоростью 100 км/ч, вторую треть — со скоростью 75
км/ч, а последнюю — со скоростью 60 км/ч. Найдите среднюю скорость
автомобиля на протяжении всего пути. Ответ дайте в км/ч.
4.
(ЕГЭ) Первые три часа
автомобиль ехал со скоростью 70 км/ч, следующий час — со скоростью 65
км/ч, а затем один час — со скоростью 45 км/ч. Найдите среднюю скорость
автомобиля на протяжении всего пути. Ответ дайте в км/ч.
5.
(ЕГЭ) Первые 120 км
автомобиль ехал со скоростью 50 км/ч, следующие 160 км — со
скоростью 100 км/ч, а затем 120 км — со скоростью 120 км/ч.
Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте
в км/ч.
3. Движение навстречу
1.
Два охотника отправились
одновременно навстречу друг другу из двух деревень, расстояние между которыми
18км. Первый шёл со скоростью 5км/час, а второй – 4км/час. Первый охотник взял
с собой собаку, которая бежала со скоростью 8км/час. Собака сразу же побежала
навстречу второму охотнику, встретила его, повернула и стой же скоростью
побежала навстречу второму охотнику и т.д. Так она бегала от одного охотника к
другому, пока те не встретились. Сколько километров пробежала собака?
2.
(ГИА 2 балла) Два пешехода
отправляются одновременно навстречу друг другу из двух пунктов, расстояние
между которыми равно 50км, и встречаются через 5 час. Определите скорость
каждого пешехода, если скорость у одного из них на 2км/час больше, чем у
другого.
3.
(ГИА 4 балла) Из города А в
город В, расстояние между которыми равно 300км, выехал автобус. Через 20мин.
Навстречу ему из В в А выехал автомобиль и через 2час. После выезда встретил автобус.
С какой скоростью ехал автомобиль, если известно, что она была на 20км/час
больше скорости автобуса?
4.
( ГИА 6 баллов) Турист и
велосипедист одновременно отправились навстречу друг другу из пунктов А и В.
Они встретились через 1,5часа, после чего каждый продолжил движение в своём
направлении. Велосипедист прибыл в пункт А через 2 часа после выезда из В. За
какое время прошёл путь от А до В турист?
5.
(ГИА 6 баллов) Из пунктов А и
В, расстояние между которыми 6км, одновременно вышли навстречу друг другу два
пешехода. После их встречи пешеход, шедший из а, пришёл в в через 24мин, а
шедший из В пришёл в А через 54 мин. На каком расстоянии от пункта А
встретились пешеходы?
6.
(ЕГЭ) Из двух городов,
расстояние между которыми равно 480 км, навстречу друг другу одновременно
выехали два автомобиля. Через сколько часов автомобили встретятся, если их
скорости равны 75 км/ч и 85 км/ч?
7.
(ЕГЭ) Из городов A и B,
расстояние между которыми равно 440 км, навстречу друг другу одновременно
выехали два автомобиля и встретились через 4 часа на расстоянии 240 км от
города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в
км/ч.
8.
(ЕГЭ) Расстояние между
городами A и B равно 440 км. Из города A в город B со скоростью 50 км/ч выехал
первый автомобиль, а через час после этого навстречу ему из города B выехал со
скоростью 80 км/ч второй автомобиль. На каком расстоянии от города A автомобили
встретятся? Ответ дайте в километрах.
9.
(ЕГЭ) Расстояние между
городами A и B равно 680 км. Из города A в город B выехал первый автомобиль, а
через два часа после этого навстречу ему из города B выехал со скоростью 80
км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили
встретились на расстоянии 360 км от города A. Ответ дайте в км/ч.
10.
(ЕГЭ) Из городов A и B навстречу
друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 1 час
раньше, чем велосипедист приехал в A, а встретились они через 40 минут после
выезда. Сколько часов затратил на путь из B в A велосипедист?
4. Движение в
противоположных направлениях
1.
Из одного пункта в
противоположных направлениях вышли два пешехода. Скорость одного из них 6
км/час, и он был в пути на 2 час больше, чем другой. Скорость другого
составляла 2/3 скорости первого. Сколько времени был в пути каждый пешеход, если
они удалились друг от друга на 28км?
2.
Папа и сын плывут на лодке
против течения. В какой то момент сын уронил за борт папину шляпу. Только через
15 мин. Папа заметил пропажу, быстро развернул лодку и они поплыли по течению с
той же собственной скоростью. За сколько минут они догонят шляпу?
5. Движение в одном
направлении
1.
На катке Ваня догоняет Мишу,
который находится от него в 24м и движется со скоростью 6м/сек. Это составляет
3/5 скорости Вани. Через сколько времени Ваня догонит Мишу и какое он проедет
расстояние при этом?
2.
(Старинная задача) Собака
усмотрела в 150 саженях зайца, который пробегает в 2 мин 500 сажен, а собака в
5 мин -1 300 сажен. Спрашивается, в какое время собака догонит зайца?
3.
(Старинная задача) Некий юноша
пошёл из Москвы к Вологде. Он проходил в день по 40 вёрст. Через день вслед за
ним был послан другой юноша, проходивший в день по 45 вёрст. Через сколько дней
второй догонит первого?
4.
(ГИА 4балла) Из пункта
А в пункт В, расстояние между которыми 60км, одновременно выехали автобус и
автомобиль. В пути автомобиль сделал остановку на 3мин, но в пункт В прибыл на
7мин. раньше автобуса. Найдите скорости автомобиля и автобуса, если известно,
что скорость автобуса в 1,2 раза меньше скорости автомобиля.
5.
(ГИА 6 баллов) Из турбазы в одном
направлении выходят три туриста с интервалом в 30минут. Первый идёт со
скоростью 5км/час, второй -4кмчас. Третий турист догоняет второго, а ещё через
4 часа догоняет первого. Найдите скорость третьего туриста.
6.
(ЕГЭ) Из пункта A в пункт B
одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь
путь. Второй проехал первую половину пути со скоростью, меньшей скорости
первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в
результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите
скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте
в км/ч.
7.
(ЕГЭ) Два велосипедиста
одновременно отправились в 154-километровый пробег. Первый ехал со скоростью,
на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа
раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ
дайте в км/ч.
8.
(ЕГЭ) Из пункта А в пункт В,
расстояние между которыми 50 км, одновременно выехали автомобилист и
велосипедист. Известно, что в час автомобилист проезжает на 40 км больше, чем
велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в
пункт В на 4 часа позже автомобилиста. Ответ дайте в км/ч.
9.
(ЕГЭ) Расстояние между
городами A и B равно 630 км. Из города A в город B выехал автомобиль, а через 2
часа следом за ним со скоростью 60 км/ч выехал мотоциклист, догнал автомобиль в
городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B.
Найдите расстояние от A до C. Ответ дайте в километрах.
10.
(ЕГЭ) Два пешехода
отправляются одновременно в одном направлении из одного и того же места на
прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго.
Через сколько минут расстояние между пешеходами станет равным 150 метрам?
11.
(ЕГЭ) Первый велосипедист
выехал из поселка по шоссе со скоростью 12 км/ч. Через час после него со
скоростью 10 км/ч из того же поселка в том же направлении выехал второй
велосипедист, а еще через час после этого — третий. Найдите скорость
третьего велосипедиста, если сначала он догнал второго, а через 2 часа 45 минут
после этого догнал первого. Ответ дайте в км/ч.
6.
Движение по окружности
(замкнутой трассе)
1.
(ГИА 4 балла) Два тела,
движущиеся в разные стороны по окружности длиной 500м с постоянными скоростями,
встречаются каждые 125сек. При движении в одну сторону первое тело догоняет
второе каждые 12,5 сек. Найдите скорости каждого тела.
2.
(ГИА 4 балла) Два тела,
двигаясь по окружности в одном направлении, встречаются через каждые 112 мин.,
а двигаясь в противоположных направлениях – через каждые 16 минут. Во втором
случае расстояние между ними уменьшилось с 40м до 26м за 12сек. Сколько метров
в минуту проходит каждое тело?
3.
(ГИА 4 балла) Два тела,
движущиеся в разные стороны по окружности длиной 500м с постоянными скоростями,
встречаются каждые 125сек. При движении в одну сторону первое тело догоняет
второе каждые 12,5 сек. Найдите скорости каждого тела.
4.
(ЕГЭ) Два мотоциклиста
стартуют одновременно в одном направлении из двух диаметрально противоположных
точек круговой трассы, длина которой равна 22 км. Через сколько минут
мотоциклисты поравняются в первый раз, если скорость одного из них на 20 км/ч
больше скорости другого?
5.
(ЕГЭ) Из одной точки круговой
трассы, длина которой равна 12 км, одновременно в одном направлении стартовали
два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20
минут после старта он опережал второй автомобиль на один круг. Найдите скорость
второго автомобиля. Ответ дайте в км/ч.
6.
(ЕГЭ) Из пункта A круговой
трассы выехал велосипедист, а через 30 минут следом за ним отправился
мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый
раз, а еще через 44 минуты после этого догнал его во второй раз. Найдите
скорость мотоциклиста, если длина трассы равна 33 км. Ответ дайте в км/ч.
7.
Движение по воде
1.
(ГИА 2 балла) Катер прошёл
20км по течению реки и такой же путь обратно, затратив на весь путь 1час 45мин.
Скорость течения реки равна 2км/час. Найдите собственную скорость катера.
2.
(ГИА 2 балла) Катер прошёл
20км по течению реки и такой же путь обратно, затратив на весь путь 1час 45мин.
Скорость течения реки равна 2км/час. Найдите собственную скорость катера.
3.
(ГИА 2 балла) Моторная лодка
прошла 10км по озеру и 4км против течения, затратив на весь путь 1час. Найдите
собственную скорость лодки, если скорость течения реки равна 3км/час.
4.
(ГИА 2 балла) Катер прошёл
15км по течению реки и 4км по озеру, затратив на весь путь 1час. Найдите
собственную скорость катера, если скорость течения реки равна 4км/час.
5.
(ГИА 2 балла) Лодка может
проплыть 15км по течению реки и ещё 6км против течения за то же время, за какое
плот может проплыть 5км по этой реке. Найдите скорость течения реки, если
известно, что собственная скорость лодки 8км/час.
6.
(ГИА 6 баллов) Плот проплывает
из пункта А в пункт В за 12 час, а моторная лодка – за 3час. За какое время
моторная лодка преодолеет такое же расстояние в стоячей воде?
7.
(ЕГЭ) Моторная лодка прошла
против течения реки 255 км и вернулась в пункт отправления, затратив на
обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если
скорость течения равна 1 км/ч. Ответ дайте в км/ч.
8.
(ЕГЭ) Теплоход проходит по
течению реки до пункта назначения 255 км и после стоянки возвращается в пункт
отправления. Найдите скорость теплохода в неподвижной воде, если скорость
течения равна 1 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход
возвращается через 34 часа после отплытия из него. Ответ дайте в км/ч.
9.
(ЕГЭ) От пристани А к пристани
В отправился с постоянной скоростью первый теплоход, а через 1 час после этого
следом за ним со скоростью на 1 км/ч большей отправился второй. Расстояние
между пристанями равно 420 км. Найдите скорость первого теплохода, если в
пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
10.
(ЕГЭ) Байдарка в 10:00 вышла
из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20
минут, байдарка отправилась назад и вернулась в пункт А в 16:00. Определите (в
км/ч) собственную скорость байдарки, если известно, что скорость течения реки 2
км/ч.
11.
(ЕГЭ) Пристани A и B расположены
на озере, расстояние между ними 195 км. Баржа отправилась с постоянной
скоростью из A в B. На следующий день она отправилась
обратно со скоростью на 2 км/ч больше прежней, сделав по пути остановку на 2
часа. В результате она затратила на обратный путь столько же времени, сколько
на путь из A в B. Найдите скорость баржи на пути
из A в B. Ответ дайте в км/ч.
12.
(ЕГЭ) Теплоход, скорость
которого в неподвижной воде равна 20 км/ч, проходит по течению реки и после
стоянки возвращается в исходный пункт. Скорость течения равна 4 км/ч, стоянка
длится 6 часов, а в исходный пункт теплоход возвращается через 36 часов после
отплытия из него. Сколько километров прошел теплоход за весь рейс?
13.
(ЕГЭ) Расстояние между
пристанями A и B равно 189 км. Из A в B по течению реки отправился плот, а
через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас
повернула обратно и возвратилась в A. К этому времени плот прошел 50 км.
Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2
км/ч. Ответ дайте в км/ч.
8. Движение протяжённых
тел
1.
(ЕГЭ) Поезд, двигаясь
равномерно со скоростью 50 км/ч, проезжает мимо придорожного столба за 72
секунды. Найдите длину поезда в метрах.
2.
(ЕГЭ) Поезд, двигаясь
равномерно со скоростью 70 км/ч, проезжает мимо лесополосы, длина которой равна
1000 метров, за 1 минуту 48 секунд. Найдите длину поезда в метрах.
3.
(ЕГЭ) По морю параллельными
курсами в одном направлении следуют два сухогруза: первый длиной 130 метров,
второй — длиной 120 метров. Сначала второй сухогруз отстает от первого, и
в некоторый момент времени расстояние от кормы первого сухогруза до носа
второго составляет 600 метров. Через 11 минут после этого уже первый сухогруз
отстает от второго так, что расстояние от кормы второго сухогруза до носа
первого равно 800 метрам. На сколько километров в час скорость первого
сухогруза меньше скорости второго?
4.
(ЕГЭ) По двум параллельным
железнодорожным путям в одном направлении следуют пассажирский и товарный
поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Длина
товарного поезда равна 800 метрам. Найдите длину пассажирского поезда, если
время, за которое он прошел мимо товарного поезда, равно 2 минутам. Ответ дайте
в метрах.
9. Движение в гору и с
горы
1.
(ГИА 4 балла) Путь от
пансионата до почты, который сначала идёт в гору, а потом под гору, пешеход
прошёл за 1час 40мин, а обратный путь – за 2час20мин. В гору он шёл со
скоростью 3км/час, а под гору- со скоростью 6км/час. Найдите расстояние от
пансионата до почты.
2.
(ГИА 4 балла) Путь от посёлка
до озера идёт сначала горизонтально, а затем в гору. От посёлка до озера
велосипедист доехал за 1 час, а обратно за 46мин. Его скорость на
горизонтальном участке была равна 12км/час, на подъёме-8км/час, а на
спуске-15км/час. Найдите расстояние от посёлка до озера.
3.
(ГИА 6 баллов) Автомобиль едет
из А в В сначала 2мин с горы, а затем 6мин в гору. Обратный же путь он проделывает
за 13мин. Во сколько раз быстрее автомобиль едет с горы, чем в гору?
4.
(ГИА 6 баллов) Дорога от
посёлка до станции идёт сначала в гору, а потом под гору, при этом её длина
равна 9км. Пешеход на подъёме идёт со скоростью, на 2км/час меньшей, чем на спуске.
Путь от посёлка до станции занимает у него 1час 50мин, а обратный путь занимает
1час 55мин. Определите длину подъёма на пути к станции и скорости пешехода на
подъёме и спуске?
- Схемы задач на движение помогают представить наглядно условие задачи и найти верное решение.
- Таблица к задачам на движение позволяет структурировать данные, чтобы наглядно видеть исходные данные и неизвестные величины.
Поэтому, чтобы решить сложные задачи на движение, нужно нарисовать схему, а в дополнение к схеме рекомендуется нарисовать таблицу, где в шапке параметры скорости, времени и расстояния. При этом везде применяется основная формула:
Рассмотрим решение следующих типов задач:
- простые задачи на скорость, время и расстояние;
- задачи на движение в разных направлениях: сближение и удаление;
- задачи на движение в одном направлении: сближение и удаление;
- решение задач на движение по реке.
Решить простые задачи на движение
Для решения простых задач на движение, как правило, схема или таблица не требуется, в них применяется формула нахождения скорости, времени или расстояния. Но иногда, чтобы не запутаться в решении, лучше воспользоваться каким-либо методом. Рассмотрим схему и таблицу, чтобы вы смогли выбрать наиболее удобный для себя способ разобраться в задаче.
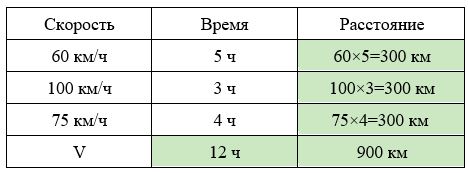
Задача 1. Средняя скорость
Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
Средняя скорость — это отношение пройденного пути ко времени, за который пройден этот путь.
- Найдем общее расстояние: 900 км.
- Найдем время в пути: 5 + 3 + 4 = 12 часов.
- Найдем среднюю скорость автомобиля: 900:12 = 75 км/ч.
Задача 2. Движение с остановкой
В 9:00 велосипедист выехал из пункта А в пункт Б. Доехав до пункта Б, он сделал остановку на полчаса, а в 11:30 выехал обратно с прежней скоростью. В 13:00 ему оставалось проехать 8 км до пункта А. Найдите расстояние между пунктами А и Б.
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности.
- Найдем скорость: 8 : 0,5 = 16 км/ч
- Найдем расстояние: 16×2=32 км.
Задача 3. Уровень ЕГЭ.
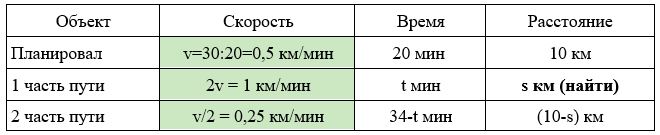
Лыжник планировал проехать 10 км с горы за 20 минут с постоянной скоростью v. Вместо этого первые несколько километров он проехал в два раза быстрее, чем планировал, а оставшиеся километры он проехал в два раза медленнее, чем планировал. В итоге весь путь занял у него 34 минуты. Сколько километров лыжник проехал в два раза быстрее, чем планировал?
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
- Найдем скорость, с которой лыжник планировал скатиться: 10 : 20 = 0,5км/мин
- Найдем скорости, с которыми лыжник скатывался: 3км/мин и 0,25км/мин.
- Составим систему уравнений:
1) 1×t=s → t=s
2) 0,25×(34-t)=10-s → 0,25×(34-s)=10-s → s=2 км.
Решить задачи на движение в разных направлениях: сближение и удаление
Задача 4. Скорость удаления
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго — 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) /
Способ 1.
1) 100× 4 = 400 (км) — проехал первый автомобиль,
2) 70 × 4 = 280 (км) — проехал второй автомобиль.
3) 400 + 280 = 680 (км).
Способ 2.
1) (100 + 70), 170 км/ч — это скорость удаления автомобилей.
2) 170× 4 = 680 км.
Задача 5. Скорость сближения
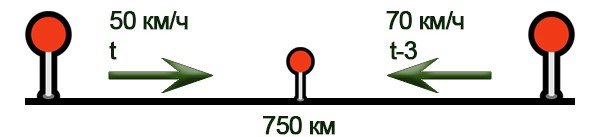
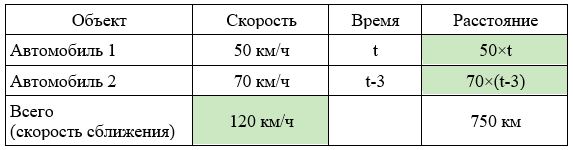
Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
Способ 1.
- Составим уравнение: 50×t + 70×(t-3) =750
- Решим уравнение: 120t=960; t=8 часов.
- По условиям задачи нужно найти расстояние от пункта А, то есть расстояние для первого автомобиля: 50×8=400км.
Способ 2.
- За первые три часа пути автомобиль, выехавший из города А, проехал 150 километров и расстояние от него до города В стало равным 600 км.
- Скорость сближения двух автомобилей равна 120 км/ч, значит, они встретятся через 5 часов после выезда второго автомобиля: 600:120=5 часов.
- Таким образом, первый автомобиль всего ехал 8 часов: 50×8=400км.
Задача 6. Скорость сближения
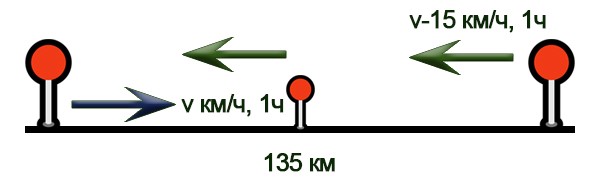
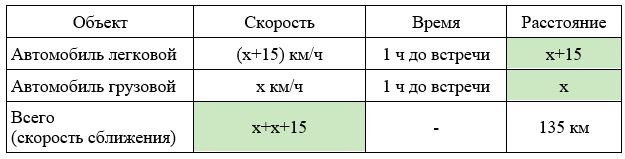
Расстояние между пунктами А и В равно 135 км. Из пункта А в пункт В выехал легковой автомобиль. Одновременно с ним из пункта В в пункт А выехал грузовой автомобиль, скорость которого на 15 км/ч меньше скорости легкового. Через час после начала движения они встретились. Через сколько минут после встречи грузовой автомобиль прибыл в пункт А?
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
- Пусть x км/ч — скорость грузового автомобиля, тогда (x + 15) км/ч — скорость легкового автомобиля. Получаем уравнение: x+x+15=135; x=60км/ч.
- Найдем сколько времени грузовой автомобиль затратил на весь путь: 135:60=2,25 часов.
- Найдем сколько времени грузовой автомобиль затратил на путь после встречи: 2,25-1=1,25 часов или 75 минут (1,25*60).
- Ответ: 75 мин.
Задача 7. Уровень ЕГЭ.
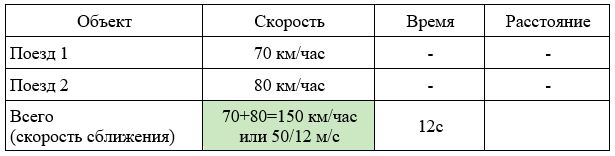
Два поезда движутся навстречу друг другу – один со скоростью 70 км/ч, другой со скоростью 80 км/ч. Пассажир, сидящий во втором поезде, заметим, что первый поезд прошел мимо него за 12 секунд. Какова длина первого поезда? Ответ дайте в метрах.
Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
- Найдем скорость сближения: 70+80=150км/ч.
- Переведем ее в другие единицы измерения: 150 км/ч = 150000/3600 = 50/12 м/с
- Заметим, что фраза “первый поезд прошел мимо пассажира за 12с” означает, что с того момента, как пассажир увидел голову поезда, до того момента, как он увидел хвост поезда, прошло 12с.
- Найдем расстояние 50/12 × 12 =50 метров.
Решить задачи на движение в одном направлении: сближение и удаление
Задача 8. Скорость сближения
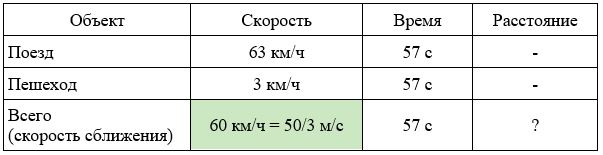
Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 3 км/ч пешехода за 57 секунд. Найдите длину поезда в метрах.
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
- Найдем скорость поезда относительно пешехода: 63 − 3 = 60 км/ч
- Переведем скорость сближения в другие единицы измерения: 60 км/ч = 60000/3600=50/3 м/с.
- Найдем длину поезда (расстояние, которое проехал поезд): (50/3)*57=950 м.
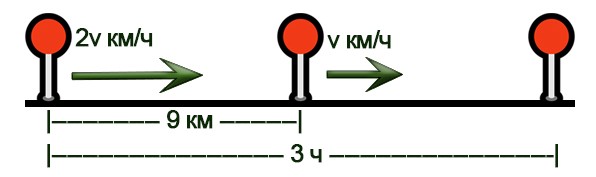
Задача 9. Скорость сближения
Два туриста одновременно вышли в одном направлении в город N. При этом вышли они из разных городов, расстояние между которыми 9 км. Известно, что турист, изначально находившийся дальше от города N, шёл со скоростью, в два раза превышающей скорость другого туриста. В город N они прибыли одновременно, через 3 часа после начала движения. Найдите скорость туриста, который шёл быстрее. Ответ дайте в км/ч.
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
- Найдем скорость сближения туристов: 9:3=3 км/ч.
- По формуле сближения получаем: 2v-v=3 → v=3 →2v=6 км/ч.
- Ответ: 6
Задача 10. Скорость удаления
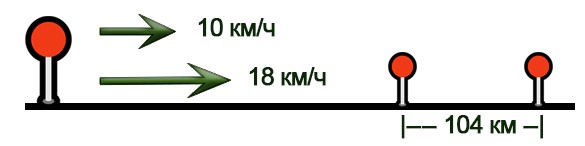
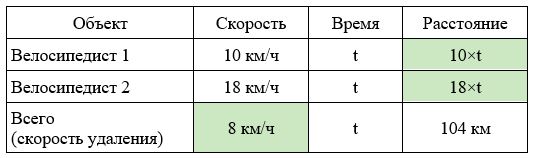
Два велосипедиста выехали из одного места в одном направлении. Скорость первого – 10 км/ч, а второго – 18 км/ч. Через сколько часов расстояние между велосипедистами будет равно 104 км?
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
- Найдем скорость удаления: 18-10=8 км/ч
- Найдем время в пути: 108:8=13 часов.
- Ответ: 13
Задача 11. Скорость удаления
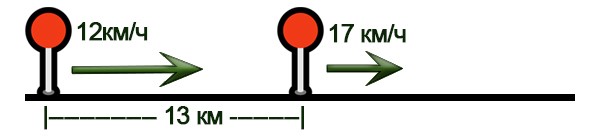
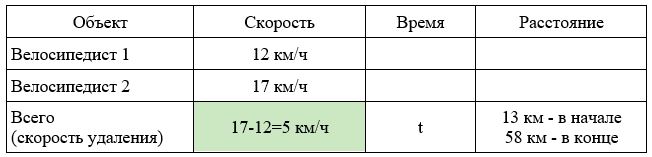
Два велосипедиста выехали в одном направлении из мест, находящихся на расстоянии 13 км друг от друга. Скорость первого – 12 км/ч, а второго – 17 км/ч, причем второй находился в начале движения впереди. Через сколько часов расстояние между велосипедистами будет равно 58 км?
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
- Найдем скорость удаления: 17-12=5 км/ч
- Найдем расстояние, на которое они удались друг от друга: 58-13=45 км.
- Найдем время: 45:5=9 часов.
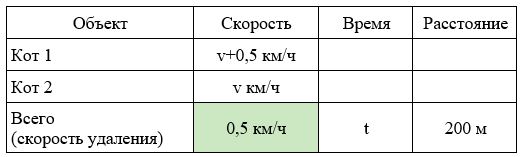
Задача 12. Уровень ЕГЭ
Два кота одновременно выбегают в одном направлении из одного и того же подъезда. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между котами станет равным 200 метрам?
Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
- Скорость удаления будет 0,5 км/ч — это скорость, с которой первый кот бежит быстрее второго.
- Найдем время: 0,2 : 0,5 = 0,4 часа
- Переведем время в другие единицы измерения: 0,4 ч = 0,4*60 = 24 мин.
Решить задачи на движение по реке
Задача 13.
Яхта движется по стоячей воде, ее собственная скорость равна 30 км/ч. Встречный ветер каждую минуту сносит яхту на 20 метров. За сколько часов яхта пройдет 259200 метров?
Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
- Переведем скорость яхты в другие единицы измерения: 30 км/ч = 500 м/с.
- Найдем скорость удаления: 500-20=480 м/с.
- Найдем время: 259200 :480=540 минут = 9 часов.
Задача 14.
Расстояние от пристани А до пристани Б по течению реки катер прошёл за 5 часов, а на обратный путь он затратил на 1 час больше. Найдите скорость катера в неподвижной воде (собственную скорость), если скорость течения реки 2 км/ч.
Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)
- Пусть скорость катера в неподвижной воде равна x км/ч.
- Составим уравнение: 5×(x+2)=6×(x-2); x=22 км/ч.
Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.
Советы для решения задач на движения
- В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
- Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.