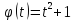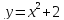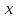Как составить сложную функцию примеры

Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x),  а f — функция от u:  f=f(u), то функция y=f(u) — сложная.

А  u  в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций.

1) y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса появится выражение, зависящее от x, даже самое простое — такая функция называется сложной. То есть y=sin u — сложная функция, если u — некоторая функция от x. Примеры сложных функций с синусом:

y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя функция f — это синус. То есть u=x+1, f=sin u.

y=sin (5x-2x³+3). Внутренняя функция u=5x-2x³+3, внешняя функция f=sin u.

y=sin (x/7). Внутренняя функция u=x/7, внешняя функция f=sin u.

2) y=cos x — «простая» функция. y=cos u — сложная функция, если u — некоторая функция, зависящая от x. Примеры сложных функций с внешней функцией — косинусом:

y=cos (4-11x). Внутренняя функция u=4-11x, внешняя функция — косинус: y=cos u.

y=cos (7x³ -4x²). Внутренняя функция u=7x³ -4x², внешняя — y=cos u.

3) y=tg x — «простая» функция. y = tg u — сложная функция, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — тангенс:

y=tg(17+5x²). Внутренняя функция u=17+5x², внешняя — y=tg u.

y=tg(9-x). Внутренняя u=9-x, внешняя — y=tg u.

4) y=ctg x — «простая» функция. y=ctg u — сложная функция, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — котангенс:

y=ctg(2x+6). Внутренняя функция u=2x+6, внешняя — y=ctg u.

y=ctg(√x).  u=√x, f=ctg u.

5) y=√x — «простая» функция. y=√u — сложная, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — квадратный корень:

   

Здесь внутренняя функция y=sin x, а внешняя — f=√u.

   

Здесь u=9x³-12x+5, f=√u.

6) y=xⁿ — «простая» функция. y=uⁿ — сложная, если u=u(x). Примеры сложных функция для случая, когда внешняя функция — степенная.

y=sin³x. Внутренняя функция y=sin x (так как sin³x=(sin x)³), внешняя — у=u³.

   

7) y=arcsin x — «простая» функция. y=arcsin u — сложная, когда u=u(x).

Например, y=arcsin (3x-9) — сложная функция. Внутренняя функция u=3x-9,  внешняя — f=arcsin u.

y=arcsin (17-5x³).  u=17-5x³, f=arcsin u.

8) y=arccos x — «простая» функция. y=arccos u — сложная, при u=u(x).

Например, y=arccos (34x+5) — сложная функция. Внутренняя функция u=34x+5, внешняя — f=arccos u.

9) y=arctg x — «простая» функция. y=arctg u — сложная, при u=u(x).

Например, y= arctg (6x+2x³-7). Внутренняя функция u =6x+2x³-7, внешняя — f=arctg u.

10) y=arcctg x — «простая функция. При u=u(x) функция y=arcctg u — сложная.

Например, y= arcctg(2-11x+x²) — сложная функция. u=2-11x+x², f= arcctg u.

11) y=ln x — «простая» функция. y= ln u — сложная, при u=u(x).

Например, y=ln(4+32x-2x³). Внутренняя функция y=4+32x-2x³, внешняя — f=ln u.

   

Это — «простая» функция. А вот при u=u(x) получаем логарифм сложной функции:

   

Например,

   

   

Эта функция — «простая» (называется экспонента). А вот если в показателе стоит не x, а некоторая функция от икса: u=u(x), то это — уже экспонента сложной функции:

   

Например,

   

   

Эта функция — «простая». А вот если в показателе стоит не x, а некоторое выражение с x — функция u=u(x), то это уже степень сложной функции:

   

Например,

   

Эта функция — сложная. Внутренняя функция u=8x³+5x, а внешняя — степень сложной функции

   

Следует добавить, что внутренняя функция u, в свою очередь, может быть сложной функцией. И таких «вложенных» функций может быть несколько (теоретически — сколько угодно).

Например,

1) y=cos³(3x-12). Здесь внутренняя функция u =cos(3x-12), а внешняя функция f=u³. Но внутренняя функция y=cos(3x-12), в свою очередь, тоже является сложной функцией. Для нее внутренняя функция u=3x-12, а внешняя f=cos x.

   

Сначала рассмотрим эту функцию, как логарифм сложной функции. Тогда внутренняя функция

   

внешняя — логарифм:

   

В свою очередь, функция

   

— тоже сложная. Это — синус сложной функции, то есть

   

Но u — снова сложная функция. Здесь уже внутренняя  функция u=2x²+5x, а внешняя f=√u.

   Раз ты зашел сюда, то уже, наверное, успел увидеть в учебнике эту формулу

((f(g(x)))’=f'(g(x))cdot g'(x))

и сделать вот такое лицо:

Друг, не переживай! На самом деле все просто до безобразия. Ты обязательно все поймешь. Только одна просьба – прочитай статью не торопясь, старайся понять каждый шаг. Я писал максимально просто и наглядно, но вникнуть в идею всё равно надо. И обязательно реши задания из статьи.

Содержание:

• Что такое сложная функция?
• 
  “Распаковка” сложной функции
• 
  Внутренняя и внешняя функция
• 
  Производная сложной функции. Примеры

Что такое сложная функция?

Представь, что ты переезжаешь в другую квартиру и поэтому собираешь вещи в большие коробки. Пусть надо собрать какие-нибудь мелкие предметы, например, школьные письменные принадлежности. Если просто скидать их в огромную коробку, то они затеряются среди других вещей. Чтобы этого избежать, ты сначала кладешь их, например, в пакет, который затем укладываешь в большую коробку, после чего ее запечатываешь. Этот “сложнейший” процесс представлен на схеме ниже:

Казалось бы, причем здесь математика? Да притом, что сложная функция формируется ТОЧНО ТАКИМ ЖЕ способом! Только «упаковываем» мы не тетради и ручки, а (x), при этом «пакетами» и «коробками» служат разные функции.

Например, возьмем x и «запакуем» его в функцию косинуса:

В результате получим, ясное дело, (cos⁡x). Это наш «пакет с вещами». А теперь кладем его в «коробку» – запаковываем, например, в кубическую функцию.

Что получится в итоге? Да, верно, будет «пакет с вещами в коробке», то есть «косинус икса в кубе».

Получившаяся конструкция и есть сложная функция. Она отличается от простой тем, что к одному иксу применяется НЕСКОЛЬКО «воздействий» (упаковок) подряд и получается как бы «функция от функции» – «упаковка в упаковке».

В школьном курсе видов этих самых «упаковок» совсем мало, всего четыре :

Давай теперь «упакуем» икс сначала в показательную функцию с основанием 7, а потом в тригонометрическую функцию тангенс. Получим:

(x → 7^x → tg⁡(7^x))

А теперь «упакуем» икс два раза в тригонометрические функции, сначала в синус, а потом в котангенс:

(x → sin⁡x → ctg⁡ (sin⁡x ))

Просто, правда?

Напиши теперь сам функции, где икс:
   – сначала «упаковывается» в косинус, а потом в показательную функцию с основанием (3);
   – сначала в пятую степень, а затем в тангенс;
   – сначала в логарифм по основанию (4), затем в степень (-2). 

Ответы на это задание посмотри в конце статьи.

А можем ли мы «упаковать» икс не два, а три раза? Да, без проблем! И четыре, и пять, и двадцать пять раз. Вот, например, функция, в которой икс «упакован» (4) раза:

(y=5^{log_2⁡{sin⁡(x^4 )}})

Но такие формулы в школьной практике не встретятся (студентам повезло больше – у них может быть и посложнее☺).

«Распаковка» сложной функции

Посмотри на предыдущую функцию еще раз. Сможешь ли ты разобраться в последовательности «упаковки»? Во что икс запихнули сначала, во что потом и так далее до самого конца. То есть – какая функция вложена в какую? Возьми листок и запиши, как ты считаешь. Можно сделать это цепочкой со стрелками как мы писали выше или любым другим способом.

Сделал?

Теперь правильный ответ: сначала икс «упаковали» в (4)-ую степень, потом результат упаковали в синус, его в свою очередь поместили в логарифм по основанию (2), и в конце концов всю эту конструкцию засунули в степень пятерки.

То есть разматывать последовательность надо В ОБРАТНОМ ПОРЯДКЕ. И тут подсказка как это делать проще: сразу смотри на икс – от него и надо плясать. Давай разберем несколько примеров.

Например, вот такая функция: (y=tg⁡(log_2⁡x )). Смотрим на икс – что с ним происходит сначала? Берется логарифм от него. А потом? Берется тангенс от результата. Вот и последовательность будет такая же:

(x → log_2⁡x → tg⁡(log_2⁡x ))

Еще пример: (y=cos⁡{(x^3 )}). Анализируем – сначала икс возвели в куб, а потом от результата взяли косинус. Значит, последовательность будет: (x → x^3 → cos⁡{(x^3 )}). Обрати внимание, функция вроде бы похожа на самую первую (там, где с картинками). Но это совсем другая функция: здесь в кубе икс (то есть (cos⁡{(x·x·x)})), а там в кубе косинус (x) (то есть, (cos⁡x·cos⁡x·cos⁡x)). Эта разница возникает из-за разных последовательностей «упаковки».

Последний пример (с важной информацией в нем): (y=sin⁡{(2x+5)}). Понятно, что здесь сначала сделали арифметические действия с иксом, потом от результата взяли синус: (x → 2x+5 → sin⁡{(2x+5)}). И это важный момент: несмотря на то, что арифметические действия функциями сами по себе не являются, здесь они тоже выступают как способ «упаковки». Давай немного углубимся в эту тонкость.

Как я уже говорил выше, в простых функциях икс «упаковывается» один раз, а в сложных – два и более. При этом любая комбинация простых функций (то есть их сумма, разность, умножение или деление) – тоже простая функция. Например, (x^7) – простая функция и (ctg x) – тоже. Значит и все их комбинации являются простыми функциями:

(x^7+ ctg x) – простая,
(x^7· ctg x) – простая,
(frac{x^7}{ctg x}) – простая и т.д.

Однако если к такой комбинации применить еще одну функцию – будет уже сложная функция, так как «упаковок» станет две. Смотри схему:

Хорошо, давай теперь сам. Напиши последовательность «заворачивания» функций:

   (y=cos{⁡(sin⁡x)})

   (y=5^{x^7})

   (y=arctg⁡{11^x})

   (y=log_2⁡(1+x))

Ответы опять в конце статьи.

Внутренняя и внешняя функции

Зачем же нам нужно разбираться во вложенности функций? Что нам это дает? Дело в том, что без такого анализа мы не сможем надежно находить производные разобранных выше функций.

И для того, чтобы двигаться дальше, нам будут нужны еще два понятия: внутренняя и внешняя функции. Это очень простая вещь, более того, на самом деле мы их уже разобрали выше: если вспомнить нашу аналогию в самом начале, то внутренняя функция – это «пакет», а внешняя – это «коробка». Т.е. то, во что икс «заворачивают» сначала – это внутренняя функция, а то, во что «заворачивают» внутреннюю – уже внешняя. Ну, понятно почему – она ж снаружи, значит внешняя.

Вот в этом примере: (y=tg⁡(log_2⁡x )), функция (log_2⁡x) – внутренняя, а  – внешняя.

А в этом: (y=cos⁡{(x^3+2x+1)}),   (x^3+2x+1) – внутренняя,  а  – внешняя.

Выполни последнюю практику анализа сложных функций, и перейдем, наконец, к тому, ради чего всё затевалось – будем находить производные сложных функций:

Заполни пропуски в таблице:

Производная сложной функции

Браво нам, мы всё ж таки добрались до «босса» этой темы – собственно, производной сложной функции, а конкретно, до той самой ужасной формулы из начала статьи.☺

((f(g(x)))’=f'(g(x))cdot g'(x))

Формула эта читается так:

И сразу смотри схему разбора “по словам” чтобы понимать, что к чему относится:

Надеюсь, термины «производная» и «произведение» затруднений не вызывают. «Сложную функцию» – мы уже разобрали. Загвоздка в «производной внешней функции по неизменной внутренней». Что это такое?

Ответ: это обычная производная внешней функции, при которой изменяется только внешняя функция, а внутренняя остается такой же. Все равно непонятно? Хорошо, давай на примере.

Пусть у нас есть функция (y=sin⁡(x^3 )). Понятно, что внутренняя функция здесь (x^3), а внешняя  . Найдем теперь производную внешней по неизменной внутренней.

Из таблицы производных мы знаем, что производная синуса икс есть косинус икс (табличные значения надо знать наизусть!):      (({sin⁡{x}})’=cos⁡{x}).

Тогда производная внешней функции по неизменной внутренней для нашего случая будет (cos⁡(x^3)). То есть, мы взяли ее как обычную производную синуса, а содержимое синуса (внутреннюю функцию) просто скопировали в полученную производную (косинус), ничего в ней не меняя.

Таким образом, на данный момент имеем:

Осталась «производная внутренней функции». Ну, это совсем легко – обычная производная от внутренней функции, при этом внешняя не влияет вообще никак. В нашем примере, производная от (x^3).

((x^3 )’=3x^2)

Все, теперь можем писать ответ:

Вот так. Давай еще один пример разберем.

Пусть надо найти производную функции (y=(sin⁡x )^3).

Анализируем. Последовательность «заворачивания» у нас такая: (x → sin⁡x → (sin⁡x )^3). Значит, в данном примере внутренняя функция это (sin⁡x), а внешняя .

Производная внешней по внутренней – это производная куба (содержимое куба при этом не меняется). Так как , а в нашем случае в куб «завернут» (sin⁡x), то производная внешней будет (3(sin⁡x)^2). То есть, имеем:

Ну, а производная внутренней – это просто производная синуса икс, то есть косинус икс.

В итоге, имеем:

(y’=((sin⁡x )^3 )’=3(sin⁡x )^2·(sin⁡x )’=3(sin⁡x )^2·cos⁡x)

Понятно?
Ладно, ладно, вот еще один пример с разбором. ☺

Пример. Найти производную сложной функции (y=ln(x^2-x)).

Разбираем вложенность функций: (x → x^2-x → ln⁡(x^2-x)).
Внутренняя: (x^2-x).            Внешняя: .  
Из таблицы производных знаем:.
То есть производная внешней по внутренней будет: (ln⁡(x^2-x)’=) (frac{1}{x^2-x}).
Производная внутренней: ((x^2-x)’= (x^2)’-(x)’=2x-1).
В итоге, согласно большой и страшной формуле имеем:

(y ‘=(ln⁡(x^2-x) )’=)(frac{1}{x^2-x})(·(2x-1))

Ну и напоследок можно немного «причесать» ответ, чтоб никто не докопался:

(y ‘=(ln⁡(x^2-x))’=)(frac{1}{x^2-x})(·(2x-1)=)(frac{2x-1}{x^2-x})

Готово.

Что, еще примеров желаешь? Легко.

Пример. Найти производную сложной функции (y=sin⁡{(cos⁡x)}).
Вложенность функций: (x → cos⁡x → sin⁡{(cos⁡x)})
Внутренняя: (cos⁡x)    Внешняя:
Производная внешней по внутренней: (sin{⁡(cos⁡x )}’=cos⁡{cos⁡x})
Производная внутренней: ((cos⁡x )’= -sin⁡x)
Имеем: (y’=(sin⁡{(cos⁡x)})’=cos⁡{cos⁡x}·(-sin⁡x )=-cos⁡{cos⁡x} ·sin⁡x)

Замечание: Обрати внимание, что заменить запись (cos⁡{cos⁡x}) на (cos^2⁡x) НЕЛЬЗЯ, так как (cos^2⁡x) – это комбинация простых функций (cos^ 2⁡x=cos⁡x·cos⁡x), а (cos⁡{cos⁡x}) – сложная функция: косинус от косинуса икс. Это абсолютно разные функции.

Еще пример с важным замечанием в нем.

Пример. Найти производную сложной функции (y=sqrt{x^6} )
Вложенность функций: (x → x^6 → sqrt{x^6})
Внутренняя: (x^6)      Внешняя:
Производная внешней по внутренней: (sqrt{x^6}’=)(frac{1}{2sqrt{x^6}})
Производная внутренней: ((x^6)’= 6x^5)
Имеем: ((sqrt{x^6})’=)(frac{1}{2sqrt{x^6}})(·6x^5)
И теперь упростим ответ. Вспомним свойство корня: (sqrt[b]{x^a} =x^{frac{a}{b}}). Тогда (sqrt{x^6}=x^{frac{6}{2}}=x^3). С учетом этого получаем:

(y’=( sqrt{x^6})’=)(frac{1}{2sqrt{x^6}})(·6x^5=)(frac{1}{2x^3})(·6x^5=)(frac{6x^5}{2x^3})(=3x^2)

Всё. А теперь, собственно, важное замечание:

Тот же самый ответ, но значительно меньшими усилиями мы могли бы получить, упростив исходную функцию сразу. Воспользуемся тем же свойством корня: (sqrt[b]{x^a} =x^{frac{a}{b}}). Тогда исходная функция приобретает вид: (y=sqrt{x^6}=x^{frac{6}{2}}=x^3). А производная куба это практически табличное значение! Готов ответ: (y’=(sqrt{x^6})’=(x^3 )’=3x^2). Немножко проще предыдущего решения, правда ☺? Поэтому прежде чем искать производную, посмотрите, можно ли исходную функцию упростить, чтоб решать было проще.

Давай рассмотрим пример, где эта идея нам сильно поможет.

Пример. Найти производную сложной функции (y=ln⁡(x^3)).
Можно, конечно, рассмотреть вложенность функций: (x → x^3 → ln⁡(x^3 )), разобрать на внутреннюю и внешнюю и так далее. Но можно вспомнить свойство логарифма: (log_a⁡{b^c}=c·log_a{⁡b}). И тогда функция получается (y=ln⁡(x^3 )=3ln⁡x). Отлично! Берем производную:

(y’=(ln⁡(x^3 ) )’=(3ln⁡x )’=3(ln⁡x )’=3·)(frac{1}{x}=frac{3}{x})

Вуаля!

Теперь задачка посложнее, для продвинутых. Решим пример с тройной вложенностью!

Пример. Найти производную сложной функции (y=3^{sin⁡(x^4+1)}).
Вложенность функций: (x → x^4+1 → sin⁡(x^4+1) → 3^{sin⁡(x^4+1)})
Внутренняя: (x^4+1)    Средняя:      Внешняя:
Сначала производная внешней по средней. Вспоминаем таблицу производных: . Значит, в нашем случае будет (3^{sin⁡(x^4+1)}·ln⁡3).
Хорошо, теперь производная средней по внутренней. По таблице: . Значит, мы получим, (sin⁡(x^4+1)’=cos⁡(x^4+1)).
И наконец, производная внутренней: ((x^4+1)’=(x^4 )’+(1)’=4x^3).
Отлично. Теперь собираем все вместе, перемножая отдельные производные:

((3^{sin⁡(x^4+1)})’=3^{sin⁡(x^4+1)} ·ln⁡3·cos⁡{(x^4+1)}·4x^3)

Готово. Да, это ответ. ☺

Ну, а что ты хотел, я сразу сказал – пример для продвинутых! А представь, что будет с четырехкратной или пятикратной вложенностью? ☺

Пример: Найти производную сложной функции (y=tg⁡(7^x)).

Разбираем вложенность функций: (x : → :7^x : → :tg⁡(7^x)).
Внутренняя: (7^x)       Внешняя: (tg⁡(7^x)).
Ищем производную самой внешней функции, внутреннюю при этом не трогаем.
Из таблицы производных знаем: .
То есть, в нашем случае производная внешней по внутренней будет:  (frac{1}{cos^2⁡(7^x)}).
Теперь ищем производную внутренней. Этой формулой мы уже пользовались, так что сразу пишем ответ: ((7^x)’=7^x·ln⁡7).
И перемножаем результаты:

(y’=tg⁡(7^x)’=)(frac{1}{cos^2⁡(7^x)}·7^x·ln⁡7)

И “причесываем”:   (y’=(tg⁡(7)^x))’=)(frac{1}{cos^2⁡(7^x )})( ·7^x·ln⁡7=)(frac{ln⁡7·7^x}{cos^2⁡(7^x)}).

Ну, теперь думаю всё понятно? И снова повторю – не пугайся сложных конструкций в ответах и промежуточных вычислениях. Они «на лицо ужасные», но зато добрые (в смысле простые) внутри. ☺ Пойми принцип и делай все последовательно.

Последний пример. Такие задания в разных вариациях весьма часто дают на контрольных и тестах. Он вроде как считается сложным. ☺ Хех, наивные учителя. ☺

Пример: Найти производную сложной функции (y=sqrt[3]{(x^5+2x-5)^2}).

Казалось бы, опять у нас тройная вложенность функций:

(x → x^5+2x-5 → (x^5+2x-5)^2 → sqrt[3]{(x^5+2x-5)^2}).

Но давай снова воспользуемся свойством корня (sqrt[b]{x^a} =x^{frac{a}{b}}) и преобразуем нашу функцию к виду:

(y=sqrt[3]{(x^5+2x-5)^2}=(x^5+2x-5)^{frac{2}{3}})

Вот так. И теперь у нас вложенность двойная: (x → x^5+2x-5 → (x^5+2x-5)^{frac{2}{3}})
При этом функция осталась той же! Удобное свойство, однако. Стоит его запомнить, да? ☺ Ладно, поехали дальше.
Внутренняя функция: (x^5+2x-5).    Внешняя: .
Производная внешней по внутренней. По таблице производных общая формула производной степенной функции:   . Получаем:   . Тогда в нашем случае будет: (frac{2}{3}(x^5+2x-5)^{-frac{1}{3}}).
Производная внутренней: ((x^5+2x-5)’=5x^4+2).
Общий результат: (y ‘=(sqrt[3]{(x^5+2x-5)^2})’=((x^5+2x-5)^{frac{2}{3}} )’=frac{2}{3}(x^5+2x-5)^{-frac{1}{3}}·(5x^4+2)).

В принципе, ответ найден. Но здесь можно сильно «причесать» результаты. Это может показаться сложным, но это не так, просто опять нагромождения символов большое и возникает такое ложное ощущение. На всякий случай помни: «не причесанный» ответ – тоже ответ. Поэтому если не поймешь дальнейших преобразований – не критично. Ладно, расческу в руки и вперед.
Вспоминаем свойство отрицательной степени (a^{-n}=)(frac{1}{a^n}). Получаем:

(y ‘=frac{2}{3}(x^5+2x-5)^{-frac{1}{3}}·(5x^4+2)=)(frac{2}{3})(·)(frac{1}{(x^5+2x-5)^{frac{1}{3}}})(·(5x^4+2))

А теперь применяем свойство корня (sqrt[b]{x^a} =x^{frac{a}{b}}) в обратную сторону. То есть, вот так (x^{frac{a}{b}}=sqrt[b]{x^a}). В результате имеем:

(y’=)(frac{2}{3})(frac{1}{(x^5+2x-5)^{frac{1}{3}}})(·(5x^4+2)=)(frac{2}{3})(frac{1}{sqrt[3]{x^5+2x-5}})(·(5x^4+2))

Ну, и перемножаем дроби.

(y’=)(frac{2}{3})(frac{1}{sqrt[3]{x^5+2x-5}})(·(5x^4+2)=)(frac{2(5x^4+2)}{3sqrt[3]{x^5+2x-5}})(=)(frac{10x^4+4}{3sqrt[3]{x^5+2x-5}})

ВСЁ!!! А теперь сам.

Найти производные функций:

a. (y=ctg⁡(x^7))
b. (y=e^{x^4+5x^3})
c. (y=sqrt{cos⁡x})
d. (y=log_5⁡{5^x})
e. (y=(tg⁡x)^3)
f. (y=sin⁡(ln⁡(x^2)))

Ответы ко всем заданиям (вперемежку).

(y=tg⁡(x^5))

(y=log^{-2}_{4}{⁡x})

(y=3^{cos⁡x})

(x → 1+x → log_2⁡{(1+x)} )

(x → 11^x → arctg⁡(11^x) )

(x → x^7 → 5^{x^7})

(x → sin⁡x → cos⁡(sin⁡x))

Сошлось? Красавчик!

Сложная функция

1. Если
   задана некоторая функция
   ,
   например,
   ,
   то это значит, что задано правило
   соответствия
   .
   Это правило предписывает произвести
   над значением аргумента
   
   определенные действия, а именно, в нашем
   случае, умножить его на 2 и затем к
   произведению прибавить 1. В итоге
   получаем определенное число –
   соответствующее значение функции
   .
   Так, если
   ,
   то
   ,
   а если
   ,
   то
   .
   При
   
   получаем
   .
   Областью определения функции является
   числовое множество, в нашем примере –
   это
   .

Рассмотрим
следующее выражение
,
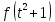
в котором вместо аргумента данной
функции подставляется некоторая функция
от другого аргумента, а именно
.
Можно записать это выражение в виде
.
Таким образом, мы имеем «функцию от
функции». Аргументом этой новой функции
является переменная
.
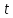
Значения функции
,
то есть
,
вычисляются следующим образом. Берется
значение аргумента,
например, равное 2, и находится значение
функции

при
.
Имеем
.
Далее вычисляем значение функции

при
.
Получаем
.
Таким образом,
.
Для произвольного значения

имеем

, то есть
,
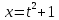
значит
.
Поэтому формула функции

имеет вид
.
Отметим, что фактически в
были проделаны те действия, которые
предусматриваются правилом
,
однако эти действия были проделаны не
над аргументом х, а над выражением
.
Функция

получена в результате описанной операции
называется сложной. Термин «сложная»
используется здесь в смысле «составная»,
то есть сложная функция составлена из
других функций.
Дадим
точное определение сложной функции.

Определение.
Пусть функция

определена на множестве
,
а функция

– на множестве
,
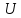
причем множество значений функции

содержится в области определения функции
.Поставим
в соответствие каждому числу

из

число
.
Тем самым на множестве

будет задана функция
.
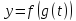
Эту функцию называют сложной функцией
или композицией функций
и
.

При
этом

называют внешней, a

— внутренней функцией композиции.

Пример
1. Пусть
.
Составьте сложную функцию
,
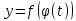
если

.

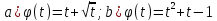
Решение.
Подставим вместо

в формулу функции
,
соответственно,

и
:

1. Получаем 1

.
В итоге
.

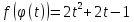
Пример
2. Даны две функции
,
соответственно,
.
Найдите сложную функцию

Решение.
,
,
.

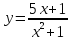
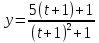
Рассмотрим
следующую задачу, в которой требуется
найти композицию функций

и
,
причем первая функция – внешняя, а
вторая – внутренняя. Для удобства имеет
смысл ввести новые обозначения для
переменных второй функции, обозначив
ее аргумент буквой
,
а зависимую переменную – буквой
.
Имеем
.
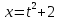
Важно понимать, что введение других
обозначений переменных никак не повлияло
на функцию. Записи

и

представляют одну и ту же функцию, с
областью определения
,
действие которой состоит в возведении
аргумента в квадрат и прибавлении числа
2.

Композицией
функций

и

является функция
.
В этом случае также ничего не мешает
обозначить другой буквой аргумент
сложной функции, а именно – буквой
,
то есть так, как обозначены аргументы
обеих функций в условии задачи. Таким
образом, получаем ответ:
.
Заметим, что тот же результат можно
получить, если формально подставить в
формулу первой функции

вместо

выражение
.
На практике, конечно, можно пользоваться
этим приемом, при этом понимая
математический смысл произведенной
операции.

Пример
3. Найдите сложную функцию, составленную
из функций

и
,
где первая функция будет внешней, а
вторая – внутренней.

Решение.
В первую функцию вместо

подставим выражение

. В итоге получаем
.

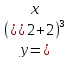
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Департамент
внутренней и  кадровой политики  Белгородской области

областное
государственное  автономное  образовательное учреждение

среднего
профессионального образования

«Белгородский 
политехнический колледж»

Методическая
разработка

открытого
урока

по
дисциплине ОДп.10 «Математика»

Тема:
«Сложная функция»

Подготовила

преподаватель
математики

Съедина
В.В.

Белгород
– 2014

Пояснительная
записка

         Урок
разработан для обучающихся 1 курса  специальностей среднего профессионального
образования,  реализующих образовательные программы среднего (полного) общего
образования.

         Разработка
может быть использована в рамках изучения раздела «Функции, их свойства и
графики», а также отдельные элементы урока могут быть использованы при изучении
темы «Производная сложной функции»  

Разработка урока снабжена авторской презентацией,
которая на всех этапах урока помогает визуализировать учебный материал, а также
осуществить первичное закрепление и контроль усвоения во время объяснения
нового материала, во время первичного закрепления и отработки навыков при
решении задач путем «дозированной» информации, выводящейся на слайдах поэтапно.

Урок рассчитан на 1 академический час (45 минут).

         Приложения
к конспекту урока;

         –
презентация «Сложная функция»;

         –
индивидуальные карты-модули для учащихся.

Конспект
открытого урока по математике

на
тему: «Сложная функция»

Тип урока –
изучение нового материала

Цели
урока:

—  Обучающие цели:

        
создать условия для формирования нового  понятия «сложная функция», обеспечить
развитие умения по распознаванию сложных функций, создать условия для освоения
навыков построения графика сложной функции.

·         
Развивающие
цели:

создать
условия для развития познавательного интереса учащихся, развития аналитического
мышления, расширения кругозора учащихся.

·         
Воспитательные
цели:

создать
условия для развития математической культуры, культуры речи, создать условия
для воспитания целеустремленности, аккуратности 

Целью
изучения данной темы является формирование  общих и профессиональных  компетенций
обучающихся:

ОК 2.
Организовывать собственную деятельность, выбирать типовые методы и способы
выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Осуществлять поиск и
использование информации, необходимой для эффективного выполнения
профессиональных задач, профессионального и личностного развития

ОК 3. Принимать
решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 8 Самостоятельно определять задачи
профессионального и личностного развития, заниматься самообразованием, осознанно
планировать повышение квалификации.

ПК
6.4 Контролировать ход и оценивать результаты выполнения работ

ПК
6.5 Вести утвержденную учетно – отчетную документацию

 Оборудование:

·       
Презентация
«Сложная функция»;

·       
Экран,
проектор, доска;

·       
Индивидуальные
карты-модули;

·       
Учебники:

 Алимов Ш.А. и др.
Алгебра и начала анализа. 10 (11) кл.   – М., 2010, Колмогоров А.Н. и др.
Алгебра и начала анализа. 10 (11) кл. – М., 2009.

Структура
урока:

I.
Организационный момент  –  0,5 мин.

II.  Этап
подготовки учащихся к активному сознательному усвоению знаний – 4,5 мин.

III. Этап
усвоения новых знаний – 30 мин.

IV. Этап
закрепления новых знаний – 8 мин.

V. Этап
информирования учащихся о домашнем задании и инструктажа по его выполнению  – 
2 мин.

Ход занятия

I.
Организационный момент

II. Этап
подготовки учащихся к активному сознательному усвоению знаний 

Слайд
1.

Тема нашего занятия «Сложная функция». С понятием
«функция» вы уже знакомы, да и понятие «сложный» так же известен вам. Однако
часто в повседневной речи мы часто считаем слова «сложный» и «трудный»
синонимами. Но на самом деле «сложный» и «Трудный» далеко не всегда означают
одно и то же.

В толковом словаре В.И. Даля можно найти  такое
определение «Сложный, составной, сложенный или составленный из разных частей…».

Наша с вами задача убедиться, что сложная функция –
это не значит трудная!

Слайд 2.

Итак, цель нашего сегодняшнего занятия разобраться,
что же такое «Сложная функция», как распознать сложную функцию и научиться
строить график сложной функции.

         Прежде
чем рассматривать сложную функцию, давайте вспомним основные понятия, которые
нам сегодня потребуются при изучении нового материала. Перед каждым из вас
лежат индивидуальные карты, прочтите 5 вопросов, которые там приведены,
подумайте и ответьте на них. У вас в распоряжении 1,5 мин.

         Вводная
беседа по ранее изученному материалу:

         1.
Что значит задать функцию?

         2.
Что такое аргумент функции?

         3.
Что такое значение функции?

         4.
Что называют областью определения функции?

         5.
Что называют областью значений функции?

Слайд 3.

Итак, еще раз обращаю ваше внимание, что функция, это
прежде всего некоторое соответствие между множеством Х (независимых переменных)
и множеством У (значений функции), при этом обязательно нужно помнить что
каждому значению х соответствует единственное значение у.

III. Этап
усвоения новых знаний

         Достаточно
часто мы сталкиваемся с задачами, где значение функции зависит не
непосредственно от аргумента, через «промежуточную» функцию. Такие функции
называют сложными

         Слайд
4.

         Или
говорят, что «сложная функция – это композиция двух и более функций». Термин
«сложная» функция не является понятием сложности  начертания или исследования,
а указывает на вид или «конструкцию» функциональной зависимости.

         Рассмотреть
слайд, обратить внимание на промежуточный шаг x₀→ t₀ →y₀.

         Слайд
5.

         Сложную
функцию можно задать формулой   y=f(g(x)), где g(x) –
внутренняя  функция,  f(t)  – внешняя
функция. Обратите внимание, эта формула есть в ваших индивидуальных картах .

         Рассмотрим
пример сложной функции

g(x) =                 
– внутренняя функция,    f(t) =         
– внешняя функция.

         Для
определения какая функция является внутренней, а какая внешней нужно задать
вопрос: «в каком порядке будут выполнены действия при необходимости вычисления
значения функции по заданному аргументу?»

          Найдите
y(2)-?

1) Сначала нужно найти значение подкоренного
выражения 2²-4=0, то есть g(x) = x²-4 – будет
внутренней функцией;

2)  затем уже
находим значение корня  =0, то есть f(t) =       будет
внешней функцией.

Слайд 6.

Перед вами на экране и в индивидуальных картах
приведены примеры сложных функций:    y = sin2x, y = (x³
– 1 )⁵ , y = cos(7x + 2),  , 

y = sin²x + sin x .

Вам необходимо определить какая функция является
внутренней, а какая внешней, и заполнить таблицу. На выполнение задания вам
дается 3 минуты.

Слайд 7.

Самопроверка (2 мин.).
Проверьте  правильность выполненного задания (около каждой функции проставьте
«+» или « – » и подсчитайте количество правильных ответов).

 Слайд 8.

Помимо умения различать в заданных функциях внутреннюю
и внешнюю функции необходимо уметь составлять композицию функций.

На экране приведены три элементарных функции. Вам
необходимо составить  композицию этих функций по заданным формулам.

Например y=h(f(x))=[ f(x)=t=x² , h(t)=sin t ] =sin x²

         Рассуждая
аналогично, составьте, пожалуйста, композицию из функций в соответствии с
заданием, на выполнение этого задания вам дается 3 минуты.

         Проверка
(1 мин.) – опрос по цепочке, сверка с доской (около каждой функции проставьте
«+» или « – » и подсчитайте количество правильных ответов).

         Слайд
9.

Итак,  мы с вами рассмотрели, как в аналитически
заданной функции определить внутреннюю и внешнюю функции.

Что бы еще раз убедиться, что сложная функция является
композицией двух функций, построим график функции .

Фронтальная беседа (2
мин):

1. Определите внутреннюю и
внешнюю функции.

2.  Укажите область
определения каждой функции

3. Что можно сказать о
четности этой функции.

Подведение итога опроса слайд
10 .

Слайд 11.

Как мы уже говорили, сложная функция – это композиция
функций.  Построим графики внутренней и внешней функции в координатных осях XOG и GOУ. Для
этого составим таблицы значений каждой функции. Заполните таблицы в
индивидуальных картах (2 минуты).

Слайд 12.

Проверьте правильность своих вычислений, и как
показано на экране, постройте графики двух функций в разных системах координат
(на  построение у вас  – 3 минуты).

Посмотрите на экран, вот что у вас должно было
получиться.

Слайд 13.

А теперь рассмотрим как, используя полученные графики,
построить график сложной функции.

 Возьмем некоторое х₀=0 и по
первому графику найдем соответствующее ему значение g₀=-1, затем
по второму графику для g₀=-1,
найдем у₀=1/2 и построим в новой системе координат точку с
координатами (0:1/2). Аналогично, можно построить и другие точки x₁=1 →g₁=0 →y₁=1→(1;1),
учитывая четность функции, получаем точку (-1;1). И строим эскиз графика
сложной функции.

Проделайте эту операцию самостоятельно в своих
индивидуальных картах, для удобства можете использовать вспомогательную
таблицу. На выполнение работы  5 мин. (пройти для проверки и
корректировки  выполнения задания, проверить выполнение заданий по определению
внутренней и внешней функции, составлению сложных функций).

IV. Этап
закрепления новых знаний

Используя имеющиеся графики, постройте график функции y=(2^x)²-1

(на выполнение 4 минуты) – первый справившийся
учащийся на доске выполняет чертеж графика

  Итак, мы рассмотрели понятие сложной функции как
композицию двух функций, внешней и внутренней. Научились распознавать эти
функции в конкретно заданной функции, а также составлять композицию двух
функций. А также посмотрели, как с помощью графиков элементарных функций можно
построить график сложной функции.

Фронтальный опрос:

1. Объясните понятие «сложная функция»

2. Как распознать внешнюю и внутреннюю функции?

3. Можно ли утверждать, что график сложной функции   –
это обязательно сложная кривая, для построения которой необходимы сложные
вычисления и преобразования?

Хочется отметить, что слова «сложный», «сложенный»
связаны с глаголом «сложить», «складывать». В словаре В.И. Даля читаем, что
«СКЛАД» – это стройность, красота, порядок, устройство, а «складный ум –
логичный, ясный и верный». Мне хотелось, что бы сложная функция оказалась для
вас в первую очередь не трудной, а интересно устроенной.

По итогам работы на уроке выставляются отметки
активным учащимся.

V. Этап
информирования учащихся о домашнем задании и инструктажа по его выполнению 

В ваших
индивидуальных картах записано домашнее задание: построить график функции

Построение выполнить в рабочих тетрадях.

Индивидуальные карты сдать для проверки на следующем
уроке.

Спасибо за урок.

Заключение

Данная разработка была опробована на группе 1 курса с
достаточно высоким уровнем подготовки, цели и задачи урока были достигнуты в
полном объеме.

Использование индивидуальных карт-модулей позволило
сократить время, как при объяснении нового материала, так и при закреплении,
что позволило рассмотреть на уроке достаточно большой объем материала.

При изучении материала была использована презентация,
в которой пошагово рассмотрены все этапы урока, что позволило увеличить
плотность урока и оптимально увеличить его темп. Чередование проверки и
самопроверки в ходе объяснения нового материала, позволило в ходе урока
проводить коррекцию усвоения и реализовать индивидуальный подход к каждому
учащемуся.

Литература

1.
Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл.   – М., 2010.

2. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 
2007.

3.
Башмаков М.И. Математика: учебник для 10 кл. – М., 2007.

4. Колмогоров А.Н. и др. Алгебра и начала анализа. 10
(11) кл.
– М., 2009.

Приложение 1.

Фамилия,
имя учащегося______________________________________

Тема
занятия: «Сложная функция»

Цель:

—  Познакомить с
понятием «сложная функция»;

—  Научить
распознавать сложные функции;

—  Научить строить
график сложной функции;

Ход
занятия:

1.
Ответьте на вопросы:

         1.
Что значит задать функцию?

         2.
Что такое аргумент функции?

         3.
Что такое значение функции?

         4.
Что называют областью определения функции?

         5.
Что называют областью значений функции?

2.
Сложная функция – это композиция двух и более функций.

Формула для задания сложной функции

y=f(g(x)) – 
сложная  функция

g(x) –
внутренняя  функция

f(t)  – внешняя
функция

Пример.

   

g(x) =                  – внутренняя
функция,    f(t)
=          – внешняя функция

3.
Заполните таблицу

Сложная функция y=f(g(x))	Внешняя функция f(t)	Внутренняя функция g(x)
1.   y = sin2x
2. y = (x3 – 1 )5
3. y = cos(7x + 2)
4.
5. y = sin2x + sin x

4.
Составьте сложную функцию, если  f(x)=x², g(x)=2x-4, h(x)=sin x

пример:
y=h(f(x))=sin x²

·     y₁=f(g(x))                              
____________________________________

—  y₂=g(f(x))                             
____________________________________

—  y₃=
f(h(x))                            
____________________________________

—  y₄=h(g(x))                            _____________________________________

5.
Пример.   Построить график функции           

Решение

–
Определим внутреннюю и внешнюю функции y=f(g(x)): g(x)=x²-1, f(g)=2^g.

– 
Построим на разных координатных плоскостях графики функций g(x)=x²-1и f(g)=2^g, для
этого составим таблицы значений каждой функции

                 
   g(x)=x²-1                                                               
f(g)=2^g

х	-2	-1	0	1	2		g	-2	-1	0	1	2	3
g							y

Примечание 1 клетка=1                                Примечание  
1 клетка=0,5

Учитывая, что сложная функция есть
композиция двух функций, т.е. составим
вспомогательную таблицу

x	-2	-1	0	1	2
g
f

Построим
график сложной функции: 1 клетка = 0,5

Задания
для самостоятельной работы:

В
рабочих тетрадях постройте график функции  y=(2^x)²-1

Домашнее задание:

Построить график функции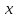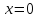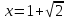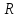