Как составить сложные суждения

Суждения это в логике? Сложные суждения примеры. Классификация суждений. Структура суждений. Простые суждения, примеры. Логические формулы.

Здравствуйте, уважаемые читатели! Продолжаем публикацию цепочки статей, раскрывающих законы формальной логики. С первой частью Вы сможете познакомиться по ссылке: № 1. Статья «Понятие это в логике? Логика Аристотеля кратко и понятно!»

Сегодня мы рассмотрим суждения. Напоминаю, что основой для данной статьи послужила книга Гусев Д. А. «Краткий курс логики: Искусство правильного мышления».

Блок 1. Суждения. Что такое суждения?

Суждение — это форма языкового мышления, которая состоит из понятий, связанных между собой, происходит утверждение либо отрицание чего-либо.

Пример:

• Федор Иванов работает менеджером по продажам.
• Некоторые менеджеры по продажам компании являются туристами.
• Никто из менеджеров по продажам не перевыполнил план продаж.

Суждения обладают набором свойств, которые в том числе отличают их от понятий.

1. Все суждения состоят из понятий, которые связаны между собой. Пример:

• Понятие «Федор Иванов» и понятие «менеджер по продажам» образуют суждение «Федор Иванов работает менеджером по продажам».

2. Все суждения выражаются в форме предложения. Однако не любое предложение является суждением. Вопросительные и восклицательные предложения не являются суждениями, потому что в них ничего не утверждается и не отрицается. Повествовательное предложение всегда содержит утверждение или отрицание. Поэтому суждение выражается повествовательным предложением. Вместе с тем существуют риторические предложения, которые могут быть и вопросительными, и восклицательными по форме, в то время как по смыслу что – либо утверждают или отрицают. Примеры:

• И кто из менеджеров по продажам не стремится заработать бонусы?
• Вы сможете заработать свои бонусы, потому что их нельзя не заработать!

3. Все суждения можно разделить на истинные или ложные. Истинным является суждение, отражающее достоверное событие. Понятие «достоверное событие» определено в теории информации. Теория информации базируется на теории вероятности и математической статистике. Важно понимать, что здесь мы переходим к аппарату математической логики. В противном случае истинность или ложность суждения становятся уязвимы для критики, поскольку объем знаний отдельного субъекта в большинстве случаев не позволяет точно определить истинность/ложность события достоверно. Пример:

• Никто из менеджеров по продажам не сможет выполнять план продаж в 10 млн руб.

Является это суждение ложным или истинным? Если менеджеры обычно продают на 1 млн. руб, то можно предположить, что суждение истинное. Однако, всегда остается вероятность того, что план продаж в 10 млн. руб. будет выполнен при случайном благоприятном стечении обстоятельств. И автор однажды столкнулся с таким «удивительным» событием, хотя математически ничего удивительного в этом нет.

В самых простых случаях, на бытовом уровне люди разделяют более-менее хорошо истинность/ложность суждений. Пример:

• Все менеджеры по продажам нашей компании мужчины.

Если Вы получили такой опыт, что Вам оказались доступны к наблюдению первичные и вторичные половые признаки, то суждение будет истинным. Однако, если Вы делаете выводы на основании вторичных и третичных половых признаков, при этом не знаете, что такое трансгендерность, интерсексуальность, то можете допустить ошибку в своем суждении.

Формальная логика – это двузначная логика, когда все факты делятся только на истинные и ложные.

4. Все суждения могут быть сложными и простыми. Простые суждения с помощью союза объединяются в сложные.

ВИДЕО «Переговоры. Как устранить контроль со стороны босса?!»

Блок 2. Суждения. Структура суждений.

2.1. Суждения по своей структуре состоят из четырех частей.

1. Субъект (S) – это предмет, о котором идет речь. Пример:

• Некоторые менеджеры по продажам являются туристами. Субъект «менеджеры по продажам».

2. Предикат (P) – это то, что говориться о субъекте. Пример:

• Некоторые менеджеры по продажам являются туристами. Предикат «туристы».

3. Связка – это то, что соединяет субъект и предикат. Пример:

• Некоторые менеджеры по продажам являются туристами. Связка «являются».

4. Квантор – это указатель на объем субъекта. Пример:

• Некоторые менеджеры по продажам являются туристами. Квантор «некоторые».

2.2. Отношения между субъектом и предикатом в суждении.

1. Равнозначность. Пример:

• Все менеджеры по продажам (S) в нашей компании – это специалисты по заключению сделок (P). Формула: S=P. Субъект равен предикату.

2. Пересечение. Пример:

• Некоторые менеджеры по продажам (S) в нашей компании являются туристами (P). Субъект и предикат – это пересекающиеся понятия.

3. Подчинение. Пример:

• Все менеджеры по продажам (S) это сотрудники отдела продаж (P). Субъект – это видовое понятие, а предикат – родовое понятие.

4. Несовместимость. Пример:

• Менеджеры по продажам (S) не являются логистами (P). Субъект и предикат – это несовместимые понятия.

2.3. Термины суждения.

Термины суждения – это субъект и предикат. Выделяют две группы терминов.

1. Распределенный термин (+). В суждении говорится о всех объектах, включенных в объем термина. Пример:

• Все работники трудоустроены в компании.

2. Нераспределенный термин (-). В суждении говорится не о всех объектах, включенных в объем термина. Пример:

• Все менеджеры по продажам (S) работают в отделе продаж (P).

Субъект суждения распределен, потому что «все». Предикат суждения не распределен, потому что в отделе продаж работают и другие сотрудники, кроме менеджеров по продажам.

---

Блок 3. Суждения. Классификация суждений.

Суждения подразделяются на три вида:

1. Атрибутивные суждения. В суждениях предикат является сущностным, неотъемлемым признаком субъекта. Пример:

• Менеджеры по продажам (S) являются сотрудниками отдела продаж (P).

Работа в отделе продаж (P) – это сущностный признак менеджера по продажам (S). Еще пример:

• Некоторые сотрудники отдела (S) продаж являются менеджерами по продажам (P).

Здесь уже субъект оказывается сущностным признаком предиката, но это также атрибутивное суждение, потому что его можно изменить и предикат станет главным признаком субъекта. Получается, что субъект может быть атрибутом предиката, а предикат может быть атрибутом субъекта.

2. Экзистенциальные суждения. В суждениях предикат указывает на существование или не существование субъекта. Пример:

• Зубные феи (S) в жизни не встречаются (P).

Предикат указывает на отсутствие субъекта.

3. Релятивные суждения. В суждениях предикат выражает отношение к субъекту. Пример:

• Федор Иванов (S) работает менеджером по продажам дольше всех (P) в своем отделе.

Предикат указывает на отношение к субъекту по времени («дольше всех»).

Заказать услугу «Переговоры — Посредничество»

Блок 4. Суждения. Простые суждения.

4.1. Что такое простое суждение?

Простое суждение содержат один субъект и один предикат.

Такие суждения разделяются по объему субъекта (общий – «все», частный – «некоторые») и по связке (утвердительная – «есть», отрицательная — «не есть»). Выделяют четыре комбинации:

1. Общеутвердительные суждения (A). Общий объем + утвердительная связка. Формула: «Все S есть P». Пример:

• Все менеджеры по продажам – это сотрудники компании.

Субъект и предикат в общеутвердительных суждениях находятся в отношениях: равнозначности или подчинения.

2. Частноутвердительные суждения (I). Частный объем + утвердительная связка. Формула: «Некоторые S есть P». Пример:

• Некоторые менеджеры по продажам являются туристами.

Субъект и предикат в частноутвердительных суждениях находятся в отношениях: пересечения или подчинения.

3. Общеотрицательные суждения (E). Общий объем + отрицательная связка. Формула: «Все S не есть P». Пример:

• Все менеджеры по продажам не являются логистами.

Субъект и предикат в общеотрицательных суждениях находятся в отношении несовместимости.

4. Частноотрицательные суждения (O). Частный объем + отрицательная связка. Формула: «Некоторые S не есть P». Пример:

• Некоторые менеджеры по продажам не выполняют план продаж.

Субъект и предикат в частноотрицательных суждениях находятся в отношениях: пересечения или подчинения.

4.2. Распределенные термины. Виды простых суждений.

А. Равнозначность. Пример:

• Все менеджеры по продажам – это специалисты по заключению сделок. Субъект всегда распределен.

А. Подчинение. Пример:

• Все менеджеры по продажам – это сотрудники компании. Субъект всегда распределен.

I. Пересечение. Пример:

• Некоторые менеджеры по продажам являются туристами.

I. Подчинение. Пример:

• Некоторые менеджеры по продажам подчиняются супервайзеру Ольге Сидоровой.

Е. Несовместимость. Пример:

• Все менеджеры по продажам не являются логистами. Субъект всегда распределен. Предикат всегда распределен.

О. Пересечение. Пример:

• Некоторые менеджеры по продажам не выполняют план продаж. Предикат всегда распределен.

О. Подчинение. Пример:

• Некоторые менеджеры по продажам не подчиняются супервайзеру Ольге Сидоровой. Предикат всегда распределен.

4.3. Способы преобразования простых суждений.

1. Обращение (конверсия). Субъект и предикат меняются местами. Пример:

• Все менеджеры по продажам являются сотрудниками отдела продаж (А-подчинение).

Преобразуем в другое суждение. Пример:

• Некоторые сотрудники отдела продаж являются менеджерами по продажам (I-пересечение).

2. Превращение (обверсия). Связки меняются. Пример:

• Все менеджеры по продажам являются сотрудниками отдела продаж.

Преобразуем в другое суждение. Пример:

• Все менеджеры по продажам не являются не сотрудниками отдела продаж.

Здесь можно наблюдать логическую закономерность – всякое утверждение равнозначно двойному отрицанию, а любое двойное отрицание равнозначно утверждению.

3. Противопоставление предикату. Состоит из двух операций, сначала происходит превращение, а затем обращение. Пример:

• Все менеджеры по продажам являются сотрудниками отдела продаж.

Сначала превращение: все менеджеры по продажам не являются не сотрудниками отдела продаж.

Затем обращение: все не сотрудники отдела продаж не являются менеджерами по продажам.

Еще раз повторим:

1. Все менеджеры по продажам являются сотрудниками отдела продаж (первоначальное суждение).
2. Некоторые сотрудники отдела продаж являются менеджерами по продажам (обращение).
3. Все менеджеры по продажам не являются не сотрудниками отдела продаж (превращение).
4. Все не сотрудники отдела продаж не являются менеджерами по продажам (противопоставление предикату).

4.4. Разделение простых суждений.

1. Несравнимые суждения.  Характеризуются разными субъектами и предикатами. Пример:

• Все менеджеры по продажам (S) стремятся выполнить план продаж (P).
• Некоторые молодые мамы (S) надолго остаются дома (P).

В этих двух суждениях субъект и предикат не совпадают.

2. Сравнимые суждения. Характеризуются одинаковыми субъектами и предикатами, способны отличаться кванторами и связками. Пример:

• Все менеджеры по продажам (S) стремятся выполнить план продаж (P).
• Некоторые менеджеры по продажам (S) не стремятся выполнить план продаж (P).

В этих двух суждениях совпадают субъекты и предикаты, кванторы и связки не совпадают.

4.5. Разделение сравнимых суждений. Логический квадрат.

1. Сравнимые совместимые суждения. Способны быть одновременно истинными. Пример:

• Некоторые менеджеры по продажам являются туристами.
• Некоторые менеджеры по продажам не являются туристами.

Оба суждения истинные.

1.1. Совместимые суждение в отношениях равнозначности. Идентичны субъект, предикат, кванторы, связки. Пример:

• Менеджеры по продажам являются сотрудниками отдела продаж.
• Специалисты по заключению сделок являются сотрудниками отдела продаж.

1.2. Совместимые суждения в отношениях подчинения. Предикаты и связки идентичны, но субъекты пребывают в отношениях вида и рода. Пример:

• Все работники отдела продаж являются сотрудниками компании.
• Все менеджеры по продажам являются сотрудниками компании.

1.3. Совместимые суждения в отношениях частичного совпадения (субконтрарность). Субъекты и предикаты совпадают, связки не совпадают. В таком отношении пребывают только частные суждения. Пример:

• Некоторые менеджеры по продажам являются туристами.
• Некоторые менеджеры по продажам не являются туристами.

2. Сравнимые несовместимые суждения. Не могут быть одновременно истинными. Если одно из суждений истинное, то второе обязательно ложное. Пример:

• Все менеджеры по продажам являются сотрудниками отдела продаж.
• Некоторые менеджеры по продажам не являются сотрудниками отдела продаж.

2.1. Несовместимые суждения в отношениях противоположности (контрарность). Субъекты и предикаты совпадают, связки различаются. В таком отношении пребывают только общие суждения. Пример:

• Все менеджеры по продажам являются сотрудниками отдела продаж.
• Все менеджеры по продажам не являются сотрудниками отдела продаж.

Такого рода суждения способны быть одновременно ложными, но не могут быть одновременно истинными.

2.2. Несовместимые суждения в отношениях противоречия (контрадикторность). Предикаты совпадают, связки не совпадают, субъекты отличаются объемами (вид и род). Пример:

• Все менеджеры по продажам являются сотрудниками отдела продаж.
• Некоторые менеджеры по продажам не являются сотрудниками отдела продаж.

Подобные два суждения не могут быть одновременно ложными и не могут быть одновременно истинными. Если ложно одно, то другое истинно.

Итого, получаем логический квадрат.

---

Блок 5. Суждения. Сложное суждение.

Суждения могут быть сложными, если содержат более, чем один субъект и предикат.

Различают следующие виды сложных суждений:

1. Конъюнктивные суждения (конъюнкция, соединение) (˄) – это сложные суждения, в которых используется соединительный союз «и». Формула: a ˄ b. Пример:

• Наступил сезон и продажи  увеличились.

2. Дизъюнктивные суждения (дизъюнкция)– это сложные суждения, в которых используется разделительный союз «или». Характер применения данного союза позволяет выделять два вида таких суждений.

2.1. Строгая дизъюнкцию (˅). Составные части исключают друг друга. Формула: a ˅ b (или a, или b). Пример:

• Менеджер выполняет план продаж или не выполняет свой план продаж.

2.2. Нестрогая дизъюнкцию (˅). Составные части сосуществуют и не исключают друг друга. Формула: a ˅ b (a или b). Пример:

• Менеджер сам хочет выполнить план продаж или его заставляют выполнять план продаж.

3. Импликативные суждения (импликация) (→) – это сложные суждение, в которых используется союз «если…, то» в условном значении. Формула: a → b (если a, то b). Пример:

• Если сотрудник работает менеджером по продажам, то он отвечает за выполнение плана продаж.

В данных суждениях из основания вытекает следствие, однако основание не вытекает из следствия. Нельзя сказать, что если сотрудник отвечает за выполнение плана продаж, то он работает менеджером по продажам.

4. Эквивалентные суждения (эквиваленция) (↔) – это сложные суждения, в которых используется союз «если …, то» не в условном значении, а в тождественном. Формула: a ↔ b (если a, то b и если b, то а). Пример:

• Если сотрудник работает менеджером по продажам, то он заключает договора с клиентами.

В эквивалентном суждении нет основания и следствия. Обе части равны между собой.

5. Отрицательные суждения (отрицание) (¬) — это сложные суждения, в которых используется союз «неверно, что…». Формула: ¬a (неверно, что a). Пример:

• Неверно, что все менеджеры компании контролируют дебиторскую задолженность.

В логики истинность или ложность сложных суждений зависит от истинности или ложности простых суждений, входящих в его состав.

---

Блок 6. Суждения. Логические формулы.

Любое сложное суждение можно выразить  с помощью формул. Пример:

• Менеджер по продажам сейчас заключает договор с клиентом, или проводит аудит торговых точек, или на складе решает свои вопросы по товару с кладовщиком.

Формула: a˅b˅c (нестрогая дизъюнкция).

Пример:

• Менеджер по продажам сейчас у клиента «А», или у клиента «Б», или у клиента «В».
• Хотя уже вечер, поэтому он точно не у клиента «В» и не у клиента «Б».
• Значит, он решает вопрос по долгам с клиентом «А».

Формула: ((a˅b˅c)˄(¬c ˄¬b))→a (первая часть в скобках – строгая дизъюнкция, вторая часть в скобках – два отрицания, связанных конъюнктивно, первая и вторая часть в больших скобках связаны конъюнктивно, данные в больших скобках связаны с суждением «а» импликативно.

6.1. Логические формулы делятся на три части:

1. Тождественно-истинные. Эти формулы истинные при условии истинности простых суждений, составляющих сложные суждения.

2. Тождественно-ложные. Эти формулы ложные, при условии истинности простых суждений, составляющих сложные суждения. Такое случается при нарушении логических законов.

3. Выполнимые (нейтральные). Эти формулы либо истинные, либо сложные, при условии истинности простых суждений, составляющих сложные суждения. Пример:

• Если менеджер работает в отделе продаж, то он может зарабатывать бонусы.
• Менеджер Иванов зарабатывает бонусы.
• Следовательно, Иванов работает в отделе продаж.

Формула: ((a→b)˄b)→а. Эта формула нейтральная. Рассуждения корректны, однако небезупречны. Это означает, что вывод может быть, как истинным, так и ложным. Менеджер Иванов может работать в отделе продаж, а может работать в другом отделе, где существует возможность зарабатывать бонусы.

На этом сегодня мы закончим, несмотря на то, что тема про суждения раскрыта не полностью. Почему заканчиваем? Потому что формат статьи блога не предусматривает развернутый и полноценный анализ этого сложного вопроса. Вместе с тем, основные аспекты с примерами были раскрыты.

Перейти на сайт «Психолог Якимов Владислав»

2. Сложные суждения

2. Сложные суждения

Образование и особенности сложных суждений. Напомним, что сложные суждения образуются из простых путем того или иного их соединения (а также, добавим здесь для полноты анализа, путем соединения простых со сложными и сложных между собой).

Подобно простым сложные суждения могут быть истинными и ложными. Но если истинность или ложность простого суждения непосредственно определяется его соответствием или несоответствием действительности, то истинность или ложность сложного суждения зависит прежде всего от истинности или ложности составляющих его простых (и иных) суждений.

Сложные суждения отличаются от простых также по своим функциям и структуре. Их функции носят более сложный характер, так как в них раскрывается не одна, а одновременно несколько — две или более — связей между предметами мысли. Их структура тоже характеризуется большей сложностью, обретая новое качество. Основными структурообразующими элементами здесь выступают уже не понятия-термины (субъект и предикат), а самостоятельные суждения (причем их внутренняя субъектно-предикатная структура уже не учитывается). И связь между ними осуществляется не с помощью связки «есть» («не есть»), а в качественно иной форме — посредством логических союзов (они называются также «логическими связками»). Это такие союзы, как «и», «или», «если… то» и др. Они близки по смыслу к соответствующим грамматическим союзам, но, как будет показано ниже, полностью с ними не совпадают. Главное их отличие сводится к тому, что они однозначны, тогда как грамматические союзы могут иметь множество смыслов и оттенков.

Каждый из логических союзов является бинарным, т.е. соединяет между собой только два суждения независимо от того, простые они или сами, в свою очередь, сложные, имеющие внутри себя собственные союзы.

Если в простых суждениях переменными были субъект и предикат (S и Р), а постоянными — логические связки «есть» и «не есть», то в сложных суждениях переменными выступают уже отдельные, далее нерасчленяемые суждения (назовем их «А» и «В»), а постоянными — логические союзы: «и», «или» и др.

В русском языке сложные суждения имеют весьма многообразные формы выражения. Они могут выражаться прежде всего сложносочиненными предложениями. Например: «Ни один виновный не должен уйти от ответственности, и ни один невиновный не должен пострадать». Они могут быть выражены также сложноподчиненными предложениями. Таково, например, высказывание Цицерона: «Ведь если бы даже ознакомление с правом представляло огромную трудность, то и тогда сознание его великой пользы должно было бы побуждать людей к преодолению этой трудности». Наконец, они могут облекаться и в особую форму простых распространенных предложений. Этого нетрудно добиться, например, в результате своеобразного «свертывания» сложных предложений. Так, сложносочиненное предложение «Аристотель был великим логиком, и Гегель тоже был великим логиком» можно превратить в простое распространенное: «Аристотель и Гегель были великими логиками». Благодаря подобному «свертыванию» достигается большая лаконичность речи, а следовательно, ее экономность и динамичность.

Таким образом, не всякое сложное суждение выражается непременно сложным предложением, но всякое сложное предложение выражает сложное суждение.

Виды сложных суждений по характеру логического союза. В сложных суждениях, как и в простых, есть свои виды. Они определяются прежде всего характером логического союза. В зависимости от смысла и назначения логического союза различаются следующие основные группы сложных суждений.

1. Конъюнктивные (или соединительные) суждения (от лат. conjunctio — связь, соединение). Они образуются из исходных посредством логического союза конъюнкции «и» (символически: «д»). Их наиболее общая схема: А?В (читается: «А и В»), где А и В — исходные суждения, а знак ? — символ их конъюнкции. Например: «Никто не забыт, и ничто не забыто».

В русском языке логический союз конъюнкции выражается многими грамматическими союзами: «и», «а», «но», «да», «хотя», «а также», «несмотря на то, что…» Вот примеры. Современное изречение: «Трудолюбие — душа бизнеса и ключ к процветанию». Философское положение одного из древнекитайских мыслителей: «Самое большое не имеет внешней границы, а самое маленькое не имеет предела внутри себя». Слова Аристотеля: «Платон друг, но истина еще больший друг». Из народной мудрости: «Русские долго запрягают, да быстро ездят». Среди юристов распространен афоризм: «Pereat mundus et fiat justitia» («Правосудие должно совершиться, хотя бы погиб мир»). Нередко грамматические союзы заменяются запятой, двоеточием, точкой с запятой и даже точкой. Например, как полагал один из семи древнегреческих мудрецов: «Наслаждения смертны, добродетели бессмертны». Или: «Тысячелетие по кирпичику создает государство — один час может превратить его в пыль».

Если конъюнкция выражена простым распространенным предложением, то она может иметь три исходных структуры:

а) один субъект и два предиката — «S есть (не есть) Р₁ и Р₂». Например: «Все равны перед законом и судом». Здесь можно вычленить два исходных суждения с общим субъектом и разными предикатами: «Все равны перед законом» и «Все равны перед судом»;

б) два субъекта и один предикат — «S₁ и S₂ есть (не есть) Р». Например: «Государственные пенсии и социальные пособия устанавливаются законом». Здесь также налицо два простых суждения;

в) два субъекта и два предиката — «S₁ и S₂ есть (не есть) Р₁ и Р₂». Например: «Основные права и свободы человека неотчуждаемы и принадлежат каждому от рождения». Здесь уже четыре простых суждения.

Понятно, что на этой основе могут быть еще более сложные мыслительные конструкции.

Пример: «Осуществление прав и свобод человека и гражданина не должно нарушать права и свободы других лиц».

Возможны четыре способа сочетания двух исходных суждений «А» и «В» в зависимости от их истинности («и») и ложности («л»). Какая здесь действует закономерность? Конъюнкция таких суждений истинна в одном случае: если истинно каждое из них в отдельности. В остальных случаях она ложна. Вот таблица (матрица) конъюнкции:

А
В
А?В

и
и
и

и
л
л

л
и
л

л
л
л

В принципе логический союз «и» в отличие от грамматического может объединять даже такие суждения, которые по смыслу очень далеки друг от друга. Классический пример: «2 ? 2 = 4, и снег бел». Правда, и здесь можно найти что-то общее, например: «Это верно, что 2 ? 2 = 4 и что снег бел». Другой пример. Что общего между такими простыми суждениями: «Существует звездное небо над головой» и «Есть нравственный закон в душе человека»? Однако их конъюнкция возможна: они могут быть сближены, если учесть, что именно то и другое больше всего поразило И. Канта. В практике мышления такие суждения бывают довольно редко, но они лишь подчеркивают универсальный характер закономерности конъюнкции: она не зависит от конкретного содержания исходных суждений, а ее истинность или ложность всецело определяется истинностью или ложностью каждого из них. Важно лишь, чтобы исходные суждения обладали свойством коммутативности (перестановочности), т.е. их истинность или ложность не менялась от перестановки.

Впрочем, иногда признают некоммутативную конъюнкцию: «Наступила зима, и мы катаемся на лыжах» (а не наоборот).

Логический союз «и» может соединять и более двух исходных суждений — по формуле: А?В?С… Вспомним в этой связи стихи Пушкина:

Теперь у нас дороги плохи,

Мосты забытые гниют,

На станциях клопы да блохи

Заснуть минуты не дают.

В подобных случаях важно другое — чтобы исходные суждения обладали свойством ассоциативности (сочетаемости), т.е. их истинность или ложность не менялась от способа сочетания: (А?В)?С или А?(В?С) и т. д. Общая закономерность конъюнкции остается здесь в силе: она истинна лишь при истинности всех ее составляющих.

Знание особенностей конъюнкции имеет немалое значение в практике мышления. Строя более или менее сложное рассуждение, следует тщательно проверять истинность исходных суждений. Ведь от этого напрямую зависит его собственная истинность или ложность. Так, достаточно одного ложного суждения, чтобы придать всей, даже весьма сложной, конъюнкции ложность. Недаром еще древние утверждали: «Дырявая пола халата делает всю одежду дырявой». Эта же мысль заложена в русских пословицах — о том, что” делает ложка дегтя в бочке меда или одна паршивая овца в стаде.

Все это важно учитывать в юридической практике, когда нередко выстраивается более или менее сложная цепь рассуждений. А из-за одного ложного звена она может распасться. В то же время достаточно обнаружить хотя бы одно ложное суждение в доводах оппонента, чтобы опровергнуть все рассуждение в целом.

2. Дизъюнктивные (разделительные) суждения (от лат. disjunctio — разобщение, обособление). Бывает две их разновидности: слабая и сильная (или нестрогая и строгая).

Слабая (нестрогая) дизъюнкция образуется логическим союзом «или» (знак «?»), Он характеризуется тем, что объединяемые им суждения не исключают друг друга. Общая формула: A?B (читается: «А или В»). Языковые средства выражения слабой дизъюнкции — грамматические союзы «или», «либо» и другие в их разделительно-соединительном значении. Например, как сказано в древнем поучении: «Мудрая книга, оставленная человеком после его смерти, более полезна, чем дворец или часовня на кладбище» (или чем то и другое вместе). Еще пример: «Право может способствовать экономическому развитию либо препятствовать ему» (но оно может одновременно способствовать в одном отношении и препятствовать в другом). Из Трудового кодекса РФ: «Комиссии по трудовым спорам образуются по инициативе работников и (или) работодателя из равного числа представителей работников и работодателя» (ст. 384).

Слабая дизъюнкция истинна в тех случаях, когда истинно, по крайней мере, одно из составляющих ее суждений (или оба вместе), и ложна, когда оба суждения ложны.

Вот таблица слабой дизъюнкции:

А
В
A?B

и
и
и

и
л
и

л
и
и

л
л
л

Как и в конъюнкции, логический союз «или» обладает свойством коммутативности. Дизъюнкция может состоять из трех и более исходных суждений — по формуле: A?B?C… Примером может служить рассуждение ходжи Насреддина, который взялся за десять лет научить падишахова ишака грамоте: «Через десять лет либо ишак сдохнет, либо падишах умрет, либо меня аллах приберет» (а может, и все вместе). Великолепный образец многочленной дизъюнкции, полезной для юристов, мы находим у Цицерона: «Люди ведь гораздо чаще руководствуются в своих решениях ненавистью, или любовью, или пристрастием, или гневом, или горем, или радостью, или надеждой, или боязнью, или заблуждением, или другим каким-либо душевным движением (а может быть, одновременно тем или иным их сочетанием. — Е. И.), чем справедливостью, или предписанием, или каким-нибудь правовым установлением, или судебным решением, или законами». В подобных случаях, как и в конъюнкции, логический союз «или» обладает свойством ассоциативности.

Дизъюнктивное суждение может не исчерпывать всех возможных случаев. Тогда в русском языке ставятся выражения типа: «и так далее», «и тому подобное», «и прочее». Они применимы даже в юридических текстах (к которым предъявляются особо строгие требования), если нет возможности перечислить все варианты чего-либо.

Сильная (строгая) дизъюнкция образуется логическим союзом «либо… либо» (символ ?). Она отличается от слабой тем, что ее составляющие исключают друг друга. Общая формула: А ? В (читается: «А либо В»). И она выражается, по существу, теми же грамматическими средствами, что и слабая: «или», «либо» и др., но уже в ином, разделительно-исключающем значении.

Примеры. «Гражданин Российской Федерации не может быть лишен своего гражданства или права изменить его» (Конституция РФ, ст. 6); «Закон, устанавливающий или отягчающий ответственность, обратной силы не имеет» (там же, ст. 54); «Виновным в преступлении признается лицо, совершившее деяние умышленно или по неосторожности» (УК РФ, ст. 24).

Для того чтобы подчеркнуть строго разделительный характер грамматических союзов, используется их усиленная, двойная форма: «или… или», «либо… либо», «то… то», «ли… ли» и др.

Примеры. Как считали древние: «De mortuus aut bene, aut nihil» («О мертвых либо хорошо, либо ничего»); у Брэгга подчеркнуто: «Человек к 40 годам либо сам себе доктор, либо он дурак»; или: «Либо я найду путь, либо проложу его».

Строгая дизъюнкция истинна лишь тогда, когда одно из составляющих ее суждений истинно, а другое ложно.

А
В
A ? B

и
и
л

и
л
и

л
и
и

л
л
л

Дизъюнктивное суждение может включать в себя три и более исходных суждения. Формула: A ? B ? C… Примеры: «Вечно он был занят либо судебной речью, либо домашними упражнениями, либо обдумывал, либо писал»; «Всякое заинтересованное лицо вправе в порядке, установленном законом, обратиться в суд за защитой нарушенного или оспариваемого права или охраняемого законом интереса». Еще более сложный случай: «При хищении, недостаче, умышленном уничтожении или умышленной порче материальных ценностей ущерб определяется по ценам, действующим в данной местности на день причинения ущерба». Строгая дизъюнкция тоже обладает свойствами коммутативности и ассоциативности.

Дизъюнкция — слабая и сильная — широко распространена в практике мышления. В ней выражаются логические операции деления, расчленения, перечисления чего-то. Юридическая практика особенно богата такого рода суждениями. Ведь здесь особое значение имеет детальное указание видов права, видов преступления и наказания, перечисление юридически важных случаев, форм осуществления того или иного права или обязанности и пр.

3. Импликативные (или условные) суждения (от лат. implicatio — сплетение, тесная связь). В них объединяются суждения на основе логического союза «если…, то» (обозначается «?»). Формула А ? В (читается: «Если А, то В»). Для выражения импликации русский язык имеет следующие грамматические союзы: «если…, то», «когда…, тогда», «в случае, если…, то» и др.

Примеры. Афоризм древних: «Cum tacent — clamant» («Когда молчат — кричат»); «Если мы хотим добиться уважения к закону, мы сначала должны создать закон, достойный уважения»; «Если правительство нарушает закон, оно порождает неуважение к нему». Грамматический союз «если» может стоять и не перед первым суждением.

Примеры. Известное крылатое выражение Достоевского, часто цитируемое, «Красота спасет мир» на самом деле есть сложное, условное суждение: «Красота спасет мир, если она добра». У Шекспира:

И добродетель стать пороком может,

Когда ее неправильно приложат.

Юридический пример. «Заседание комиссии по трудовым спорам считается правомочным, если на нем присутствует не менее половины членов, представляющих работников, и не менее половины членов, представляющих работодателя» (Трудовой кодекс РФ, ст. 387).

В условных суждениях отражаются прежде всего многообразные реальные зависимости между предметами и явлениями — причинно-следственные, пространственно-временные, функциональные и т. д. Но они могут, как и предыдущие, представлять собой соединение разнородных по конкретному содержанию суждений типа: «Если 2 ? 2 = 4, то снег бел». Именно в таком обобщенном смысле импликация используется в классической логике. Суждение, стоящее после слов «если», «когда», называется «антецедентом» (предшествующим) или «основанием», а после «то» — «консеквентом» (последующим) или «следствием».

Импликация истинна во всех случаях, кроме одного: когда предшествующее (основание) есть, а последующего (следствия) нет. Таблица истинности импликации:

А
В
А ? В

и
и
и

и
л
л

л
и
и

л
л
и

Импликация может включать в себя три и более суждений. Например: «Участие прокурора в разбирательстве гражданского дела обязательно в случаях, когда это предусмотрено законом или когда необходимость участия прокурора в данном деле признана судом».

Законодательство и юридическая практика его применения свидетельствуют, что в форме импликации выражаются не только объективные зависимости одних предметов и явлений от других, но и также права и обязанности людей, связанные с теми или иными условиями. Например: «Каждый вправе в соответствии с международными договорами Российской Федерации обращаться в межгосударственные органы по защите прав и свобод человека, если исчерпаны все имеющиеся внутригосударственные средства правовой защиты» (Конституция РФ, ст. 46).

4. Эквивалентные (равнозначные) суждения (от лат. aequivalens — равноценный, равнозначный). В них объединяются суждения с взаимной (прямой и обратной) условной зависимостью. Они называются еще «двойной импликацией». Их образует логический союз «если и только если…, то» (символ «?»). Формула эквивалентности: А ? В (читается: «Если и только если А, то В»), Грамматически эквивалентность выражается союзами: «тогда и только тогда…, когда», «лишь в том случае, если…, то», «только при условии, если…, то» и др. Примеры: «Если число делится на два, то оно четное»; «Если и только если человек достиг пенсионного возраста, то он имеет право на получение пенсии по возрасту».

Эквивалентное суждение истинно в двух случаях: когда оба составляющие его суждения истинны и когда они оба ложны. Таблица истинности эквивалентности:

А
В
А ? В

и
и
и

и
л
л

л
и
л

л
л
и

Отрицание суждений. При характеристике сложных суждений широко используется еще один логический союз: «неверно, что» или просто «не» (знак отрицания «?» ). В отличие от бинарных союзов он относится к одному суждению. Прибавление его к какому-либо суждению означает образование нового суждения, которое находится в определенной зависимости от исходного. Например, исходное суждение: «Все судьи неподкупны». Его отрицание: «Неверно, что все судьи неподкупны» или «Не все судьи неподкупны», «Некоторые судьи не неподкупны».

Отрицание истинно, если исходное суждение ложно, и наоборот. Таблица отрицания суждений:

А
?А

и
л

л
и

Логические союзы, рассмотренные из методических соображений порознь, в реальной практике мышления нередко переплетаются друг с другом, образуя порой весьма сложные мыслительные конструкции. Например: «Суд не принимает отказа истца от иска, признания иска ответчиком и не утверждает мирового соглашения сторон, если эти действия противоречат закону или нарушают чьи-либо права и охраняемые законом интересы». Здесь налицо сочетание нескольких конъюнкций с дизъюнкцией и импликацией. Или: «Судья, народный заседатель, прокурор, секретарь судебного заседания, эксперт и переводчик не могут участвовать в рассмотрении дела и подлежат отводу, если они лично, прямо или косвенно, заинтересованы в исходе дела или имеются иные обстоятельства, вызывающие сомнения в их беспристрастности».

Различия между логическими союзами относительны. Подобно тому как один и тот же логический союз может соединять самые разные по конкретному содержанию суждения, так одно и то же конкретное суждение может быть выражено разными логическими союзами. Например: «День прошел, и настала ночь»; «Если день прошел, то настала ночь»; «Или день не прошел, или настала ночь»; «День не прошел, ночь не настала»; «Если ночь не настала, то день не прошел». Взаимосвязь и взаимозаменяемость логических союзов имеет большое значение для преобразования символических формул в процессе исчисления высказываний.

Суждения
бывают простые и сложные; последние
состоят из нескольких простых. Суждение
«Некоторые звери делают запасы на зиму»
— простое, а суждение «Наступила осень,
дни стали короче, и перелетные птицы
отправились в теплые края» — сложное,
состоящее из трех простых суждений.

Виды простых
ассерторических суждений

Это суждения, в
которых один субъект и один предикат.
Простые суждения бывают трех видов:

1 . Суждения свойства
(атрибутивные).

В
них утверждается или отрицается
принадлежность предмету известных
свойств, состояний, видов деятельности.
Примеры: «Мед сладкий», «Шопен не является
драматургом». Схемы этого вида суждения:
« S
есть Р » или «S
не есть Р».

2. Суждения с
отношениями.

В них говорится
об отношениях между предметами. Например:
«Всякий протон тяжелее электрона»,
«Французский писатель Виктор Гюго
родился позднее французского писателя
Стендаля», «Отцы старше своих детей» и
др.

Формула,
выражающая суждение с двуместным
отношением, записывается как аRb
или R(а,
b),
где а и b
— имена предметов, а К — имя отношения.
В суждении с отношением может что-либо
утверждаться или отрицаться не только
о двух, но и о трех, четырех или большем
числе предметов, например: «Москва
находится между Санкт-Петербургом и
Киевом». Такие суждения выражаются
формулой R(а„
а₂,
а₃,
…, а„).

3. Суждения
существования (экзистенциальные).

В них утверждается
или отрицается существование предметов
(материальных или идеальных) в
действительности. Примеры этих суждений:
«Существуют атомные электростанции»,
«Не существует беспричинных явлений».

Категорические
суждения и их виды (деление по количеству
и качеству)

В
традиционной логике все три указанных
вида суждений представляют собой простые
категорические суждения. По качеству
связки («есть» или «не есть») категорические
суждения делятся на утвердительные и
отрицательные. Суждения «Некоторые
учителя являются талантливыми
воспитателями» и «Все ежи колючие»
утвердительные. Суждения «Некоторые
книги не являются букинистическими» и
«Ни один кролик не является хищным
животным» отрицательные. Связка «есть»
в утвердительном суждении отражает
присущность предмету (предметам)
некоторых свойств. Связка «не есть»
отражает то, что предмету (предметам)
не присуще некоторое свойство.

Некоторые логики
считали, что в отрицательных суждениях
нет отражения действительности. На
самом деле отсутствие определенных
признаков также представляет собой
действительный признак, имеющий
объективную значимость. В отрицательном
истинном суждении наша мысль разъединяет
(разделяет), то, что находится разделенным
в объективном мире.

В познании
утвердительное суждение имеет в общем
случае большее значение, чем отрицательное,
ибо важнее раскрыть, каким признаком
обладает предмет, чем то, каким он не
обладает, так как любой предмет не
обладает очень многими свойствами
(например, дельфин не рыба, не насекомое,
не растение, не пресмыкающееся и т. д.).

В зависимости от
того, обо всем ли классе предметов, о
части этого класса или об одном предмете
идет речь в субъекте, суждения делятся
на общие, частные и единичные. Например:
«Все соболи — ценные пушные звери» и
«Все здравомыслящие люди хотят долгой,
счастливой и полезной жизни» (П.Брэгг)
общие суждения; «Некоторые животные —
водоплавающие» — частное; «Везувий
действующий вулкан» — единичное.

Структура
общего суждения: «Все S
суть (не суть) Р». Единичные суждения
будут трактоваться как общие, так как
их субъектом является одноэлементный
класс.

Среди общих суждений
встречаются выделяющие суждения, в
состав которых входит кванторное слово
«только». Примеры выделяющих суждений:
«Брэгг пил только дистиллированную
воду»; «Смелый человек не боится правды.
Ее боится только трус» (А. К. Доил).

Среди общих суждений
имеются исключающие суждения, например:
«Все металлы при температуре 20°С, за
исключением ртути, твердые». К числу
исключающих суждений относятся и те, в
которых выражены исключения из тех или
иных правил русского или иных языков,
правил логики, математики, других наук.

Частные
суждения имеют структуру: «Некоторые
S
суть (не суть) Р». Они делятся на
неопределенные и определенные. Например,
«Некоторые ягоды ядовиты» ‑
неопределенное частное суждение. Мы не
установили, обладают ли признаком
ядовитости все ягоды, но не установили
и то, что признаком ядовитости не обладают
некоторые ягоды. Если мы установили,
что «только некоторые S
обладают признаком Р», то это будет
определенное частное суждение, структура
которого: «Только некоторые S
суть (не суть) Р». Примеры: «Только
некоторые ягоды ядовиты»; «Только
некоторые фигуры являются сферическими»;
«Только некоторые тела легче воды».

В
определенных частных суждениях часто
применяются кванторные
слова:
большинство,
меньшинство, немало, не все, многие,
почти все, несколько и др.

В
единичном суждении субъектом является
единичное понятие. Единичные суждения
имеют структуру: «Это S
есть (не есть) Р». Примеры единичных
суждений: «Озеро Виктория не находится
в США»; «Аристотель — воспитатель
Александра Македонского»; «Эрмитаж —
один из крупнейших в мире художественных
и культурно-исторических музеев».

Объединенная
классификация простых категорических
суждений по количеству и качеству

В
каждом суждении имеется количественная
и качественная характеристики. Поэтому
в логике применяется объединенная
классификация суждений по количеству
и качеству, на основе которой, выделяются
следующие четыре типа суждений:

1.
А — общеутвердительное суждение.
Структура его: «Все «S
суть Р». Например: «Все люди хотят
счастья».

2.
I
— частноутвердительное суждение.
Структура его: «Некоторые S
есть Р». Например, «Некоторые уроки
стимулируют творческую активность
учащихся». Условные обозначения для
утвердительных суждений взяты от слова
AFFIRMO,
или утверждаю; при этом берутся две
первые гласные буквы: А — для обозначения
общеутвердительного и I
— для обозначения частноутвердительного
суждения.

1. Е
   — общеотрицательное суждение. Его
   структура: «Ни одно S
   не есть Р». Пример: «Ни один океан не
   является пресноводным».

2. О
   — частноотрицательное суждение.
   Структура его: «Некоторые S
   не есть Р». Например, «Некоторые
   спортсмены не являются чемпионами
   Олимпийских игр». Условное обозначение
   для отрицательных суждений взяты от
   слова NEGO,
   или отрицаю [28].

Распределенность
терминов в категорических суждениях

Так
как простое категорическое суждение
состоит из терминов S
и Р, которые, являясь понятиями, могут
рассматриваться со стороны объема, то
любое отношение между S
и Р в простых суждениях может быть
изображено при помощи круговых схем
Эйлера, отражающих отношения между
понятиями. В суждениях термины S
и Р могут быть либо распределены, либо
не распределены. Термин считается
распределенным, если его объем полностью
включается в объем другого термина или
полностью исключается из него. Термин
будет нераспределенным, если его объем
частично включается в объем другого
термина или частично исключается из
него. Проанализируем четыре вида
суждений: А, I,
E,
О (мы рассматриваем типичные случаи).

Суждение
А — общеутвердительное. Его структура:
«Все S
суть Р». Рассмотрим два случая.

1. В суждении «Все
караси — рыбы» субъектом является
понятие «карась», а предикатом — понятие
«рыба». Квантор общности — «все». Субъект
распределен, так как речь идет о всех
карасях, т.е. его объем полностью включен
в объем предиката. Предикат не распределен,
так как в нем мыслится только часть рыб,
которые совпадают с карасями; речь идет
лишь о той части объема предиката,
которая совпадает с объемом субъекта.

2.
В суждении «Все квадраты — равносторонние
прямоугольники» термины такие: S
— «квадрат», Р — «равносторонний
прямоугольник» и квантор общности —
«все». В этом суждении S
распределен и Р распределен, ибо их
объемы полностью совпадают.

Если
S
равен по объему Р, то Р распределен. Это
бывает в определениях и в выделяющих
общих суждениях.

Суждение
I
— частноутвердительное. Его структура:
«Некоторые S
суть Р». Рассмотрим два случая.

1. В суждении
«Некоторые подростки — филателисты»
термины такие:

S
— «подросток», Р — «филателист», квантор
существования — «некоторые». Субъект
не распределен, так как в нем мыслится
только часть подростков, т.е. объем
субъекта лишь частично включается в
объем предиката. Предикат тоже не
распределен, так как он также лишь
частично включен в объем субъекта
(только некоторые филателисты являются
подростками).

2.
В суждении «Некоторые писатели —
драматурги» термины такие: S
— «писатель», Р — «драматург» и квантор
существования — «некоторые». Субъект
не распределен, так как в нем мыслится
только часть писателей, т. е. объем
субъекта лишь частично включается в
объем предиката. Предикат распределен,
ибо объем предиката полностью входит
в объем субъекта. Таким образом, Р
распределен, если объем Р меньше объема
S,
что бывает в частных выделяющих суждениях.

Суждение
Е — общеотрицательное. Его структура:
«Ни одно S
не суть Р». Например: «Ни один лев не
есть травоядное животное». В нем термины
такие: S
— «лев», Р — «травоядное животное» и
кванторное слово — «ни один». Здесь
объем субъекта полностью исключается
из объема предиката, и наоборот.

Суждение
О — частноотрицательное. Его структура:
«Некоторые S
не суть Р». Например: «Некоторые учащиеся
не являются спортсменами». В нем такие
термины: S
— «учащийся», Р — «спортсмен» и квантор
существования — «некоторые». Субъект
не распределен, так как мыслится лишь
часть учащихся, а предикат распределен,
ибо в нем мыслятся все спортсмены, ни
один из которых не включен в ту часть
учащихся, которая мыслится в субъекте.

Итак,
S
распределен в общих суждениях и не
распределен в частных; Р всегда распределен
в отрицательных суждениях, в утвердительных
же он распределен тогда, когда по объему
Р ≤
S
[15].

Отношения между
простыми суждениями

Отношения
между простыми суждениями определяются,
с одной стороны, их конкретным
содержанием, а с другой —
логической формой: характером субъекта,
предиката,
логической связки. Поскольку по характеру
предиката простые суждения делятся,
прежде всего, на атрибутивные и суждения
с отношением, то рассмотрим каждый
из этих видов в отдельности.

Отношения
между атрибутивными суждениями. По
своему содержанию атрибутивные суждения
могут находиться в двух важнейших
отношениях сравнимости
и несравнимости.

Несравнимые
суждения. У
них разные субъекты или предикаты или
то и другое вместе.
Таковы, например, суждения “Космос
необъятен” и “Закон суров”. В
подобных
случаях истинность или ложность одного
из суждений непосредственно не зависит
от истинности или ложности другого. Она
прямо определяется отношением к
действительности
соответствием или несоответствием ей.
Правда, в условиях универсальной
связи и взаимодействия предметов и
явлений действительности суждения о
них не могут быть абсолютно независимыми
друг от друга. Очевидна лишь
их относительная самостоятельность и
независимость с точки зрения истинности
или
ложности. Так если истинно суждение
“Энергия сохраняется” (а не исчезает,
и не возникает
из ничего, как гласит закон сохранения
и превращения энергии), то будет ложным
суждение “Вечный двигатель возможен”,
хотя по конкретному содержанию они
не имеют ничего общего, ни субъекта, ни
предиката, а, следовательно, являются
несравнимыми.

Так
в предложении может быть одинаковым
субъект или предикат. Например: “Закон
суров” и “Закон вступил в силу”
или “Закон вступил в силу” и “Указ
вступил в
силу”. И хотя смысловое различие здесь
меньше, чем в предыдущем случае,
они тоже не могут соотноситься между
собой по истинности или ложности.
Поэтому в дальнейшем их анализ не
производится.

Сравнимые
суждения. Они,
наоборот, имеют одинаковые термины —
и субъект, и
предикат, но могут различаться по
количеству и качеству. Это суждения,
как говорят,
“одинаковой материи”, а, следовательно,
сопоставимы по истинности и ложности.

По
своей логической форме, прежде всего,
по количеству и качеству сравнимые
суждения подразделяются на совместимые
и несовместимые.

Совместимые
суждения содержат одну и ту же мысль
полностью или частично. Между
ними возникают следующие логические
отношения: эквивалентности, подчинения,
частичной совместимости.

Эквивалентность
(равнозначность) это отношение между
суждениями, у которых
субъект и предикат выражены одни и теми
же или равнозначными понятиями (хотя
и разными словами), причем и количество
и качество одни и те же. Таково например,
общеутвердительные суждения “Все
адвокаты юристы” и “Все защитники
в
суде имеют специальное юридическое
образование”. Аналогично может
обстоять дело
и с общеотрицательными, частноутвердительными
и частноотрицательными суждениями.
Отношения между такого рода суждениями
по их истинности или ложности
характеризуются взаимно однозначным
соответствием: они или одновременно
истинны, или одновременно ложны. Поэтому
если истинно одно, то истинно
другое, а если одно ложно, то и другое
ложно.

Последующие
отношения между простыми атрибутивными
суждениями – А, Е, I,
О
– для наглядности изображают графически
в виде логического квадрата.

Его
вершины символизируют простые
категорические суждения – А, Е, I,
О; стороны
и диагонали отношения между суждениями.
Противоположность
(контрарность) (рис. 3.2.1).

Рис. 3.2.1. Логический
квадрат

Подчинение
—
это отношение между такими суждениями,
у которых количество различно,
а качество одно и то же. В таком отношении
находятся общеутвердительное (А)
и частноутвердительное (I),
общеотрицательное (Е) и частноотрицательное
(О) суждения.
При подчинении действуют следующие
закономерности:

а) из
истинности подчиняющего (А или Е) следует
истинность подчиненного (соответственно
I
или О), но не наоборот;

б) из
ложности подчиненного (I
или О) следует ложность подчиняющего
(соответственно
А или Е), но не наоборот.

Примеры.
Если истинно А, что “Все адвокаты –
юристы”, то тем более истинно, что
“По крайней мере, некоторые адвокаты
– юристы”. Но если истинно, что “Некоторые
свидетели правдивы”, то отсюда еще
не следует, что истинно А: “Все свидетели
правдивы”. В данном случае это ложное
суждение. В других случаях А может
быть истинным. Например: если истинно,
что “Некоторые адвокаты – юристы”,
то
истинно А, что “Все адвокаты – юристы”.
В свою очередь, если ложно I,
что “Некоторые граждане вправе
нарушать законы”, то тем более ложно
А, что “Все граждане
вправе нарушать законы”. Но если ложно
А, что “Все свидетели правдивы”, то
отсюда еще не следует, что ложно I:
“Некоторые свидетели правдивы”. В
данном случае
это истинное суждение. В других случаях
I
может быть ложным. Например: если
ложно А, что “Все граждане вправе
нарушать законы”, то ложно и I,
что “Некоторые
граждане вправе нарушать законы”.
Истинным будет Е, что “Ни один гражданин
не вправе нарушать законы”.

Частичная
совместимость (субконтрарность)
— это
отношение между суждениями
одинакового количества, но разного
качества: между частноутвердительными
(I)
и частноотрицательными (О) суждениями.
Для нее характерна
следующая закономерность: оба суждения
могут быть одновременно истинными, но
не могут быть одновременно ложными. Из
ложности одного из них следует
истинность другого, но не наоборот.
Например, при истинности I,
что “Некоторые
свидетели правдивы”, может быть
истинно и О, что “Некоторые свидетели
не правдивы”. Но оно может быть и
ложным. Например, если истинно, что
“Некоторые
адвокаты — юристы”, то это не значит,
что истинно О: “Некоторые адвокаты
– не юристы”. Оно ложно. Однако если
ложно I,
что “Некоторые граждане вправе
нарушать законы”, то не может быть
ложным О, что “По крайней мере, некоторые
граждане не вправе нарушать законы”.
Оно будет непременно истинным.

Несовместимые
суждения. Они
имеют следующие логические отношения:
противоположности и противоречия.

Противоположность
—
это отношение между общеутвердительными
(А) и общеотрицательными
(Е) суждениями. Оба таких суждения не
могут быть одновременно
истинными, но могут быть одновременно
ложными. Из истинности одного
непременно следует ложность другого,
но не наоборот. Тут, следовательно,
закономерность,
обратная той, что характеризовала
отношения частичной совместимости.
Так, если истинно А, что “Все адвокаты
—
юристы”, то ложно Е, что “Ни
один адвокат —
не юрист”. И если истинно Е, что “Ни
один гражданин не вправе нарушать
законы”, то ложно А, что “Все граждане
вправе нарушать законы”. Но если ложно
А, что “Все свидетели правдивы”, то
отсюда еще не следует истинность Е, что
“Ни один свидетель не правдив”. В
данном случае оно тоже ложное. Истинно
здесь I,
что
“Некоторые свидетели правдивы”.
Ложно, что “Некоторые свидетели не
правдивы”.
В других случаях Е может быть истинным.
Так, если ложно А, что “Все граждане
вправе нарушать законы”, то истинно
Е, что “Ни один гражданин не вправе
нарушать
законы”.

Противоречие
(контрадикторность) —
отношение между такими суждениями, как
общеутвердительное (А) и частноотрицательное
(О), общеотрицательное (Е) и частноутвердительное
(I).
Им присущи следующие закономерности:
они не могут быть одновременно
истинными и не могут быть одновременно
ложными. Из истинности одного
непременно следует ложность другого и
наоборот. Это “самые несовместимые”
из всех суждений, межу ними, образно
говоря, отношения “кошки и собаки”,
поскольку те не могут ужиться друг с
другом.

Примеры.
Если истинно А, что “Все адвокаты –
юристы”, то ложно О, что “Некоторые
адвокаты — не юристы”. Если ложно А,
что “Все свидетели правдивы”, то
истинно О, что “Некоторые свидетели
не правдивы”.

Знание
отношений между простыми атрибутивными
суждениями по их истинности
и ложности важно в познавательном и
практическом отношении. Оно помогает,
прежде всего, избегать возможных
логических ошибок в собственных
рассуждениях.
Так, из истинности частного суждения
(I
или О) нельзя выводить истинность
общего (А или Е). Например, из того, что
“Некоторые судьи неподкупны”, еще
не следует, что “Все судьи неподкупны”.
Подобная ошибка называется в логике
поспешным
обобщением и допускается часто [58].

В
дискуссии, споре, в частности по
юридическим вопросам чтобы опровергнуть
общее ложное суждение, вовсе не обязательно
прибегать к противоположному общему
суждению, так как легко попасть впросак:
оно может оказаться тоже ложным.
Вспомним пример: если ложно А, что “Все
свидетели правдивы”, то это еще
не значит, что истинно Е: “Ни один
свидетель не правдив”. Оно тоже ложно,
хотя в других случаях Е может оказаться
истинным. В логическом отношении
достаточно привести противоречащее
суждение О: “Некоторые свидетели не
правдивы”.
Если А ложно, то О всегда истинно. Это
самый безопасный и неуязвимый,
наиболее надежный способ опровержения
[41].

Отношения
между
суждениями
с отношениями. Реляционные
суждения (или суждения
об отношениях между предметами мысли),
как уже отмечалось, имеют нечто
общее с атрибутивными суждениями:
трехчленность строения (xRy),
наличие количества
и качества. Поэтому они могут находиться
тоже в отношениях подчинения, частичной
совместимости, противоположности,
противоречия или же логической
независимости.
Так, если истинно I,
что “Некоторые металлы легче воды”,
то это еще не значит, что истинно А: “Все
металлы легче воды”, но означает, что
ложно Е —
“Ни один
металл не легче воды” и что неопределенно
О, “Некоторые металлы не легче воды”
(в данном случае оно истинно).

В
то же время реляционные суждения
отличаются от атрибутивных тем, что
раскрывают не свойства предметов, а
отношения между предметами и, следовательно,
имеют
не одночленный (одноместный) предикат,
а многочленный (n-местный
от двух и более). Поэтому в зависимости
от характера отношения R
между предметами х
и у
внутри
суждения устанавливаются свои, особые
отношения.

Отношения
между х и у могут быть, прежде всего,
симметричными и несимметричными.

Симметричные
(от
греч. symmetria
—
соразмерность) —
это такие отношения между
х и у, для которых не имеет значения,
какой из этих членов предшествующий,
а какой последующий. Иначе говоря, их
можно менять местами,
при этом истинность или ложность не
изменится. Это раскрываемые в суждениях
отношения равенства, сходства, подобия,
одновременности и др. Например: “Иван
– брат Петра”. Следовательно, “Петр
– брат Ивана”. Такие два реляционных
суждения могут быть одновременно
истинными либо одновременно
ложными. Если истинно одно из них, то
истинно и другое, и наоборот,
если ложно одно из них, то ложно и другое.

Несимметричными
являются
такие отношения между х и у, при которых
важен порядок их расположения. Поэтому
менять их местами нельзя без изменения
смысла суждения,
следовательно, его истинности или
ложности. Например: “Иван —
отец Степана”.
Но это не значит, что “Степан – отец
Ивана”. Если истинно одно из этих
суждений,
то ложно другое. Истинным здесь будет
“Степан сын Ивана”. Несимметричными
оказываются и такие отношения: “Иван
любит Марью”. Отсюда вовсе
не следует, что “Марья любит Ивана”,
но может любить его, а может и не любить.
Если истинно одно из таких суждений, то
другое – неопределенно.

Важно
также учитывать относительный характер
различий между симметричностью
и несимметричностью. Симметричное в
одном отношении может
быть несимметричным и в другом и наоборот.
Например: если “Иван -брат
Петра”, то “Петр – брат Ивана”. Но
если “Иван – брат Елены”, то это
значит, что
“Елена – естра Ивана”.

Отношения между
х и у могут быть транзитивными и
нетранзитивными.

Транзитивные,
или переходные
отношения (от лат. transitive
– переход). Если, например,
х эквивалентно у, а у эквивалентно z,
то и х эквивалентно z.
Это могут быть также
отношения величины (больше —
меньше), пространственные (дальше —
ближе), временные
(раньше —
позже) и др. Например: “Иван — брат
Петра”, “Петр —
брат Елены”,
значит, “Иван — брат Елены”. Такие
суждения могут быть либо одновременно
истинными,
либо одновременно ложными.

Нетранзитивные
(непереходные)
отношения обладают обратной зависимостью
по сравнению
с предыдущей. Так, если “Иван —
отец Степана”, а “Степан —
отец Николая”,
то это вовсе не значит, что “Иван отец
Николая”. Он ему дед, следовательно,
такие суждения не могут быть одновременно
истинными. Если истинно
одно, то ложно другое.

Есть еще отношения
рефлексивности и нерефлексивности.

Рефлексивные
отношения
(от лат. reflexio
— обращение назад, отражение)
характеризуются тем, что каждый
член отношения находятся в таком же
отношении к самому себе. Если два события
произошли одновременно, то они одновременны
между собой. Оба суждения могут
быть либо истинными, либо ложными.

Нерефлексивные
отношения
таковы, что если 2 меньше 3, то это не
значит, что 2
меньше 2 и 3 меньше 3. Из истинности одного
следует ложность другого.

Знание
особенностей подобных отношений между
реляционными суждениями по их
истинности или ложности важны всюду,
где есть такого рода отношения. Особое
значение
это имеет в сфере правовых отношений.
Так, в судебной практике учитываются
одновременность или разновременность
событий, отношения родства, знакомства
между людьми и т.д. Например, если Иванов
знает Петрова, а Петров —
Сидорова, то это еще не значит, что Иванов
знает Сидорова. Тут отношения нетранзитивные
со всеми вытекающими отсюда последствиями
по истинности и ложности
между раскрывающими их реляционными
суждениями [6].

Сложные суждения

Сложные
суждения отличаются от простых также
по своим функциям и структуре.
Их функции носят более сложный характер,
так как в них раскрывается не одна,
а одновременно несколько —
две или более —
связей между предметами мысли. Их
структура тоже характеризуется большей
сложностью, обретая новое качество.
Основными структурообразующими
элементами здесь выступают уже не
понятия-термины (субъект и предикат), а
самостоятельные суждения (причем их
внутренняя субъектно-предикатная
структура уже не учитывается). И связь
между ними осуществляется
не с помощью связки “есть” (“не
есть”), а в качественно иной формы —
посредством логических союзов (они
называются также логическими связками).
Это такие
союзы, как “и”, “или”, “либо”,
“если… то” и др. Они близки по смыслу
к соответствующим
грамматическим союзам, но, как будет
показано ниже, полностью с ними
не совпадают. Главное их отличие сводится
к тому, что они однозначны, тогда как
грамматические союзы могут иметь
множество смыслов и оттенков [20, 59].

Каждый
из логических союзов является бинарным,
т.е. соединяет между собой только
два суждения независимо от того, простые
они или сами, в свою очередь, сложные,
имеющие внутри себя собственные союзы.

Если
в простых суждениях переменными были
субъект и предикат (S
и Р), а постоянными
—
логические связки “есть” и “не
есть”, то в сложных суждениях переменными
выступают уже отдельные, далее
нерасчленяемые суждения (назовем их
“А” и “В”), а постоянными —
логические союзы: “и”, “или” и
др.

В
русском языке сложные суждения имеют
весьма многообразные формы выражения.
Они могут выражаться, прежде всего,
сложносочиненными предложениями.
Например: “Ни один виновный не должен
уйти от ответственности, и ни один
невиновный не должен пострадать”.
Они могут быть выражены также
сложноподчиненными
предложениями. Таково, например,
высказывание Цицерона: “Ведь
если бы даже ознакомление с правом
представляло огромную трудность, то и
тогда
сознание его великой пользы должно было
бы побуждать людей к преодолению этой
трудности”.

Наконец,
они могут облекаться и в особую форму
простых распространенных
предложений. Этого нетрудно добиться,
например, в результате своеобразного
“свертывания” сложных предложений.
Так, сложносочиненное предложение
“Аристотель был великим логиком, и
Гегель тоже был великим логиком”
можно превратить в простое распространенное:
“Аристотель и Гегель были великими
логиками”. Благодаря такому “свертыванию”
достигается большая лаконичность речи,
следовательно, ее экономность и
динамичность.

Таким образом, не
всякое сложное суждение выражается
непременно сложным предложением, но
всякое сложное предложение выражает
сложное суждение.

Сложным
называют
суждение, включающее в качестве составных
частей другие суждения,
связанные логическими связками —
конъюнкцией,
дизъюнкцией или импликацией.
В
соответствии с функциями логических
связок основными видами сложных суждений
являются: 1) соединительные, 2) разделительные,
3) условные и 4)
эквивалентные суждения.

Соединительным
(конъюнктивным) суждением называют
суждение, включающее
в качестве составных частей другие
суждения-конъюнкты, объединяемые
связкой “и”. Например: “Кража и
мошенничество относятся к умышленным
преступлениям”. Если одно из составляющих
суждений —
“Кража
относится
к умышленным преступлениям” —
обозначить символом р, другое суждение
— “Мошенничество относится к умышленным
преступлениям” — символом q,
а связь между
ними знаком, то в целом соединительное
суждение можно символически выразить
как рлq.

В естественном
языке соединительные суждения могут
быть выражены одним из трех способов.

1. Соединительная
   связка выражена в сложном субъекте,
   состоящем
   из конъюнктивно
   связанных понятий, по схеме: S₁,
   и
   S₂,
   есть
   Р. Например,
   “Конфискация
   имущества и лишение звания являются
   дополнительными видами уголовного
   наказания”.

2. Соединительная
   связка выражена в сложном предикате,
   состоящем
   из конъюнктивно
   связанных признаков, по схеме: S
   есть
   Р₁
   и Р₂.
   Например,
   “Преступление
   —
   это общественноопасное и противоправное
   деяние”.

3. Соединительная
   связка представлена сочетанием первых
   двух способов по
   схеме: S₁
   и
   S₂
   есть
   P₁
   и Р₂.
   Например,
   “С полицеймейстером и прокурором
   Ноздрев тоже был на “ты” и обращался
   по-дружески” (Н. В. Гоголь, “Мертвые
   души”).

4. Конъюнктивная
   связка
   грамматически выражается не только
   союзом “и”, но и словами
   “а”, “но”, “также”, “как”,
   “так и”, “хотя”, “однако”,
   “несмотря на”, “вместе с тем”
   и др.

На основе выше
изложенного можно составить структурную
схему соотношения простых и сложных
суждений (рис. 3.3.1).

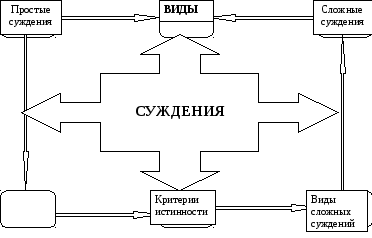
Виды
и типы

простых

суждений

Рис. 3.3.1. Структурная
схема соотношения простых и сложных
суждений

4. Сложные суждения: логическая структура и виды

Сложные суждения – это суждения, образованные их простых посредством той или иной логической связи. Структура сложных суждений отличается от структуры простых суждений. Основными структурообразующими элементами здесь выступают не понятия (термины – субъект и предикат), а самостоятельные простыесуждения, внутренняя субъектно-предикатная структура которых уже не учитывается. Связь между элементами сложного суждения осуществляется с помощью логических союзов: «и», «или»; «если…то…»; «если и только если…, то»; «неверно, что…», которые близки к соответствующим грамматическим союзам, но полностью с ними не совпадают. Главное их отличие состоит в том, что логические союзы однозначны, тогда как грамматические союзы имеют множество смыслов и оттенков.

Эти типы связи простых суждений выражаются соответствующими логическими связками: конъюнкцией («и»), дизъюнкцией («или»), строгой дизъюнкцией («либо, …либо»), импликацией («если…, то»), эквиваленцией (тогда и только тогда, когда…», отрицанием («неверно, что…»). Логические связки обозначают символами:
~ соответственно. Каждый из этих логических союзов, за исключением отрицания, является бинарным, т.е. соединяет только два суждения, независимо от того простые они или сами, в свою очередь, сложные, имеющие внутри себя собственные союзы.

Сложные суждения рассматриваются в логике только с точки зрения их истинностных значений, которые зависят от истинностных значений простых суждений, входящих в него, а также от характера связи этих суждений. Характер связи определяется смыслом логических союзов, который состоит в ответе на вопрос: при каких условиях сложное суждение будет истинно, а при каких – ложно. Иначе говоря, при каких сочетаниях истинности и ложности простых суждений, входящих в сложное, данный логический союз дает истинную связь, а при каких – ложную. Смысл логических союзов можно определить с помощью, так называемойистинностной таблицы, в которой на входе (см. Табл.1, столбцы 1,2) выписываются все возможные комбинации истинностных значений простых суждений(входящих в рассматриваемое сложное), а на выходе (Таблица 1 – столбцы 3 – 9) – значения сложного суждения, образованного из данных простых с помощьюсоответствующего логического союза. При этом, исходные простые суждения обозначают буквами: А,В,С,D…, а значения истинности символами: «и» – истино; «л» – ложно.

Таблица 1.

NN	1	2	3	4	5	6	7	8	9
А	В	А В	А В	А В	А В	А В	~А	~В
1.	и	и	и	и	л	и	и	л	л
2.	и	л	л	и	и	л	л	л	и
3.	л	и	л	и	и	и	л	и	л
4.	л	л	л	л	л	и	и	и	и

Виды сложных суждений

По характеру логической связи выделяют пять основных видов сложных суждений: соединительные (конъюнктивные), разделительные (дизъюнктивные), условные (импликативные), эквивалентные, отрицаемые.

Соединительное или конъюнктивное суждение – это сложное суждение, образованное из исходных суждений посредством логического союза «и», обозначаемого символом « ».  Например, суждение: «Сегодня я пойду на лекцию по логике и в кино» является конъюнктивным суждением, состоящим из двух простых суждений (обозначим их соответственно – А, В): : «Сегодня я пойду на лекцию по логике» (А), «Сегодня я пойду в кино» (В). Символически данное сложное суждение можно записать как: А В, где А, В – элементы конъюнкции; « » – символ логического союза – конъюнкции. В русском языке конъюнктивный логический союз выражается многими грамматическими союзами: и, а, но, да, хотя, однако, а также… Нередко подобные грамматические союзы заменяются запятой, двоеточием, точкой с запятой. Например, в суждении «Русские долго запрягают, да быстро ездят».

Конъюнктивное суждение истинно только при истинности всех составляющих его элементов и ложно при ложности хотя бы одного из них (см. табл.1 – столбец 3).

Знание особенностей истинностного значения конъюнкции имеет особое значение в практике мышления, т.к. достаточно одного ложного суждения, чтобы придать всей, даже весьма сложной, конъюнктивной мысли ложность. Этот факт лежит в основе многих русских пословиц, например, о том, что делает ложка дегтя в бочке меда. Эту особенность важно учитывать в юридической практике, в дискуссиях – когда выстраивается сложная цепь мыслей, которая при одном ложном звене может распасться. С другой стороны, достаточно обнаружить хотя бы один ложный аргумент в доводах оппонента, чтобы опровергнуть все его рассуждение в целом.

Разделительное или дизъюнктивное суждение – это сложное суждение, образованное из исходных суждений посредством логического союза «или», обозначаемого символом « ». Например, суждение: «Право может способствовать экономическому развитию или препятствовать ему» является дизъюнктивным суждением, состоящим из двух простых: «Право может способствовать экономическому развитию», «Право может препятствовать экономическому развитию». Соответственно обозначив их через буквы А, В – выделим его логическую форму: А В.

Поскольку связка «или» употребляется в двух разных значениях – неисключающем и исключающем, то различают слабую и сильную дизъюнкции соответственно. Выше приведенный пример является слабой дизъюнкцией, т.к. право одновременно в одном отношении может способствовать развитию экономики, но препятствовать в другом. Слабая дизъюнкция является истинной в тех случаях, когда истинно по крайней мере одно из составляющих ее суждений (или оба вместе) и ложна, когда оба составляющих ее суждения ложны (Табл.1 – столбец 4).

Сильная дизъюнкция (символ « ») отличается от слабой тем, что ее составляющие исключают друг друга. Например: «Преступление может быть умышленным или по неосторожности». Для того, чтобы подчеркнуть строго разделительный, исключающий характер связи, в естественном языке используется усиленная двойная форма разделения: «…либо…либо», «или…или», например: «Либо я найду путь, либо я проложу его». Строгая дизъюнкция истинна лишь тогда, когда одно из составляющих ее суждений истинно, а другое – ложно (Табл. 1 – столбец 5).

Среди дизъюнктивных суждений следует различать также полную и неполную дизъюнкцию, когда соответственно: перечислены все признаки, виды определенного рода или это перечисление остается открытым (неполным), что в естественном языке выражается словами: «и т.д.», «и др.».

Дизъюнктивные суждения широко распространены в практике мышления. Именно в них выражается логическая операция деления.

Условное или импликативное суждение – это сложное суждение, в котором суждения объединяются логическим союзом «если…, то» (символ « »), например: «Если правительство нарушает закон, то порождает неуважение к нему», «Если число делится на 2 без остатка, то оно четное». Условное суждение состоит из двух составляющих его суждений. Суждение, выраженное после слова «если» называется основанием или антецедентом (предыдущим), а суждение – после слова «то» называется следствием или консеквентом (последующим). Формула условного суждения: А В, где А – основание, В – следствие. При этом, суждения, выполняющие роль основания и следствия, сами по себе могут быть как простыми, так и сложными суждениями.

Образуя условное суждение, прежде всего, имеют в виду, что не может быть так, чтобы то, о чем говорится в основании имело место, а то, о чем говорится в следствии отсутствовало. Иными словами, не может случится, чтобы антецедент был истинным, а консеквент – ложным. Это и определяет то, что условное суждение истинно во всех случаях, кроме одного: когда предшествующее есть, а последующего нет (т.е. – суждение по форме А В – ложно только в одном случае, когда А – истинно, а В – ложно). Это выражено в таблице 1 – столбец 6.

В форме условных суждений выражают как объективные зависимости одних объектов от других, так и права и обязанности людей, связанные с теми или иными условиями.

Эквивалентное суждение – это сложное суждение, в котором объединяются суждения с взаимной условной зависимостью. Поэтому они также называются двойной импликацией. Они образуются с помощью логического союза «если и только если…, то», который обозначается символом « ». Формула эквивалентности: А В,где А, В – суждения, из которых образуется эквивалентное суждение, например: «Человек имеет право  на пенсию по возрасту, если и только если он достиг пенсионного возраста». В естественном языке, в том числе в экономических и юридических текстах, для выражения эквивалентных суждений используются грамматические союзы: «лишь при условии, что…, то», «только тогда, когда…, то», «в том и только в том случае, когда…, тогда».

Условия истинности эквивалентных суждений представлены в 7-ом столбце таблицы 1: эквивалентное суждение истинно в двух случаях – когда оба составляющих его суждения истинны или когда оба ложны. Иными словами, связь (отношение) между элементами эквивалентного суждения можно охарактеризовать как необходимую: истинность А достаточна для признания истинности В и наоборот; ложность А служит показателем ложности В и наоборот.

Отрицаемое суждение – это сложное суждение, образованное с помощью логического союза «неверно, что…» (или просто «не»), который именуется знаком отрицания (символ «~»). В отличие от вышеотмеченных бинарных союзов он относится к одному суждению. Прибавление его к какому-либо суждению означает образование нового суждения, которое находится в определенной зависимости от исходного: отрицаемое суждение истинно, если исходное ложно, и наоборот. Это выражено в таблице1 – столбцы 8,9. Например, если исходное суждение: «Все свидетели правдивы», то  отрицаемое: «Неверно, что все свидетели правдивы».

Все выделенные виды сложных суждений используются в обычных рассуждениях и контекстах, в том числе экономических и правовых. Для более точного уяснения смысла этих контекстов важно овладение навыками логического анализа сложных суждений с использованием символического языка для выражения их логической структуры. Часто для достижения определенности высказывания необходимо выявить главную связь в суждении. Например, высказывание «Преступление совершено А и В или С» не отличается определенностью, поскольку не ясно, какая из двух логических связок – конъюнкция или дизъюнкция – является главной. Поэтому данное высказывание может быть истолковано как конъюнктивное суждение (1): «А и (В или С)», а может и как дизъюнктивное суждение (2): «(А и В) илиС». Но по логической значимости, т.е. по их истинностному значению, они не эквиваленты. Это можно определить, построив для них истинностные таблицы, и по ним сравнить истинностные значения этих суждений.

С этой целью важно знать, как вообще строятся истинностные таблицы для различных сложных суждений. Осуществляется это следующим образом.

На входе таблицы:

1.       Выписывают все простые суждения (А, В, С, D…), входящие  в  рассматриваемое  сложное суждение. Пусть их число будет n.

2.       Определяют число к строк в таблице по формуле к = 2ⁿ

3.       В столбцах входа таблицы выписывают все возможные комбинации истинностных значений простых суждений в следующем порядке: в самом правом столбце чередуют и и л по одному; во втором справа столбце чередуют подряд два значения и и два значения л; в третьем столбце чередуют подряд четыре значения и и четыре значения л; в четвертом столбце – восемь значений и подряд и восемь значений л подряд и т.д.

На выходе таблицы:

4.       Слева направо выписывают логические формы всех сложных суждений, входящих в рассматриваемое суждение, по порядку: в начале суждения 1-ой степени сложности (т.е. с одним логическим знаком); затем 2-ой степени (с двумя логическими союзами); далее 3-ей степени (с тремя логическими союзами) и так до тех пор, пока последнее суждение не будет представлять логическую форму исходного сложного суждения.

5.       Столбцы истинностных значений для выписанных логических форм образуют исходя из: (1) смысла логического союза (см. таблицу 1) и (2) значений истинности, которые принимают простые суждения, входящие в данную форму (см. строки входа таблицы).

Мы можем сравнить вышеотмеченные суждения (1) и (2). С этой целью теперь построим таблицу 2 для конъюнктивного суждения (1), выразив его символически как «А (В С)», и таблицу 3 для дизъюнктивного суждения (2), записав его символически как «(А В) С».

Таблица 2		Таблица 3
А	В	С	В С	А (В С)		А	В	С	А В	(А В) С
и	и	и	и	и		и	и	и	и	и
и	и	л	и	и		и	и	л	и	и
и	л	и	и	и		и	л	и	л	и
и	л	л	л	л		и	л	л	л	л
л	и	и	и	л		л	и	и	л	и
л	и	л	и	л		л	и	л	л	л
А	В	С	В С	А (В С)		А	В	С	А В	(А В) С
л	л	и	и	л		л	л	и	л	и
л	л	л	л	л		л	л	л	л	л

Из таблиц 2 и 3 видно, что истинностные значения суждений (1) и (2) не одинаковы (в двух строках – когда одно ложно, другое истинно), и следовательно они не эквивалентны, и представляют суждения, выражающие различные связи между их структурными элементами.

Таким образом, для осуществления логического анализа формы сложных суждений необходимо записать их символически в виде формулы и построить соответствующие истинностные таблицы с последующим их сравнением.

4. Отношения между суждениями

Между суждениями существуют логические отношения. Суждения как и понятия, могут быть сравнимыми и несравнимыми, совместимыми и несовместимыми. Но есть существенные различия, вызванные их различной логической структурой. Если сравнимые понятия соотносятся друг с другом по их объему, то между сравнимыми суждениями имеются многообразные отношения прежде всего по их истинностным значениям. Анализ этих отношений предполагает выяснение таких вопросов: могут ли рассматриваемые суждения быть вместе истинными, вместе ложными, обусловливает ли истинность одного истинность другого и ложность одного ложность другого. Такой анализ имеет важное теоретическое и практическое значение, но его осуществление имеет свою специфику относительно простых и сложных суждений, поскольку они различаются своей логической структурой.

Отношения суждений по их истинностным значениям исследуются в логике между сравнимыми суждениями.

Несравнимые простые суждения имеют разные субъекты и предикаты, например: «Закон суров» и «Небо ясное». Истинность и ложность таких суждений не зависит друг от друга. Сравнимые простые суждения имеют одинаковые субъект и предикат (поэтому они и сравнимы по содержанию), но различаются количественными и качественными характеристиками логической формы. Несравнимые сложные суждения включают в себя полностью или частично разные по содержанию простые суждения. Например, суждения: «Прокуроры и следователи имеют юридическое образование» и «Прокуроры и следователи стоят на страже законности». Сравнимые сложные суждения включают одинаковые исходные простые суждения, а различаются типом связи между ними (т.е. логическими союзами). Например: «Кража и мошенничество строго караются по закону», «Кража или мошенничество строго караются по закону», «Неверно, что кража и мошенничество строго караются по закону».

Между сравнимыми суждениями выделяются два типа отношений: совместимость и несовместимость. Суждения рассматриваются как совместимые, если онимогут быть одновременно истинными, и как несовместимые, если они не могут быть одновременно истинными.

Совместимость бывает трех видов: эквивалентность, подчинение и частичная совместимость.

1.       Суждения эквивалентны, если они всегда принимают одинаковые истинностные значения. Простые категорические суждения (А, Е, J, О) находятся в отношении эквивалентности, если они различны по количеству и качеству, и одно из них стоит под отрицанием: ~ А эквивалентно О («Неверно, что все юристы адвокаты» эквивалентно «Некоторые юристы не адвокаты»); ~ О эквивалентно А («Неверно, что некоторые адвокаты не юристы» эквивалентно «Все адвокаты юристы»); ~ J эквивалентно Е («Неверно, что некоторые студенты профессора» эквивалентно «Ни один студент не профессор»); ~ Е эквивалентно J («неверно, что ни один гриб не ядовит» эквивалентно «Некоторые грибы ядовиты»).

Сложные суждения находятся в отношении эквивалентности, когда при одних и тех же значениях истинности исходных простых суждений они принимают одинаковые значения. Это всегда можно установить построением истинностных таблиц для рассматриваемых сложных суждений.

2.       Суждение находится в отношении подчинения к другому (подчиняющему), если оно истинно во всех тех случаях, когда истинно подчиняющее. Это отношение имеет место между простыми категорическим суждениями, у которых количество различно, а качество одно и то же. В таком отношении находятся: общеутвердительные (А) и частноутвердительные (J) суждения; общеотрицательные (Е) и частноотрицательные (О) суждения. Здесь действуют такие закономерности: (1) из истинности общего (А или Е) следует соответственно истинность частного (J или О), но не наоборот; (2) из ложности частного (J или О) следует ложность общего (А или Е), но не наоборот. Например, если истинно «Все студенты нашей группы – успевающие» (А), то тем более истинно «Некоторые студенты нашей группы успевающие» (J). В свою очередь, если ложно «Некоторые люди вправе нарушать закон» (J), то тем более ложно, что «Все люди вправе нарушать закон» (А).

Отношение подчинения в сложных суждениях имеет свойства логического следования, которое характеризуется тем, что при истинности подчиняющего суждения В подчиненное суждение С всегда истинно, и не может быть так, что суждение В истинно, а суждение С – ложно. Например: «Если у человека повышенная температура (В), то он болен (С)». При наличии температуры у человека (В) – истинно, следует с необходимостью истинность суждения (С). Но при ложности В, суждение С может быть как истинным, так и ложным.

3.       Отношение частичной совместимости также имеет место как между простыми, так и сложными суждениями. Для этого отношения характерна следующаязакономерность: невозможна совместная ложность суждений, находящихся в отношении частичной совместимости. В случае простых суждений – это отношение между суждениями одинакового количества, но разного качества: между частноутвердительными (J) и частноотрицательными (О) суждениями. Из ложности одного из них следует истинность другого, но не наоборот: из истинности одного из них не следует с необходимостью ложность другого – оно также может быть истинным. Эту закономерность особо следует учитывать в практике мышления. Так, при истинности (J) – «Некоторые следователи независимы» может быть истинным и (О) – «Некоторые следователи не являются независимыми». Но при ложности суждения (J) – «Некоторые следователи независимы» необходимо будет истиннымпротивоположное по качеству суждение, т.е. (О) – «Некоторые следователи не являются независимыми».

Рассмотрим теперь несовместимые суждения. Различают два вида несовместимости: противоречие и противоположность.

Противоречие – это такое отношение между суждениями, при котором истинность одного необходимо влечет ложность другого и наоборот. Иными словами, противоречивые суждения не могут вместе быть ни истинными, ни ложными. Среди простых суждений это отношение имеет место между: общеутвердительными (А) и частноотрицательными (О) суждениями; общеотрицательными (Е) и частноутвердительными (J) суждениями. Так, если ложно суждение «Все следователи независимы», то истинно «Некоторые следователи не являются независимыми». Отношение противоречия между сложными суждениями означает, что их истинностные значения могут лишь исключать друг друга.

Противоположность между суждениями проявляется в том, что данные суждения не могут быть вместе истинными, но могут быть вместе ложными. Для этого отношения характерна закономерность обратная той, которая характерна для отношения частичной совместимости: если одно из двух суждений истинно, то другоенеобходимо ложно, но при ложности одного из них другое может быть как истинным, так и ложным. Иными словами, возможна ложность обоих суждений.

В случае простых суждений, это отношение имеет место между общеутвердительными (А) и общеотрицательными (Е) суждениями. Так, если истинно (А) – «Все адвокаты – юристы», то ложно (Е) – «Ни один адвокат не юрист». Но если ложно (А) – «Все свидетели правдивы», то из него не следует истинность суждения (Е) – «Ни один свидетель не правдив», оно тоже ложно. Но в других случаях (Е) может быть истинным. Так, если ложно суждение (А) – «Все граждане вправе нарушать закон», то истинно (Е) – «Ни один гражданин не вправе нарушать закон».

Знание отношений между суждениями по их истинным значениям важно в познавательном и практическом планах, поскольку помогает избегать возможных ошибок в собственных рассуждениях, позволяет грамотно анализировать различные контексты, высказывания оппонентов. Часто встречаются ситуации, когда суждениями оперируют как исключающими друг друга. Например, когда кто-то выдвигает суждение в форме «Некоторые S есть Р», а другой – в форме «Некоторые S не есть Р». Логический же анализ этих суждений показывает, суждения, высказанные в такой форме, не исключают друг друга, а являются частично совместимыми, и оба могут оказаться истинными. Весьма часто также в споре из истинности частного суждения (J или О) выводят истинность общего (А или Е) соответственно, что нарушает правильность отношений между ними.

В дискуссии, споре, в частности по юридическим и экономическим вопросам, чтобы опровергнуть общее ложное суждение, часто используют противоположное ему общее суждение. Но так легко попасть впросак: оно тоже может оказаться ложным. В логическом отношении для точного опровержения достаточно привестипротиворечащее суждение (см. ниже схему логического квадрата). Смешение противоположных и противоречащих суждений довольно частая ошибка в практике мышления. Поэтому важно уметь осуществлять логический анализ отношений между суждениями.

Для осуществления логического анализа отношений между простыми суждениями используют графическую схему, называемую «логическим квадратом»: его вершины символизируют четыре вида простых категорических суждений – А, Е, J, О; стороны и диагонали – отношения между этими суждениями.

Общая характеристика сложных суждений

Виды сложных суждений – это выделенные по тем или иным основаниям классы сложных суждений, т. е. формы мышления, в которых утверждается или отрицается что-либо относительно существования предметов и явлений, их свойств, связей и отношений между ними, причем в составе этих суждений можно выделить простые суждения (они не являются неделимыми).

В обычной речи суждения выражаются с помощью предложений. Но не каждое предложение является суждением. Предложения в зависимости от цели высказывания делятся на:

• повествовательные (цель – сообщение),
• вопросительные (цель – вопрос),
• побудительные (цель – побуждение).

Только в повествовательных предложениях может выражаться суждение. При этом предложение должно содержать в себе какую-то информацию. В вопросительных и побудительных предложениях суждения выражаться не могут, поскольку они ничего не утверждают и не отрицают, не являются истинными или ложными. Здесь есть два исключения:

• риторические вопросы могут содержать суждение в особой форме – хотя они и являются вопросительными, по сути передают какую-то информацию;
• побудительные предложения также могут содержать суждение, если выражают призыв, лозунг или приказ. Это модальные суждения, подразумевающие слово-побуждение или слово-запрещение.

Образование сложных суждений производится из нескольких простых суждений. В каждом из простых суждений выделяют:

• субъект – понятие о предмете, которому в суждении отведена центральная роль,
• предикат – признак предмета, которые утверждается или отрицается,
• связка – постоянное слово, выражающее реальность утверждения («есть», «суть», «является»),
• кванторные слова, говорящие о том, что признак предмета причисляется к указываемому кванторным словом объему («все», «некоторые», «ни один»).

Сложные суждения, как и простые, бывают истинными и ложными. При этом их истинностная характеристика определяется не непосредственно соответствием действительности, а истинностью или ложностью входящих в его состав простых суждений, а также особенностями используемого союза.

«Виды сложных суждений» 👇

Логическая структура сложных суждений тоже имеет особенность, отличающую их от простых суждений. В сложных суждениях основной структурообразующей единицей является простое суждение (в то время как в простых суждениях это понятие). Связь между простыми суждениями в составе сложного осуществляется с помощью логических союзов:

• «и»,
• «или»,
• «либо»,
• «если … то …».

Чтобы определить истинность сложного суждения, обычно используют табличный способ. Для этого в первых столбцах таблицы записывают все возможные комбинации истинности для простых суждений, затем определяют истинность сложных суждений, входящих в основное сложное суждение как компоненты (начиная от простых к более сложным в соответствии с порядком выполнения логических операций).

Виды сложных суждений в зависимости от логической связки

В сложных суждениях могут использоваться разные логические союзы. В зависимости от того, какой союз использован, выделяют следующие виды сложных суждений:

• конъюнктивными (соединительными) суждениями называют суждения, включающие в качестве компонентов суждения-конъюнкты, связанные союзом «и». Например: «Дождь закончился, и выглянуло солнце». Сложное конъюнктивное суждение истинно только в том случае, если оба простых истинны;
• дизъюнктивными (разделительными) суждениями называют суждения, включающие в качестве компонентов суждения-дизъюнкты, связанные союзом «или». Например: «Я плотно пообедаю или закажу пиццу на ужин». Выделяют слабую дизъюнкцию, когда союз «или» выражает соединительно-разделительный смысл, т. е. составляющие сложного суждения не исключают друг друга, например: «Я надену синие брюки или синюю куртку». Сильная дизъюнкция соответствует случаю употребления логических союзов «или» и «либо» в исключающе-разделяющем смысле, т.е. когда компоненты сложного высказывания исключают друг друга. Например: «Сейчас я пойду в кино или на каток» (невозможно пойти в два места одновременно). Сложное дизъюнктивное суждение истинно, если хотя бы одно из простых истинно;
• условными (импликативными) суждениями называют суждения, образованные из двух простых с использованием логического союза «если … то …». Например: «Если не поливать комнатное растение, то оно засохнет». Часть, которая начинается со слова «если», называется «основание», а часть, которая начинается со слова «то» – следствие. Условные суждения отражают объективные причинно-следственные, функциональные, пространственно-временные и другие связи, сформировавшиеся между явлениями и предметами реального мира. Нужно понимать, что в русском языке союз «если … то …» может употребляться не только для построения условного суждения, но и для простой последовательности. Условное суждение истинно во всех случаях, кроме одного: когда из истины следует ложь (т.е. из ложного простого суждения может следовать как истинное, так и ложное, а из истинного – только истинное).

Рассмотренные виды сложных суждений могут комбинироваться между собой, образуя многокомпонентные конструкции.

Пример сочетания нескольких видов сложных суждений: «Если государство снизит налоги или реализует другие меры поддержки, то инвестиционный климат станет более благоприятным». Это импликативное суждение, основанием которого служит дизъюнктивное суждение.

Виды сложных суждений по количеству терминов

По количеству терминов сложные суждения бывают трех видов:

• несколько субъектов и один предикат. Схематически такое суждение может быть представлено: «S1, S2, S3 есть (не есть) P». Например: «Торты, пирожные и конфеты – это сласти»;
• один субъект и несколько предикатов. Схематически такое суждение представляется: «S есть (не есть) P1, P2, P3». Например: «Англоязычные страны – это Великобритания, США и Австралия»;
• несколько субъектов и несколько предикатов. Схематическое представление суждения: «S1, S2, S3 есть (не есть) P1, P2, P3». Например: «Продавцами и покупателями могут выступать юридические и физические лица».