Алгоритм вычисления собственных значений — алгоритм, позволяющий определить собственные значения и собственные векторы заданной матрицы. Создание эффективных и устойчивых алгоритмов для этой задачи является одной из ключевых задач вычислительной математики.
Собственные значения и собственные векторы[править | править код]
Если задана n × n квадратная матрица A над вещественными или комплексными числами, то собственное значение λ и соответствующий ему корневой вектор v — это пара, удовлетворяющая равенству[1]
где v ненулевой n × 1 вектор-столбец, E является n × n единичной матрицей, k — положительным целым, а λ и v могут быть комплексными, даже если A вещественна. Если k = 1, вектор просто называется собственным вектором. В этом случае Av = λv. Любое собственное значение λ матрицы A имеет простой[note 1] собственный вектор, соответствующий ему так, что если k — наименьшее целое, при котором (A – λE)k v = 0 для корневого вектора v, то (A – λE)k-1 v будет простым собственным вектором. Значение k всегда можно взять меньше либо равным n. В частности, (A – λE)n v = 0 для всех корневых векторов v, соответствующих λ.
Для любого собственного значения λ матрицы A ядро ker(A – λE) состоит из всех собственных векторов, соответствующих λ, (вместе с 0) и называется собственным подпространством числа λ, а векторное подпространство ker((A – λE)n) состоит из всех корневых векторов (дополненное нулевым вектором) и называется корневым подпространством. Геометрическая кратность значения λ является размерностью его собственного подпространства. Алгебраическая кратность значения λ является размерностью его корневого подпространства. Дальнейшие термины связаны с равенством
Здесь det — определитель, λi — все различные собственные значения матрицы A, а αi — соответствующие алгебраические кратности. Функция pA(z) — это характеристический многочлен матрицы A. Таким образом, алгебраическая кратность является кратностью собственных значений как корней характеристического многочлена. Поскольку любой собственный вектор является корневым вектором, геометрическая кратность меньше либо равна алгебраической кратности. Сумма алгебраических кратностей равна n степени характеристического многочлена. Уравнение pA(z) = 0 называется характеристическим уравнением, поскольку его корни являются в точности собственными значениями матрицы A. По теореме Гамильтона — Кэли сама матрица A удовлетворяет тому же самому уравнению: pA(A) = 0[note 2]. Как следствие, столбцы матрицы 

Любой набор корневых векторов различных собственных значений линейно независим, так что базис для всего C n можно выбрать из набора корневых векторов. Точнее этот базис {vi}n
i=1 можно выбрать и выстроить так, что
-
- если vi и vj имеют одно и то же собственное значение, то тоже будет верно для любого vk при k между i и j;
- если vi не является простым собственным вектором и если λi его собственное значение, то (A – λiE )vi = vi-1 (в частности v1 должен быть простым собственным вектором).
Если эти базисные вектора расположить как столбцы матрицы V = [ v1 v2 … vn ], то V можно использовать для преобразования матрицы A в её нормальную жорданову форму:
где λi — собственные значения, βi = 1 если (A – λi+1)vi+1 = vi и βi = 0 в других случаях.
Если W является обратимой матрицей и λ — собственное значение матрицы A с соответствующим корневым вектором v, то (W -1AW – λE )k W –kv = 0. Таким образом, λ является собственным значением матрицы W -1AW с соответствующим корневым вектором W –kv. Таким образом, подобные матрицы имеют те же самые собственные значения.
Нормальные, эрмитовы и вещественные симметричные матрицы[править | править код]
Эрмитово-сопряжённая матрица M* к комплексной матрице M — это траспонированная матрица с заменой всех элементов на сопряжённые значения: M * = M T. Квадратная матрица A называется нормальной, если она коммутирует с эрмитово-сопряжённой: A*A = AA*. Матрица называется эрмитовой, если она равна своей сопряжённой: A* = A. Все эрмитовы матрицы нормальны. Если A имеет только вещественные элементы, то сопряжённая к ней — это просто транспонированная матрица, и она будет эрмитовой в том и только в том случае, когда она симметрична. Если применить это к столбцам, сопряжённость можно использовать для определения канонического скалярного произведения в C n: w • v = w* v[note 3]. Нормальные, эрмитовы и вещественные симметричные матрицы имеют ряд полезных свойств:
-
- Каждый корневой собственный вектор нормальной матрицы является простым собственным вектором.
- Любая нормальная матрица подобна диагональной, поскольку её нормальная жорданова форма является диагональной матрицей.
- Собственные вектора, соответствующие различным собственным значениям нормальной матрицы, ортогональны.
- Для любой нормальной матрицы A C n имеет ортонормальный базис, состоящий из собственных векторов матрицы A. Соответствующая матрица собственных векторов является унитарной.
- Собственные значения эрмитовой матрицы являются вещественными числами, поскольку (λ – λ)v = (A* – A)v = (A – A)v = 0 для ненулевого собственного вектора v.
- Если матрица A вещественна, существует ортонормальный базис для R n, состоящий из собственных векторов матрицы A, в том и только в том случае, когда A симметрична.
Возможно как для вещественных, так и для комплексных матриц иметь все собственные значения вещественными, не будучи при этом эрмитовой матрицей. Например, вещественная треугольная матрица имеет все свои собственные значения на диагонали, но, в общем случае, не симметрична.
Число обусловленности[править | править код]
Любую задачу вычислительной математики можно рассматривать как вычисление некоторой функции ƒ от некоторого аргумента x. Число обусловленности κ(ƒ, x) задачи — это отношение относительной ошибки результата вычисления к относительной ошибке параметра функции и зависит как от функции, так и от параметра. Число обусловленности описывает насколько возрастает ошибка во время вычислений. Десятичный логарифм этого числа говорит о количестве знаков, которые мы теряем по отношению к исходным данным. Число обусловленности относится к наилучшему сценарию, отражая нестабильность самой задачи, независимо от способа решения. Никакой алгоритм не может дать результат лучше, чем определённый числом обусловленности, разве что случайно. Однако плохо разработанный алгоритм может дать существенно более плохие результаты. Например, как будет упомянуто ниже, задача нахождения собственных значений нормальной матрицы всегда хорошо обусловлена, однако задача нахождения корней многочлена может быть очень плохо обусловлена[en]. Такие алгоритмы вычисления собственных значений, которые работают путём нахождения корней характеристического многочлена, могут оказаться плохо обусловленными, даже если сама задача хорошо обусловлена.
Для задачи решения системы линейных уравнений Av = b, где A является обратимой, число обусловленности κ(A-1, b) определяется выражением ||A||op||A-1||op, где || ||op — операторная норма, подчинённая обычной евклидовой норме на C n. Поскольку это число не зависит от b и является тем же самым как для A, так и для A-1, оно обычно называется числом обусловленности κ(A) матрицы A. Это значение κ(A) является также абсолютным значением отношения наибольшего собственного значения матрицы A к её наименьшему собственному значению. Если A является унитарной, то ||A||op = ||A-1||op = 1, так что κ(A) = 1. В общем случае для матриц часто сложно вычислить операторную норму. По этой причине обычно используют другие нормы матрицы для оценки числа обусловленности.
Для задачи вычисления собственных значений Бауэр и Файк доказали[en], что если λ является собственным значением диагонализируемой n × n матрицы A с матрицей собственных векторов V, то абсолютная ошибка вычисления λ ограничена произведением κ(V) и абсолютной ошибкой в A:
[2]. Как следствие, число обусловленности для вычисления λ равно
κ(λ, A) = κ(V) = ||V ||op ||V -1||op. Если матрица A нормальна, то V является унитарной и κ(λ, A) = 1. Таким образом, задача вычисления собственных значений нормальных матриц хорошо обусловлена.
Было показано, что число обусловленности задачи вычисления собственного подпространства нормальной матрицы A, соответствующего собственному значению λ, обратно пропорционально минимальному расстоянию между λ и другими, отличными от λ, собственными значениями матрицы A[3]. В частности, задача определения собственного подпространства для нормальных матриц хорошо обусловлена для изолированных собственных значений. Если собственные значения не изолированы, лучшее, на что мы можем рассчитывать, это определение подпространства всех собственных векторов близлежащих собственных значений.
Алгоритмы[править | править код]
Любой нормированный многочлен является характеристическим многочленом сопровождающей матрицы, поэтому алгоритм для вычисления собственных значений можно использовать для нахождения корней многочленов. Теорема Абеля — Руффини показывает, что любой такой алгоритм для размерности большей 4 должен либо быть бесконечным, либо вовлекать функции более сложные, чем элементарные арифметические операции или дробные степени. По этой причине алгоритмы, вычисляющие точно собственные значения за конечное число шагов, существуют только для специальных классов матриц. В общем случае алгоритмы являются итеративными, дающими на каждой итерации очередное приближение к решению.
Некоторые алгоритмы дают все собственные значения, другие дают несколько значений или даже всего одно, однако и эти алгоритмы можно использовать для вычисления всех собственных значений. Как только собственное значение λ матрицы A определено, его можно использовать либо для приведения алгоритма к получению другого собственного значения, либо для сведения задачи к такой, которая не имеет λ в качестве решения.
Приведение обычно осуществляется сдвигом: A заменяется на A – μE для некоторой константы μ. Собственное значение, найденное для A – μE, должно быть добавлено к μ, чтобы получить собственное значение матрицы A. Например, в степенном методе μ = λ. Итерация степенного метода находит самое большое по абсолютной величине значение, так что даже если λ является приближением к собственному значению, итерация степенного метода вряд ли найдёт его во второй раз. И наоборот, методы, основанные на обратных итерациях находят наименьшее собственное значение, так что μ выбирается подальше от λ в надежде оказаться ближе к какому-нибудь другому собственному значению.
Приведение можно совершить путём сужения матрицы A к пространству столбцов матрицы A – λE. Поскольку A – λE вырождена, пространство столбцов имеет меньшую размерность. Алгоритм вычисления собственных значений можно тогда применить к этой суженой матрице. Процесс можно продолжать, пока не будут найдены все собственные значения.
Если алгоритм не даёт к собственные значения, общей практикой является применение алгоритма, основанного на обратной итерации, с приравниванием μ к ближайшей аппроксимации собственного значения. Это быстро приводит к собственному вектору ближайшего к μ собственного значения. Для небольших матриц альтернативой служит использование столбцового подпространства произведения A – λ́E для каждого из остальных собственных значений λ́.
Матрицы Хессенберга и трёхдиагональные матрицы[править | править код]
Поскольку собственными значениями треугольной матрицы являются диагональные элементы, в общем случае не существует конечного метода, подобного исключениям Гаусса, для приведения матрицы к треугольной форме, сохраняя при этом собственные значения, однако можно получить нечто близкое к треугольной матрице. Верхняя матрица Хессенберга — это квадратная матрица, у которой все элементы ниже первой поддиагонали равны нулю. Нижняя матрица Хессенберга — это квадратная матрица, у которой все члены выше первой наддиагонали равны нулю. Матрицы, которые являются как нижними, так и верхними матрицами Хессенберга — это трёхдиагональные матрицы. Матрицы Хессенберга и трёхдиагональные матрицы являются исходными точками многих алгоритмов вычисления собственных значений, поскольку нулевые значения уменьшают сложность задачи. Существует несколько методов сведения матриц к матрицам Хессенберга с теми же собственными значениями. Если исходная матрица симметрична или эрмитова, то результирующая матрица будет трёхдиагональной.
Если нужны только собственные значения, нет необходимости вычислять матрицу подобия, поскольку преобразованная матрица имеет те же собственные значения. Если также нужны и собственные векторы, матрица подобия необходима для преобразования собственных векторов матрицы Хессенберга к собственным векторам исходной матрицы.
| Метод | Применим к матрицам | Результат | Цена без матрицы подобия | Цена с матрицей подобия | Описание |
|---|---|---|---|---|---|
| Преобразования Хаусхолдера | общего вида | матрица Хессенберга | 2n3⁄3 + O(n2)[4] | 4n3⁄3 + O(n2)[4] | Отражение каждого столбца относительно подпространства для обнуления нижних элементов столбца. |
| Повороты Гивенса | общего вида | матрица Хессенберга | 4n3⁄3 + O(n2)[4] | Осуществляется плоское вращении для обнуления отдельных элементов. Вращения упорядочены так, что следующие вращения не затрагивают нулевые элементы. | |
| Итерации Арнольди | общего вида | матрица Хессенберга | Осуществляется ортогонализация Грама ― Шмидта на подпространствах Крылова. | ||
| Алгоритм Ланцоша[en][5] | эрмитова | трёхдиагональная матрица | Итерации Арнольди для эрмитовых матриц. |
Итеративные алгоритмы[править | править код]
Итеративные алгоритмы решают задачу вычисления собственных значений путём построения последовательностей, сходящихся к собственным значениям. Некоторые алгоритмы дают также последовательности векторов, сходящихся к собственным векторам. Чаще всего последовательности собственных значений выражаются через последовательности подобных матриц, которые сходятся к треугольной или диагональной форме, что позволяет затем просто получить собственные значения. Последовательности собственных векторов выражаются через соответствующие матрицы подобия.
| Метод | Применим к матрицам | Результат | Цена за один шаг | Сходимость | Описание |
|---|---|---|---|---|---|
| Степенной метод | общего вида | наибольшее собственное значение и соответствующий вектор | O(n2) | Линейная | Многократное умножение матрицы на произвольно выбранный начальный вектор с последующей нормализацией. |
| Обратный степенной метод | общего вида | ближайшее к μ собственное значение и соответствующий вектор | Линейная | Степенная итерация с матрицей (A – μE )-1 | |
| Метод итераций Рэлея | общего вида | ближайшее к μ собственное значение и соответствующий вектор | Кубическая | Степенная итерация с матрицей (A – μiE )-1, где μi является отношением Рэлея от предыдущей итерации. | |
| Предобусловленная обратная итерация[6] или LOBPCG[en] | положительно определённая вещественная симметричная | ближайшее к μ собственное значение и соответствующий вектор | Обратная итерация с предобуславливанием (приближённое обращение матрицы A). | ||
| Метод деления пополам[7] | вещественная симметричная трёхдиагональная | любое собственное значение | Линейная | Использует метод бисекции для поиска корней характеристического многочлена и свойства последовательности Штурма. | |
| Итерации Лагерра | вещественная симметричная трёхдиагональная | любое собственное значение | Кубическая[8] | Использует метод Лагерра[en] вычисления корней характеристического многочлена и свойства последовательности Штурма. | |
| QR-алгоритм[9] | хессенберга | все собственные значения | O(n2) | Кубическая | Разложение A = QR, где Q ортогональная, R ― треугольная, затем используется итерация к RQ. |
| все собственные значения | 6n3 + O(n2) | ||||
| Метод Якоби | вещественная симметричная | все собственные значения | O(n3) | квадратичная | Использует поворот Гивенса в попытке избавиться от недиагональных элементов. Попытка не удаётся, но усиливает диагональ. |
| Разделяй и властвуй[en] | эрмитова трёхдиагональная | все собственные значения | O(n2) | Матрица разбивается на подматрицы, которые диагонализируются, затем воссоединяются. | |
| все собственные значения | (4⁄3)n3 + O(n2) | ||||
| Метод гомотопии | вещественная симметричная трёхдиагональная | все собственные значения | O(n2)[10] | Строится вычисляемая гомотопия. | |
| Метод спектральной свёртки[en] | вещественная симметричная | ближайшее к μ собственное значение и соответствующий собственный вектор | Предобусловленная обратная итерация, применённая к (A – μE )2 | ||
| Алгоритм MRRR[11] | вещественная симметричная трёхдиагональная | некоторые или все собственные значения и соответствующие собственные вектора | O(n2) | «Multiple Relatively Robust Representations» — Осуществляется обратная итерация с разложением LDLT смещённой матрицы. |
Прямое вычисление[править | править код]
Не существует простых алгоритмов прямого вычисления собственных значений для матриц в общем случае, но для многих специальных классов матриц собственные значения можно вычислить прямо. Это:
Треугольные матрицы[править | править код]
Поскольку определитель треугольной матрицы является произведением её диагональных элементов, то для треугольной матрицы T 
Разложимые полиномиальные уравнения[править | править код]
Если p ― любой многочлен и p(A) = 0, то собственные значения матрицы A удовлетворяют тому же уравнению. Если удаётся разложить многочлен p на множители, то собственные значения A находятся среди его корней.
Например, проектор ― это квадратная матрица P, удовлетворяющая уравнению P2 = P. Корнями соответствующего скалярного полиномиального уравнения λ2 = λ будут 0 и 1. Таким образом, проектор имеет 0 и 1 в качестве собственных значений. Кратность собственного значения 0 ― это дефект P, в то время как кратность 1 ― это ранг P.
Другой пример ― матрица A, удовлетворяющая уравнению A2 = α2E для некоторого скаляра α. Собственные значения должны быть равны ±α. Операторы проектирования
удовлетворяют равенствам
и
Пространства столбцов матриц P+ и P– являются подпространствами собственных векторов матрицы A, соответствующими +α и -α, соответственно.
Матрицы 2×2[править | править код]
Для размерностей от 2 до 4 существуют использующие радикалы формулы, которые можно использовать для вычисления собственных значений. Для матриц 2×2 и 3×3 это обычная практика, но для матриц 4×4 растущая сложность формул корней[en] делает этот подход менее привлекательным.
Для матриц 2×2
характеристический многочлен равен
Собственные значения можно найти как корни квадратного уравнения:
Если определить 
с подобными формулами для c и d. Отсюда следует, что вычисление хорошо обусловлено, если собственные значения изолированы.
Собственные векторы можно получить, используя теорему Гамильтона — Кэли. Если λ1, λ2 — собственные значения, то (A – λ1E )(A – λ2E ) = (A – λ2E )(A – λ1E ) = 0, так что столбцы (A – λ2E ) обнуляются матрицей (A – λ1E ) и наоборот. Предполагая, что ни одна из матриц не равна нулю, столбцы каждой матрицы должны содержать собственные векторы для другого собственного значения (если же матрица нулевая, то A является произведением единичной матрицы на константу и любой ненулевой вектор является собственным).
Например, пусть
тогда tr(A) = 4 – 3 = 1 и det(A) = 4(-3) – 3(-2) = -6, так что характеристическое уравнение равно
а собственные значения равны 3 и −2. Теперь
,
В обеих матрицах столбцы отличаются скалярными коэффициентами, так что можно выбирать любой столбец. Так, (1, -2) можно использовать в качестве собственного вектора, соответствующего собственному значению −2, а (3, -1) в качестве собственного вектора для собственного числа 3, что легко можно проверить умножением на матрицу A.
Матрицы 3×3[править | править код]
Если A является матрицей 3×3, то характеристическим уравнением будет:
Это уравнение можно решить с помощью методов Кардано или Лагранжа, но аффинное преобразование матрицы A существенно упрощает выражение и ведёт прямо к тригонометрическому решению. Если A = pB + qE, то A и B имеют одни и те же собственные векторы и β является собственным значением матрицы B тогда и только тогда, когда α = pβ + q является собственным значением матрицы A. Если положить 

Подстановка β = 2cos θ и некоторое упрощение с использованием тождества cos 3θ = 4cos3 θ – 3cos θ сводит уравнение к cos 3θ = det(B) / 2. Таким образом,
Если det(B) является комплексным числом или больше 2 по абсолютной величине, арккосинус для всех трёх величин k следует брать из одной и той же ветви. Проблема не возникает, если A вещественна и симметрична, приводя к простому алгоритму:[12]
% Given a real symmetric 3x3 matrix A, compute the eigenvalues p1 = A(1,2)^2 + A(1,3)^2 + A(2,3)^2 if (p1 == 0) % A is diagonal. eig1 = A(1,1) eig2 = A(2,2) eig3 = A(3,3) else q = trace(A)/3 p2 = (A(1,1) - q)^2 + (A(2,2) - q)^2 + (A(3,3) - q)^2 + 2 * p1 p = sqrt(p2 / 6) B = (1 / p) * (A - q * E) % E is the identity matrix r = det(B) / 2 % In exact arithmetic for a symmetric matrix -1 <= r <= 1 % but computation error can leave it slightly outside this range. if (r <= -1) phi = pi / 3 elseif (r >= 1) phi = 0 else phi = acos(r) / 3 end % the eigenvalues satisfy eig3 <= eig2 <= eig1 eig1 = q + 2 * p * cos(phi) eig3 = q + 2 * p * cos(phi + (2*pi/3)) eig2 = 3 * q - eig1 - eig3 % since trace(A) = eig1 + eig2 + eig3 end
Снова, собственные векторы A можно получить путём использования теоремы Гамильтона — Кэли. Если α1, α2, α3 — различные собственные значения матрицы A, то (A – α1E)(A – α2E)(A – α3E) = 0. Тогда столбцы произведения любых двух из этих матриц содержат собственные векторы третьего собственного значения. Однако если a3 = a1, то (A – α1E)2(A – α2E) = 0 и (A – α2E)(A – α1E)2 = 0. Таким образом, корневое собственное подпространство α1 натянуто на столбцы A – α2E, в то время как обычное собственное подпространство натянуто на столбцы (A – α1E)(A – α2E). Обычное собственное подпространство α2 натянуто на столбцы (A – α1E)2.
Например, пусть
Характеристическое уравнение равно
с собственными значениями 1 (кратности 2) и −1. Вычисляем
,
а затем
.
Тогда (-4, -4, 4) является собственным вектором для −1, а (4, 2, -2) является собственным вектором для 1. Векторы (2, 3, -1) и (6, 5, -3) являются корневыми векторами, соответствующими значению 1, любой из которых можно скомбинировать с (-4, -4, 4) и (4, 2, -2), образуя базис корневых векторов матрицы A.
См. также[править | править код]
- Список алгоритмов вычисления собственных значений[en]
Комментарии[править | править код]
- ↑ Термин «простой» здесь употребляется лишь для подчёркивания различия между «собственным вектором» и «корневым вектором».
- ↑ где постоянный член умножается на единичную матрицу E.
- ↑ Такой порядок в скалярном произведении (с сопряжённым элементом слева) предпочитают физики. Алгебраисты часто предпочитают запись w • v = v* w.
Примечания[править | править код]
- ↑ Sheldon Axler. Down with Determinants! // American Mathematical Monthly. — 1995. — Вып. 102. — С. 139—154.
- ↑ F. L. Bauer, C. T. Fike. Norms and exclusion theorems // Numer. Math. — 1960. — Вып. 2. — С. 137—141.
- ↑ S. C. Eisenstat, I. C. F. Ipsen. Relative Perturbation Results for Eigenvalues and Eigenvectors of Diagonalisable Matrices // BIT. — 1998. — Т. 38, вып. 3. — С. 502—9. — doi:10.1007/bf02510256.
- ↑ 1 2 3 William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Numerical Recipes in C. — 2nd. — Cambridge University Press, 1992. — ISBN 0-521-43108-5.
- ↑ Х. Д. Икрамов. Разреженные матрицы. — 1982. — Т. 20. — (Итоги науки и техники. Сер. Мат. анал).
- ↑ K. Neymeyr. A geometric theory for preconditioned inverse iteration IV: On the fastest convergence cases. // Linear Algebra Appl. — 2006. — Т. 415, вып. 1. — С. 114—139. — doi:10.1016/j.laa.2005.06.022.
- ↑ Уилкинсон, 1970, стр. 274, Метод деления пополам
- ↑ T. Y Li, Zhonggang Zeng. Laguerre’s Iteration In Solving The Symmetric Tridiagonal Eigenproblem – Revisited // SIAM Journal on Scientific Computing. — 1992.
- ↑ Парлетт, 1983, стр. 156, глава 8, Алгоритмы QR и QL
- ↑ Moody T. Chu. A Note on the Homotopy Method for Linear Algebraic Eigenvalue Problems // Linear Algebra Appl. — 1988. — Т. 105. — С. 225—236. — doi:10.1016/0024-3795(88)90015-8.
- ↑ Inderjit S. Dhillon, Beresford N. Parlett, Christof Vömel. The Design and Implementation of the MRRR Algorithm // ACM Transactions on Mathematical Software. — 2006. — Т. 32, вып. 4. — С. 533—560. — doi:10.1145/1186785.1186788.
- ↑ Oliver K. Smith. Eigenvalues of a symmetric 3 × 3 matrix // Communications of the ACM. — Т. 4, вып. 4. — С. 168. — doi:10.1145/355578.366316.
Литература[править | править код]
- Дж. Голуб, Ч. Ван Лоун. Матричные вычисления. — Москва: «Мир», 1999. — ISBN 5-03-002406-9.
- Б. Парлетт. Симметричная проблема собственных значений. — Москва: «Мир», 1983.
- Дж. Х. Уилкинсон. Алгебраическая проблема собственных значений. — Москва: «Наука» Главная редакция физико-математической литературы, 1970.
Дополнительная литература[править | править код]
- Adam W. Bojanczyk, Adam Lutoborski. Computation of the Euler angles of a symmetric 3X3 matrix // SIAM Journal on Matrix Analysis and Applications. — Jan 1991. — Т. 12, вып. 1. — С. 41—48. — doi:10.1137/0612005.
Собственные векторы и собственные значения матрицы
Пусть — числовая квадратная матрица n-го порядка. Матрица
называется характеристической для
, а ее определитель
характеристическим многочленом матрицы
(7.12)
Характеристическая матрица — это λ-матрица. Ее можно представить в виде регулярного многочлена первой степени с матричными коэффициентами. Нетрудно заметить, что степень характеристического многочлена равна порядку характеристической матрицы.
Пусть — числовая квадратная матрица n-го порядка. Ненулевой столбец
, удовлетворяющий условию
(7.13)
называется собственным вектором матрицы . Число
в равенстве (7.13) называется собственным значением матрицы
. Говорят, что собственный вектор
соответствует {принадлежит) собственному значению
.
Поставим задачу нахождения собственных значений и собственных векторов матрицы. Определение (7.13) можно записать в виде , где
— единичная матрица n-го порядка. Таким образом, условие (7.13) представляет собой однородную систему
линейных алгебраических уравнений с
неизвестными
(7.14)
Поскольку нас интересуют только нетривиальные решения однородной системы, то определитель матрицы системы должен быть равен нулю:
(7.15)
В противном случае по теореме 5.1 система имеет единственное тривиальное решение. Таким образом, задача нахождения собственных значений матрицы свелась к решению уравнения (7.15), т.е. к отысканию корней характеристического многочлена матрицы
. Уравнение
называется характеристическим уравнением матрицы
. Так как характеристический многочлен имеет n-ю степень, то характеристическое уравнение — это алгебраическое уравнение n-го порядка. Согласно следствию 1 основной теоремы алгебры, характеристический многочлен можно представить в виде
где — корни многочлена кратности
соответственно, причем
. Другими словами, характеристический многочлен имеет п корней, если каждый корень считать столько раз, какова его кратность.
Теорема 7.4 о собственных значениях матрицы. Все корни характеристического многочлена (характеристического уравнения (7-15)) и только они являются собственными значениями матрицы.
Действительно, если число — собственное значение матрицы
, которому соответствует собственный вектор
, то однородная система (7.14) имеет нетривиальное решение, следовательно, матрица системы вырожденная, т.е. число
удовлетворяет характеристическому уравнению (7.15). Наоборот, если
— корень характеристического многочлена, то определитель (7.15) матрицы однородной системы (7.14) равен нулю, т.е.
.В этом случае система имеет бесконечное множество решений, включая ненулевые решения. Поэтому найдется столбец
, удовлетворяющий условию (7.14). Значит,
— собственное значение матрицы
.
Свойства собственных векторов
Пусть — квадратная матрица n-го порядка.
1. Собственные векторы, соответствующие различным собственным значениям, линейно независимы.
В самом деле, пусть и
— собственные векторы, соответствующие собственным значениям
и
, причем
. Составим произвольную линейную комбинацию этих векторов и приравняем ее нулевому столбцу:
(7.16)
Надо показать, что это равенство возможно только в тривиальном случае, когда . Действительно, умножая обе части на матрицу
и подставляя
и
имеем
Прибавляя к последнему равенству равенство (7.16), умноженное на , получаем
Так как и
, делаем вывод, что
. Тогда из (7.16) следует, что и
(поскольку
). Таким образом, собственные векторы
и
линейно независимы. Доказательство для любого конечного числа собственных векторов проводится по индукции.
2. Ненулевая линейная комбинация собственных векторов, соответствующих одному собственному значению, является собственным вектором, соответствующим тому же собственному значению.
Действительно, если собственному значению соответствуют собственные векторы
, то из равенств
, следует, что вектор
также собственный, поскольку:
3. Пусть — присоединенная матрица для характеристической матрицы
. Если
— собственное значение матрицы
, то любой ненулевой столбец матрицы
является собственным вектором, соответствующим собственному значению
.
В самом деле, применяя формулу (7.7) имеем . Подставляя корень
, получаем
. Если
— ненулевой столбец матрицы
, то
. Значит,
— собственный вектор матрицы
.
Замечания 7.5
1. По основной теореме алгебры характеристическое уравнение имеет п в общем случае комплексных корней (с учетом их кратностей). Поэтому собственные значения и собственные векторы имеются у любой квадратной матрицы. Причем собственные значения матрицы определяются однозначно (с учетом их кратности), а собственные векторы — неоднозначно.
2. Чтобы из множества собственных векторов выделить максимальную линейно независимую систему собственных векторов, нужно для всех раз личных собственных значений записать одну за другой системы линейно независимых собственных векторов, в частности, одну за другой фундаментальные системы решений однородных систем
Полученная система собственных векторов будет линейно независимой в силу свойства 1 собственных векторов.
3. Совокупность всех собственных значений матрицы (с учетом их кратностей) называют ее спектром.
4. Спектр матрицы называется простым, если собственные значения матрицы попарно различные (все корни характеристического уравнения простые).
5. Для простого корня характеристического уравнения соответствующий собственный вектор можно найти, раскладывая определитель матрицы
по одной из строк. Тогда ненулевой вектор, компоненты которого равны алгебраическим дополнениям элементов одной из строк матрицы
, является собственным вектором.
Нахождение собственных векторов и собственных значений матрицы
Для нахождения собственных векторов и собственных значений квадратной матрицы n-го порядка надо выполнить следующие действия.
1. Составить характеристический многочлен матрицы .
2. Найти все различные корни характеристического уравнения
(кратности
корней определять не нужно).
3. Для корня найти фундаментальную систему
решений однородной системы уравнений
, где
Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы (см. пункт 3 замечаний 5.3, пункт 1 замечаний 5.5).
4. Записать линейно независимые собственные векторы матрицы , отвечающие собственному значению
(7.17)
где — отличные от нуля произвольные постоянные. Совокупность всех собственных векторов, отвечающих собственному значению
, образуют ненулевые столбцы вида
. Здесь и далее собственные векторы матрицы будем обозначать буквой
.
Повторить пункты 3,4 для остальных собственных значений .
Пример 7.8. Найти собственные значения и собственные векторы матриц:
Решение. Матрица . 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(1). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов второй строки матрицы , то есть
. Умножив этот столбец на (-1), получим
.
3(2). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(2). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , т.е.
. Поделив его на (- 3), получим
.
Матрица . 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(1). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , то есть
. Умножив этот столбец на (-1), получим
.
3(2). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(2). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , т.е.
. Умножив его на (-1), получим
.
Матрица 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду (ведущие элементы выделены полужирным курсивом):
Ранг матрицы системы равен 2 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисные переменные
через свободную
и, полагая
, получаем решение
.
4(1). Все собственные векторы, соответствующие собственному значению , вычисляются по формуле
, где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , то есть
, так как
Разделив его на 3, получим .
3(2). Для собственного значения имеем однородную систему
. Решаем ее методом Гаусса:
Ранг матрицы системы равен единице , следовательно, фундаментальная система решений состоит из двух решений
. Базисную переменную
, выражаем через свободные:
. Задавая стандартные наборы свободных переменных
и
, получаем два решения
4(2). Записываем множество собственных векторов, соответствующих собственному значению , где
— произвольные постоянные, не равные нулю одновременно. В частности, при
получаем
; при
. Присоединяя к этим собственным векторам собственный вектор
, соответствующий собственному значению
(см. пункт 4(1) при
), находим три линейно независимых собственных вектора матрицы
Заметим, что для корня собственный вектор нельзя найти, применяя пункт 5 замечаний 7.5, так как алгебраическое дополнение каждого элемента матрицы
равно нулю.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Собственные числа и собственные векторы линейного оператора
Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x 1, x 2, . x m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x 1, x 2, . x m оператора A с попарно различными собственными числами λ1, λ2, …, λm линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x 1, x 2, . x n, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 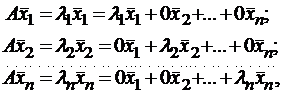

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе < ε i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса – собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
Пример №1 . Линейный оператор A действует в R3 по закону A· x =(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, . xn – координаты вектора x в базисе e 1=(1,0,0), e 2=(0,1,0), e 3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e 1=(1,4,6)
A· e 2=(-3,-7,-7)
A· e 3=(4,8,7) 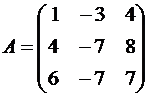
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
Пример №2 . Дана матрица 
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x – собственный вектор
Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой ai k =ak i .
Замечания .
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Свойства собственных векторов
Для любого собственного значения Хк(А) существует п- кг линейно независимых собственных векторов
образующих фундаментальную систему решений однородной системы уравнений (А – ХкЕ)Х = 0. Здесь гк = г(А – ХкЕ) — ранг матрицы А – ХкЕ.
Множество всех собственных векторов А(Хк), соответствующих собственному значению Хк <А)матрицы Л, совпадает с общим решением однородной системы уравнений (Л – ХкЕ)Х = ©, т. е.
Любые два собственных вектора F и F(X2), соответствующие различным собственным значениям А, ф А2 характеристического уравнения А – ХЕI = 0 матрицы А, являются линейно независимыми.
Если F(A,j), F(Х2) линейно независимые, то равенство F(X<)a + + Е(А9)Р = 0 выполняется только при а = Р = 0. Предположим, что F(Xl)а + Е(А9)Р = 0 при р * 0. Так как F(Xl) и F(X2) — собственные векторы, то они удовлетворяют уравнению АХ = XX, т. е.
Умножим первое равенство на а, второе на Р и сложим, получим
По предположению F(Xx)a + Е(А9)р = 0, тогда Составим и решим систему уравнений
Так как по условию X,, * Xv а по предположению р * 0, то F(X2) = 0. Это противоречит тому, что собственным вектором может быть только ненулевой вектор.
Система собственных векторов, составленная из систем собственных векторов, соответствующих различным собственным значениям АДА!), А2(Л). АП(Л), является линейно независимой.
Пример 7.1. Найти собственные значения и собственные векторы матрицы
Решение. Составим систему (А – ХЕ)Х = 0, которая в координатной записи имеет вид
Приравняем определитель матрицы этой системы к нулю
Раскроем этот определитель по правилу треугольника, получим характеристическое уравнение
Найдем характеристические значения матрицы А (корни этого уравнения):
Для каждого из характеристических значений найдем собственные векторы.
При = 1 система (7.1) принимает вид
Система является разрешенной. Включим в набор разрешенных неизвестных х< и хт Свободной неизвестной х3 придадим значение д’3 = 1, получим решение С(Х1) = (1, 0, -1), которое является собственным вектором.
Аналогично найдем соответствующие собственным значениям Х2 и Х3 собственные векторы
Приведение квадратной матрицы к диагональному виду
Матрицу А можно привести к диагональному виду с помощью матрицы Г, если матрица Т
г АТявляется диагональной.
Для нахождения матрицы Т необходимо найти собственные значения и собственные векторы матрицы А. Матрицу Т составляют из собственных векторов-столбцов. Если эта матрица является квадратной, то матрицу А можно привести к диагональному виду.
Пример 7.2. Матрицу
привести к диагональному виду.
Решение. В предыдущем примере для матрицы А были найдены собственные значения
и соответствующие им собственные векторы Из этих векторов составим матрицу Т
Найдем обратную матрицу Т 1 с использованием присоединенной матрицы.
Найдем произведение матриц Т 1 АТ:
Упражнения
7.1. Найти собственные значения и собственные векторы матрицы А. Записать матрицу Т приводящую матрицу А к диагональному виду и Гр
Приведение квадратной матрицы к диагональному виду. Критерии приводимости квадратной матрицы к диагональному виду
Страницы работы
Фрагмент текста работы
§ 2. Приведение квадратной матрицы к диагональному виду
Говорят, что квадратная матрица А с элементами из поля P приводится к диагональному виду над P, если существует невырожденная квадратная матрица Т с элементами из P такая, что матрица – диагональная.
Критерии приводимости квадратной матрицы к диагональному виду. 1. Если А – квадратная матрица -го порядка с элементами из поля P, – линейное пространство над Р, – тот линейный оператор, матрица которого в некотором базисе пространства совпадает с А, то для приводимости матрицы А к диагональному виду над полем Р необходимо и достаточно, чтобы в существовал базис, состоящий из собственных векторов оператора f.
2. Для того чтобы квадратная матрица А n-го порядка приводилась к диагональному виду над полем Р необходимо и достаточно, чтобы все корни ее характеристического уравнения принадлежали этому полю и для каждого из них выполнялось условие
, (7)
где – кратность корня характеристического уравнения матрицы А.
При решении задач первый критерий, пожалуй, проще в применении, хотя студенты обычно предпочитают второй.
В том случае, когда все характеристические числа матрицы А различны и принадлежат полю Р, эта матрица приводится к диагональному виду над Р. Если матрица А приводится к диагональному виду – матрице , то диагональными элементами последней являются собственные значения матрицы А, а матрица Т, приводящая А к диагональному виду, есть не что иное, как матрица перехода от исходного базиса к базису из собственных векторов.
Из всего вышесказанного вытекает, что для приведения квадратной матрицы к диагональному виду над полем Р следует:
1) составить характеристический многочлен матрицы А и найти его корни. Если какой-либо из них не принадлежит полю Р, то А к диагональному виду не приводится;
2) если все корни характеристического уравнения принадлежат полю Р, то для кратных корней проверить условие (7) (для однократных оно выполняется всегда). Если для какого-то из корней (7) не выполняется, то А к диагональному виду не приводится;
3) если для каждого из собственных значений условие (7) выполняется, то А к диагональному виду приводится. Записываем этот диагональный вид – матрицу , располагая на ее главной диагонали собственные значения в произвольном порядке, причем каждое из значений повторяется столько раз, какова его кратность;
4) для каждого из найденных собственных значений находим собственные векторы и составляем из них базис;
5) записываем матрицу Т, приводящую А к диагональному виду, – матрицу перехода от исходного базиса к базису из собственных векторов, сохраняя порядок, установленный матрицей .
Пример 1. Найти диагональный вид матрицы А над полем действительных чисел и невырожденную матрицу Т, приводящую к этому диагональному виду, если
.
►Проводим решение по намеченному плану.
+
.
2.Все корни действительны и однократны, поэтому матрица А приводится к диагональному виду.
3. .
4. Все собственные векторы можно найти с помощью алгебраических дополнений. Кроме того, вспомним, что, если мы нашли один собственный вектор, то любой вектор, ему коллинеарный, также является собственным с тем же самым собственным значением.
: ; ,
(алгебраические дополнения к элементам первой строки);
: ; =
(алгебраические дополнения к элементам второй строки);
: ; ,
(алгебраические дополнения к элементам первой строки).
5. Составляем матрицу перехода от исходного базиса к, построенному базису , записывая в столбцы матрицы координатные столбцы векторов , и соответственно:
.◄
Пример 2. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.
.
►Составляем и решаем характеристическое уравнение:
.
Матрица имеет только одно собственное значение , но его кратность равна трем. Проверяем выполнение условия (4.58):
.
Условие не выполняется, значит, матрица к диагональному виду не приводится.◄
Пример 3. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.
.
► Решение опять проводим по намеченному плану.
–
.
2. Проверяем выполнение условия (7) для кратного корня:
. (8)
Таким образом, , условие выполняется, матрица к диагональному виду приводится.
3. .
4. Так как , то , т. е для первого собственного значения можно найти два линейно независимых собственных вектора. По одной из строк матрицы (8), разделив все ее элементы на общий множитель, выписываем единственное уравнение для отыскания координат собственных векторов и решаем его: , . В качестве двух линейно независимых решений можно взять, например
[spoiler title=”источники:”]
http://bstudy.net/719731/estestvoznanie/svoystva_sobstvennyh_vektorov
http://vunivere.ru/work86118
[/spoiler]
In linear algebra, eigendecomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way. When the matrix being factorized is a normal or real symmetric matrix, the decomposition is called “spectral decomposition”, derived from the spectral theorem.
Fundamental theory of matrix eigenvectors and eigenvalues[edit]
A (nonzero) vector v of dimension N is an eigenvector of a square N × N matrix A if it satisfies a linear equation of the form
for some scalar λ. Then λ is called the eigenvalue corresponding to v. Geometrically speaking, the eigenvectors of A are the vectors that A merely elongates or shrinks, and the amount that they elongate/shrink by is the eigenvalue. The above equation is called the eigenvalue equation or the eigenvalue problem.
This yields an equation for the eigenvalues
We call p(λ) the characteristic polynomial, and the equation, called the characteristic equation, is an Nth order polynomial equation in the unknown λ. This equation will have Nλ distinct solutions, where 1 ≤ Nλ ≤ N. The set of solutions, that is, the eigenvalues, is called the spectrum of A.[1][2][3]
If the field of scalars is algebraically closed, then we can factor p as
The integer ni is termed the algebraic multiplicity of eigenvalue λi. The algebraic multiplicities sum to N: 
For each eigenvalue λi, we have a specific eigenvalue equation
There will be 1 ≤ mi ≤ ni linearly independent solutions to each eigenvalue equation. The linear combinations of the mi solutions (except the one which gives the zero vector) are the eigenvectors associated with the eigenvalue λi. The integer mi is termed the geometric multiplicity of λi. It is important to keep in mind that the algebraic multiplicity ni and geometric multiplicity mi may or may not be equal, but we always have mi ≤ ni. The simplest case is of course when mi = ni = 1. The total number of linearly independent eigenvectors, Nv, can be calculated by summing the geometric multiplicities
The eigenvectors can be indexed by eigenvalues, using a double index, with vij being the jth eigenvector for the ith eigenvalue. The eigenvectors can also be indexed using the simpler notation of a single index vk, with k = 1, 2, …, Nv.
Eigendecomposition of a matrix[edit]
Let A be a square n × n matrix with n linearly independent eigenvectors qi (where i = 1, …, n). Then A can be factorized as
where Q is the square n × n matrix whose ith column is the eigenvector qi of A, and Λ is the diagonal matrix whose diagonal elements are the corresponding eigenvalues, Λii = λi. Note that only diagonalizable matrices can be factorized in this way. For example, the defective matrix ![{displaystyle left[{begin{smallmatrix}1&1\0&1end{smallmatrix}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86645fac7ab74a9bf79acc20abb7a56a1a1ce54b)
The n eigenvectors qi are usually normalized, but they need not be. A non-normalized set of n eigenvectors, vi can also be used as the columns of Q. That can be understood by noting that the magnitude of the eigenvectors in Q gets canceled in the decomposition by the presence of Q−1. If one of the eigenvalues λi has more than one linearly independent eigenvectors (that is, the geometric multiplicity of λi is greater than 1), then these eigenvectors for this eigenvalue λi can be chosen to be mutually orthogonal; however, if two eigenvectors belong to two different eigenvalues, it may be impossible for them to be orthogonal to each other (see Example below). One special case is that if A is a normal matrix, then by the spectral theorem, it’s always possible to diagonalize A in an orthonormal basis {qi}.
The decomposition can be derived from the fundamental property of eigenvectors:
The linearly independent eigenvectors qi with nonzero eigenvalues form a basis (not necessarily orthonormal) for all possible products Ax, for x ∈ Cn, which is the same as the image (or range) of the corresponding matrix transformation, and also the column space of the matrix A. The number of linearly independent eigenvectors qi with nonzero eigenvalues is equal to the rank of the matrix A, and also the dimension of the image (or range) of the corresponding matrix transformation, as well as its column space.
The linearly independent eigenvectors qi with an eigenvalue of zero form a basis (which can be chosen to be orthonormal) for the null space (also known as the kernel) of the matrix transformation A.
Example[edit]
The 2 × 2 real matrix A
may be decomposed into a diagonal matrix through multiplication of a non-singular matrix B
Then
for some real diagonal matrix ![{displaystyle left[{begin{smallmatrix}x&0\0¥d{smallmatrix}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07484076f3ceb15c58acdc7f415a075bd45d7fac)
Multiplying both sides of the equation on the left by B:
The above equation can be decomposed into two simultaneous equations:
Factoring out the eigenvalues x and y:
Letting
this gives us two vector equations:
And can be represented by a single vector equation involving two solutions as eigenvalues:
where λ represents the two eigenvalues x and y, and u represents the vectors a and b.
Shifting λu to the left hand side and factoring u out
Since B is non-singular, it is essential that u is nonzero. Therefore,
Thus
giving us the solutions of the eigenvalues for the matrix A as λ = 1 or λ = 3, and the resulting diagonal matrix from the eigendecomposition of A is thus ![{displaystyle left[{begin{smallmatrix}1&0\0&3end{smallmatrix}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1493b65cef1e702f043de193bab6fbe625b9dce5)
Putting the solutions back into the above simultaneous equations
Solving the equations, we have
Thus the matrix B required for the eigendecomposition of A is
that is:
Matrix inverse via eigendecomposition[edit]
If a matrix A can be eigendecomposed and if none of its eigenvalues are zero, then A is invertible and its inverse is given by
If 




Practical implications[edit]
When eigendecomposition is used on a matrix of measured, real data, the inverse may be less valid when all eigenvalues are used unmodified in the form above. This is because as eigenvalues become relatively small, their contribution to the inversion is large. Those near zero or at the “noise” of the measurement system will have undue influence and could hamper solutions (detection) using the inverse.[4]
Two mitigations have been proposed: truncating small or zero eigenvalues, and extending the lowest reliable eigenvalue to those below it. See also Tikhonov regularization as a statistically motivated but biased method for rolling off eigenvalues as they become dominated by noise.
The first mitigation method is similar to a sparse sample of the original matrix, removing components that are not considered valuable. However, if the solution or detection process is near the noise level, truncating may remove components that influence the desired solution.
The second mitigation extends the eigenvalue so that lower values have much less influence over inversion, but do still contribute, such that solutions near the noise will still be found.
The reliable eigenvalue can be found by assuming that eigenvalues of extremely similar and low value are a good representation of measurement noise (which is assumed low for most systems).
If the eigenvalues are rank-sorted by value, then the reliable eigenvalue can be found by minimization of the Laplacian of the sorted eigenvalues:[5]
where the eigenvalues are subscripted with an s to denote being sorted. The position of the minimization is the lowest reliable eigenvalue. In measurement systems, the square root of this reliable eigenvalue is the average noise over the components of the system.
Functional calculus[edit]
The eigendecomposition allows for much easier computation of power series of matrices. If f (x) is given by
then we know that
Because Λ is a diagonal matrix, functions of Λ are very easy to calculate:
The off-diagonal elements of f (Λ) are zero; that is, f (Λ) is also a diagonal matrix. Therefore, calculating f (A) reduces to just calculating the function on each of the eigenvalues.
A similar technique works more generally with the holomorphic functional calculus, using
from above. Once again, we find that
Examples[edit]
which are examples for the functions 

Decomposition for special matrices[edit]
Subsets of important classes of matrices
|
This section needs expansion. You can help by adding to it. (June 2008) |
When A is normal or real symmetric matrix, the decomposition is called “spectral decomposition”, derived from the spectral theorem.
Normal matrices[edit]
A complex-valued square matrix A is normal (meaning A*A = AA*, where A* is the conjugate transpose) if and only if it can be decomposed as
where U is a unitary matrix (meaning U* = U−1) and Λ = diag(λ1, …, λn) is a diagonal matrix.[6] The columns u1, …, un of U form an orthonormal basis and are eigenvectors of A with corresponding eigenvalues λ1, …, λn.
If A is restricted to be a Hermitian matrix (A = A*), then Λ has only real valued entries. If A is restricted to a unitary matrix, then Λ takes all its values on the complex unit circle, that is, |λi| = 1.
Real symmetric matrices[edit]
As a special case, for every n × n real symmetric matrix, the eigenvalues are real and the eigenvectors can be chosen real and orthonormal. Thus a real symmetric matrix A can be decomposed as
where Q is an orthogonal matrix whose columns are the real, orthonormal eigenvectors of A, and Λ is a diagonal matrix whose entries are the eigenvalues of A.[7]
Useful facts[edit]
Useful facts regarding eigenvalues[edit]
- The product of the eigenvalues is equal to the determinant of A
Note that each eigenvalue is raised to the power ni, the algebraic multiplicity.
- The sum of the eigenvalues is equal to the trace of A
Note that each eigenvalue is multiplied by ni, the algebraic multiplicity.
- If the eigenvalues of A are λi, and A is invertible, then the eigenvalues of A−1 are simply λ−1
i. - If the eigenvalues of A are λi, then the eigenvalues of f (A) are simply f (λi), for any holomorphic function f.
Useful facts regarding eigenvectors[edit]
- If A is Hermitian and full-rank, the basis of eigenvectors may be chosen to be mutually orthogonal. The eigenvalues are real.
- The eigenvectors of A−1 are the same as the eigenvectors of A.
- Eigenvectors are only defined up to a multiplicative constant. That is, if Av = λv then cv is also an eigenvector for any scalar c ≠ 0. In particular, −v and eiθv (for any θ) are also eigenvectors.
- In the case of degenerate eigenvalues (an eigenvalue having more than one eigenvector), the eigenvectors have an additional freedom of linear transformation, that is to say, any linear (orthonormal) combination of eigenvectors sharing an eigenvalue (in the degenerate subspace) is itself an eigenvector (in the subspace).
Useful facts regarding eigendecomposition[edit]
Useful facts regarding matrix inverse[edit]
- A can be inverted if and only if all eigenvalues are nonzero:
- If λi ≠ 0 and Nv = N, the inverse is given by
Numerical computations[edit]
Numerical computation of eigenvalues[edit]
Suppose that we want to compute the eigenvalues of a given matrix. If the matrix is small, we can compute them symbolically using the characteristic polynomial. However, this is often impossible for larger matrices, in which case we must use a numerical method.
In practice, eigenvalues of large matrices are not computed using the characteristic polynomial. Computing the polynomial becomes expensive in itself, and exact (symbolic) roots of a high-degree polynomial can be difficult to compute and express: the Abel–Ruffini theorem implies that the roots of high-degree (5 or above) polynomials cannot in general be expressed simply using nth roots. Therefore, general algorithms to find eigenvectors and eigenvalues are iterative.
Iterative numerical algorithms for approximating roots of polynomials exist, such as Newton’s method, but in general it is impractical to compute the characteristic polynomial and then apply these methods. One reason is that small round-off errors in the coefficients of the characteristic polynomial can lead to large errors in the eigenvalues and eigenvectors: the roots are an extremely ill-conditioned function of the coefficients.[8]
A simple and accurate iterative method is the power method: a random vector v is chosen and a sequence of unit vectors is computed as
This sequence will almost always converge to an eigenvector corresponding to the eigenvalue of greatest magnitude, provided that v has a nonzero component of this eigenvector in the eigenvector basis (and also provided that there is only one eigenvalue of greatest magnitude). This simple algorithm is useful in some practical applications; for example, Google uses it to calculate the page rank of documents in their search engine.[9] Also, the power method is the starting point for many more sophisticated algorithms. For instance, by keeping not just the last vector in the sequence, but instead looking at the span of all the vectors in the sequence, one can get a better (faster converging) approximation for the eigenvector, and this idea is the basis of Arnoldi iteration.[8] Alternatively, the important QR algorithm is also based on a subtle transformation of a power method.[8]
Numerical computation of eigenvectors[edit]
Once the eigenvalues are computed, the eigenvectors could be calculated by solving the equation
using Gaussian elimination or any other method for solving matrix equations.
However, in practical large-scale eigenvalue methods, the eigenvectors are usually computed in other ways, as a byproduct of the eigenvalue computation. In power iteration, for example, the eigenvector is actually computed before the eigenvalue (which is typically computed by the Rayleigh quotient of the eigenvector).[8] In the QR algorithm for a Hermitian matrix (or any normal matrix), the orthonormal eigenvectors are obtained as a product of the Q matrices from the steps in the algorithm.[8] (For more general matrices, the QR algorithm yields the Schur decomposition first, from which the eigenvectors can be obtained by a backsubstitution procedure.[10]) For Hermitian matrices, the Divide-and-conquer eigenvalue algorithm is more efficient than the QR algorithm if both eigenvectors and eigenvalues are desired.[8]
Additional topics[edit]
Generalized eigenspaces[edit]
Recall that the geometric multiplicity of an eigenvalue can be described as the dimension of the associated eigenspace, the nullspace of λI − A. The algebraic multiplicity can also be thought of as a dimension: it is the dimension of the associated generalized eigenspace (1st sense), which is the nullspace of the matrix (λI − A)k for any sufficiently large k. That is, it is the space of generalized eigenvectors (first sense), where a generalized eigenvector is any vector which eventually becomes 0 if λI − A is applied to it enough times successively. Any eigenvector is a generalized eigenvector, and so each eigenspace is contained in the associated generalized eigenspace. This provides an easy proof that the geometric multiplicity is always less than or equal to the algebraic multiplicity.
This usage should not be confused with the generalized eigenvalue problem described below.
Conjugate eigenvector[edit]
A conjugate eigenvector or coneigenvector is a vector sent after transformation to a scalar multiple of its conjugate, where the scalar is called the conjugate eigenvalue or coneigenvalue of the linear transformation. The coneigenvectors and coneigenvalues represent essentially the same information and meaning as the regular eigenvectors and eigenvalues, but arise when an alternative coordinate system is used. The corresponding equation is
For example, in coherent electromagnetic scattering theory, the linear transformation A represents the action performed by the scattering object, and the eigenvectors represent polarization states of the electromagnetic wave. In optics, the coordinate system is defined from the wave’s viewpoint, known as the Forward Scattering Alignment (FSA), and gives rise to a regular eigenvalue equation, whereas in radar, the coordinate system is defined from the radar’s viewpoint, known as the Back Scattering Alignment (BSA), and gives rise to a coneigenvalue equation.
Generalized eigenvalue problem[edit]
A generalized eigenvalue problem (second sense) is the problem of finding a (nonzero) vector v that obeys
where A and B are matrices. If v obeys this equation, with some λ, then we call v the generalized eigenvector of A and B (in the second sense), and λ is called the generalized eigenvalue of A and B (in the second sense) which corresponds to the generalized eigenvector v. The possible values of λ must obey the following equation
If n linearly independent vectors {v1, …, vn} can be found, such that for every i ∈ {1, …, n}, Avi = λiBvi, then we define the matrices P and D such that
Then the following equality holds
And the proof is
And since P is invertible, we multiply the equation from the right by its inverse, finishing the proof.
The set of matrices of the form A − λB, where λ is a complex number, is called a pencil; the term matrix pencil can also refer to the pair (A, B) of matrices.[11]
If B is invertible, then the original problem can be written in the form
which is a standard eigenvalue problem. However, in most situations it is preferable not to perform the inversion, but rather to solve the generalized eigenvalue problem as stated originally. This is especially important if A and B are Hermitian matrices, since in this case B−1A is not generally Hermitian and important properties of the solution are no longer apparent.
If A and B are both symmetric or Hermitian, and B is also a positive-definite matrix, the eigenvalues λi are real and eigenvectors v1 and v2 with distinct eigenvalues are B-orthogonal (v1*Bv2 = 0).[12] In this case, eigenvectors can be chosen so that the matrix P defined above satisfies
or
,
and there exists a basis of generalized eigenvectors (it is not a defective problem).[11] This case is sometimes called a Hermitian definite pencil or definite pencil.[11]
See also[edit]
- Eigenvalue perturbation
- Frobenius covariant
- Householder transformation
- Jordan normal form
- List of matrices
- Matrix decomposition
- Singular value decomposition
- Sylvester’s formula
Notes[edit]
- ^ Golub & Van Loan (1996, p. 310)
- ^ Kreyszig (1972, p. 273)
- ^ Nering (1970, p. 270)
- ^ Hayde, A. F.; Twede, D. R. (2002). Shen, Sylvia S. (ed.). “Observations on relationship between eigenvalues, instrument noise and detection performance”. Imaging Spectrometry VIII. Proceedings of SPIE. 4816: 355. Bibcode:2002SPIE.4816..355H. doi:10.1117/12.453777.
- ^ Twede, D. R.; Hayden, A. F. (2004). Shen, Sylvia S; Lewis, Paul E (eds.). “Refinement and generalization of the extension method of covariance matrix inversion by regularization”. Imaging Spectrometry IX. Proceedings of SPIE. 5159: 299. Bibcode:2004SPIE.5159..299T. doi:10.1117/12.506993.
- ^ Horn & Johnson (1985), p. 133, Theorem 2.5.3
- ^ Horn & Johnson (1985), p. 136, Corollary 2.5.11
- ^ a b c d e f Trefethen, Lloyd N.; Bau, David (1997). Numerical Linear Algebra. SIAM. ISBN 978-0-89871-361-9.
- ^ Ipsen, Ilse, and Rebecca M. Wills, Analysis and Computation of Google’s PageRank, 7th IMACS International Symposium on Iterative Methods in Scientific Computing, Fields Institute, Toronto, Canada, 5–8 May 2005.
- ^ Quarteroni, Alfio; Sacco, Riccardo; Saleri, Fausto (2000). “section 5.8.2”. Numerical Mathematics. Springer. p. 15. ISBN 978-0-387-98959-4.
- ^ a b c Bai, Z.; Demmel, J.; Dongarra, J.; Ruhe, A.; Van Der Vorst, H., eds. (2000). “Generalized Hermitian Eigenvalue Problems”. Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide. Philadelphia: SIAM. ISBN 978-0-89871-471-5.
- ^ Parlett, Beresford N. (1998). The symmetric eigenvalue problem (Reprint. ed.). Philadelphia: Society for Industrial and Applied Mathematics. p. 345. doi:10.1137/1.9781611971163. ISBN 978-0-89871-402-9.
References[edit]
- Franklin, Joel N. (1968). Matrix Theory. Dover Publications. ISBN 978-0-486-41179-8.
- Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Baltimore: Johns Hopkins University Press, ISBN 978-0-8018-5414-9
- Horn, Roger A.; Johnson, Charles R. (1985). Matrix Analysis. Cambridge University Press. ISBN 978-0-521-38632-6.
- Horn, Roger A.; Johnson, Charles R. (1991). Topics in Matrix Analysis. Cambridge University Press. ISBN 978-0-521-46713-1.
- Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley, ISBN 978-0-471-50728-4
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
- Strang, G. (1998). Introduction to Linear Algebra (3rd ed.). Wellesley-Cambridge Press. ISBN 978-0-9614088-5-5.
External links[edit]
- Interactive program & tutorial of Spectral Decomposition.















































![{displaystyle left[Lambda ^{-1}right]_{ii}={frac {1}{lambda _{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f57c7c286afe19b02c6d88e723c53eac4f4fedb8)



![{displaystyle left[fleft(mathbf {Lambda } right)right]_{ii}=fleft(lambda _{i}right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92325f5010257b3d8d0d004f524f8ae147bdc95c)



















