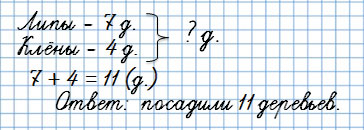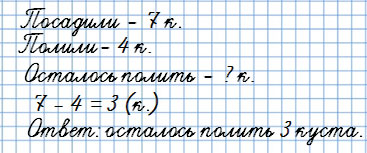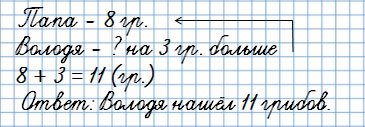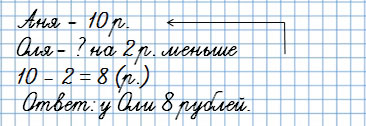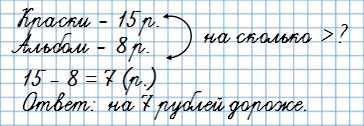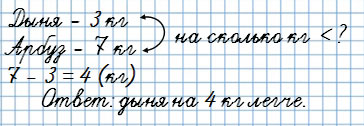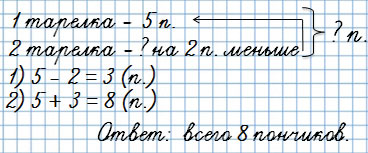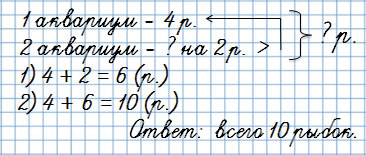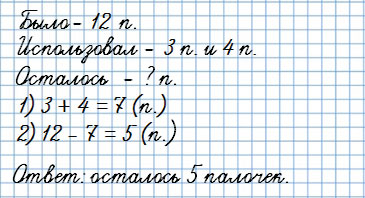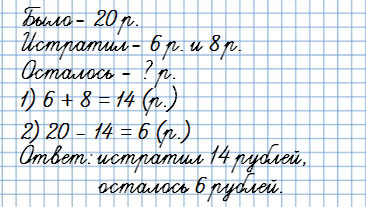Преобразование пар простых взаимосвязанных задач в составную
Простая задача №1
«Свете подарили 6 конфет, а Маше на 3 конфеты больше. Сколько конфет подарили Маше?»
С.-6к.
М.-? на 3 к. больше
Простая задача №2
«Свете подарили 6 конфет, а Маше 9 конфет. Сколько всего конфет подарили девочкам?»
С.- 6 к.
М.-9 к.
Составная задача
«Свете подарили 6 конфет, а Маше на 3 конфеты больше. Сколько всего конфет подарили девочкам?»
С.-6к.
М.-? на 3 к. больше
-Прочитайте задачу самостоятельно
-Прочитайте условие задачи
-Прочитайте вопрос задачи
-О чем говорится в задаче? (о конфетах, которые подарили Свете и Маше)
-Что о них сказано? (Свете подарили 6 конфета, а Маше на 3 конфеты больше)
-Давайте составим краткую запись
-Какие слова возьмем для краткой записи? (Света и Маша)
-Запишите заглавные буквы
-Сколько Свете подарили конфет? (6)
-Сколько Маше подарили конфет? (неизвестно)
-Значит ставим знак «вопроса» напротив буквы «М»
-А что сказано про конфеты, которые подарили Маше? (Маше подарили на 3 конфеты больше)
-Чего не хватает в краткой записи? (знака «вопроса»- сколько всего подарили конфет девочкам)
-Можем ли мы сразу ответить на главный вопрос задачи? (нет)
-Почему? (неизвестно, сколько конфет подарили Маше)
-А мы можем это узнать? (да)
-Каким действием? (сложением)
-Назовите выражение. (6+3)
-Почему действием сложения? (потому что Маше подарили столько же конфет, сколько и Свете, но на 3 конфеты больше)
-Мы ответили на главный вопрос задачи? (нет)
-Как узнать сколько всего конфет подарили девочкам? (сложить число конфет Светы и число конфет Маши)
-Теперь мы можем ответить на главный вопрос задачи? (да)
-Сколько действий в задаче? (2)
-Запишите решение задачи по действиям с пояснением и выражением.
1) 6+3=9 (к.)- подарили Маше
2) 6+9=15 (к.)- подарили всего девочкам
(6+3) +6=15 (к.)
Ответ: 15 конфет.
Виды дополнительной работы с задачей:
1)Изменение условия так, чтобы задача решалась другим действием.
«Свете подарили 6 конфет, а Маше на 3 конфеты меньше. Сколько всего конфет подарили девочкам?»
1)6-3=3 (к.)- подарили Маше
2)6+3=9 (к.)- подарили всего девочкам
2)Сравнение содержания данной задачи и ее решения с содержанием и решением другой задачи.
Задача:
«У Оли 4 мяча, а у Кати на 2 мяча меньше. Сколько всего мячей у девочек?»
1)4-2=2 (м.)- у Кати
2)4+2=6 (м.)- всего у девочек
В данной задаче первое действие- вычитание.
В первой задаче первое действие- сложение.
3)Установление соответствия между содержанием задачи и краткой записью.
-Подходит ли эта краткая запись данной задачи?
С.-6 к.
М.-3 к.
(нет, так как в ней «известно» сколько конфет подарили Маше)
-Что нужно изменить в данной краткой записи, чтобы она соответствовала задаче? (нужно изменить данные про конфеты, подаренные Маше)
-Как можно изменить задачу, чтобы данная краткая запись подходила этой задаче? («Свете подарили 6 конфет, а Маше 3 конфеты. Сколько всего конфет подарили девочкам?»)
Одной из важнейших задач начальной школы является математическое
развитие ребёнка путём обучения решению задач.
Не только учителя, но и родители младших школьников хорошо
знают, что труднее всего в математике многим детям даются задачи. Именно
поэтому очень важно с первых же дней ребёнка в школе правильно подойти к
процессу обучения его решению задач, иначе объективные и субъективные трудности
этого процесса со временем могут превратить изучение математики для ребёнка в
тяжёлую и неприятную повинность.
Слайд №2:
Цели и задачи
Знакомство с составными задачами на уроках математики происходит
уже в конце 1 класса. Поэтому учитель ставит перед собой цель: используя
различные формы и приемы работы над составными задачами, развивать логическое
мышление, интеллект младших школьников, активизировать учебно-познавательную
деятельность, формировать у учащихся универсальные учебные действия:
1) читать задачу, правильно представлять ситуацию, заданную условием,
выделять главные (опорные) слова;
2) выделять условие и вопрос, известное и неизвестное (данные и
искомое);
3) выбирать арифметические действия для решения задачи;
4) записывать решение и ответ задачи.
Слайд №3
Главным
условием успешного обучения решению составных задач является овладение
учащимися умением решать простые задачи.
Чтобы
научить учащихся решать задачи, учитель может использовать приемы, которые
отрабатываются сначала при обучении решению простых задач, а затем они же
используются при решении составных задач, но в более сложной форме.
Так, при
формировании умения решать задачи хорошо использовать приём моделирования.
Моделирование может быть предметным (модель строится с использованием
наглядных средств), графическим (ситуация изображается с помощью схемы,
схематического чертежа) и мысленным (ученик представляет себе ситуацию в уме и,
пользуясь ею, сразу может составить запись решения).
Для того, чтобы решить задачу, ученик должен уметь переходить от
текста к представлению ситуации, а от неё к записи решения с помощью
математических символов. Для решения любой математической задачи ученик должен
уметь выполнить двойной переход: текст – образ – запись решения.
Самым простым способом моделирования задачи является моделирование
на наглядных предметах.
Затем постепенно его можно заменить другим способом
моделирования задачи – схематическим (упрощённый вариант графической модели).
Например, схема, соответствующая действию сложения, может выглядеть
так:
 |
|||
Схема, соответствующая действию вычитания, может выглядеть
так:
 |
Главным достоинством такой схемы является то, что она визуально
и по смыслу точно отражает характер операций сложения и вычитания. Также она
отражает количественные соотношения ситуации, показывает связь между данными и
искомым.
Слайд №4
При решении задач, в которых требуется либо увеличить (уменьшить)
множество на несколько единиц, либо сравнить два множества для выяснения,
которое из них больше (меньше) и на сколько (разностное сравнение) для введения
новой схемы можно использовать игру «Вычислительная машина»

В пустом квадратике помещаются числа, которые «машина» уменьшает или
увеличивает.
При работе с такой схемой важно обсудить с учениками вопрос о том, что
стрелка в данном случае показывает на то число, которое надо найти в
результате.
Можно использовать задания на классификацию задач с
использованием схем. Для этого демонстрируется несколько схем, структурно
различных, но с одинаковыми числами. Детям по одному предлагаются тексты задач,
и по мере чтения текстов им нужно выбрать схему, помогающую решить задачу, и
объяснить при этом свой выбор.
Слайд №5
На
подготовительном этапе также можно использовать следующие формы и приемы
работы над задачами:
а) составление задач по картинке, по схеме, по краткой записи, по решению
б) решение задач-вопросов
в) решение задач с недостающими либо с избыточными данными
г) решение логических задач
д) решение задач с неопределенными данными
е) решение задач-цепочек ( когда вторая задача является продолжением первой) и
другие.
Слайд №6
Составление задач по картинке,
по схеме, по краткой записи, по решению.
Слайд №7
Решение задач-вопросов:
Что нужно знать, чтобы найти, сколько всего грибов в
двух корзинах?
Что нужно знать, чтобы найти, на сколько подосиновиков
больше, чем лисичек?
Слайд №8
Постановка вопроса к данному условию задачи.
а) Было 3 ромашки. Стало на 2 больше. Сколько … ?
б) На автостоянке было 8 легковых автомобилей и 2 грузовых. Потом 4
легковых автомобиля уехали. Объясни, что ты узнаешь, выполнив действия: 8 +
2, 8 – 2, 8 – 4.
в) Поставь к каждому условию вопрос, чтобы задача решалась так: 8 – 6.
1.
На одной полке 8 книг, а
на другой 6 книг.
2.
В прошлом году Петя вырос
на 8 см, а в этом году – на 6 см.
Слайд №9
Решение задач с недостающими данными (ответить
на вопрос нельзя, так как неизвестно одно данное, как и в составных задачах)
Девочка нарисовала красные и 3 зелёных шарика. Сколько
всего шариков нарисовала девочка?
Слайд №10
Выбор из предложенных вопросов к определенному
условию таких, на которые можно ответить, пользуясь данным условием.
«От ленты длиной 10 см отрезали сначала 2 см, а потом еще 4 см».
а) Сколько всего сантиметров ленты отрезали?
б) На сколько сантиметров меньше отрезали в первый раз, чем во второй?
в) На сколько сантиметров лента стала короче?
г) Сколько сантиметров ленты осталось?
Слайд №11
Подбор нужной схемы к задаче.
1.На первой полке 6 книг. На второй – на 4 книги больше. Сколько книг на
двух полках?
2.На первой полке 6 книг. На второй – на 4 книги больше. Сколько книг на
второй полке?
Слайд №12
Решение задач-цепочек (вторая задача является
продолжением первой):
В вазе лежало 4 яблока, а груш- на 2 больше. Сколько груш
лежало в вазе?
В вазе лежало 4 яблока и 6 груш. Сколько всего
яблок и груш лежало в вазе?
Слайд №13
У Саши было 6 легковых машин и 2 самосвала. Сколько всего машин у
Саши?
У Саши было 8 машин. 3 машины он подарил другу. Сколько машин у
него осталось?
Слайд №14
Выбор действия в задаче: читаются задачи, а дети показывают карточки «+» или «-»
Решение задач с неопределенными данными
В
линейку тетрадей
В клетку тетрадей
Решение логических задач.
– В коробке умещается 10 красных бусинок или 6 зеленых. Какие
бусинки меньшего размера: красные или зеленые?
Слайд №15
Постепенно дети,
решая задачу под руководством учителя, приучаются действовать по определенному
алгоритму. Но для самостоятельной или домашней работы полезна бывает памятка
по решению составных задач.
Памятка по решению составных задач
Читай задачу и представляй себе, о чем в ней
говорится.
Сделай краткую запись или построй схему.
Объясни, что показывает каждое число, и назови вопрос
задачи.
Подумай, какое число получится в ответе: больше или
меньше, чем данные числа.
Подумай, можно ли сразу ответить на вопрос задачи.
Если нет, то почему. Что можно узнать сначала, что потом? Составь план решения.
Выполни решение.
Ответь на вопрос задачи.
Проверь решение.
Слайд №16
Приемы,
способствующие формированию умения решать составные задачи во многом повторяют
те же приемы для решения простых задач:
1)
Из двух простых составить
одну задачу
2) Из одной
составной выделить несколько простых задач
3) К условию
придумать вопрос, чтобы задача решалась в одно (два) действия.
4) К вопросу
придумать условие, чтобы задача решалась в одно (два) действия.
5) Составление
задач по рисунку, схеме, чертежу, решению.
6) Решение задач
в сравнении
7) Решение задач
разными способами.
8) Решение задач
с недостающими и лишними данными.
9)Решение
логических задач
Слайд №17
1)
Из двух простых
составить одну составную задачу
В вазе лежало 4
яблока, а груш- на 2 больше.
Сколько груш лежало в вазе?
В вазе лежало 4
яблока и 6 груш. Сколько всего фруктов лежало в вазе?
В вазе лежало 4
яблока, а груш- на 2 больше. Сколько всего фруктов лежало в вазе?
2)
Из одной составной
выделить несколько простых задач.
Слайд №18
К условию
придумать вопрос, чтобы задача решалась в одно (два) действия.
На полянке росло 3
подосиновика, а белых грибов – на 2 больше.
Сколько…..?
К вопросу
придумать условие, чтобы задача решалась в одно (два) действия.
Сколько всего подосиновиков
и белых грибов росло на полянке?
Слайд №19
Составление
задач по рисунку, ( пауза) чертежу, (пауза) решению
Слайд №20
Составление
задач по схемам
Слайд №21
Решение
задач в сравнении
Первоклассники взяли
в библиотеке 18 книг. 11 книг они уже прочитали. Сколько книг осталось
прочитать?
и
Первоклассники взяли
в библиотеке 10 сказок и 8 книг о животных. 11 книг они уже прочитали. Сколько
книг осталось прочитать?
На полянке росло 3
белых гриба и 2 лисички. Сколько всего грибов росло на полянке?
и
На полянке росло 3
белых гриба, а лисичек на 2 больше. Сколько всего грибов росло на полянке?
Слайд №22
Решение задач
различными способами
В детском саду было
15 кукол, машин на 8 больше, чем кукол, а мячей на 6 меньше, чем машин. Сколько
мячей было в детском саду?
I способ
1)
15+8=23 (шт.) –машин
2)
23-6=17 (шт.)-мячей
Ответ: 17 мячей.
II
способ
1)
8-6=2 (шт.)- больше мячей,
чем кукол
2)
15+2=17 (шт.)-мячей
Ответ: 17 мячей.
Слайд №23
Решение задач
с недостающими и лишними данными.
На станции
юннатов живут 18 кроликов, а кур- на 12 меньше, чем голубей. Сколько всего
зверей и птиц у юннатов?
–Измени условие
или вопрос так, чтобы можно было решить эту задачу.
На уроках труда дети делали игрушки. Они
сделали 11 зайчиков и 7 медвежат. Детскому саду они подарили 9 игрушек. На
сколько больше дети сделали зайчиков, чем медвежат?
–Все ли данные
нужны для решения?
-Измените условие,
исключив лишние данные.
-Измените вопрос
так, чтобы все данные были нужны.
Слайд №24
Решение
логических задач
1.В трех коробках
лежат скрепки, кнопки и спички. Известно, что все три записи неверные.
Определите, где что лежит.
2.Один сосуд 3-х
литровый, а другой -5-ти литровый. Как с помощью этих сосудов налить в кувшин 4
литра воды из водопроводного крана?
Эксперты
утверждают, что занятия математикой учат обобщать, находить закономерности и
выстраивать логические цепочки – важное умение для освоения многих школьных
предметов, да и просто для решения каких-либо жизненных ситуаций.
Решение
задач формирует ещё один важный навык – прогнозирование, то есть умение
просчитывать свои шаги и поступки, видеть на несколько шагов вперёд.
Кроме того,
занятия математикой учат быстро соображать, работать одновременно сразу со
многими понятиями из разных областей, приучают понимать, а не зазубривать
нужную информацию, развивают абстрактное мышление.
Учёные в
один голос утверждают: отсутствие способностей к математике не более чем миф.
На самом деле головной мозг можно и нужно развивать хотя бы на школьных уроках.
Список
использованной литературы:
1.
Т.А.Лавриненко «Как
научить детей решать задачи». Методические рекомендации для учителей начальных
классов. Саратов, Издательство «Лицей», 2010 г.
2.
О.В.Узорова, Е.Н.Нефедова
«500 задач с пояснением, пошаговым решением и правильным оформлением 2 класс»
Москва, АСТ Астрель, Профиздат, 2013 г.
3.
О.В.Узорова, Е.Н.Нефедова
«700 заданий и упражнений по математике
1-2 классы» Москва, АСТ Астрель, Профиздат, 2012 г.
4.
Т.В.Ушакова «Учимся
считать быстро1-2 классы» Санкт-Петербург Издательский дом «Литера», 2014 г.
Автор: Смирнова Татьяна Сергеевна
Организация: МБОУ «Гимназия №6»
Населенный пункт: Московская область, город Ивантеевка
В математике задачи играют важную роль. Решения задач помогают формировать умение развивать у детей не только логическое мышление и речь, но и возможности для формирования доступных для них обобщений. Что такое задача? Задача- это условие, о ком или о чем ,говорится в задаче, вопрос , решение и ответ. Большое значение уделяется решению и составлению простых задач, так как с помощью решения простых задач формируется одно из важных понятий начального курса математики – понятие об арифметических действиях. Учащиеся узнают, в каких случаях применяется то или иное арифметическое действие. Работа по формированию данного умения начинается уже в процессе решения простых задач, выполняя в данном случае не только функцию подготовки к знакомству с составной задачей, но и оказывая положительное влияние на их развитие.
Дети должны научиться понимать отличие составной задачи от простой – ее нельзя решить сразу, т.е. одним действием, а для решения сначала из нее вычисляются простые задачи, устанавливаются соответствующие связи между данными и искомым. Главной целью составных задач является, разъяснения свойств суммы и разности, сопоставления случаев применения различных действий.
В процессе обучения решению составной задачи в начальной школе я использую методические приёмы: методический приём сравнения; методический приём выбора;
Методический приём сравнения :
Формирование умения пользоваться этим приёмом следует осуществлять поэтапно, в тесной связи с изучением конкретного содержания.
Задание 1.
«Девочки вырезали 15 снежинок, а мальчики на 5 снежинок меньше.
Сколько снежинок вырезали девочки и мальчики вместе ?»
«Девочки вырезали 15 снежинок, а мальчики на 5 снежинок больше.
Сколько снежинок вырезали девочки и мальчики вместе ?»
Сравниваем тексты задач.
Чем они похожи? Чем различаются?
Сравнивая тексты задач, ученик устанавливает, что в них сюжет один и тот же, числовые данные одни и те же и вопрос сформулирован одинаковый. Различаются тексты условием:
в первом случае мальчики на 5 снежинок меньше, а во втором – на 5 больше.
Методический приём выбора используется для формирования у учащихся умения обосновывать свои суждения, используя для этого математическое содержание задания.
Этот приём позволяет осознать сущность формируемых понятий, общих способов действий и содержательную зависимость между ними. Процесс выполнения любого задания должен всегда представлять цепочку суждений, для обоснования истинности которых учащиеся используют различные способы.
Выбор ответа к данной задаче;
Задача.
«Арбуз вес 8 кг, а тыквы на 2 кг больше. Сколько весят арбуз и тыква вместе?»
Решив задачу, ученик подчёркивает верный ответ.
1) 18 кг 2) 14 кг 3) 15 кг
Использование данного приёма стимулирует учащихся к анализу текста, к установлению зависимости между данными и искомым.
Подобные задачи помогают готовиться к итоговому тестированию.
Методический приём преобразования Действия учеников в ходе выполнения соответствующих заданий направляются в основном указанием: «измени …», «представь …», «замени …» и др.
Приведу примеры заданий.
Приём преобразования вопроса.
Задача.
«В одной коробке 20 карандашей, а в другой на 3 карандаша меньше. Сколько карандашей в двух коробках?
Измени вопрос так, чтобы задача решалась в одно действие.
Приём преобразования отношений в соответствии с математической записью.
Подумай, что можно изменить в тексте задачи, чтобы выражение 15 –7 было её решением.
Задача.
«У Тани 15 тетрадей в линейку , а в клетку на 7 больше. Сколько всего тетрадей у Тани?»
В процессе анализа учащиеся приходят к выводу, что задача решается в два действия. Им необходимо изменить условие и вопрос таким образом, чтобы задача решалась в одно действие. Для этого следует внести изменения в условие задачи и сформулировать вопрос.
Дети учатся доказывать свою точку зрения, мыслить и рассуждать при анализе условия задачи.
Составить задания нетрудно, ориентируясь на задачи учебника.
Например, задачу:
У Светы 6 значков, а у Стаса на 2 значка больше. Сколько значков у Стаса?» неплохо предложить в таком виде: «У Светы 6 значков, у Стаса на 2 значка меньше, а у Коли 3 значка. Сколько значков у Светы и у Коли вместе?
Уместно дать и такую задачу:
На дереве сидело 10 птичек. Сначала улетело 2 птички, а потом еще 3. Сколько птичек улетело? Работа с такой задачей может быть дополнена заданием: «Придумайте еще вопрос, на который можно ответить в этой задаче». (Сколько птичек осталось на дереве?)
Например, учитель предлагает детям решить самостоятельно две простые задачи (их текст записан на доске или на плакате)
В первой коробке 8 карандашей, а во второй на 2 карандаша больше. Сколько карандашей во второй коробке?
В первой коробке 4 карандаша, а во второй 6. Сколько карандашей в двух коробках?
При знакомстве с составной задачей полезно использовать различные методические приемы.
Можно, например, сразу приступить к решению задачи, разъяснив учащимся, что такое условие, вопрос, данные. В этом случае, используя метод беседы, учитель выясняет, что нужно знать, чтобы ответить на вопрос задачи нужно знать, сколько карандашей в первой коробке и сколько карандашей во второй).
Используя иллюстрацию, данную в учебнике, учитель выясняет, каким действием можно узнать, сколько карандашей впервой коробке, что говорится про вторую коробку. Записывается первое действие. Затем учитель показывает, как записать второе действие и вопрос задачи. Здесь можно показать запись решения задачи выражением.
Аналогично разбирается вторая задача. Для записи ее решения учитель может вызвать к доске ученика, а остальные учащиеся выполнят запись решения задачи в тетрадях. Данный прием следует использовать в том случае, если учащиеся на предшествующих уроках испытывали затруднения при выполнении заданий, связанных с подготовкой к решению составных задач:
Если же подготовительная рабе та к решению составных задач была организована и была результативной, то знакомство учащихся с составной задачей можно провести по-другому.
После решения задач внимание детей обращается на связь, существующую между этими задачами.
Для этого проводится беседа по вопросам: прочитайте еще раз внимательно задачи. Обратили ли вы внимание на то. что они связаны между собой? (И в той и в другой задаче речь идет о двух коробках, в которых лежат карандаши.) Кто сможет из двух задач составить одну с двумя вопросами?
После попыток учащихся составить текст задачи с двумя вопросами учитель открывает на доске запись: «В первой коробке 8 карандашей, а во второй– на 2 карандаша больше. Сколько всего карандашей в двух коробках? Сколько карандашей во второй коробке?» Учитель подчеркивает, что в этой задаче два вопроса. Он просит учащихся внимательно прочитать каждый из них и подумать, на какой вопрос можно ответить сначала — на первый или на второй.
В зависимости от ответа на поставленный вопрос строится дальнейшая работа. Если учащиеся дают предполагаемый ответ, то учитель стирает (закрывает) второй вопрос и спрашивает: «Можно ли сразу ответить на этот вопрос задачи?» (Нет, сначала нужно узнать, сколько карандашей во второй коробке.) А затем говорит, что задача, в которой нельзя ответить на вопрос одним действием, называется составной. Учитель показывает запись решения составной задачи (по действиям или выражением).
На последующих уроках следует разъяснить взаимосвязь этих двух форм записи решения задачи.
Учитель сначала организует работу класса по решению простых задач. Затем он предлагает текст составной задачи. Для того, чтобы обратить внимание учащихся на взаимосвязь данной составной задачи с простыми, полезно выделить составную задачу в тексте простых (подчеркнуть или обвести на доске). Данный прием поможет увидеть в составной задаче простые. Умение выделять в составной задаче простые будет полезным в дальнейшем при решении некоторых составных задач.
В уроки следует включать не только решение простых и составных задач, но и сравнение их, а также творческое использование различных заданий, направленных на формирование умения решать составные задачи.
Выполнению данного задания должна предшествовать работа по анализу и сравнению текстов задач, в процессе которой учащиеся отметят, что условия задач одинаковые, различие только в вопросах.
Уделяя особое внимание решению простых задач и организуя самостоятельное решение их учащимися, необходимо продуманно сочетать эту работу с формированием умения решать составные задачи.
Так, например, предложив для самостоятельного решения задачу: «Девочка купила булку за 8 р. Сколько сдачи она получила с 20 р.?», не следует ограничиваться только ее фронтальной проверкой или использовать для этой цели решение задачи на индивидуальной доске. Полезно после самостоятельного решения задачи привлечь учеников, не справившихся с заданием, к «проигрыванию» задачи. Покупатель держит в руке 20 р. (демонстрационная модель), а продавец имеет набор монет. Он должен дать покупателю сдачу. Как это можно сделать? Учащиеся предлагают различные варианты набора монет, которые в сумме составляют 12 р.
После этого на столе учителя появляется еще один предмет, например тетрадь за 3 р.
Учитель обращается к классу: «А если девочка купит еще сок за 7 р., она получит сдачи больше или меньше, чем 12 р.? Как узнать, сколько рублей сдачи получит девочка в этом случае?»
После того как «проиграна» составная задача, учитель дополняет условие: «Девочка купила булку за 8 рублей, а сок за 7 рублей. Сколько получит сдачи с 12 рублей? и спрашивается : «Чем отличается эта задача от той, которая дана в учебнике?»
Таким образом, планируя на уроке решение простых и составных задач, следует творчески использовать в работе различные методические приемы.
Литература
- Демидова А.Е. Обучение решению некоторых видов составных задач / А.Е. Демидова // Начальная школа: плюс до и после. – 2003. –№ 4. – С.34–37.
- Истомина Н.Б. Методика обучения математике в начальных классах: Учеб. пособие для студ. сред. и высш. пед. учеб. заведений / Н.Б. Истомина – М.: Издательский центр “Академия”, 2002. – 512с.
- Прием графического моделирования при обучении решению задач / А.В. Белошистая // Начальная школа. – 2006. №8. С. 36–39.
- Моро–Методика математики начального курса.
Приложения:
- file0.docx.. 22,5 КБ
Опубликовано: 15.05.2020
Если задача решается в одно действие, то она называется простой, если в несколько (в два и более), то составной (сложной)
СОСТАВНЫЕ ЗАДАЧИ НА НАХОЖДЕНЕ СУММЫ (385-446)
1. На первой полке 5 книг, а на второй на 3 больше. Сколько книг на двух полках?
Р е ш е н и е .
1)Если на первой полке 5 книг, а на второй на три больше, то на второй будет 5 + 3 = 8 книг.
2)Если на первой полке 5 книг, а на второй 8 книг, то на обоих будет 5 + 8 = 13 книг.
О т в е т: на обоих полках 13 книг.
2. (399) В саду росло 6 гвоздик, маков на 2 меньше, а астр столько, сколько гвоздик и маков вместе. Сколько астр росло в саду? Сколько всего цветов росло в саду?
Р е ш е н и е .
1)Если в саду росло 6 гвоздик, а маков на 2 меньше, то маков было 6 – 2 = 4.
2)Если в саду росло 6 гвоздик и 4 мака, то астр росло 6 + 4 = 10.
3)Если в саду гвоздик и маков было 10, а астр тоже 10, то всего росло 10 + 10 =20 цветов.
О т в е т: астр росло 10; всего было 20 цветов.
Из Пчелко.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Образцы оформления задачи
В разделе “Задачи” мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
1. Задачи на нахождение суммы
В вопросе задач такого типа всегда есть “Сколько всего?”
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
В вопросе “Сколько … осталось?”
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
3. Задачи на увеличение или уменьшение числа на несколько единиц
В условии “на … больше”
Папа с Володей собирали грибы. Папа нашёл 8 грибов, а Володя на 3 гриба больше.
Сколько грибов нашёл Володя?
В условии “на … меньше”
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
В вопросе “На сколько больше…?”
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
“На сколько меньше…?”
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии “Было…Стало…”
В вопросе “Сколько добавили?”
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии “Было… Осталось…”
В вопросе “Сколько уехало?”
“Сколько человек вышло?”
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии “Убрали… Осталось…”
В вопросе “Сколько было сначала?”
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Первый вид
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Второй вид
В классе два маленьких аквариума. В первом аквариуме 4 рыбки, а во втором – на 2 рыбки больше.
Сколько рыбок в двух аквариумах?
Третий вид
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
Четвёртый вид
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
или
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
II тип:
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
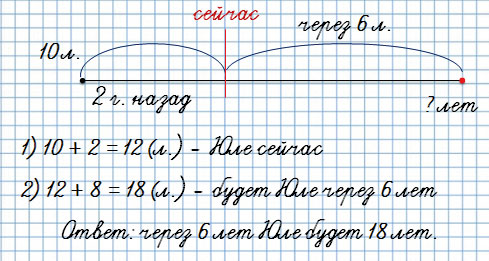
Задачи с составлением рисунка по условию:
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Советуем посмотреть:
Обратные задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 15,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 19,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 23,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 24,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 25,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 30,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 44,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
2 класс
Страница 55. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 13,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 44,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 49,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 45,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 21,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 73,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 37. ПР 4. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 75. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 18,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 49,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 57,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 60,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 38. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 70,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 385,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 80,
Мерзляк, Полонский, Якир, Учебник
Номер 246,
Мерзляк, Полонский, Якир, Учебник
Номер 250,
Мерзляк, Полонский, Якир, Учебник
Номер 265,
Мерзляк, Полонский, Якир, Учебник
Номер 464,
Мерзляк, Полонский, Якир, Учебник
Номер 465,
Мерзляк, Полонский, Якир, Учебник
Номер 482,
Мерзляк, Полонский, Якир, Учебник
Номер 484,
Мерзляк, Полонский, Якир, Учебник
Номер 497,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 366,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 371,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 382,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 383,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 404,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 409,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 432,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 443,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 448,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 450,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник