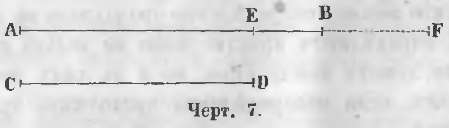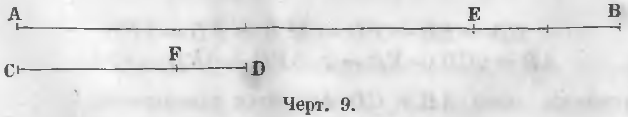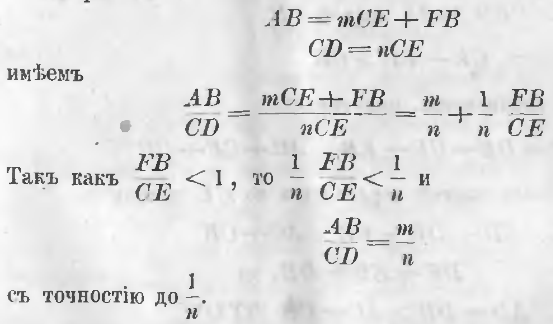Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Прямая
Понятие прямой, также как и понятие точки является основными понятиями геометрии. Как известно основные понятия не определяется. Это не является и исключением для понятия прямой. Поэтому рассмотрим суть этого понятия через его построение.
Возьмем линейку и, не отрывая карандаша, проведем линию произвольной длины (рис. 1).
Полученную линию мы и будем называть прямой. Однако тут необходимо отметить, что это не вся прямая, а только её часть. Всю же прямую построить не имеется возможным, она является бесконечной на обоих своих концах.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Прямые будем обозначать маленькой латинской буквой, либо двумя её точками в круглых скобках (рис. 2).
Понятия прямой и точки связаны тремя аксиомами геометрии:
Аксиома 1: Для каждой произвольной прямой существует как минимум две точки, которые на ней лежат.
Аксиома 2: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.
Аксиома 3: Через $2$ произвольные точки всегда проходит прямая, причем эта прямая единственна.
Для двух прямых актуально их взаимное расположение. Возможны три случая:
- Две прямые совпадают. В этом случае каждая точка одной будет также и точкой другой прямой.
- Две прямые пересекаются. В этом случае только какая-то одна точка из одной прямой будет также принадлежать и другой прямой.
- Две прямые параллельны. В этом случае у каждой из этих прямых свой набор различных друг от друга точек.
«Прямая и отрезок, измерение и сравнение отрезков» 👇
В этой статье мы не будем подробно останавливаться на этих понятиях.
Отрезок
Пусть нам дана произвольная прямая и две точки, принадлежащие ей. Тогда
Определение 1
Отрезком будет называться часть прямой, которая ограничена двумя ее произвольными различными точками.
Определение 2
Точки, которыми ограничен отрезок в рамках определения 1 называются концами этого отрезка.
Отрезки будем обозначать двумя её точками концов в квадратных скобках (рис. 3).
Сравнение отрезков
Рассмотрим два произвольных отрезка. Очевидно, что они могут быть либо равными, либо неравными. Чтобы разобраться в этом, нам нужна следующая аксиома геометрии.
Аксиома 4: Если оба конца двух различных отрезков совпадут при их наложении, то такие отрезки будут равными.
Итак, для сравнения выбранных нами отрезков (обозначим их отрезок 1 и отрезок 2) наложим конец отрезка 1 на конец отрезка 2, так, чтобы, отрезки оставались по одну сторону от этих концов. После такого наложения возможны два следующих случая:
-
Вторые концы этих отрезков также совпадут. В таком случае по аксиоме 5 мы получим, что такие отрезки будут равны друг другу
(рис. 4). -
Вторые корцы не совпадут. Здесь, без ограничения общности, будем считать, что конец отрезка 1 будет принадлежать отрезку 2. Тогда здесь мы говорим, что данные отрезки не равны, причем отрезок 1 короче отрезка 2.
Длина отрезка
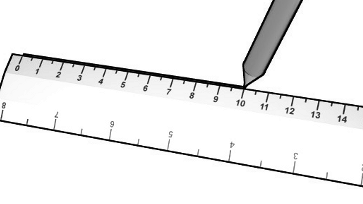
Помимо сравнения одних отрезков с другими также часто необходимо измерение отрезков. Измерить отрезок означает найти его длину. Для этого необходимо выбрать какой-то «эталонный» отрезок, который мы будем принимать за единицу ( к примеру отрезок, длина которого равняется 1 сантиметру). После выбора такого отрезка мы проводим с ним сравнение отрезков, длину которого нужно найти. Рассмотрим пример.
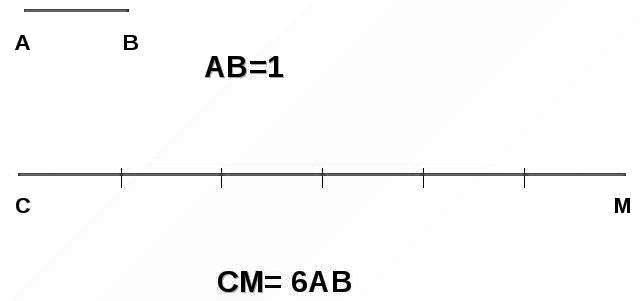
Пример 1
Найти длину следующего отрезка
если следующий отрезок равняется 1
Решение.
Для его измерения возьмем за эталон отрезок $[AB]$. Будем откладывать его на отрезок $[CM]$. Получим:
Ответ: $6$ см.
Понятие длины отрезка связаны со следующими аксиомами геометрии:
Аксиома 5: Выбрав определенную единицу измерения отрезков, длина любого отрезка будет положительна.
Аксиома 6: Выбрав определенную единицу измерения отрезков, мы можем для любого положительного числа найти отрезок, у которого длина равняется данному числу.
После определения длины отрезков у нас появляется второй способ для сравнения отрезков. Если при одном и том же выборе единицы длины отрезок $1$ и отрезок $2$ будут иметь одинаковую длину, то такие отрезки будут называться равными. Если же, без ограничения общности, отрезок 1 будет иметь длину по числовому значению меньше длины отрезка $2$, то отрезок $1$ будет меньше отрезка $2$.
Самым простым способом измерения длины отрезков является измерение, с помощью линейки.
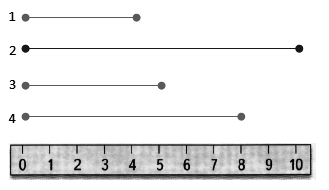
Пример 2
Записать длины следующих отрезков:
Решение.
Измерим их с помощью линейки:
Получим.
Ответ:
- $4$ см.
- $10$ см.
- $5$ см.
- $8$ см.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
В практической деятельности для определения расстояния между пунктами находят длину отрезка, соединяющего рассматриваемые пункты. Если не принимать во внимание физические свойства предметов, то многие из них дают представление об отрезках, например карандаши, балки различных металлических конструкций и т. д.
Рассмотрим понятие отрезка. Для определения отрезка воспользуемся основным свойством (аксиомой) расположения точек на прямой, которое формулируется следующим образом:
Аксиома: Из трех точек на прямой единственная точка лежит между двумя другими.
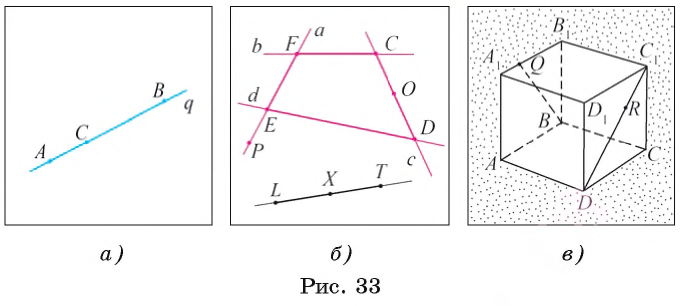
Пусть на прямой q лежат три точки А, В и С (рис. 33, а). Точка С лежит между точками А и В. Можно говорить также, что точки А и В лежат по разные стороны от точки С или что точки А и С лежат по одну сторону от точки Б.
Определение. Отрезком называется геометрическая фигура, состоящая из двух точек прямой и всех ее точек, лежащих между данными точками.
Данные точки называются концами отрезка, остальные его точки называются внутренними точками.
Отрезок, концами которого являются точки А и В, обозначается АВ или ВА. Иногда отрезки обозначаются также строчными буквами латинского алфавита а, b, с и т. д.
Если точки А и B — концы отрезка АВ, то говорят, что отрезок АВ соединяет эти точки.
Можно сказать, что отрезок АВ есть фигура, состоящая из двух точек А, В и части прямой, ими ограниченной.
Подчеркнем, что отрезок LТ состоит из точек L, T и всех точек X прямой LТ, лежащих между точками L и Т (рис. 33, б).
Например, на рисунке 33, B изображены отрезки ЕF, FС, СD и DЕ, которые лежат на прямых а, b, с и d соответственно.
Точка О является внутренней точкой отрезка СD, а точка Р не является внутренней точкой отрезка ЕF. На рисунке 33, в изображены отрезки BQ и DC1, которые лежат в гранях куба, и точка R, являющаяся внутренней точкой отрезка DC1.
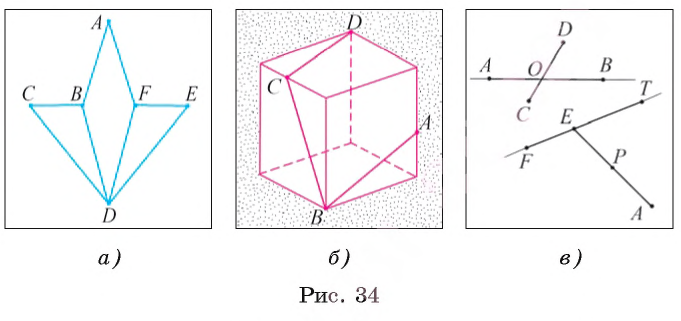
Пользуясь отрезками, мы можем конструировать новые геометрические фигуры. Например, на рисунке 34, а изображена фигура, образованная отрезками АВ, ВС, СD, DЕ, DB, DF, ЕF, FА.
На рисунке 34, B изображен куб и геометрическая фигура, образованная отрезками АВ, ВС, СD, которые лежат в гранях этого куба.
На рисунке 34, в изображены отрезки АВ и СD, которые пересекаются в точке О. Точка О является внутренней точкой каждого из этих отрезков.
Отрезки FТ и ЕА, изображенные на рисунке 34, в, имеют общую точку Е. Точка Е одновременно является внутренней точкой отрезка FТ и концом отрезка ЕА.
Если отрезок АВ не пересекает прямую l, то говорят, что точки А и В лежат по одну сторону от прямой l.
Например, точки Р и А лежат по одну сторону прямой FТ, так как отрезок РА и прямая FТ не пересекаются (см. рис. 34, в).
Если отрезок АВ пересекается с прямой l во внутренней точке отрезка АВ, то говорят, что точки А и В лежат по разные стороны от прямой l.
Например, точки С и D лежат по разные стороны от прямой АВ (см. рис. 34, в).
Более подробное объяснение:
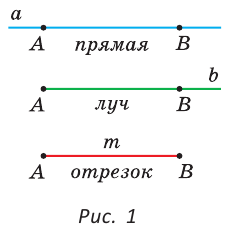
Прямую можно представить как туго натянутую нить, бесконечную в обе стороны. Прямая изображается отрезком, который может быть продолжен в обе стороны.
Луч и отрезок — это части прямой. Луч можно представить как луч от фонарика, а отрезок — как карандаш. Луч состоит из точки прямой (начало луча) и всех ее точек, лежащих по одну сторону от данной точки. Отрезок состоит из двух точек прямой (концов отрезка) и всех ее точек, лежащих между двумя данными точками.
На рисунке 1 показаны: прямая АВ (или ВА, или 
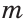
Измерение отрезков
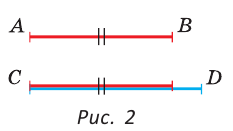
Для сравнения отрезков их можно наложить друг на друга. Если отрезки совпадут своими концами, то они равны, если нет — то отрезок, который лежит внутри другого отрезка, считается меньшим. На рисунке 2 отрезок АВ меньше отрезка CD, то есть АВ < CD. Равные отрезки на чертеже иногда обозначают равным числом черточек на них.
Отрезки можно сравнить, измерив их длины. Отрезок измеряется при помощи других отрезков, которые приняты за единицу длины: 1 мм, 1 см, 1 дм, 1 м, 1 км и т. д. Если на данном отрезке АВ укладывается три отрезка по 1 дм, пять отрезков по 1 см и два отрезка по 1 мм, то длина отрезка АВ равна 3 дм 5 см 2 мм. При решении геометрических задач длины всех отрезков обычно записывают в одних единицах: АВ = 352 мм или АВ = 3,52 дм. Если в условии размерность не указана, то считается, что длины отрезков выражены в одних единицах.
Часто вместо слов «длина отрезка равна 12 см» говорят «отрезок равен 12 см», вместо «найдите длину отрезка» — «найдите отрезок».
Ломаная
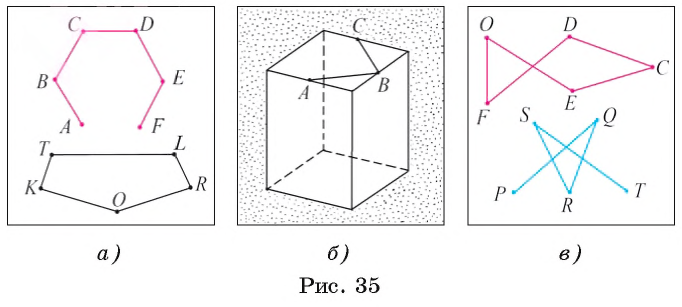
Среди множества геометрических фигур, образованных отрезками, выделяются такие, которые называются ломаными.
Определение. Ломаной называется геометрическая фигура, состоящая из отрезков А1А2, А2А3, …, Аn-1Аn, последовательно соединяющих точки A1,A2, A3, …, Аn-1, Аn.
Точки A1,A2, A3, …, Аn-1, Аn называются вершинами ломаной, а отрезки А1А2, А2А3, …, Аn-1Аn называются звеньями ломаной.
Точки А1 и Аn называются концами ломаной.
Два звена ломаной называются смежными, если они имеют общую вершину.
Ломаная называется простой ломаной, если любые ее два звена, кроме смежных, не имеют общих точек и никакие два смежных звена не лежат на одной прямой.
Ломаная называется замкнутой, если ее концы совпадают.
Например, на рисунке 35, а изображены простая ломаная ABCDEF, которая не является замкнутой, и ОKTLR — простая замкнутая ломаная. На рисунке 35, B изображена незамкнутая простая ломаная ABC, звенья AB и ВС которой лежат в грани параллелепипеда.
На рисунке 35, в изображены ломаные FOECD и PQRST, которые не являются простыми, так как некоторые их несмежные звенья имеют общие точки.
Заметим, что отрезки могут образовывать ломаную, все звенья которой не лежат в одной плоскости. Такая ломаная называется пространственной.
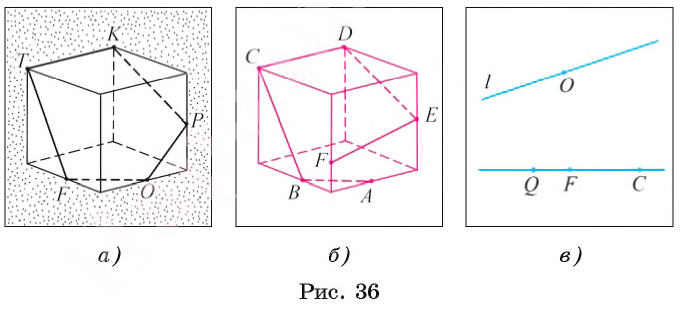
Например, на рисунках 36, а изображена замкнутая ломаная FТКРО, звенья которой лежат в гранях куба и не содержатся в одной плоскости.
Примером пространственной незамкнутой ломаной служит фигура, образованная отрезками АВ, ВС, СD, DЕ и ЕF, которые лежат в гранях куба (рис. 36, б).
Луч
Пусть О — некоторая точка прямой l. Тогда точка О разделяет множество остальных точек прямой l на два множества, каждое из которых вместе с точкой О называется лучом с началом в точке О (рис. 36, в).
Луч с началом О характеризуется следующим образом. Если две точки лежат по одну сторону от точки О, то эти точки лежат на одном луче с началом О. Если две точки лежат по разные стороны от точки О, то эти точки лежат на разных лучах с началом О.
Например, точки F и С луча с началом в точке Q, изображенного на рисунке 36, в, лежат по одну сторону от начала Q этого луча.
Определение. Лучом называется геометрическая фигура, состоящая из точки прямой и всех ее точек, лежащих по одну сторону от данной точки.
Данная точка называется началом луча.
Луч обозначается либо строчной латинской буквой, например h, р, либо двумя заглавными буквами латинского алфавита, первая из которых обозначает начало луча, а вторая — некоторую другую его точку.
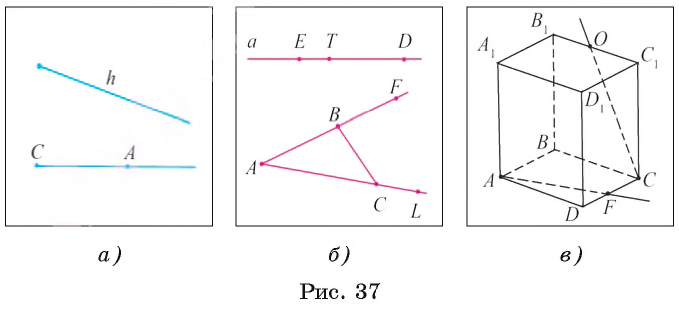
Например, на рисунке 37, а изображены лучи h и СА.
Противоположными лучами называются два различных луча одной прямой, имеющие общее начало.
Лучи ТD и ТЕ прямой а, изображенные на рисунке 37, б, являются противоположными.
На рисунке 37, B изображены лучи АF и АL, имеющие общее начало А. Отрезок АВ является частью луча АF, а концы B и С отрезка ВС принадлежат лучам АF и АL соответственно.
На рисунке 37, в изображены прямоугольный параллелепипед АВСDА1В1С1D1 и луч СО, который лежит в той же плоскости, что и грань СВВ1С1. Луч АF лежит в плоскости грани АВСD данного параллелепипеда.
Сравнение отрезков
В практической деятельности для того, чтобы сравнить длины двух предметов, их прикладывают один к другому.
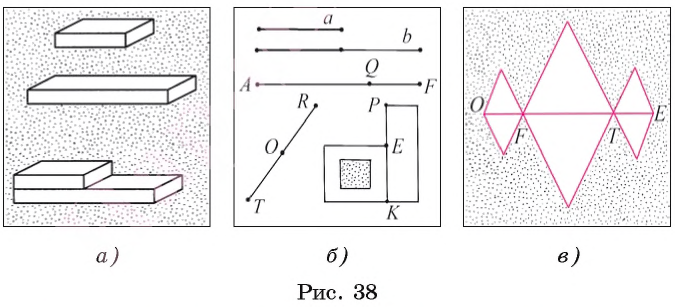
Например, приложив друг к другу два деревянных бруска, мы можем выяснить, равны длины этих брусков или один из них длиннее другого (рис. 38, а).
Пусть даны два отрезка а и b (рис. 38, б). Для сравнения этих отрезков наложим один отрезок на другой так, чтобы конец одного совпал с концом другого. Если два других конца отрезков также совпадут, то эти отрезки совместятся, и, значит, они равны.
Отрезки называются равными, если при наложении они совмещаются.
Если же два других конца отрезков не совместятся, то меньшим считается тот отрезок, который составляет часть другого.
Если отрезок а равен отрезку b, то пишут а = b и говорят: «Отрезок а равен отрезку b». Если отрезок а составляет часть отрезка b, то пишут: а < b и говорят: «Отрезок а меньше отрезка b» или пишут: b>а и говорят: «Отрезок b больше отрезка а».
Например, на рисунке 38, B отрезок АQ составляет часть отрезка АF, отрезок КЕ — часть отрезка КР.
Если точка С является внутренней точкой отрезка АВ, то говорят, что она разбивает, или делит, отрезок на два отрезка АС и СВ.
Например, на рисунке 38, в точка F разбивает отрезок ОЕ на отрезки ОF и FЕ, а точка Т разбивает отрезок ЕF на отрезки ЕТ и ТF.
В дальнейшем будем предполагать, что выполняется следующая аксиома.
Аксиома откладывания отрезка. На любом луче от его начала можно отложить единственный отрезок, равный данному.
Эта аксиома означает, что если дан какой-либо отрезок АВ и произвольный луч h с началом в точке О, то на луче h существует единственная точка X, такая, что отрезок ОХ равен отрезку АВ.
Серединой отрезка называется точка, делящая его на два равных отрезка.
Например, на рисунке 38, B изображена точка О — середина отрезка ТR (О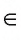
Измерение длин отрезков
В практической деятельности часто необходимо измерять длины отрезков. Знание длин отрезков позволяет сравнивать их, не накладывая один на другой.
Измерение длин отрезков основано на сравнении их с некоторым отрезком, который принимается за единицу измерения (единичный отрезок).
Длина отрезка — это геометрическая величина, которая показывает, сколько раз единица измерения и ее части укладываются в измеряемом отрезке.
Длина отрезка АВ обозначается АВ.
Длина отрезка может измеряться в миллиметрах (мм), сантиметрах (см), дециметрах (дм), метрах (м) и т. д.
Например, если за единицу измерения принять отрезок в 1 см, то для определения длины отрезка необходимо узнать, сколько раз в измеряемом отрезке укладывается сантиметр и его части.
Если в отрезке АВ отрезок в 1 см укладывается 3 раза, то говорят, что отрезок АВ имеет длину, равную 3 см, и пишут: АВ = 3 см. Если в отрезке CD сантиметр укладывается 2 раза и в остатке 5 раз укладывается десятая часть сантиметра, то длина отрезка СD равна 2,5 см, т. е. СD = 2,5 см.
При выбранной единице измерения длину отрезка можно выразить некоторым положительным числом. Если два отрезка равны, то единичный отрезок и его части укладываются в этих отрезках одинаковое число раз, т. е. равные отрезки имеют равные длины.
При измерении отрезков опираются на следующие свойства длины отрезков.
- При выбранной единице измерения каждый отрезок имеет длину, которая больше нуля.
- При выбранной единице измерения для любого положительного числа существует отрезок, длина которого выражается этим числом.
- Равные отрезки имеют равные длины.
- Отрезки, имеющие равные длины, равны.
- Длина отрезка равна сумме длин отрезков, на которые он делится любой точкой.
Длиной ломаной называется сумма длин ее звеньев.
Теперь дадим определение расстояния между точками.
Определение. Расстоянием между двумя точками называется длина отрезка, соединяющего данные точки.
Если две точки совпадают, то расстояние между ними считается равным нулю.
Расстояние между двумя точками А и B обозначается АB или ВА.
Пример:
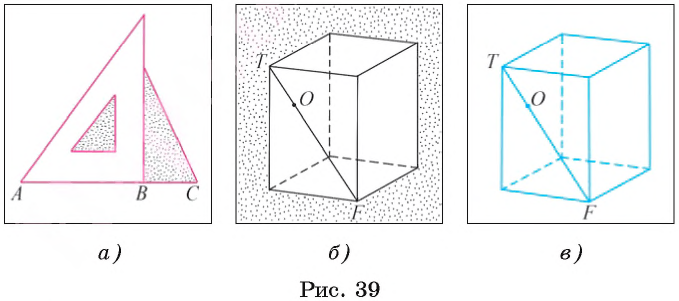
Точка B делит отрезок АС на два отрезка АВ и ВС. Вычислите длину отрезка АС, если известно, что АB = 2 см, а ВС = 1 см (рис. 39, а).
Решение.
Длина отрезка АС равна сумме длин отрезков, на которые он делится точкой B. Следовательно, АС=АВ + ВС = 2+1 = 3 (см).
Ответ: 3 см.
Пусть точка О делит отрезок ТF — диагональ грани прямоугольного параллелепипеда — на отрезки ТО и ОF (рис. 39, б, в).
Тогда, если ТF = 10 см, а ТО = 2 см, то OF= 8 см. Действительно, ТF = ТО + ОF, значит, ОF = ТF-ТО = 10 – 2 = 8 (см).
Окружность и круг
Дадим определение еще одной геометрической фигуры.
Определение. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, находящихся на заданном расстоянии от данной точки этой плоскости.
Данная точка называется центром окружности.
Радиусом окружности называется отрезок, соединяющий центр окружности с какой-либо точкой окружности.
Иногда радиусом окружности называют длину отрезка, соединяющего центр окружности с какой-либо ее точкой.
Из определения следует, что все радиусы окружности равны.
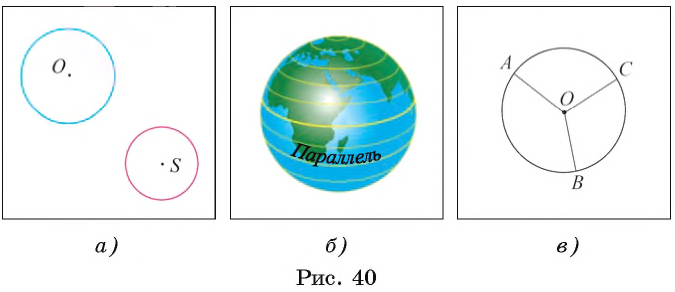
На рисунке 40, а изображены окружности с центрами в точках О и S. Параллели имеют форму окружностей, расположенных на поверхности земного шара (рис. 40, б).
Например, на рисунке 40, в изображены радиусы ОА, ОВ и ОС. Окружность с центром в точке О и радиусом R обозначается 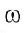
Хордой окружности называется отрезок, соединяющий две точки окружности.
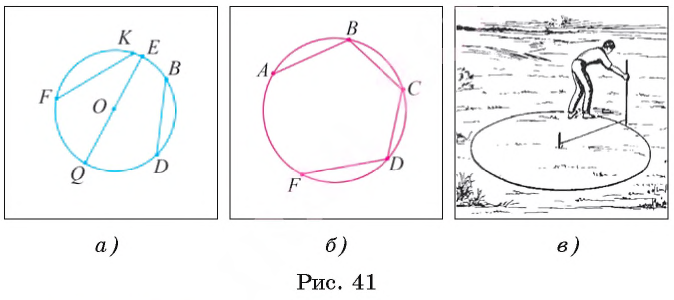
Например, на рисунке 41, а изображены хорды FК, DB и QЕ, а на рисунке 41, B изображена ломаная АВСDF, каждое звено которой является хордой окружности.
Диаметром окружности называется хорда, проходящая через центр окружности (или длина такой хорды). Центр окружности делит любой ее диаметр на два равных отрезка.
Например, хорда QЕ является диаметром окружности, так как проходит через центр О этой окружности (см. рис. 41, а).
Дугой окружности называется каждая из частей, на которые делят окружность любые две ее точки.
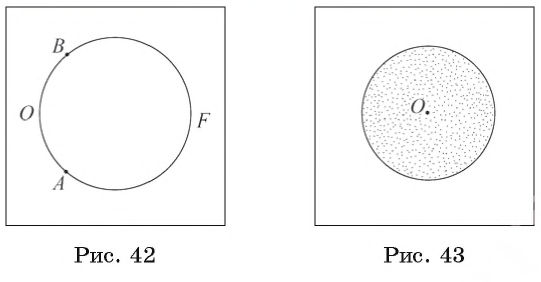
Например, на рисунке 42 точки А и B делят окружность на две дуги АОВ и АFB, которые обозначаются 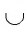
Прочертить окружность на местности для разбивки цветочной клумбы можно с помощью веревки и колышка (рис. 41, в).
Определение. Кругом называется геометрическая фигура, состоящая из окружности и части плоскости, ограниченной этой окружностью (рис. 43).
Окружность называется границей круга.
Круг с центром в точке О и радиусом R обозначается 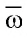
Окружность с центром в точке О и радиусом R называется границей круга с центром в точке О и радиусом R.
Центром, радиусом, хордой и диаметром круга называются центр, радиус, хорда и диаметр его границы.
Плоская геометрическая фигура называется ограниченной, если все ее точки принадлежат некоторому кругу, и называется неограниченной, если не существует круга, содержащего все точки этой фигуры.
Любой отрезок АВ — ограниченная фигура, так как для него существует круг некоторого, быть может, достаточно большого радиуса, которому принадлежат все точки этого отрезка. Например, любой отрезок АВ принадлежит кругу с центром в точке А и радиусом R=АВ.
Примером неограниченной фигуры является любая прямая или луч. Не существует круга, которому принадлежат все точки прямой. Для круга сколь угодно большого радиуса найдутся точки прямой, которые не принадлежат этому кругу.
Сравнение и измерение углов
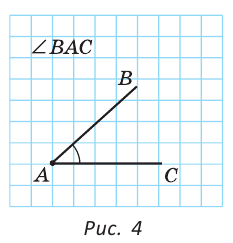
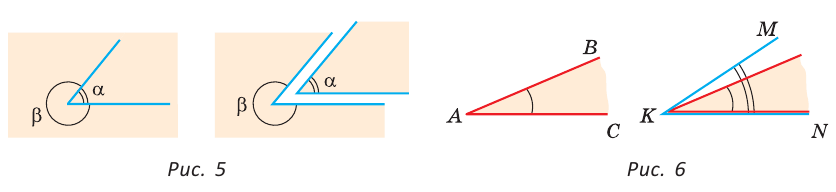
Если из точки провести два луча, то получим угол. Эти лучи называются сторонами угла, а их общая точка — его вершиной. При записи угла тремя большими буквами вершина угла записывается в центре.
На рисунке 4 лучи АВ и АС — стороны угла ВАС (или CAB), точка А — вершина угла. Если понятно из рисунка, о каком угле идет речь, то его обозначают одной буквой при вершине угла: 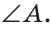
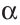
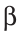
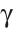
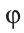
Угол, изображенный на плоскости, делит ее на две части, каждая из которых называется плоским углом. На рисунке 5 это углы 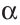
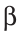
Сравнить углы можно наложением, совместив сторону одного угла со стороной другого. Если углы совпадут, то они равны; если нет, то угол, который лежит внутри другого угла, считается меньшим. На рисунке 6 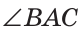
Измерение углов
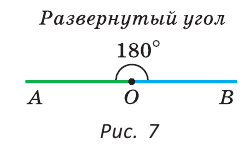
Если стороны угла повернуть вокруг его вершины так, чтобы они образовали прямую, то получим развернутый угол (рис. 7).
Углы можно сравнить, измерив их величины. Углы измеряются в градусах. Величину развернутого угла принимают за 180°. Тогда 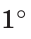
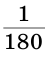
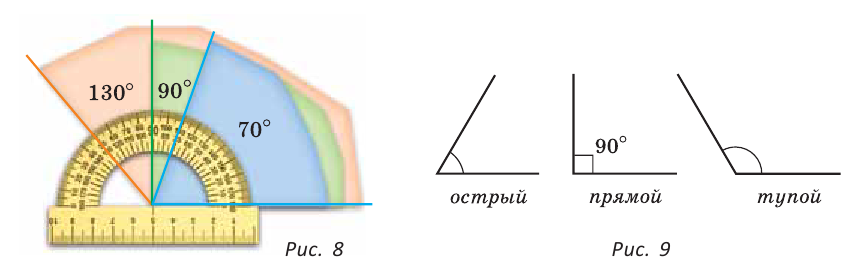
Виды углов: угол, меньший 90°, называется острым; равный 90°, — прямым; больший 90°, но меньший 180°, — тупым углом (рис. 9).
Неизвестный угол при решении задач иногда обозначают 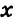
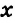
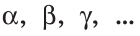
Полуплоскость
Пусть l — некоторая прямая на плоскости. Тогда эта прямая разделяет множество остальных точек плоскости на два множества, каждое из которых вместе с прямой l называется полуплоскостью. Прямая l называется границей каждой из полуплоскостей.
Полуплоскость с границей l характеризуется следующим образом. Если две точки лежат по одну сторону от прямой l, то эти точки лежат в одной полуплоскости с границей l. Если две точки лежат по разные стороны от прямой l, то эти точки лежат в разных полуплоскостях с границей l.
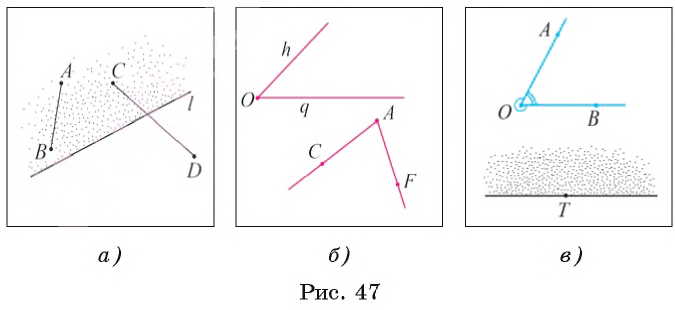
Например, точки А и В лежат в одной полуплоскости с границей l, а точки С и D лежат в разных полуплоскостях с границей l (рис. 47, а).
Определение. Полуплоскостью называется геометрическая фигура, состоящая из прямой и всех точек плоскости, лежащих по одну сторону от данной прямой.
Данная прямая называется границей полуплоскости.
Угол и его определение
Пусть на плоскости даны два луча h, q, имеющие общее начало О. Тогда остальные точки плоскости разделяются этими лучами на две части, каждая из которых вместе с лучами h и q называется углом (рис. 47, б).
Определение. Углом называется геометрическая фигура, состоящая из двух лучей с общим началом и одной из частей плоскости, на которые эти лучи разделяют остальные точки плоскости.
Лучи называются сторонами угла, а их общее начало — вершиной угла.
Угол с вершиной О и сторонами h, q обозначается 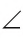
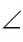
Если на сторонах угла с вершиной А указаны, например, точки С и F, тогда этот угол можно обозначать 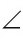
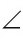
Заметим, что два луча с общим началом являются сторонами двух углов. Тот из углов, который хотят рассматривать, на рисунке отмечается дугой.
На рисунке 47, в дугой отмечен один из углов, а двумя дугами — другой из углов, сторонами которых служат лучи ОА и ОВ.
Развернутым углом называется угол, стороны которого являются противоположными лучами. На рисунке 47, в изображен развернутый угол с вершиной Т.
Если два луча с общим началом совпадают, то говорят, что они являются сторонами нулевого угла.
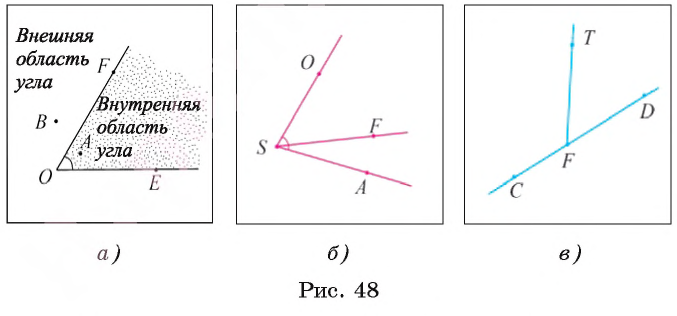
Для каждого ненулевого угла определены его внутренняя и внешняя области. Внутренней областью угла называется множество точек этого угла, не принадлежащих его сторонам.
Внешней областью угла называется множество точек плоскости, не принадлежащих углу.
На рисунке 48, а показаны точка А, которая лежит во внутренней области неразвернутого угла FOE, и точка В, лежащая во внешней области этого угла.
Если начало луча совпадает с вершиной угла и луч лежит во внутренней области данного угла, то говорят, что этот луч делит угол на два угла.
Например, на рисунке 48, B луч SF делит угол ASO на два угла: 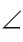
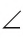
Любой луч с началом в вершине развернутого угла, не совпадающий с его сторонами и лежащий в его внутренней области, делит этот развернутый угол на два угла.
Например, луч FT, не совпадающий с лучами FC и FD, делит развернутый угол CFD с вершиной F на два угла: CFT и TFD (рис. 48, в).
Сравнение углов
Пусть 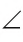
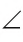
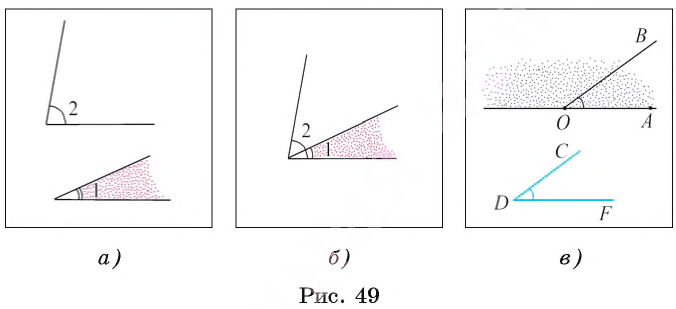
Если две другие стороны также совместятся, то совместятся и сами углы, а следовательно, они равны. Если при наложении эти стороны не совместятся, то меньшим считается тот угол, который является частью другого угла.
Например, на рисунке 49, B 
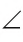
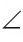
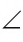
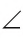
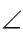
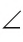
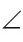
Если угол неразвернутый, то он может быть меньше или больше развернутого.
В дальнейшем, если не будет оговорено иное, будем рассматривать углы, меньшие развернутого угла или развернутые.
Далее будем пользоваться следующей аксиомой.
Аксиома откладывания угла в данную полуплоскость. От любого луча в данную полуплоскость можно отложить единственный угол, равный данному неразвернутому углу.
Эта аксиома означает, что если дан какой-либо луч OA и некоторый угол CDF, то в каждой из двух полуплоскостей, границей которой является прямая ОА, существует единственный луч ОВ, такой, что угол CDF равен углу АОВ (рис. 49, в).
Определение. Биссектрисой угла называется луч с началом в вершине этого угла и делящий его на два равных угла.
Измерение углов
Измерение углов основано на сравнении их с некоторым углом, который принимается за единицу измерения. За единицу измерения углов принят угол в один градус (градус) — угол, равный 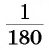
Некоторые части градуса имеют специальное название. Например, 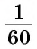
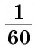
Градусная мера угла — это геометрическая величина, которая показывает, сколько раз угол в один градус и его части укладываются в данном угле.
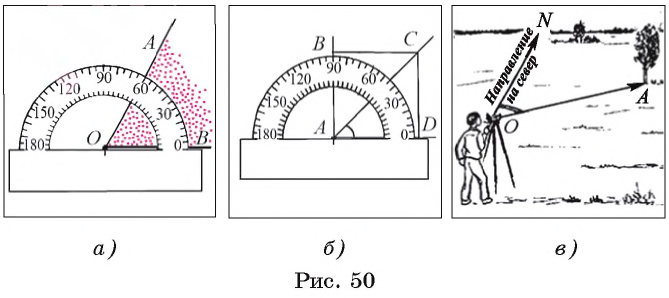
Для измерения углов используется транспортир (рис. 50, а).
Например, на рисунке 50, а изображен угол АОВ, градусная мера которого равна 60°. На рисунке 50, B изображен угол CAD, градусная мера которого равна 45° и 
Угол, градусная мера которого равна 35 градусов 40 минут и 12 секунд, обозначают следующим образом: 35°40’12”.
Так как градус составляет 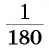
Каждый угол имеет определенную градусную меру.
Если два угла равны, то угол в один градус и его части укладываются в этих углах равное число раз, т. е. равные углы имеют равные градусные меры.
Если один угол меньше другого, то угол в один градус или его части укладываются в нем меньшее число раз, чем в другом угле.
При измерении углов опираются на следующие свойства градусной меры углов.
- Каждый ненулевой угол имеет градусную меру, которая больше нуля,
- Для любого числа 0
180 существует угол, градусная мера которого равна
°.
- Равные углы имеют равные градусные меры.
- Углы, имеющие равные градусные меры, равны.
- Градусная мера угла равна сумме градусных мер углов, на которые он делится любым, лучом.
Понятие угла и его градусной меры используется на практике, например при определении курса корабля или в геодезии при определении азимута предмета — градусной меры угла между направлением на север и направлением на предмет (рис. 50, в).
Если дан угол, градусная мера которого равна 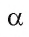
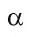
Угол называется прямым, если его градусная мера равна 90° (рис. 51, а), острым — если больше 0° и меньше 90° (рис. 51, б), тупым — если больше 90° и меньше 180° (рис. 51, в).
Ранее мы обсуждали, что понимается под теоремой. Теперь докажем теоремы, которые характеризуют свойства смежных и вертикальных углов.
Свойства смежных и вертикальных углов
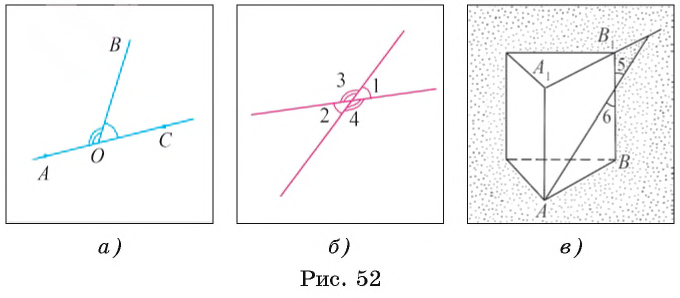
Два угла называются смежными, если у них одна сторона общая, а две другие стороны этих углов являются противоположными лучами.
Например, углы АОВ и ВОС, изображенные на рисунке 52, а, являются смежными.
Два угла называются вертикальными, если они имеют общую вершину и стороны одного угла являются лучами, противоположными сторонам другого.
Например, на рисунке 52, B изображены вертикальные углы 1 и 2, 3 и 4. На рисунке 52, в изображены вертикальные углы 5 и 6, лежащие в той же плоскости, в которой лежит грань АВВ1А1 прямой призмы.
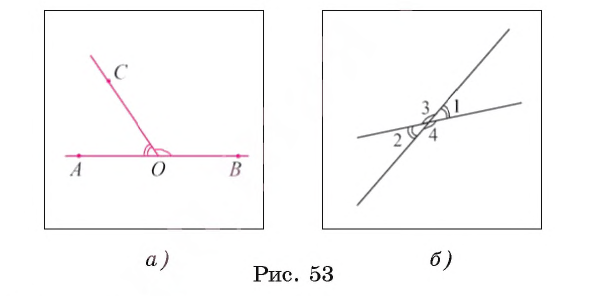
Теорема 1 (о свойстве смежных углов). Сумма градусных мер смежных углов равна 180°.
Доказательство.
Пусть углы АОС и ВОС смежные (рис. 53, а). Так как луч ОС делит развернутый угол с вершиной О на два угла АОС и BОС, то 


А поскольку 


Теорема доказана.
Теорема 2 (о свойстве вертикальных углов). Вертикальные углы равны.
Доказательство.
Пусть 





















Теорема доказана.
Перпендикулярные прямые
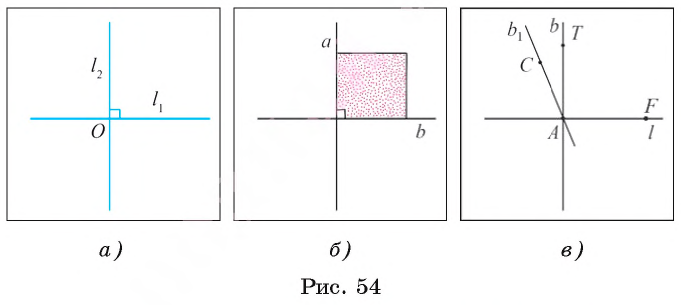
Теперь рассмотрим понятие перпендикулярных прямых. Пусть две прямые l1 и l2 пересекаются в точке О. При этом образуются четыре неразвернутых угла, сторонами которых являются лучи данных прямых с началом в точке О. Если один из этих углов прямой (рис. 54, а), то, как следует из теорем 1 и 2, и остальные углы также прямые. В этом случае говорят, что прямые l1 и l2 при пересечении образуют прямые углы.
Определение. Две прямые называются перпендикулярными (или взаимно перпендикулярными), если они при пересечении образуют прямые углы.
Если прямые а и b (АВ и СD) перпендикулярные, то используется обозначение а 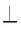
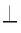
Лучи и отрезки называются перпендикулярными, если они лежат на перпендикулярных прямых.
Отрезок называется перпендикулярным прямой, если он лежит на прямой, перпендикулярной данной прямой.
На рисунке 54, B изображены перпендикулярные прямые а и b, содержащие две стороны квадрата.
Теорема 3. Через каждую точку прямой в плоскости проходит единственная прямая, перпендикулярная данной прямой.
Доказательство.
1. Докажем, что такая прямая существует.
Пусть l — данная прямая, А — произвольная точка прямой l. Пусть AF — один из лучей этой прямой с началом в точке А.
На основании аксиомы откладывания угла отложим от луча AF прямой угол TAF. Тогда прямая b, содержащая луч AT, перпендикулярна прямой l (рис. 54, в).
2. Докажем, что такая прямая единственная.
Допустим, что существует еще одна прямая b1, проходящая через точку А и перпендикулярная прямой l.
Пусть АС — луч этой прямой, лежащий в одной полуплоскости с лучом AT. Каждый из углов FAT и FAC — прямой и отложен от данного луча в одной полуплоскости.
Согласно аксиоме откладывания угла, от данного луча в данную полуплоскость можно отложить только один прямой угол. Следовательно, не может быть другой прямой, проходящей через точку А и перпендикулярной прямой l.
Теорема доказана.
Доказательство от противного
При доказательстве предыдущей теоремы применялся способ, который называется доказательством от противного.
Этот способ доказательства состоит в том, что сначала делают предположение о верности утверждения, противоположного тому, которое необходимо доказать. Затем путем рассуждений, опираясь на аксиомы и доказанные ранее теоремы, приходят к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании делают вывод, что сделанное предположение было неверным, а, следовательно, верно утверждение теоремы.
- Первый признак равенства треугольников
- Перпендикуляр и наклонная в геометрии
- Медианы, высоты и биссектрисы треугольника
- Равнобедренный треугольник и его свойства
- Окружность и круг
- Описанные и вписанные окружности
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
Прямая линия
Прямая линия есть кратчайшее расстояние между двумя точками.
Свойства прямой. a) Положение прямой линии вполне определяется теми двумя точками, между которыми она проведена.
Это свойство зависит от того, что b) между двумя точками можно провести только одну прямую линию, ибо между двумя точками существует только одно кратчайшее расстояние.
Определение прямой линии, вытекающее из непосредственного усмотрения ее свойства, некоторые называют аксиомой. Это понятие о прямой линии называют иногда основным.
В прямой линии нужно отличить ее положение и ее длину.
Прямую линию можно неопределенно продолжать в обе стороны.
Две точки определяют прямую линии не только в тех точках, которые лежат между ними, но и в тех точках, которые получаются, если неопределенно продолжать прямую линию в обе стороны.
c) Две прямые линии пересекаются в одной точке, ибо точка их пересечения находится на конце прямой линии.
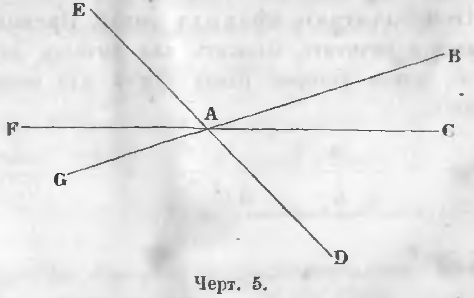
d) Через одну точку можно провести бесчисленное множество прямых линий.
Все линии на чертеже 5 проходят через общую точку A.
e) Если две прямые имеют две общие точки, то они совпадают всеми остальными точками.
f) Расстояние между двумя точками определяется длиной прямой линии, их соединяющей.
Равные прямые. Две прямые линии, имеющие одинаковую длину, называются равными. Линии AB с CD (черт. 6) будут равными линиями.
Равные прямые совпадают при наложении друг на друга.
Сравнение прямых линий
Чтобы сравнить две данные прямые AB и CD по длине (черт. 7) накладывают линию CD на линию AB так, чтобы точка C совпадала с точкой A.
Здесь могут быть три случая:
-
Если точка D упадет в точку E, находящуюся между A и B, линия CD меньше AB.
-
Если точка D упадет в точку B, линия CD равна AB.
-
Если точка D упадет в точку F, находящуюся на продолжении линии AB, линия CD больше AB.
Сложение и вычитание прямых линий. Прямые линии можно складывать и вычитать. Сложить или вычесть линии значит найти линию, длина которой равна сумме или разности длин данных линий.
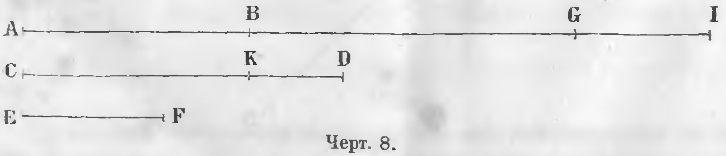
Чтобы сложить прямые линии AB, CD, EF (черт. 8), продолжают линию AB и от точки B откладывают линию BG, равную CD, от точки G линию GI равную EF. Линия AI равна сумме всех этих трех линий.
AI = AB + CD + EF.
Чтобы найти разность линий CD и AB, откладывают на линии CD от точки C линию CK, равную AB, тогда линия KD равна разности линий CD и AB.
KD = CD – AB.
Отношение двух прямых линий
Сравнивая две прямые линии по длине, определяют их взаимное отношение. При этом сравнении имеет значение линия, называемая общей мерой двух линий.
Общая мера двух линий есть такая линия, которая содержится целое число раз в обеих линиях.
При определении взаимного отношения двух прямых линий по длине, могут встретиться два случая:
-
Когда эти линии имеют общую меру.
-
Когда они ее не имеют.
В первом случае они называются соизмеримыми, во втором — несоизмеримыми. В первом случае отношение двух линий выражается каким-нибудь рациональным, т. е. целым или дробным числом; во втором оно не может быть точно выражено ни целым, ни дробным числом.
Если две прямые линии соизмеримы, то находят их общую меру.
Определение общей меры двух линий
Общая мера двух линий большей AB и меньшей CD (черт. 9) не может быть больше линии CD. Удостоверимся сначала, не будет ли меньшая линия CD этой общей мерой.
Для этого накладывают меньшую линию на большую и определяют, сколько раз она уложится в большей. Если она укладывается ровное число раз, например, m раз, тогда отношение двух линий выражается этим целым числом m.
Действительно, тогда
AB = m * CD и AB/CD = m.
Если же она не укладывается ровное число раз, то последовательно накладывают линию CD до тех пор, пока не получится остатка EB меньшего CD.
Положим, линия CD уложилась в AB два раза и получился еще остаток EB. Общая мера линий AB и CD не может быть более остатка EB.
Действительно, из равенства
AB = 2CD + EB
видно, что общая мера линий AB и CD должна содержаться равное число раз в линии EB. Она может или равняться линии EB или быть меньше ее.
Отсюда заключение:
Общая мера двух линий AB и CD должна быть общей мерой меньшей линии и остатка EB.
Отыскивая общую меру CD и EB, поступаем по предыдущему. Откладываем линию EB на линии CD до тех пор, пока не получится остатка FD, меньшего линии EB. Общая мера CD и EB будет по предыдущему заключению общей мерой EB и FD.
Линию FD снова откладываем по линии EB. Пусть линия FD отложится на линии EB ровно два раза, тогда линия FB и будет этой общей мерой.
Связь между линиями выразится рядом равенств:
AB = 2CD + EB
CD = EB + FD
EB = 2FD
откуда
CD = EB + FD = 2FD + FD = 3FD
AB = 2CD + EB = 2 * 3FD + 3FD = 8FD.
Отношение линий AB и CD выразится равенством:
AB/CD = 8FD/3FD = 8/3.
Мы видим, что при нахождении общей меры нужно поступать точно так же, как при нахождении общего наибольшего делителя между целыми числами. Отсюда
Правило нахождения общей меры двух линий. Чтобы найти общую меру, нужно меньшую линию наложить на большую, первый остаток на меньшую, второй остаток на первый, и поступить так до тех пор, пока последний остаток не уложится ровное число раз в предпоследнем.
Чтобы найти отношение двух линий, нужно при помощи общей меры выразить обе линии и потом найти частное этих выражений.
2-й случай: две прямые линии несоизмеримы. Если две линии несоизмеримы, мы никогда не получим такого остатка, который содержался бы в предпоследнем остатке целое число раз. В этом случае определяют отношение прямых линий с каким угодно приближением. Для этого разделив меньшую линию на n равных частей, накладывают это часть CE на большую линию AB (черт. 10). Положим, что эта часть повторяется в большей линии m раз и еще получается остаток FB меньше CE.
Из равенств
AB = mCE + FB
CD = nCE
имеем
Так как n можно увеличивать произвольно, то и отношение длин двух прямых можно выразить с каким угодно приближением.
(См. о несоизмеримости диагонали квадрата с его стороной).
Измерение линий. Измерить линию значит найти ее отношение к другой линии, принятой за единицу. Это отношение называют длиной данной линии. Длина линии всегда выражается в каких-нибудь единицах.
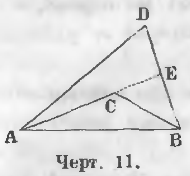
Ломаные линии
Две линии ACB и ADB (черт. 11), соединяющие концы прямой AB, называются ломаными. При этом линия ACB называется внутренней, а линия ADB внешней ломаной линией.
Теорема 1. Внешняя ломаная больше внутренней.
Даны две ломаные линии: внешняя ADB и внутренняя ACB (черт. 11).
Требуется доказать, что ADB больше ACB или
AD + DB > AC + CB.
Доказательство. Продолжим линию AC до пересечения с линией DB в точке E.
Линия ADE как ломаная больше прямой AE.
AD + DE > AC + CE
Ломаная линия CEB больше прямой CB
CE + EB > CB
Сложив эти неравенства, получим:
AD + DE + CE + EB > AC + CE + CB
Вычтя из обоих частей неравенства по CE, получим:
AD + DE + EB > AC + CB
Так как DE + EB = DB, то
AD + DB > AC + CB.
Что и требовалось доказать.
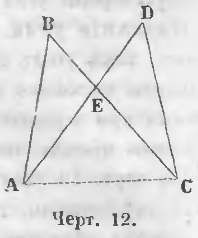
Теорема 2. Сумма пересекающихся частей ломаных больше суммы непересекающихся.
Даны пересекающиеся ломаные ABC и ADC (черт. 12), AD и BC их пересекающиеся части.
Требуется доказать, что
AD + BC > AB + DC.
Доказательство. Из того, что ломаная AEB больше прямой AB и ломаная CED больше прямой DC вытекают неравенства:
AE + BE > AB
ED + EC > DC
Сложив их, находим:
AE + BE + ED + EC > AB + DC
Так как
AE + ED = AD
BE + EC = BC
то
AD + BC > AB + DC
Что и требовалось доказать.
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой (общее уравнение прямой на плоскости и его исследование). Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и его исследование, как осуществлять переходы от общего уравнения к другим типам уравнений прямой (неполного уравнения, полного уравнения). Всю теорию закрепим иллюстрациями и решением практических задач на уравнения.
Общее уравнение прямой: основные сведения
Как найти уравнение прямой? Пусть на плоскости задана прямоугольная система координат Oxy.
Любое уравнение первой степени, имеющее вид Ax+By+C=0, где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид Ax+By+C=0 при некотором наборе значений А, В, С.
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение Ax+By+C=0 определяет на плоскости прямую.
Пусть существует некоторая точка М0(x0, y0), координаты которой отвечают уравнению Ax+By+C=0. Таким образом: Ax0+By0+C=0. Вычтем из левой и правой частей уравнений Ax+By+C=0 левую и правую части уравнения Ax0+By0+C=0, получим новое уравнение, имеющее вид A(x-x0)+B(y-y0)=0. Оно эквивалентно Ax+By+C=0.
Полученное уравнение A(x-x0)+B(y-y0)=0 является необходимым и достаточным условием перпендикулярности векторов n→=(A, B) и M0M→=(x-x0, y-y0). Таким образом, множество точек M(x, y) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n→=(A, B). Можем предположить, что это не так, но тогда бы векторы n→=(A, B) и M0M→=(x-x0, y-y0) не являлись бы перпендикулярными, и равенство A(x-x0)+B(y-y0)=0 не было бы верным.
Следовательно, уравнение A(x-x0)+B(y-y0)=0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение Ax+By+C=0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени Ax+By+C=0.
Зададим в прямоугольной системе координат на плоскости прямую a; точку M0(x0, y0), через которую проходит эта прямая, а также нормальный вектор этой прямой n→=(A, B).
Пусть также существует некоторая точка M(x, y) – плавающая точка прямой. В таком случае, векторы n→=(A, B) и M0M→=(x-x0, y-y0) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n→, M0M→=A(x-x0)+B(y-y0)=0
Перепишем уравнение Ax+By-Ax0-By0=0, определим C: C=-Ax0-By0 и в конечном результате получим уравнение Ax+By+C=0.
Так, без какой-либо помощи онлайн мы смогли доказать и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид Ax+By+C=0 – это общее уравнение прямой на плоскости в прямоугольной системе координат Oxy (уравнение прямой параллельной оси ox).
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой Ax+By+C=0.
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2x+3y-2=0, которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n→= (2, 3). Изобразим заданную прямую линию из уравнения с вектором на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2x+3y-2=0, поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ·Ax+λ·By+λ·C=0, умножив обе части общего уравнения прямой на число λ, не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой Ax+By+C=0, в котором числа А, В, С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А=0, В≠0, С≠0, общее уравнение принимает вид By+C=0. Такое неполное общее уравнение задает в прямоугольной системе координат Oxy прямую, которая параллельна оси Ox, поскольку при любом действительном значении x переменная y примет значение -CB . Иначе говоря, общее уравнение прямой Ax+By+C=0, когда А=0, В≠0, задает геометрическое место точек (x, y), координаты которых равны одному и тому же числу -CB.
- Если А=0, В≠0, С=0, общее уравнение принимает вид y=0. Такое неполное уравнение определяет ось абсцисс Ox.
- Когда А≠0, В=0, С≠0, получаем неполное общее уравнение Ax+С=0, задающее прямую, параллельную оси ординат.
- Пусть А≠0, В=0, С=0, тогда неполное общее уравнение примет вид x=0, и это есть уравнение координатной прямой Oy.
- Наконец, при А≠0, В≠0, С=0, неполное общее уравнение принимает вид Ax+By=0. И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел (0, 0) отвечает равенству Ax+By=0, поскольку А·0+В·0=0.
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 27, -11. Необходимо написать общее уравнение заданной прямой. Попробуем его составить.
Решение
Решение лежит на поверхности. Прямая, параллельная оси ординат, задается уравнением вида Ax+C=0, в котором А≠0. Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения Ax+C=0, т.е. верно равенство:
A·27+C=0
Из него возможно определить C, если придать A какое-то ненулевое значение, к примеру, A=7. В таком случае получим: 7·27+C=0⇔C=-2. Нам известны оба коэффициента A и C, подставим их в уравнение Ax+C=0 и получим требуемое уравнение прямой: 7x-2=0
Ответ: 7x-2=0
На чертеже изображена прямая, необходимо записать ее уравнение. Как будем это находить?
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси Ox и проходит через точку (0, 3).
Прямую, которая будет являться параллельной оси абсцисс, определяет неполное общее уравнение By+С=0. Найдем значения B и C. Координаты точки (0, 3), поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой By+С=0, тогда справедливым является равенство: В·3+С=0. Зададим для В какое-то значение, отличное от нуля. Допустим, В=1, в таком случае из равенства В·3+С=0 можем найти С: С=-3. Используем известные значения В и С, получаем требуемое уравнение прямой: y-3=0.
Ответ: y-3=0.
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М0(x0, y0), тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: Ax0+By0+C=0. Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A(x-x0)+B(y-y0)+C=0, это уравнение эквивалентно исходному общему, проходит через точку М0(x0, y0) и имеет нормальный вектор n→=(A, B).
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М0(-3, 4), через которую проходит прямая, и нормальный вектор этой прямой n→=(1, -2). Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А=1, В=-2, x0=-3, y0=4. Тогда:
A(x-x0)+B(y-y0)=0⇔1·(x-(-3))-2·y(y-4)=0⇔⇔x-2y+22=0
Задачу можно решать иначе. Как она будет решаться? Общее уравнение прямой имеет вид Ax+By+C=0. Заданный нормальный вектор (векторная прямая) позволяет получить значения коэффициентов A и B в уравнении прямой, тогда:
Ax+By+C=0⇔1·x-2·y+C=0⇔x-2·y+C=0
Теперь найдем значение С, используя заданную условием задачи точку М0(-3, 4), через которую проходит прямая. Координаты этой точки отвечают уравнению x-2·y+C=0, т.е. -3 – 2·4+С=0. Отсюда С=11. Требуемое уравнение прямой принимает вид: x – 2·y + 11=0.
Ответ: x – 2·y + 11=0.
Задана прямая 23x-y-12=0 и точка М0, лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна -3. Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М0 как x0 и y0. В исходных данных указано, что x0=-3. Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
23×0-y0-12=0
Определяем y0: 23·(-3)-y0-12=0⇔-52-y0=0⇔y0=-52
Ответ: -52
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида Ax+By+C=0 к каноническому уравнению x-x1ax=y-y1ay.
Если А≠0, тогда переносим слагаемое By в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: Ax+CA=-By.
Это равенство возможно записать как пропорцию: x+CA-B=yA .
В случае, если В≠0, оставляем в левой части общегь уравнения только слагаемое Ax, прочие переносим в правую часть, получаем: Ax=-By-C. Выносим –В за скобки, тогда: Ax=-By+CB.
Перепишем равенство в виде пропорции: x-B=y+CBA .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3y-4=0. Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3y-4=0. Далее действуем по алгоритму: в левой части остаётся слагаемое 0x; а в правой части выносим -3 за скобки; получаем: 0x=-3y-43.
Запишем полученное равенство как пропорцию: x-3=y-430. Так, мы получили уравнение канонического вида.
Ответ: x-3=y-430.
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Перед нами задание. Прямая задана уравнением 2x-5y-1=0. Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2x-5y-1=0⇔2x=5y+1⇔2x=5y+15⇔x5=y+152
Теперь примем обе части полученного канонического уравнения равными λ, тогда:
x5=λy+152=λ⇔x=5·λy=-15+2·λ, λ∈R
Ответ: x=5·λy=-15+2·λ, λ∈R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y=k·x+b, но только тогда, когда В≠0. Для перехода в левой части оставляем слагаемое By, остальные переносятся в правую. Получим: By=-Ax-C. Разделим обе части полученного равенство на B, отличное от нуля: y=-ABx-CB.
Задано общее уравнение прямой: 2x+7y=0. Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2x+7y=0⇔7y-2x⇔y=-27x
Ответ: y=-27x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида xa+yb=1. Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на –С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y:
Ax+By+C=0⇔Ax+By=-C⇔⇔A-Cx+B-Cy=1⇔x-CA+y-CB=1
Необходимо преобразовать общее уравнение прямой x-7y+12=0 в уравнение прямой в отрезках.
Решение
Перенесем 12 в правую часть: x-7y+12=0⇔x-7y=-12.
Разделим на -1/2 обе части равенства: x-7y=-12⇔1-12x-7-12y=1.
Преобразуем далее в необходимый вид: 1-12x-7-12y=1⇔x-12+y114=1.
Ответ: x-12+y114=1.
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
xa+yb⇔1ax+1by-1=0⇔Ax+By+C=0y=kx+b⇔y-kx-b=0⇔Ax+By+C=0
Каноническое уравнение преобразуется к общему по следующей схеме:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax(y-y1)⇔⇔ayx-axy-ayx1+axy1=0⇔Ax+By+C=0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔Ax+By+C=0
Заданы параметрические уравнения прямой x=-1+2·λy=4. Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x=-1+2·λy=4⇔x=-1+2·λy=4+0·λ⇔λ=x+12λ=y-40⇔x+12=y-40
Перейдем от канонического к общему:
x+12=y-40⇔0·(x+1)=2(y-4)⇔y-4=0
Ответ: y-4=0
Задано уравнение прямой в отрезках x3+y12=1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x3+y12=1⇔13x+2y-1=0
Ответ: 13x+2y-1=0.
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A(x-x0)+B(y-y0)=0. Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2x-3y+33=0. Также известна точка M0(4, 1), через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n→=(2, -3): 2x-3y+33=0. Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A(x-x0)+B(y-y0)=0⇔2(x-4)-3(y-1)=0⇔2x-3y-5=0
Ответ: 2x-3y-5=0.
Заданная прямая проходит через начало координат перпендикулярно прямой x-23=y+45. Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x-23=y+45.
Тогда n→=(3, 5). Прямая проходит через начало координат, т.е. через точку О(0, 0). Составим общее уравнение заданной прямой:
A(x-x0)+B(y-y0)=0⇔3(x-0)+5(y-0)=0⇔3x+5y=0
Ответ: 3x+5y=0.
Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.
Здесь будет калькулятор
Уравнение прямой с угловым коэффициентом
y=kx+by=kx+b,
где kk — угловой коэффициент, а bb — свободный коэффициент.
Уравнения данного вида составляются следующим образом по формуле:
y−y0=k(x−x0)y-y_0=k(x-x_0),
где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.
Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.
Решение
Подставляем значения в формулу:
y−y0=k(x−x0)y-y_0=k(x-x_0)
y−2=1⋅(x−1)y-2=1cdot(x-1)
Приводим подобные слагаемые:
y=x+1y=x+1
Ответ
y=x+1y=x+1
Общее уравнение прямой
Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:
y−x−1=0y-x-1=0
Уравнение прямой по двум точкам
Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},
где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.
Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).
Решение
x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}
x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}
x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}
x−4=−y−12x-4=frac{-y-1}{2}
y+1=2⋅(4−x)y+1=2cdot(4-x)
y=8−2x−1y=8-2x-1
y=−2x+7y=-2x+7
Ответ
y=−2x+7y=-2x+7
Уравнение прямой при помощи точки и вектора нормали
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.
Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).
Решение
x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,
x−7+40−5y=0x-7+40-5y=0
x−5y=−40+7x-5y=-40+7
x−5y=−33x-5y=-33
5y=x+335y=x+33
y=x5+335y=frac{x}{5}+frac{33}{5}
Проверка
Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.
8=75+3358=frac{7}{5}+frac{33}{5}
8=88=8 — верно, ответ правильный.
Ответ
y=x5+335y=frac{x}{5}+frac{33}{5}
Прямая в пространстве
Уравнение прямой, заданной в пространстве имеет такой вид:
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.
Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).
Решение
x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Проверка
Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:
1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.
Такой вид уравнения прямой называется каноническим.
Ответ
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}


![Отрезок [AB]](https://spravochnick.ru/assets/files/handbook/images/56/e8/56e842f0a1f35ce72c937dc5f2c62356)




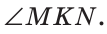
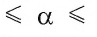 180 существует угол, градусная мера которого равна
180 существует угол, градусная мера которого равна 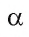 °.
°.