Построение статистического ряда
Для построения
статистического ряда определяют отрезок
числовой оси, содержащий все элементы
выборки xn=(x1,…,xn),
т.е. интервал (xmin,
хmax).
Затем необходимо провести разбиение
элементов выборки на группы (выполнить
процедуру группировки выборки), то есть
интервал (xmin,
хmax)
разбить на полуинтервалы (разряды). Для
этого необходимо разделить точками х1,
х2,…,хq
действительную ось на q
непересекающихся разрядов (хj,
хj+1),
j=1,q,
одинаковой длины.
Количество разрядов
вычисляем по формуле: q=
,q=5-20,
а длину разряда вычисляем по формуле:
l
= r/q.
Причем xmin
= х0,
хmax
= хq.
После этого для
каждого из разрядов находят представителей
разрядов, т.е. устанавливают координаты
средних точек разрядов
:
=
.
Затем находят
число элементов выборки nj
(абсолютная
частота разряда), попадающих в j-ый
разряд. Наконец, вычисляется относительная
частота разряда p*j
:
p*j=nj/n
(j=1,q).
Ряд относительных
частот p*j,
(j=1,q)
называется статистическим рядом.
Статистический
ряд необходим для упорядочивания
информации и строится в виде таблицы.
Статистические оценки закона распределения случайной величины
Построение
статистических оценок функции
распределения
Эмпирической
(статистической) функцией распределения
называют функцию F*(x),
определяющую для каждого значения x
относительную частоту события X<x.
Статистическая
функция распределения F*(x)
рассчитывается по формуле:
F*(x)
=
где
–
число вариантов (значений) вариационного
ряда, расположенных левее текущего
значенияx
включительно,
n
– объем выборки.
Из теоремы Бернулли
следует, что при неограниченном увеличении
n
относительная частота события Х<
х, т.е. F*(xi)
стремится по вероятности к F(x)
этого события, так как
.
Отсюда следует
целесообразность использования
эмпирической функции распределения
выборки для приближенной оценки
теоретической функции распределения
генеральной совокупности. Это
подтверждается тем, что F*(x)
обладает всеми свойствами F(x):
-
значения эмпирической
функции принадлежат отрезку [0,1]; -
F*(x)–
неубывающая функция; -
если х1
– наименьшая варианта, то F*(x)=0
при х <
х1
; -
если хk
– наибольшая варианта, то F*(x)=1
при х >=
хk.
Пример графика
статистической функции распределения
представлен на рис.1.
Рис.1. Статистическая
функция распределения.
Второй оценкой
функции распределения является
кумулятивная ломаная.
При
достаточно больших объемах выборки
измерений (наблюдений) повторение
ступенчатой оценки F*(x)
становится неудобным.
В этом случае,
для построения оценки функции
распределения, удобнее использовать
данные статистического ряда, а именно:
F**(
)
=0
F**(
)
=
F**(
)
=
+
………………….
F**(
)
=
=
где
=1.
Используя эти
формулы, можно построить ломаную F**(x),
проходящую через точки (
),j=
и принять ее в качестве графика оценки
функции распределения. Ее называют
кумулятивной ломаной.
Пример расчетов
приведен в табл.2.
|
Номер |
1 |
2 |
3 |
4 |
5 |
6 |
|
Границы |
[14,01;14.74) |
[14.74;15.58) |
[15.58;16.32) |
[16.32;17.93) |
[17.93;18.71) |
[18.71;19.55] |
|
Относительная |
0.18 |
0.16 |
0.16 |
0.16 |
0.16 |
0.16 |
|
F**(x) |
0.18 |
0.34 |
0.48 |
0.64 |
0.84 |
1 |
Таблица 2
Значения F**(x)
для примера, приведенного в табл. 2,
вычисляются по формуле:
F**(
)
= 0
F**(
)
=
F**(
)
=
+
.
F**(
)
=
+
+
…………………………….
F**(
)
=
+
+…+
= 1
График
кумулятивной ломаной представлен на
рис.2.
Рис.2. Кумулятивная
ломаная
5) Построение
статистических оценок плотности
распределения f(x):
гистограммы f*(x)
и полигона частот f**(x).
Статистической
оценкой (статистическим аналогом)
плотности распределения является
полигон частот и гистограмма.
Гистограммой
называют
ступенчатую фигуру, состоящую из
прямоугольников, основаниями которых
служат интервалы длиною
,
а высота равна отношению
(плотность относительной частоты).
Учитывая свойство
плотности распределения можно записать:
P(xj-1
X<xj
)=
f(
j)*lj
, (
)
,
где lj
– длина j-го
интервала (разряда), f(
j)-
средняя на интервале Ij
плотность распределения f(x),
вычисляемая в точке
j
(средняя точка разряда).
Заменяя P(xj-1
X<xj
)
относительной частотой p*j
статистического
ряда, получим следующее выражение для
приближенного значения f*j
плотности распределения на разряде:
f*j=
p*j/
lj
,
здесь
– относительная частота разряда,
– длина разряда,f*j
– плотность
относительной частоты разряда,
– номер разряда (
).
Таким образом,
гистограмма относительных частот
строится следующим образом: на оси Оx
отложим длины разрядов и на них, как на
основаниях, построим прямоугольники,
имеющие площадь p*j
и высоту равную f*j
(см. рис.3.).
Площадь гистограммы
относительных частот равна сумме всех
относительных частот:
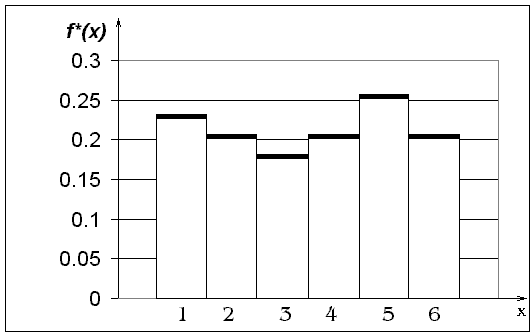
Рис.3. Гистограмма
– оценка плотности распределения,
построенная по относительным частотам.
Сглаженную
гистограмму относительных частот в
виде ломаной линии называют полигоном
относительных частот f**(х).
Полигон относительных частот является
вторым способом оценки f(x).
Она строится по точкам (
,
f*j),
(
)
(см. рис.4).
Рис.4. Полигон
относительных частот
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема:
Элементы математической статистики
Статистика
возникла существенно раньше теории вероятностей. Еще в глубокой древности
проводились переписи населения, велись земельные кадастры. Эти операции были
связаны с наблюдениями и вычислениями. На протяжении многих веков статистика
искала свой математический аппарат и нашла его в теории вероятностей. В
результате возник такой раздел математики, как математическая статистика.
Математическая
статистика – это раздел математики, изучающий методы
сбора, систематизации и обработки результатов наблюдений с целью выявления
статистических закономерностей, т.е. отыскания законов распределения.
Математическая
статистика, как и теория вероятностей, имеет дело с массовыми явлениями.
Отличие математической статистики от теории вероятностей в том, что теория
вероятностей изучает закономерности случайных явлений на основе абстрактного
описания действительности, а математическая статистика оперирует
непосредственно результатами наблюдений над случайными явлениями.
Описательная
статистика
В
практике статистических наблюдений различают два вида наблюдений:
– сплошное
(изучают все объекты совокупности);
– выборочное
(изучается лишь часть объектов совокупности).
Определение:
Генеральной совокупностью называют
всю подлежащую изучению совокупность объектов.
Определение:
Выборочной совокупностью (выборкой)
называют часть объектов, которая отобрана для непосредственного наблюдения из
генеральной совокупности. Обычно выборка составляет 5% – 10% от генеральной
совокупности.
Числа объектов в
генеральной совокупности и выборке называют их объемами. Генеральная
совокупность может иметь как конечный, так и бесконечный объем. На практике всю
генеральную совокупность изучают сравнительно редко, поскольку если
совокупность содержит очень большое число объектов, то провести сплошное
обследование невозможно.
Пример
1:
1. Вся
продукция предприятия есть генеральная совокупность, а отдельные экземпляры,
подвергнутые контролю, составляют выборку.
2. Из
10 000 студентов для контрольной флюорографии отобрано 1000 человек. Объем
генеральной совокупности равен 10 000; объем выборки равен 1000.
Сущность
выборочного метода состоит в том, чтобы по некоторой
части генеральной совокупности выносить суждения об ее свойствах в целом.
Основной
недостаток выборочного метода – ошибки исследования, называемыми ошибками
репрезентативности (представительства).
Требования
к выборке. Чтобы по выборке можно было судить о
генеральной совокупности, она должна быть репрезентативной, т.е. она
должна достаточно хорошо воспроизводить генеральную совокупность. Выборка будет
обладать таким свойством, если каждый объект генеральной совокупности будет
иметь один и тот же шанс быть выбранным, в этом случае выборка является
случайной.
Вариационный
и статистический ряды
Выборка
является труднообозримым множеством. Для дальнейшего изучения выборку
подвергают перегруппировке.
Определение:
Вариационным рядом называется
последовательность всех элементов выборки, расположенных в неубывающем порядке.
Одинаковые элементы повторяются.
Запись
вариационного ряда: 
Ему соответствует
следующая таблица:
|
i |
1 |
2 |
3 |
… |
n |
|
|
|
|
|
… |
|
Элементы
вариационного ряда 
называют его вариантами
или порядковыми статистиками.
Пример
2: Студенты получили следующие баллы по
тесту: 11, 8, 9, 10, 8, 6, 7, 7, 9, 11, 10, 6, 5, 11, 10. Записать
статистический и вариационный ряды.
Р
е ш е н и е :
11,
8, 9, 10, 8, 6, 7, 7, 9, 11, 10, 6, 5, 11, 10 – это статистический ряд.
Расположим
данные в порядке возрастания:
5,
6, 6, 7, 7, 8, 8, 9, 9, 10, 10, 10, 11, 11, 11 – это вариационный ряд.
Представим
данный ряд в виде таблицы (с учетом повторений) и в порядке возрастания
значений признака, получим ранжированный вариационный ряд.
|
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
1 |
2 |
2 |
2 |
2 |
3 |
3 |
Здесь
значение признака
(варианта), 
его частота («вес»
значения признака, количество повторений). Сумма всех частот значений признака
равна объему выборки: 
= 1
+ 2 + 2 + 2 + 2 + 3 + 3 = 15.
Дискретный
статистический ряд
Вариационный
ряд называется дискретным, если любые его варианты отличаются на
конечную постоянную величину, и называется непрерывным (или интервальным),
если его варианты могут отличаться друг от друга на сколь угодно малую
величину.
Определение:
Дискретным статистическим рядом
называется последовательность различных вариант с указанием частот
повторения элементов. При этом вместо абсолютных частот 
можно задавать
распределение относительных частот 
.
.
Дискретный
статистический ряд (выборочное распределение)
можно записать в виде таблицы:
|
|
|
|
… |
|
|
|
|
|
… |
|
Для наглядного
представления выборки часто используют различные графические изображения.
Простейшими графическими изображениями являются полигон и гистограмма
выборки.
Определение:
Ломаная линия на координатной плоскости с вершинами в точках 
называется полигоном частот, а ломаная с вершинами 
полигоном относительных частот.
При
большом объеме выборки более наглядное представление дает гистограмма
выборки. Для построения гистограммы частот выборки промежуток от
наименьшего значения выборки до наибольшего значения разбивается на несколько
частичных промежутков шириной h.
Для каждого частичного промежутка подсчитывают сумму 
частот значений выборки,
попавшей в этот промежуток. Затем на каждом интервале, как на основании,
строится прямоугольник высотой, равной 
.
Пример
3: Дана выборка, состоящая из чисел 1, 3,
1, 2, 3, 5, 1, 3, 1, 2. Составить вариационный и статистический ряды. Построить
полигон относительных частот.
Р
е ш е н и е :
Вариационный
ряд имеет следующий вид: 1, 1, 1, 1, 2, 2, 3, 3, 3, 5.
Объем
выборки 
.
Статистический ряд
приведен в таблице:
|
|
1 |
2 |
3 |
5 |
|
|
4 |
2 |
3 |
1 |
|
|
0,4 |
0,2 |
0,3 |
0,1 |
Полигон
относительных частот имеет вид:
Числовые характеристики выборки
Полигон
относительных частот дает хорошее представление о распределении частот в
выборке. Для анализа статистических данных используются различные
статистические характеристики.
Определение:
Элемент, отвечающий наибольшей частоте по сравнению с соседними элементами
статистического ряда, называется модой
(mod).
Или, проще говоря, мода – это наиболее часто встречающееся значение наблюдаемой
величины.
Определение:
Минимальный и максимальный элементы называются крайними, иначе – экстремальными элементами вариационного
ряда.
Определение:
Разность между максимальным и минимальным элементами называется размахом, или широтой выборки:
Определение:
Выборочным математическим ожиданием (выборочным
средним) называют среднее арифметическое значение выборки:
Если
выборка задана статистическим (ранжированным) рядом, то выборочное среднее
можно найти по формуле:
Определение:
Выборочной дисперсией называют
среднее арифметическое квадратов отклонений значений выборки от выборочного
среднего:
Если
выборка задана статистическим (ранжированным) рядом, то выборочную дисперсию
можно найти по формуле:
Определение:
Медианой (med)
называется значение наблюдаемой величины, приходящееся на середину
вариационного ряда. Если выборка содержит четное число членов, то в качестве медианы
берут среднее арифметическое двух средних членов.
Пример
4: При измерении роста девушек некоторого
института была получена следующая выборка: 179, 160, 155, 183, 155, 153, 167,
186, 163, 155, 157, 175, 170, 166, 160, 173, 182, 167, 171, 169, 179, 165, 156,
179, 158, 171, 175, 173, 165, 171. Сделайте статистический анализ данной
выборки.
Р
е ш е н и е :
Вариационный ряд – 153,
155, 155, 155, 156, 157, 158, 160, 160, 163, 165, 165, 166, 167, 167, 169, 170,
171, 171, 171, 173, 173, 175, 175, 179, 179, 179, 182, 183, 186.
Объем выборки: 
.
Размах выборки: 
.
Медиана: 
, т.к. ряд четный и для
нахождения медианы мы должны взять два числа в середине этого ряда, т.е. числа,
стоящие на 15 и 16 местах, и найти среднее арифметическое.
Мода: 
Ранжированный
вариационный ряд:
|
|
153 |
155 |
156 |
157 |
158 |
160 |
163 |
165 |
166 |
167 |
169 |
170 |
171 |
173 |
175 |
179 |
182 |
183 |
186 |
|
|
1 |
3 |
1 |
1 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
1 |
3 |
2 |
2 |
3 |
1 |
1 |
1 |
Выборочное
распределение:
|
|
153 |
155 |
156 |
157 |
158 |
160 |
163 |
165 |
166 |
167 |
169 |
170 |
171 |
173 |
175 |
179 |
182 |
183 |
186 |
|
|
0,03 |
0,1 |
0,03 |
0,03 |
0,03 |
0,07 |
0,03 |
0,07 |
0,03 |
0,07 |
0,03 |
0,03 |
0,1 |
0,07 |
0,07 |
0,1 |
0,03 |
0,03 |
0,03 |
Полигон
относительных частот:
Среднее значение
выборки:
Выборочная
дисперсия:
Задания:
1. Дана
выборка: 1, 2, 2, 3, 4, 5, 5, 5. Определите моду и медиану. Найдите выборочное
среднее, выборочную дисперсию и постройте полигон.
2. При
подсчете количества листьев у одного из лекарственных растений были получены
следующие данные: 8, 10, 7, 9, 11, 6, 9, 8, 10, 7, 7, 11, 13, 10, 8. Сделайте
статистический анализ этой выборки.
3. В
опыте по измерению заряда электрона были получены следующие значения: 4,758;
4,765; 4,760; 4,758; 4,775; 4,778; 4,765; 4,758; 4,766; 4,765; 4,758; 4,760;
4,772; 4,772; 4,758; 4,775; 4,760; 4,766; 4,775; 4,771; 4,772; 4,766; 4,771;
4,758; 4,773. Сделайте статистический анализ этой выборки.
4. Задан
ранжированный вариационный ряд некоторого испытания. Сделайте статистический
анализ этого ряда.
|
|
0 |
1 |
5 |
7 |
8 |
10 |
13 |
|
|
4 |
6 |
4 |
9 |
11 |
7 |
9 |
5.
Данные о количестве пациентов
кардиологического отделения больницы приведены в таблице. Сделайте
статистический анализ этих данных.
|
62 |
54 |
84 |
59 |
75 |
43 |
49 |
89 |
28 |
49 |
|
40 |
53 |
18 |
18 |
55 |
51 |
26 |
68 |
76 |
65 |
|
43 |
39 |
47 |
65 |
55 |
29 |
33 |
42 |
51 |
95 |
|
85 |
46 |
45 |
42 |
48 |
6 |
73 |
54 |
70 |
56 |
|
69 |
66 |
33 |
100 |
58 |
42 |
89 |
41 |
36 |
72 |
|
54 |
50 |
54 |
45 |
48 |
11 |
62 |
33 |
32 |
61 |
|
36 |
31 |
84 |
61 |
26 |
53 |
64 |
50 |
66 |
63 |
|
77 |
31 |
84 |
61 |
26 |
53 |
64 |
50 |
66 |
63 |
|
9 |
30 |
69 |
60 |
9 |
30 |
4 |
27 |
74 |
62 |
|
19 |
42 |
55 |
79 |
77 |
31 |
92 |
30 |
39 |
96 |
6.
Придумайте свою задачу по теме «Статистические
характеристики» и решите ее. Объем выборки должен быть не менее 30 значений.
ЛАБОРАТОРНАЯ
РАБОТА
Тема:
Обработка статистических данных выборочным методом.
Цель:
Экспериментально составить выборку, определить параметры выборки, и представить
ее графически в виде полигона.
Ход
работы:
1.
Подсчитайте пульс в течении 1 минуты. Из
значений, полученных каждым студентом группы, составьте выборку.
2. Запишите
выборку в виде вариационного ряда.
3. Определите
объем выборки .
4. Определите
размах выборки 
.
5. Определите
медиану 
.
6. Запишите
выборку в виде ранжированного (статистического) ряда.
7. Определите
моду 
.
8. Запишите
выборку в виде выборочного распределения.
9. Постройте
полигон частот выборки.
10. Вычислите
среднее значение выборки.
11. Вычислите
выборочную дисперсию.
12. Сделайте
вывод.
- Главная
- Полезные советы
- Построить интервальный статистический ряд и гистограмму распределения.
Построить интервальный статистический ряд и гистограмму распределения.
Для имеющейся совокупности опытных данных (выборки) требуется:
1) Построить интервальный статистический ряд и гистограмму распределения;
2) Вычислить выборочную среднюю, выборочную дисперсию, выборочное среднеквадратичное отклонение, коэффициент вариации;
3) Выбрать теоретический закон распределения.
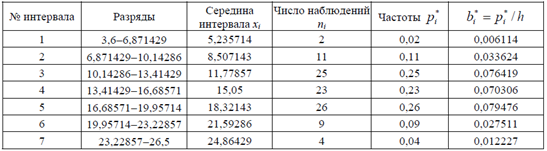
Решение:
Для построения интервального ряда, определим по формуле Старджесса число интервалов: 
Тогда величина интервала равна 
− разность между наибольшим и наименьшим значениями признака.
Отсюда имеем: 
По этим данным составим интервальный статистический ряд:
Выборочное среднее определим по формуле среднего арифметического взвешенного:
Выборочная дисперсия равна:
Выборочное среднеквадратичное отклонение равно квадратному корню из дисперсии: 
Коэффициент вариации равен: 
Полученному статистическому ряду соответствует нормальное распределение. В качестве теоретического закона распределения используем нормальное распределение с математическим ожиданием 15,148 и дисперсией 19,79.
Если испытываете трудности в написании курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена – от 99 рублей.
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Статистическое распределение выборки
Содержание:
- Примеры использования формул и таблиц для решения практических задач
- Статистический интервальный ряд распределения
Предположим случай, когда из генеральной совокупности извлекается некоторая выборка, при этом каждому значению соответствует некоторый параметр, означающий количество раз, когда появлялось данное значение. Здесь $x_1$ было зафиксировано $n_1$ раз, $x_2$ было обнаружено $n_2$$x_k$ выявлено $n_k$. При этом
$sum_{i=1}^{k}n_i=n$
Где n — объём рассматриваемой выборки.
Определение 1
Используется следующая терминология: $x_k$ носят наименование вариантов, а последовательность таких вариантов, зафиксированный по возрастанию именуется вариационным рядом. Количество наблюдений каждого из вариантов носят название частот. При этом частное частот и выборки называют относительными частотами.
Определение 2
Статистическое распределение —это название всего набора вариантов и частот, которые с ними соотносятся. Чаще всего задаётся с помощью специальной таблицы, где представлены частоты, а также интервалы им соответствующие.
| $x_1$ | $x_2$ | … | $x_k$ |
| $n_1$ | $n_2$ | … | $n_k$ |
| $frac{n_1}{n}$ | $frac{n_2}{n}$ | $frac{n_k}{n}$ |
Здесь в первой строке представлены варианты, во второй частоты, в третьеq взяты относительные частоты.
Для определения размера интервала используется следующее выражение:
$d=frac{x_{max}- x_{min}}{1+3,332cdot lg n}$
Здесь $x_{max}$, $x_{min}$ наибольшее и наименьшее значения ряда вариантов, а n характеризуем объём выборки.
Примеры использования формул и таблиц для решения практических задач
Пример 1
В ходе проведения измерений в однородных группах, были определены следующие значения выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74. Необходимо использовать данные значения, что определить ряд распределения частот и ряд распределения относительных частот.
Решение.
1) Составим статистический ряд распределения частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| ni | 2 | 4 | 8 | 2 | 4 |
2) Рассчитаем суммарный размер выборки: n=2+4+8+2+4=20. Определим относительные частоты, для этого используем формулы: ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Теперь зафиксируем в таблице распределение относительных частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| wi | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
Контрольная сумма должна равняться единице: 0,1+0,2+0,4+0,1+0,2=1.
Полигон частот
Название «полигоном частот» применяют для обозначения ломаной линии, каждый отрезок, которой соединяют точки $(х_1,n_1),(х_2,n_2),…,(х_k,n_k)$. Для построения на графике полигона частот по оси абсцисс отмечают варианты $х_2$, при этом на оси ординат отсчитывают– соответствующие частоты $n_i$. Когда полученные точки $(х_i,n_i)$ соединяются с помощью отрезков, то автоматически получают полигон частот.
Статистический интервальный ряд распределения.
Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются, если число различающихся вариант в полученной выборке не слишком большое. Также применение возможно, когда дискретность имеет важное значение для экспериментатора. В тех случаях, когда важный для задачи признак генеральной совокупности Х распределяется непрерывным образом, либо его дискретность нет возможности учесть, то варианты предпочтительнее всего группировать, чтобы получить интервалы.
Статистическое распределение допустимо задавать в том числе в качестве последовательности интервалов и частот, соответствующих этим интервалам. При это за частоту какого-либо интервала принимается сумма всех частот, вошедших в данный интервал.
Особенно следует отметить ,что $h_i-h_{i-1}=h$ при всех i, т.е. группировка проводится с равным шагом h. Также в вопросе группировки можно ориентироваться на ряд полученных опытным путём рекомендацийу, касающихся таких параметров, как а, k и $h_i$:
1. $Rраз_{мах}=X_{max}-X_{min}$
2. $h=R/k$; k-число групп
3.$ kgeq 1+3.321lgn$ (формула Стерджеса)
4. $a=x_{min}, b=x_{max}$
5.$ h=a+h_i, i=0,1…k$
Определённую в ходе решения задачи группировку удобнее всего скомпоновать и перевести в вид специальной таблицы, которая также может именоваться — «статистический интервальный ряд распределения»:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Частоты | n1 | n2 | … | nk-1 | nk |
Таблицу подобного вида можно сделать, поменяв частоты $n_i$ на относительные частоты:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Отн. частоты | w1 | w2 | … | wk-1 | wk |
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример 2
На склад пришла крупная партия деталей. Из них методом случайного отбора взято 50 экземпляров. Рассматривая изделия по одному, особенно интересующему признаку — размеру, определённому с точностью до 1 см, получим следующий вариационный ряд: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Требуется произвести расчёт и определить статистический интервальный ряд распределения.
Решение
Найдём параметры выборки используя сведения из условия задачи.
$k geq1+3,321cdot lg50=1+3.32lg(5cdot10)=1+3.32(lg5+lg10)=6.6$
Получили a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.
| Интервалы группировки | 22-26 | 26-30 | 30-34 | 34-38 | 38-42 | 42-46 | 46-50 |
| Частоты | 1 | 4 | 10 | 18 | 9 | 5 | 3 |
| Отн. частоты | 0.02 | 0.08 | 0.2 | 0.36 | 0.18 | 0.1 | 0.06 |
Десятичные логарифмы от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| lnn≈ | 0 | 0.3 | 0.48 | 0.6 | 0.7 | 0.78 | 0.85 | 0.9 | 0.95 | 1 |
Не получается написать работу самому?
Доверь это кандидату наук!
Итак, установление закономерностей, которым подчинены массовые случайные явления основано на изучении статистических данных — результатах наблюдений. Математическая статистика решает две главные задачи: указать способы сбора и группировки (если данных очень много) статистических сведений (результатов наблюдений) и разработать методы анализа собранных статистических данных в зависимости от целей исследования.
Пусть требуется изучить совокупность однородных объектов относительно качественного или количественного признака, характеризующего эти объекты.
Пример 14.1.1
Некоторое предприятие выпускает партию одинаковых деталей. Если контролируют детали по размеру – это количественный признак.
Можно производить этот контроль сплошным обследованием, то есть измерять каждый из объектов совокупности. Но на практике сплошное обследование применяется редко:
а) из-за очень большого числа объектов;
б) из-за того, что иногда обследование заключается в физическом уничтожении, например, проверяем взрываемость гранат или проверяем на крепость произведенную посуду и т.д.
В таких случаях производится случайный отбор ограниченного (небольшого) числа объектов, которые и подвергают изучению.
Выборочной совокупностью (выборкой) называется совокупность случайно отобранных однородных объектов.
Генеральной совокупностью называется совокупность всех однородных объектов, из которых производится выборка.
Объемом совокупности (выборочной или генеральной) называется число объектов этой совокупности.
При наборе выборки можно поступать двояко: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В связи с этим выборки подразделяются на повторные и бесповторные.
Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Это требование коротко формулируется так: выборка должна быть репрезентативной (представительной).
Способы отбора выборки:
1. Отбор, не требующий расчленения генеральной совокупности на части:
а) простой случайный бесповторный;
б) простой случайный повторный.
2. Отбор, при котором генеральная совокупность разбивается на части (если объем генеральной совокупности слишком большой):
а) типический отбор. Объекты отбираются не из всей генеральной совокупности, а из ее «типичных» частей. Например, цех из тридцати станков производит одну и ту же деталь. Тогда отбор делается по одной или по две детали с каждого станка в случайные моменты времени;
б) механический отбор. Например, если нужно выбрать 5% деталей, то выбирают не случайно, а каждую двадцатую деталь;
в) серийный отбор. Объекты выбирают не по одному, а сериями.
Итак, пусть из генеральной совокупности значений некоторого количественного признака произведена выборка объема N:
.
Таблица вида
Таблица 14.1.1
| № | 1 | 2 | 3 | … | N |
 |
 |
 |
 |
… |  |
называется простым статистическим рядом, являющимся первичной формой представления статистического материала.
Из данных табл. 14.1.1 находят 
и 
, соответственно наименьшее и наибольшее значения выборки. Затем данные табл. 14.1.1 называемые вариантами, располагают в порядке возрастания. Тогда выборка , записанная в порядке возрастания, называется вариационным рядом.
Размах выборки – это длина основного интервала 
, в который попадают все значения выборки. Вычисляется размах выборки следующим образом: 
. Затем по формуле
, (14.1.1)
где 
— целая часть числа 
, определяется число 
. Данное число задает количество подынтервалов (классов), на которые разбиваем основной интервал. Длины h подынтервалов и их границы 
вычисляются по формулам
, (14.1.2)
; 
;…; 
; … ; 
. (14.1.3)
Далее находятся частоты 
и относительные частоты 
попадания значений выборки 
в 
-й подынтервал. Причем для частот должно выполняться равенство 
, а для относительных частот соответственно 
.
Результаты проведенных расчетов сводятся в таблицы:
Таблица 14.1.2
|
 |
 |
… |  |
 |
 |
 |
… |  |
Таблица 14.1.3
|
|
|
… | |
 |
 |
 |
… |  |
Далее находятся середины подынтервалов:
; 
; … ; 
и после этого составляется еще одна таблица (табл. 14.1.4), которая называется статистическим рядом распределения. Статистический ряд распределения является оценкой теоретического ряда распределения и сходится к нему по вероятности. Поскольку ряд распределения является одной из форм задания закона распределения дискретной случайной величины, то мы получили эмпирический закон распределения исследуемой дискретной случайной величины.
Таблица 14.1.4
|
 |
 |
… |  |
|
|
|
… | |
Сгруппированные данные табл. 14.1.4 несут в себе меньше информации, чем выборочные, так как в них теряется информация о порядке следования выборочных значений. При группировке также фактически происходит округление наблюдаемых значений выборки внутри -го класса (подынтервала) до значения 
, что приводит к потере информации о распределении исследуемой случайной величины внутри каждого класса. Это распределение в дальнейшем предполагается равномерным. Преимуществом же сгруппированных данных является их компактность и большая наглядность.
В целях визуального изучения полученных в табл. 14.1.2, 14.1.3, 14.1.4 данных пользуются различными способами их графического изображения. К ним относятся гистограмма и полигон.
Для построения гистограммы относительных частот используются данные табл. 14.1.3. В декартовой системе координат на оси 
откладываются границы подынтервалов. По оси 
откладываются величины 
(плотности вероятностей) 
.
Гистограммой относительных частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные подынтервалы длины 
, а высоты равны числам 
(плотности вероятностей). Аналогичным образом, по данным табл. 1.2 строится гистограмма частот.
Для построения полигона относительных частот используются данные табл. 1.4. В декартовой системе координат на оси находятся и , то есть изображаются границы основного интервала. Затем наносятся значения середин подынтервалов 
. По оси откладываются значения, соответствующие относительным частотам 
.
Полигоном относительных частот называется ломаная, отрезки которой соединяют точки 
; 
; … ; 
. Полигон относительных частот есть визуальное представление эмпирического закона распределения выборки.
Любая функция выборки 
называется статистикой. Статистика является случайной величиной, так как на различных реализациях выборки она получает различные наблюдаемые значения. Статистиками являются: частоты 
, границы классов 
и их середины , размах. Статистический ряд распределения также является статистикой. Из определения статистики следует, что любая функция от статистик также является статистикой, поэтому статистикой является любая функция от сгруппированных данных (табл. 14.1.4).
Статистики служат для оценки любых характеристик изучаемой случайной величины: вероятностей случайных событий, связанных с изучаемой величиной, ее числовых характеристик, параметров закона распределения и так далее. Изучение статистик на основе теории вероятностей есть теоретическое ядро математической статистики.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
