Муниципальное
автономное общеобразовательное учреждение
Лицей
№ 1
Городского
округа город Стерлитамак
Республики
Башкортостан
Исследовательская
работа
Стомахион
Выполнили: Ишембетова
Карина и
Трофимова
Екатерина
ученицы 6 класса
Руководитель Сологуб
О.В.
учитель математики
Стерлитамак
2017
Содержание
Введение
1. Немного истории
2. Практическая работа
3. Наши эксперименты
4. Заключение
5. Приложение
6. Список литературы
Введение
Головоломки считаются
одними из самых старейших игр на земле. При решении головоломок необходимо
проявлять такие качества как смекалка, сообразительность, внимательность. Очень
часто при решении головоломок нужна хорошая зрительная память. Головоломка
— непростая задача, для решения которой, как правило, требуется
сообразительность, а не специальные знания высокого уровня. К головоломкам
можно отнести кроссворды, шарады, ребусы, пазлы. Головоломные задачи можно
задавать при помощи кубиков, спичек, монет. Головоломки есть простые, которые
можно сделать самим из картона или палочек, а есть сложные в изготовлении, но
которые можно приобрести в магазинах, такие как – танграм, пентамино,
стомахион.
28 октября 1998 года
Греция упустила возможность приобрести на аукционе в Нью-Йорке Палимпсест
Архимеда: его купил за 2.000.000 долларов неизвестный коллекционер….
Большое значение имеет
тот факт, что только в Палимпсесте содержится трактат «Стомахион» – древнейший
труд, посвященный комбинаторике, жизненно важному разделу информатики.
Считается, что Архимед пытался выяснить, сколькими способами можно
рекомбинировать 14 сегментов, при этом создав идеальный квадрат. Полученный им
ответ – 17.152 комбинаций.
Наряду с трудами Архимеда
в Палимпсесте был найден скрытый комментарий по поводу «Категорий» Аристотеля,
а также тексты Гиперида – афинского оратора «Золотого века».
При доставке палимпсеста
в SSRL, на первой странице было обнаружено и имя писца, удалившего рукопись
Архимеда – это был Иоаннис Миронас, закончивший написание молитв на древнейшем
пергаменте 14 апреля 1229 года в Иерусалиме….
Таким образом, мы поставили себе цель:
изучить историю происхождения игры Стомахион, как в нее играть, какие
существуют варианты игры.
Познакомиться:
с правилами игры,
видами схем,
основами построения схем
1.
Немного истории
Две тысячи двести лет
назад великий древнегреческий математик Архимед написал трактат под названием
“Стомахион” (Stomachion). В отличие от других текстов, принадлежащих
перу Архимеда, содержание этого трактата и даже смысл самого названия в течение
столетий были покрыты мраком. Историки математики из Стэнфорда, разбирая записи
на древнем пергаменте, который был подчищен и использован вторично в более
поздние времена монахами (это так называемый палимпсест), а затем, почти
необратимо разрушен сыростью почвы, заявили, что способны все-таки пролить
некоторый свет на тайну содержания этого трактата. В процессе изучения древнего
палимпсеста открылось столько удивительного, что самое время кричать
“Эврика! “, подобно Архимеду, когда ему, согласно древней легенде, в
ванне пришла в голову гениальная идея, как определить точный состав золотой
царской короны. Доктор Ревил Нетз (Reviel Netz) считает, что этот трактат был
посвящен, ни много ни мало, как комбинаторике, то есть науке, о которой, как
считалось ранее, древнегреческие ученые ничего еще в те времена не знали.
Основной целью комбинаторики является определение, сколькими путями может быть
решена та или иная задача. И обнаружение числа путей, которыми может быть
решена проблема, изложенная в “Стомахионе”, оказалось столь
непростым, что доктор Нетз был вынужден попросить проделать это группу из
четырех экспертов по комбинаторике. На решение задачи современными средствами
потребовалось шесть недель. Доктор Нетз признает, что их результаты не могут
быть доказаны с абсолютной уверенностью, однако заявляет, что представил эту
работу вниманию собрания многих известных специалистов в Принстонском
университете, и они согласились с его интерпретацией.
Среди всех работ Архимеда
“Стомахион” в наименьшей степени привлекал внимание историков,
поскольку его содержимое считалось либо незначительным, либо непонятным. За
прошедшие тысячелетия сохранился только крошечный фрагмент введения, а
поскольку название, казалось, совпадало с названием детского желудочного
заболевания, то это автоматически лишало текст в глазах многих ученых всякого
интереса. Фактически смысл рукописи был просто неверно истолкован, считает
Нетз. Архимед на самом деле пробовал установить, сколькими путями 14 полос,
имеющих неправильную форму, могли быть соединены вместе так, чтобы в результате
получился квадрат. Ответ – 17 152 – потребовал тщательного и систематического
подсчета всех возможностей. “Это было непросто”, – говорит доктор
Перси Диаконис (Persi Diaconis), статистик из Стэнфорда, который работал над
этой проблемой вместе со своей коллегой и женой доктором Сьюзен Холмс (Susan
Holmes), а также со специалистами по комбинаторике доктором Рональдом Грэмом
(Ronald Graham) и доктором Фан Чанг (Fan Chung) из Калифорнийского университета
в Сан-Диего. Независимо от них ученый – компьютерщик доктор Уильям
Х. Катлер (William H. Cutler) из Чикаго написал соответствующую
программу, которая подтвердила, что ответ математиков верен. Возможно,
столь же замечательной, как известие о том, что Архимед знал комбинаторику,
является история самой рукописи, которая датируется 975 годом и написана
по-гречески на пергаменте.
Это один из трех наборов
копий работ Архимеда, которые были доступны в Средневековье. (Остальные
потеряны, и ни один из них не содержал “Стомахиона”.) “В случае
с Архимедом, как и с другими античными авторами, мы не имеем оригинальных
работ, – говорит доктор Нетз. – Мы знакомы лишь с копиями копий.” В
тринадцатом столетии христианские монахи, нуждаясь в пергаменте для своих
молитвенников, разорвали эту рукопись, отмыли страницы от прежнего текста и
покрыли их религиозными письменами. После столетий использования в своем новом
качестве этот молитвенник оказался в монастыре в Константинополе. Датский
ученый Йохан Людвиг Хейберг (Johan Ludvig Heiberg, был писатель с таким именем (14.12.1791 –
25.8.1860), возможно, здесь какая-то неточность…) нашел его в
1906 году в библиотеке Церкви Святого Погребения в Стамбуле. Он заметил слабые
следы, оставшиеся от математического трактата. Используя лупу, Хейберг
транскрибировал то, что смог, и сфотографировал в общей сложности две трети
страниц.
Однако вскоре
документ исчез, потерянный наряду с другими драгоценными рукописями в ходе
споров между греками и турками. Вновь о нем заговорили в 1970-х годах. Тогда он
оказался в руках некого французского семейства, что купило его в Стамбуле в начале
20-х годов и хранило документ в течение пяти десятилетий перед попыткой
продать. В результате возник скандал (вряд ли французы имели право
распоряжаться артефактом), к тому же рукопись выглядела ужасно. Она была
испорчена почвой, так как ее попросту зарыли, чтобы сохранить. В 1998 году
анонимный миллиардер выкупил рукопись за 2 миллиона долларов и предоставил ее
Художественному музею в Балтиморе, где она в настоящее время и хранится. Слабые
следы старых записей читаются только с помощью ультрафиолетового освещения, да
и то приходится проводить дополнительную обработку изображений с помощью
компьютера, убирая “шум”. Отчасти этой работе помогают и старые
фотографии, сделанные еще Хейбергом. Во всей этой истории, правда, остается
неясным вопрос о том, решил ли сам Архимед поставленную им самим задачу.
“Я уверен, что он решил ее, иначе, не стал бы заявлять об этом, – говорит
доктор Нетз. – Однако я не знаю, решил ли он ее правильно”.
Древние греки занимались
геометрией, не только измеряя земельные участки и расстояния до кораблей в
море. Они любили геометрические игры. Одна из них называлась «СТОМАХИОН». В
этой игре надо было из 14 частей квадрата складывать различные фигуры.
Создателем ее считали Архимеда. В 1899 г. Швейцарский историк Генрих Зютер
обнаружил в книгохранилищах Берлина и Кембриджа арабскую рукопись “Книга
Архимеда о разбиении фигуры стомахиона на 14 частей, находящихся в рациональных
отношениях”. Позже датский историк математики Гейберг подтвердил, что
создателем игры является Архимед.
2.
Практическое применение

состоит из 14 частей. Выразительны фигуры бегущего человека, сидящей собаки,
двугорбого верблюда. Эта игра сложнее танграма.
Принципы игры.
Сущность игр состоит в
том, чтобы создать на плоскости силуэты предметов по образцу или по замыслу.
Игры на первый взгляд кажутся разными, но их объединяет общность цели, способов
действия и результата.
Игры предлагаются от простого к сложному.
Все игры результативны:
получается плоскостное силуэтное изображение предмета. Оно условно, схематично,
но образ легко угадывается по характерным признакам предметов, строению,
соотношению частей, форме. Из любого набора можно составить изображения
разнообразной конфигурации, узоры, геом.фигуры.
Все собираемые фигуры должны
иметь равную площадь, т.к. собираются из одинаковых элементов. Отсюда следует
что:
1.
В
каждую собираемую фигуру должны войти непременно все 14
элементов.
2.
При
составлении фигуры элементы не должны налегать друг на друга, т.е.
располагаться только в одной плоскости.
3.
Элементы
фигур должны примыкать один к другому
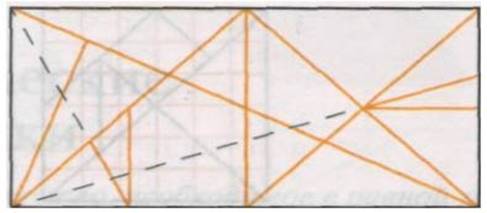
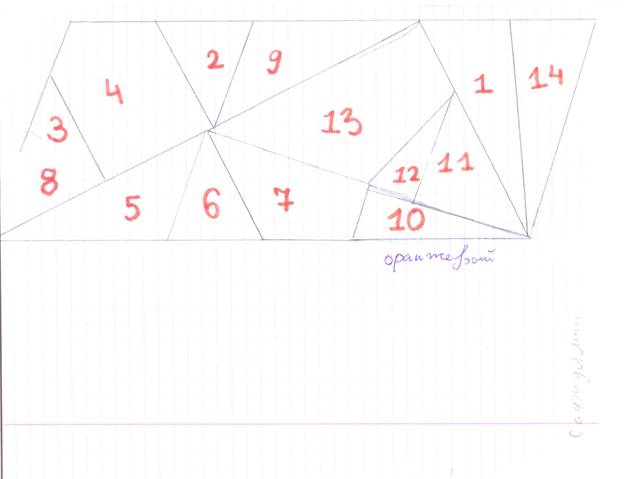
Разрежь стомахион по
указанным линиям попробуй сложить из его частей фигуры, указанные в Приложении
Игра
“Стомахион” требует большего терпения. Ведь она намного сложнее игры
“Танграм”, недаром слово “стомахион” переводится как
“приводящая в ярость”.
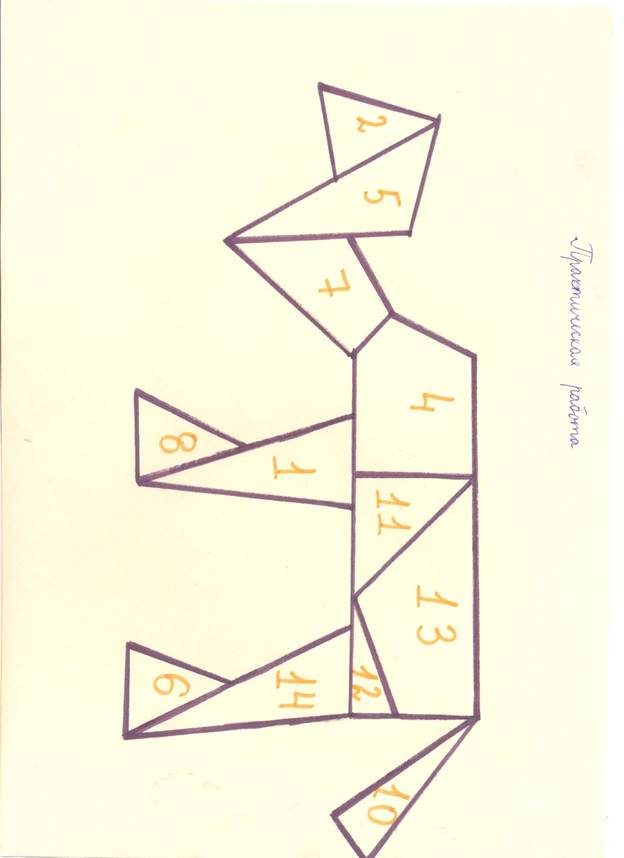
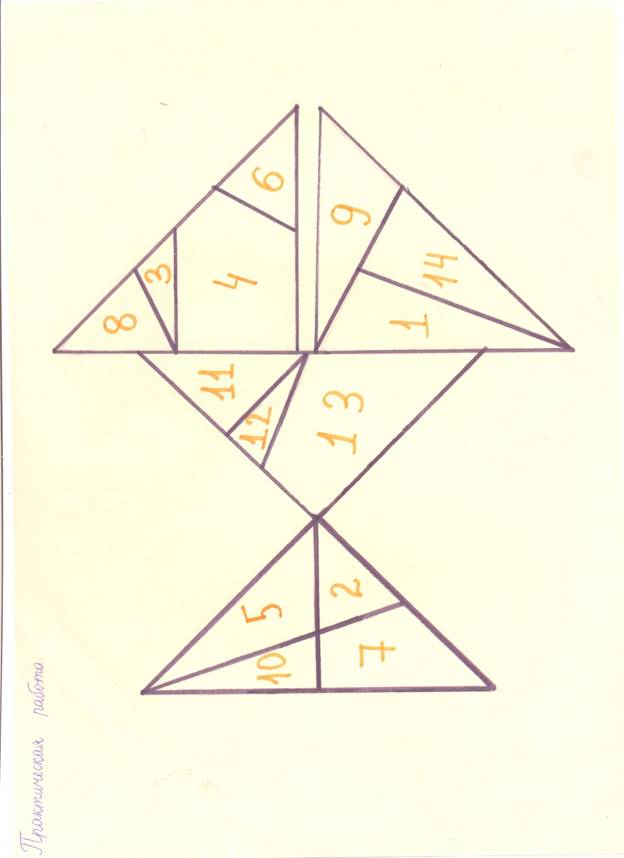
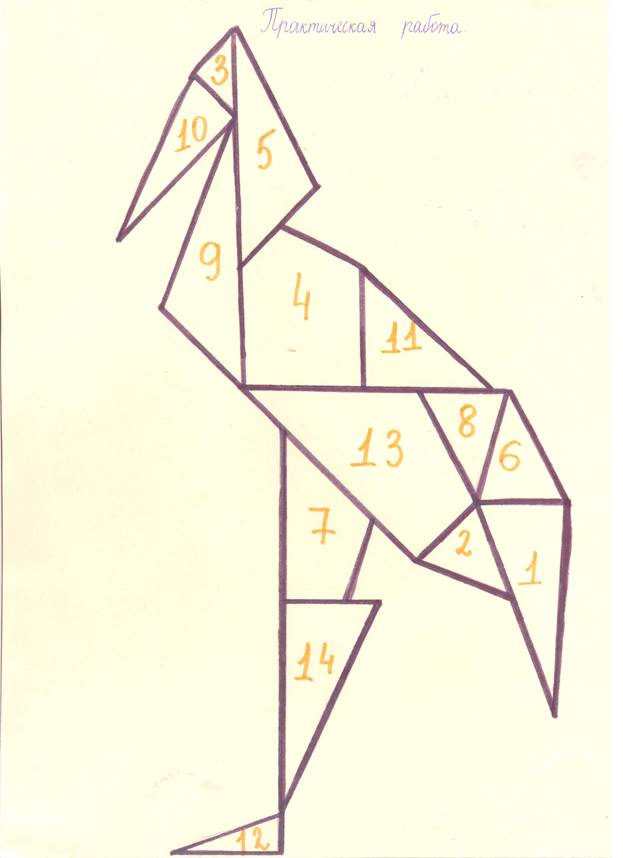
В ходе практической
работы по построению фигур мы обнаружили некоторые закономерности. Например,
если посмотреть на схему, то можно увидеть 4 прямоугольных треугольника. Все
фигуры складываются из одного набора, значит их площади равны, т.е. все фигуры
равновелики. Если стороны исходного прямоугольника целочисленные, то и площадь
каждой части фигуры – тоже целое число. Чтобы это проверить, мы познакомились с
формулой Пика. Об этом в следующей части нашей работы.
4.
Наши
эксперименты.
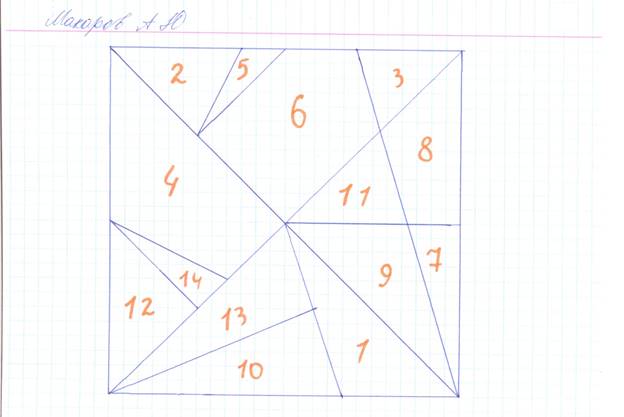
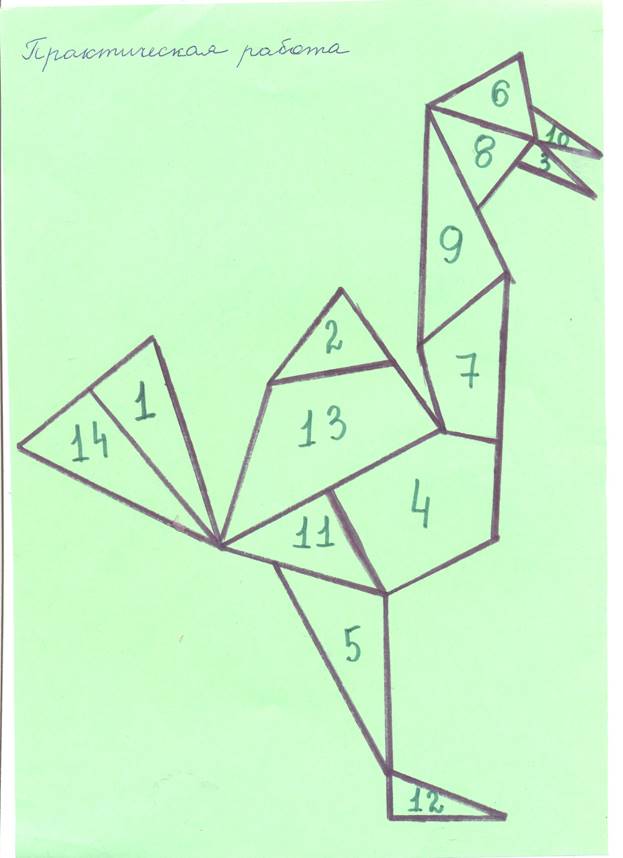
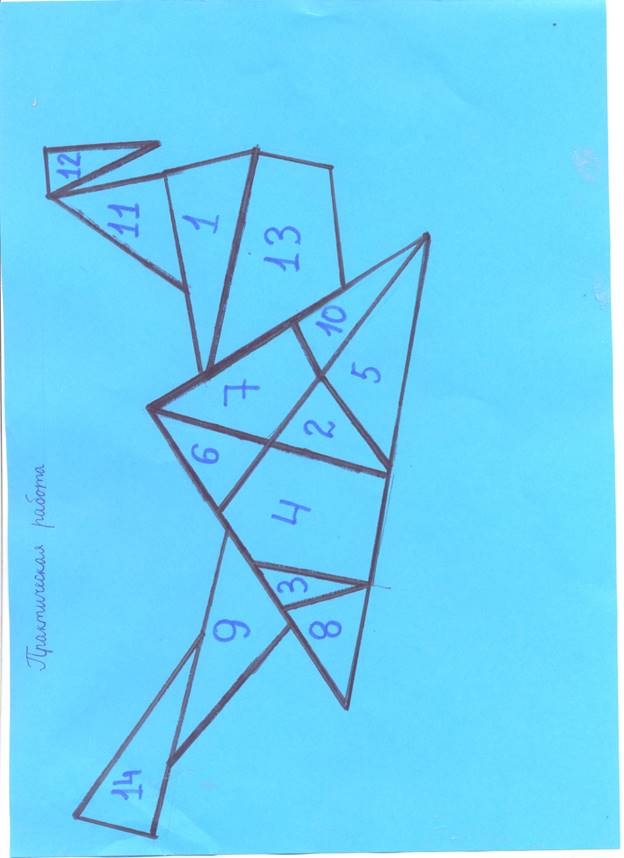
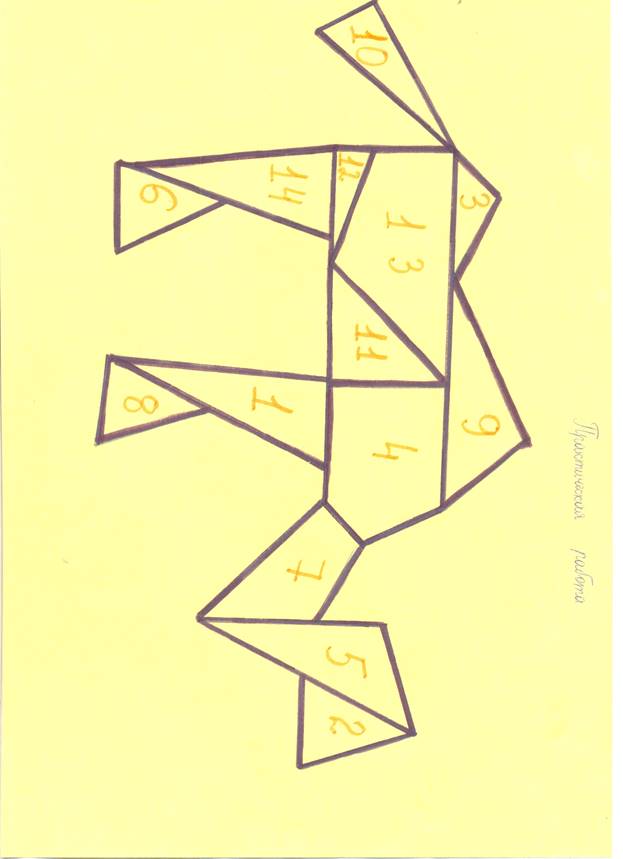
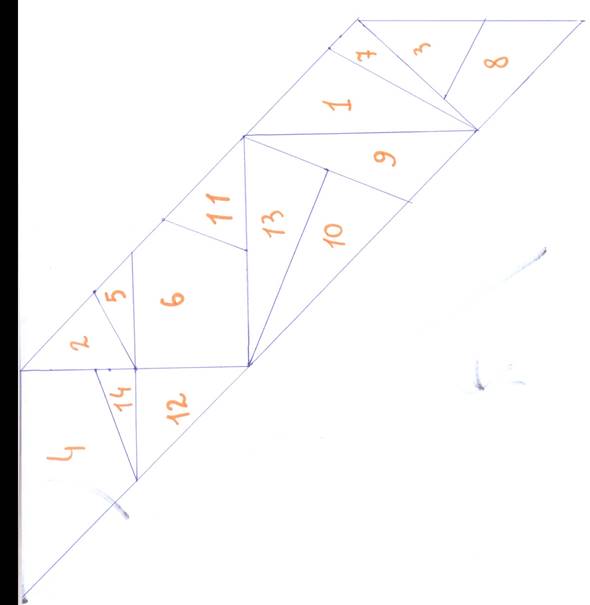
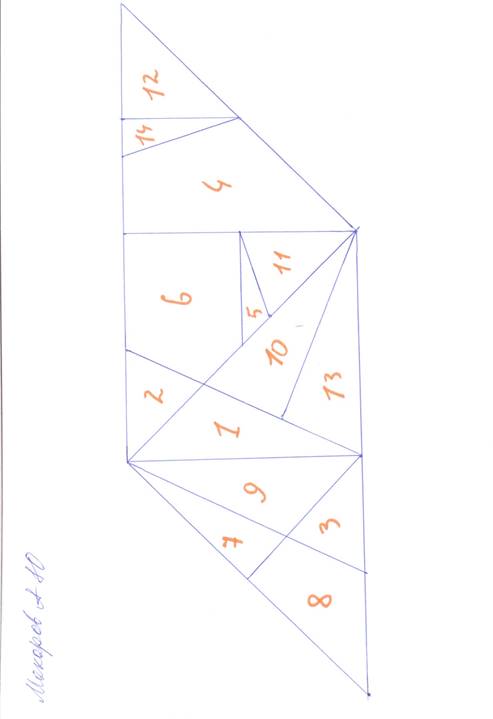
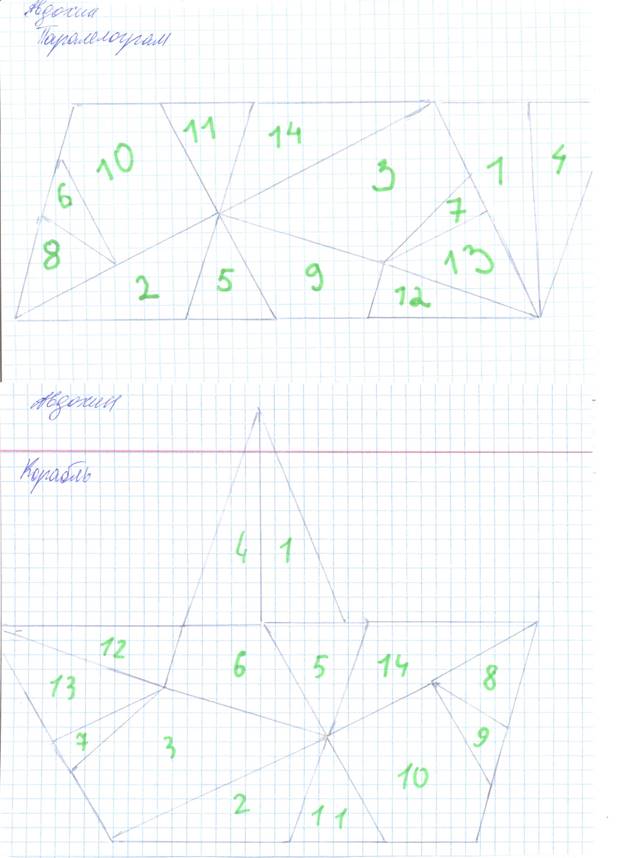
В ходе практической работы мы провели
эксперимент: сможем ли сами собрать фигуры из 14 частей. Что получилось –
смотрите сами.
5. Заключение
Две тысячи двести лет
назад великий древнегреческий математик Архимед написал трактат под названием
“Стомахион”. В отличие от других текстов, принадлежащих перу
Архимеда, содержание этого трактата и даже смысл самого названия в течение
столетий были покрыты мраком. В ходе изучения правил игры, знакомства с
историей игры мы узнали о палимпсестах, выяснили, что комбинаторика – один из
древних разделов математики и, самое главное: нас увлек процесс создания фигур.
Мы, 6-ники, научились
вычислять площади фигур, не зная основных формул, с помощью формулы Пика. Но и
самое главное: наша работа имеет продолжение – некоторым нашим одноклассникам
понравился процесс построения различных фигур. Что из этого получится, в
следующей нашей работе.
5. Приложения
Стомахион
схема
Схемы
фигур
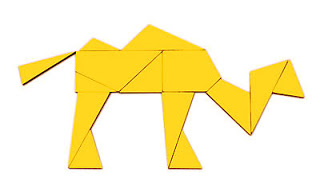
Схема
«верблюд»
Древняя
рукопись
6. Список
используемой литературы
1. Гарднер
М. Математические головоломки и развлечения. – М.: Оникс, 1994.
2. Кордемский
Б.А., «Математическая смекалка», «Манускрипт», Санкт-Петербург, 1994.
3. Кордемский
Б.А., Русалев Н.В. «Удивительный квадрат», Москва, 1994, «Столетие»;
4. Перельман
Я.И., «Занимательная геометрия», издательство «АСТ», Москва 2003.
5.
И.Ф.
Шарыгин, Л.Н. Ерганжиева: «Наглядная геометрия, 5-6 класс».
Г. К. Муравин, О. В. Муравина: «Математика, 5 класс».
Л. Кэрролл: «Алиса в стране чудес».
Скачано с www.znanio.ru
Муниципальное автономное общеобразовательное учреждение
Содержание Введение 1. Немного истории 2
Введение Головоломки считаются одними из самых старейших игр на земле
Таким образом, мы поставили себе цель : изучить историю происхождения игры
Немного истории Две тысячи двести лет назад великий древнегреческий математик
Среди всех работ Архимеда “Стомахион” в наименьшей степени привлекал внимание историков, поскольку его содержимое считалось либо незначительным, либо непонятным
Рональдом Грэмом (Ronald Graham) и доктором
Используя лупу, Хейберг транскрибировал то, что смог, и сфотографировал в общей сложности две трети страниц
Одна из них называлась «СТОМАХИОН»
Практическое применение Игра состоит из 14 частей
Разрежь стомахион по указанным линиям попробуй сложить из его частей фигуры, указанные в
Исследовательская работа “Стомахион”
Исследовательская работа “Стомахион”
Исследовательская работа “Стомахион”
Исследовательская работа “Стомахион”
Исследовательская работа “Стомахион”
Исследовательская работа “Стомахион”
Наши эксперименты. В ходе практической работы мы провели эксперимент: сможем ли сами собрать фигуры из 14 частей
Исследовательская работа “Стомахион”
Исследовательская работа “Стомахион”
Исследовательская работа “Стомахион”
Исследовательская работа “Стомахион”
Заключение Две тысячи двести лет назад великий древнегреческий математик
Приложения Стомахион схема
Схемы фигур
Схема «верблюд» Древняя рукопись
Список используемой литературы 1
Для решения головоломок нам понадобится не только знание
геометрии, но и хорошее воображение. Хорошее воображение – это качество,
которое необходимо в равной мере и математику, и поэту. Великий французский
просветитель Вольтер сказал: «В голове у Архимеда было гораздо больше
воображения, чем в голове у Гомера».
Давайте выполним задание. Выясним, на что пойдёт больше
краски: на окрашивание квадрата или необычного кольца, которые изображены на
рисунке.
Решение.
На окрашивание квадрата пойдёт столько же краски, сколько и на
окрашивание кольца.
Среди геометрических головоломок встречается множество
занимательных задач на разрезание квадрата.
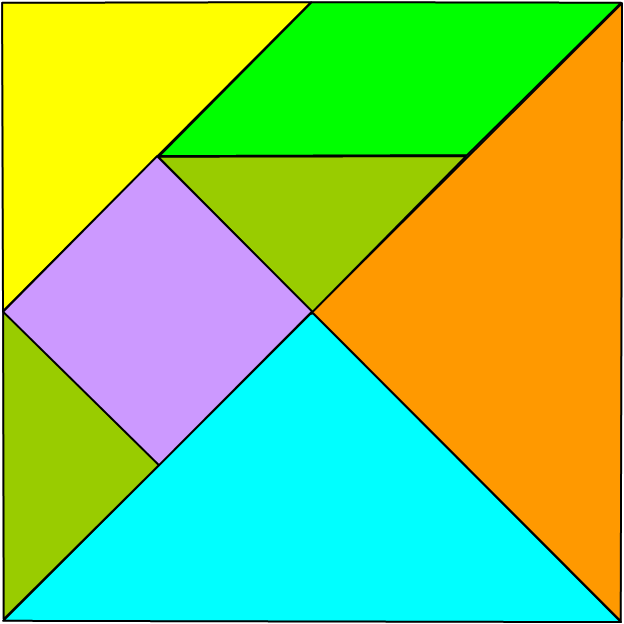
Возьмём квадрат размером клеток.
Разрежем его на 7 частей вот таким образом…
Получилось 2 больших треугольника, 2 маленьких и 1 средний, а
также 2 четырёхугольника, один из которых – квадрат.
Это популярная китайская головоломка танграм. Каждый из 7
элементов называют таном.
В Китае головоломку называют «чи чао ту», что означает «умственная
головоломка из семи частей». Доказательством тому, что головоломку
действительно изобрели в Китае, служит первая известная книга о танграме
«Собрание фигур из семи частей». Название «танграм» возникло в Европе, скорее
всего, от слова «тань» (что означает «китаец») и корня «грамма» (в переводе с
греческого означает «буква»).
Головоломку вы можете изготовить самостоятельно. Для этого
переведите на плотную бумагу квадрат, разделённый на семь частей, и разрежьте
его.
Суть игры заключается в конструировании на плоскости из семи
элементов различных более сложных фигур, которые обычно задаются в виде силуэта
или внешнего контура.
В каждую собираемую фигуру должны войти все 7 элементов танграма.
При составлении фигуры элементы не должны накладываться друг на друга. Также
элементы фигуры должны примыкать один к другому.
Отметим, что удобнее начинать складывать фигуру с самого большого
треугольника.
Используя все 7 элементов танграма, составьте фигурки, которые
изображены на рисунке. Также вы можете попробовать придумать свою фигурку,
используя все 7 частей головоломки.
В танграме среди его 7 частей уже есть треугольники разных
размеров, но из его частей можно ещё складывать различные треугольники.
Сложим треугольник, используя 4 части танграма. Возьмём 1 большой
треугольник, 2 маленьких треугольника и квадрат.
Теперь возьмём 1 большой треугольник, 1 средний треугольник и 2
маленьких треугольника и сложим из этих фигур такой же треугольник.
Мы можем составить треугольник из 2 частей, а также 3 частей, из 5
частей, из 7 частей.
А вот из 6 частей танграма составить треугольник нельзя.
Очевидно, что из всех семи фигур танграма составляется квадрат.
Также квадрат мы можем составить из 2 фигур, 3 фигур, 4 фигур.
Прямоугольник можно составить, например, из 2 маленьких
треугольников и четырёхугольника или с помощью 2 маленьких треугольников и
квадрата.
Также можно составить прямоугольник из 5 частей танграма или из
всех 7 частей.
А ещё из частей этой головоломки можно составить, например,
пятиугольник.
Выполним задание. Составьте каждую картинку, изображённую
на рисунке, из 7 частей танграма.
Решение.
Популярность танграма привела к созданию других подобных
головоломок. Так, например, возьмём квадрат размером клеток и разделим его на 4 равные части вот таким образом…
Из этих 4 равных фигур мы можем выложить, например, квадрат с
квадратным отверстием, прямоугольник с квадратным отверстием или вот такие
четырёхугольники.
Сейчас познакомимся с ещё одной известной игрой, которая
называется стомахион.
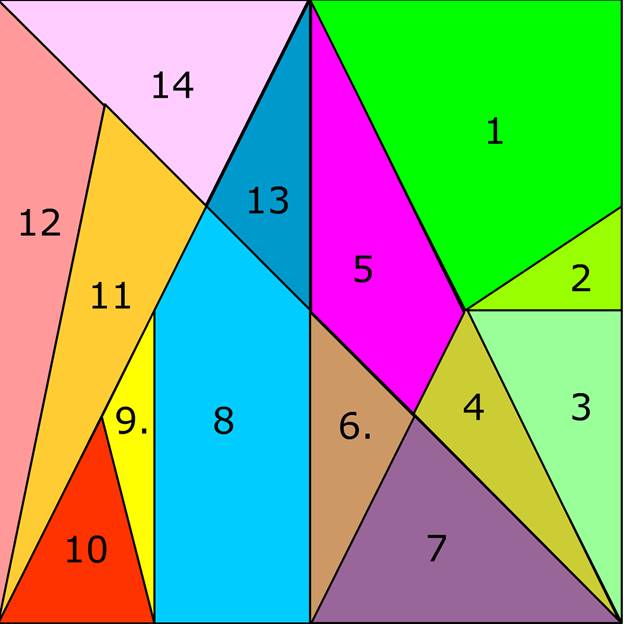
Возьмём прямоугольник, одна сторона которого в 2 раза больше
другой, и разделим его на 14 частей – геометрических фигур (1 пятиугольник, 2
четырёхугольника и 11 треугольников). Может показаться, что прямоугольник разбит
на части случайным образом, но на самом деле это не так.
Этой известной игре уже более 2000 лет. Её создателем считали
Архимеда. В 1899 году швейцарский историк Генрих Зутер обнаружил в
книгохранилищах Берлина и Кембриджа арабскую рукопись «Книга Архимеда о
разбиении стомахиона на 14 частей, находившихся в рациональных отношениях». Позже
датский математик Гейберг подтвердит, что создателем игры является Архимед.
Из элементов игры можно составлять различные фигуры – силуэты
животных, геометрические фигуры и так далее.
Давайте выполним задание. Составьте картинку, изображённую
на рисунке, из четырнадцати элементов стомахиона.
На рисунке изображена фигура, которая напоминает бегущего человека.
Игра стомахион требует большого терпения, ведь она намного сложнее
игры танграм. Недаром слово «стомахион» переводится как «приводящая в ярость».
Познакомимся ещё с одной головоломкой, которая называется «Колумбово
яйцо». В этой головоломке так же, как и в рассмотренных выше, необходимо
создавать фигуры из элементов, которые получаются из овала. Для изготовления
игры берут за основу овал (например, размером см) и разрезают его на десять частей вот таким образом…
В результате получается 4 треугольника (2 больших и 2 маленьких), 2
фигуры, похожие на четырёхугольник, одна из сторон которого округлой формы, 4
фигуры (большие и маленькие), которые имеют сходство с треугольником, но с
одной закруглённой стороной.
В «Колумбово яйцо» можно играть, составляя из частей фигурки
всевозможных предметов, животных, птиц. При этом элементы игры должны
соединяться таким образом, чтобы они не перекрывали друг друга. В составленной
фигуре должны использоваться все 10 элементов головоломки.
Выполним задание. Составьте картинку, изображённую на
рисунке, из 10 элементов игры «Колумбово яйцо».
Фигура, изображённая на рисунке, напоминает зайчика.
Интересно, что элементы геометрических головоломок участвуют в
жизни современного человека. Так, танграм во всех его проявлениях можно
встретить, например, в дизайне одежды, а также в архитектуре. Танграм часто
можно встретить в дизайне мебели.
Стомахион
Один из способов сложения стомахиона.
Стомахион, остомахион (др.-греч. Ὀστομάχιον, лат. loculus Archimedius) — древнегреческий математический трактат, приписываемый Архимеду. Это сочинение дошло до нашего времени в сокращённом арабском переводе и единственной греческой копии, обнаруженной при исследовании палимпсеста Архимеда. Содержание трактата посвящёно анализу одноимённой игры, головоломки наподобие танграма.
История
Арабский текст был обнаружен в 1899 году швейцарским учёным Генрихом Зутером, однако ещё крупнейший специалист первой половины XX века по научному наследию Архимеда Э. Дейкстерхёйс (1892—1965) не мог ничего определённого сказать о содержании этого трактата[1].
К моменту обнаружения текста трактата в палимпсесте об игре стомахион было известно, что в ней требовалось сложить квадрат из 14 элементов. Арабская рукопись, обнаруженная Зутером, добавляла к этому знанию информацию об устройстве стомахиона[2]. Об этой игре также упоминали античные авторы — Викторин, Цезий Басс[en], Эннодий и Лукреций.
Перевод
Первый параграф «Стомахиона» был переведён первым исследователем палимпсеста, Й. Л. Гейбергом. Из этого текста следовало, что Архимед, путём измерения углов, пытался определять пригодность различных сочетаний фигур для решения задачи[3]. На основе сведений от античных авторов, Гейберг понял текст в том смысле, что Архимед рассматривал возможность построения разнообразных не непрерывных фигур.
Из этого следовало, что трактат был посвящён малоинтересному рассмотрению бесконечного множества таких фигур[4]. После прочтения рукописи стало понятно, что предметом рассмотрения Архимеда в его трактате было определение количества различных комбинаций, с помощью которых можно было бы собрать квадрат.
Результат 17 152 был получен в декабре 2003 года путём компьютерного перебора всех вариантов[5].
Примечания
- ↑ Netz, Noel, 2007, p. 235.
- ↑ Netz, Noel, 2007, p. 237.
- ↑ Netz, Noel, 2007, p. 239.
- ↑ Netz, Noel, 2007, p. 241.
- ↑ Netz, Noel, 2007, pp. 257-260.
Литература
- Netz R., Noel W. The Archimedes Code. — Weidenfeld & Nicolson, 2007. — 313 p. — ISBN 0–306–81580–X.
Ссылки
- Борисов М. Загадочная рукопись свидетельствует о том, что Архимед знал комбинаторику. Грани.ру (25 декабря 2003). Проверено 13 декабря 2013.
На Викискладе есть медиафайлы по теме Стомахион
Вы любите играть?
- Значимость и незаменимость игры в нашей жизни давно уже доказана многими психологами, учеными и самой жизнью. Мы играем с самого детства, учимся общаться в процессе игры, строить отношения.
Собраться всей семьей или с друзьями, поболтать о разном, угостить всех чем-нибудь вкусненьким, сыграть несколько увлекательных партий в настольную игру – все это то, что придает нашей жизни особый колорит.
Сегодня увлечение настольными играми принимает тотальный характер. Ведь современные настольные игры – это не только «бродилки», но и стратегические, экономические, детективные, логические игры.
В мире существует уже до 10 тысяч настольных игр разной тематики. Конечно, за всеми новшествами не угнаться, а некоторые игры слишком дорого стоят. Но ведь игру можно сделать и своими руками
Вот несколько игр.
Танграм
Игры-головоломки, на воссоздание из геометрических фигур образных изображений используются для совершенствования зрительного восприятия, и анализа, зрительной памяти, комбинаторики. Наборы фигур представляют собой части разрезанной определенным образом фигуры: квадрата, прямоугольника, круга или овала. Они интересны детям. Детей увлекал результат – составить увиденное на образце или задуманное.
Успешность освоения игры у детей зависит от сенсорного развития детей. Дети называли геометрические фигуры, их свойства, их отличительные признаки, свободно перемещать фигуры. У детей развивается умение анализировать изображения, выделять геометрические формы, видоизменять фигуры путем разрезания и составлять их из частей.
Существуют различные игры- головоломки, на воссоздание из геометрических фигур плоскостных изображений предметов, животных, птиц, домов, кораблей такие как: «Танграм», «Пифагор», «Сфинкс», «Волшебный круг», «Колумбово яйцо», «Листик», «Вьетнамская игра», «Пентамино».
Но мы сейчас рассмотрим только одну из них – “Танграм”.
Появление этой китайской головоломки связано с красивой легендой. Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по летам. Одно беспокоило старого императора Мальчику доставляло большое удовольствие целый день забавляться игрушками. Император призвал к себе трех мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали “Ши-Чао-Тю” – квадрат, разрезаннный на семь частей.
Говорят, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, «упражняя свое терпение и находчивость»
Суть игры заключается в том, чтобы на плоскости из семи частей квадрата создавать самые разнообразные фигуры, силуэты предметов по образцу или замыслу. В коммерческих наборах обычно прилагаются карточки с заданиями.
1 вариант: Самый простой. Если ребенок маленький предложите ему составить фигуру путём наложения элементов на образец разделенными на составные части.
2 вариант: Если с первым разобрались ,то можно составлять фигуры по примеру, то есть картинка перед вами а элементы составляете уже смотря на фигуры разделённую на части.
3 вариант: Для детей постарше, можно оставлять в фигуре только контуры.
4 вариант: Собственно творческие задания – самому придумать и сложить фигуру.
Малыши тоже могут приобщаться к головоломке. Для них можно придумать совсем простенькие задания. Например, сложить из двух треугольников или из двух прямоугольников – квадратики, из треугольников – большой треугольник или параллелограмм. Таким методом можно изучить основные геометрические фигуры.
Сделать танграм можно самому. Это очень просто. Вам понадобятся шаблон головоломки. Распечатайте Танграм или нарисуйте сами по образцу. Можно использовать разноцветные элементы, если ребёнок маленький – заодно вспомните цвета, да и интереснее работать – играть с красочным
материалом.
При решении головоломки требуется соблюдать два правила: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны перекрываться друг другом. Взяв на вооружение математическую науку – комбинаторику, было получено более 5000 возможных вариантов сложенных фигурок.
Примеры сборки :
“ПИФАГОР”
Головоломка Пифагор очень похожая на старый добрый Танграм. Головоломка имеет форму квадрата, разрезанного на 7 частей, комбинируя которые, можно создать огромное количество геометрических фигур, силуэтов животных, людей, разных предметов и т.п. Все детали разного размера, в этом и заключается сложность, поэтому сложить фигуру из них достаточно сложно.
В инструкции к головоломке предлагаются 15 разных заданий. Головоломку Пифагор можно использовать на занятиях по математике, дома или в школе, ведь она отлично способствует развитию воображения, логики, внимания, пространственного мышления, математических и творческих способностей. Вы можете сделать из картона или вырезать из пластика головоломку Пифагор и Вашей семье гарантированы положительные эмоции и хорошее нестроение.
ВОЛШЕБНЫЙ КВАДРАТ
Геометрическая головоломка Волшебный квадрат относится ко второму уровню сложности и подходит для детей в возрасте от 4 лет. Занимаясь с головоломкой, ребенок познакомится с простыми геометрическими фигурами: треугольником, трапецией, квадратом.
Головоломка “Монгольская игра”
Разновидность геометрической головоломки, на подобии “Танграма” или “Квадрата Пифагора”.
Головоломка представляет собой квадрат разрезанный на 11 частей: 2 квадрата, один большой прямоугольник, 4 маленьких прямоугольника, 4 треугольника. Лучше всего изготовить такую головоломку из двустороннего картона или пластика.
Суть игры – собирать фигурки из данных элементов по принципу мозаики.
Как можно играть:
Составлять геометрические фигуры по образцу. В интернете можно найти готовые задания с ответами,, а можно придумать задания для своего ребенка и самим.
Для того, чтобы нарисовать фигуры Вам потребуется лист в клетку. Можно взять обычный лист из школьной бумаги. Элементы из которых состоит “Монгольская игра” очень просты, и вам не составит большого труда составить из них композиции.
Вот, для примера, несколько фигур, составленных их элементов головоломки.
Если ребенок маленький, то можно составлять фигуры по примеру, то есть фигурам, разделенными на составные части. Для детей постарше, можно оставлять в фигуре только контуры.
Малыши тоже могут приобщаться к головоломке. Для них можно придумать совсем простенькие задания. Например, сложить из двух треугольников или из двух прямоугольников – квадратики, из треугольников – большой треугольник или параллелограмм. Таким методом можно изучить основные геометрические фигуры.
Головоломка “СФИНКС”
Головоломка «Сфинкс» состоит из разнообразных геометрических фигур: из
4 треугольников и 3 четырехугольников с разным соотношением сторон. Из
элементов можно собрать силуэты птиц, человека, животных, развивая
наблюдательность и геометрическое воображение.
Инструкция содержит
схемы для построения более двух десятков фигур:
Игры – головоломки развивают пространственное воображение, комбинаторные способности, сообразительность, смекалку, находчивость. Простые в понимании, но достаточно трудные в решении, головоломки находятся на тонкой грани, соединяющей увлекательную игру и интеллектуальное развитие.
Головоломки от Алексея Шамшина
И ещё одна
Головоломка Архимеда СТОМАХИОН
Предлагаемая головоломка Архимедова игра — уникальный геометрический конструктор, в который играли еще в глубокой древности. Ее иное название “Стомахион”.
Элементы игры получаются путем произвольного деления прямоугольника на 14 частей. Из получившихся деталей конструируют на плоскости разнообразные предметные силуэты, например, сидящей собаки, бегущего человека, разнообразных цветов, птиц. Можно сложить и многофигурные композиции. Знакомить ребенка с игрой необходимо постепенно.
Поупражняйте малыша в различении геометрических фигур. Можно предложить ребенку сосчитать стороны, углы, сгруппировать фигуры по форме, размеру, назвать их. Затем попробуйте конструировать простейшие изображения. Для облегчения головоломки Архимедова игра, предлагается сначала выкладывать фигуры по прилагаемым схемам.
Головоломка “ЛИСТИК”
Геометрическая головоломка-мозаика Листик разработана для детей в возрасте от 4 лет Фигура, напоминающая лист сирени. Этот лист сирени выложен из других фигур: треугольников, квадратов, трапеций.
Работа с головоломкой развивает глазомер ребенка, восприятие им формы, зрительно-моторную координацию, пространственное мышление и воображение. Способствует развитию произвольности (умения играть по правилам и выполнять инструкции), познавательной активности, мелкой моторики, воображения, сформированности сенсорных эталонов цвета, величины и формы, комбинаторных способностей, абстрактного мышления.
“Волшебный круг”
Круг разрезается на 10 частей. Правила игры те же, что и в других подобных играх: использовать для составления силуэта все 10 частей, не накладывая одну не другую. Разрезанный круг должен быть окрашен одинаково, с двух сторон.
ВЬЕТНАМСКАЯ ИГРА
В состав “Вьетнамской игры” входит разделенный на семь частей круг и рамка, в которую укладываются элементы. Все детали головоломки имеют обтекаемую форму, некоторые из них одинаковы по размеру. Предложите малышу сконструировать из замысловатых деталей силуэт какого-нибудь животного или птицы. Сначала можно задействовать не все элементы, затем постепенно усложнять задания.
Можно конструировать по схемам, а можно выдумывать свои сюжетные композиции.
Конструируя простые образные фигуры, дети учатся восприятию формы, способности выделять, фигуру из фона, выделению основных признаков объекта. Головоломка развивает глазомер, аналитико-синтетические функции, воображение (репродуктивное и творческое), зрительно-моторную координацию, умение работать по правилам. Игра предназначена для детей от 4 лет
КОЛУМБОВО ЯЙЦО
Существует рассказ – может быть, и
вымышленный. Открыватель Америки Колумб был приглашен к всемогущему кардиналу
Мендозе. За столом, по просьбе гостей, он начал рассказывать, как именно был им
открыт Новый Свет (который, впрочем, он считал Индией). Кто-то из присутствующих,
человек ограниченный, но самоуверенный, пожав плечами, сказал: «Так просто
всё?»
Колумб взглянул на
него и протянул ему лежавшее на блюде куриное яйцо: «Сделайте так, чтобы оно
стояло на своем носке». Разумеется, попытки установить яйцо успехом не
увенчались. «Это немыслимо…» – сказал обескураженный собеседник Колумба. «Это
очень просто!» – с усмешкой ответил мореплаватель и, разбив о стол носок яйца,
без труда заставил его стоять.
Выражение
«колумбово яйцо» – стало воплощением остроумного и неожиданного выхода из
затруднения, синонимом простого разрешения трудных вопросов.
Знакомимся с увлекательной головоломкой Колумбово яйцо, которая отлично скрасит время в дороге, ожиданиt в поликлинике и конечно же, разовьет логику и мышление ребенка. Принцип игры прост. Разрезаем по линиям фигурку яйца на мелкие детали. Задача ребенка – собрать фигурку по образцу. Но иногда можно пофантазировать и придумать свои варианты, разглядеть в фигуре знакомый образ.
Вот фигуры с заданиями
Пентамино
Известная логическая игра-головоломка. Именно эта игра вдохновила Алексея Пажитнова на создание популярной компьютерной игры тетриса.
Пентамино – очень популярная логическая игра и головоломка одновременно. Элементы в игре – плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов. Всего существуют 12 элементов пентамино, обозначаемых латинскими буквами, форму которых они напоминают
Можно изготовить пентамино из кубиков, но тогда Вам нужно будет склеить и обклеить цветной пленкой 60 кубиков – трудновато. Предлагаем сделать элементы их плотного картона.
- Рисуем каждый элемент на твердом картоне, вырезаем, проверяем, чтобы элемент входил в элемент “U”. Подрезаем , если надо лишнее. Мы рисовали детали из квадратиков 2,5х2,5 см.
- Обводим готовый картонный элемент на сложенной вдвое цветной бумаге и вырезаем сразу две цветные детали. Лучше цветные детали делать меньше, чем картонные, и приклеиваются лучше, и углы поровнее будут.
- Клеим клеем-карандашом цветную бумагу с двух сторон картонки.
- Находим коробочку для хранения деталей, куда потом будем складывать также схемы и задания к игре.
Сложи прямоугольник.
Самая распространённая задача о пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20.
Существует ровно 2339 различных укладок пентамино в прямоугольник 6×10, а вот вариантов прямоугольника 3х20 всего 2.
Один из двух способов складывания прямоугольника 3х20
Честно скажу, пыталась весь вечер сложить – не получилось, поэтому ребенку такую задачу лучше не предлагать.
Детям лучше тренироваться на маленьких прямоугольниках из нескольких деталей.
Вот нарисовали варианты складывания прямоугольников из трех деталей.
Сложи фигуру
Их элементов можно складывать различные фигуры, симметричные узоры, буква алфавита, цифры.
Для маленьких детей, лучше фигуры складывать по образцу, как мозаику.
Фигурки можно распечатать или перерисовать на листочек в клеточку

Ответы
ГЕКСАМИНО
Гексамино — это развивающая геометрическая головоломка-мозаика. На поле головоломки из отдельных деталей собрана причудливая геометрическая фигура. Все детали отличаются друг от друга по форме. Головоломка имеет четвертый уровень сложности и предназначена для детей в возрасте от 6 лет.
ГЕКСАТРИОН
ТЕТРИС
Классический Тетрис – случайные фигурки падают сверху, в игре игрок может переворачивать фигурки, двигать их горизонтально и ускорять движение вниз. Фигурка двигается пока не соприкоснется с другой фигуркой или не упадет на самый низ.
Если в игре заполняется ряд, то ряд исчезает и все что выше этого ряда опускается на одну клетку вниз. Игра постепенно наращивает темп. Если одновременно фигурки заполняют 4 ряда – это Тетрис, от этого и происходит название игры. В игре игрок получает очки за каждую фигурку и за каждый исчезнувший ряд. Игра Тетрис заканчивается когда верхняя фигурка касается верхней границы экрана.
Одна из самых классических игр, игра Тетрис (Tetris) обладает воистину магической притязательностью, сколько в неё не играешь, а хочется всё больше и больше.
В игру Тетрис (Tetris) смогут играть не только взрослые, но и маленькие исследователи этого загадочного мира, игра тетрис всегда выручит и взбодрит скучными зимними вечерами. Итак, правила в игре такие же классические как и сама игра, складываем фигурки, так чтобы получилась одна сплошная линия.
Тетрис – это одна из первых электронных игр, которая появилась еще тогда, когда ни у кого не было домашних компьютеров.
Это самая современная и красочная версия тетриса. Дизайн и управление тут на высоте, кроме того добавлены некоторые интересные фишки. Цель игры – расставить падающие сверху фигурки таким образом, чтобы они заняли всё пространство по горизонтали, в этом случае они испарятся и дадут вам игровые очки.
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Содержание
-
1.
Проект “Потомки Стомахиона Архимеда” 11 класс -
2.
Из разных видов головоломок хотелось рассмотреть именно -
3.
Цель:Ознакомление с этими головоломкамиЗадачи: Узнать больше об -
4.
Игра стомахион была известна еще до нашей -
5.
Сделаем игру стомахион: возьмем прямоугольник, одна сторона -
6.
Первое ее изображение (1780) обнаружено -
7.
Сделаем несколько фигурЛошадькошкаДом -
8.
Игра пентаминоЭта игра была придумана в 50-ых -
9.
Игра яйцо Колумба -
10.
Из этих фигур можно сделать заповедник -
11.
Давайте проиллюстрируем с детства известную нам сказку « Курочка ряба».Жили-были дед да баба. -
12.
Была у них курочка ряба. -
13.
Снесла курочка яичко.Яичко не простое, золотое. -
14.
Дед бил, бил – не разбил. -
15.
Баба била, била – не разбила. -
16.
Мышка бежала, хвостиком махнула. Яичко упало и разбилось. -
17.
Дед и баба плачут. Курочка кудахчет: «Не -
18.
Заключение Стомахион, танграм, пентамино, яйцо Колумба -
19.
Литература: Шарыгин И. Ф., Ерганжиева Л. Н. -
20.
Скачать презентанцию
Из разных видов головоломок хотелось рассмотреть именно «стомахион», «танграм», «пентамино», «яйцо Колумба», так как это игры: заставляющие думать, предоставляющие возможность проверить и развить свои способности, способствуют их самоутверждению, развивают настойчивость, стремление
Слайды и текст этой презентации
Слайд 1
Потомки Стомахиона Архимеда
1
Выполнила ученица 11 класса Мишарина Ксения Владимировна
Руководитель Иванова
Нина Николаевна
учитель математики МОУ «СОШ»
с. Большелуг Корткеросский район
Республика
Коми

Слайд 2Из разных видов головоломок хотелось рассмотреть именно «стомахион», «танграм», «пентамино»,
«яйцо Колумба», так как это игры:
заставляющие думать,
предоставляющие
возможность проверить и развить свои способности, способствуют их самоутверждению,
развивают настойчивость, стремление к успеху и различные мотивационные качества,
в таких играх совершенствуется мышление, включая действия по планированию, прогнозированию, взвешиванию шансов на успех, выбору альтернатив.

Слайд 3Цель:
Ознакомление с этими головоломками
Задачи:
Узнать больше об играх: стомахион, танграм,
пентамино, яйцо Колумба
Составить из них несколько фигур
Совместить эти игры на практической работе
Введение:

Слайд 4Игра стомахион была известна еще до нашей эры. Создателем ее
считали Архимеда. В переводе из древнегреческого стомaxион означает то, что
вызывает злость. Прямоугольник, длины сторон которого относятся, как 1:2, нужно разрезать на 14 частей. Тогда оказывается, что из них можно составить силуэты разных животных, предметов, сооружений и т.д. Испытав свою сообразительность в этой игре, вы убедитесь, что название целиком оправдано. Игра воспитывает изобретательность, тренирует зрение, умение видеть геометрические формы в окружающих предметах.
Игра стомахион

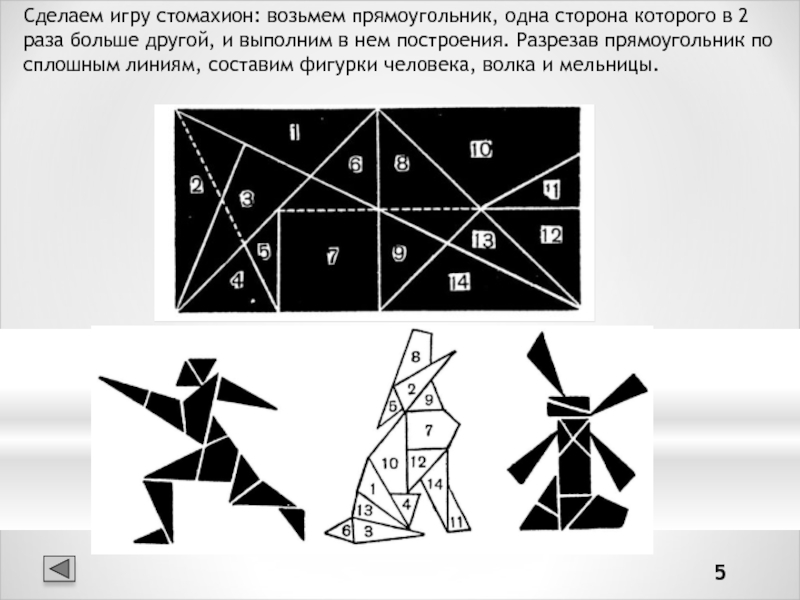
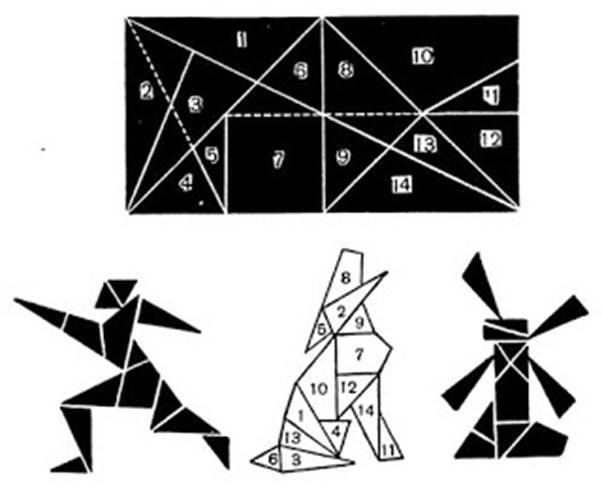
Слайд 5Сделаем игру стомахион: возьмем прямоугольник, одна сторона которого в 2
раза больше другой, и выполним в нем построения. Разрезав прямоугольник
по сплошным линиям, составим фигурки человека, волка и мельницы.
Слайд 6 Первое ее изображение (1780) обнаружено на ксилографии японского
художника Утомаро, где две девушки складывают фигурки. Название “Танграмм” возникло
в Европе. Вероятнее всего, от слова “тань” (что означает “китаец”) и корня “грамма” (в переводе с греческого “буква”). На первых порах ею пользовались не для развлечения, а для обучения геометрии.
Суть игры заключается в том, чтобы на плоскости из семи частей квадрата создавать самые разнообразные фигуры, силуэты предметов по образцу или замыслу.
Игра танграм

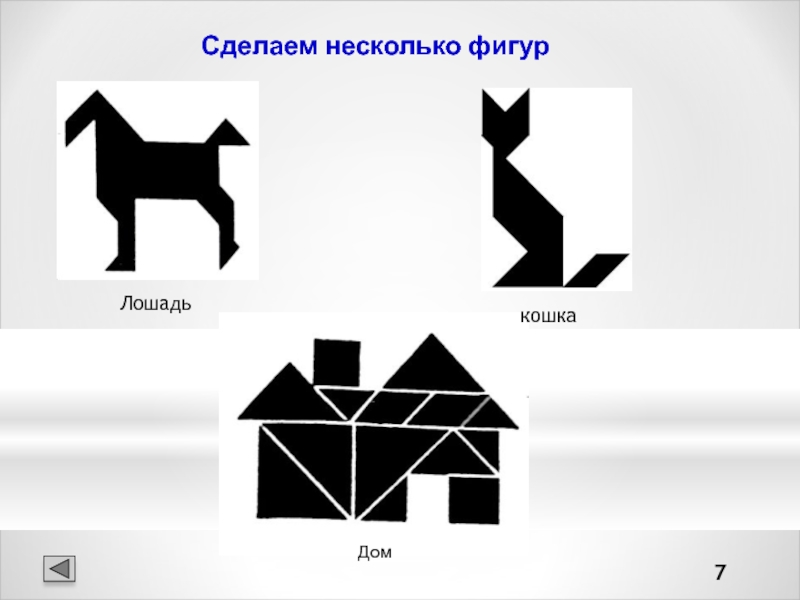
Слайд 7Сделаем несколько фигур
Лошадь
кошка
Дом
Слайд 8
Игра пентамино
Эта игра была придумана в 50-ых годах ХХ века
американским математиком С. Голомбом и очень быстро увлекла не только
школьников и студентов, но и профессоров математики. Она заключается в складывании различных фигур из заданного набора пентамино. Набор пентамино содержит 12 фигурок, каждая из которых составлена из пяти («пента» в переводе с греческого означает «пять») одинаковых квадратов, причем квадраты «соседствуют» друг с другом, только сторонами.

Слайд 10Из этих фигур можно сделать заповедник

Слайд 11
Давайте проиллюстрируем с детства известную
нам сказку « Курочка ряба».
Жили-были
дед да баба.

Слайд 13Снесла курочка яичко.
Яичко не простое, золотое.

Слайд 16Мышка бежала, хвостиком махнула.
Яичко упало и разбилось.

Слайд 17Дед и баба плачут.
Курочка кудахчет: «Не плачь, дед, не
плачь, баба.
Я снесу вам яичко другое, не золотое –
простое».

Слайд 18
Заключение
Стомахион, танграм, пентамино, яйцо Колумба имеют тысячелетнюю историю.
Их решали люди разных эпох и национальностей. Разрезать на части
и обратно собрать простую геометрическую фигуру (квадрат, круг, прямоугольник) всегда было для человека сложной и увлекательной задачей.
К сожалению, сохранились до наших дней не все древние головоломки, а только наиболее интересные и удачные.
Суть этих игр не просто в собирании первоначальной фигуры. Из полученных деталей можно складывать самые разные силуэты (животных, людей, различные предметы). Однако существуют определенные правила: в каждую собираемую фигуру должны войти все ее элементы, но так чтобы они примыкали один к другому, а не накладывались друг на друга. Сделать это непросто. Чем больше деталей имеет головоломка, тем труднее их правильно разместить.
Эти головоломки интересны людям любого возраста, но в первую очередь они несут огромную пользу детям, поскольку стимулируют образное, пространственное и творческое мышление, развивают память, логику и воображение.

Слайд 19Литература:
Шарыгин И. Ф., Ерганжиева Л. Н. Наглядная геометрия. 5
– 6 кл.: Учебное пособие. – М.: Дрофа, 1998.
Конфорович А.
Г., А. Андриевская А. М. История развития математики. Альбом. Киев. Головное издательство издательского объединения «ВЫША ШКОЛА» 1988.
Оплеснина Л. С., Юрченко И. М. Коми Республиканский Институт Усовершенствования Учителей. Использование листов с печатной основой. Сыктывкар, 1979.
http://igrushka.kz/vip87/aib1.jpg
http://nattik.ru/wp-content/uploads/2010/09/tangram_kartinki7.jpg
http://nattik.ru/wp-content/uploads/2010/09/tangram_kartinki8.jpg
http://www.babylessons.ru/wp-content/uploads/2010/03/_45031.jpg
http://igrushka.kz/vip87/aib2.jpg






































.jpg)



















.jpg)















