
Рассмотрим ситуацию, когда исследовательская группа ищет мнения о религии среди различных возрастных групп. Вместо того чтобы собирать отзывы 326 044 985 граждан США, для исследования можно выбрать случайную выборку примерно из 10000 человек. Эти 10000 граждан можно разделить на группы в соответствии с возрастом, т.е. группы 18-29, 30-39, 40-49, 50-59, 60 и старше. Каждая страта будет иметь отдельных членов и количество членов. Возраст, социально-экономическое деление, национальность, религия, уровень образования и другие подобные классификации подпадают под стратифицированную случайную выборку.
Что такое стратифицированная случайная выборка?
Стратифицированная случайная выборка – это тип вероятностной выборки, с помощью которой исследовательская организация может разделить всю совокупность на несколько непересекающихся, однородных групп (страт) и случайным образом выбрать конечных членов из различных страт для исследования, что снижает затраты и повышает эффективность. Члены каждой из этих групп должны быть разными, чтобы каждый член всех групп получил равную возможность быть отобранным с помощью простой вероятности. Этот метод выборки также называется “случайной квотной выборкой”.
Выбор респондентов
8 шагов для выбора стратифицированной случайной выборки:
- Определите целевую аудиторию.
- Определите стратификационную переменную или переменные и определите количество страт, которые будут использоваться. Эти стратификационные переменные должны соответствовать цели исследования. Каждая дополнительная информация определяет переменные стратификации. Например, если цель исследования – понять все подгруппы, то переменные будут связаны с подгруппами, и вся информация, касающаяся этих подгрупп, будет влиять на переменные. В идеале в выборке должно использоваться не более 4-6 переменных стратификации и не более 6 страт, поскольку увеличение числа переменных стратификации увеличивает вероятность того, что одни переменные нивелируют влияние других переменных.
- Используйте уже существующую выборочную совокупность или создайте совокупность, включающую всю информацию о переменной стратификации для всех элементов целевой аудитории.
- Внести изменения после оценки выборочной совокупности на основе недостаточного охвата, избыточного охвата или группировки.
- С учетом всего населения каждая страта должна быть уникальной и охватывать всех и каждого члена населения. Внутри страты различия должны быть минимальными, в то время как каждая страта должна сильно отличаться друг от друга. Каждый элемент популяции должен принадлежать только к одной страте.
- Присвойте случайный уникальный номер каждому элементу.
- Определите размер каждой страты в соответствии с вашими требованиями. Численное распределение между всеми элементами во всех стратах определит тип выборки. Это может быть пропорциональная или непропорциональная стратифицированная выборка.
- Исследователь может выбрать случайные элементы из каждой страты для формирования выборки. Из каждой страты должен быть выбран минимум один элемент, чтобы обеспечить представительство каждой страты, но если из каждой страты выбраны два элемента, то можно легко рассчитать пределы погрешности при подсчете собранных данных.
Узнайте больше: Простая случайная выборка
Типы стратифицированной случайной выборки:
- Пропорциональная стратифицированная случайная выборка:
При таком подходе размер выборки каждой страты прямо пропорционален размеру популяции всей совокупности страт. Это означает, что каждая стратовая выборка имеет одинаковую долю выборки.
Формула пропорциональной стратифицированной случайной выборки: nh = ( Nh / N ) * n
nh= Объем выборки для hth страты
Nh= Размер популяции для hth страты
N = Размер всей популяции
n = Размер всей выборки
Если у вас есть 4 страты с соответствующими размерами 500, 1000, 1500, 2000 и исследовательская организация выбирает ? в качестве выборочной доли. Исследователь должен отобрать 250, 500, 750, 1000 человек из соответствующей страты.
| Страта | A | B | C | D |
| Размер населения | 500 | 1000 | 1500 | 2000 |
| Фракция выборки | 1/2 | 1/2 | 1/2 | 1/2 |
| Результаты окончательного размера выборки | 250 | 500 | 750 | 1000 |
Независимо от размера выборки совокупности, доля выборки останется одинаковой для всех страт.
Узнайте больше: Систематическая выборка
- Непропорциональная стратифицированная случайная выборка:
Доля выборки является основным отличительным фактором между пропорциональной и непропорциональной стратифицированной случайной выборкой. При непропорциональной выборке каждая страта будет иметь свою фракцию выборки.
Успех этого метода выборки зависит от точности исследователя при распределении фракций. Если выделенные фракции не точны, результаты могут быть необъективными из-за перепредставленных или недопредставленных страт.
| Страта | A | B | C | D |
| Размер популяции | 500 | 1000 | 1500 | 2000 |
| Доли выборки | 1/2 | 1/3 | 1/4 | 1/5 |
| Результаты окончательного размера выборки | 250 | 333 | 375 | 400 |
Узнайте больше: Кластерная выборка
Примеры стратифицированной случайной выборки:
Исследователи и статистики используют стратифицированную случайную выборку для анализа отношений между двумя или более стратами. Поскольку стратифицированная случайная выборка включает несколько слоев или страт, очень важно рассчитать страты до расчета значения выборки.
Узнайте больше: Количественные исследования рынка
Следующий пример классической стратифицированной случайной выборки:
Допустим, 100 (Nh) ученикам школы с 1000 (N) учениками были заданы вопросы об их любимом предмете. Факт, что ученики 8-го класса будут иметь другие предпочтения по предметам, чем ученики 9-го класса. Чтобы опрос дал точные результаты, идеальным способом будет разделение каждого класса на различные страты.
Здесь представлена таблица количества учеников в каждом классе:
| Глава | Количество учеников (n) |
| 5 | 150 |
| 6 | 250 |
| 7 | 300 |
| 8 | 200 |
| 9 | 100 |
Расчитайте выборку каждого класса, используя формулу стратифицированной случайной выборки:
| Стратифицированная выборка (n5) = 100 / 1000 * 150 = 15 |
| Стратифицированная выборка (n6) = 100 / 1000 * 250 = 25 |
| Стратифицированная выборка (n7) = 100 / 1000 * 300 = 30 |
| Стратифицированная выборка (n8) = 100 / 1000 * 200 = 20 |
| Стратифицированная выборка (n9) = 100 / 1000 * 100 = 10 |
Узнайте больше: Удобная выборка
Преимущества стратифицированной случайной выборки:
- Большая точность результатов по сравнению с другими вероятностными методами выборки, такими как кластерная выборка, простая случайная выборка, систематическая выборка или не вероятностные методы, такие как удобная выборка. Эта точность будет зависеть от разграничения различных страт, т.е, Результаты будут высокоточными, если все страты будут сильно различаться.
- Удобно обучать команду стратификации выборки из-за точности природы этого метода выборки.
- Вследствие статистической точности этого метода, меньшие размеры выборки также могут получить очень полезные результаты для исследователя.
- Этот метод выборки охватывает максимальное количество населения, поскольку исследователи полностью контролируют деление на страты.
Узнайте больше: Кластерная выборка против стратифицированной
Когда использовать стратифицированную случайную выборку?
- Стратифицированная случайная выборка является чрезвычайно продуктивным методом выборки в ситуациях, когда исследователь намерен сосредоточиться только на определенных стратах из имеющихся данных о населении. Таким образом, в выборке исследования можно найти желаемые характеристики страт.
- Исследователи полагаются на этот метод выборки в случаях, когда они намерены установить связь между двумя или более различными стратами. Если такое сравнение проводится с помощью простой случайной выборки, существует большая вероятность того, что целевые группы не будут представлены в равной степени.
- При использовании метода стратифицированной случайной выборки можно легко вовлечь в процесс исследования население, к которому трудно получить доступ или связаться с ним.
- Точность статистических результатов выше, чем при простой случайной выборке, поскольку элементы выборки выбираются из соответствующих страт. Диверсификация внутри страт будет намного меньше, чем диверсификация, существующая в целевой популяции. Благодаря точности, необходимый размер выборки будет гораздо меньше, что поможет исследователям сэкономить время и усилия.
Выбор респондентов
Читать подробнее:
- Последовательная выборка
- Квотная выборка
- Выборка снежного кома
- Количественные исследования рынка
- Количественные исследования рынка
Понятие
стратифицированной выборки.
Вероятностная
выборка с любой техникой отбора (простая
случайная, систематическая, серийная
или многоступенчатая) становится
стратифицированной,
если
процедурам отбора предшествует выделение
в генеральной совокупности однородных
частей, называемых стратами.
В статистическом
смысле стратификация соответствует
выделению таких статистически
однородных групп, колеблемость изучаемых
признаков которых внутри меньше, чем
между ними.
Эта дифференциация
внутри генеральной совокупности на
качественно более однородные группы
содержательно связана с предметом
исследования.
Стратификация
совокупности оказывается необходимой
во всех случаях, когда совокупность
является неоднородной по социальным,
экономическим и другим характеристикам
единиц наблюдения.
Так, исследуя
профессиональную ориентацию школьников
в пределах одного города, можно в
одну страту отнести 16 школ, расположенных
в районе старых застроек, во вторую —
20 школ, расположенных в районах
новостроек. Для опроса можно отобрать
выпускников из двух школ первой
страты, а также из двух школ второй
страты. Если такая группировка школ
действительно отражает различия
районов, которые существенно учитывать
в исследовании профессиональной
структуры, то колеблемость изучаемых
признаков внутри каждой группы школ
должна быть меньше, чем между группами.
В качестве страт
могут быть использованы как естественные
образования, так и специально формируемые
для определенного исследования. Например,
такими стратами могут выступать
экономико-географические регионы
или области страны, города, классифицированные
по их административному статусу и по
численности населения. Стратами могут
выступать и идеальные образования.
Примером является выделение в генеральной
совокупности при исследовании
отношения молодежи к труду, шести групп
по содержанию труда119.
Стратифицирующий
признак.
Признак, по значениям которого производится
стратификация генеральной совокупности,
называется признаком стратификации.
Стратификация может проводиться по
одному или нескольким признакам.
Организация
стратифицированной выборки.
Организация стратифицированной
выборки требует представления о характере
распределения по всей совокупности
тех признаков, которые должны быть
положены в основу образования типических
групп, или страт.
Неправильный выбор
признака для группировки элементов
генеральной совокупности может не
увеличить репрезентативность выборочных
данных по сравнению со случайной выборкой
того же объема.
Организация
стратифицированной репрезентативной
выборки связана на практике с известными
трудностями, особенно если выделенные
страты неравночисленны Математическая
статистика рекомендует в этих случаях,
чтобы размеры выборки из каждой страты
были пропорциональны средним квадратическим
отклонениям в соответствующих стратах
генеральной совокупности. Но дисперсии,
как правило, неизвестны. Поэтому часто
при организации отбора из страт
генеральной совокупности производится
отбор пропорционально их размеру
(доле) в общей численности совокупности.
Еще один употребляемый
в социологии вариант выбора — это отбор
одинакового количества единиц наблюдения
из неравных типических групп.
Выборка организуется
в зависимости от рассмотренных вариантов
отбора с объемом, который рассчитывается
по следующим формулам.
1. Пропорционально
среднеквадратическому отклонению 5; в
1-й типической группе, найденному по
результатам пробного исследования.
Размер (![]() )
)
выборки изi-й
типической группы равен

где п
— объем всей
выборки; ![]()
— объем
i-й
группы в генеральной совокупности; l
— количество
групп. Весь объем выборки равен
![]()
2.
Пропорционально размеру групп:
![]() ,
,
гдеN
объем генеральной совокупности. Весь
объем выборки равен
![]() .
.
3. Отбор равного
числа единиц наблюдения
![]() .
.
Весь объем выборки определяется по
формуле![]() .
.
Расчет характеристик
стратифицированной выборки.
Характеристики такой выборки
рассчитываются как взвешенные величины:
показатели по каждой страте комбинируются
в общую среднюю; вклад групповых средних
пропорционален весу каждой страты в
выборочной или генеральной совокупности.
В стратифицированной
выборке общая дисперсия выборки имеет
как бы два источника: дисперсию групповых
средних, которые характеризуют каждую
страту ![]() ,
,
и среднюю дисперсию из дисперсий внутри
каждой из этих страт
![]() .
.
Первую
составляющую принято называть межгрупповой
дисперсией,
а вторую — внутригрупповой
дисперсией.
Это
записывается следующим образом:
![]() (7)
(7)
Расчет средней
ошибки при отборе, пропорциональном
численности единиц в стратах,
производится по формуле
 (8)
(8)
или, если пренебречь
отношением
n/N,
![]() (9)
(9)
В выражениях (8) и
(9)
![]() вычисляется исходя из формулы (7), т. е.
вычисляется исходя из формулы (7), т. е.![]() ,
,
где![]() — общая дисперсия
— общая дисперсия
выборки — подсчитывается как для
простой выборки, не принимая во внимание
стратификацию.
Таблица 19.
Данные к примеру
|
Семья |
Группа (i) |
||||
|
I |
II |
III |
IV |
V |
|
|
Размер на подписку, |
|||||
|
1 2 |
3 2 |
10 6 |
15 12 |
17 11 |
14 20 |
|
|
|
|
|
|
|
Из соотношения
для средней ошибки (7) следует, что ошибка
стратифицированной выборки меньше
средней ошибки чисто случайной
выборки либо равна ей, когда межгрупповая
дисперсия равна нулю.
Пример.
Предположим, что выборка содержит 5
страт (группы семей по среднему доходу120).
Необходимо определить величину расходов
на годовую подписку. Из каждой i-й
страты взяты по две семьи (объем выборки
п =
10, см. табл. 19),
Расчет:
|
|
|
|
|
|
2,5 8,0 13,5 14,0 17,0 |
—8,5 —3 2,5 3,0 6,0 |
72,25 9,00 6,25 9,00 36,00 |
|
|
|
= 132,5 |
Найдем дисперсию,
не учитывая расслоение семей на 5 групп:
|
№ п/п |
|
|
|
|
|
1 2 3 4 5 6 7 8 9 10 |
3 2 10 6 15 12 11 17 14 20 |
—8 —9 —1 —5 4 1 0 6 3 9 |
64 81 1 25 16 1 0 36 9 81 |
|
|
|
= 314 |
Отсюда внутригрупповая
дисперсия
![]() ,
,
ошибка для стратифицированной выборки![]() .
.
Для случайной
выборки
![]() .
.
Таким образом, как
видно из рассмотренного примера,
стратифицированная выборка при
прочих равных условиях дает более точные
результаты.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Стратифицированная выборка – это такая, которая гарантирует, что каждая подгруппа (страта) данной совокупности адекватно представлена во всей выборочной совокупности исследовательского исследования. Например, можно разделить выборку взрослых на подгруппы по возрасту: 18–29, 30–39, 40–49, 50–59, 60 и старше. Чтобы стратифицировать эту выборку, исследователь случайным образом выбирал пропорциональное количество людей из каждой возрастной группы. Это эффективный метод выборки для изучения того, как тенденция или проблема может отличаться в разных подгруппах.
Важно отметить, что слои, используемые в этом методе, не должны перекрываться, потому что если они действительно, у одних людей шансы быть отобранными выше, чем у других. Это приведет к искажению выборки, что приведет к смещению результатов исследования и сделает результаты недействительными.
Некоторые из наиболее распространенных слоев, используемых в стратифицированной случайной выборке, включают возраст, пол , религия, раса, уровень образования, социально-экономический статус и национальность.
Содержание
- Когда использовать стратифицированную выборку
- Пропорциональная стратифицированная случайная выборка
- Непропорциональная стратифицированная случайная выборка
- Преимущества стратифицированной выборки
- Недостатки стратифицированной выборки
Когда использовать стратифицированную выборку
Есть много ситуаций в котором исследователи предпочли бы стратифицированную случайную выборку другим типам выборки. Во-первых, он используется, когда исследователь хочет изучить подгруппы в популяции. Исследователи также используют этот метод, когда они хотят наблюдать отношения между двумя или более подгруппами, или когда они хотят изучить редкие крайности популяции. При таком типе выборки исследователю гарантируется, что субъекты из каждой подгруппы включены в окончательную выборку, тогда как простая случайная выборка не гарантирует, что подгруппы представлены в выборке одинаково или пропорционально.
Пропорциональная стратифицированная случайная выборка
В пропорциональной стратифицированной случайной выборке размер каждой страты пропорционален размеру генеральной совокупности страт при исследовании всей генеральной совокупности. Это означает, что каждая страта имеет одинаковую долю выборки.
Например, предположим, что у вас есть четыре страты с размерами населения 200, 400, 600 и 800 Если вы выбираете долю выборки, равную ½, это означает, что вы должны случайным образом выбрать 100, 200, 300 и 400 субъектов из каждой страты соответственно. Для каждой страты используется одна и та же фракция выборки, независимо от различий в размере генеральной совокупности страт.
Непропорциональная стратифицированная случайная выборка
При непропорциональной стратифицированной случайной выборке разные страты не имеют одинаковых долей выборки друг с другом. Например, если ваши четыре страты содержат 200, 400, 600 и 800 человек, вы можете выбрать разные фракции выборки для каждой страты. Возможно, первая страта из 200 человек имеет фракцию выборки ½, в результате чего для выборки выбрано 100 человек, в то время как последняя группа из 800 человек имеет фракцию выборки, в результате чего для выборки выбрано 200 человек..
Точность использования непропорциональной стратифицированной случайной выборки сильно зависит от фракций выборки, выбранных и используемых исследователем. Здесь исследователь должен быть очень осторожным и точно знать, что делает. Ошибки, допущенные при выборе и использовании фракций выборки, могут привести к чрезмерному или недостаточному представлению страты, что приведет к искаженным результатам.
Преимущества стратифицированной выборки
Использование стратифицированной выборки всегда обеспечивает более высокую точность, чем простая случайная выборка, при условии, что страты были выбраны таким образом, чтобы члены одной и той же страты были максимально похожи с точки зрения интересующей характеристики . Чем больше разница между стратами, тем больше выигрыш в точности.
С административной точки зрения часто удобнее стратифицировать выборку, чем выбирать простой случайный образец. Например, интервьюеров можно обучить тому, как лучше всего работать с одним определенным возрастом или этнической группой, в то время как других обучат тому, как лучше всего работать с другим возрастом или этнической группой. Таким образом, интервьюеры могут сконцентрироваться на небольшом наборе навыков и усовершенствовать его, и это будет менее своевременным и дорогостоящим для исследователя.
Стратифицированная выборка также может быть меньше по размеру, чем простые случайные выборки, что может сэкономить много времени, денег и усилий исследователям. Это связано с тем, что этот тип метода выборки имеет высокую статистическую точность по сравнению с простой случайной выборкой.
Последним преимуществом является то, что стратифицированная выборка гарантирует лучший охват Население. Исследователь контролирует подгруппы, включенные в выборку, тогда как простая случайная выборка не гарантирует, что какой-либо один тип людей будет включен в окончательную выборку.
Недостатки стратифицированной выборки
Одним из основных недостатков стратифицированной выборки является то, что бывает трудно определить подходящие страты для исследования. Второй недостаток – сложность организации и анализа результатов по сравнению с простой случайной выборкой.
Обновлено Ники Лиза Коул, Доктор философии

When we wish to conduct an experiment on a population – for example, the entire population of a country – it is not always practical or realistic to include every subject (citizen) in the experiment.
Instead, we rely on a sample, which is a subset of the population, and then draw conclusions about the population based on the sample’s results.
Now, drawing a sample from a population is known as sampling technique, and the manner in which the sample is drawn is essential to the result.
There are lot of sampling techniques out there, but in this tutorial we will look at one of them called stratified random sampling and how it works. Without further ado, let’s get started.
Before we go into the details of stratified random sampling, let’s break the term down into bits so we can grasp it better. Let’s start with stratified.
In the context of sampling, stratified means splitting the population into smaller groups or strata based on a characteristic. To put it another way, you divide a population into groups based on their features.
Random sampling entails randomly selecting subjects (entities) from a population. Each subject has an equal probability of being chosen from the population to form a sample (subpopulation) of the overall population.
So therefore, stratified random sampling is a sampling approach in which the population is separated into groups or strata depending on a particular characteristic. Then subjects from each stratum (the singular of strata) are randomly sampled.
You divide the population into groups based on a characteristic and then choose a subject or entity at random from each group.
Types of Stratified Random Sampling
Stratified sampling is divided into two categories, which are:
- Proportionate stratified random sampling.
- Disproportionate stratified random sampling.
Proportionate stratified random sampling is a type of sampling in which the size of the random sample obtained from each stratum is proportionate to the size of the entire stratum’s population.
In other words, the proportion of the entire stratum equals the proportion of the sample stratum. Consider the following example:
students = {
"Name": ["Ibrahim", "Ganiyat", "Joel", "Elijah", "Yusuf", "Nurain",
"Dayo", "David", "Olu", "Tobi"],
"ID": ['001', '002', '003', '004', '005', '006','007', '008', '009', '010'],
"Grade": ['A', 'B', 'C', 'A', 'B', 'C', 'A', 'A', 'B', 'A'],
"Category": [1, 2, 2, 1, 3, 3, 1, 2, 3, 3]
}
df = pd.DataFrame(students)
>>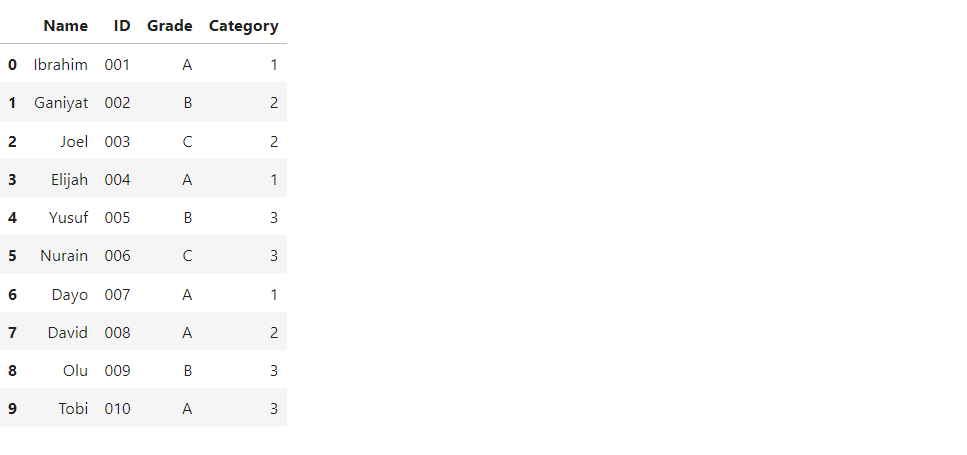
The above dataframe contains students’ names, IDs, grades, and categories. Assume we wish to stratify students based on their grade characteristics and sample 60% of students from each group. That means we will have three strata in the above dataframe, because we have three different grades.
We can sample it by typing the following:
df_sample = df.groupby("Grade", group_keys=False).apply(lambda x:x.sample(frac=0.6))Now what we did above is to group the dataframe into different strata using the groupby() method. Then we passed in the Grade feature. For each group (stratum) we randomly sampled out 0.6(60%) of observation from it.

Now if we look at the proportion for df_sample and df, we will see that the proportions for both dataframes are the same.

Disproportionate stratified random sampling, on the other hand, involves randomly selecting strata without regard for proportion. In other words, sampling is done based on a specified number. Let’s look at an example.
df.groupby('Grade', group_keys=False).apply(lambda x: x.sample(n=2))In this code, you can see that we only specified the actual number of samples we want to achieve.

Most of the time, you’ll use proportionate stratified sampling. Disproportionate requires more expert knowledge. When performing stratified sampling you will most likely use proportionate sampling.
Applications of Stratified Random Sampling
1. Sampling Based on Shared Characteristic:
When one or more subjects in an experiment share characteristics, it suggests they are members of the same group (one subject can only be in a particular group).
For example, suppose 50 students take a test, and the grade range for the examination is merely A-E. So we can have students who are in the same grade group, for example, students who received an A (and it is impossible for a student to have two grades). As a result, they share the same characteristic or feature, which is grade.
So when you want to sample subjects based on shared characteristics, you should use stratified random sampling. This ensures that a member of a specific group will be included.
This is because stratified random sampling differs from simple random sampling, which is also a sampling technique. Stratified random sampling randomly samples out the population with no characteristics (that is, each subject of the population has equal chances of being picked).
As a result, simple random sampling cannot guarantee that a certain member of a particular group will be included in the sample.
Let’s have a look at an example to see what we’re talking about. Let’s say we want to sample out 60% of students using both stratified and simple random sampling.
We can see the result for stratified random sampling below:
df.groupby('Grade', group_keys=False).apply(lambda x: x.sample(frac=0.6))
And this is the result of simple random sampling:
df.sample(frac= 0.6)
We can see that students with C grades are not included in the sample. This is because in simple random sampling, every observation has an equal chance of being chosen because we are not sampling based on characteristics. This means that there is a chance that an observation will not be chosen.
In stratified random sampling, on the other hand, we consider all the groups we want to sample and then randomly sample from each group.
2. Imbalanced Dataset:
An imbalanced dataset is a machine learning classification problem in which the two class labels in the target variable are not proportional to one another. In other words, one class has a higher count than the other, resulting in an imbalance.
In machine learning, stratified sampling is also used to obtain the same sample proportion for a train and test set if there is an imbalance in the dataset.
For example, a chronic disease dataset has an imbalance label as shown below. You can click here to download the dataset.
df = pd.read_csv("kidney_disease.csv")
df.head()
If we check the proportion label feature which is classification, we can see that it is imbalanced.

Now let’s say we want to split the train and test set using simple random sampling. We won’t achieve the same proportion for the train and test set as the population proportion.
from sklearn.model_selection import train_test_split
X = df.drop(columns = ["classification"])
y = df["classification"]
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8)
We can see that the label proportion for both y_train and y_test is not the same as the population proportion. To achieve the same proportion we can make use of the stratify parameter in train_test_split as shown below:
from sklearn.model_selection import train_test_split
X = df.drop(columns = ["classification"])
y = df["classification"]
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8, stratify=y)The above code shows that the dataset was stratified on the label. So with that we will achieve the same proportion as the population proportion.

Conclusion
In this tutorial, we looked at stratified sampling and how you can use it in statistics and machine learning. We also looked at the types of stratified sampling.
Thank you for your time.
Learn to code for free. freeCodeCamp’s open source curriculum has helped more than 40,000 people get jobs as developers. Get started
17 авг. 2022 г.
читать 1 мин
Исследователи часто берут образцы из населения и используют данные из выборки, чтобы сделать выводы о населении в целом.
Одним из широко используемых методов выборки является стратифицированная случайная выборка , при которой население разбивается на группы, и определенное количество членов из каждой группы случайным образом отбирается для включения в выборку.
В этом руководстве объясняется, как выполнить стратифицированную случайную выборку в R.
Пример: стратифицированная выборка в R
Средняя школа состоит из 400 учеников, которые являются первокурсниками, второкурсниками, младшими или старшими. Предположим, мы хотим взять стратифицированную выборку из 40 учащихся, чтобы в выборку было включено по 10 учащихся каждого класса.
В следующем коде показано, как создать образец фрейма данных для 400 учащихся:
#make this example reproducible
set.seed(1)
#create data frame
df <- data.frame(grade = rep(c('Freshman', 'Sophomore', 'Junior', 'Senior'), each =100),
gpa = rnorm(400, mean=85, sd=3))
#view first six rows of data frame
head(df)
grade gpa
1 Freshman 83.12064
2 Freshman 85.55093
3 Freshman 82.49311
4 Freshman 89.78584
5 Freshman 85.98852
6 Freshman 82.53859
Стратифицированная выборка с использованием количества строк
В следующем коде показано, как использовать функции group_by() и sample_n() из пакета dplyr для получения стратифицированной случайной выборки из 40 учащихся по 10 учащихся в каждом классе:
library(dplyr)
#obtain stratified sample
strat_sample <- df %>%
group_by(grade) %>%
sample_n (size=10)
#find frequency of students from each grade
table(strat_sample$grade)
Freshman Junior Senior Sophomore
10 10 10 10
Стратифицированная выборка с использованием доли строк
В следующем коде показано, как использовать функции group_by() и sample_frac() из пакета dplyr для получения стратифицированной случайной выборки, в которой мы случайным образом выбираем 15% учащихся из каждого класса:
library(dplyr)
#obtain stratified sample
strat_sample <- df %>%
group_by(grade) %>%
sample_frac (size=.15)
#find frequency of students from each grade
table(strat_sample$grade)
Freshman Junior Senior Sophomore
15 15 15 15
Дополнительные ресурсы
Типы методов отбора проб
Кластерная выборка в R
Систематическая выборка в R

