Структурная
группировка заключается в расчленении
однородной в качественном отношении
совокупности статистических единиц на
группы, характеризующие состав сложного
объекта. Посредством структурной
группировки изучается внутреннее
строение типов, статистических
совокупностей. В связи с этим она может
проводиться на основе типологической
группировки. Вместе с тем нередко
изучается структура общих совокупностей,
включающих неоднородные явления.
Например, исследуется структура всех
организаций и хозяйств в системе АПК:
сельскохозяйственных, вспомогательных,
перерабатывающих, сбытовых и др.
Структурные
группировки могут проводиться как по
качественным, так и по количественным
признакам. В зависимости от целей, задач,
масштабности и сложности статистического
объекта за основу группировки берут
либо один, либо несколько существенных
группировочных признаков. В связи с
этим структурные группировки могут
быть простыми
или сложными
(комбинированными).
Структурная
группировка проводится в следующем
порядке:
-
выбирается
один или несколько группировочных
признаков, по которым намечено провести
группировку; -
выделяются
группы по качественным признакам или
определяются интервалы по количественным
признакам; -
статистические
единицы группируются согласно выделенным
группам; по каждой группе рассчитываются
необходимые относительные и средние
показатели; -
оцениваются
результаты структурной группировки.
Выбор
группировочных признаков определяется
поставленной задачей структурной
группировки. Так, если необходимо выявить
структуру численности работников по
уровню образования, то очевидно, что
все работники будут распределены по
качественному признаку. Если же поставлена
задача определить структуру работников
по возрасту, то их численность необходимо
распределить по количественному
признаку. При необходимости изучения
совместной структуры численности
работников по уровню образования и по
возрасту возможно применение этих двух
признаков в сочетании (комбинации).
Выделение
групп по намеченным качественным
признакам в структурной группировке
ограничивается, как правило, характером
признака. При этом количество групп, на
которые делится изучаемая статистическая
совокупность, нередко определяется
числом разновидностей качественного
признака. Так, группировка работников
системы АПК по профессиям допускает
формирование стольких групп, сколько
различных профессий имеют работники
этой отрасли экономики.
В
качестве примера простой структурной
группировки по качественному признаку
можно привести данные о составе всей
рабочей силы Республики Беларусь по
уровню образования (табл. 3.3).
Т а б
л и ц а 3. 3. Распределение
численности работников по уровню
образования (на
начало года, в % к итогу)
|
Показатели |
2001 |
2006 |
2009 |
|
Всего работников |
100,0 |
100,0 |
100,0 |
|
В высшее среднее специальное среднее общее базовое (неполное среднее) |
18,8 22,4 50,6 8,2 |
22,8 22,8 31,2 4,3 |
23,8 22,7 29,8 3,4 |
Данные
таблицы 3.3 показывают, что в структуре
общей численности работников Беларуси
за период 2001 – 2009 гг. значительная доля
была представлена группой лиц, имевших
среднее образование. Удельный вес этих
групп имеет тенденцию к снижению.
Сокращается также доля группы работников,
имевших базовое (неполное среднее)
образование. В структуре всех работников
Беларуси значительный удельный вес
занимали группы лиц, имевших среднее
специальное и высшее образование. Доля
каждой из этих групп за рассматриваемый
период повысилась.
Структурные
сдвиги в распределении численности
работников свидетельствуют об улучшении
качественного состава рабочей силы в
Республике Беларусь по уровню образования.
Построение
структурной группировки по количественным
признакам обычно связано с определением
рационального числа интервальных групп
и расчётом величины интервалов. Возможное
рациональное число групп может колебаться
в различных приделах и зависит от объема
статистического объекта (количества
единиц) и однородности группировочных
признаков.
При
расчете величины интервалов, т.е. пределов
колебания между наибольшими и наименьшими
значениями признака в каждой группе,
необходимо стремиться к тому, чтобы не
исчезли особенности изучаемого явления.
Например, при изучении структурных
особенностей перерабатывающих организации
АПК по числу работников необходимо,
чтобы число групп было не слишком большим
и не слишком малым. В настоящее время
перерабатывающая сфера АПК представлена
сочетанием небольших (20 – 30 работников),
средних (100-200 человек) и крупных (700-800 и
более работников) организаций.
При
условии формирования малого числа
интервальных групп возможно попадание
в одну и ту же группу перерабатывающих
организаций, существенно различающихся
по их размеру. В то же время если образовать
большое число групп, то в них могут
сгладиться характерные особенности,
выражающие различия по численности
работников в организациях.
Одно
из важнейших требований формирования
групп заключается в том, чтобы в каждую
вошло достаточно большое число
статистических единиц для обеспечения
представительности результатов
структурной группировки. Это достигается
регулированием величины интервалов в
группах, т.е. путем использования равных
и неравных интервалов. Применение приёма
равных интервалов во всех группах может
быть обеспечено только в условиях
однородности группировочного признака,
т.е. когда вариация этого признака не
превышает 10 %. В условиях же неоднородности
группировочного признака формирование
интервальных групп чаще всего связано
с неравными интервалами.
Примером
простой структурной группировки,
построенной по количественному признаку,
могут быть данные о составе рабочей
силы Республики Беларусь по возрасту
(табл. 3.4).
Т а б
л и ц а 3.4. Распределение
численности работников по возрастным
группам
(на начало года, в
% к итогу)
|
Показатели |
2001 г. |
2006 г. |
2009 г. |
|
Всего работников |
100,0 |
100,0 |
100,0 |
|
в т.ч. в возрасте, лет: |
|||
|
до 25 |
10,6 |
11,4 |
11,6 |
|
12,0 |
12,1 |
12,4 |
|
27,5 |
24,4 |
23,4 |
|
28,7 |
28,8 |
26,6 |
|
11,8 |
12,5 |
13,6 |
|
9,6 |
10,8 |
12,4 |
|
средний возраст, лет |
39,4 |
39,7 |
40,1 |
Из
данных табл. 3.4. видно, что в структуре
общей численности работников Беларуси
за период 2001 – 2009 гг. основной удельный
вес занимали группы лиц в возрасте 30–39
и 40–49 лет, которые составляли вместе
не менее 55 % всего числа работников. В
динамике доля групп работников в возрасте
до 25 лет, 25–29 и 50–54 года, 55 лет и старше
имела тенденцию повышения, доля работников
в возрасте 30–39 лет – снижения. Структурные
изменения, имевшие место в составе общей
численности работников Беларуси за
период 2001– 2009гг. привели к повышению
среднего возраста работавшего населения
с 39,4 до 40,1 года.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
6.2. Структурная группировка
Напоминаю, это группировка качественно однородной совокупности по числовому признаку. Примеры только что были выше, и мы
продолжаем. Суровая задача местного Политеха для студентов около- и машиностроительных специальностей:
Пример 38
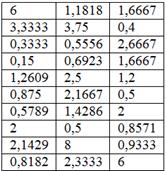
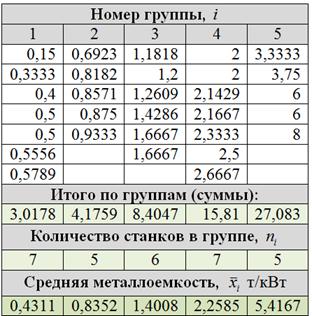
В результате выборочного исследования 30 станков рассчитаны их относительные показатели металлоёмкости (т/кВт):
Требуется:
а) вычислить общую (выборочную) среднюю;
б) выполнить структурную равноинтервальную группировку;
в) выполнить структурную равнонаполненную группировку;
г) выбрать наиболее удачную группировку и вычислить выборочные средние; результаты оформить в виде групповой
таблицы;
д) по выбранной группировке построить интервальный вариационный ряд;
е) сделать краткие выводы.
Но прежде, немного о содержании. Согласно автору методички, относительная металлоемкость – это частное от деления веса
станка на мощность его двигателя (тонн на киловатт). Разделили, например, 5 тонн на 2 кВт и получили 2,5 тонны на один кВт.
Эти значения и представлены в таблице. Правильность и достоверность перечисленных фактов я снова оставлю на совести автора, да
и, в конце концов, нам требуется обработать числа, а уж что это такое – не особо важно, хоть объём талии пчёлок. …И всё-таки
математика немного шизофреническая наука 🙂
Решение:
ну, с пунктом а) справится даже неподготовленный человек. Очевидно, что для нахождения выборочной средней нужно просуммировать все значения и разделить полученный результат
на объём выборки:
т/кВт (не забываем указать
размерность!)
Эти и другие вычисления лучше проводить в Экселе, и чуть ниже будет ролик о том, как быстро выполнить все пункты задания.
Ибо на калькуляторе щёлкать 30 слагаемых муторно (хотя, вариант вполне рабочий).
6.2.1. Равноинтервальная группировка
б) Выполним структурную равноинтервальную группировку. Пугаться не нужно, это задание уже было
– нам нужно построить обычный интервальный вариационный ряд
с равными интервалами, и я кратко повторю алгоритм.
В условии ничего не сказано о количестве интервалов, и поэтому для определения их оптимального количества используем формулу Стерджеса:
интервалов (результат
округляем влево).
Найдём минимальное и максимальное
значения и вычислим размах вариации:
т/кВт. Таким образом, длина частичного интервала составит:
т/кВт. Теперь «нарезаем» интервалы и
подсчитываем количество станков в
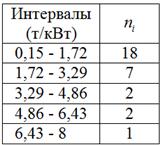
каждом из них:
Контроль: , что и требовалось
проверить.
И уже сейчас мы видим, что построенный вариационный ряд не слишком хорош – по той причине, что в трёх последних
интервалах слишком мало станков, и считать по ним средние значения и другие показатели не вполне корректно. Во избежание этого
недостатка используют разные методы, в частности, другой метод группировки:
6.2.2. Равнонаполненная группировка
в) Это разбиение совокупности на группы с одинаковым (или примерно одинаковым)количеством объектов,
станков в данном случае. Но интервалы здесь получатся разной длины.
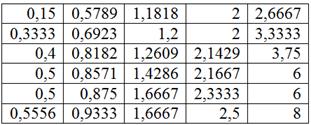
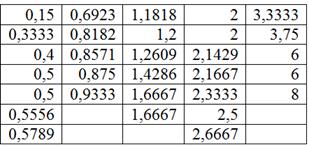
Отсортируем числа по возрастанию и выделим 5 групп по станков в каждой:
Формально всё выглядит тип-топ (и можно оставить так), но некоторые значения логичнее перенести в соседние группы. Так,
значение 0,5789 (верхняя строка) явно ближе к 1-й группе, а значение 2,6667 – к предпоследней группе; туда их и
перенесём:
г) Очевидно, что равнонаполненная группировка более удачна, с ней и работаем. По каждой
группе подсчитаем сумму, объём (количество станков) и выборочную среднюю – как результат деления
суммы на соответствующий объём. Вычисления сведём в групповую таблицу:
И на всякий пожарный пример расчёта первой групповой средней:
т/кВт;
Да, кстати, не забываем предварительно проконтролировать объём выборки:
, ч.т.п.
д) Построим интервальный вариационный ряд по равнонаполненной группировке. Границы интервалов можно
брать как средние арифметические «стыковых» значений, например: (граница между 1-м и 2-м интервалом). Но вполне допустимо (и даже
лучше) разметить интервалы «на глазок», выбирая удобные «круглые» значения:
Полученный интервальный ряд имеет разную длину интервалов, но для него
точно так же можно построить гистограмму, эмпирическую функцию распределения, а также рассчитать типовые характеристики. Правда, с модой
проблема будет и для её нахождения таки лучше использовать равноинтервальную группировку (пункт б).
Теперь смотрим ролик по быстрому и эффективному выполнению
расчётов.
Выражаясь научно, мы выполнили статистическую сводку.
Статистическая сводка – это комплекс действий по обработке статистических данных с целью получения обобщающих
показателей и анализа стат. совокупности.
Причём, в пункте а) была простая статическая сводка (подсчёт общих показателей), которая
переросла в сводку сложную, включающую в себя группировку данных, расчёт групповых характеристик и сведение
результатов в групповую таблицу.
Но это ещё не всё:
е) Сделаем краткие выводы.
Я не случайно выделил данный пункт. Довольно часто в заданиях по статистике требуется сделать выводы – в них нужно
отразить основные результаты выполненных действий и особенности исследуемой совокупности. Собственно, это и
есть цель статистического исследования – сделать выводы.
И за нами дело не станет. Сказать здесь можно следующее. В результате исследования рассчитана средняя металлоёмкость т/кВт по выборке и средние значения по группам
равнонаполненной (наиболее удачной) группировки. Большинство станков (18 шт. в первых трёх группах) имеют показатель
металлоёмкости меньший, чем средняя металлоёмкость по выборке. Пять станков (группа 5) обладают значительно бОльшей
металлоёмкостью, чем остальные, и причины этого требуют отдельного анализа (возможно, станки морально устарели).
Несколько строчек вполне достаточно, даже многовато получилось. Но это на пользу – грамотный аналитик или чиновник должен
мастерски уметь «лить воду» J. …Вот видите, какой полезный курс….
Следующее задание для самостоятельного решения:
Пример 39
По результатам выборочного исследования 50 предприятий получены данные об их квартальной прибыли (числа в экселевском файле), млн. руб. Требуется:
1) вычислить среднюю прибыль;
2) провести равнонаполненную группировку и вычислить групповые средние;
3) построить соответствующий вариационный ряд;
4) сделать выводы.
Вообще, здесь удобно разбить выборку на 5 интервалов (и такой вариант вполне себе неплох), но от греха подальше лучше
использовать формулу Стерджеса, что я и сделал в образце решения, который, как обычно, находится в конце книги. Ваш вариант
решения может немного отличаться от моей версии. И выводы, разумеется, тоже.
Теперь вернёмся к пункту «бэ» Примера 38, где была выполнена не слишком удачная равноинтервальная группировка, скопирую табличку сверху:
Как вы помните, от «куцых» последних интервалов мы избавились, выполнив равнонаполненную группировку. Но есть и другой метод «лечения», который
называется


| Оглавление |
Содержание курса лекций «Статистика»
Статистическая сводка и группировка. В результате проведения статистического наблюдения получают данные о признаках каждой обследованной единицы статистической совокупности. Однако эти массивы данных, содержащие подробные сведения о каждой единице совокупности, собирают не для того, чтобы получить характеристики каждой из них, а с целью изучить совокупность в целом, выявить ее характерные группы и закономерности. Для этого необходимо обобщить и систематизировать сведения, полученные в ходе статистического наблюдения.
Обобщение и систематизация первичных статистических данных – это самостоятельный этап статистического исследования, основная задача которого получить полную и всестороннюю характеристику как совокупности в целом, так и отдельных ее частей и представить полученную информацию об изучаемой совокупности в наиболее удобной для пользователей форме. В статистической практике данный этап статистического исследования называют этапом сводки и группировки статистических данных.
Статистическая сводка
Сводка – это научная обработка первичных данных с целью получения обобщенных характеристик изучаемого социально-экономического явления по ряду существенных для него признаков с целью выявления типичных черт и закономерностей, присущих изучаемому явлению в целом.
По глубине и точности обработки материала различают простую сводку и сложную сводку.
Простая сводка – это операция по подсчету общих итогов по совокупности единиц наблюдения и оформление этого материала в статистических таблицах.
Сложная сводка – это комплекс последовательных операций, включающих группировку полученных при наблюдении материалов, составление системы показателей для характеристики типичных групп и подгрупп изучаемой совокупности явлений, подсчет числа единиц и итогов по каждой группе и подгруппе, и по всему объекту и представление результатов в виде статистических таблиц.
Этапы проведение сводки
- Выбор группировочного признака.
- Определение порядка формирования групп.
- Разработка системы статистических показателей для характеристики групп и объекта в целом
- Разработка макетов статистических таблиц для представления результатов сводки.
Статистическая группировка
Группировка – разбиение общей совокупности единиц объекта наблюдения по одному или нескольким существенным признакам на однородные группы, различающиеся между собой в количественном и качественном отношении и позволяющие выделить социально-экономические типы, изучить структуру совокупности и проанализировать связи между отдельными признаками.
Задачи, решаемые с помощью метода группировок:
- выделение социально-экономических типов явлений;
- изучение структуры явления и структурных сдвигов, происходящих в нем;
- выявление взаимосвязи и взаимозависимости между явлениями.
Виды группировок. В соответствии с познавательными задачами, решаемыми в ходе построения статистических группировок, различают следующие их виды: типологические, структурные, аналитические.
Типологическая группировка – это разбиение разнородной совокупности единиц наблюдения на отдельные качественно однородные группы и выявление на этой основе социально-экономических типов явлений. При построении группировки этого вида основное внимание должно быть уделено идентификации типов и выбору группировочного признака. Решение вопроса об основании группировки должно осуществляться на основе анализа сущности изучаемого социально-экономического явления.
Структурная группировка – предназначена для изучения состава однородной совокупности по какому-либо варьирующему признаку, а также структуры и структурных сдвигов, происходящих в нем.
Аналитическая группировка – выявляет взаимосвязи между изучаемыми явлениями и признаками, их характеризующими.
!!!В статистике при изучении связей социально-экономических явлений признаки подразделяют на факторные и результативные.
Факторные признаки, под их воздействием изменяются результативные признаки. Взаимосвязь проявляется в том, что с возрастанием или убыванием значения факторного признака систематически возрастает или убывает значение признака результативного и наоборот.!!!
Особенности построения аналитической группировки:
- единицы статистической совокупности группируются по факторному признаку;
- каждая выделенная группа характеризуется средними величинами результативного признака.
По способу построения группировки бывают простые и комбинационные.
Простая группировка – группы образованы только по одному признаку.
Комбинационная группировка – разбиение совокупности на группы производится по двум и более признакам, взятым в сочетании (комбинации).
Сначала группы формируются по одному признаку, затем группы делятся на подгруппы по другому признаку, а эти в свою очередь делятся по третьему и так далее. Таким образом, комбинационные группировки дают возможность изучить единицы совокупности одновременно по нескольким взаимосвязанным признакам.
При построении комбинационной группировки возникает вопрос о последовательности разбиения единиц объекта по признакам. Как правило, рекомендуется сначала производить группировку по атрибутивным признакам, значения которых имеют ярко выраженные качественные различия.
Этапы построения статистических группировок
- Определение группировочного признака.
- Определение размаха вариации.
- Определение числа групп.
- Расчет ширины интервала группировки.
- Определение признаков, которые в комбинации друг с другом будут характеризовать каждую выделенную группу.
При небольшом объеме совокупности (n<50) не следует образовывать большого количества групп, так как группы будут включать недостаточное число единиц объекта. Показатели, рассчитанные для таких групп, не будут представительными и не позволят получить адекватную характеристику исследуемого явления.
Часто группировка по количественному признаку имеет задачу отразить распределение единиц совокупности по этому признаку. В этом случае количество групп зависит, в первую очередь, от степени колеблемости группировочного признака: чем больше его колеблемость, тем больше можно образовать групп.
При определении числа групп необходимо принять во внимание размах вариации признака (R), который позволяет оценить вариацию признака между крайними значениями признака – максимальным (Хmax) и минимальным (Xmin) и определяется по формуле 5.1): 
Чем больше размах вариации признака, положенного в основание группировки, тем, как правило, может быть образовано большее число групп. При этом может возникнуть проблема получения пустых групп, т.е. групп, не содержащих ни одной единицы наблюдения.
Определение числа групп можно осуществить несколькими способами. Формально-математический способ предполагает использование формулы Стерджесса (формула 5.2): 
где n – число групп; N – число единиц совокупности.
Согласно этой формуле выбор числа групп зависит только от объема изучаемой совокупности.
Применение данной формулы дает хорошие результаты в том случае, если совокупность состоит из большого числа единиц наблюдения (n>50).
Другой способ определения числа групп основан на применении показателя среднего квадратического отклонения (σ). Если величина интервала равна 0,5σ, то совокупность разбивается на 12 групп, а когда величина интервала равна 2/3σ и σ, то совокупность делится, собственно, на 9 и 6 групп. Однако при определении групп данными методами существует большая вероятность получения «пустых» или малочисленных групп, характеристики изучаемого явления на основе которых будут недостаточно типичными для выделенной группы и изучаемой совокупности в целом.
Когда определено число групп, то следует определить интервалы группировки.
Интервал – это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет верхнюю и нижнюю границы или одну из них. Нижней границей интервала называется наименьшее значение признака в интервале. Верхней границей интервала называется наибольшее значение признака в интервале. Величина интервала представляет собой разность между верхней и нижней границами интервала.
Интервалы группировки бывают: равные и неравные; открытые и закрытые.
Ширина равного интервала определяется по (формуле 5.3):

Если максимальные или минимальные значения сильно отличаются от смежных с ними значений вариантов в упорядоченном ряду значений группировочного признака, то для определения величины интервала следует использовать не максимальное или минимальное значения, а значения, несколько превышающие минимум, и несколько меньше, чем максимум.
Полученную по формуле (5.3) величину округляют и она будет являться шириной интервала.
Существуют следующие правила определения ширины интервала.
Если величина интервала, рассчитанная по формуле (5.3) представляет собой величину, которая имеет один знак до запятой (например: 0,67; 1,487; 3,82), то в этом случае полученные значения целесообразно округлить до десятых и их использовать в качестве ширины интервала. В приведенном выше примере это будут соответственно значения: 0,7; 1,5; 3,8.
Если рассчитанная величина интервала имеет две значащие цифры до запятой и несколько после запятой (например, 14,876), то это значение необходимо округлит до целого числа (15).
В случае, когда рассчитанная величина интервала представляет собой трехзначное, четырехзначное и так далее число, то эту величину следует округлить до ближайшего числа, кратного 100 или 50. Например, 652 следует округлить до 650 или до 700.
Если размах вариации признака в совокупности велик и значения признака варьируют неравномерно, то надо использовать группировку с неравными интервалами.
Неравные интервалы могут быть получены в процессе объединения пустых, не содержащих ни одной единицы совокупности, равных интервалов. Это происходит в том случае, если после построения равных интервалов по изучаемому признаку образуются группы, содержащие мало или не содержащие вообще ни одной единицы, т.е. группы, не отражающие определенных типов изучаемого явления по признаку. В этом случае возникает необходимость в увеличении интервалов группировки.
Также неравные интервалы могут быть прогрессивно-возрастающие или прогрессивно-убывающие в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической и геометрической прогрессии, определяется следующим образом:hi+1=hi+а,
а в геометрической прогрессии: hi +1= hi ×q, где:
а – константа: для прогрессивно-возрастающих интервалов имеет знак «+», а при прогрессивно-убывающих – знак «-».
q — константа: для прогрессивно-возрастающих – больше «1»; для прогрессивно-убывающих ‑ меньше «1».
Применение неравных интервалов обусловлено тем, что в первых группах небольшая разница в показателях имеет большое значение, а в последних группах эта разница не существенна.
Например, при построении группировки строительных компаний города по показателю численности работающих, который варьирует от 500 человек до 3500 человек, нецелесообразно рассматривать равные интервалы, т. к. учитываются как малые, так и крупнейшие строительные фирмы города. Поэтому следует образовывать неравные интервалы: 500–1000, 1000–2000, 2000–3500, т.е. величина каждого последующего интервала больше предыдущего на 500 человек и увеличивается в арифметической прогрессии. Выбор исследователя в построении равных или неравных интервалов зависит от степени заполнения каждой выделенной группы, т.е. от числа единиц в них. Если величина интервала существенна и содержит большое число единиц совокупности, то эти интервалы необходимо дробить, а в противном случае – объединять.
Интервалы статистической группировки
Интервалы группировок могут быть закрытыми и открытыми.
Закрытые интервалы – это интервалы, у которых есть и верхняя и нижняя границы.
Открытые интервалы – это интервалы, у которых указана только одна граница: как правило, верхняя – у первого интервала и нижняя – у последнего.
Например, группы страховых компаний по числу работающих в них сотрудников (чел.): до 50, 50–100, 100–150, 150 и более. Применение открытых интервалов целесообразно в тех случаях, когда в совокупности встречается незначительное число единиц наблюдения с очень малыми или очень большими значениями вариантов, которые резко, в несколько раз, отличаются от всех остальных значений изучаемого признака.
Если основанием группировки служит непрерывный признак (например, группы строительных фирм по объему строительно-монтажных работ, выполненных собственными силами (тыс. руб.): 1200–1400, 1400–1600, 1600–1800, 1800–2000), то одно и то же значение признака выступает и верхней и нижней границами двух смежных интервалов. В данном случае объем работ 1400 тыс. руб. составляет верхнюю границу первого интервала и нижнюю границу второго, 1600 тыс. руб. ‑ соответственно второго и третьего и т.д., т.е. верхняя граница i-го интервала равна нижней границе (i+1)-го интервала.
При таком обозначении границ может возникнуть вопрос, в какую группу включать единицы наблюдения, значения признака у которых совпадают с границами интервалов.
Например, во вторую или третью группу должна войти строительная фирма с объемом строительно-монтажных работ 1600 тыс. рублей? Если верхняя граница формируется по принципу «исключительно», то фирма должна быть отнесена к третьей группе, в противном случае – ко второй. Для того, чтобы правильно отнести к той или иной группе единицу совокупности, значение признака которой совпадает с границами интервалов, можно ориентироваться на открытые интервалы (по нашему примеру группы строительных фирм по объему строительно-монтажных работ преобразуются в следующие: до 1400, 1400–1600, 1600–1800, 1800 и более). В данном случае, вопрос отнесения отдельных единиц совокупности, значения которых являются граничными, к той или иной группе решается на основе анализа последнего открытого интервала. Возможны два случая обозначения последнего открытого интервала: 1) 1800 тыс. руб. и более; 2) более 1800 тыс. руб. В первом случае, строительные фирмы с объемом строительно-монтажных работ 1600 тыс. руб. попадут в третью группу; во втором случае – во вторую группу.
Если в основании группировки лежит дискретный признак, то нижняя граница 1-го интервала равна верхней границе i-1-го интервала, увеличенной на 1.
Например, группы строительных фирм по числу занятого персонала (чел.) будут иметь вид: 100–150, 151–200, 201–300.
Строя такую группировку, следует дифференцированно устанавливать границы интервалов для разных отраслей народного хозяйства. Это достигается путем использования группировок со специализированными интервалами.
Специализированные интервалы – применяются дли выделения из совокупности одних и тех же типов по одному и тому же признаку для явлений, находящихся в различных условиях.
При изучении социально-экономических явлений на макроуровне часто применяют группировки, интервалы которых не будут ни прогрессивно-возрастающими, ни прогрессивно-убывающими. Такие интервалы называются произвольными и, как правило, используются при группировке предприятий, например, по уровню рентабельности.
Пример. Далее на примере данных приведенных в табл. 5.1. произведем аналитическую группировку совокупности, включающей 30 банков.
Таблица 5.1 ‑ Совокупность 30 банков Российской Федерации
(на 01.01.19 г., цифры условные)
| Номер банка | Капитал, млн. руб. | Активы, млн. руб. |
Работающие активы, млн. руб |
| 1 | 2 | 3 | 4 |
| 1 | 207,7 | 2,48 | 1,14 |
| 2 | 200,3 | 2,40 | 1,10 |
| 3 | 190,2 | 2,28 | 1,05 |
| 4 | 323,2 | 3,88 | 1,88 |
| 5 | 247,1 | 2,96 | 1,36 |
| 6 | 177,7 | 2,12 | 0,97 |
| 7 | 242,5 | 2,90 | 1,33 |
| 8 | 182,9 | 2,18 | 0,99 |
| 9 | 315,6 | 3,78 | 1,73 |
| 10 | 183,2 | 2,20 | 1,01 |
| 11 | 320,2 | 3,84 | 1,76 |
| 12 | 207,3 | 2,48 | 1,14 |
| 13 | 181,0 | 2,17 | 0,99 |
| 14 | 172,4 | 2,06 | 0,94 |
| 15 | 234,3 | 2,81 | 1,29 |
| 16 | 189,5 | 2,27 | 1,04 |
| 17 | 187,8 | 2,24 | 1,03 |
| 18 | 166,9 | 1,99 | 0,91 |
| 19 | 157,7 | 1,88 | 0,86 |
| 20 | 168,3 | 2,02 | 0,93 |
| 21 | 224,4 | 2,69 | 1,23 |
| 22 | 166,5 | 1,99 | 0,91 |
| 23 | 198,5 | 2,38 | 1,09 |
| 24 | 240,4 | 2,88 | 1,32 |
| 25 | 229,3 | 2,75 | 1,26 |
| 26 | 175,2 | 2,10 | 0,96 |
| 27 | 156,0 | 1,87 | 0,86 |
| 28 | 160,1 | 1,92 | 0,88 |
| 29 | 178,7 | 2,14 | 0,98 |
| 30 | 171,6 | 2,05 | 0,94 |
По данным табл.5.1 группировочным (факторным) признаком является капитал, результативным – прибыль. Группировку производим по факторному признаку. Зададим количество групп (условно) – 4, а величину интервала определим по формуле (5.3).
Обозначим границы групп:
1-я группа – 156,0-197,8;
2-я группа – 197,8-239,6;
3-я группа – 239,6-281,4;
4-я группа – 281,4-323,2.
После того, как определен группировочный признак – капитал, задано число групп – 4 и образованы сами группы, необходимо отобрать показатели, которые характеризуют группы, и определить их величины по каждой группе.
Далее показатели, характеризующие банки, разносятся по четырем указанным группам и подсчитываются групповые итоги. Результаты группировки заносятся в таблицу и определяются общие итоги по совокупности единиц наблюдения по каждому показателю.
Таблица 5.2 ‑ Группировка коммерческих банков по величине капитала
| Группы банков
по величине капитала, млн. руб |
Число
банков |
Капитал,
млн. руб |
Активы,
млн. руб |
Работающие
активы, млн. руб |
| 156,0-197,8
197,8-239,6 239,6-281,4 281,4-323,2 |
17
7 3 3 |
2966,5
1501,8 730,0 958,8 |
35,48
17,99 8,74 11,5 |
16,25
8,25 4,01 5,37 |
| Итого | 30 | 6157,1 | 73,71 | 33,88 |
Структурная группировка коммерческих банков на основе данных таблицы 5.2 будет иметь вид:
Таблица 5.3 ‑ Группировка коммерческих банков по величине капитала (в % к итогу)
| Группы банков по величине капитала, млн. руб. | Число банков в % к итогу | Капитал | Активы | Работающие активы |
| 156,0-197,8 | 56,7 | 48,2 | 48,1 | 48,0 |
| 197,8-239,6 | 23,3 | 24,4 | 24,4 | 24,3 |
| 239,6-281,4 | 10,0 | 11,9 | 11,9 | 11,8 |
| 281,4-323,2 | 10,0 | 15,5 | 15,6 | 15,9 |
| Итого | 100,0 | 100,0 | 100,0 | 100,0 |
Из таблицы 5.3 видно, что в основном преобладают малые банки ‑ 56,7%, на долю которых приходится 48,2% всего капитала. Более конкретный анализ взаимосвязи показателей можно сделать на основе аналитической группировки.
Таблица 5.4 ‑ Группировка коммерческих банков по величине капитала
|
Группы банков по величине капитала, млн. руб. |
Число банков | Капитал, млн. руб. | Активы, млн. руб. | Работающие активы, млн. руб. | |||
| всего | в среднем на один банк | всего | в среднем на один банк | всего | в среднем на один банк | ||
| 156,0-197,8 | 17 | 2966,5 | 174,5 | 35,48 | 2,09 | 16,25 | 0,96 |
| 197,8-239,6 | 7 | 1501,8 | 214,5 | 17,99 | 2,57 | 8,25 | 1,18 |
| 239,6-281,4 | 3 | 730,0 | 243,3 | 8,74 | 2,91 | 4,01 | 1,34 |
| 281,4-323,2 | 3 | 958,8 | 319,6 | 11,5 | 3,83 | 5,37 | 1,79 |
| Итого | 30 | 6157,1 | 205,2 | 73,71 | 2,46 | 33,88 | 1,13 |
Величина капитала, все активы банка и работающие активы прямо зависят между собой, и чем крупнее банк, тем эффективнее управление работающими активами.
Мы рассмотрели примеры группировок по одному признаку. Однако в ряде случаев для решения поставленных задач такая группировка является недостаточной. В этих случаях переходят к группировке исследуемой совокупности по двум и более существенным признакам во взаимосвязи (комбинационной группировке).
От группировок следует отличать классификацию. Классификацией называется систематизированное распределение явлений и объектов на определенные группы, классы, разряды на основании их сходства и различия.
Ряды распределения представляют собой простейшую группировку, в которой каждая выделенная группа характеризуется только частотой.
В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения, построенные по качественным признакам, то есть признакам, характеризующим состояние изучаемого явления и не имеющим числового выражения.
Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Взятые за несколько периодов, эти данные позволяют исследовать изменение структуры.
Вариационными рядами называют ряды распределения, построенные по количественному признаку, т.е. признаку, имеющему числовое выражение у отдельных единиц совокупности. Вариационный ряд состоит из двух элементов: вариантов и частот.
Вариантами называются отдельные значения признака, которые он принимает в вариационном ряду, то есть конкретное значение варьирующего признака.
Частотами называются численности отдельных вариант, или каждой группы вариационного ряда. Частоты показывают, как часто встречаются те или иные значения признака в изучаемой совокупности. Сумма всех частот определяет численность всей совокупности, ее объем.
Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100%.
В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды.
Дискретный вариационный ряд ‑ это ряд распределения в котором группы составлены по признаку, изменяющемуся прерывно, т.е. через определенное число единиц и характеризуют распределение единиц совокупности по дискретному признаку, принимающему только целые значения.
Например, группы студентов по баллу в сессию по предмету: 5,4,3,2.
Интервальный вариационный ряд распределения – это ряд распределения, в котором группировочный признак, составляющий основание группировки, может принимать в интервале любые значения, отличающиеся друг от друга на сколь угодную малую величину
Построение интервальных вариационных рядов целесообразно прежде всего при непрерывной вариации признака, а также если дискретная вариация признака проявляется в широких пределах, то есть число вариантов дискретного признака достаточно велико.
Правила построения рядов распределения аналогичны правилам построения группировки.
Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения.
Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении оси абсцисс (х) и оси ординат (у) точки соединяются прямыми линиями, в результате чего получают ломаную линию, называемую полигоном частот. Иногда для замыкания полигона предлагается крайние точки (слева и справа на ломаной линии) соединить с точками на оси абсцисс, в результате чего получается многоугольник.
Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенным на соответствующих интервалах. Высота столбиков должна быть пропорциональна частотам. В результате получается график, на котором ряд распределения изображен в виде смежных друг с другом столбиков.
Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить прямыми линиями.
При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо сделать для устранения влияния величины интервала на распределение интервала и получения возможности сравнивать частоты.
Плотность распределения – это частота, рассчитанная на единицу ширины интервалу то есть, сколько единиц в каждой группе приходится на единицу величины интервала.
Для графического изображения вариационных рядов может использоваться кумулятивная кривая. При помощи кумуляты изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам. Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение.
При построении кумуляты интервального вариационного ряда по оси абсцисс (х) откладываются варианты ряда, а по оси ординат (у) накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, то есть кумуляту.
Если при графическом изображении вариационного ряда в виде кумуляты оси х и у поменять местами, то получим огиву.
Контрольные задания
- В чем суть и каково значение сводки как второго этапа статистического исследования?
- Какова роль группировок в статистике?
- Что такое ряды распределения?
- Дайте характеристику вариационному ряду.
- Пользуясь формулой Стерджесса, определите интервал группировки сотрудников фирмы по уровню доходов, если общая численность сотрудников составляет 50 человек, а минимальный и максимальный доход соответственно равен 50000 и 300000 рублей.
- По данным статистических сборников, постройте группировку численности безработных двух регионов по полу и возрасту (% к итогу) с целью приведения их к сопоставимому виду. Сделайте сравнительный анализ результатов.
- Имеются следующие данные об успеваемости в летнюю сессию 2019 г.: 5, 4, 4, 4. 3. 2, 5, 3, 4, 4, 4, 3, 2, 5, 2, 5, 5, 2, 3, 3. Постройте по этим данным: а) ряд распределения студентов по баллам оценок, полученных в сессию; б) ряд распределения студентов по уровню успеваемости, выделив в нем 2 группы студентов: не успевающие (2 балла), успевающие (3 балла и выше); в) каким видом ряда распределения (вариационным или атрибутивным) является каждый из этих двух рядов?
- Какие из указанных ниже группировок являются типологическими: а) группировка населения по полу; б) группировка населения по отраслям, занятого в народном хозяйстве; в) группировка вложений на строительство объектов производственного и непроизводственного назначения; г) группировка предприятий общественного питания по формам собственности.
Содержание курса лекций «Статистика»
11. Практическая работа №
4. Алгоритм построения группировки
В данной практической
работе мы с Вами подробно разберем алгоритмы построения группировки.
Из предыдущей лекции Вы
узнали, что группировки бывают структурные, типологические, аналитические и
сложные.
Рассмотрим каждый вид.
Структурные группировки
Пример 1:
требуется произвести группировку с равными интервалами по данным о стаже работы
рабочих участка. На участке работает 50 рабочих, со стажем работы от 0 до 26
лет.
1)
По формуле Стерджесса, рассмотренной в
предыдущей лекции рассчитаем оптимальное количество групп:
m = 1 + 3,322 × lg N ,
m
= 1 + 3,322 × lg 50
m
= 1+3,322×1,698970004336
m=6,64397835
Примем
оптимальное количество групп равным 7 исходя из правил округления.
2)
Далее рассчитывается постоянная ширина
интервалов. Так как вариация признака проявляется в сравнительно узких
границах, и распределение статистических единиц носит достаточно равномерный
характер, то строим группировку с равными интервалами.
Для равноинтервальной
группировки ширина интервала аi определяется
по формуле:
аi
= (Xmax
– Xmin)
/ m
аi =
(26-0) / 7
аi
= 3,71
Здесь округление идет по
правилам в большую сторону, следовательно
аi
= 4
3)
Определяются границы каждого интервала
4)
Подсчитывают число единиц, попавших в
интервал. Причём единицы, имеющие значение признака, равное граничному, относят
только к одному из интервалов
5)
Данные заносятся в таблицу
Пункт 4) и частично пункт
5) мы пока не выполняем, в рамках данной практической работы, так как для этого
необходимы знания из следующих лекций.
Итак, структурная
группировка, выполненная по рассчитанным параметрам приведена в таблице 1.
Таблица 1
Определение границ группировки по
интервалам
|
Номер группы |
Параметры групп, лет |
|
|
Границы интервалов |
||
|
нижняя |
верхняя |
|
|
1 |
0 |
4 |
|
2 |
4 |
8 |
|
3 |
8 |
12 |
|
4 |
12 |
16 |
|
5 |
16 |
20 |
|
6 |
20 |
24 |
|
7 |
24 |
28 |
|
Итого |
0 |
28 |
Определенных
выводов мы сейчас сделать не сможем, так как у нас намеренно нет данных о
конкретном стаже каждого из работников. Но если бы они у нас были, то таблица ,
например, выглядела бы уже так:
Таблица 2
Группировка рабочих участка по стажу
работы
|
Номер группы |
Параметры групп, лет |
Число рабочих в группе |
Удельный |
|
|
Границы интервалов |
||||
|
нижняя |
верхняя |
|||
|
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
4 |
6 |
12 |
|
2 |
4 |
8 |
8 |
16 |
|
3 |
8 |
12 |
11 |
22 |
|
4 |
12 |
16 |
13 |
26 |
|
5 |
16 |
20 |
6 |
12 |
|
6 |
20 |
24 |
4 |
8 |
|
7 |
24 |
28 |
2 |
4 |
|
Итого |
0 |
28 |
50 |
100 |
Дублирую
информацию, что исходные данные для заполнения столбца 4 «Число рабочих групп»
были намеренно не предоставлены, так как тема «Ряды распределения» еще не
изучена и ждет нас в следующей лекции.
Удельный
вес был рассчитан как деление параметра «Число рабочих в группе» на итоговое
значение (общее количество рабочих на участке).
Теперь, по проведенной
группировке можно сделать следующие выводы:
1. Больше всего на
участке имеется рабочих со стажем работы от 12 до 16 лет, они составляют 26% от
общей численности рабочих участка; меньше всего – со стажем от 24 до 28 лет, их
доля составляет 4%.
2. С увеличением стажа
работы число рабочих вначале растет, достигает максимума в 4-ой группе, а затем
снижается.
Типологические группировки
Пример 2.
Необходимо выполнить группировку населения поселка городского типа по
возрастному составу.
Выделяются 4 возрастные
категории: дошкольный возраст – до 7лет; школьный – с 7 до 17 лет; рабочий – с
17 до 55(60) лет; пенсионный – с 55 (60) лет.
По технике выполнения
типологическая группировка похожа на структурную группировку, за исключением
первых этапов – группировочный признак, количество групп, их параметры
определяются на основе качественного анализа.
В таких группировках
очень часто применяются специализированные интервалы. Типологические
группировки представляются в табличной форме, объектом анализа в них являются
показатели структуры.
Пример типологической
группировки приведен в Таблице 3.
Таблица 3
Определение границ группировки
|
Возрастные категории |
Границы интервалов , |
|
|
нижняя |
верхняя |
|
|
1 |
2 |
3 |
|
дошкольный |
до |
7 |
|
школьный |
7 |
17 |
|
рабочий |
17 |
55(60) |
|
пенсионный |
55(60) |
и более |
|
Итого |
Аналогично предыдущему
примеру вывод сделать невозможно, так как у нас нет данных о конкретном
количестве населения и их возрасте. Но если бы они у нас были, то таблица, выглядела
бы так:
Таблица 4
Группировка населения поселка городского
типа по возрастным категориям.
|
Возрастные категории |
Границы интервалов , |
Численность в |
Показатель структуры |
|
|
нижняя |
верхняя |
|||
|
1 |
2 |
3 |
4 |
5 |
|
дошкольный |
до |
7 |
192 |
14,32 |
|
школьный |
7 |
17 |
218 |
16,26 |
|
рабочий |
17 |
55(60) |
574 |
42,80 |
|
пенсионный |
55(60) |
и более |
357 |
26,62 |
|
Итого |
1341 |
100 |
Вывод: наибольшее
количество человек в поселке относятся к группе «рабочие» – 574 человека, и
они составляют 42,8% от общей численности; меньше всего группа «Дошкольники» – 192
человека, их доля составляет 14,32%.
Аналитические группировки
Аналитические группировки
отличаются от структурных и типологических по технике выполнения, которая
заключается в следующем:
1. Производится
группировка единиц совокупности по факторному признаку, она выполняется как
структурная.
2. В каждой выделенной
группе отбираются соответствующие значения результативного признака, и на их
основе рассчитывается некоторый обобщающий показатель, обычно, среднее
значение.
3. Анализируются
изменения обобщающего показателя – среднего значения результативного признака
по группам, и делается вывод о наличии или отсутствии взаимосвязи и ее
направлении. Если при изменении значений факторного признака, положенного в
основу группировки изменяется величина результативного, то признается наличие
связи между признаками; при этом, если с увеличением значений факторного
признака увеличивается значение результативного, то связь относится к прямой;
в противном случае – к обратной.
Пример 3.
Необходимо установить зависимость между стажем работы и величиной заработной
платы рабочих участка. По каждому рабочему известны стаж работы и месячная
заработная плата.
В рассматриваемом примере
факторным признаком является стаж работы, результативным – величина заработной
платы.
По факторному признаку
ранее была проведена структурная группировка (см. пример 1). Рабочие были
разбиты на 7 однородных групп.
Дополнительно в каждой
группе была рассчитана суммарная заработная плата рабочих за месяц и средняя ее
величина по формуле средней арифметической.
Результаты расчета
приведены в таблице 5.
Таблица 5.
Исследование зависимости заработной платы
рабочих участка от стажа работы.
|
Номер группы |
Параметры групп, лет |
Число рабочих в группе |
Общая |
Средняя |
|
|
Границы интервалов |
|||||
|
нижняя |
верхняя |
||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
4 |
6 |
18000 |
3000 |
|
2 |
4 |
8 |
8 |
28000 |
3500 |
|
3 |
8 |
12 |
11 |
41800 |
3800 |
|
4 |
12 |
16 |
13 |
59800 |
4600 |
|
5 |
16 |
20 |
6 |
34800 |
5800 |
|
6 |
20 |
24 |
4 |
27200 |
6800 |
|
7 |
24 |
28 |
2 |
14800 |
7400 |
|
Итого |
0 |
28 |
50 |
224405 |
Объектом анализа в этой
таблице является среднее значение результативного признака – среднемесячная заработная
плата рабочих в группах. Если среднее значение результативного признака,
установленное по группам имеет некоторое различие, то связь между признаками
можно считать установленной. Если средний результат при переходе от одной
группе к другой практически не меняется, то связь между признаками отсутствует.
В рассматриваемом примере изменение стажа работы приводит к изменению
заработной платы. Таким образом, с помощью аналитической группировки можно
установить наличие связи между признаками, но описать ее нельзя.
Сложные группировки
Сложные группировки
делятся на комбинационные и многомерные.
Комбинационные группировки
выполнятся по нескольким признакам последовательно. Последовательность
устанавливается исходя из логики взаимосвязи показателей. Как правило,
группировку начинают с атрибутивного признака. При комбинационной группировке
совокупность логически последовательно разбивается на однородные части по
отдельным признакам: на группы – по одному признаку, затем внутри каждой группы
по второму признаку – на подгруппы и т.д.
Комбинационная
группировка по двум признакам (X, Y) оформляется в виде шахматной
таблицы, в которой значения одного признака X откладываются по строкам,
а значения второго признака Y – по столбцам. На пересечении j–ого
столбца и i-ой строки (в теле таблицы) находятся частоты совместного
проявления значения признака Y в j-ом столбце и значения признака
X в i -ой строке.
При выполнении
многомерных группировок могут быть использованы два основных подхода:
• Первый заключается в
том, что рассчитывается обобщающий показатель по совокупности группировочных признаков
и проводится простая группировка по этому обобщающему показателю.
• Второй подход состоит в
использовании методом кластерного анализа.
Представителем первого
подхода является метод многомерной средней, алгоритм которого
заключается в следующем:
1. Составляется матрица
абсолютных значений признаков по всем статистическим единицам xij ,
i=1,n
– статистические единицы
j=1,k
– признаки
2. Абсолютные значения
признаков заменяются их нормированными по среднему значению уровнями:
Pij
= xij /хj,
где
Pij –
нормированное значение j-ого признака у i-ой
статистической единицы
xj
– среднее значение j-того признака
3. Для каждой
статистической единицы рассчитывается многомерная средняя:
k – число оснований
группировки
4. В соответствии со
значениями многомерной средней совокупность разделяется на однородные группы,
то есть выполняется простая группировка по многомерной средней.
Пример 4.
Необходимо выделить однородные группы статистических единиц по трем признакам,
объем статистической совокупности составляет 10 объектов, каждый из которых
характеризуется условными значениями признаков. Исходные данные и расчет
многомерной средней представлен в таблице 6.
Таблица 6
Расчет многомерной средней
|
Номер объекта |
Абсолютные значения признаков |
Нормированные значения признаков |
Расчет многомерной средней |
|||||
|
xi1 |
xi2 |
xi3 |
Pi1 |
Pi2 |
Pi3 |
Сумма нормированных по среднему значению уровней |
многомерная средняя |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
2 |
18 |
62 |
0,57 |
1,67 |
1,00 |
3,24 |
1,08 |
|
2 |
1 |
5 |
40 |
0,29 |
0,46 |
0,64 |
1,39 |
0,46 |
|
3 |
2 |
7 |
40 |
0,57 |
0,65 |
0,64 |
1,86 |
0,62 |
|
4 |
6 |
15 |
77 |
1,71 |
1,39 |
1,24 |
4,34 |
1,45 |
|
5 |
1 |
9 |
43 |
0,29 |
0,83 |
0,69 |
1,81 |
0,60 |
|
6 |
6 |
20 |
95 |
1,71 |
1,85 |
1,53 |
5,10 |
1,70 |
|
7 |
5 |
9 |
62 |
1,43 |
0,83 |
1,00 |
3,26 |
1,09 |
|
8 |
1 |
1 |
46 |
0,29 |
0,09 |
0,74 |
1,12 |
0,37 |
|
9 |
8 |
15 |
84 |
2,29 |
1,39 |
1,35 |
5,03 |
1,68 |
|
10 |
3 |
9 |
72 |
0,86 |
0,83 |
1,16 |
2,85 |
0,95 |
|
Итого |
35 |
108 |
621 |
10,00 |
10,00 |
10,00 |
10,00 |
10,00 |
|
среднее значение |
3,50 |
10,80 |
62,10 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1)
Итак, абсолютные значения признаков
(столбец 2,3,4) нам даны, мы их не рассчитывали, это просто исходные данные.
2)
Далее , столбец 5 рассчитывается по
формуле из пункта 2.
Например,
для объекта под номером 1 нормированное значение признака Pi1 рассчитывается следующим образом –
2/3,5
= 0,57
Для
объекта под номером 2 –
1/3,5
= 0,29
И
так далее.
3)
Столбцы 6 и 7 рассчитываются аналогично с
подстановкой своих абсолютных значений признака и средней.
4)
Далее рассчитываем сумму
нормированных по среднему значению уровней, это наш числитель из формулы многомерной
средней (пункт 3).
Например для объекта номер 1, сумма считается следующим образом :
0,57+1,67+1,00 = 3,24
Для объекта номер 2 –
0,29+0,46+0,64 = 1,39
И далее, по аналогии, для каждого объекта.
5)
Для каждой статистической единицы рассчитывается
многомерная средняя по формуле из пункта 3.
Например
, для объекта номер 1 формула расчет будет следующий:
3,24/3
= 1,08
Для
объекта номер 2 :
1,39/3
= 0,46
И далее, по аналогии, для каждого объекта.
Таким образом, для
каждого из 10 объектов рассчитана условная характеристика – многомерная
средняя, заменяющая три первоначальных признака.
По многомерной средней как
группировочному признаку, необходимо выполнить одномерную структурную
группировку.
Для этого определяется:
• Количество однородных
групп по уже известной нам формуле Стерджесса.
m = 1 + 3,322 × lg N ,
m
= 1 + 3,322 × lg 10
m
= 1+3,322×1
m=4,322
m
= 4
• Ширина интервалов
аi
= (Xmax
– Xmin)
/ m
аi =
(1,7-0,37) / 4
аi
= 0,33
Структурная группировка
представлена в таблице 7.
Таблица 7
Группировка объектов по многомерной
средней
|
Номер групп |
Параметры групп |
Номера объектов |
Количество объектов |
|
|
xiн |
xiв |
|||
|
1 |
2 |
3 |
5 |
6 |
|
1 |
0,38 |
0,71 |
2, 3, 5, 8 |
4 |
|
2 |
0,71 |
1,04 |
10 |
1 |
|
3 |
1,04 |
1,37 |
1,7 |
2 |
|
4 |
1,37 |
1,7 |
4,6,9 |
3 |
|
Итого |
0,38 |
1,7 |
10 |
В столбце номер 5 мы
указали номера объектов, которые подходят (включаются) в данную группировку,
исходя из значения многомерной средней (таблица 6), а в столбце 6 мы просто
указали общее число объектов, включенных в ту или иную группу.
Таким образом, 10 объектов
были распределены по 4-м однородным группам.
При втором подходе
к выполнению многомерных группировок каждая единица совокупности, обладающая
набором из k признаков рассматривается как точка в k-мерном пространстве –
пространстве признаков, а каждому признаку придается смысл координаты.
Задача классификации в
этом случае сводится к выделению сгущений объектов в этом пространстве. Для
этого используются различные алгоритмы, но всегда однородные группы выделяются
на основании близости объектов по совокупности признаков.
Мерой близости объектов,
то есть мерой сходства единиц совокупности, могут служить различные критерии.
Выделяют три типа мер
сходства:
• коэффициенты подобия;
• коэффициенты корреляции;
• показатели расстояния.
Коэффициенты подобия
используются для измерения степени близости между парой объектов, каждый из
признаков которых принимает значения 0 или 1.
Наиболее простой
коэффициент подобия рассчитывается по формуле:
Sij
= Pij /
m
Где, Pij –
число совпадений признаков у объектов i и j;
m – общее число
признаков, по которым осуществляется сравнение.
0 ≤ Pij ≤ 1
Коэффициенты корреляции
используются как измерители силы связи между статистическими единицами или
между признаками. Для измерения тесноты связи количественных признаков
применяют коэффициенты линейной корреляции.
В кластерном анализе
мерой сходства является мера расстояния между двумя объектами i
и j.
Для количественных
признаков используется Евклидово расстояние:
где Pi1 , Pj1
– стандартизованные значения 1-ого признака i-ого и j-ого объекта наблюдения.
Статистическая сводка и группировка
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Статистическая сводка
Процесс
упорядочения, систематизации и обобщения данных называется статистической
сводкой. В результате определенным образом выполненной обработки статистических
данных представляется возможным выявить сущность социально-экономических
явлений, характерные черты и существенные особенности отдельных объектов или их
групп, обнаружить закономерности и тенденции их развития.
Сводка
статистических данных осуществляется по заранее разработанным программе и
плану. При разработке программы определяются статистические подлежащее и
сказуемое. Подлежащее – это объект исследования, расчлененный на группы и
подгруппы; сказуемое – статистические показатели, которые характеризуют
подлежащее сводки.
Программа
сводки определяется задачами статистического исследования, которые можно свести
к следующим положениям:
-
выделение групп, на которые может быть расчленена изучаемая совокупность
явлений; -
определение перечня группировочных признаков, позволяющих произвести
разграничение единиц совокупности; -
обозначение границ интервалов групп при классификации по количественным
признакам; -
разработка системы статистических показателей для характеристики выделенных
групп.
В плане
сводки решаются вопросы о способах ее осуществления (вручную или с
использованием средств вычислительной техники), последовательности отдельных
операций сводки, выделении этапов сводки, выполняемых в децентрализованном и
централизованном порядке, сроках выполнения каждого этапа сводки, способах
представления результатов сводки (ряды распределения, статистические таблицы,
статистические графики и т. д.).
Статистическая группировка
Группировка
– это разделение изучаемой совокупности по значениям одного или нескольких
признаков на качественно однородные группы и характеристика этих групп с помощью
определенной системы показателей.
В
зависимости от поставленной цели и конкретного содержания исследуемого
материала посредством группировок решают три основные задачи:
- выделение социально-экономических типов явлений (процессов);
- выявление состава (структуры) изучаемой совокупности;
- установление причинно-следственных связей между признаками явлений (процессов).
Соответственно
перечисленным выше задачам используются три вида группировок: типологические,
структурные и аналитические (факторные).
Построение
группировки предполагает определение группировочного признака или основания
группировки, т. е. признака, по которому совокупность будет расчленена на
группы. Группировочные признаки могут быть количественными (возраст, уровень
производительности труда, рентабельность и т. д.) и атрибутивными (пол,
профессия, регионы и т. д.).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Величина интервалов и формула Стерджесса
При
построении группировки по количественному признаку устанавливаются границы
выделяемых групп. В этом случае, решая вопрос о величине интервала группировки
(или о числе групп), следует выбирать такое число групп, чтобы сводную
информацию можно было достаточно легко интерпретировать.
Величина
интервала при выборе равных интервалов группировки и известном числе групп
определяется по формуле:
где
и
– максимальное и минимальное значения
группировочного признака;
– число выделяемых групп.
Хороший
способ приближенного определения интервала группировки при неизвестном
изначально числе групп может быть получен на основании формулы Стерджесса:
где
– число единиц совокупности
Величина
равного интервала при построении используется обычно в тех случаях, когда
соотношение максимального и минимального значений группировочного признака в
вариационном ряду распределения не превышает десятикратного значения. При
значительной вариации группировочного признака целесообразно применять кратные
интервалы. В практике статистических исследований обычно используют удвоенные
кратные интервалы, т. е. величина каждого последующего интервала по сравнению с
предыдущим удваивается.
В
отдельных случаях статистика использует также неравные интервалы (например, при
большом объеме изучаемой совокупности, сильной колеблемости группировочного
признака и т. д.) и стандартные шкалы интервалов.
Интервалы
группировки считаются обоснованными, если коэффициенты вариации анализируемых
признаков по группам не превышают 33 %.
Вторичная группировка
Специфическим
видом группировок является так называемая вторичная группировка — операция
образования новых групп на основании уже имеющейся группировки.
Вторичная
группировка может строиться путем непосредственного укрупнения групп и по
способу пропорционального дробления групп.
Смежные темы решебника:
- Полигон, гистограмма, кумулята, огива
- Показатели вариации
- Эмпирическое корреляционное отношение
Примеры решения задач
Пример 1
По данным
таблицы произвести группировку заводов по производству продукции за отчетный
период, образовав пять групп заводов. Каждую группу охарактеризуйте числом
заводов, числом работающих, среднегодовой стоимостью ОПФ. Наряду с абсолютными
показателями по группам, вычислить их процентное соотношение. Сделать выводы.
Показатели 24-х заводов отрасли
| Номер п/п |
Среднегодовая стоимость ОПФ, млн. руб. |
Среднесписочное число работающих за отчетный период, чел. |
Производство продукции за отчетный период, млн.р. |
| 1 | 4,3 | 142,0 | 1,8 |
| 2 | 3,5 | 143,0 | 4,0 |
| 3 | 4,3 | 134,0 | 12,7 |
| 4 | 2,1 | 159,0 | 9,2 |
| 5 | 7,2 | 137,0 | 5,7 |
| 6 | 3,2 | 88,0 | 16,7 |
| 7 | 7,5 | 91,0 | 6,1 |
| 8 | 5,2 | 57,0 | 19,5 |
| 9 | 5,7 | 157,0 | 7,9 |
| 10 | 9,1 | 79,0 | 15,8 |
| 11 | 2,6 | 97,0 | 16,1 |
| 12 | 1,1 | 85,0 | 12,2 |
| 13 | 6,0 | 100,0 | 7,1 |
| 14 | 2,4 | 149,0 | 11,7 |
| 15 | 3,7 | 151,0 | 13,2 |
| 16 | 5,4 | 138,0 | 11,7 |
| 17 | 5,7 | 74,0 | 1,2 |
| 18 | 2,7 | 91,0 | 16,8 |
| 19 | 4,3 | 77,0 | 1,2 |
| 20 | 4,5 | 160,0 | 3,0 |
| 21 | 2,1 | 90,0 | 6,3 |
| 22 | 3,9 | 88,0 | 8,7 |
| 23 | 1,0 | 83,0 | 8,5 |
| 24 | 3,4 | 109,0 | 17,1 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
При построении группировки с равными
интервалами величина интервала h определяется по формуле
где
– наибольшее
и наименьшее значения признака в исследуемой совокупности
k- число групп
При
. границы интервалов имеют следующий вид:
| Номер группы | Нижняя граница, млн. руб. | Верхняя граница, млн. руб. |
| 1 | 1,2 | 4,9 |
| 2 | 4,9 | 8,6 |
| 3 | 8,6 | 12,3 |
| 4 | 12,3 | 16 |
| 5 | 16 | 19,7 |
Расположим предприятия по
возрастанию группировочного признака:
Расчетная вспомогательная таблица
| Группы предприятий, млн.р. | Номер п/п |
Среднегодовая стоимость ОПФ, млн. руб. |
Среднесписочное число работающих за отчетный период, чел. |
Производство продукции за отчетный период, млн.р. |
| 1,2 – 4,9 | 17 | 5,7 | 74 | 1,2 |
| 19 | 4,3 | 77 | 1,2 | |
| 1 | 4,3 | 142 | 1,8 | |
| 20 | 4,5 | 160 | 3 | |
| 2 | 3,5 | 143 | 4 | |
| Всего | 5 | 22,3 | 596 | 11,2 |
| 4,9 – 8,6 | 5 | 7,2 | 137 | 5,7 |
| 7 | 7,5 | 91 | 6,1 | |
| 21 | 2,1 | 90 | 6,3 | |
| 13 | 6 | 100 | 7,1 | |
| 9 | 5,7 | 157 | 7,9 | |
| 23 | 1 | 83 | 8,5 | |
| Всего | 6 | 29,5 | 658 | 41,6 |
| 8,6 – 12,3 | 22 | 3,9 | 88 | 8,7 |
| 4 | 2,1 | 159 | 9,2 | |
| 14 | 2,4 | 149 | 11,7 | |
| 16 | 5,4 | 138 | 11,7 | |
| 12 | 1,1 | 85 | 12,2 | |
| Всего | 5 | 14,9 | 619 | 53,5 |
| 12,3 – 16 | 3 | 4,3 | 134 | 12,7 |
| 15 | 3,7 | 151 | 13,2 | |
| 10 | 9,1 | 79 | 15,8 | |
| Всего | 3 | 17,1 | 364 | 41,7 |
| 16 – 19,7 | 11 | 2,6 | 97 | 16,1 |
| 6 | 3,2 | 88 | 16,7 | |
| 18 | 2,7 | 91 | 16,8 | |
| 24 | 3,4 | 109 | 17,1 | |
| 8 | 5,2 | 57 | 19,5 | |
| Всего | 5 | 17,1 | 442 | 86,2 |
Получаем следующую группировку:
Группировка предприятий по признаку “Производство продукции”
|
Производство продукции за отчетный период, млн. р. |
Число предприятий | Число работающих |
Среднегодовая стоимость ОПФ |
|||
| ед. | в % к итогу | чел. | в % к итогу | млн.р. | в % к итогу | |
| 1,2 – 4,9 | 5 | 20,8 | 596 | 22,2 | 22,3 | 22,1 |
| 4,9 – 8,6 | 6 | 25,0 | 658 | 24,6 | 29,5 | 29,2 |
| 8,6 – 12,3 | 5 | 20,8 | 619 | 23,1 | 14,9 | 14,8 |
| 12,3 – 16 | 3 | 12,5 | 364 | 13,6 | 17,1 | 16,9 |
| 16 – 19,7 | 5 | 20,8 | 442 | 16,5 | 17,1 | 16,9 |
| Итого | 24 | 100,0 | 2679 | 100,0 | 100,9 | 100,0 |
Вывод к задаче
Таким образом наиболее у наиболее
многочисленной группы предприятий производство продукции находится в пределах
от 4,9 до 8,6 млн.р. Эта группа по численности составляет 25% от исследуемой
совокупности, в ней работает 24,6% работающих, а стоимость ОПФ составляет 29,5%
от итоговой. В самой малочисленной группе производится от 12,3 до 16 млн.р., в
ней работает 13,6% работающих, а стоимость ОПФ составляет 16,9% от итоговой.
Пример 2
Для
выявления взаимосвязи между среднегодовой стоимостью основных фондов и стоимостью
произведенной продукции произведите аналитическую группировку предприятий,
выделив четыре группы предприятий по стоимости основных фондов с равными
интервалами.
Стоимость основных фондов и
произведенной продукции по 20 предприятиям отрасли, млн. ден.ед.
| № п/п |
Среднегодовая стоимость основных фондов |
Стоимость произведенной продукции |
| 1 | 62 | 71 |
| 2 | 72 | 79 |
| 3 | 74 | 85 |
| 4 | 24 | 30 |
| 5 | 41 | 52 |
| 6 | 46 | 56 |
| 7 | 54 | 54 |
| 8 | 144 | 166 |
| 9 | 140 | 160 |
| 10 | 118 | 139 |
| 11 | 122 | 143 |
| 12 | 78 | 84 |
| 13 | 82 | 95 |
| 14 | 82 | 92 |
| 15 | 88 | 99 |
| 16 | 86 | 104 |
| 17 | 90 | 101 |
| 18 | 94 | 112 |
| 19 | 100 | 115 |
| 20 | 112 | 123 |
| Итого | 1709 | 1960 |
Определите
по каждой группе и в целом по отрасли:
- количество предприятий;
- стоимость основных фондов: всего и в среднем на одно предприятие;
- стоимость произведенной продукции: всего и в среднем на одно предприятие;
- стоимость произведенной продукции на рубль основных фондов (фондоотдачу);
Результаты
расчетов представьте в таблице. Сделайте выводы.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
При построении группировки с равными
интервалами величина интервала h определяется по формуле
где
– наибольшее
и наименьшее значения признака в исследуемой совокупности
k- число групп
При
границы интервалов
имеют следующий вид:
| Номер группы | Нижняя граница, млн. д.е. | Верхняя граница, млн. д.е. |
| 1 | 24 | 54 |
| 2 | 54 | 84 |
| 3 | 84 | 114 |
| 4 | 114 | 144 |
Расположим
предприятия по возрастанию группировочного признака:
Расчетная вспомогательная таблица
|
Группы предприятий, млн.д.е. |
№ п/п |
Среднегодовая стоимость основных фондов, млн.д.е. |
Стоимость произведенной продукции, млн.д.е. |
| 4 | 24 | 30 | |
| 24-54 | 5 | 41 | 52 |
| 6 | 46 | 56 | |
| Итого | 3 | 111 | 138 |
| 7 | 54 | 54 | |
| 54-84 | 1 | 62 | 71 |
| 2 | 72 | 79 | |
| 3 | 74 | 85 | |
| 12 | 78 | 84 | |
| 13 | 82 | 95 | |
| 14 | 82 | 92 | |
| Итого | 7 | 504 | 560 |
| 16 | 86 | 104 | |
| 84-114 | 15 | 88 | 99 |
| 17 | 90 | 101 | |
| 18 | 94 | 112 | |
| 19 | 100 | 115 | |
| 20 | 112 | 123 | |
| Итого | 6 | 570 | 654 |
| 10 | 118 | 139 | |
| 114-144 | 11 | 122 | 143 |
| 9 | 140 | 160 | |
| 8 | 144 | 166 | |
| Итого | 4 | 524 | 608 |
Получаем следующую группировку:
Группировка предприятий отрасли
| Группы предприятий, млн.д.е. | Число предприятий | Среднегодовая стоимость основных фондов, млн.д.е. | Стоимость произведенной продукции, млн.д.е. | Фондоотдача, ден.ед. | ||
| всего | на одно предприятие | всего | на одно предприятие | |||
| 24-54 | 3 | 111 | 37,0 | 138 | 46 | 1,243 |
| 54-84 | 7 | 504 | 72,0 | 560 | 80 | 1,111 |
| 84-114 | 6 | 570 | 95,0 | 654 | 109 | 1,147 |
| 114-144 | 4 | 524 | 131,0 | 608 | 152 | 1,160 |
| Итого | 20 | 1709 | 85,5 | 1960 | 98 | 1,147 |
Вывод к задаче
Таким
образом с увеличением среднегодовой стоимости основных фондов увеличивается
стоимость произведенной продукции. Фондоотдача также имеет тенденцию к
увеличению. Средняя фондоотдача по всей совокупности предприятий составила
1,147 ден.ед.
Пример 3
Имеются
данные об уровне выполнения норм выработки рабочими двух цехов
машиностроительного предприятия:
| Цех №1 | Цех №2 | ||
| Уровень выполнения норм выработки | Число рабочих | Уровень выполнения норм выработки | Число рабочих |
| до 90 | 4 | до 93,9 | 6 |
| 90 – 90,9 | 16 | 94 – 98,9 | 15 |
| 94 – 99,9 | 24 | 99 – 100,9 | 14 |
| 100-105,9 | 66 | 101 – 104,9 | 28 |
| 106-109,9 | 40 | 105 – 108,9 | 36 |
| 110 и выше | 25 | 109 – 114,9 | 18 |
| 115 и выше | 13 | ||
| Итого | 175 | Итого | 130 |
Приведите
данные к сопоставимости. Определите, какова доля не выполняющих норму рабочих в
каждом цехе. Сделайте вывод, в каком из цехов уровень выполнения норм выработки
лучше.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Осуществим
вторичную группировку по обеим цехам по способу пропорционального дробления.
Данные
разобьем на 4 группы по выработке:
до 100
100 –
104,9
105-
109,9
110 и
выше
Цех №1:
Число рабочих в 1-й
группе (<100):
Число рабочих во 2-й
группе (100-104,9):
Число рабочих во 3-й
группе (105-109,9):
Число рабочих во 3-й
группе (110 и выше):
Цех №2:
Число рабочих в 1-й группе
(<100)
Число рабочих во 2-й
группе (100-104,9)
Число рабочих во 3-й
группе (105-109,9)
Число рабочих во 3-й
группе (110 и выше)
Получаем:
Вторичная группировка
| Цех №1 | Цех №2 | ||
| Уровень выполнения норм выработки | Число рабочих | Уровень выполнения норм выработки | Число рабочих |
| до 100 | 44 | до 100 | 28 |
| 100 – 104,9 | 55 | 100 – 104,9 | 35 |
| 105 – 109,9 | 51 | 105 – 109,9 | 39 |
| 110 и выше | 25 | 110 и выше | 28 |
| Итого | 175 | 130 |
Доля
рабочих, не выполняющих норму в 1-м цехе:
Доля
рабочих, не выполняющих норму во 2-м цехе:
Вывод к задаче
Таким
образом, выполнение норм выработки во 2-м цехе лучше, чем в первом.
Пример 4
Имеются
следующие данные о распределении сельскохозяйственных предприятий региона по
величине валовой продукции:
|
Группы сельскохозяйственных предприятий по величине валовой продукции, млн.руб. |
Число предприятий, в % к итогу | Валовая продукция, в % к итогу |
| до 100 | 10 | 17,9 |
| 100-300 | 60 | 42,4 |
| свыше 300 | 30 | 39,7 |
| Итого | 100,0 | 100,0 |
Применяя
метод вторичной группировки, образуйте группы сельскохозяйственных предприятий
по величине валовой продукции, млн.р.
до 10,
10-50, 50-100, 100-200, 200-250, свыше 250.
По каждой
группе рассчитайте оба показателя.
Решение
Осуществим
вторичную группировку по способу пропорционального дробления групп:
В первую группу
войдет 1/10 часть 1-го интервала
Во вторую группу
войдет 2/5 части 1-го интервала
В третью группу
войдет половина 1-го интервала
В четвертую группу
войдет 4/5 части 2-го интервала
В пятую группу войдет
1/5 часть 2-го интервала и 3-й интервал
Вторичная группировка
|
Группы сельскохозяйственных предприятий по величине валовой продукции, млн.руб. |
Число предприятий, % к итогу |
Стоимость реализованной продукции, % к итогу |
| до 10 | 1 | 1,79 |
| 10-50 | 4 | 7,16 |
| 50-100 | 5 | 8,95 |
| 100-250 | 48 | 33,92 |
| свыше 250 | 42 | 48,18 |
| Итого | 100,0 | 100,0 |
Задачи контрольных и самостоятельных работ
Задача 1
1.
Произведите группировку магазинов №№5…27 по признаку относительного уровня
издержек обращения (в% к розничным продажам), образовав при этом 4 группы с
равными интервалами.
2.
Охарактеризуйте каждую группу и всю совокупность магазинов числом магазинов,
размером розничных продаж, издержек обращения и торговой площади.
3.
Определите средние размеры розничных продаж, издержек обращения и торговой
площади, приходящиеся на один магазин.
4.
Определите средний относительный уровень издержек обращения по каждой группе и
в целом.
Полученные
результаты оформите в виде статистической таблицы. Сделайте выводы.
| Номер магазина |
Розничные продажи (млрд. руб.) |
Издержки обращения (млрд. руб.) | Стоимость основных средств (среднегодовая) (млрд. руб.) | Численность продавцов (чел.) | Торговая площадь (м2) |
| 5 | 235 | 24,8 | 7,8 | 132 | 1335 |
| 6 | 80 | 9,2 | 2,2 | 41 | 946 |
| 7 | 113 | 10,9 | 3,2 | 40 | 1435 |
| 8 | 300 | 30,1 | 6,8 | 184 | 1820 |
| 9 | 142 | 16,7 | 5,7 | 50 | 1256 |
| 10 | 280 | 46,8 | 6,3 | 105 | 1353 |
| 11 | 156 | 30,4 | 5,7 | 57 | 1138 |
| 12 | 213 | 28,1 | 5,0 | 100 | 1216 |
| 13 | 298 | 38,53 | 6,7 | 112 | 1352 |
| 14 | 242 | 34,2 | 6,5 | 106 | 1445 |
| 15 | 130 | 20,1 | 4,8 | 62 | 1246 |
| 16 | 184 | 22,3 | 6,8 | 60 | 1332 |
| 17 | 96 | 9,8 | 3,0 | 34 | 680 |
| 18 | 304 | 38,7 | 6,9 | 109 | 1435 |
| 19 | 95 | 11,7 | 2,8 | 38 | 582 |
| 20 | 352 | 40,1 | 8,3 | 115 | 1677 |
| 21 | 101 | 13,6 | 3,0 | 40 | 990 |
| 22 | 148 | 21,6 | 4,1 | 50 | 1354 |
| 23 | 74 | 9,2 | 2,2 | 30 | 678 |
| 24 | 135 | 20,2 | 4,6 | 52 | 1380 |
| 25 | 320 | 40,0 | 7,1 | 140 | 1840 |
| 26 | 155 | 22,4 | 5,6 | 50 | 1442 |
| 27 | 262 | 29,1 | 6,0 | 102 | 1720 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Имеются
следующие данные об урожайности картофеля и количеством внесенных минеральных
удобрений по 10 сельскохозяйственным предприятиям:
| Номер колхоза | Урожайность, ц/га |
Внесено минеральных удобрений на 1 га, кг |
Номер колхоза | Урожайность, ц/га |
Внесено минеральных удобрений на 1 га, кг |
| 1 | 128 | 140 | 6 | 183 | 197 |
| 2 | 179 | 262 | 7 | 201 | 246 |
| 3 | 221 | 289 | 8 | 195 | 276 |
| 4 | 136 | 191 | 9 | 141 | 187 |
| 5 | 164 | 202 | 10 | 192 | 253 |
Для
изучения зависимости между урожайностью картофеля и внесенными минеральными
удобрениями произведите группировку сельскохозяйственных предприятий, образовав
3 группы предприятий с равными интервалами. По каждой группе и по совокупности
в целом подсчитайте:
1) число
предприятий;
2)
среднюю урожайность картофеля;
3)
средний объем внесенных минеральных удобрений на 1 га, кг.
Результаты
представьте в таблице и сделайте выводы.
Задача 3
Имеются
следующие данные о распределении сельскохозяйственных предприятий региона по
величине валовой продукции:
|
Группы сельскохозяйственных предприятий по величине валовой продукции, млн.руб. |
Число предприятий, в % к итогу | Валовая продукция, в % к итогу |
| до 100 | 10 | 17,9 |
| 100-300 | 60 | 42,4 |
| свыше 300 | 30 | 39,7 |
| Итого | 100,0 | 100,0 |
Применяя
метод вторичной группировки, образуйте группы сельскохозяйственных предприятий
по величине валовой продукции, млн.р.
до 10,
10-50, 50-100, 100-200, 200-250, свыше 250.
По каждой
группе рассчитайте оба показателя.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Используя
данные по варианту задания, выполнить следующие расчеты:
1.
Сгруппировать показатели.
2.
Согласно полученной группировки рассчитать моду и медиану.
3.
Рассчитать средние величины, дисперсию и коэффициент вариации.
4. Найти
уровень взаимосвязи между показателями при помощи корреляционно-регрессионного
анализа.
Имеются
данные о деятельности банков одного из регионов.
| № п/п |
Срок функционирования, лет |
Объем привлеченных средств, млн. ден.ед. |
| 1 | 7 | 46 |
| 2 | 4 | 40 |
| 3 | 3 | 38 |
| 4 | 7 | 49 |
| 5 | 2 | 41 |
| 6 | 9 | 55 |
| 7 | 6 | 60 |
| 8 | 12 | 58 |
| 9 | 3 | 38 |
| 10 | 9 | 56 |
| 11 | 5 | 48 |
| 12 | 2 | 40 |
| 13 | 10 | 62 |
| 14 | 4 | 54 |
| 15 | 7 | 57 |
| 16 | 2 | 43 |
| 17 | 3 | 46 |
| 18 | 10 | 58 |
| 19 | 5 | 53 |
| 20 | 8 | 51 |
| 21 | 3 | 42 |
| 22 | 6 | 58 |
| 23 | 8 | 56 |
| 24 | 9 | 49 |
| 25 | 10 | 47 |
| 26 | 4 | 43 |
| 27 | 9 | 46 |
| 28 | 11 | 48 |
| 29 | 5 | 57 |
| 30 | 8 | 59 |
| Итого |
На основе соответствующих вашему
варианту данных построить интервальный вариационный ряд банков по объему
привлеченных средств (4 интервала) и изобразить графически.
По данным подсчитайте:
1) Средний размер привлекаемых
средств (способ моментов и квадратов);
2) Моду, медиану привлекаемых
средств;
3) Показатели вариации;
4) Показатели корреляции и
регрессии.
Сделать вывод. Начертить 4 вида
графиков.
Задача 5
По
имеющимся данным о сбыте продукции (в тыс. руб.) в различных фирмах города
произвести группировку данных, образовав 4 равных интервалов. Оформить в
таблице.
По
полученному интервальному ряду определить (аналитически и графически): средний
объем сбыта, моду, медиану.
87, 75,
66, 60, 87, 67, 66, 69, 89, 74, 90, 78, 99, 86, 76, 95, 69, 68, 87, 63
Задача 6
Произвести
анализ 20 банков, применив метод группировок, используя данные, приведенные в
таблице ниже:
Основные
показатели деятельности банков (млн.руб.)
|
Номер банка |
Капитал |
Чистые активы |
Прибыль |
| 1 | 5170 | 74104 | 1222 |
| 2 | 6412 | 22311 | 502 |
| 3 | 6424 | 30978 | 1372 |
| 4 | 4467 | 46331 | 1845 |
| 5 | 9454 | 7741 | 214 |
| 6 | 4357 | 19422 | 215 |
| 7 | 4033 | 9203 | 336 |
| 8 | 2755 | 12082 | 504 |
| 9 | 6868 | 57821 | 2635 |
| 10 | 3896 | 23787 | 794 |
| 11 | 3660 | 37528 | 694 |
| 12 | 7301 | 43129 | 934 |
| 13 | 3564 | 40927 | 1405 |
| 14 | 3327 | 17881 | 220 |
| 15 | 3280 | 21955 | 654 |
| 16 | 5153 | 31627 | 2173 |
| 17 | 5400 | 16068 | 1463 |
| 18 | 2613 | 13851 | 229 |
| 19 | 5196 | 6588 | 570 |
| 20 | 2609 | 22781 | 445 |
Задача 7
Используя
данные таблицы по 20 фирмам, сгруппируйте фирмы по следующим признакам:
низкорентабельные, рентабельные, высокорентабельные. В качестве основы
группировки возьмите прибыль на одного работающего. Для каждого выделенного
типа рассчитайте число фирм, среднюю численность персонала, стоимость
реализованной продукции на одного работающего. Результаты представьте в виде
таблицы и изобразите графически. Предложите анализ возможных факторов повышения
рентабельности.
Итоги деятельности фирм,
расположенных на территории района
| Номер в реестре | Заявленная отпускная стоимость реализованной продукции (млн. руб.) | Среднесписочная численность персонала | Заявленная прибыль (млн. руб.) | Расходы на рекламу (млн. руб.) |
| 6 | 195,2 | 181 | 16,3 | 4,0 |
| 7 | 157,8 | 1123 | 12,5 | 1,2 |
| 8 | 98,3 | 265 | 7,8 | 0,4 |
| 9 | 541,2 | 312 | 28,1 | 3,5 |
| 10 | 325,1 | 198 | 35,3 | 7,8 |
| 11 | 398,5 | 253 | 23,4 | 4,9 |
| 12 | 38,4 | 126 | 6,7 | 2,2 |
| 13 | 137,6 | 78 | 14,3 | 5,6 |
| 14 | 56,5 | 44 | 3,4 | 2,7 |
| 15 | 41,2 | 58 | 6,5 | 2,4 |
| 16 | 168,5 | 87 | 13,9 | 3,7 |
| 17 | 174,3 | 128 | 10,2 | 5,1 |
| 18 | 184,1 | 165 | 20,5 | 5,9 |
| 19 | 241,6 | 188 | 13,3 | 1,8 |
| 20 | 58,0 | 39 | 10,2 | 3,4 |
| 21 | 302,7 | 155 | 16,7 | 2,9 |
| 22 | 87,5 | 61 | 5,3 | 0,2 |
| 23 | 611,5 | 3875 | 58,3 | 10,7 |
| 24 | 257,6 | 189 | 25,0 | 3,2 |
| 25 | 107,4 | 98 | 8,8 | 3,7 |
Задача 8
Имеются
данные о распределении коммерческих банков по объявленному уставному фонду:
| Регион 1 | Регион 2 | ||
| Группы банков по уставному фонду | Удельный вес банков в общем их числе | Группы банков по уставному фонду | Удельный вес банков в общем их числе |
| до 100 | 7 | до 100 | 2 |
| 100-500 | 9 | 100-300 | 5 |
| 500-1000 | 18 | 300-500 | 6 |
| 1000-5000 | 34 | 500-700 | 7 |
| 5000-20000 | 22 | 700-1000 | 12 |
| свыше 20000 | 10 | 1000-3000 | 28 |
| 3000-5000 | 18 | ||
| 5000-10000 | 14 | ||
| свыше 10000 | 8 | ||
| Итого | 100 | Итого | 100 |
С целью
сравнения осуществите вторичную группировку коммерческих банков, для чего
выделите следующие группы банков по объявленному уставному фонду:
до 100,
100-500, 500-1000, 1000-5000, 5000-10000, свыше 10000 тыс.у.е. Сделайте выводы.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 9
Имеются
следующие данные по предприятиям по численности рабочих в 2012 г. Данные
представлены в таблице:
Исходные
данные
|
Предприятия со среднегодовой численностью рабочих (чел.) |
Число предприятий в процентах к итогу, % |
|
до 100 |
33,9 |
| 100-200 | 20,0 |
| 200-500 | 23,7 |
| 500-1000 | 11,8 |
| 1000-3000 | 8,0 |
| 3000-5000 | 2,3 |
|
5000 и более |
0,3 |
| Итого | 100,0 |
Используя
данные таблицы, необходимо провести перегруппировку предприятий по
численности рабочих, приняв следующие интервалы:
до 50
чел.
50 – 300
чел.
300 – 800
чел.
800 -1500
чел.
1500 –
4000 чел.
4000 –
9000 чел.
более
9000 чел.
Задача 10
Имеются
следующие данные о распределении промышленных предприятий двух регионов по
численности занятого на них промышленно-производственного персонала.
| Регион 1 | Регион 2 | ||||
|
Группы предприятий по численности работающих, чел. |
Число предприятий, % |
Численность промышленно-производственного персонала, тыс.чел. |
Группы предприятий по численности работающих, чел. |
Число предприятий, % |
Численность промышленно-производственного персонала, тыс.чел. |
| до 100 | 32 | 1 | до 300 | 34 | 1 |
| 101-500 | 38 | 4 | 301-600 | 28 | 6 |
| 501-1000 | 17 | 10 | 601-1000 | 20 | 10 |
| 1001-2000 | 9 | 15 | 1001-2000 | 13 | 15 |
| 2001-5000 | 3 | 32 | 2001-4000 | 4 | 43 |
| 5001 и более | 1 | 38 | 4001 и более | 1 | 25 |
| Итого | 100 | 100 | Итого | 100 | 100 |
Постройте
вторичную группировку данных о распределении промышленных предприятий, пересчитав
данные:
а)
региона 2 в соответствии с группировкой региона 1;
б)
региона 1 в соответствии с группировкой региона 2;
в)
регионов 1 и 2, образовав следующие группы промышленных предприятий по
численности ППП: до 500, 500-1000, 1000-2000, 2000-3000, 3000-4000, 4000-5000,
5000 и более.
Задача 11
По данным
таблицы 2 произвести вторичную группировку, образовав три группы предприятий по
среднегодовой стоимости ОПФ.
|
Группы предприятий по среднегодовой стоимости ОПФ, тыс.руб. |
Число предприятий, % |
Объем продукции, % |
Среднегодовая численность работающих |
Среднегодовая стоимость ОПФ |
| до 75 | 6.4 | 0.1 | 0.8 | 0.0 |
| 75-200 | 5.5 | 0.2 | 0.5 | 0.1 |
| 200-300 | 15.4 | 1.8 | 2.4 | 0.4 |
| 300-2500 | 36.6 | 9.7 | 12.4 | 4.4 |
| 2500-5000 | 30.4 | 17.2 | 17.3 | 9.6 |
| 5000-10000 | 1.9 | 27.7 | 29.0 | 20.8 |
| и более | 3.8 | 43.3 | 37.6 | 64.7 |
| Итого | 100.0 | 100.0 | 100.0 | 100.0 |
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ