Структура алу
Обобщенная
структурная схема АЛУ (рис. 7.1) включает:
–
блок регистров для приема и размещения
операндов и результатов;
–
операционный блок, в котором осуществляется
преобразование операндов в соответствии
с реализуемыми алгоритмами;
–
схемы контроля, обеспечивающие непрерывный
оперативный контроль и диагностирование
ошибок;
–
блок управления (БУ), в котором после
приема кода операции (КОП) из центрального
устройства управления формируются
управляющие сигналы (УС), координирующие
взаимодействие всех узлов АЛУ между
собой и с другими блоками процессора.
Блок
регистров связан с РОН центрального
процессора и кэш-памятью данных.
Иногда
АЛУ не содержит своего БР, в этом случае
операционный блок непосредственно
работает с регистрами общего назначения
процессора. Для оперативного управления
выполнением операции в ОБ на разных
этапах анализируется преобразуемая
информация и формируются сигналы
признаков (флаги), которые используются
в БУ для выработки и посылки в процессор
сигнала признака результата (ПРез).
Для
оценки АЛУ используются следующие
характеристики: множество выполняемых
операций, разрядность, время выполнения
операций, надежностные и энергетические
характеристики.
Рис. 7.1. Обобщенная
структурная схема АЛУ.
Сумматоры
Сумматоры АЛУ
делятся:
-
по типу использования
для суммирования базовых элементов
(комбинационные и накапливающие); -
по способу
осуществления операции суммирования
(последовательные и параллельные).
Сумматоры
последовательного действия выполняются,
как правило, на комбинационных элементах;
на сегодняшний день устройства такого
типа почти не применяются. В АЛУ
современных ЭВМ средней и высокой
производительности применяются сумматоры
параллельного действия, выполняемые
на накапливающих или комбинационных
элементах.
Рис. 7.2. Сумматор
параллельного действия (на накапливающих
элементах).
В качестве
накапливающих элементов могут служить
обычные T-триггеры. Перед суммированием
триггеры сумматора устанавливаются в
нулевое состояние сигналом сброс. Затем
на счетные входы триггеров подается
первое слагаемое и запоминается. В
следующем такте на входы триггеров
подается второе слагаемое.
Триггеры тех
разрядов, в которых второе слагаемое
равно 1, меняют свое состояние на
противоположное. В тех разрядах, в
которых триггеры перешли из единичного
состояния в нулевое, возникают сигналы
переносов, последовательно передаваемые
в старшие разряды сумматора. Арифметические
операции сумматора выполняются с учетом
знаков операндов.
Классификация алу
По способу
представления чисел:
-
для чисел с
фиксированной точкой; -
для чисел с
плавающей точкой; -
для десятичных
чисел.
По способу
действия над операндами:
-
последовательные;
В параллельных
АЛУ операнды представляются параллельным
кодом и операции совершаются параллельно
во времени над всеми разрядами операндов.
-
параллельные.
В последовательных
АЛУ операнды представляются в
последовательном коде, а операции
производятся последовательно во времени
над их отдельными разрядами. Такие АЛУ,
как правило, используют конвейерный
метод обработки, при котором совмещаются
во времени фазы выполнения операции
для различных разрядов операндов.
По выполняемым
функциям АЛУ подразделяются на:
-
многофункциональные;
В многофункциональных
АЛУ все возможные операции для всех
форм представления чисел выполняются
одними и теми же схемами, которые
коммутируются нужным образом в зависимости
от требуемого режима работы.
-
функциональные
(блочные).
В блочном АЛУ
операции над числами с фиксированной
и плавающей точкой, десятичными и
алфавитно-цифровыми полями, операции
умножения выполняются в отдельных
блоках. Такой подход позволяет увеличить
скорость работы АЛУ за счет использования
быстродействующих блоков, а также за
счет организации параллельной работы
этих блоков. Однако в этом случае
значительно увеличиваются затраты на
оборудование.
По структурной
организацииАЛУ подразделяются на
устройства, имеющие:
-
регистровую
структуру с непосредственными связями
и закрепленной логикой; -
магистральную
структуру с сосредоточенной памятью
и логикой.
В АЛУ с регистровой
структуройза каждым из регистров
закреплена своя логическая схема,
используемая для выполнения микрооперации
(см. рис. 7.3).
Пример:
С регистром Рг1непосредственно связан преобразователь
кодаПК1. С регистромРг3объединенКСМпо схеме накапливания сумматора,
а сКСМ, в свою очередь, связаныПК2и комбинационная схемаКСдля
мультиплексирования входных данных.
На регистреРг3выполняются
микрооперации сдвига вправо или влево
и сброс. РегистрРг4выполняет
микрооперации сдвига и непосредственно
связан сПК3. Таким образом, в АЛУ с
такой структурой функции хранения и
преобразования информации выполняются
одним и тем же операционным блоком.
Рис. 7.3. Регистровая
структура с закрепленной логикой
В АЛУ с магистральной
структуройрегистры выделены в
отдельный блок, а схемы для преобразования
информации выделены также в отдельный
операционный блок (ОБ), который связан
с блоками регистров по входам и выходам
(см. рис. 7.4). Блок регистров (БР) осуществляет
функции приема, хранения и выдачи
операндов и результатов, а ОБ выполняет
весь набор микроопераций над словами,
хранимыми в блоке регистров. В АЛУ с
такой структурой блок регистров может
быть реализован или как СОЗУ, или как
совокупность отдельных регистров с
индивидуальными схемами управления.СтруктуражеОБимеет следующие
модификации:
-
последовательное
соединение операционных узлов; -
параллельное
соединение операционных узлов.
ПримерАЛУ с
магистральной структурой с последовательным
соединением узлов ОБ.
В этом АЛУ
преобразователь кода ПК, комбинационный
сумматорКСМи сдвигательСДВсоединены последовательно, причемПКиКСМпо входам связаны с выходными
шинами блока регистров, а выходСДВ– с входной шиной блока регистров. Такая
организация операционного блока дает
возможность выполнять с высокой скоростью
последовательности микроопераций,
обеспечивающие выполнение одного слова.
Рис. 7.4. Магистральная
структура с последовательным соединением
операционных узлов
В случае же
параллельного соединения операционных
блоков АЛУ все операционные блоки: СМ,СДВ,КС,ПКпараллельно
соединяются с входными и выходными
шинами блока регистров, что позволяет
выполнять несколько микроопераций
параллельно. Выглядит это так, как
показано на рис. 7.5.
Рис. 7.5. Магистральная
структура с параллельным соединением
операционных узлов
Соседние файлы в папке гос
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 июля 2022 года; проверки требует 1 правка.
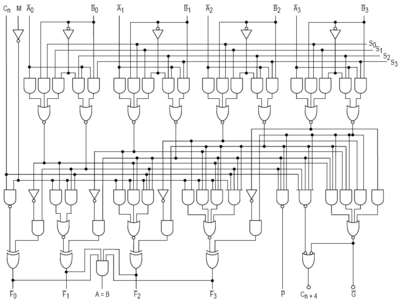
Комбинационная логическая схема 4-битного АЛУ, реализованная в 24-выводной микросхеме ТТЛ, модель 74181, впервые разработанная и ранее изготавливаемая фирмой Texas Instruments. Выполняет сложение, вычитание, все элементарные логические функции и битовые сдвиги над двумя 4-битовыми операндами. Не содержит в своем составе регистров
Арифме́тико-логи́ческое устро́йство (АЛУ; англ. arithmetic logic unit, ALU) — блок процессора, который под управлением устройства управления служит для выполнения арифметических и логических преобразований (начиная от элементарных) над данными, называемыми в этом случае операндами. Разрядность операндов обычно называют размером или длиной машинного слова.
Концепция арифметико-логического устройства предложена в 1945 году Джоном фон Нейманом в публикации по EDVAC; она стала одной из составляющих ставшей классической фон-неймановской компьютерной архитектуры.
Организация и принципы действия[править | править код]
Обобщённая блок-схема арифметико-логического устройства (АЛУ). Стрелками указаны входные и выходные слова. Флаги — признаки (например, результата сравнения операндов) выполнения предыдущей операции (вход) и результата выполнения текущей операции (выход). В одноместных операциях таких, например, как инверсия битов слова или битовый сдвиг второй операнд (B) не участвует в операции. Слово команды указывает необходимую операцию.
Арифметико-логическое устройство в зависимости от выполнения функций можно разделить на две части:
- микропрограммное устройство (устройство управления), задающее последовательность микрокоманд (команд);
- операционное устройство, в котором реализуется заданная последовательность микрокоманд (команд).
В состав арифметико-логического устройства условно включаются регистры Рг1 — Рг7, которые служат для обработки информации, поступающей из оперативной или пассивной памяти N1, N2, … NS и логические схемы, которые используются для обработки слов по микрокомандам, поступающим из устройства управления.
Различают два вида микрокоманд: внешние — такие микрокоманды, которые поступают в АЛУ от внешних источников и вызывают в нём преобразование информации и внутренние — те, которые генерируются в АЛУ и оказывают влияние на микропрограммное устройство, изменяя таким образом нормальный порядок следования команд.
Типовые функции регистров, входящих в арифметико-логическое устройство:
- Рг1 — аккумулятор (или аккумуляторы) — главный регистр АЛУ, в котором образуется результат вычислений;
- Рг2, Рг3 — регистры операндов (слагаемого, сомножителя, делителя, делимого и других) в зависимости от выполняемой операции;
- Рг4 — регистр адреса (или адресные регистры), предназначенные для запоминания (бывает, что формирования) адреса операндов результата;
- Рг6 — k индексных регистров, содержимое которых используется для формирования адресов;
- Рг7 — l вспомогательных регистров, которые по желанию программиста могут быть аккумуляторами, индексными регистрами или использоваться для запоминания промежуточных результатов.
Часть операционных регистров могут быть адресованы в команде для выполнения операций с их содержимым, и их называют программно-доступными. К таким регистрам относятся: сумматор, индексные регистры и некоторые вспомогательные регистры. Остальные регистры нельзя адресовать в программе, то есть они являются программно-недоступными.
Операционные устройства можно классифицировать по виду обрабатываемой информации, по способу её обработки и по логической структуре.
Такая сложная логическая структура АЛУ может характеризоваться количеством отличающихся друг от друга микроопераций, которые необходимы для выполнения всего комплекса задач, поставленных перед арифметико-логическим устройством. На входе каждого регистра собраны соответствующие логические схемы, обеспечивающие такие связи между регистрами, что позволяет реализовать заданные микрооперации. Выполнение операций над словами сводится к выполнению определённых микроопераций, которые управляют передачей слов в АЛУ и действиями по преобразованию слов. Порядок выполнения микрокоманд определяется алгоритмом выполнения операций. То есть, связи между регистрами АЛУ и их функциями зависят в основном от принятой методики выполнения логических операций, в том числе арифметических или специальной арифметики.
Пример работы АЛУ на операции сложения[править | править код]
Функционально АЛУ состоит из двух регистров (Регистр1, Регистр 2), схемы управления и сумматора[1]. Арифметическая операция выполняется по тактам:
- значения операнда 1, участвующего в арифметической операции по шине данных поступает в Регистр 1 или уже там находится;
- значения операнда 2, участвующего в арифметической операции по шине данных поступает в Регистр 2 или уже там находится;
- по шине инструкций поступает инструкция на выполнение операции в схему управления;
- данные из регистров поступают в сумматор, схема управления дает команду на выполнение сложения;
- результат сложения поступает в Регистр 1;
- признаки выполнения операции в АЛУ поступают в регистр флагов.
Пример работы АЛУ на операции вычитания:
- значение операнда 1, участвующего в арифметической операции по кодовой шине данных поступает в Регистр 1;
- значение операнда 2, участвующего в арифметической операции по кодовой шине данных поступает в Регистр 2;
- по кодовой шине инструкций, поступает инструкция на выполнение операции вычитания в схему управления;
- схема управления преобразовывает положительное число в отрицательное (в формате дополнительного кода до двух);
- результат преобразования операнда поступает в сумматор;
- сумматор складывает два числа;
- результат сложения поступает в Регистр 1;
- результат операции АЛУ поступает в результирующий блок.
Операции[править | править код]
Все выполняемые в арифметико-логическом устройстве операции являются логическими операциями (функциями), которые можно разделить на следующие группы:
- операции двоичной арифметики для чисел с фиксированной точкой;
- операции двоичной (или шестнадцатеричной) арифметики для чисел с плавающей точкой;
- операции десятичной арифметики;
- операции индексной арифметики (при модификации адресов команд);
- операции специальной арифметики;
- операции над логическими кодами (логические операции);
- операции над алфавитно-цифровыми полями.
Современные компьютеры общего назначения обычно реализуют операции всех приведённых выше групп, а малые и микроЭВМ, микропроцессоры и специализированные ЭВМ часто не имеют аппаратуры арифметики чисел с плавающей точкой, десятичной арифметики и операций над алфавитно-цифровыми полями. В этом случае эти операции выполняются специальными подпрограммами.
К арифметическим операциям относятся сложение, вычитание, вычитание модулей («короткие операции») и умножение и деление («длинные операции»). Группу логических операций составляют операции дизъюнкция (логическое ИЛИ) и конъюнкция (логическое И) над многоразрядными двоичными словами, сравнение кодов на равенство. Специальные арифметические операции включают в себя нормализацию, арифметический сдвиг (сдвигаются только цифровые разряды, знаковый разряд остаётся на месте), логический сдвиг (знаковый разряд сдвигается вместе с цифровыми разрядами). Обширна группа операций редактирования алфавитно-цифровой информации.
Каждая операция в АЛУ является логической функцией или последовательностью логических функций описываемых двоичной логикой для двоичных ЭВМ, троичной логикой для троичных ЭВМ, четверичной логикой для четверичных ЭВМ, десятичной логикой для десятичных ЭВМ и так далее.
Классификация[править | править код]
По способу действия над операндами арифметико-логические устройства делятся на последовательные и параллельные. В последовательных устройствах операнды представляются в последовательном коде, а операции производятся последовательно во времени над их отдельными разрядами; в параллельных — параллельным кодом и операции совершаются параллельно во времени над всеми разрядами операндов.
По способу представления чисел различают арифметико-логические устройства:
- для чисел с фиксированной точкой;
- для чисел с плавающей точкой;
- для десятичных чисел.
По характеру использования элементов и узлов АЛУ делятся на блочные и многофункциональные. В блочном устройстве операции над числами с фиксированной и плавающей точкой, десятичными числами и алфавитно-цифровыми полями выполняются в отдельных блоках, при этом повышается скорость работы, так как блоки могут параллельно выполнять соответствующие операции, но значительно возрастают затраты оборудования. В многофункциональных АЛУ операции для всех форм представления чисел выполняются одними и теми же схемами, которые коммутируются нужным образом в зависимости от требуемого режима работы.
По своим функциям арифметико-логическое устройство является операционным блоком, выполняющим микрооперации, обеспечивающие приём из других устройств (например, памяти) операндов, их преобразование и выдачу результатов преобразования в другие устройства. Арифметико-логическое устройство управляется управляющим блоком, генерирующим управляющие сигналы, инициирующие выполнение в АЛУ определённых микроопераций. Генерируемая управляющим блоком последовательность сигналов определяется кодом операции команды и оповещающими сигналами.
Примечания[править | править код]
- ↑ Макаровой Н. В. Информатика: Учебник. — М.: Финансы и статистика, 2006. — 768 с. — ISBN 978-5-279-02202-1.
Литература[править | править код]
- Каган Б. М. Электронные вычислительные машины и системы. — 3-е изд., перераб. и доп. — Энергоатомиздат, 1991. — ISBN 5-283-01531-9.
- Угрюмов Е. П. Цифровая схемотехника. Учеб. пособие для вузов. Изд. 2. — БХВ-Петербург, 2004.
- Самофалов К. Г., Романкевич А. М., Валуйский В. Н., Каневский Ю. С., Пиневич М. М. Прикладная теория цифровых автоматов. — К.: Вища школа, 1987. — С. 375.
- Ершов А. П., Монахов В. М., Бешенков С. А. и др. 1 // Основы информатики и вычислительной техники: Проб. учеб. пособие для сред. учеб. заведений. В 2 ч. — М.: Просвещение, 1985. — С. 96.
- Ершов А. П., Монахов В. М., Кузнецов А. А. и др. 2 // Основы информатики и вычислительной техники: Проб. учеб. пособие для сред. учеб. заведений. В 2 ч. — М.: Просвещение, 1986. — С. 143.
- IX Арифметико-логическое устройство. Логические основы ЭВМ. Пособие к курсам «Радиоэлектроника» и «Микропроцессорные средства». Республика Карелия, г. Петрозаводск, ПетрГУ. Кафедра информационно-измерительных систем и физической электроники. Дата обращения: 18 сентября 2010. Архивировано 3 июня 2004 года.
- Исследование эффективности ALU и FPU процессоров разных поколений от TestLabs.kz
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Арифметико-логическое устройство (АЛУ) предназначено для выполнения арифметических и логических преобразований над числами и словами.
В АЛУ кроме классических арифметических операций, логического сложения и логического умножения двух слов выполняются сдвиги слов, преобразования кодов и некоторые другие операции.
Современные АЛУ выполняют:
-
функции двоичной арифметики для данных в формате с фиксированной точкой;
-
функции двоичной арифметики для данных в формате с плавающей точкой;
-
функции арифметики двоично-десятичного представления данных;
-
логические операций (в том числе сдвиги арифметические и логические);
-
операции пересылки данных;
-
работу с символьными данными;
-
работу с графическими данными.
Основные характеристики АЛУ можно разделить на количественные и качественные.
Количественные характеристики определяют скорость выполнения операций, время выполнения одной операции, точность представления данных, количество выполняемых операций.
Среднюю скорость выполнения операций Vср. в АЛУ можно определить как отношение N(T)- количества операций, выполненных за отрезок времени Т к данному отрезку времени:
Vср = N(T)/T (1)
Среднее время, которое АЛУ тратит на выполнение операции равно: Tср = 1/Vср (2)
Точность представления данных в АЛУ зависит от разрядной сетки АЛУ и выбранного формата данных.
К качественным характеристикам АЛУ относятся:
-
структурные особенности АЛУ;
-
форматы представления данных (с фиксированной или плавающей точкой);
-
способы кодирования данных.
АЛУ можно классифицировать по ряду признаков, приведенных ниже.
1. Классификация по способу представления данных:
-
с фиксированной запятой;
-
с плавающей запятой.
2. Классификация по способу действия над операндами:
·последовательные АЛУ, где каждая операция выполняется последовательно над каждым разрядом;
·параллельные АЛУ, операция выполняется над всеми разрядами данных одновременно;
·последовательно – параллельные АЛУ, где слово данных делится на слоги, обработка данных ведется параллельно над разрядами слога и последовательно над слогами.
3. Классификация по использованию систем счисления:
-
двоичная;
-
двоично- десятичная;
-
восьмеричная;
-
шестнадцатеричная;
-
и т.д.
4. Классификация по характеру использования элементов и узлов:
-
блочные – для выполнения отдельных арифметических операций в структуру АЛУ вводят специальные блоки, что позволяет процесс обработки информации вести параллельно;
-
конвейерные – в конвейерных АЛУ операция разбивается на последовательность микроопераций, выполняемых за одинаковые промежутки времени (такты) на разных ступенях конвейера, что позволяет выполнять операцию над потоком операндов каждый такт;
-
многофункциональные – это универсальные АЛУ, выполняющие множество операций в одном устройстве. В таких АЛУ требуется настройка на выполнение данной операции при помощи кода операции.
5.Классификация по временным характеристикам.
По временным характеристикам АЛУ делятся на:
-
синхронные – в синхронных АЛУ каждая операция выполняется за один такт.
-
Асинхронные – не тактируемые АЛУ, обеспечивающие высокое быстродействие, так как выполняются на комбинационных схемах.
6.Классификация по структуре устройства управления:
-
АЛУ с жесткой логикой устройства управления;
-
АЛУ с микропрограммным управлением.
Структура АЛУ представлена на рисунке 1.
Рисунок 1 – Структура АЛУ
Исходные данные (операнды) по командам УУ (см выше) считываются из ОЗУ в регистры первого и второго операндов (связь 1).
Из УУ в блок управления АЛУ поступает команда на выполнение той или иной операции (связь 2), которая передается им в операционную часть (связь 3).
В соответствии с этой командой операционная часть выполняет нужное действие с данными, которые выбираются из регистров первого и второго операндов (связь 6). Результат заносится в регистр результата (связь 4), откуда – в ОЗУ (связь 5).
Структура регистров АЛУ, куда помещаются исходные и результирующие данные, а также размер регистров (число двоичных разрядов t) формируют понятие разрядной сетки (далее – сетки), которое используется ниже.
Таким образом, структура АЛУ определяется набором микроопераций, необходимых для выполнения заданных арифметических, логических и специальных операций, а задачу построения АЛУ можно свести к задаче определения набора микроопераций, который позволяет составить микропрограмму любой из заданных операций. Такой набор легко получить, если записать микропрограммы всех операций, выполняемых в АЛУ, и выбрать из них все микрооперации, входящие в микропрограммы хотя бы один раз. Однако, если при этом алгоритм операций выбирать произвольно, то количество микроопераций, входящих в полный набор, может оказаться слишком большим и, следовательно, АЛУ будет сложным.
Для получения более простой схемы АЛУ алгоритмы арифметических и логических операций следует выбирать из условия получения минимального набора микроопераций. При этом необходимо учитывать требование обеспечения заданного быстродействия АЛУ: слишком ограниченный набор микроопераций может привести к «длинным микропрограммам некоторых операций», что увеличивает время выполнения данных операций.
Список использованных источников
-
Арифметико-логическое устройство [Электронный ресурс] Режим доступа: http://www.studfiles.ru/preview/3565590/page:3/ Дата обращения: 07.02.2017
-
Арифметико-логическое устройство [Электронный ресурс] Режим доступа: http://www.intuit.ru/studies/courses/60/60/lecture/1770%3Fpage%3D1 Дата обращения:07.02.2017
-
Арифметико-логическое устройство. Общие сведения, функции и классификация [Электронный ресурс] Режим доступа: http://www.studfiles.ru/preview/716008/ Дата обращения: 07.02.2017
Теперь мы можем перейти к знакомству с внутренним миром АЛУ. Как и в первой части статьи я не буду рассматривать какую то определенную микросхему или какой то определенный тип АЛУ. При этом предполагается, что читатели знакомы с основами цифровой логики.
Оптимизации логический выражений, которые реализуются на аппаратном уровне, внимание уделяться не будет. Точно так же не будет уделяться внимание синхронизации и гонкам из-за разных времен путей прохождения сигналов. Иллюстрации в статье будут функциональными схемами, а не принципиальными, так как вряд ли кто то будет сегодня собирать АЛУ из дискретных элементов. В основном будет рассматриваться построение статического АЛУ, причем невысокой разрядности. Вопросы разрядности мы уже обсуждали в первой части статьи.
В работе АЛУ нет никакой мистики. Но некоторую сложность представляет многообразие и разнородность выполняемых функций. Поэтому АЛУ часто строятся как набор отдельных функциональных блоков. При этом, построение этих блоков и их объединение в единое целое могут быть разными. Во с этого и начнем.
Но сначала необходимо сделать еще одно важное уточнение. Набор выполняемых АЛУ операций не тождественен набору команд процессора! Операции АЛУ это лишь базовый набор элементов, из которого и строятся все выполняемые процессором операции. И этот базовый набор не обязательно должен быть большим.
Статья не является учебником. Это не копия каких либо книг или учебников. Это не компиляция других источников и статей. Как и другие статьи канала, это мой личный опыт.
Первую часть статьи можно прочитать здесь – Элементы ЭВМ. АЛУ – арифметико-логическое устройство. Часть 1
Объединить разнородное в единое целое
Самым простым и очевидным, но далеко не всегда самым эффективным и целесообразным, решением является просто использовать столько разных блоков, сколько операций должно выполнять АЛУ. А код операции будет выбирать, выходной сигнал какого именно блока будет поступать на выход АЛУ.
Такой принцип построения АЛУ действительно применяется на практике. Такие АЛУ одни из самых быстрых, но их схемотехника может быть избыточной. При этом они исключают наличие “недокументированных” функций, что можно рассматривать и как достоинство, и как недостаток. Чуть позже мы еще вернемся к этому вопросу.
Большое количество выполняемых операций требует и большого количества функциональных блоков, которые работают параллельно, даже в том случае, если функционал блоков частично перекрывается. Поскольку по входам все блоки включены параллельно, это может создавать излишнюю нагрузку на предшествующие узлы процессора с которых и поступают входные сигналы a и b. Для исключения этого на входах операндов АЛУ устанавливаются буферные усилители, я показал их а иллюстрации.
Однако, можно уменьшить схемотехническую избыточность АЛУ за счет объединения функционала отдельных блоков. При этом для управления многофункциональными блоками потребуются дополнительные сигналы, что усложняет управление АЛУ. Но зато это повышает гибкость и уменьшает схемотехническую избыточность.
На первый взгляд, различия невелики. Однако, это не так. Во первых, теперь каждый блок может выполнять несколько различных функций, что управляется дополнительными сигналами с1 и с2. Более того, блоки могут быть взаимосвязанным (на иллюстрации не показано). Однако, это не исключает необходимости коммутатора выходных сигналов блоков, который управляется сигналом sw.
Такие АЛУ немного медленнее, так как путь сигналов операндов от входов до выхода более длинный (мы это скоро увидим). Но они и более гибкие в применении. И именно такие АЛУ мы и будем далее рассматривать в статье.
Однако, сначала пару слов о “предельном случае”
ПЗУ в роли АЛУ
Давайте представим, что и сигналы операндов, и сигналы выбора операции, являются полностью равноправными и образуют некое “множество входных данных”. В таком представлении нет ничего искусственного и неестественного. Достаточно просто абстрагироваться от функционального значения отдельных сигналов.
Теперь мы можем представить АЛУ как функциональный модуль, который ставит в соответствие множеству входных сигналов заранее определенное множество выходных сигналов. Такое функциональное преобразование можно записать в табличной форме. Ничего не напоминает?
Да, именно так, мы можем представить АЛУ как ПЗУ. Сигналы входных операндов, входящий перенос, код операции, в совокупности будут являться адресом ячейки ПЗУ, а ее содержимое будет сигналами результата операции и исходящим переносом.
И такие АЛУ действительно иногда используются. Особенно в случаях, когда требуется выполнение нетривиальных операций при высоком быстродействии. Например, специализированное АЛУ выполняющее операции преобразования между системами координат для навигационного процессора.
Несмотря на все преимущества подобных АЛУ, они используются нечасто. С ростом разрядности обрабатываемых операндов, даже небольшим, резко возрастает требуемый объем ПЗУ, что приводит к увеличению занимаемого им на кристалле места. И размер АЛУ получается слишком большим, а стоимость высокой. Такие АЛУ в статье рассматриваться далее не будут.
Многофункциональный логический блок
Давайте начнем с самого простого – одноразрядного многофункционального логического блока. Предположим, что нам требуется выполнение четырех логических операций:
- НЕ
- И
- ИЛИ
- ИСКЛЮЧАЮЩЕЕ ИЛИ
Давайте вспомним формулы де-Моргана
которые устанавливают зависимость между операциями И и ИЛИ для прямой и инверсной логики. Это позволяет нам использовать всего один логический элемент, например, И, для выполнения как операции И, так и операции ИЛИ. Просто для ИЛИ нам потребуется инверсия входных сигналов и выходного сигнала.
Точно так же можно использовать элемент ИЛИ для выполнения операции И если инвертировать входные и выходной сигналы.
Таким образом, наша задача сводится к управлению инверсией сигналов. И сделать это можно, например, с помощью инвертора и мультиплексора
Здесь сигнал передается на выход без инверсии если управляющий сигнал p/n равен “0” и с инверсией если p/n равно “1”. На иллюстрации слева показана принципиальная схема с использованием элементарных логических элементов, а справа функциональная схема. Элементы DD2-DD5 и образуют тот самый мультиплексор.
Можно использовать и другой вариант, с использованием элемента исключающее ИЛИ
В данном случае сигнал, точно так же, как в предыдущем варианте, передается без инверсии если p/n равно “0” и с инверсией если p/n равно “1”. На иллюстрации слева показан один из распространенных вариантов реализации функции ИСКЛЮЧАЮЩЕЕ ИЛИ на элементах 2И-НЕ, а справа функциональная схема.
Время задержки прохождения сигнала в обоих вариантах примерно одинакового. На практике используются оба варианта, хотя построение элемента ИСКЛЮЧАЮЩЕЕ ИЛИ может быть и иным.
Теперь мы можем нарисовать схему блока выполняющего операции И и ИЛИ, причем тип операции будет задаваться внешними сигналами
Здесь у нас есть три дополнительных управляющих сигнала (s0, s1, s2), что может показаться излишним. Однако, это дает нам дополнительную гибкость и функциональность. Давайте посмотрим, какие операции может выполнять этот наш многофункциональных элемент
Как вы помните, мы планировали свести в одном элементе две функции, И и ИЛИ, но результат получился более интересным. В частности, получилась и функция ЗАПРЕТ, о которой я уже упоминал в статьях
Феррит-диодные ячейки. Старая импульсная логика. История цифровой техники.
и
Феррит-транзисторная динамическая логика. История цифровой схемотехники
Эти дополнительные операции могут оказаться полезными. Если же они не нужны, а на первом месте стоит простота управления, то мы можем объединить сигналы в s0-s2 в один сигнал. И у нас останется только две возможные функции, И и ИЛИ, как мы изначально и планировали.
Этот блок, без каких либо изменений, позволяет выполнять и операцию НЕ, причем для любого операнда. Например, для инверсии операнда a нам нужно задать s0=”1″ s1=”0″ s2=”0″ и зафиксировать b=”1″. Фиксация операнда b=”1″ может быть выполнена внешней, по отношению к АЛУ, схемой, например, декодером команд или блоком микропрограммного управления процессора. То есть, теми же узлами процессора, которые формируют и сигналы s0-s2.
Но можно добавить еще один управляющий сигнал и дополнительный мультиплексор, который позволит выбирать в качестве операнда или выход схемы передача/инверсия, или предопределенные “0” или “1”. Все зависит от функциональных требований к АЛУ. Я не буду отдельно иллюстрировать эти варианты.
Однако, наши начальные требования к функционалу блока все еще выполнены не полностью. Нет реализации операции ИСКЛЮЧАЮЩЕЕ ИЛИ. Давайте добавим недостающее.
Недостающую операцию нам пришлось добавить в виде отдельного элемента ИСКЛЮЧАЮЩЕЕ ИЛИ и мультиплексора. Обратите внимание, что при выполнении операции ИСКЛЮЧАЮЩЕЕ ИЛИ сигнал s2 не имеет значения.
Это лишь один из вариантов построения логического блока, причем даже не столько вариант, сколько набросок варианта. Он вполне работоспособен, но далеко не оптимален. И многие важные при построении реальных АЛУ вопросы оставлены “за кадром”. Да и в управляющих сигналах порядок надо навести.
Многоразрядное АЛУ будет содержать несколько таких многофункциональных логических блоков. Их информационные входы и выходы будут раздельными, а управляющие сигналы общими.
Арифметические операции. Сумматоры. Полноценное одноразрядное АЛУ
Из всех арифметических операций АЛУ зачастую поддерживают только сложение и вычитание. Причем выполняет обе операции сумматор. Давайте, но кратко, поговорим о сумматорах. Я не сомневаюсь, что вы все про них знаете, но отдельные моменты, с точки зрения АЛУ, уточнить будет полезно.
В первой части статьи я говорил, что операция ИСКЛЮЧАЮЩЕЕ ИЛИ является и арифметической. Это действительно так. Если не считать переносов между разрядами двоичных чисел. Полусумматор вычисляет сумму двух чисел без учета входящего переноса и формирует сигнал исходящего переноса, который возникает как результат операции. Полный сумматор вычисляет сумму двух чисел с учетом входящего переноса и формирует сигнал исходящего переноса. Полусумматоры нам не интересны.
Без сомнения вы все знаете эту схему. Ci это входящий перенос от предыдущего разряда (младшего). Co это исходящий перенос для следующего разряда (старшего). Сигнал исходящего переноса имеет самую большую задержку формирования и определяет быстродействие сумматора. Для многоразрядных сумматоров переносы вычисляются последовательно, разряд за разрядом. Это сильно снижает быстродействие. Проблему позволяют решить схемы ускоренного переноса. Однако, я сегодня не буду касаться этого вопроса.
В данном случае, мы же строим АЛУ, нам важен лишь один элемент схемы сумматора – элемент ИСКЛЮЧАЮЩЕЕ ИЛИ (левый верхний) на который поступают сигналы a и b. Дело в том, что такой элемент у нас уже есть в логическом блоке. Почему бы его не использовать? Давайте попробуем
Позвольте, а откуда же взялась операция вычитания? Все очень просто, у нас уже есть элементы обеспечивающие инверсию сигналов входных операндов. Например, если мы установим s1=”1″, то сигнал b будет инвертироваться, а результирующая операция будет a-b. Вот так вот все просто!
На самом деле, здесь еще будет полезной возможность инверсии входящего переноса. Точно так же, как мы это реализовали для сигналов a и b. Я не буду показывать это на иллюстрации. Оставлю это читателям в качестве упражнения.
Увеличение количества управляющих сигналов полезно, так как увеличивает количество выполняемых операций. Включая арифметические. Я показал два сигнала управления выходным мультиплексором, s3 и s4. Теперь у нас нужно выбирать один из трех сигналов с внутренних блоков АЛУ для передачи на выход.
Не все комбинации управляющих сигналов действующие и не все имеют смысл. Но, как я говорил в начале данной статьи, вопросы оптимизации логических функций сегодня не будут рассматриваться.
Сдвигатели даных
А как же сдвиги? Это ведь важная операция. Важная, но ее не обязательно реализовывать внутри АЛУ, так как сдвиги имеют более широкое использование внутри процессоров. Тем не менее, сдвигатели могут устанавливаться на входах и внутри АЛУ. До рассмотренных ранее элементов АЛУ. Мы не будем их подробно рассматривать сегодня, но упрощенную функциональную схему сдвигателя на один разряд вправо и влево я приведу
В данном случае я не стал показывать управляющие сигналы мультиплексоров, что бы не загромождать картинку. Думаю, принцип работы сдвигателей понятен. Сдвиг не обязательно должен быть на один разряд. Можно использовать многоразрядные мультиплексоры и реализовать сдвиг на любое число разрядов, причем число разрядов можно задавать и управляющими сигналами.
Если вместо фиксированных значений “0” выводы мультиплексоров подключить к сигналам входящего переноса, то можно каскадировать сдвигатели точно так же, как сумматоры и АЛУ. Можно реализовать и циклические сдвиги, в том числе, с участием переносов. Но этот вопрос выходит за рамки сегодняшней статьи.
Сдвигатели данных могут включаться не только на входах АЛУ, но и на выходе. Это позволяет строить сложные схемы управления данными и выполнения операций уже на уровне процессора.
Умножение и деление
Очень кратко. Умножение и деление сложные операции, которые зачастую выполняются итерационно на уровне микропрограмм. Однако, в некоторых процессорах могут использоваться и аппаратные блоки умножения/деления.
Умножение реализовать проще. Достаточно последовательного включения сумматоров и сдвигателей данных, что бы получить аппаратный эквивалент всем известного умножения столбиком. Причем нужно понимать, что произведение двух двоичных чисел разрядностью N имеет разрядность 2N. Почему это так, я описывал в статье
Простые типы данных. Машинное представление простых типов. Операции с простыми типами.
Умножители не столько сложны, сколько громоздки. Их структура регулярна, но количество элементов велико. И время выполнения операции умножения, даже аппаратно реализованной, велико.
Деление сложнее умножения, так как к схемам сдвига и вычитания необходимо добавлять схемы сравнения (цифровые компараторы), которые не только формируют разряды частного и остатка, но и влияют на ход процесса деления.
Кроме уже упомянутой особенности, два выходных значения, частное и остаток, нельзя не сказать, что делимое имеет удвоенную разрядность по сравнению с частным и остатком. Причины так же описаны в статье по приведенной ссылке. А что бы сложность деления стала более понятной, можете почитать статью
Машинное деление целых двоичных чисел
В которой я рассказываю об алгоритмах деления на примере архитектуры микроконтроллеров PIC.
Заключение
Сегодня мы, чрезвычайно кратко и упрощенно, познакомились с некоторыми принципами лежащими в основе построения и работы центрального элемента любого процессора – АЛУ, арифметическо-логического устройства. Заглянули в его внутренний мир, который оказался не столь страшен, как казалось со стороны. Во всяком случае, для рассмотренных нами примеров.
Будут и другие статьи посвященные устройству и работе узлов процессоров и ЭВМ в целом. В дополнение к уже ведущемуся циклу статей “Микроконтроллеры для начинающих”. Правда пока сложно сказать, насколько этот новый цикл окажется для вас интересным. А от интереса будет зависеть и тематика новых статей, и их количество.
Как всегда, можете задавать вопросы в комментариях. И можете предлагать интересующие вас темы статей. Или вопросы требующие более глубокого и подробного рассмотрения.
До новых встреч!
Содержание
- Назначение и состав АЛУ
- Операция деление в АЛУ
- Назначение и состав умножителя-акумулятора в АЛУ
- Основные режимы умножителя-аккумулятора АЛУ
- Операция переполнения в АЛУ
- Операция насыщения в АЛУ
- Операция округления в АЛУ
- Назначение и состав устройства сдвига
- Принцип работы устройства
- Определение экспоненты (степени) блока
- Команда немедленные сдвиги
- Логические сдвиги
- Денормализация
- Нормализация
Назначение и состав АЛУ
Арифметическо–логическое устройство предназначено:
● для реализации стандартного набора арифметических и логических операций над 16–разрядными операндами X, Y, а также многоцикловой операции деления с использованием двух имеющихся примитивов. Ниже приводится список стандартных функций АЛУ: R=X+Y сложение X и Y R=X+Y+CI сложение X и Y с переносом; R=X–Y вычитание Y из X; R=X–Y–CI–1 вычитание Y из X с заемом; R=Y–X вычитание X из Y; R=Y–X–CI–1 вычитание X из Y с заемом; R=–X арифметическое отрицание X;
R=–Y арифметическое отрицание Y; R=Y+1 инкремент Y; R=Y–1 декремент Y; R= PASS X результат равен операнду X; R= PASS Y результат равен операнду Y; R=0 (PASS 0) очистить результат; R=ABS X абсолютное значение X; R=X AND Y логическое умножение; R=X OR Y логическое сложение; R=X XOR Y сложение по модулю 2; R=NOT X логическое отрицание X; R=NOT Y логическое отрицание Y;
● для выдачи информации о состоянии процессора. После выполнения операции АЛУ генерирует (или обновляет) шесть флагов:
- AZ — флаг нулевого результата (при всех стандартных операциях);
- AN — флаг отрицательного результата (при всех стандартных операциях);
- AV — флаг переполнения (при всех стандартных операциях);
- АС — флаг переноса (при всех Стандартных операциях);
- AS — флаг знака входного Х–операнда (при операции ABS);
- AQ — флаг примитива деления (при делении).

- непосредственно ALU с двумя регистрами для входных операндов X, Y и регистром результата R;
- входные регистры АХ0, АХ1 и AY0, AY1 для хранения Х– и Y–операндов;
- регистр результата AR, в который загружаются результаты выполненной в АЛУ операции для их вывода на шину результата R или на шину данных памяти данных DMD;
- регистр обратной связи AF, в который загружаются результаты выполненной в АЛУ операции с целью их использования в качестве операнда Y;
- мультиплексоры для выбора загружаемых 16–разрядных операндов в регистры AY0, AY1, AR, X, Y. Арифметическо–логическое устройство содержит два набора (банка) программно доступных регистров AХ0, AХ1, AY0, AY1, AR, AF. В каждый момент времени доступным является лишь один набор. Для активизации набора можно использовать бит SEC_REG в позиции MSTAT.0 регистра режима и статуса MSTAT (табл. 8.3.9) или команды DIS SEC_REG, ENA SEC_REG.

- максимальное положительное число 0111111111111111, если флаг переноса AC = 0;
- максимальное отрицательное число 1000000000000000, если AC = 1. Бит AV_LATCH = 1 (позиция MSTAT.2 в регистре режима и статуса процессора) позволяет установить режим «защелки». В этом режиме:
- после переполнения АЛУ флаг AV остается поднятым (AV = 1) и в тех случаях, когда последующие команды не вызывают переполнения АЛУ;
- флаг AV может быть очищен только прямой записью нуля в позицию ASTAT.2 регистра арифметического статуса ASTAT (табл. 8.3.8).
Операция деление в АЛУ
Для операции деления в АЛУ используется дополнительная сдвиговая логика, не показанная на рис. 8.3.1. Деление может быть знаковым и беззнаковым. Деление беззнаковых чисел реализуется с помощью команды–примитива DIVQ, при выполнении которой формируется один бит частного за процессорный цикл. Шестнадцатикратное выполнение команды DIVQ позволяет получить 16 бит частного.
При делении знаковых чисел предварительно определяется знак частного с помощью другой команды–примитива DIVS.
После этого 15–кратное использование команды–примитива DIVQ позволяет получить значение частного с одинарной точностью. 
- старшая часть делимого Y может располагаться в регистрах AY1 или AF, младшая часть — в регистре AY0;
- делитель X может располагаться в AХ0, AХ1 или любом регистре результата. При выполнении команды DIVS:
- с помощью операции исключающее ИЛИ над старшими битами делимого и делителя определяется знаковый бит частного, который загружается в самый младший разряд регистра AY0, а также в регистр арифметического статуса ASTAT как флаг AQ;
- содержимое регистра AY0 сдвигается влево на один разряд, при этом самый старший бит AY0 займет место самого младшего бита LSB в регистре AF;
- пятнадцать младших бит регистра результата R ALU займут место оставшихся пятнадцати старших разрядов регистра AF. Таким образом, в результате выполненной операции DIVS начальное содержимое пары регистров AF–AY0 сдвигается влево на один разряд, а знаковый бит частного помещается в самый младший разряд AY0. Для рассмотрения операции деления беззнаковых чисел (DIVQ) воспользуемся схемой на рис. 8.3.3.

- старшая часть делимого Y должна располагаться в регистре AF, младшая часть — в регистре AY0;
- делитель X может располагаться в AX0, AX1 или любом регистре результата AR;
- флаг AQ должен быть сброшен (AQ = 0). При выполнении команды DIVQ;
- действия ALU определяются состоянием флага AQ. При AQ = 1 на выходе ALU результат R = Y+X; при AQ = 0 — R = Y–X;
- с помощью операции исключающее ИЛИ над старшими битами делителя и операнда R на выходе ALU определяется флаг AQ, который загружается в регистр арифметического статуса ASTAT, а также после инвертирования в самый младший разряд регистра AY0 как очередной бит частного;
- содержимое регистра AY0 сдвигается влево на один разряд, при этом самый старший бит AY0 займет место самого младшего бита LSB в регистре АF;
- пятнадцать младших бит регистра результата AR ALU займут мест оставшихся пятнадцати старших разрядов регистра AF. Формат частного определяется из формата делимого и делителя: NL – DL + 1 — число бит слева от десятичной точки частного; NR – DR – 1 — число бит справа от десятичной точки частного, где NL, NR — число бит слева и справа от десятичной точки делимого; DL, DR — число бит слева и справа от десятичной точки делителя.
Для получения правильного результата при делении двух целых чисел (делимое в формате 32.0 и делитель в формате 16.0) необходимо предварительно сдвинуть делимое влево на один разряд, т. е. перевести делимое в формат 1.31.
Умножитель–аккумулятор.
Назначение и состав умножителя-акумулятора в АЛУ
Умножитель–акумулятор МАС позволяет выполнить умножение двух 16–разрядных операндов (Х*Y), умножение с накоплением суммы и разности (MR+X*Y; MR–X*Y), очистку результата MR, где MR — содержимое регистра результата. 
- умножитель, содержащий два входных 16–разрядных порта X, Y и один 32–разрядный выходной порт произведения P. Умножитель позволяет перемножать любые комбинации операндов X и Y: знаковый на знаковый (SS), беззнаковый на знаковый (US), знаковый на беззнаковый (SU), беззнаковый на беззнаковый (UU);
- два входных регистра MX0, MX1 и MY0, MY1 для хранения Х– и Y– операндов;
- сумматор–вычитатель, предназначенный для сложения и вычитания 40–разрядного операнда и 32–разрядного произведения. Разрядность сумматора–вычитателя превышает 32 бита, чтобы разрешить промежуточные переполнения при выполнении нескольких операций подряд. При появлении значащих бит выше 32–разрядной границы устанавливается флаг переполнения умножителя MV;
- регистр результате MR шириной 40 бит, в который загружаются результаты выполненной в сумматоре–вычитателе операции для их вывода на шину результата R или на шину данных памяти данных DMD. Регистр MR состоит из двух 16–разрядных регистров MR0, MR1 и одного 8–разрядного регистра MR2. Каждый из этих регистров может быть напрямую загружен через шину DMD. Загрузка MR0 не влияет на содержимое регистров MR1, MR2. При загрузке регистра MR1 с шины DMD все биты MR2 автоматически заполняются знаковым битом. Для заполнения регистра MR2 другими значениями, его следует загружать после MR1. Выводы регистра MR2 подключены к младшим битам шины DMD. При чтении регистра MR2 на шины DMD и R старшие 8 разрядов заполняются знаковыми битами;
- регистр обратной связи MF, в который загружаются результаты (биты 16–31), выполненной в сумматоре–вычитателе операции, с целью их использования в качестве операнда Y;
- мультиплексоры для выбора источника операндов при их загрузке в регистры MY0, MY1, MR0, MR1, MR2 и порты X, Y умножителя, а также для вывода результатов из регистров MR0, MR1, MR2 на шину DMD. Умножитель–аккумулятор содержит два набора программно доступных регистров MX0, MX1, MY0, MY1, MR0, MR1, MR2, MF. В каждый момент времени доступным является лишь один набор. Для активизации набора используется бит SEC_REG в позиции MSTAT.0 регистра режима и Статуса MSTAT (табл. 8.3.9).
Основные режимы умножителя-аккумулятора АЛУ
Умножитель–аккумулятор обеспечивает выполнение операций в двух стандартных режимах:
- в дробном режиме (для чисел в формате 1.15) при загрузке 32–битного произведения Р в регистр результата MR происходит знаковое расширение и сдвиг содержимого влево на 1 бит. В частности, 31–й бит произведения Р соответствует 32–у биту регистра MR (или биту 0 регистра MR2), а нулевой бит Р — первому биту регистра MR (или MR0). Младший (нулевой) бит MR (или MR0) очищается, старшие семь бит MR (или MR2) заполняются знаком (или 31–м битом) произведения P;
- в целочисленном режиме (для целых чисел в формате 16.0) 32–битный регистр произведения P загружается в регистры MR0, MR1. Восемь бит регистра MR2 заполняются знаком произведения Р. Выбор режима осуществляется битом M_MODE (позиция MSTAT.4) регистра режима и состояния MSTAT (табл. 8.3.9): M_MODE=0 — дробный режим; M_MODE = 1 — целочисленный режим. В обоих режимах произведение P подается на вход сумматора–вычитателя.
Операция переполнения в АЛУ
После выполнения каждой операции в сумматоре–вычитателе формируется флаг переполнения MV, который заносится в позицию ASTAT.6 регистра арифметического статуса ASTAT (табл. 8.3.7). Флаг переполнения устанавливается (MV = 1) в том случае, если результат на выходе сумматора–вычитателя, интерпретируемый как число с дополнением до 2, пересекает 32–битную границу. В этом случае 9 старших (знаковых) разрядов 40–битного регистра результата не равны одновременно 0 или 1.
Операция насыщения в АЛУ
Эта операция выполняется при установленном флаге переполнения (MV = 1) в регистре арифметического статуса ASTAT (табл. 8.3.7). В результате операции содержимое регистра результата MR принимает максимальное:
- положительное значение 00000000 0111111111111111 1111111111111111, если старший разряд регистра MR1 равен 0;
- отрицательное значение 11111111 1000000000000000 0000000000000000, если старший разряд регистра MR1 равен 1. Операция насыщения используется после умножений–аккумуляций для контроля правильности полученных результатов. Если MV = 0, то операция насыщения оставляет результат неизменным.
Операция округления в АЛУ
С помощью опции RND аккумулятор позволяет округлять 40–битный результат до 16–битного. Округленный результат передается в регистр MR или MF. При использовании регистра MR округленный 16–битный результат содержится в регистре MR1. Содержимое регистров MR2, MR1 можно рассматривать как результат, округленный до 24 бит. 
Назначение и состав устройства сдвига
Устройство сдвига SHIFTER предназначено для выполнения сдвиговых операций 16–разрядных операндов, включающих арифметические и логические сдвиги, нормализацию и денормализацию, определение экспоненты. Устройство сдвига содержит (рис. 8.3.5):
- сдвиговый массив размерности 16×32, в котором исходный 16–разрядный операнд за один цикл помещается на любую позицию в 32–разрядном выходном слове, начиная с полностью сдвинутого операнда вправо и кончая полностью сдвинутым операндом влево;
- детектор экспоненты дляопределения степени операнда (см. ниже);
- регистр операндов SI (Shifter InOut), обеспечивающий 16–разрядный операнд для сдвигового массива и детектора экспоненты;
- регистр результата SR (Shifter Result) для хранения 32–разрядного результата сдвигового массива, состоящий из двух 16–битных регистров SR0, SR1. Информация в регистр SR может быть занесена с шины данных памяти данных DMD и считана на шины DMD и R. Регистр SR может быть также задействован в цепи обратной связи через логику управления OR/PASS для реализации сдвигов с двойной точностью;
- восьмиразрядный регистр экспоненты SE (Shifter Exponent), содержащий порядок в виде 8–разрядного дополнительного кода при выполнении операций нормализации и денормализации;
- пятиразрядный регистр для блочных операций с плавающей точкой SB (Shifter Block). Он содержит значение экспоненты блока, т. е. то значение, на которое компоненты блока должны быть сдвинуты, чтобы нормализовать самое большое значение. Чтение и запись регистра осуществляется через 5 младших разрядов шины DMD. Значения записываются в дополнительном коде в формате 5.0;
- логику OR/PASS, позволяющую получить правильный результат (см. приведенные ниже примеры) при операциях с двойной точностью. При выборе модификатора PASS результат сдвигового массива загружается в регистр SR без изменения. С помощью модификатора OR выполняется операция ИЛИ над результатом сдвигового массива и текущим содержимым регистра SR. Результат операции ИЛИ помещается в регистр SR. При считывании информации из регистров SE, SB на шину DMD происходит расширение знака до 16–битного значения. Устройство сдвига содержит два банка регистров SI, SE, SR, SB. Для выбора банка используется бит SEC_REG в позиции MSTAT.0 регистра режима и статуса MSTAT (табл. 8.3.9).
Принцип работы устройства
Сдвиг входного 16–разрядного операнда осуществляется под действием контрольного кода и сигнала HI/LO, поступающих соответственно на входы С и R сдвигового массива.
Контрольный код представляет собой 8–разрядный операнд, указывающий направление сдвига и число разрядов, на которое следует произвести сдвиг. Положительное значение операнда указывает на левый сдвиг (или сдвиг вверх), отрицательное — на правый сдвиг (или сдвиг вниз). Контрольным кодом могут служить содержимое регистра SE в прямой и инверсной форме или непосредственно команда.
Сигнал HI/LO определяет начальную точку сдвига: в режиме HI сдвиги производятся относительно SR1 (верхней половины выходного поля); в режиме LO — относительно SR0 (нижней половины). Устройство сдвига заполняет все биты 32–битного результата справа от позиции операнда нулями, слева — битом расширения X, который может быть взят из трех источников: знаковый бит операнда, бит переноса АС из регистра ASTAT и 0.
Детектор экспоненты (степени) позволяет выделить степень из входного 16–разрядного операнда и может находиться в трех состояниях, по–разному интерпретирующих степень входного операнда:
- в состоянии HI входной операнд воспринимается как двоичное число с одинарной точностью или верхняя половина двоичного числа с двойной точностью. Детектор экспоненты определяет степень операнда — число ведущих знаковых разрядов, на которое должен быть сдвинут влево входной операнд, чтобы остался только один (старший) знаковый бит, и вырабатывает отрицательный код для реализации требуемого сдвига. Этот код может служить экспонентой для мантиссы, полученной удалением знаковых бит;
- в состоянии HIX (HI–eXtend stade) входной операнд интерпретируется как результат операции сложения–вычитания, при выполнении которой в АЛУ могло произойти переполнение. В этом состоянии детектор экспоненты принимает во внимание флаг AV арифметического переполнения. Если AV = 1, детектор экспоненты выдает степень +1. Это свидетельствует о том, что необходим лишний бит в нормализованной мантиссе, в качестве которого служит флаг переноса АС в АЛУ. При AV=0 разницы между состояниями HIX и HI не существует. В состояниях HIX и HI при определении степени детектор экспоненты выдает бит SS (Shifter Sign), который заносится в регистр арифметического статуса ASTAT (бит ASTAT.7). При AV = 0 бит SS является старшим разрядом входного операнда. При AV = 1 выводится инверсия бита SS для сохранения знака переполнившегося значения;
- в состоянии LO входной операнд интерпретируется как младшая половина числа с двойной точностью, а выводимый в регистр арифметического статуса ASTAT сигнал SS — как знак числа. Регистр экспоненты SE загружается результатом детектора экспоненты в том случае, когда старшая половина 32–битного числа с двойной точностью, обработанная первой, содержит лишь знаковые биты. При этом вывод детектора экспоненты сдвигается на –16, чтобы принять во внимание тот факт, что операнд на самом деле является младшей половиной 32–разрядного операнда. В табл. 8.3.1 для рассмотренных состояний приведены входные операнды и соответствующие им значения экспоненты (в графе ДЭ — детектор экспоненты).

Определение экспоненты (степени) блока
Эта операция, выполняемая с помощью команды EXPANDJ, позволяет определить степень самого большого по масштабу числа из массива чисел. 
В противном случае содержимое SB остается неизменным.
Подобным образом обрабатываются последующие элементы массива. После обработки всех элементов массива регистр SB будет содержать наибольшую степень, значение которой лежит в пределах от –15 до 0. Отметим, что операция определения экспоненты является просмотровой операцией. Для выполнения операции нормализации необходимо скопировать содержимое регистра SB в регистр экспоненты SE. В табл. 8.3.2 приведен пример определения экспоненты блока из трех элементов. Из табл. 8.3.2 следует, что степень самого большого из приведенных чисел массива составляет –3.
Команда немедленные сдвиги
С помощью команд немедленного сдвига выполняются операции логического или арифметического сдвига влево (вверх)/вправо (вниз) на требуемое число разрядов. В командах определено направление и размер сдвига. Сдвиг происходит под действием контрольного кода в виде 8–битного знакового числа, который берется из команды. Регистр экспоненты SE в немедленных сдвигах не задействован.
Примеры. Рассмотрим случай, когда входной операнд в виде 16–разрядного двоичного кода 10110110 10100011 (0xB6A3) загружается в регистр операндов SI.
Логические сдвиги
- Логический сдвиг (LSHIFT) вправо на 5 разрядов относительно старшей половины регистра результата SR (SR1). Команды: SI = 0xB6A3; SR = LSHIFT SI BY –5 (HI); Вход SI 10110110 10100011 Значение сдвига –5 Регистр SR 00000101 10110101 00011000 00000000
- Логический сдвиг (LSHIFT) влево на 5 разрядов относительно младшей половины регистра результата SR (SR0). Команды: SI = 0xB6A3; SR = LSHIFT SI BY 5 (LO); Вход SI 10110110 10100011 Значение сдвига +5 Регистр 00000000 00010110 11010100 01100000 3. Арифметический сдвиг (ASHIFT) вправо на 5 разрядов относительно старшей половины регистра результата SR (SR1). Команды: SI = 0xB6A3; SR = ASHIFT SI BY –5 (HI); Вход SI 10110110 10100011 Значение сдвига –5 Регистр SR 11111101 10110101 00011000 00000000
Денормализация
Денормализация числа — это его сдвиг на заданное число разрядов, которое хранится в регистре экспоненты SE. Поэтому при денормализации контрольный код берется из регистра SE, а не из команды как при немедленных сдвигах. Фактически денормализация преобразует число с плавающей точкой в число с фиксированной точкой. Пример. Покажем особенности этой операции на примере денормализации числа с двойной точностью. Пусть содержимое регистра SE = –3. В этом случае необходимо выполнить в два этапа (в любой последовательности):
- арифметический сдвиг на три разряда вправо старшей половины числа, представленного в виде дополнительного кода, или логический сдвиг старшей половины беззнакового числа;
- логический сдвиг на три разряда вправо младшей половины числа. На втором этапе при сдвиге всегда используется модификатор OR, чтобы не затиралась предыдущая половина результата. 1 –й этап. SR = ASHIFT SI (HI); Первый операнд 10110110 10100011 (старшая половина) Регистр SR 11110110 11010100 01100000 00000000 2–й этап. SR = SR OR LSHIFT (LO); Второй операнд 01110110 01011101 (младшая половина) Регистр SR 11110110 11010100 01101110 11001011 Отметим, что при выполнении на втором этапе логического сдвига пропадают три младших разряда второго операнда.
Нормализация
Нормализация числа в виде дополнительного кода — ото такой сдвиг числа, при котором остается только один знаковый бит. При выполнении операции нормализации фиксируется число разрядов, на которое сдвигается операнд. Поэтому операцию нормализации можно считать как преобразование числа с фиксированной точкой в число с плавающей точкой, имеющее порядок и мантиссу. На первом этапе нормализации чисел с одинарной точностью по команде EXP определяется порядок числа, на втором по команде NORM реализуется требуемый сдвиг.
Обе команды выполняются с использованием модификаторов HI или LO, а команда NORM дополнительно распознает также модификаторы PASS и OR.
При выполнении команды NORM используется содержимое регистра экспоненты SE со знаком минус (рис. 8.3.5), чтобы произвести сдвиг в нужную сторону. Нормализация чисел с двойной точностью выполняется по приведенной схеме, однако на первом этапе старшая половина числа обработать первой. При определении порядка старшей половины числа значение порядка загружается в регистр экспоненты SE. Младшая половина числа изменит содержимое SE только в том случае, когда все биты старшей половины являются знаковыми, т.е. при SE = –15. В этом случае в регистр SE будет загружен порядок (–16…–31, табл. 8.3.1) младшей половины числа. Зафиксированное в SE значение порядка используется на втором этапе для сдвига обоих частей числа с двойной точностью. При этом порядок обработки (старшей или младшей половины числа) может быть выбран любой с помощью модификаторов HI и LO. Первая половина числа нормализуется без модификатора OR, вторая половина числа — с модификатором OR, чтобы получить правильный результат.
Примеры.
- Нормализация числа 11110110 11010100, хранящегося в регистре результата AR (АЛУ), с одинарной точностью. SE = EXP AR (HI); {в SE устанавливается –3} SR = NORM AR (HI) {SR = 10110110 10100000 00000000 00000000} Так как использовался модификатор HI, результат помещен в регистр SR1.
- Нормализации с двойной точностью числа, хранящегося в регистре результата MR1 = 11110110 11010100 (старшая половина) и MR0 = 01101110 11001011 (младшая половина) умножителя–аккумулятора — типичный случай. SE = EXP MR1 (HI); {определение порядка старшей половины числа;} {в SE устанавливается –3} SE = EXP MR0 (LO); {определение порядка младшей половины числа:} {в SE сохраняется –3} SR = NORM MR1 (HI) {нормализация старшей половины числа (SE = –3):} {SR = 10110110 10100000 00000000 00000000} SR = SR OR NORM MR0 (LO) {нормализация младшей половины числа} {(SE = –3):} {SR = 10110110 10100000 00000000 00000000}
- Нормализации числа с двойной точностью, хранящегося в регистре результата MR1 = 11111111 11111111 (старшая половина) и MR0 = 11110110 11010100 (младшая половина) умножителя–аккумулятора — случай, когда старшая половина числа содержит только знаковые биты. SE = EXP MR1 (HI); {определение порядка старшей половины числа:} {в SE устанавливается –15} SE = EXP MR0 (LO); {определение порядка младшей половины числа:} {в SE устанавливается –19} SR = NORM MRl (HI) {нормализация старшей половины числа (SE = –19):} {SR = 00000000 00000000 00000000 00000000} {старшая половина сдвигается вне пределов видимости} SR = SR OR NORM MR0 (LO) {нормализация младшей половины числа} {(SE = –19):} {SR = 10110110 10100000 00000000 00000000}
- Нормализация числа 11111010 00110010 с одинарной точностью, хранящегося в регистре результата AR (АЛУ). Случай, когда в AR произошло переполнение, т. е. флаг переполнения AV = 1, при этом флаг переноса АС, фиксирующий истинный знаковый бит операнда, равен 0. В рассматриваемом случае при определении порядка используется расширенный модификатор HIX (см. табл. 8.3.1). SE = EXP AR (HIX); {в SE устанавливается +1} SR = NORM AR (HI) {SR = 01111101 00011001} Следует отметить, что нормализация с модификатором HIX при определении порядка дает правильный результат и при AV = 0, что обусловлено тождественностью модификаторов HIX и HI для этого случая.