Приветствую Вас, уважаемые Читатели! Близятся долгожданные праздники, поэтому вопрос развлечений во время длительных посиделок становится всё более актуальным. Сегодня покажу, как создать магический квадрат из чисел, который будет обладать интересными свойствами. Запомнить, как его делать, очень легко, впрочем, как и достигнуть вау-эффекта после его заполнения. Поехали!
Магический квадрат проще всего привязать к конкретному человеку, “бросившему Вам вызов”. Попросите его назвать свой возраст, а затем расчертите после 4 на 4. Если Возраст Вашего собеседника – 31, то мы получим вот такой магический квадрат:
Обратите внимание, суммы все вертикальных, горизонтальных линий и диагоналей равны 31. Кроме того, все квадраты 2х2 также в сумме дают искомое число. Сейчас покажу, как составить такой квадрат на память (листайте галерею):
Данный математический фокус работает для людей с возрастом до 65 лет. В случае, если собеседнику менее 21 года, квадрат содержит отрицательные числа. Спасибо за внимание!
ССЫЛКА НА ДЗЕН-КАНАЛ и TELEGRAM.
16
Существует несколько различных классификаций магических квадратов
пятого порядка, призванных хоть как-то их систематизировать. В книге
Мартина Гарднера [ГМ90, сс. 244-345] описан один из таких способов –
по числу в центральном квадрате. Способ любопытный, но не более того.
Сколько существует квадратов шестого порядка, до сих пор неизвестно, но их примерно 1.77 х 1019. Число огромное, поэтому нет никаких надежд пересчитать их с помощью полного перебора, а вот формулы для подсчёта магических квадратов никто придумать не смог.
Как составить магический квадрат?
Придумано очень много способов построения магических квадратов. Проще всего составлять магические квадраты нечётного порядка. Мы воспользуемся методом, который предложил французский учёный XVII века А. де ла Лубер (De La Loubère). Он основан на пяти правилах, действие которых мы рассмотрим на самом простом магическом квадрате 3 х 3 клетки.
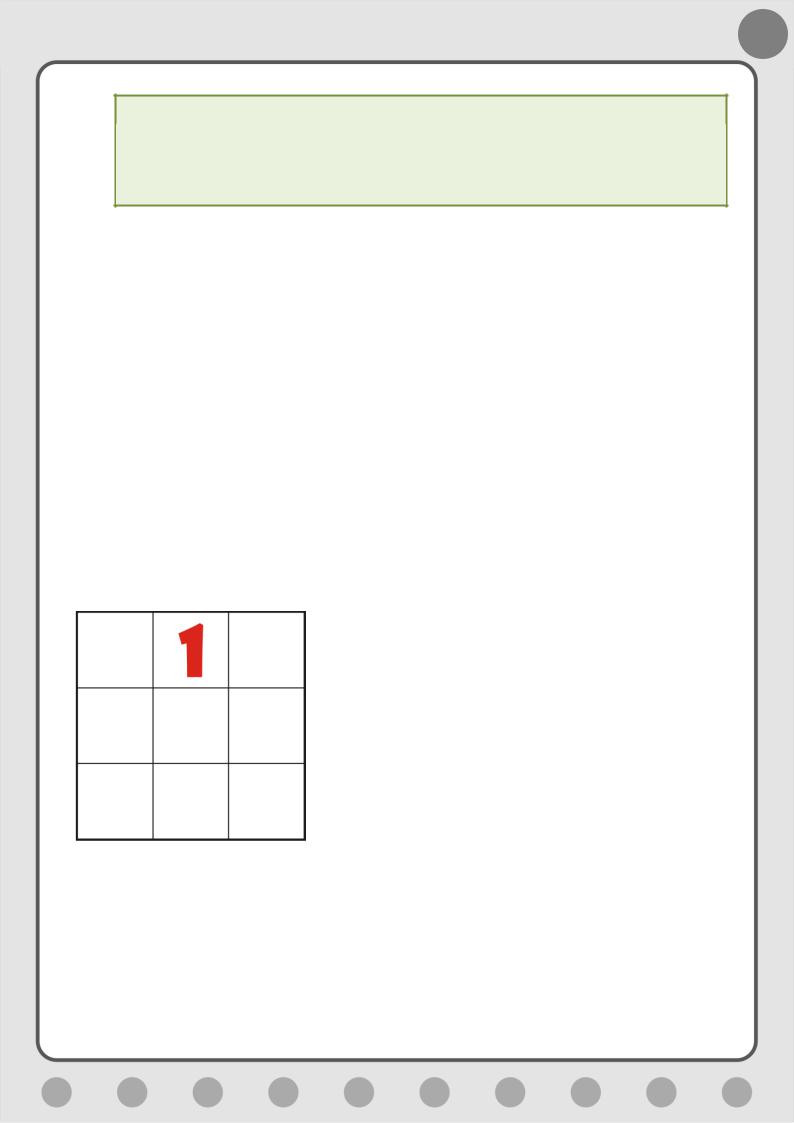
Правило 1. Поставьте 1 в среднюю колонку первой строки (Рис. 5.7).
Рис. 5.7. Первое число
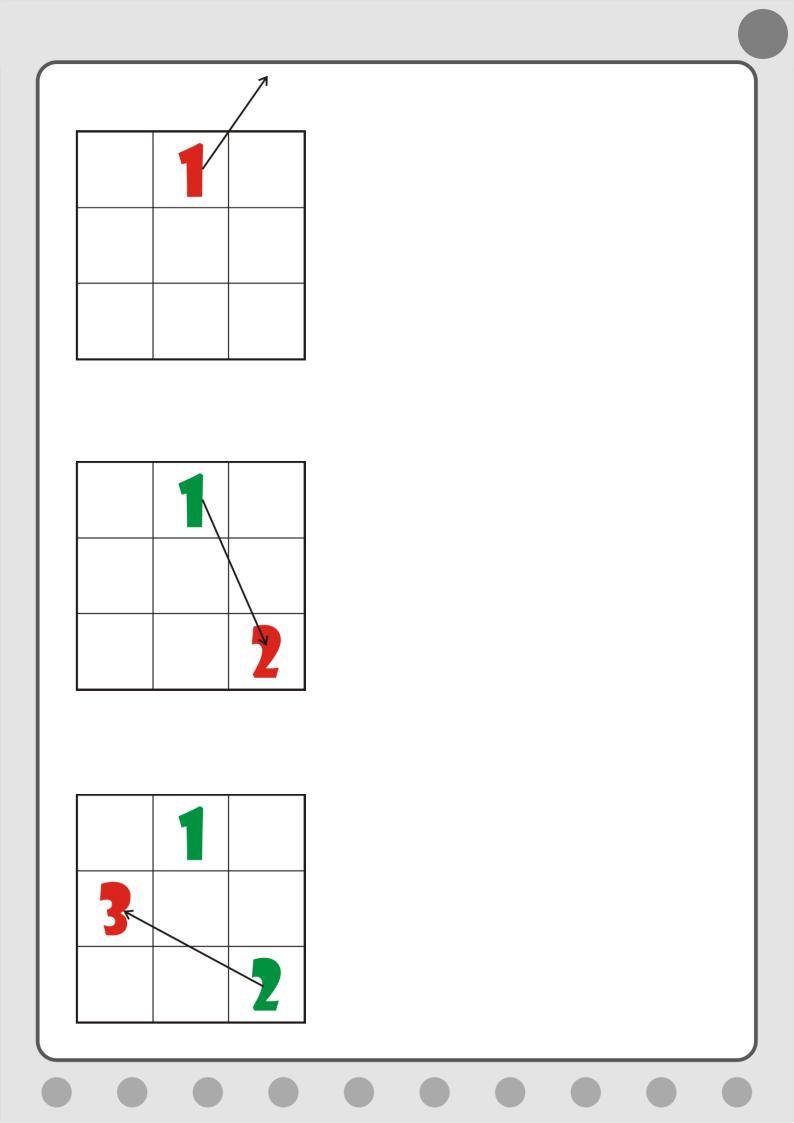
Правило 2. Следующее число поставьте, если возможно в клетку, соседнюю с текущей по диагонали правее и выше (Рис. 5.8).
17
Рис. 5.8. Пытаемся поставить второе число
Правило 3. Если новая клетка выходит за пределы квадрата сверху, то запишите число в самую нижнюю строку и в следующую колонку (Рис. 5.9).
Рис. 5.9. Ставим второе число
Правило 4. Если клетка выходит за пределы квадрата справа, то запишите число в самую первую колонку и в предыдущую строку (Рис. 5.10).
Рис. 5.10. Ставим третье число
18
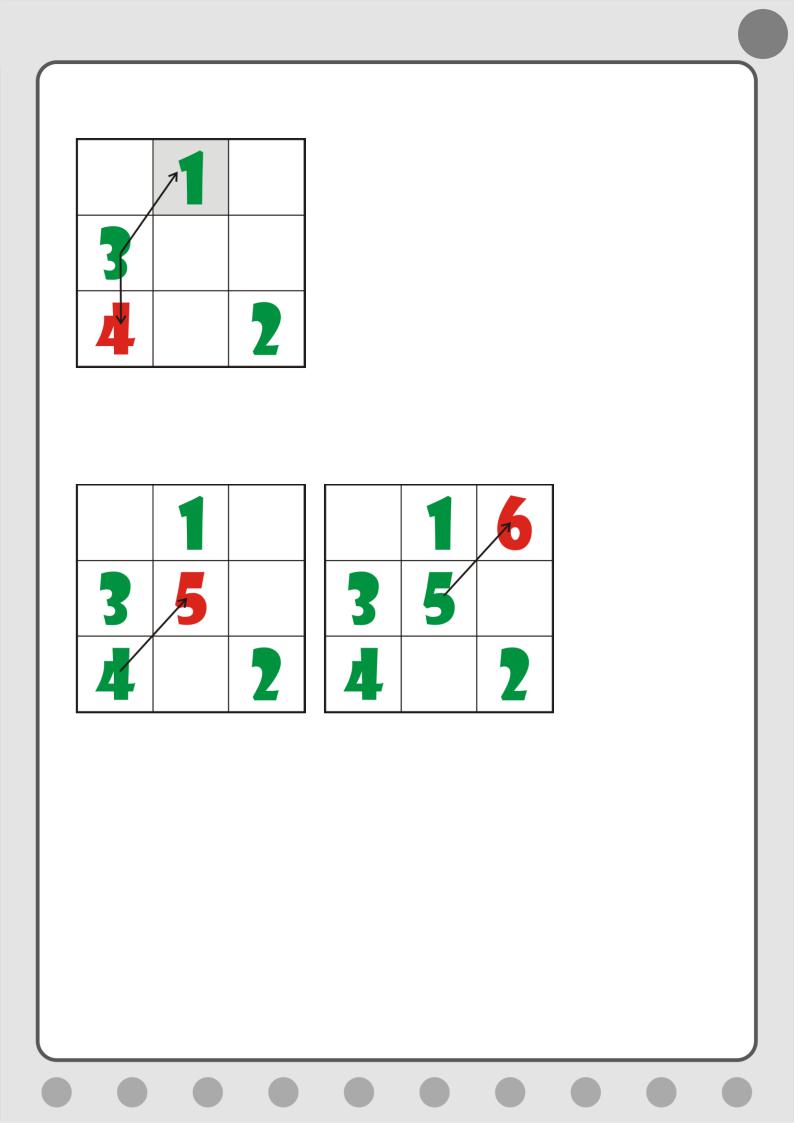
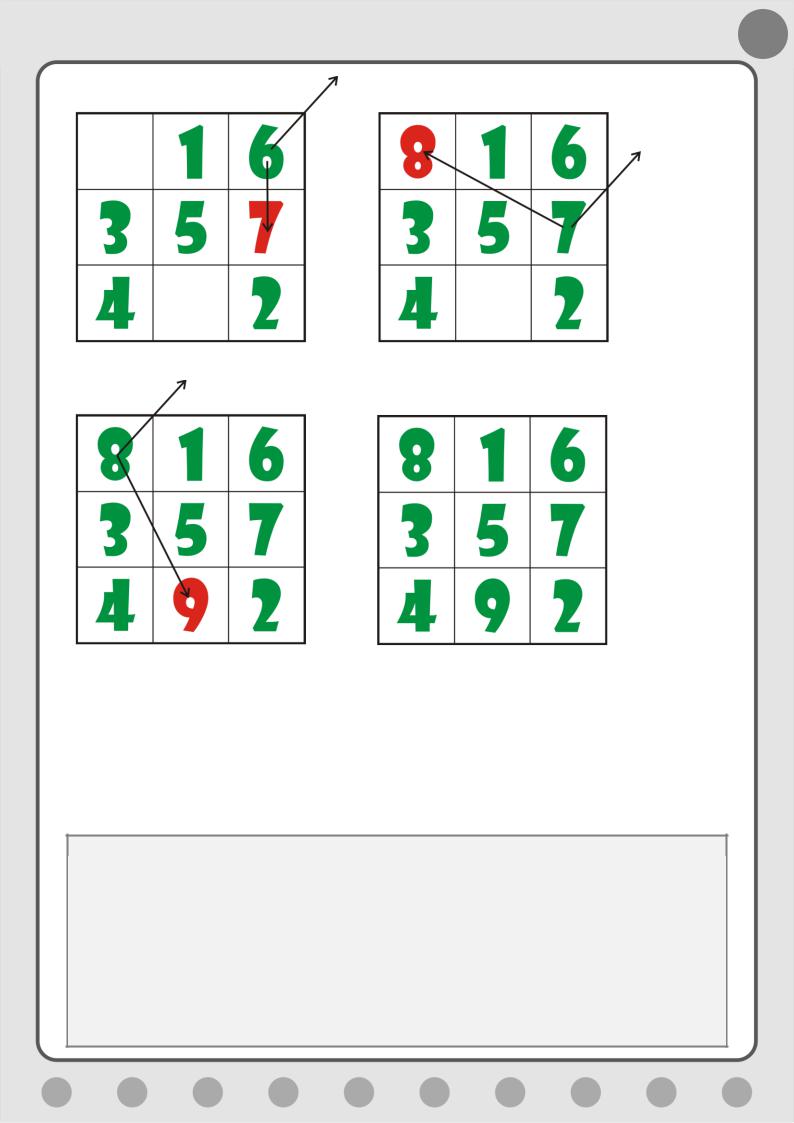
Правило 5. Если в клетке уже занята, то очередное число запишите под текущей клеткой (Рис. 5.11).
Рис. 5.11. Ставим четвёртое число
Далее переходите к Правилу 2 (Рис. 5.12).
Рис. 5.12. Ставим пятое и шестое число
Снова выполняйте Правила 3, 4, 5, пока не составите весь квадрат (Рис.
5.13).
Не правда ли, правила очень простые и понятные, но всё равно довольно утомительно расставлять даже 9 чисел. Однако, зная алгоритм построения магических квадратов, мы сможем легко перепоручить компьютеру всю рутинную работу, оставив себе только творческую, то есть написание программы.
19
Рис. 5.13. Заполняем квадрат следующими числами
Проект Магические квадраты (Magic)
Набор полей для программы Магические квадраты совершенно очевиден:
//ПРОГРАММА ДЛЯ ГЕНЕРИРОВАНИЯ
//НЕЧЕТНЫХ МАГИЧЕСКИХ КВАДРАТОВ
//ПО МЕТОДУ ДЕ ЛА ЛУБЕРА
public partial class Form1 : Form
{
//макс. размеры квадрата: const int MAX_SIZE = 27; //var
int n=0; // порядок квадрата int [,] mq; // магический квадрат
int number=0;// текущее число для записи в квадрат
20
int col=0; // текущая колонка int row=0; // текущая строка
Метод де ла Лубера годится для составления нечётных квадратов любого размера, поэтому мы можем предоставить пользователю возможность самостоятельно выбирать порядок квадрата, разумно ограничив при этом свободу выбора 27-ью клетками.
После того как пользователь нажмёт заветную кнопку btnGen Генерировать!, метод btnGen_Click создаёт массив для хранения чисел и переходит в метод generate:
//НАЖИМАЕМ КНОПКУ “ГЕНЕРИРОВАТЬ”
private void btnGen_Click(object sender, EventArgs e)
{
//порядок квадрата:
n = (int)udNum.Value;
//создаем массив:
mq = new int[n+1, n+1];
//генерируем магический квадрат: generate();
lstRes.TopIndex = lstRes.Items.Count-27;
}
Здесь мы начинаем действовать по правилам де ла Лубера и записываем первое число – единицу – в среднюю клетку первой строки квадрата (или массива, если угодно):
//Генерируем магический квадрат void generate(){
//первое число: number=1;
rule1:
//колонка для первого числа – средняя: col = n / 2 + 1;
//строка для первого числа – первая: row=1;
//заносим его в квадрат: mq[row,col]= number;
Теперь мы последовательно пристраиваем по клеткам остальные числа – от двойки до n * n:
//переходим к следующему числу:
21
nextNumber:
number++;
Запоминаем на всякий случай координаты актуальной клетки
int tc=col; int tr = row;
и переходим в следующую клетку по диагонали:
col++; row–;
Проверяем выполнение третьего правила:
rule3:
if (row < 1) row= n;
А затем четвёртого:
rule4:
if (col > n) { col=1;
goto rule3;
}
И пятого:
rule5:
if (mq[row,col] != 0) { col=tc;
row=tr+1; goto rule3;
}
Как мы узнаем, что в клетке квадрата уже находится число? – Очень просто: мы предусмотрительно записали во все клетки нули, а числа в готовом квадрате больше нуля. Значит, по значению элемента массива мы сразу же определим, пустая клетка или уже с числом! Обратите внимание, что здесь нам понадобятся те координаты клетки, которые мы запомнили перед поиском клетки для следующего числа.
Рано или поздно мы найдём подходящую клетку для числа и запишем его в соответствующую ячейку массива:
22
//заносим его в квадрат: mq[row, col] = number;
Попробуйте иначе организовать проверку допустимости перехода в но-
вую клетку!
Если это число было последним, то программа свои обязанности выполнила, иначе она добровольно переходит к обеспечению клеткой следующего числа:
//если выставлены не все числа, то if (number < n*n)
//переходим к следующему числу: goto nextNumber;
И вот квадрат готов! Вычисляем его магическую сумму и распечатываем на экране:
//построение квадрата закончено: writeMQ();
} //generate()
Напечатать элементы массива очень просто, но важно учесть выравнивание чисел разной «длины», ведь в квадрате могут быть одно-, дву- и трёхзначные числа:
//Печатаем магический квадрат void writeMQ()
{
lstRes.ForeColor = Color.Black;
string s = “Магическая сумма = ” + (n*n*n +n)/2; lstRes.Items.Add(s);
lstRes.Items.Add(“”);
// печатаем магический квадрат: for (int i= 1; i<= n; ++i){
s=“”;
for (int j= 1; j <= n; ++j){
if (n*n > 10 && mq[i,j] < 10) s += ” “; if (n*n > 100 && mq[i,j] < 100) s += ” “; s= s + mq[i,j] + ” “;
}
lstRes.Items.Add(s);
}
lstRes.Items.Add(“”); }//writeMQ()
23
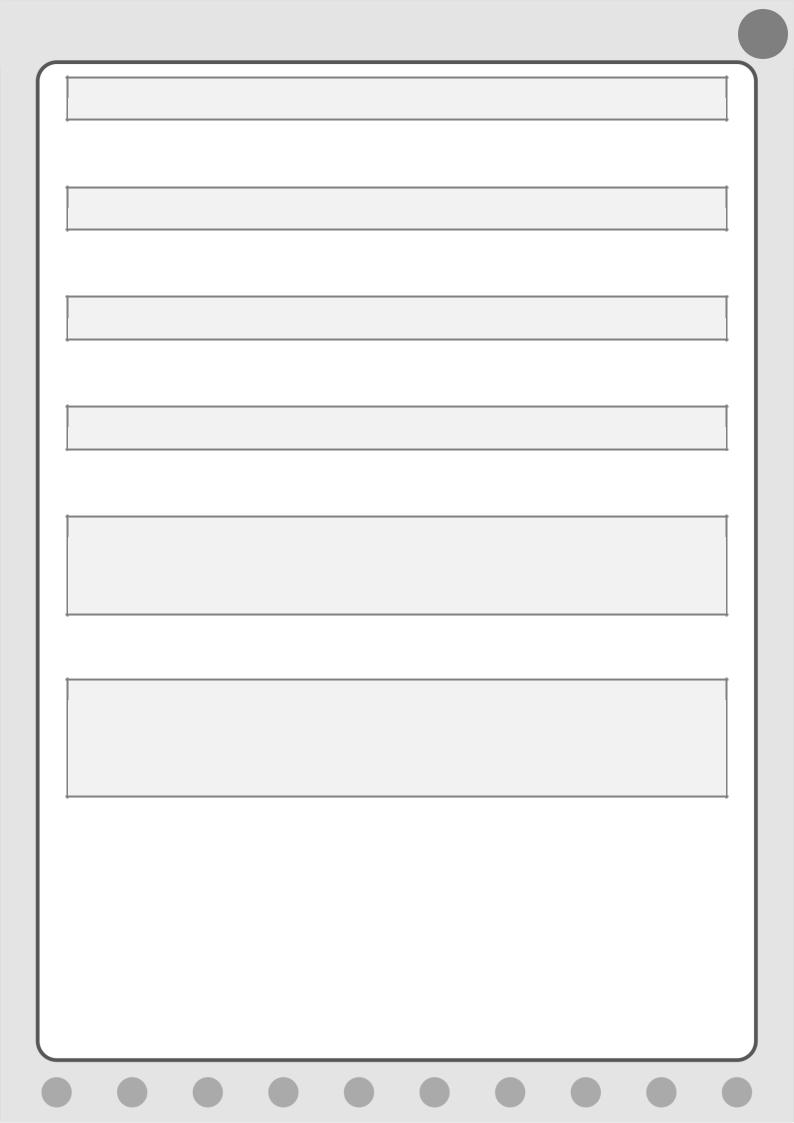
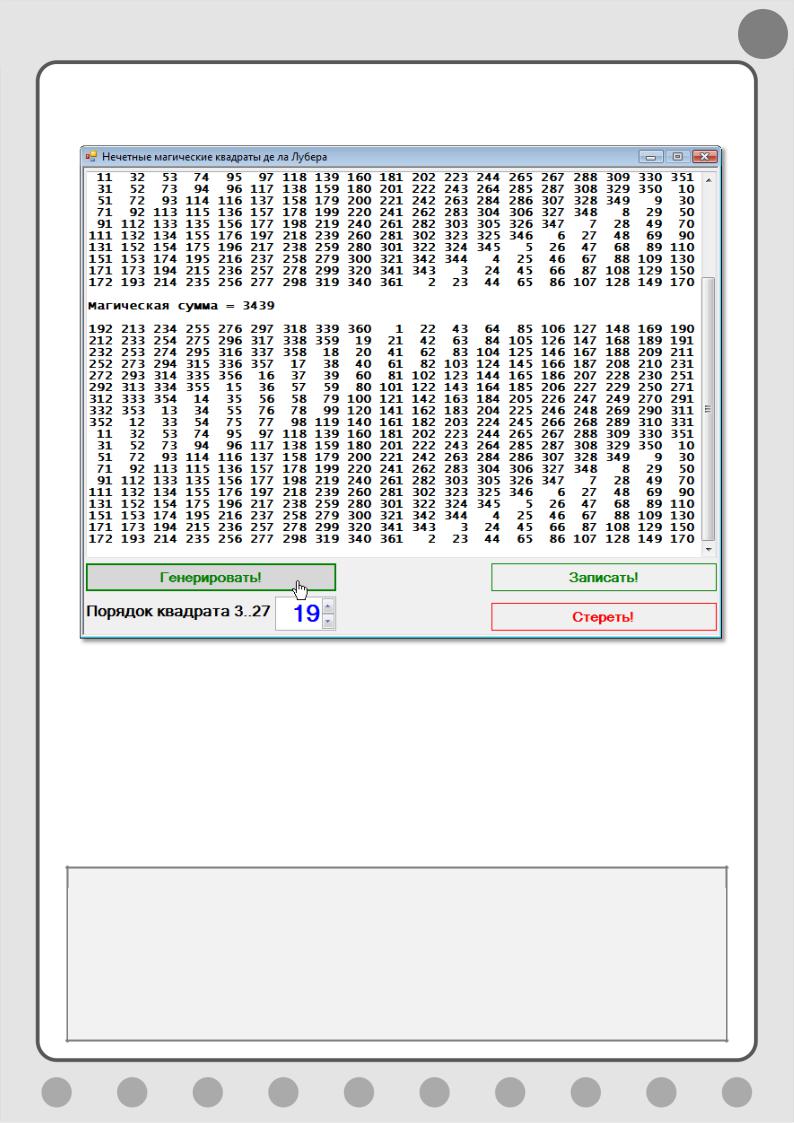
Запускаем программу – квадраты получаются быстро и на загляденье (Рис.
5.14).
Рис. 5.14. Изрядный квадратище!
В книге С.Гудман, С.Хидетниеми Введение в разработку и анализ алгорит-
мов, на страницах 297-299 мы отыщем тот же самый алгоритм, но в «сокращённом» изложении. Он не столь «прозрачен», как наша версия, но работает верно.
Добавим кнопку btnGen2 Генерировать 2! и запишем алгоритм на языке
Си-шарп в метод btnGen2_Click:
//Algorithm ODDMS
private void btnGen2_Click(object sender, EventArgs e)
{
//порядок квадрата: n = (int)udNum.Value;
//создаем массив:
mq = new int[n + 1, n + 1];
//генерируем магический квадрат: int row = 1;
24
int col = (n+1)/2;
for (int i = 1; i <= n * n; ++i)
{
mq[row, col] = i; if (i % n == 0)
{
++row;
}
else
{
if (row == 1) row = n;
else
–row;
if (col == n) col = 1;
else
++col;
}
}
//построение квадрата закончено: writeMQ();
lstRes.TopIndex = lstRes.Items.Count – 27;
}
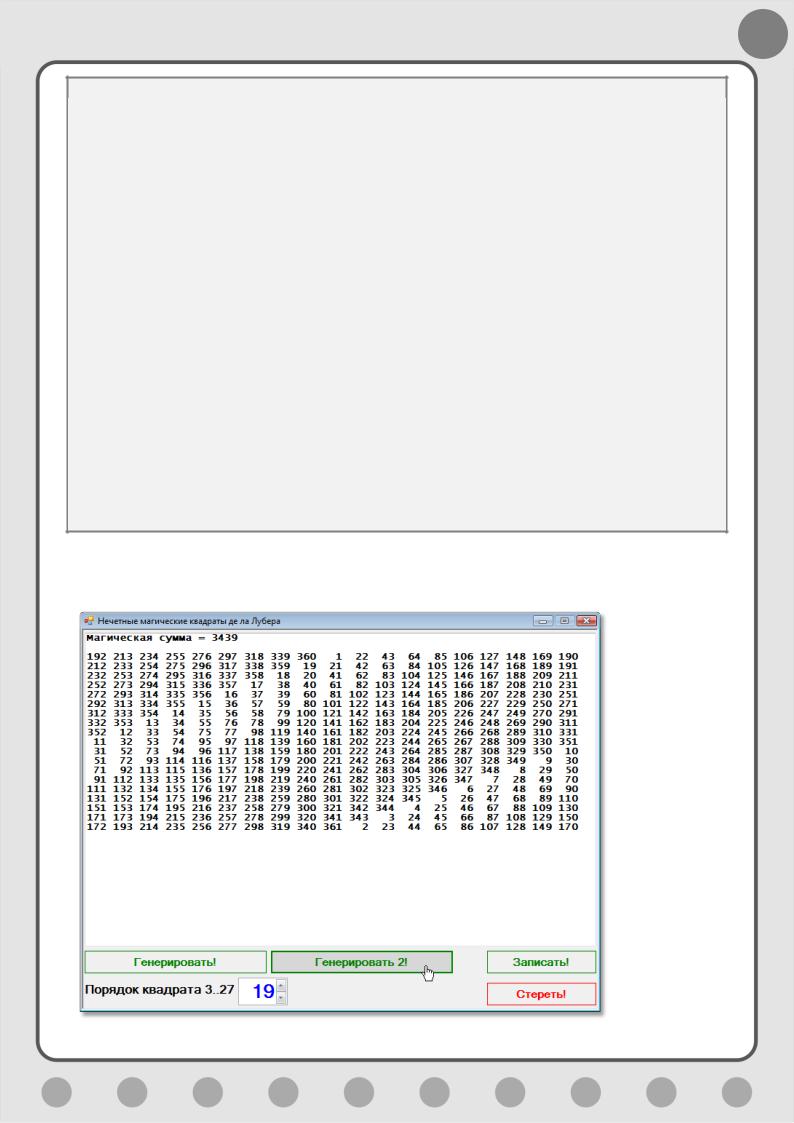
Кликаем кнопку и убеждаемся, что генерируются «наши» квадраты (Рис.
5.15).
Рис. 5.15. Старый алгоритм в новом обличии
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Личный талисман “Магический квадрат Пифагора”
«Магнит» для богатства, здоровья и прочего-прочего…
Пифагор составил магический квадрат, способный «притягивать» энергию богатства.
Между прочим, квадратом Пифагора пользовался сам Генри Форд.
Он начертил его на долларовой купюре и всегда носил с потайном отделении бумажника как талисман.
На бедность, как известно, Форд не жаловался. В возрасте 83 лет Генри передав бразды правления корпорацией и немалое состояние в размере 1 млрд. долларов (с учётом инфляции — более 36 млрд по нынешним ценам) своим внукам.
*** *** *** *** ***
Цифры, особым образом вписанные в квадрат, способны не только притянуть богатство.
Например, великий врач Парацельс составил свой квадрат — «талисман здоровья».
В общем, если грамотно построить магический квадрат, можно впустить в жизнь те энергетические потоки, которые вам необходимы.
Как сделать личный талисман магический квадрат Пифагора Надеюсь, вы умеете писать цифры и считать до десяти?
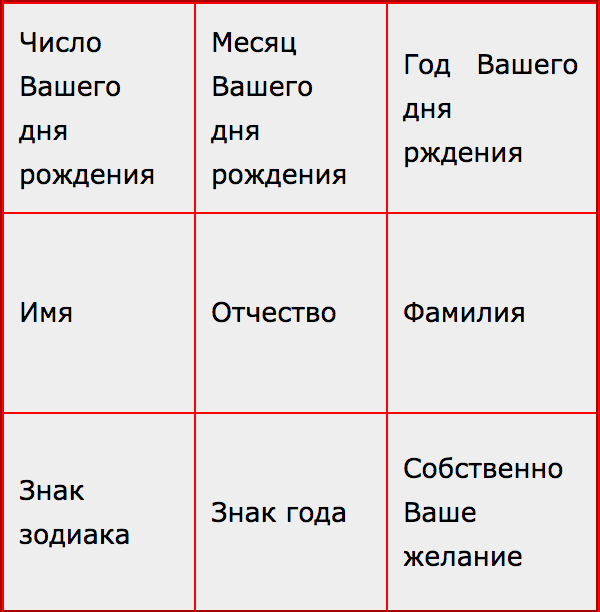
Тогда вперед. Чертим энергетический квадрат, который может стать вашим личным талисманом.
В нем три колонки и три ряда. Всего девять цифр, которые составляют ваш индивидуальный нумерологический код.
Как вычислить этот код?
В первый ряд поставим три цифры:
* цифру вашего дня рождения,
* месяца рождения
* года рождения.
Например, вы появились на свет 25 мая 1971 года. Тогда ваше первое число — число дня: 25. Это сложное число, по законам нумерологии, его надо сократить до простого, сложив цифры 2 и 5. Получается — 7: вот семерку мы и поставим в первую клеточку квадрата.
Второе — число месяца: 5, ведь май — пятый месяц. Обратите внимание: если человек родился в декабре, то есть в месяце под номером 12, нам бы пришлось сокращать число до простого: 1+2 = 3.
Третье — число года. Тут уж сокращать до простого придется всем. Итак: 1971 (год рождения) раскладываем на составные цифры и считаем их сумму. 1+9+7+1 = 18, 1+8 =9.
Вписываем в первый ряд цифры: 7, 5, 9.
Во второй ряд поставим цифры:
* четвертая — вашего имени,
* пятая — отчества,
* шестая — фамилии.
Их определяем по таблице буквенно-цифровых соответствий.
Руководствуясь ею, вы складываете цифровые значения каждой буквы своего имени, при необходимости приводите сумму к простому числу.
Точно также действуем с отчеством и фамилией.
Например, Кротов= 3+9+7+2+7+3=31=3+1=4
Теперь у нас имеется три цифры для второй строки энергетического квадрата
Третий ряд
Чтобы заполнить третий ряд, найти седьмую, восьмую и девятую цифры, придется обратиться к астрологии.
Седьмая цифра — номер вашего знака Зодиака.
Тут все просто. Овен — первый знак, ему соответствует цифра 1. Рыбы — двенадцатый знак, им соответствует цифра 12.
Внимание: в данном случае сокращать двузначные цифры до простых не следует, числа 10, 11 и 12 имеют собственное значение!
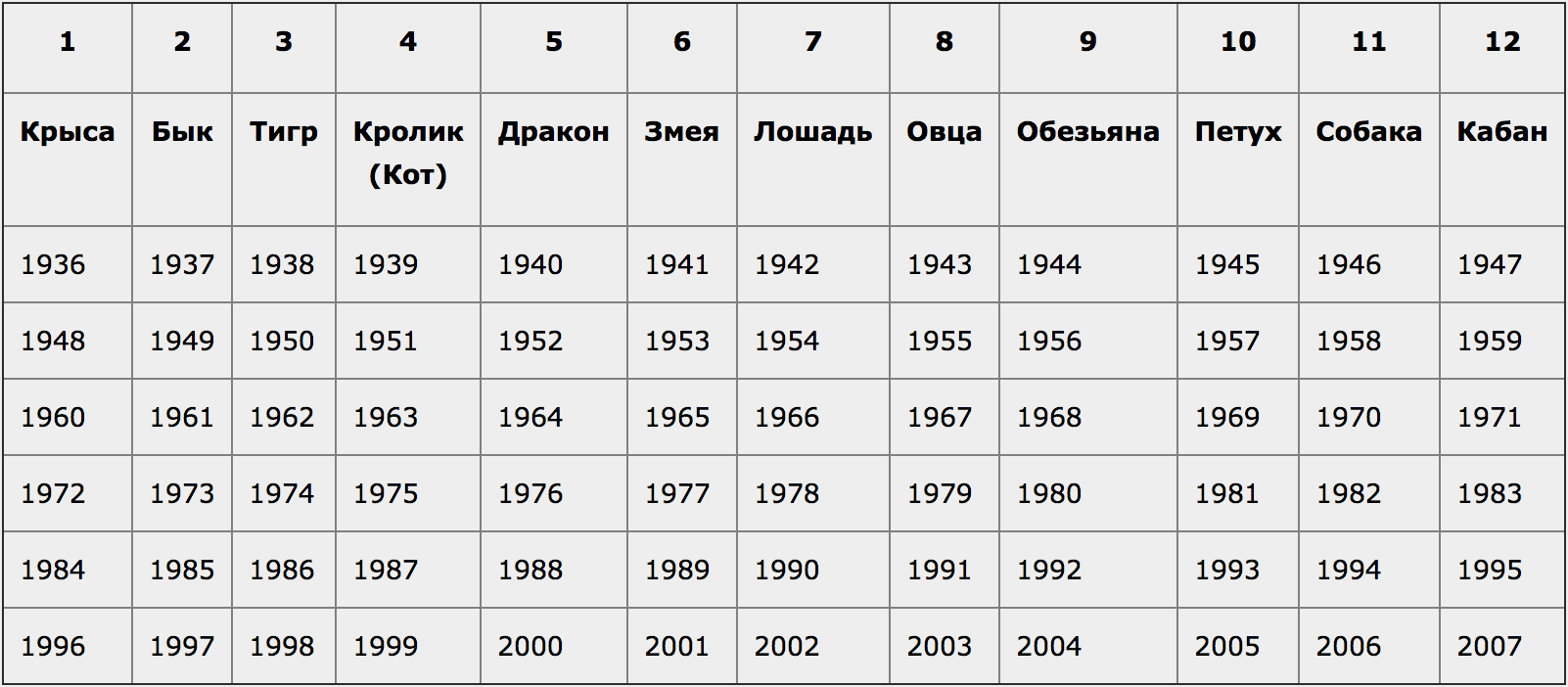
Восьмая цифра — номер вашего знака по Восточному календарю. Найти его несложно по таблице ниже:
То есть, если вы родились в 1974 году, номер вашего знака — 3 (Тигр), а если в 1982 году — 11 (Собака).
Девятая цифра — нумерологический код вашего желания.
Например, вы набираете энергию ради здоровья. Значит, ключевое слово — «здоровье». Складываем буквы снова по первой таблице:
З — 9, Д — 5, О — 7, Р — 9, О — 7, В — 3, Ь — 3, Е — 6 = 49, то есть 4+9=13. Поскольку у нас снова получилось сложное число, продолжаем сокращать: 1+3=4
Имейте в виду: если у вас получились числа 10, 11 и 12, то и в этом случае их сокращать не следует.
Ну а если вам не хватает денег, то вы можете высчитать значение слов «богатство», «деньги» или конкретно «доллар», «евро».
Итак, последней девятой цифрой в вашем магическом квадрате будет число — нумерологическое значение вашего ключевого слова или другими словами код желания.
Спойте свою «квадратную» медитацию
А теперь расположим девять цифр в три ряда по три цифры в нашем магическом квадрате.
Нарисованный квадрат можно вставить в рамку и повесить дома или в офисе.
А можно положить в папочку и убрать подальше от посторонних глаз. Прислушайтесь к своему внутреннему голосу, он подсказывает, что подходит именно вам.
Но и это еще не все. Выучите цифры своего личного нумерологического кода в той последовательности, как они стоят в клеточках.
Зачем? Это ваша личная мантра, ваша прямой провод с Богом, если хотите. Она настраивает вас на нужный поток из огромного множества сил во Вселенной, а с другой стороны — вас слышат и отвечают на ваши вибрации.
Поэтому свою мантру надо выучить наизусть. И — медитировать.
Повторяя мысленно свой нумерологический код, сядьте в удобное кресло или прилягте на диван. Расслабьтесь. Руки держите ладонями вверх, как бы принимая энергию. Через некоторое время вы ощутите покалывание в пальцах, вибрацию, может быть — тепло или, напротив, холодок в ладонях.
Отлично: энергия пошла! Медитация длится до тех пор, пока вам не захочется ее прекратить, пока не появится потребность встать или… пока вы не задремлете.
————–
Не сильны в математике? Не желаете производить подсчёты?
Не беда ! Все подсчёты за Вас произведёт компьютер на сайте www.savespace.ru
Магический квадрат
40390 Просмотров
40390 ПросмотровМатериал не мой , если уважаемый модератор посчитает нужным оставить этот материал , тогда я с удовольствием выложу – пользуйтесь.
Как составить Ваш личный магический квадрат и притянуть в свою жизнь желаемое? Потратьте несколько минут и вы получите сильнейший магический талисман, которым пользовался сам Генри Форд!
Чертим энергетический квадрат, который станет вашим личным талисманом. В нем три цифры по три ряда – то есть всего девять цифр. Вот эти-то девять цифр нам с вами и предстоит вычислить, чтобы составить ваш нумерологический код.
► Первое число: день вашего рождения
Например, вы появились на свет 25 мая 1971 года. Тогда ваше первое число – число дня: 25. Это сложное число. По законам нумерологии его надо сократить до простого, сложив цифры 2 и 5. Получается – 7: вот семерку мы и поставим в первую клеточку квадрата.
► Второе число: число месяца
Например, у нас это число 5, ведь май – пятый месяц. Обратите внимание: если человек родился в декабре, то есть в месяце под номером 12, нам бы пришлось сокращать число до простого: 1+2 = 3.
► Третье число: число года
Тут уж сокращать до простого придется всем. Итак: 1971 (год рождения) раскладываем на составные цифры и считаем их сумму. 1+9+7+1 = 18, 1+8 =9.
Вписываем в первый ряд цифры: 7, 5, 9.
► Четвертое число: число имени
Переведите свое имя в простое число по таблице. Если у вас получается двузначное число, складывайте его, пока не получите однозначное число
► Пятое число: число отчества
Переведите свое отчество в простое число по таблице. Если у вас получается двузначное число, складывайте его, пока не получите однозначное число.
Записан
► Шестое число: число фамилии
Переведите свою фамилию в простое число по таблице. Если у вас получается двузначное число, складывайте его, пока не получите однозначное число.
Записан
Чтобы заполнить третий ряд, найти седьмую, восьмую и девятую цифры, придется обратиться к астрологии.
► Седьмое число: номер Знака Зодиака
ЗНАКИ ЗОДИАКА
№1 знак зодиака Овен 21.03-20.04
№2 знак зодиака Телец 21.04-20.05
№3 знак зодиака Близнецы 21.05-21.06
№4 знак зодиака Рак 22.06-22.07
№5 знак зодиака Лев 23.07-23.08
№6 знак зодиака Дева 24.08-23.09
№7 знак зодиака Весы 24.09-23.10
№8 знак зодиака Скорпион 24.10-22.11
№9 знак зодиака Стрелец 23.11-21.12
№10 знак зодиака Козерог 22.12-20.01
№11 знак зодиака Водолей 21.01-20.02
№12 знак зодиака Рыбы 21.02-20.03
Внимание: в данном случае сокращать двузначные цифры до простых не следует, числа 10, 11 и 12 имеют собственное значение!
► Восьмое число: номер вашего знака по Восточному календарю
Найти его несложно по таблице:
Записан
► Девятое число: нумерологический код вашего желания
Например, вы набираете энергию ради здоровья. Значит, ключевое слово – «здоровье». Складываем буквы по приведенной выше таблице:
Записан
получается 49, то есть 4+9=13. Поскольку у нас снова получилось сложное число, продолжаем сокращать: 1+3=4.
Имейте в виду: числа 10, 11 и 12 и в этом случае сокращать не следует.
Ну а если вам не хватает денег, то вы можете высчитать значение слов «богатство», «деньги» или конкретно «рубль», «доллар», «евро», «тенге». Нумерологическое значение вашего ключевого слова и будет последней девятой цифрой магического квадрата.
А теперь расположим девять цифр в три ряда по три цифры в нашем магическом квадрате. Нарисованный квадрат можно вставить в рамку и повесить дома или в офисе. А можно положить в папочку и убрать подальше от посторонних глаз: если внутренний голос подсказывает, что именно этот способ вам подходит.
Хотите ускорить исполнение вашего желания? Есть один секрет:
Для того, чтобы ускорить исполнение вашего желания, следует выучить цифры своего личного нумерологического кода, то есть все числа, входящие в квадрат в той последовательности, как они стоят в клеточках. И – медитировать. Повторяя мысленно свой нумерологический код, сядьте в удобное кресло или прилягте на диван. Расслабьтесь. Руки держите ладонями вверх, как бы принимая энергию. Через некоторое время вы ощутите покалывание в пальцах, вибрацию, может быть – тепло или, напротив, холодок в ладонях. Отлично: энергия пошла! Медитация длится до тех пор, пока вам не захочется ее прекратить, пока не появится потребность встать или… пока вы не задремлете.
С первого раза не получилось? Не беда – видимо, это просто не ваш час. Подождите какое-то время. Ваш час придет!
Записан
Выглядеть ваш квадрат должен так
1 2 3
4 5 6
7 8 9
я высчитала свои цифры , написала их на листочке , вырезала небольшой квадратик , а дальше кто чего себе загадал , если деньги – можно в кошелек , если удачу можно с собой носить , ну и т.д. У кого получились двухзначные цифры (в пунктах 7,8,9) – их и пишите – согласно рекомендации. Кстати квадрат Деньги – можно нарисовать на денежной купюре и носить в кошельке, только денежку не скручивайте .
Записан
Вы пользовались? Мб есть отзовы, интересно насколько он рабочий.
Записан
Он рабочий , как и все то во что верите .
Цитата : Квадратом Пифагора, заряженным на богатство, пользовался сам Генри Форд: он начертил его на долларовой купюре и всегда носил с собой в потайном отделении бумажника как талисман. На бедность, как известно, Форд не жаловался.
В любом случае вреда он вам не принесет
Записан
Я встречала в инете маг.треугольник в углах было написано Бог Адам Ева и еще чего то .Он тоже для денег и исполнения желания.Но вот больше никак не могу его найти.Может кто видел и разъяснит что в нем написано и на каком языке.
Записан
Уважаемая Анаэль, скажите, пожалуйста, из какого источника Вы брали информацию? Спрашиваю потому что квадрат который вы выложили в теме расположен в горизонтальных рядах, я же везде находила в инете квадрат Пифагора с вертикальными рядами. Хотелось бы узнать как правильно его наносить на бумагу, чтобы не напортачить
Записан
Нашла этот магический треугольник.Что скажите,кто пользовался?
Возьмите небольшой лист бумаги.
На его лицевую сторону черной ручкой перерисуйте изображенный на рисунке символ.
На обороте напишите свое желание.
Делать это можно в любой день, но обязательно вечером – с 19 часов до полуночи. Затем закопайте талисман в укромном месте.
Повторите ритуал трижды, каждый раз перерисовывая изображение заново на новый лист бумаги. После этого можете играть в лотерею. Вам обязательно повезет! Помните: ваша вера прямо пропорционально реализации желания.
Другой способ использования данного талисмана: не закапывайте его, а носите с собой в кошельке 40 дней. На 41-й – выкиньте, а лучше сожгите, остатки пепла высыпьте в проточную воду или спустите в канализацию.
Что же представляет собой данный чудодейственный талисман? В его символике зашифровано число 331 – триада, состоящая из ангела, мужчины и женщины.
Адам олицетворяет мужское начало, Ева – женское, а ангел указывает на Яхве (каждый из четырех архангелов символизирует одну букву священного слова IHVH в следующем порядке: Михаил, Гавриил, Рафаил и Ариэль).
Адам в глазах Евы узрел Бога. Именно этот постулат в математической форме выражен на нашем рисунке.
Как уже говорилось, нарисованный вами каббалистический символ следует носить у себя в кошельке. Его матрица способна притягивать денежные массы и деловых партнеров. Чтобы усилить это свойство, на обратной стороне листочка напишите свое желание, а под ним – слово KALHIVI (что значит: «Будьте, как боги»).
Подобное сочетание символов подарит выигрыш даже самому неспособному к удаче человеку, сделав деньги практически из воздуха! Но запомните главное: подобной формулой можно воспользоваться один-единственный раз.Для людей, которым патологически не везет, данный рецепт очень пригодится: он откроет дорогу удаче в деньгах.
Записан
Уважаемая Анаэль, скажите, пожалуйста, из какого источника Вы брали информацию? Спрашиваю потому что квадрат который вы выложили в теме расположен в горизонтальных рядах, я же везде находила в инете квадрат Пифагора с вертикальными рядами. Хотелось бы узнать как правильно его наносить на бумагу, чтобы не напортачить
http://treedream.ru/news или https://vk.com/treedrea в контакте велось бурное обсуждение как правильно составлять квадрат.
Записан
Анаэль а сам квадрат рисовать нужно?или только цифры?и цвет имеет значение?
Записан
тут уже можете проявить свой креатив , и цветовую гамму можете использовать по соотношениям и рамку применить , кому , что нравится 
Записан
у меня тоже совпадают только первые числа, да и двухзначные числа они похоже складывают…
У кого-нибудь результат был хоть в каком-нибудь варианте? 
Записан
- Черная магия и Руны
- Предсказательные техники
- Нумерология (Модератор: Margete)
- Магический квадрат
Маги́ческий, или волше́бный квадра́т — квадратная таблица 
, заполненная 
различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный натуральными числами от 
до . Магический квадрат называется ассоциативным или симметричным, если сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна 
.
Нормальные магические квадраты существуют для всех порядков 
, за исключением 
, хотя случай 
тривиален — квадрат состоит из одного числа. Минимальный нетривиальный случай показан ниже, он имеет порядок 3.
Сумма чисел в каждой строке, столбце и на диагоналях называется магической константой, M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой
Первые значения магических констант приведены в следующей таблице (последовательность A006003 в OEIS):
Порядок 
|
3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
15 | 34 | 65 | 111 | 175 | 260 | 369 | 505 | 671 | 870 | 1105 |
Исторически значимые магические квадраты[править | править код]
Квадрат Ло Шу[править | править код]
Изображение Ло Шу в книге эпохи Мин
Ло Шу (кит. трад. 洛書, упр. 洛书, пиньинь luò shū) Единственный нормальный магический квадрат 3×3. Был известен ещё в Древнем Китае, первое изображение на черепаховом панцире датируется 2200 г. до н. э.
В Западноевропейской традиции этот квадрат называется «Печать Сатурна» (Sigillum Saturni). Параметры квадрата: 3, 9, 15, 45 (3х3, 9 ячеек, сумма по всем направлениям 15, сумма всех чисел в квадрате — 45).[1]
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
45 : 3 = 15
Квадрат, найденный в Кхаджурахо (Индия)[править | править код]
Самый ранний уникальный магический квадрат обнаружен в надписи XI века в индийском городе Кхаджурахо:
| 7 | 12 | 1 | 14 |
| 2 | 13 | 8 | 11 |
| 16 | 3 | 10 | 5 |
| 9 | 6 | 15 | 4 |
Это первый магический квадрат, относящийся к разновидности так называемых «дьявольских» квадратов[2].
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 = 136
136 : 4 = 34
Магический квадрат Ян Хуэя (Китай)[править | править код]
В XIII в. математик Ян Хуэй занялся проблемой методов построения магических квадратов. Его исследования были потом продолжены другими китайскими математиками. Ян Хуэй рассматривал магические квадраты не только третьего, но и больших порядков. Некоторые из его квадратов были достаточно сложны, однако он всегда давал правила для их построения. Он сумел построить магический квадрат шестого порядка, причем последний оказался почти ассоциативным (в нем только две пары центрально противолежащих чисел не дают сумму 37)[3]:
| 27 | 29 | 2 | 4 | 13 | 36 |
| 9 | 11 | 20 | 22 | 31 | 18 |
| 32 | 25 | 7 | 3 | 21 | 23 |
| 14 | 16 | 34 | 30 | 12 | 5 |
| 28 | 6 | 15 | 17 | 26 | 19 |
| 1 | 24 | 33 | 35 | 8 | 10 |
Сумма всех 36 чисел равна 666
666 : 6 = 111
Квадрат Альбрехта Дюрера[править | править код]
Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера «Меланхолия I», считается самым ранним в европейском искусстве[4]. Два средних числа в нижнем ряду указывают дату создания гравюры (1514).
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Сумма чисел на любой горизонтали, вертикали и диагонали равна 34. Эта сумма также встречается во всех угловых квадратах 2×2, в центральном квадрате (10+11+6+7), в квадрате из угловых клеток (16+13+4+1), в квадратах, построенных «ходом коня» (2+12+15+5 и 3+8+14+9), в вершинах прямоугольников, параллельных диагоналям (2+8+15+9 и 3+12+14+5), в прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12). Большинство дополнительных симметрий связано с тем, что сумма любых двух центрально симметрично расположенных чисел равна 17.
Данный квадрат является «Печатью Юпитера» (Sigillum Iouis), имеет параметры: 4, 16, 34, 136 (размер 4х4, 16 ячеек, сумма по направлениям — 34, сумма всех чисел равна 136).[1]
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 = 136
136 : 4 = 34
Магические квадраты Афанасия Кирхера[1][править | править код]
Квадрат Марса[править | править код]
Квадрат или печать Марса (Sigillum Martis) имеет параметры: 5, 25, 65, 325 (размер 5х5, 25 ячеек, сумма по направлениям — 65, сумма всех чисел равна 325).
| 12 | 25 | 8 | 21 | 4 |
| 5 | 13 | 26 | 9 | 17 |
| 18 | 6 | 14 | 22 | 10 |
| 11 | 19 | 2 | 15 | 23 |
| 24 | 7 | 20 | 3 | 16 |
325 : 5 = 65
Квадрат Солнца[править | править код]
Печать Солнца (Sigillum Solis) имеет параметры: 6, 36, 111, 666 (размер 6х6, 36 ячеек, сумма по направлениям — 111, сумма всех чисел равна 666).
| 6 | 32 | 3 | 34 | 35 | 1 |
| 7 | 11 | 27 | 28 | 8 | 30 |
| 19 | 14 | 16 | 15 | 23 | 24 |
| 18 | 20 | 22 | 21 | 17 | 13 |
| 25 | 29 | 10 | 9 | 26 | 12 |
| 36 | 5 | 33 | 4 | 2 | 31 |
666 : 6 = 111
Квадрат Венеры[править | править код]
Печать Венеры (Sigillum Veneris) имеет параметры: 7, 49, 175, 1225 (размер 7х7, 49 ячеек, сумма по направлениям — 175, сумма всех чисел — 1225).
| 22 | 47 | 16 | 41 | 10 | 35 | 4 |
| 5 | 23 | 48 | 17 | 42 | 11 | 29 |
| 30 | 6 | 24 | 49 | 18 | 36 | 12 |
| 13 | 31 | 7 | 25 | 43 | 19 | 37 |
| 38 | 14 | 32 | 1 | 26 | 44 | 20 |
| 21 | 39 | 8 | 33 | 2 | 27 | 45 |
| 46 | 15 | 40 | 9 | 34 | 3 | 28 |
1225 : 7 = 175
Квадрат Меркурия[править | править код]
Печать Меркурия (Sigillum Mercurio) имеет параметры: 8, 64, 260, 2080 (размер 8х8, 64 ячейки, сумма по направлениям — 260, сумма всех чисел — 2080).
| 8 | 58 | 59 | 5 | 4 | 62 | 63 | 1 |
| 49 | 15 | 14 | 52 | 53 | 11 | 10 | 56 |
| 41 | 23 | 22 | 44 | 45 | 19 | 18 | 48 |
| 32 | 34 | 35 | 29 | 28 | 38 | 39 | 25 |
| 40 | 26 | 27 | 37 | 36 | 30 | 31 | 33 |
| 17 | 47 | 46 | 20 | 21 | 43 | 42 | 24 |
| 9 | 55 | 54 | 12 | 13 | 51 | 50 | 16 |
| 64 | 2 | 3 | 61 | 60 | 6 | 7 | 57 |
2080 : 8 = 260
Квадрат Луны[править | править код]
Печать Луны (Sigillum Lune) имеет параметры: 9, 81, 369, 3321 (размер 9х9, 81 ячейка, сумма по направлениям — 369, сумма всех чисел — 3321).
| 37 | 78 | 29 | 70 | 21 | 62 | 13 | 54 | 5 |
| 6 | 38 | 79 | 30 | 71 | 22 | 63 | 14 | 46 |
| 47 | 7 | 39 | 80 | 31 | 72 | 23 | 55 | 15 |
| 16 | 48 | 8 | 40 | 81 | 32 | 64 | 24 | 56 |
| 57 | 17 | 49 | 9 | 41 | 73 | 33 | 65 | 25 |
| 26 | 58 | 18 | 50 | 1 | 42 | 74 | 34 | 66 |
| 67 | 27 | 59 | 10 | 51 | 2 | 43 | 75 | 35 |
| 36 | 68 | 19 | 60 | 11 | 52 | 3 | 44 | 76 |
| 77 | 28 | 69 | 20 | 61 | 12 | 53 | 4 | 45 |
3321 : 9 = 369
Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл.[править | править код]
Если в квадратную матрицу n × n заносится не строго натуральный ряд чисел, то данный магический квадрат — нетрадиционный. Ниже представлены два таких магических квадрата, заполненные простыми числами (хотя 1 в современной теории чисел не считается простым числом). Первый имеет порядок n=3 (квадрат Дьюдени); второй (размером 4×4) — квадрат Джонсона. Оба они были разработаны в начале двадцатого столетия[5]:
|
Есть еще несколько подобных примеров:
| 17 | 89 | 71 |
| 113 | 59 | 5 |
| 47 | 29 | 101 |
| 1 | 823 | 821 | 809 | 811 | 797 | 19 | 29 | 313 | 31 | 23 | 37 |
| 89 | 83 | 211 | 79 | 641 | 631 | 619 | 709 | 617 | 53 | 43 | 739 |
| 97 | 227 | 103 | 107 | 193 | 557 | 719 | 727 | 607 | 139 | 757 | 281 |
| 223 | 653 | 499 | 197 | 109 | 113 | 563 | 479 | 173 | 761 | 587 | 157 |
| 367 | 379 | 521 | 383 | 241 | 467 | 257 | 263 | 269 | 167 | 601 | 599 |
| 349 | 359 | 353 | 647 | 389 | 331 | 317 | 311 | 409 | 307 | 293 | 449 |
| 503 | 523 | 233 | 337 | 547 | 397 | 421 | 17 | 401 | 271 | 431 | 433 |
| 229 | 491 | 373 | 487 | 461 | 251 | 443 | 463 | 137 | 439 | 457 | 283 |
| 509 | 199 | 73 | 541 | 347 | 191 | 181 | 569 | 577 | 571 | 163 | 593 |
| 661 | 101 | 643 | 239 | 691 | 701 | 127 | 131 | 179 | 613 | 277 | 151 |
| 659 | 673 | 677 | 683 | 71 | 67 | 61 | 47 | 59 | 743 | 733 | 41 |
| 827 | 3 | 7 | 5 | 13 | 11 | 787 | 769 | 773 | 419 | 149 | 751 |
Последний квадрат, построенный в 1913 г. Дж. Н. Манси, примечателен тем, что он составлен из 143 последовательных простых чисел за исключением двух моментов: привлечена единица, которая не является простым числом, и не использовано единственное чётное простое число 2.
Квадраты с дополнительными свойствами[править | править код]
Пандиагональный магический квадрат[править | править код]
Пандиагональный или дьявольский квадрат — магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям[en] (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях.
Существует 48 дьявольских квадратов 4×4 в стандартной форме Френикля[fr] — с точностью до поворотов и отражений. Пандиагональный квадрат сохраняет свойства при параллельном переносе строк или столбцов. Поэтому единицу можно переместить в левый верхний угол. Таких пандиагональных квадратов на плоскости 12. Они приведены ниже:
|
|
|
|
|
|
|
|
|
|
|
|
На торе каждой четвёрке таких квадратов соответствует один квадрат. Это происходит потому, что если разрезать тор, начиная с единичной клетки как угловой, то это можно сделать четырьмя способами, сопоставляя каждому из четырёх углов единичной клетки угол плоского квадрата. Поэтому пандиагональных квадратов на торе всего 3. Для изображения торического квадрата на плоскости можно использовать любой из соответствующей ему четвёрки.
Пандиагональные квадраты существуют для нечётного порядка n>3, для любого порядка двойной чётности n=4k (k=1,2,3…) и не существуют для порядка одинарной чётности 
(
).
Пандиагональные квадраты четвёртого порядка обладают рядом дополнительных свойств, за которые их называют совершенными. Совершенных квадратов нечётного порядка не существует. Среди пандиагональных квадратов двойной чётности выше 4 имеются совершенные[6].
С учётом торических параллельных переносов имеется 144 различных пандиагональных квадратов. Один из них показан ниже.
| 1 | 15 | 24 | 8 | 17 |
| 9 | 18 | 2 | 11 | 25 |
| 12 | 21 | 10 | 19 | 3 |
| 20 | 4 | 13 | 22 | 6 |
| 23 | 7 | 16 | 5 | 14 |
Разломанные диагонали пандиагонального квадрата
Если пандиагональный квадрат ещё и ассоциативный, то он носит название идеальный[7]. Пример идеального магического квадрата:
| 21 | 32 | 70 | 26 | 28 | 69 | 22 | 36 | 65 |
| 40 | 81 | 2 | 39 | 77 | 7 | 44 | 73 | 6 |
| 62 | 10 | 51 | 58 | 18 | 47 | 57 | 14 | 52 |
| 66 | 23 | 34 | 71 | 19 | 33 | 67 | 27 | 29 |
| 4 | 45 | 74 | 3 | 41 | 79 | 8 | 37 | 78 |
| 53 | 55 | 15 | 49 | 63 | 11 | 48 | 59 | 16 |
| 30 | 68 | 25 | 35 | 64 | 24 | 31 | 72 | 20 |
| 76 | 9 | 38 | 75 | 5 | 43 | 80 | 1 | 42 |
| 17 | 46 | 60 | 13 | 54 | 56 | 12 | 50 | 61 |
Известно, что не существует идеальных магических квадратов порядка n = 4k+2 и квадрата порядка n = 4. В то же время существуют идеальные квадраты порядка n = 8.
Методом построения составных квадратов можно построить на базе данного квадрата восьмого порядка идеальные квадраты порядка n = 8k, k=5,7,9…и порядка n = 8^p, p=2,3,4… В 2008 г. разработан комбинаторный метод построения идеальных квадратов порядка n = 4k, k = 2, 3, 4,…
Построение магических квадратов[править | править код]
Метод террас[править | править код]
Описан Ю. В. Чебраковым в «Теории магических матриц».
Для заданного нечетного n начертим квадратную таблицу размером n на n. Пристроим к этой таблице со
всех четырех сторон террасы (пирамидки). В результате получим ступенчатую симметричную фигуру.
Начиная с левой вершины ступенчатой фигуры, заполним её диагональные ряды последовательными натуральными числами от 1 до 
.
После этого для получения классической матрицы N-го порядка числа, находящиеся в террасах, поставим на те места таблицы размером NxN, в которых они оказались бы, если перемещать их вместе с террасами до того момента, пока основания террас не примкнут к противоположной стороне таблицы.
| 3 | 16 | 9 | 22 | 15 |
| 20 | 8 | 21 | 14 | 2 |
| 7 | 25 | 13 | 1 | 19 |
| 24 | 12 | 5 | 18 | 6 |
| 11 | 4 | 17 | 10 | 23 |
Кроме того, данный способ является верным и в том случае, если магический квадрат нужно составить не из чисел от 1 до N, но и от K до N, где 1 <= K< N.
Прочие способы[править | править код]
Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата: нечетен, равен удвоенному нечетному числу или равен учетверенному нечетному числу. Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы.[8][9]
Найти все магические квадраты порядка удается только для 
, поэтому представляют большой интерес частные процедуры построения магических квадратов при 
. Проще всего конструкция для магического квадрата нечетного порядка. Нужно в клетку с координатами 
(где 
и 
меняются от 1 до ) поставить число (Примечание: данная формула верна для всех квадратов нечётного порядка, кроме квадратов вида 
.
Ещё проще построение выполнить следующим образом. Берётся матрица n x n . Внутри её строится ступенчатый ромб. В нём ячейки слева вверх по диагоналям заполняются последовательным рядом нечётных чисел. Определяется значение центральной ячейки C. Тогда в углах магического квадрата значения будут такими: верхняя правая ячейка C-1 ; нижняя левая ячейка C+1 ; нижняя правая ячейка C-n; верхняя левая ячейка C+n. Заполнение пустых ячеек в ступенчатых угловых треугольниках ведётся с соблюдением простых правил: 1)по строкам числа слева направо увеличиваются с шагом n + 1; 2) по столбцам сверху вниз числа увеличиваются с шагом n-1.
Также разработаны алгоритмы построения пандиагональных квадратов[10][11]
и идеальных магических квадратов 9×9.[12]
[13] Эти результаты позволяют строить идеальные магические квадраты порядков 
для 
.[7][14] Существуют также общие методы компоновки идеальных магических квадратов нечётного порядка 
.[15]
[16]
Разработаны методы построения идеальных магических квадратов порядка n=8k, k=1,2,3…[17] и совершенных магических квадратов.[18]
Пандиагональные и идеальные квадраты четно-нечётного порядка удаётся скомпоновать лишь в том случае, если они нетрадиционные.[19][20]
[21] Тем не менее, можно находить почти пандиагональные квадраты[22] Найдена особая группа идеально-совершенных магических квадратов (традиционных и нетрадиционных)[23].
Примеры более сложных квадратов[править | править код]
Методически строго отработаны магические квадраты нечётного порядка и порядка двойной чётности.[24] Формализация квадратов порядка одинарной чётности намного труднее, что иллюстрируют следующие схемы:
|
|
|
Существуют несколько десятков других методов построения магических квадратов
Шахматный подход[править | править код]
Известно, что шахматы, как и магические квадраты, появились десятки веков назад в Индии. Поэтому не случайно возникла идея шахматного подхода к построению магических квадратов. Впервые эту мысль высказал Эйлер. Он попытался получить полный магический квадрат непрерывным обходом коня. Однако, это сделать ему не удалось, поскольку в главных диагоналях суммы чисел отличались от магической константы. Тем не менее шахматная разбивка позволяет создавать любой магический квадрат. Цифры заполняются регулярно и построчно с учётом цвета ячеек.
Изображение схем построения магических квадратов
См. также[править | править код]
- Математическая магия
- Латинский квадрат
- Магический граф
- Магический куб
- Магический шестиугольник
- Чисугвимундо
- Палиндром
- Рамочный магический квадрат
- Судоку
- Супермагический квадрат
- Супермагический куб
Примечания[править | править код]
Литература[править | править код]
- Я. В. Успенский. Избранные математические развлечения. — Сеятель, 1924.
- Б. А. Кордемский. Математическая смекалка. — М.: ГИФМЛ, 1958. — 576 с.
- М. М. Постников. Магические квадраты. — М.: Наука, 1964.
- Н. М. Рудин. От магического квадрата к шахматам. — М.: Физкультура и спорт, 1969.
- Е. Я. Гуревич. Тайна древнего талисмана. — М.: Наука, 1969.
- М. Гарднер. Математические досуги. — М.: Мир, 1972.
- Энциклопедический словарь юного математика / Сост. А. П. Савин. — М. : Педагогика, 1989. — 352 с. — ISBN 5-7155-0218-7.
- Ю. В. Чебраков. Магические квадраты. Теория чисел, алгебра, комбинаторный анализ. — СПб.: СПб гос. техн. ун-т, 1995.
- Ю. В. Чебраков. Теория магических матриц. — СПб., 2008.
- М. Гарднер. Глава 17. Магические квадраты и кубы // Путешествие во времени. — М.: Мир, 1990. (недоступная ссылка)
- Чирказов Д. Буквенные магические квадраты как симметричные текстовые массивы. // Современные научные исследования и инновации. — № 11 Ноябрь 2012
Ссылки[править | править код]
- Магические квадраты (недоступная ссылка) (англ.)
- последовательность A164843 в OEIS
- М. Гарднер »Рецензия на книгу Кэтлин Оллереншоу и Дэвида Бри”
- H. Heinz Magic Squares, Magic Stars & Other Patterns (англ.)
- Н. Скрябина, В.Дубовской Магические квадраты
- Шахматный подход
- Нетрадиционные магические квадраты из простых чисел
- Наименьшие магические квадраты из простых чисел
- «Общие формулы магических квадратов.»
- Магические квадраты // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
