Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет – это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.
Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются – как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?
Оказывается, эти дети – ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине). Это не вундеркинды – ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!
Секреты устного счёта
Существуют приемы устного счета – простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Примеры:
56+7=56+10-3=63
47+8=47+10-2=55
73+9=73+10-1=82
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».
Примеры:
54+39=54+40-1=93
26+38=26+40-2=64
Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем – единицы.
Пример:
57+32=57+30+2=89
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
32+57=32+60-3=89
Складываем в уме трехзначные числа
Быстрый счет и сложение трехзначных чисел – это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Пример:
249+533=(200+500)+(40+30)+(9+3)=782
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Примеры:
67-9=67-10+1=58
576-88=576-100+12=488
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Пример:
843-596=843-500-90-6=343-90-6=253-6=247
Умножить и разделить
Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения – это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения – с 11 до 19!
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
15*16=15*10+(10*6+5*6)=150+60+30=240
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
-
умножить на 4 – это дважды умножить на 2;
-
умножить на 6 – это значит умножить на 2, а потом на 3;
-
умножить на 8 – это трижды умножить на 2;
-
умножить на 9 – это дважды умножить на 3.
Например:
37*4=(37*2)*2=74*2=148;
412*6=(412*2)·3=824·3=2472
Аналогично:
-
разделить на 4 – это дважды разделить на 2;
-
разделить на 6 – это сначала разделить на 2, а потом на 3;
-
разделить на 8 – это трижды разделить на 2;
-
разделить на 9 – это дважды разделить на 3.
Например:
412:4=(412:2):2=206:2=103
312:6=(312:2):3=156:3=52
Как умножать и делить на 5
Число 5 – это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.
Пример:
326*5=(326*10):2=3260:2=1630
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
326:5=(326·2):10=652:10=65,2.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
37*9=(37*3)*3=111*3=333
или
37*9=37*10 – 37=370-37=333
Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко – это примеры занимательные, так называемые маленькие хитрости.
Счет на пальцах
Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы – это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
- Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
- Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
- Оставшееся количество пальцев слева будет соответствовать десяткам, справа – единицам. В нашем примере – 4 пальца слева и 5 справа. Ответ: 45.
Да, действительно, решение быстрое и наглядное! Но это – из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Устный счёт на автомате
-
Во-первых, необходимо хорошо знать состав числа и таблицу умножения.
-
Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.
-
В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» – упражняться в устных вычислениях, используя тот или иной алгоритм.
Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку – и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.
Как освоить устный счёт школьникам и взрослым
Лайфхакер подобрал простые советы, сервисы и приложения.

Кроме отличных оценок по математике, умение считать в уме даёт массу преимуществ на протяжении всей жизни. Упражняясь в вычислениях без калькулятора, вы:
- Держите мозг в тонусе. Для эффективной работы интеллект, как и мускулатура, нуждается в постоянных тренировках. Счёт в уме развивает память, логическое мышление и концентрацию, повышает способность к обучению, помогает быстрее ориентироваться в ситуации и принимать правильные решения.
- Заботитесь о своём психическом здоровье. Исследования показывают, что при устном счёте задействованы участки мозга, ответственные за депрессию и тревожность. Чем активнее работают эти зоны, тем меньше риск неврозов и чёрной тоски.
- Страхуетесь от проколов в бытовых ситуациях. Способность быстро посчитать сдачу, размер чаевых, количество калорий или проценты по кредиту защищает вас от незапланированных трат, лишнего веса и мошенников.
Освоить приёмы быстрого счёта можно в любом возрасте. Не беда, если сначала вы будете немного «тормозить». Ежедневно практикуйте основные арифметические операции по 10–15 минут и уже через пару месяцев достигнете заметных результатов.
Как научиться складывать в уме
Суммируем однозначные числа
Начните тренировку с элементарного уровня — сложения однозначных чисел с переходом через десяток. Эту технику осваивают в первом классе, но почему-то часто забывают с возрастом.
- Предположим, вам нужно сложить 7 и 8.
- Посчитайте, сколько семёрке не хватает до десяти: 10 − 7 = 3.
- Разложите восьмёрку на сумму трёх и второй части: 8 = 3 + 5.
- Добавьте вторую часть к десяти: 10 + 5 = 15.
Тот же приём «опоры на десятку» используйте при суммировании однозначных чисел с двузначными, трёхзначными и так далее. Оттачивайте простейшее сложение, пока не научитесь совершать одну операцию за пару секунд.
Суммируем многозначные числа
Основной принцип — разбить слагаемые числа на разряды (тысячи, сотни, десятки, единицы) и суммировать между собой одинаковые, начиная с самых крупных.
Допустим, вы прибавляете 1 574 к 689.
- 1 574 раскладывается на четыре разряда: 1 000, 500, 70 и 4. 689 — на три: 600, 80 и 9.
- Теперь суммируем: тысячи с тысячами (1 000 + 0 = 1 000), сотни с сотнями (500 + 600 = 1 100), десятки с десятками (70 + 80 = 150), единицы с единицами (4 + 9 = 13).
- Группируем числа так, как нам удобно, и складываем то, что получилось: (1 000 + 1 100) + (150 + 13) = 2 100 + 163 = 2 263.
Основная сложность — удержать в голове все промежуточные результаты. Упражняясь в таком счёте, вы заодно тренируете память.
Как научиться вычитать в уме
Вычитаем однозначные числа
Снова возвращаемся в первый класс и оттачиваем навык вычитания однозначного числа с переходом через десяток.
Предположим, вы хотите отнять 8 от 35.
- Представьте 35 в виде суммы 30 + 5.
- Из 5 вычесть 8 нельзя, поэтому раскладываем 8 на сумму 5 + 3.
- Вычтем 5 из 35 и получим 30. Затем отнимем от 30 оставшуюся тройку: 30 − 3 = 27.
Вычитаем многозначные числа
В отличие от сложения, при вычитании многозначных чисел на разряды нужно разбивать только то, которое вы отнимаете.
Например, вас просят отнять 347 от 932.
- Число 347 состоит из трёх разрядных частей: 300 + 40 + 7.
- Сначала вычитаем сотни: 932 − 300 = 632.
- Переходим к десяткам: 632 − 40. Для удобства 40 можно представить в виде суммы 30 + 10. Сперва вычтем 30 и получим 632 − 30 = 602. Теперь отнимем от 602 оставшиеся 10 и получим 592.
- Осталось разобраться с единицами, используя всё ту же «опору на десятку». Сперва вычитаем из 592 двойку: 592 − 2 = 590. А затем то, что осталось от семёрки: 7 − 2 = 5. Получаем: 590 − 5 = 585.
Как научиться умножать в уме
Лайфхакер уже писал о том, как быстро освоить таблицу умножения.
Добавим, что наибольшие трудности и у детей, и у взрослых вызывает умножение 7 на 8. Есть простое правило, которое поможет вам никогда не ошибаться в этом вопросе. Просто запомните: «пять, шесть, семь, восемь» — 56 = 7 × 8.
А теперь перейдём к более сложным случаям.
Умножаем однозначные числа на многозначные
По сути, здесь всё элементарно. Разбиваем многозначное число на разряды, перемножаем каждый на однозначное число и суммируем результаты.
Разберём на конкретном примере: 759 × 8.
- Разбиваем 759 на разрядные части: 700, 50 и 9.
- Умножаем каждый разряд по отдельности: 700 × 8 = 5 600, 50 × 8 = 400, 9 × 8 = 72.
- Складываем результаты, разбивая их на разряды: 5 600 + 400 + 72 = 5 000 + (600 + 400) + 72 = 5 000 + 1 000 + 72 = 6 000 + 72 = 6 072.
Умножаем двузначные числа
Тут уже рука сама тянется к калькулятору или хотя бы к бумаге и ручке, чтобы воспользоваться старым добрым умножением в столбик. Хотя ничего сверхсложного в этой операции нет. Просто нужно немного потренировать краткосрочную память.
Попробуем умножить 47 на 32, разбив процесс на несколько шагов.
- 47 × 32 — это то же, что и 47 × (30 + 2) или 47 × 30 + 47 × 2.
- Сначала умножим 47 на 30. Проще некуда: 47 × 3 = 40 × 3 + 7 × 3 = 120 + 21 = 141. Приписываем справа нолик и получаем: 1 410.
- Поехали дальше: 47 × 2 = 40 × 2 + 7 × 2 = 80 + 14 = 94.
- Осталось сложить результаты: 1 410 + 94 = 1 500 + 4 = 1 504.
Этот принцип можно применять и к числам с большим количеством разрядов, но удержать в уме столько операций не каждому под силу.
Упрощаем умножение
Кроме общих правил, есть несколько лайфхаков, облегчающих умножение на определённые однозначные числа.
Умножение на 4
Можно умножить многозначное число на 2, а потом снова на 2.
Пример: 146 × 4 = (146 × 2) × 2 = (200 + 80 + 12) × 2 = 292 × 2 = 400 + 180 + 4 = 584.
Умножение на 5
Умножьте исходное число на 10, а потом разделите на 2.
Пример: 489 × 5 = 4 890 / 2 = 2 445.
Умножение на 9
Умножьте на 10, а затем отнимите от результата исходное число.
Пример: 573 × 9 = 5 730 − 573 = 5 730 − (500 + 70 + 3) = 5 230 − (30 + 40) − 3 = 5 200 − 40 − 3 = 5 160 − 3 = 5 157.
Умножение на 11
Приём сводится к следующему: впереди и сзади подставляем первую и последнюю цифры исходного числа. А между ними последовательно суммируем все цифры.
При умножении на двузначное число всё выглядит крайне просто.
Пример: 36 × 11 = 3(3+6)6 = 396.
Если сумма переходит через десяток, в центре остаётся разряд единиц, а к первой цифре добавляем один.
Пример: 37 × 11 = 3(3+7)7 = 3(10)7 = 407.
Чуть сложнее с умножением на более крупные числа.
Пример: 543 × 11 = 5(5+4)(4+3)3 = 5 973.
Как научиться делить в уме
Это операция, обратная умножению, поэтому и успех во многом зависит от знания всё той же школьной таблицы. Остальное — дело практики.
Делим на однозначное число
Для этого разбиваем исходное многозначное число на удобные части, которые точно будут делиться на наше однозначное.
Попробуем разделить 2 436 на 7.
- Выделим из 2 436 наибольшую часть, которая нацело разделится на 7. В нашем случае это 2 100. Получаем (2 100 + 336) / 7.
- Продолжаем в том же духе, только теперь с числом 336. Очевидно, что на 7 разделится 280. А в остатке будет 56.
- Теперь делим каждую часть на 7: (2 100 + 280 + 56) / 7 = 300 + 40 + 8 = 348.
Делим на двузначное число
Это уже высший пилотаж, но мы всё равно попытаемся.
Предположим, вам надо поделить 1 128 на 24.
- Прикидываем, сколько раз 24 может поместиться в 1 128. Очевидно, что 1 128 примерно в два раза меньше, чем 24 × 100 (2 400). Поэтому для «пристрелки» возьмём множитель 50: 24 × 50 = 1 200.
- До 1 200 нашему делимому 1 128 не хватает 72. Сколько раз 24 поместится в 72? Правильно, 3. А значит, 1 128 = 24 × 50 − 24 × 3 = 24 × (50 − 3) = 24 × 47. Стало быть, 1128 / 24 = 47.
Мы взяли не самый трудный пример, но пользуясь методом «пристрелки» и дроблением на удобные части, вы научитесь совершать и более сложные операции.
Что поможет освоить устный счёт
Для упражнений придётся ежедневно придумывать новые и новые примеры, только если вы сами этого хотите. В противном случае воспользуйтесь другими доступными способами.
Настольные игры
Играя в те, где необходимо постоянно вычислять в уме, вы не просто учитесь быстро считать. А совмещаете полезное с приятным времяпрепровождением в кругу семьи или друзей.
Карточные забавы вроде «Уно» и всевозможные варианты математического домино позволяют школьникам играючи освоить простое сложение, вычитание, умножение и деление. Более сложные экономические стратегии а-ля «Монополия» развивают финансовое чутьё и оттачивают сложные навыки счёта.
Что купить
- «Уно»;
- «7 на 9»;
- «7 на 9 multi»;
- «Трафик Джем»;
- «Хекмек»;
- «Математическое домино»;
- «Умножариум»;
- «Код фараона»;
- «Суперфермер»;
- «Монополия».
Мобильные приложения
С ними вы сможете довести устный счёт до автоматизма. Большинство из них предлагают решить примеры на сложение, вычитание, умножение и деление по программе младших классов. Но вы удивитесь, насколько это непросто. Особенно если задачи нужно щёлкать на время, без ручки и бумаги.
Математика: устный счёт, таблица умножения
Охватывает задания на устный счёт, которые соответствуют 1–6 классам школьной программы, включая и задачи на проценты. Позволяет тренировать скорость и качество счёта, а также настраивать сложность. Например, от простой таблицы умножения можно перейти к умножению и делению двузначных и трёхзначных чисел.
Математика в уме
Ещё один простой и понятный тренажёр устного счёта с подробной статистикой и настраиваемой сложностью.
1 001 задача для счёта в уме
В приложении используются примеры из пособия по математике «1 001 задача для умственного счёта», которое ещё в XIX веке составил учёный и педагог Сергей Рачинский.
Математические хитрости
Приложение позволяет легко и ненавязчиво освоить основные математические приёмы, которые облегчают и ускоряют устный счёт. Каждый приём можно отработать в тренировочном режиме. А потом поиграть на скорость вычислений с собой или соперником.
Quick Brain
Цель игры — правильно решить как можно больше математических примеров за определённый промежуток времени. Тренирует знание таблицы умножения, сложение и вычитание. А ещё содержит популярный математический пазл «2 048».
Веб-сервисы
Регулярно заниматься интеллектуальной зарядкой с числами можно и на математических онлайн-тренажёрах. Выбирайте необходимый вам тип действия и уровень сложности — и вперёд, к новым интеллектуальным вершинам. Вот лишь несколько вариантов.
- Математика.Club — тренажёр устного счёта.
- Школа Аристова — тренажёр устного счёта (охватывает двузначные и трёхзначные числа).
- «Развивайка» — тренировка устного счёта в пределах ста.
- 7gy.ru — тренажёр по математике (вычисления в пределах ста).
- Chisloboy — онлайн-игра на развитие скорости счёта.
- kid-mama — тренажёры по математике для 0–6 классов.
Читайте также 🧠🎓😤
- 10 эффективных способов стать умнее
- Как выучить английский язык, уделяя этому 1 час в день
- Почему учить новые языки так сложно и как это преодолеть
- 5 книг, которые помогут освоить скорочтение
- Как запоминать больше, используя метод 50/50
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью “Пределы для чайников” в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.
Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
8*4=8+8+8+8=32
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
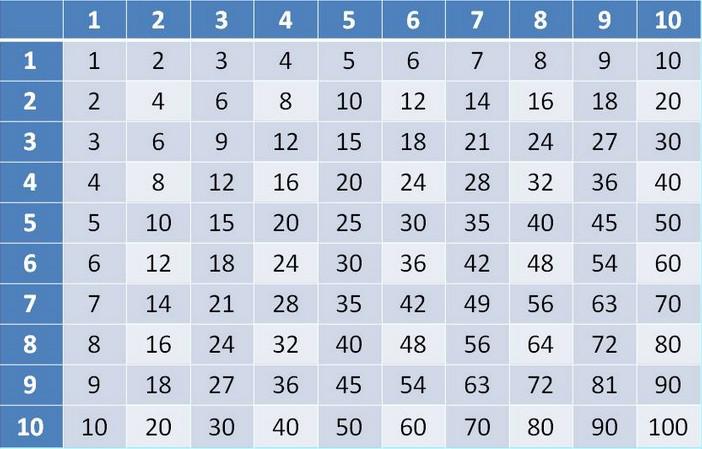
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
- 79*50=(70+9)*50=3500+450=3950
- 79*7=(70+9)*7=490+63=553
- 3950+553=4503
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число – результат умножения исходного числа на 11.
Проверим и умножим 54 на 11.
- 5+4=9
- 54*11=594
Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами – эта хитрость работает!
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.
Проверим! Возведем в квадрат число 75.
- 7*8=56
- 5*5=25
- 75*75=5625

Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
64:8=8
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
- Не забывайте тренироваться каждый день;
- не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
- скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
- почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Устный счет: как научиться считать в уме
 Математику уже за то любить следует, что она ум в порядок приводит» – говорил Михаил Ломоносов. Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него.
Математику уже за то любить следует, что она ум в порядок приводит» – говорил Михаил Ломоносов. Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него.
И вот сразу небольшой пример видео, где Евгений Буянов рассказывает как легко умножать в уме числа до 100 и даже до 1000.
Но возможность обходиться без специальных девайсов и в нужный момент оперативно решить поставленную арифметическую задачу – это не единственное применение данного навыка. Помимо утилитарного назначения, приемы устного счета позволят вам научиться организовывать себя в различных жизненных ситуациях.
К примеру, они позволяют грамотно и оперативно планировать семейный бюджет, высчитывать проценты по кредитам и понимать уровень переплаты, делать более выгодные покупки и видеть экономию. Кроме того, умение считать в уме положительно сказывается на имидже интеллектуальных способностей и выгодно выделяет человека среди окружающих его «гуманитариев».
В дополнение к этому можно уверенно сказать, что устный счет служит отличной тренировкой мышления. Согласитесь: если человек будет месяцами сидеть на диване и выходить из дома разве что в магазин, через некоторое время он заплывет жиром, наберет вес и серьезно ухудшит свое здоровье. Точно так же и с мозгом – если им не пользоваться, он перестанет работать должным образом и просто-напросто атрофируется.
Так вот практика счета в уме как раз и не дает мозгу «набрать вес и заплыть жиром». Именно поэтому мы считаем, что данный «мягкий» навык требует развития и тренировки, и именно для этого мы и создали наш курс.
Содержание:
- Цели и задачи курса
- Что такое устный счет и зачем он нужен?
- Как научиться устному счету?
- Уроки устного счета
- Как проходить курс?
- Цитаты известных людей о математике
Однако чтобы более конкретно указать на важность умения считать в уме, а также на возможность овладеть этим умением, мы хотим познакомить вас с нашим курсом подробнее.
Цели и задачи курса
Задача курса состоит не просто в том, чтобы познакомить вас с понятием устного счета, обучить интересным техникам и приемам и научить считать в уме. На самом деле преследуются значительно большие цели. Перечислим лишь несколько наиболее существенных:
| ✔ | Тренировка внимания и концентрации. Устный счет требует активизации многих интеллектуальных способностей, в том числе и умения сосредотачиваться на решении сложных задач, требующих времени. Чем больше вы будете практиковаться, тем более гибким и податливым будет ваше мышление и тем лучше вы будете сосредотачиваться, причем на совершенно любых задачах. |
| ✔ | Тренировка логического мышления. Устный счет, логика и последовательность мыслей связаны друг с другом очень тесно. Именно благодаря последним вы можете без проблем и очень даже быстро определить, что выйдет дешевле: 10 упаковок семян чиа весом 150 граммов по 280 рублей или 7 упаковок весом 180 граммов по цене 315 рублей. Порой даже нужно не столько считать, сколько рассуждать логически. |
| ✔ | Тренировка аналитического мышления. Считая, к примеру, на калькуляторе, мы, строго говоря, выполняем всего лишь одно простое действие – нажимаем на клавиши счетного устройства или сенсор смартфона. Если же мы считаем в уме, мы и производим и вычисления, и анализируем полученные данные, и продолжаем считать дальше, если это необходимо, а затем делаем заключительные выводы. |
| ✔ | Борьба с зависимостью от гаджетов. |
| ✔ | Профилактика болезней мозга. Неочевидно, неправда ли? Между тем, ученые уже давно установили, что отсутствие интеллектуальной деятельности провоцирует множество недугов, связанных с мозгом (болезнь Альцгеймера, деменция и т.д.) Если же вы будете чаще считать в уме, вы тем самым будете чаще задействовать свой мозг и нагружать его работой, что позволит предупредить серьезные проблемы. |
Думаем, что этого более чем достаточно, чтобы в общих чертах понять, для чего нужно уметь считать в уме. Но что если копнуть чуть глубже и разобраться в вопросе подробнее?
Что такое устный счет и зачем он нужен?
Устный счет – процесс произведения математических операций в уме, т.е. без использования вспомогательных устройств, таких как калькуляторы, компьютеры, телефоны, смартфоны и т.п., а также без сторонних приспособлений, таких как ручка и бумага. Устный счет объединяет в себе представления человека о числах, знание арифметических алгоритмов и умение выполнять математические операции.
Но зачем же современному человеку уметь считать в уме, если перед ним открыто столько возможностей этого не делать? К тому же сегодня устный счет все чаще оказывается ненужным, особенно когда дело касается нынешних школьников, выросших с планшетами в руках. Но тут важно вспомнить о том, что как только мы перестаем считать в уме, мы перестаем развиваться, и это касается не только подрастающего поколения.
Все мы знаем, что мозг составляют два полушария. Правое отвечает за интуитивное мышление, художественное восприятие и творчество. Левое же отвечает за логику, речь, память, аналитику. И чем больше в мозге нейронных связей между полушариями, тем полноценнее и гармоничнее он развит. А каким образом можно развивать эти межполушарные связи? Именно таким способом и является устный счет.
Еще 3 тысячи лет назад в Древнем Вавилоне использовались счеты под названием абакус, позволявшие моментально производить в уме вычисления. Позже их использование было отмечено и в Древнем Китае, а в современном мире навыки такого счета стали известны как ментальная арифметика, и, кстати, сегодня данная дисциплина даже входит в образовательную программу некоторых азиатских стран.
Цель ментальной арифметики – натренировать мозг человека на максимально быструю обработку информации. И эти тренировки дают свою плоды, ведь благодаря специальным заданиям гармонично развиваются оба полушария мозга, вследствие чего намного легче и проще воспринимается как гуманитарная, так и техническая информация.
Особое внимание в ментальной арифметике уделяется именно устному счету, служащему эффективным тренажером для мозга. И не нужно быть гением, чтобы понять, какие преимущества имеет развитый мозг и развитое мышление. Они пригождаются везде, всегда и в любой области жизни.
Посему можно заключить, что такой, казалось бы, «простенький» или «обычный» навык, как умение считать в уме, способен повлиять на всю жизнь человека, его успехи, жизненные результаты и даже личные качества. Так что если все это имеет для вас значение, предлагаем узнать, как научиться устному счету.
Как научиться устному счету?
Есть люди, которые умеют совершать несложные арифметические операции в уме. Умножить двузначное число на однозначное, умножать в пределах 20, перемножить два небольших двузначных числа и т.д. – все эти действия они могут производить в уме и достаточно быстро, быстрее среднего человека. Часто этот навык оправдан необходимостью постоянного практического использования. Как правило, люди, которые хорошо считают в уме, имеют математическое образование или, по крайней мере, опыт решения многочисленных арифметических задач.
Несомненно, опыт и тренировка играют важнейшую роль в развитии любых способностей. Но навык устного счета не опирается на один лишь опыт. Это доказывают люди, которые, в отличие от вышеописанных, способны считать в уме гораздо более сложные примеры. Например, такие люди могут умножать и делить трехзначные числа, совершать сложные арифметические операции, которые не каждый человек и в столбик сможет посчитать.
Что же необходимо знать и уметь обычному человеку, чтобы овладеть такой феноменальной способностью? На сегодняшний день существуют различные методики, помогающие научиться быстро считать в уме. Изучив многие подходы к обучению навыку считать устно, можно выделить три основных составляющих данного навыка:
|
1 |
Способности. Способность концентрировать внимание и умение удерживать в краткосрочной памяти несколько вещей одновременно. Предрасположенность к математике и логическому мышлению. |
|
2 |
Алгоритмы. Знание специальных алгоритмов и умение оперативно подобрать нужный, максимально эффективный алгоритм в каждой конкретной ситуации. |
|
3 |
Тренировка и опыт. Постоянные тренировки и постепенное усложнение решаемых задач и упражнения позволят вам улучшить скорость и качество устного счета. |
Нужно отметить, что третий фактор имеет ключевое значение. Не обладая необходимым опытом, вы не сможете удивить окружающих быстрым счетом, даже если вы знаете самый удобный алгоритм.
Однако не стоит недооценивать важность первых двух составляющих, поскольку, имея в своем арсенале способности и набор нужных алгоритмов, вы сможете «переплюнуть» даже самого опытного «счетовода», при условии, что вы тренировались одинаковое время.
Наряду с этим, и обучаться устному счету лучше всего, используя для этого правильную и эффективную систему. С учетом этой системы и разработан наш курс, и сейчас будет логичным вкратце познакомить вас с содержанием его уроков.
Уроки устного счета
Уроки устного счета, представленные в нашем курсе, направлены именно на развитие трех вышеназванных составляющих. Вот их краткое описание:
Урок 1. Внимание и концентрация
Чтобы научиться считать в уме по-настоящему быстро, необходимо уметь концентрироваться на конкретном примере. Этот навык полезен не только для совершения математических операций, но и для решения любых жизненных задач. Умение быть внимательным в нужный момент – этот навык, который выделяет великих ученых, спортсменов, политиков, несомненно, пригодится и вам.
Урок 2. Простые арифметические закономерности
Чтобы уметь решать сложные арифметические задачи, нужно для начала усвоить некоторые базовые закономерности. От того, как быстро вы сможете считать простейшие примеры, напрямую зависит ваше умение быстро выполнять более сложные математические операции. По сути, это можно считать базой для всего последующего обучения.
Урок 3. Традиционное умножение в уме
В этом уроке мы рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно, однако важно понимать, что это лишь вершина айсберга. В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.
Урок 4. Частные методики умножения двузначных чисел до 30
Способы умножения двузначных чисел хороши тем, что они универсальны для любых чисел, и при хорошем навыке могут позволить вам достаточно быстро прийти к правильному ответу. Однако эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов. В этом уроке вы узнаете, как можно быстро умножать любые числа до 30. Здесь представлены специальные методики, в том числе и введение в использование опорного числа.
Урок 5. Опорное число при умножении чисел до 100
Наиболее популярной методикой умножения больших чисел в уме является прием использования так называемого опорного числа. Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100. В уроке вы познакомитесь с данной методикой и научитесь сами ее применять.
Урок 6. Умножение в уме любых чисел до 100
Чтобы умножать любые числа до 100 в уме, важно быстро подобрать нужный алгоритм. Для удобства этого подбора в данном уроке выделены наиболее эффективные случаи для каждой методики умножения. В уроке будут рассмотрены как универсальные методики (подходящие для любых чисел), так и частные (удобные для конкретных случаев).
Урок 7. Возведение в квадрат в уме
Умение считать в уме квадраты чисел может пригодиться в разных жизненных ситуациях, например, для быстрой оценки инвестиционных сделок, для подсчета площадей и объемов, а также во многих других случаях. Кроме того, умение считать квадраты в уме может служить демонстрацией ваших интеллектуальных способностей. В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.
Также в нашем курсе представлены дополнительные материалы, помогающие тренировать и развивать умение считать устно:
Книги, учебники и ссылки на материалы по устному счету
К сожалению, в Интернете далеко не всегда удается найти качественные материалы, посвященные именно обучению счету в уме. Однако есть ряд интересных книг и сайтов, связанных с вопросами устного счета. С некоторыми из них вы и сможете познакомиться поближе, изучив данный раздел.
Дополнительные материалы по устному счету
Уместить в один курс всю важную и нужную информацию очень проблематично. Но она, несомненно, нужна, так что вы сможете углубить свои знания по рассматриваемой теме. В этом разделе вы найдете небольшую подборку полезных материалов (а именно эффективных обучающих программ и статей), которые помогут вам лучше изучить отдельные вопросы.
Далее предлагаем познакомиться с краткой инструкцией по прохождению курса.
Как проходить курс?
Уроки данного курса мы настоятельно рекомендуем проходить последовательно, не пропуская ни один из них, подробно рассматривая каждую тему и выполняя все практические указания. Лучше всего, если после изучения предлагаемых примеров вы будете придумывать несколько своих. Это позволит вам лучше понять и закрепить материал.
Если вам что-либо непонятно, перечитайте урок еще раз. Для более надежного закрепления материала в памяти советуем по окончании курса еще раз вернуться к наиболее сложным для вас темам. И, конечно же, по завершении обучения не примените возможностью познакомиться со всеми дополнительными материалами.
Цитаты известных людей о математике
Теперь же мы хотим, чтобы вы немного отдохнули перед основной работой. Ниже мы подобрали несколько цитат известных людей об умении считать. Пусть их слова станут для вас дополнительной мотивацией и еще раз напомнят о том, как важна математика:
Математика – это язык, на котором написана книга природы.
Галилео Галилей
Часто говорят, что цифры управляют миром; по крайней мере нет сомнения в том, что цифры показывают, как он управляется.
Иоганн Вольфганг фон Гете
В математике есть своя красота, как в живописи и поэзии.
Николай Жуковский
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.
Алексей Крылов
Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.
Михаил Калинин
Первое условие, которое надлежит выполнять в математике, – это быть точным, второе – быть ясным и, насколько можно, простым.
Готфрид Лейбниц
Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.
Алексей Маркушевич
Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!
Дьердь Пойа
Счет и вычисления – основа порядка в голове.
Иоганн Генрих Песталоцци
Устройство нашего мира непостижимо без знания математики.
Роджер Бэкон
А сейчас вы можете проверить, насколько быстро вы считаете в уме:
Теперь давайте приступим к занятиям.
1 Внимание и концентрация →
Как научиться считать в уме
Считать в уме, по мнению многих, в наше время уже неактуально, ведь калькулятор есть в каждом смартфоне, компьютере и ноутбуке. Однако калькулятор не будет сопровождать вас при каждом вашем шаге, а считать необходимо постоянно и много. Способность сосчитать в уме – умение весьма нужное даже в 21 веке. А тем более это нужно школьникам для решения примеров по математике из нелёгкой школьной программы. И им весьма полезно будет уметь считать быстро, не пребегая к электронным устройствам.
Опыт и постоянные тренировки играют важную роль в развитии любых способностей, но навык устного счета не состоит только лишь из опыта. Это могут доказать люди, умеющие считать в уме гораздо более сложные примеры: например, умножать и делить трех- и четырехзначные числа, находить суммы и разности огромных примеров.
Что необходимо знать и делать человеку, дабы повторить такое?
• Во-первых, концентрация или же умение ненадолго удерживать в памяти несколько вещей одновременно.
• Во-вторых, алгоритмы, специальные методы вычислений и математические уловки, значительно облегчающие процесс устного счёта.
• В-третьих, практика. Постоянные тренировки и постепенное усложнение решаемых задач позволят улучшить скорость и качество устного счета.

Важно отметить, что именно практика имеет наибольшее значение. Не обладая достаточным опытом, вы не сможете быстро применять удобные алгоритмы, подходящие под определённые ситуации. И помните, что максимальный эффект будет достигнут при оптимальном использовании всех трёх составляющих. Тренировать сразу все аспекты этого навыка Вы можете в онлайн тренажере устного счёта.
Внимание и концентрация
Чтобы максимально быстро считать в уме, необходимо уметь концентрироваться на конкретном примере. Этот навык полезен не только для совершения математических операций, но и для решения любых жизненных задач. Существует несколько способов улучшить свою внимательность и способность к концентрации:
При счете в уме, важно ясно представлять себе решаемый пример – визуализировать его. Запоминать промежуточные результаты нужно не на слух, а так как они выглядят в записи, например, на бумаге. Тренировать подобное восприятие можно разными способами, и отчасти визуализация решения приходит с опытом.
Старайтесь всегда находить что-то интересное в рутине, превращая действие в игру. Так поступают и некоторые родители, желающие, чтобы их ребёнок выполнил какую-либо скучную работу.
Огромное количество людей всегда хотят «быть лучше» соперника. Именно поэтому состязательность является еще одним способом развить свою внимательность. В устном счете Вы можете найти себе соперника и пытаться его в этом превзойти.
Еще одним фактором, создающим азарт при счете, может стать борьба с самим собой при достижении определенного результата, то есть личные рекорды. Их можно ставить, например, в скорости счета, в количестве решенных примеров и своей точности ответов.
Наконец, максимальная концентрация может быть достигнута при спонтанном увлечении процессом счета. Как пример, во время чтения Вы перестаёте думать об окружающих вас предметах, людях, ситуациях, полностью погружаетесь в книгу. Именно неподдельный интерес к чему-либо способен заставить вас приобрести наибольшую внимательность в этом деле.
Безусловно, все эти способы надо отрабатывать, практиковать. В этом могут помочь различные тренажеры зрительной памяти и улучшения внимательности.
Простые арифметические закономерности
Решение любой по сложности задачи всегда сводится к применению базовых принципов, и именно эти принципы и закономерности позволят вам быстро выполнять различного рода операции. Существует определенный набор таких правил и закономерностей, которые необходимо довести до автоматизма с помощью разных онлайн тренажеров по математике.
Вычитание 7, 8, 9. Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам необходимо привыкнуть к этому новому способу.
Таблица умножения. Для быстрого устного счета хорошо бы безупречно знать таблицу умножения, которая является основой счета. Если у Вас с этим еще проблемы, можете воспользоваться онлайн Тренажером таблицы умножения.
Умножение на 2. Для умножения на 2 некруглых чисел пробуйте округлять их до ближайших более удобных. Так 139×2 проще считать, если сначала умножить 140 на 2 (140×2=280), а потом вычесть 1×2=2 (именно 1 нужно прибавить к 139, чтобы получить 140). Итого: 140×2–1×2=280–2=278.
Деление на 2. Несмотря на то, что многим умножение и деление на 2 дается достаточно просто, в сложных случаях так же пытайтесь округлять числа. Например, чтобы разделить 198 на 2, нужно сначала разделить 200 (это 198+2) на 2 и отнять 2 деленое на 2. Итого: 198:2=200:2-2:2=100-1=99.
Деление и умножение на 4 и 8. Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно. Например, 46×4=46×2×2=92×2=184.
Умножение на 5 и 25. Умножение на 5, и деление на 2 – практически одно и то же, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10: 88×5=88:2×10=440. Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120×25 = 120:4×100 = 30×100 = 3000.
Умножение на 9. Быстро умножить любое число на 9 можно следующим образом: сначала умножьте это число на 10, а затем вычтите из результата само число. Например: 89×9=890-89=801.
Умножение на 11. Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры. Например: 23×11= 2 (2+3) 3 = 253. Или если сумма чисел в центре дает результат больше 10: 29×11 = 2 (2+9) 9 = 2 (11) 9 = 319.
И наконец, полезно знать деление чисел, кратных 10 на числа, кратные двум: 1000 = 2×500 = 4×250 = 8×125 = 16×62,5.
Более сложные методики
Эффективность умножения в уме некоторых двузначных чисел может быть выше за счет меньшего количества действий, если использовать специальные алгоритмов. Ниже представлены три специальные методики, в том числе введение и использование опорного числа.
Квадрат суммы и квадрат разности
Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:
232= (20+3)2 = 202 + 2×3×20 + 32 = 400+120+9 = 529
692 = (70-1)2 = 702 – 70×2×1 + 12 = 4 900-140+1 = 4 761
Возведение в квадрат чисел, заканчивающихся на 5
Чтобы возвести в квадрат числа, заканчивающиеся на 5, необходимо число до последней пятерки, умножить на сумму этого же числа и единицы. К результату дописываем 25. Вот несколько примеров:
252 = (2×(2+1)) 25 = 625
852 = (8×(8+1)) 25 = 7 225
1552 = (15×(15+1)) 25 = (15×16)25 = 24 025
Опорное число
Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа. Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. А методика использования этого числа зависит от того, являются ли множители больше или меньше него самого.
Оба множителя меньше опорного. Допустим, мы хотим умножить 48 на 47. Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа. Далее действуем так: из 47 вычетаем столько, сколько не хватает 48 до 50 (либо из 48 вычетаем столько, сколько не хватает 47 до 50), полученный результат умножаем на опорное число и прибавляем к нему произведение разностей опроного числа с каждым сомножителем. Наглядный пример:
(48–(50–47))×50 + (50–47)×(50–48) = 2250 + 6 = 2256
Оба множителя больше опорного. Действовать нужно точно так же, но не вычитать недостаток, а прибавлять избыток:
(51+(63–50))×50 + (63–50)×(51–50) = 3200 + 13 = 3213
Один множитель меньше, другой больше опорного. Схема та же, но произведение недостатка и избытка нужно вычитать:
(45+(52–50))×50 – (52–50)×(50–45) = 2350 – 10 = 2340
В заключение
Как уже было сказано ранее, навык устного счета набирается из трех составляющих: это способность концентрироваться конкретном примере, грамотный подбор метода быстрого счета и, конечно, опыт. Запомните, даже зная наизусть все алгоритмы, упрощающие вам устный счет, вы не сможете сосчитать без пракики так же быстро, как если бы вы занимались этим каждый день уже несколько лет. Именно потоянные тренировки на разного рода тренажерах устного счета позволят вам отточить мастрство в этом деле и приобрести тот самый бесценный навык быстрого устного счета.
 |
Онлайн тренажер устного счета 192 разнообразных режима тренировок: |