Как составить свой японский кроссворд

Рассмотрим технологию создания японского кроссворда в MS Excel на следующем примере

Источник кроссворда >>>

В данном кроссворде 18 строк и 18 столбцов (3 — для ввода чисел-заданий, остальные 15 — рабочее поле).

Скачать исходник кроссворда по данной статье >>>

ШАГ 1.
Создание рабочего поля кроссворда

Для работы нам понадобится поле размером 21х21 (19х19 — рабочее поле плюс добавим три строки и три столбца для создания границ кроссворда).

Создадим квадратное поле 19х19 из ячеек равного размера.

Выделим столбцы B–T. Для этого щелкнем левой кнопкой мыши по названию столбца B и, удерживая ее, переместим курсор к столбцу T. Обращаем внимание на то, что около курсора есть надпись, показывающая количество выделенных столбцов. Нам необходимо, чтобы это число было равно 19.

Уменьшим ширину этих столбцов вручную до 30 пикселей (можно выбрать другое значение, количество пикселей отображается в подсказке рядом с курсором при ручном изменении ширины столбцов). Как изменить ширину столбцов и высоту строк в Excel?

Выделим строки 2-20 (19 строк), изменим их высоту до 30 пикселей.

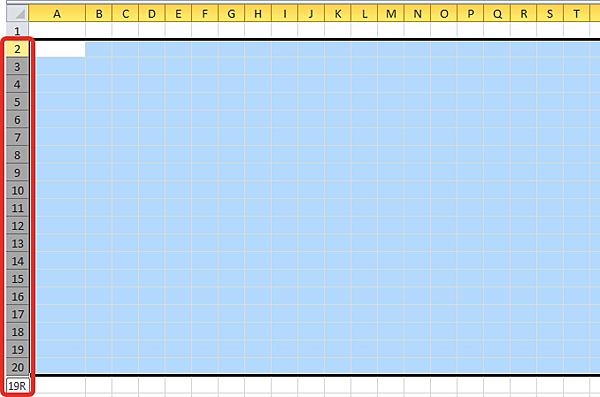
Мы получили квадратное поле размером 19х19 ячеек.

Выделим ячейки, ограничивающие это поле (ячейки А1-U1, A1-A21, A21-U21, U1-U21). На вкладке Главная в группе Шрифт выберем черную заливку для этих ячеек.

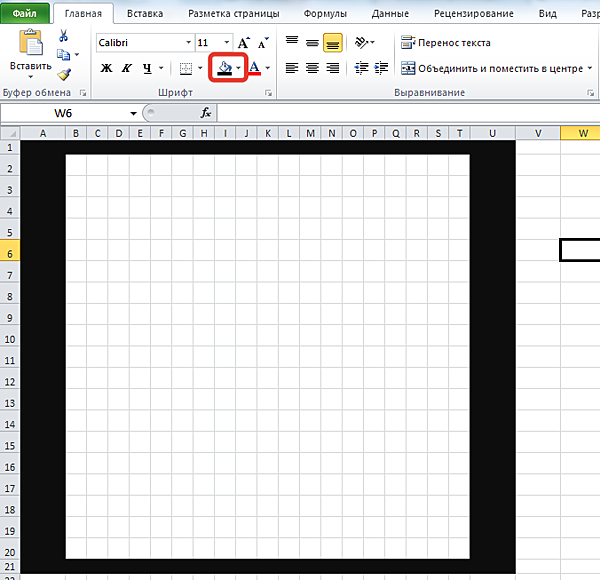
Уменьшим ширину столбцов A и U до 8 пикселей (можно выбрать другое значение). Аналогично изменим высоту строк 1 и 21 до 8 пикселей.

Выполним заливку столбца E и строки 5, уменьшим их ширину и высоту соответственно до 8 пикселей.

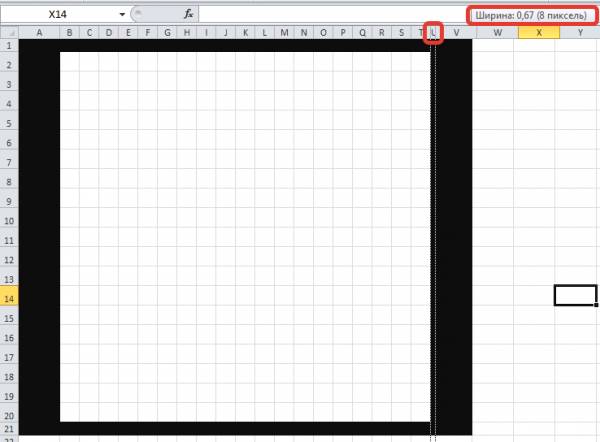
Мы получили чёткую границу по контуру нашего кроссворда и разделили области чисел и рабочее поле.

Выделим все ячейки кроссворда и на вкладке Главная в группе Шрифт раскроем список с вариантами границ (треугольник рядом с кнопкой Границы) — Все границы.

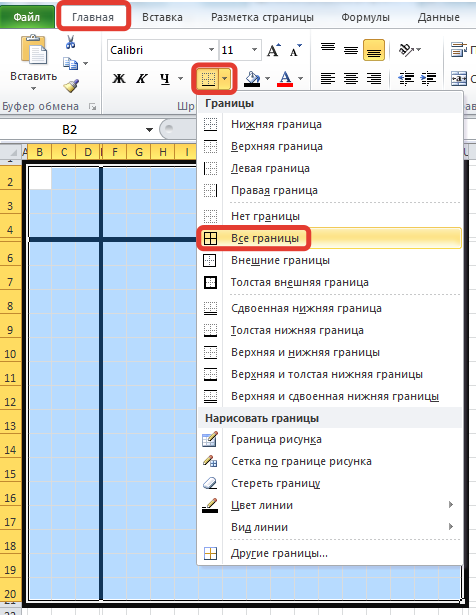
Выделим квадрат размером 3х3 в левом верхнем углу и выберем Границы — Нет границ.

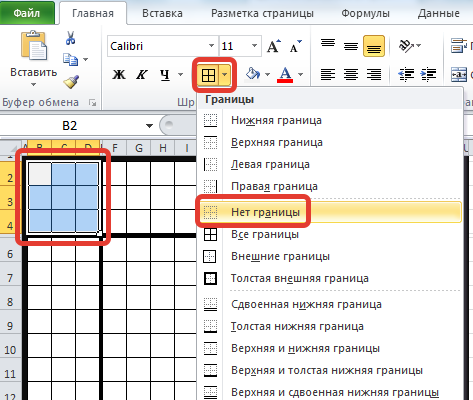
Введем числа в области указания количества заштрихованных клеток. Выделим всю область кроссворда и на вкладке Главная выберем выравнивание в ячейках по центру и по вертикали, и по горизонтали.

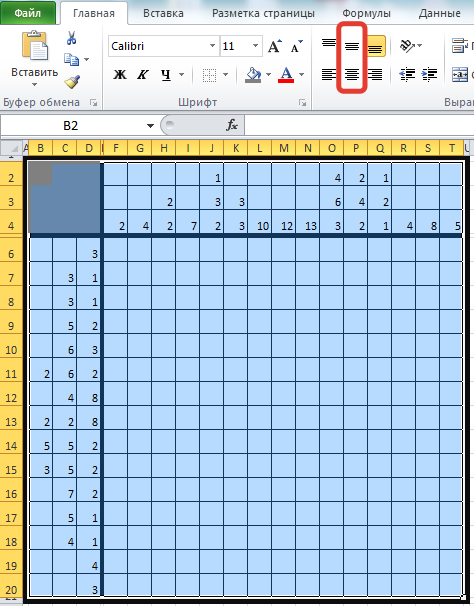
Область, где будет находиться наше изображение, для удобства разделим на группы по 5 клеток. Для этого на вкладке Главная щелкнем треугольник Границы — Вид линии — выберем широкую линию.

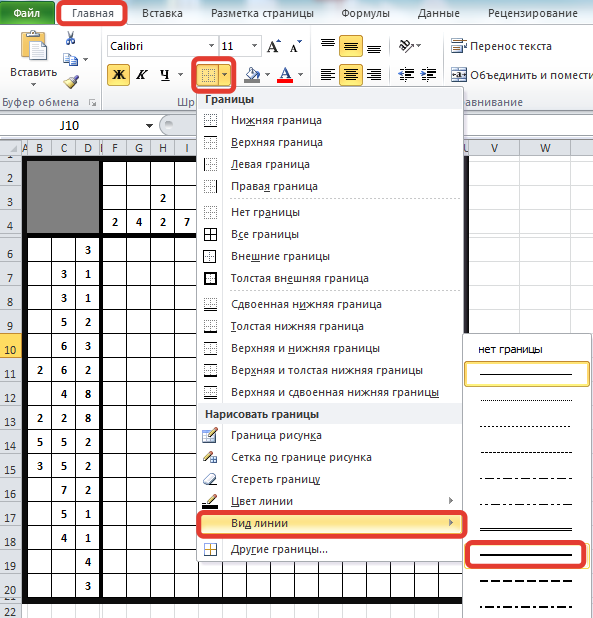
После этого курсор мыши примет вид карандаша, с его помощью можно разделить рабочее поле кроссворда на группы по 5 клеток.

Рабочее поле готово:

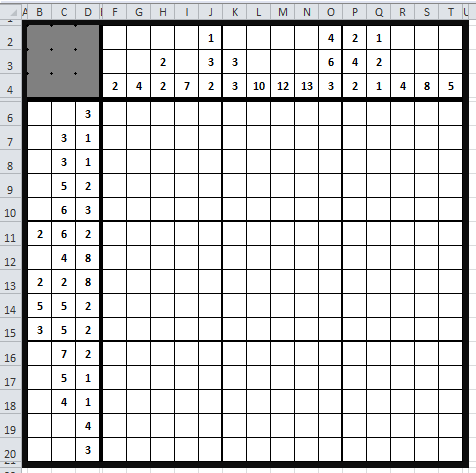
ШАГ 2.
Создание формул

Для удобства создания формул рядом с рабочим полем вставим картинку решенного кроссворда. Удерживая клавишу Ctrl, выделим ячейки, которые должны быть закрашены при решении кроссворда. Выберем для этих ячеек заливку (Главная — Цвет заливки).

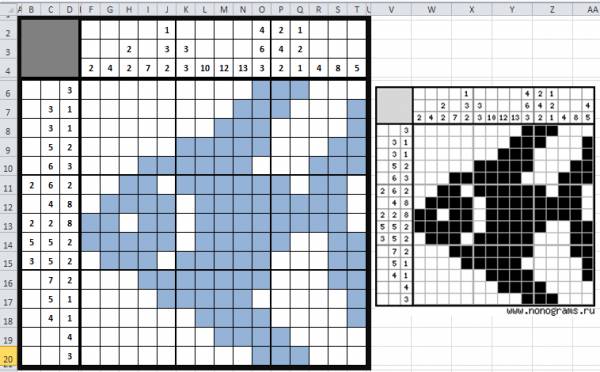
Теперь картинку-решение можно удалить. Выделим рабочую область кроссворда, скопируем ее и вставим рядом с нашим кроссвордом. Обратим внимание на то, что эта область должна располагаться в тех же строках, что и наш кроссворд — так будет удобнее. В этой области мы будем создавать формулы, необходимые для автоматического подсчета баллов, в дальнейшем формулы и все рабочие ячейки мы скроем.

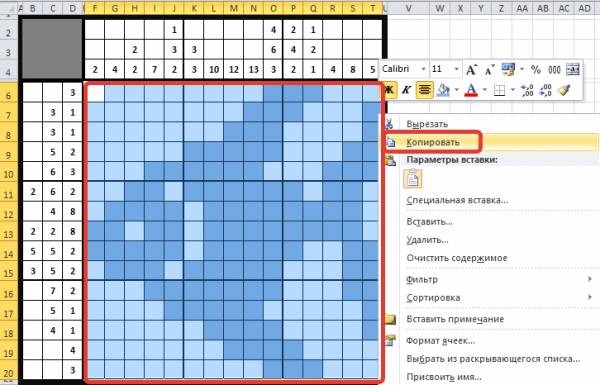
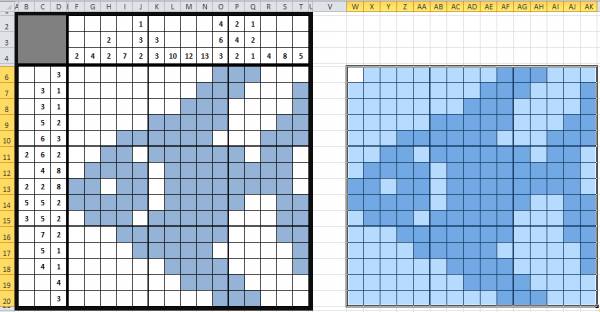
Условимся, что при разгадывании кроссворда в ячейки, которые должны быть закрашены, пользователь будет вводить цифру 2, а в ячейки, которые должны быть пустыми, — цифру 1.

В ячейке AF6 вспомогательной области (она соответствует ячейке О6 рабочей области) создадим формулу: =ЕСЛИ(О6=2;1;0).

Пояснение: функция ЕСЛИ проверяет, выполняется условие или нет, и в зависимости от полученного результата выводит соответствующее значение. Синтаксис функции следующий: =Если(условие;значение 1; значение 2). В скобках через точку с запятой указываются:

• проверяемое условие;
• значение 1 — выводится, если проверяемое условие выполняется; 
• значение 2 — выводится, если условие не выполняется.

Применительно к формуле =ЕСЛИ(О6=2;1;0), которую мы ввели в ячейку AF6, мы получим следующее: если пользователь отметит ячейку О6 как закрашенную (т.е. введет в нее цифру 2), то ячейка AF6 примет значение 1. В противном случае (если будет введена цифра 1 или ячейка будет пуста) значение ячейки AF6 будет равно 0.

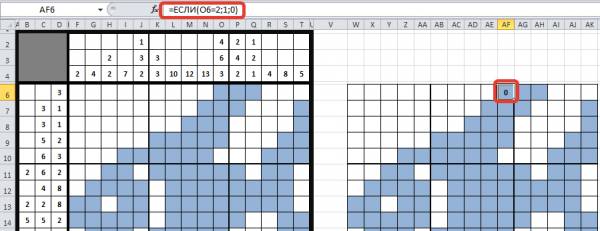
Остается только скопировать формулу на все выделенные цветом ячейки. Для этого выделим ячейку AF6 с формулой. Обратим внимание, что в правом нижнем углу этой ячейки находится маркер автозаполнения (черный квадратик). Если навести на него курсор мыши, то курсор примет вид черного крестика. Теперь нужно нажать левую кнопку мыши и, удерживая ее, потянуть вправо на две выделенные цветом ячейки. Отпустим кнопку мыши, в этих ячейках появится значение 0 (ячейки заполнились формулами). Теперь копируем формулы ячеек вниз, влево, вправо или вверх, заполняя тем самым все выделенные цветом ячейки формулами. Имена ячеек при копировании будут меняться автоматически, т.к. при создании формул мы использовали относительные ссылки.

Получим следующее:

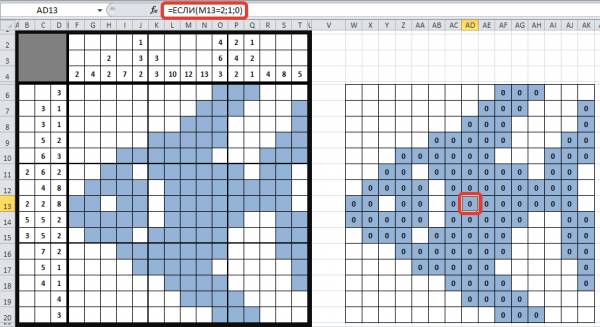
Аналогично создадим формулы и для ячеек, которые не должны быть выделены цветом (напомним, что в эти ячейки пользователь будет вводить цифру 1). Например, в ячейку W6 (она соответствует ячейке F6 кроссворда) мы вводим формулу: =ЕСЛИ(F6=1;1;0). Заметим, что эти формулы будут отличаться тем, что мы будем проверять значение не 2, а 1.

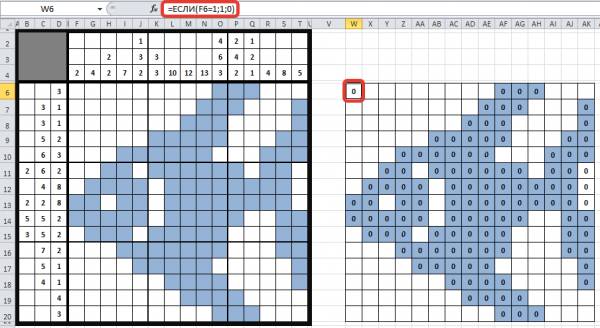
Копируем эти формулы на все ячейки, невыделенные цветом.

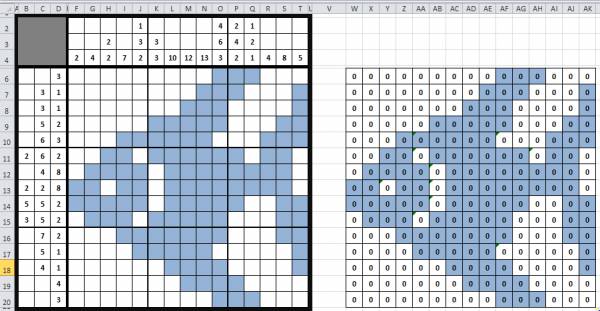
Справа от дополнительной области в столбце AO создадим формулы:

1. ячейка AO6: =СЧЁТ(W6:AK20) — в ней мы посчитаем количество ячеек нашего кроссворда (подсчет идет по диапазону вспомогательной области с формулами)

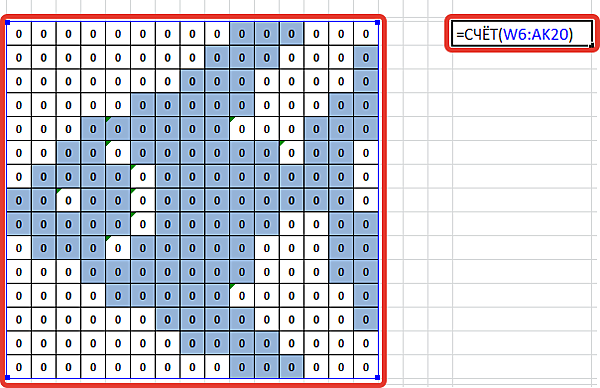
1. ячейка АО9: =СУММ((W6:AK20) — в ней мы посчитаем сумму баллов, которые набрал пользователь, разгадывая кроссворд (подсчет идет по диапазону вспомогательной области с формулами)

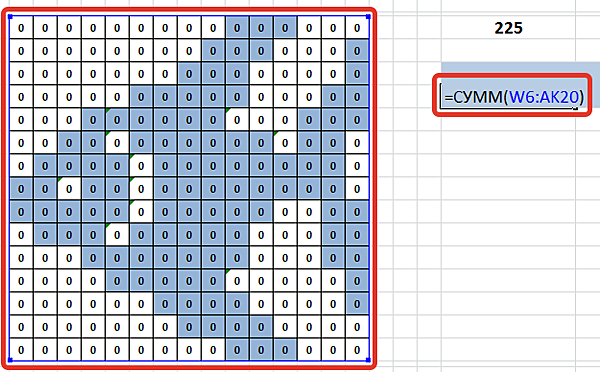
1. ячейка АО11: =ЕСЛИ(AO9=225;1;0) — если пользователь во все ячейки кроссворда ввел верные значения, т.е. получил 225 баллов за весь кроссворд (эту сумму мы вычислили в ячейке АО9), то значение ячейки АО11 будет равно 1, в противном случае — 0. Эта ячейка и ее значение нужны для использования условного форматирования.

ШАГ 3.
Условное форматирование

Выделим ячейки в рабочей области кроссворда, которые должны быть закрашены цветом (в них пользователь вводит цифру 2). Для этого щелкаем по ячейкам левой кнопкой мыши при нажатой клавише Ctrl. Читайте также: Основы Excel. Как выделять ячейки, задавать имена диапазонов и сохранять файлы?

После выделения всех ячеек на вкладке Главная выбираем Условное форматирование — Правила выделения ячеек — Другие правила.

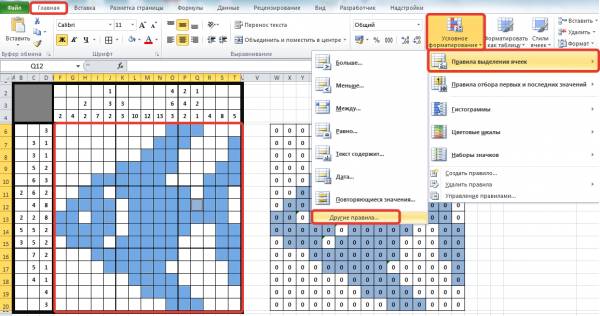
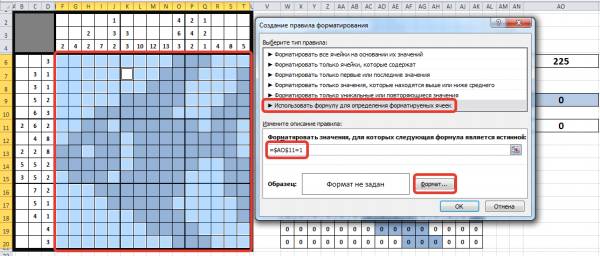
В диалоговом окне Создание правила форматирования выбираем Использовать формулу для определения форматируемых ячеек. В строку для ввода формул вводим формулу, истинность которой будет проверяться: =$AО$11=1. Т.е. если значение ячейки АО11 будет равно 1, то ячейки, которые мы выделили, будут отформатированы.

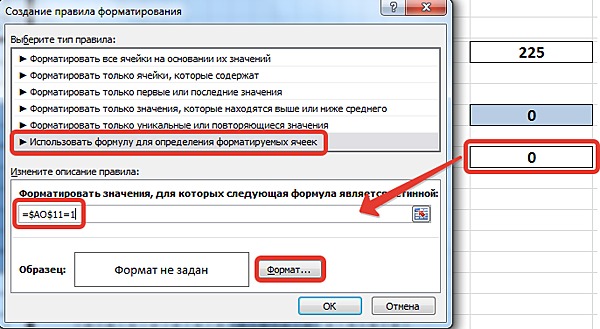
После создания формулы зададим формат условного форматирования (щёлкнем Формат).

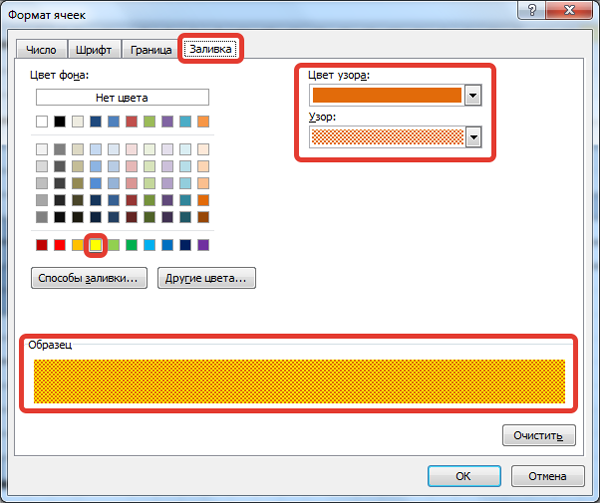
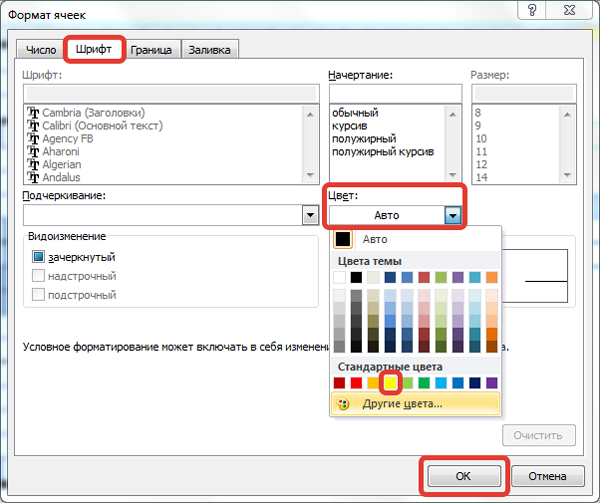
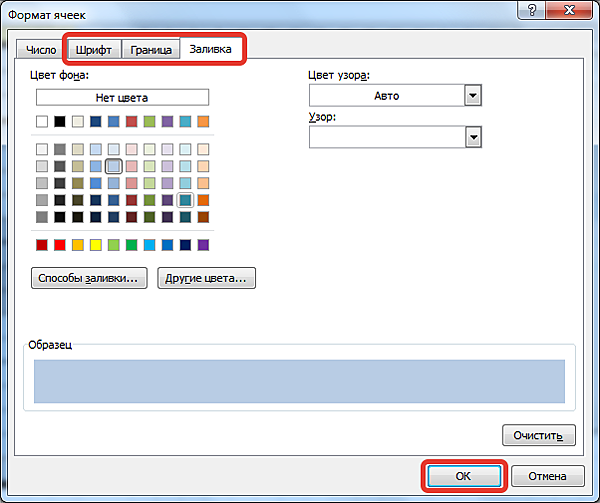
В диалоговом окне Формат ячеек на вкладке Заливка выберем цвет заливки, можно задать узор и его цвет. Обращаем внимание на Образец внизу.

На вкладке Граница выберем Тип линии — Нет.

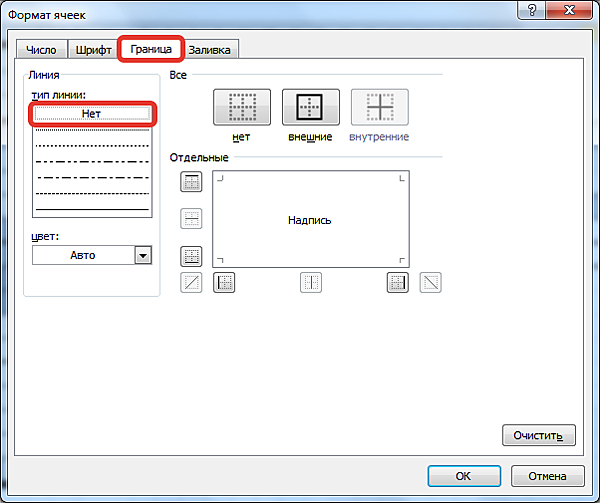
На вкладке Шрифт выберем цвет шрифта такой же, как и цвет заливки ячеек, который мы выбирали на вкладке Заливка.

После выбора всех параметров нажимаем ОК.

Теперь аналогично создадим условное форматирование для ячеек кроссворда, которые должны быть пустыми (в них пользователь вводит цифру 1).

Для этого выделим эти ячейки, выберем Главная — Условное форматирование — Правила выделения ячеек — Другие правила — Использовать формулу для определения форматируемых ячеек — создаем формулу =$AO$11=1 — Формат.

Устанавливаем цвет заливки для этих ячеек, цвет шрифта должен быть такой же, границ быть не должно (Тип линий — Нет) — ОК.

Что же у нас получилось? Введем цифры 1 и 2 в рабочую область кроссворда. Обратим внимание на изменение значений во вспомогательной области справа. Как только мы введем последнее значение в кроссворд и нажмем Enter, наш кроссворд поменяет свое оформление.

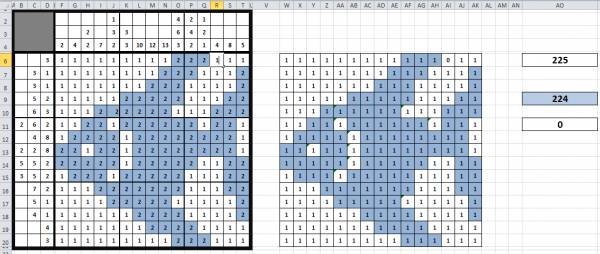
Теперь у ячеек нет границ. Цифры, которые мы вводили в ячейки, стали невидны (в нашем примере мы выбрали узор для заливки ячеек, поэтому цифра 2 видна, но это не портит вид нашей рыбки). Обратим внимание на формулы в столбце АО: как только сумма набранных пользователем баллов стала равна 225, значение ячейки АО11 стало равно 1, поэтому сработало условное форматирование.

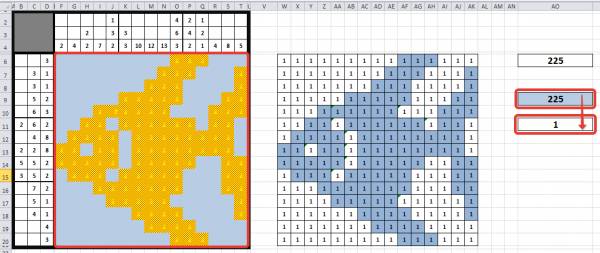
ШАГ 4. Заключительный этап

Остается скрыть формулы и столбцы от пользователя, защитить ячейки. Для этого выделим столбцы W-АО, в которых находятся формулы и вспомогательная область, щелкнем по ним правой кнопкой мыши и выберем Скрыть.

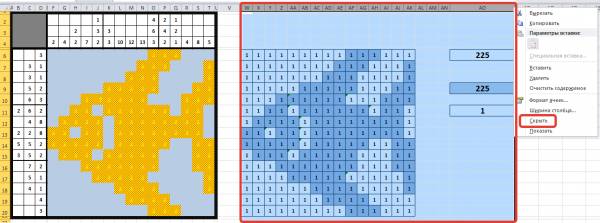
Удалим с рабочего поля все цифры (1 и 2), мы получим следующий вид нашего листа:

Для защиты всех ячеек выделим все ячейки листа, для этого щелкнем на прямоугольник в верхнем левом углу между названиями столбца А и строки 1. Далее щелкнем правой кнопкой мыши по любой ячейке и выберем Формат ячеек.

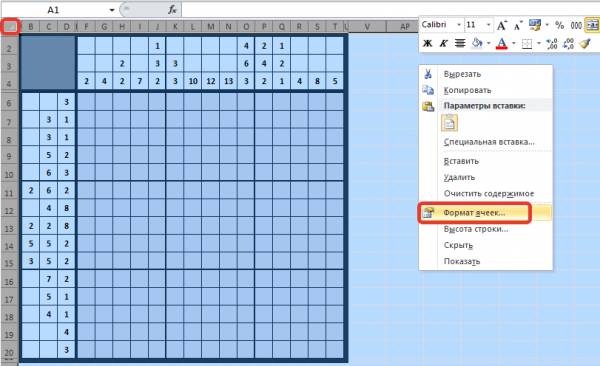
В диалоговом окне Формат ячеек на вкладке Защита установим флажки Защищаемая ячейка и Скрыть формулы — ОК.

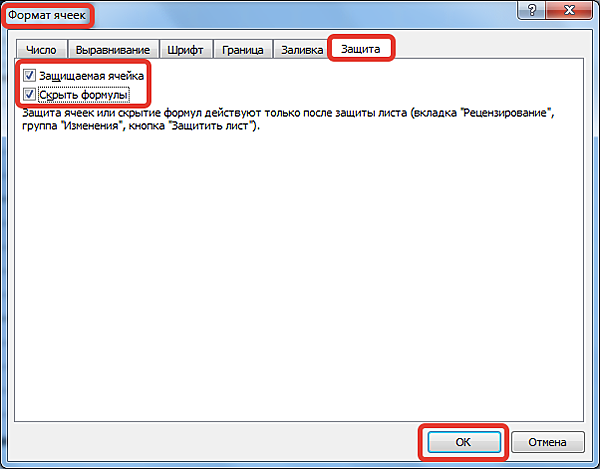
Выделим диапазон ячеек рабочей области, где пользователь будет расставлять 1 и 2, щелкнем правой кнопкой мыши по ним и выберем в контекстном меню Формат ячеек. На вкладке Защита снимем флажок Защищаемая ячейка — ОК.

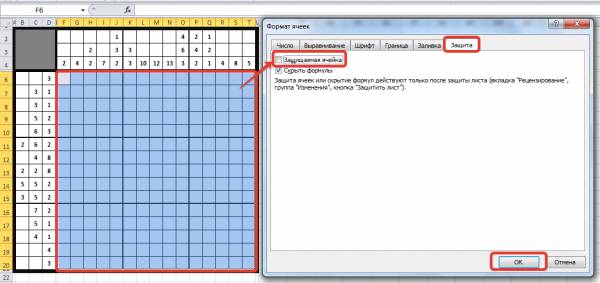
Защитим лист от редактирования. Для этого на вкладке Рецензирование выберем Защитить лист. В диалоговом окне Защита листа введем пароль для защиты. Будьте внимательны! Забытый пароль восстановить невозможно, поэтому или записывайте его в надежном месте, или создавайте такой пароль, который точно не забудете.

Устанавливаем флажок Выделение незаблокированных ячеек. Таким образом, мы разрешаем пользователю выделять незаблокированные ячейки. Можно разрешить форматирование ячеек, чтобы пользователь мог заливать ячейки цветом. Нажимаем ОК.

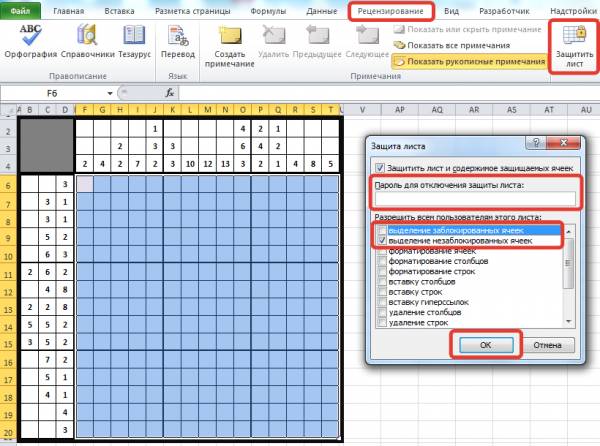
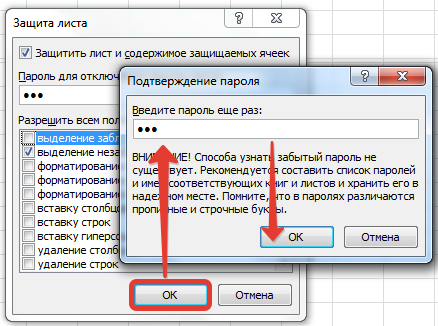
Повторно вводим пароль и нажимаем ОК.

Мы получили готовый японский кроссворд, выполненный в MS Excel.

ВАЖНО

Скачать исходник кроссворда по данной статье >>>

Японские кроссворды интересно разгадывать, но не менее увлекательно их создавать. Вы можете внести свои дополнения и идеи при использовании данного материала в своей работе. Готовые японские кроссворды, сделанные в т.ч. по этой инструкции, вы можете опубликовать на нашем сайте и получить бесплатное электронное свидетельство. Следуйте инструкции >>>

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ “СОШ”, с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

---

автор вопроса выбрал этот ответ лучшим

Как составить японский кроссорд?

Если Вы умеете разгадывать японские кроссворды, да еще и рисуете не плохо, то и составить его для Вас не составит труда. Сначала разбейте чистый лист бумаги не поле из клеток, как на японском кроссворде.

Далее следует определиться с тем, что хотите нарисовать, и нанести рисунок точечным способом, примерно так:

Теперь дело за малым — считаем количество закрашенных клеточек и вписываем поочередно слева направо, сверху вниз. В качестве примера можете изучить картинки выше.

Как составить японский кроссворд

Здесь вы можете создавать и редактировать японские кроссворды онлайн.

Слева, в панели инструментов, выберите режим редактора японских кроссвордов и укажите ширину и высоту. В случае конвертации картинки в кроссворд выберите файл изображения и нажмите на кнопку «Конвертировать». Чтобы обрезать фото перед конвертацией используйте сервис фотошоп онлайн.

Сразу после создания нового японского кроссворда его можно отправить на сайт , который будет опубликован после модерации.

Внимание! Отправляя кроссворды на сайт Вы передаете все права на дальнейшие использования этих кроссвордов, включая публикацию и редактирование!

Японские кроссворды на QtQuick

Люблю в свободное время что-нибудь прототипировать. Это позволяет поизучать что-то новое. Данный прототип является клиентом для ресурса http://www.nonograms.ru/, разработчиком которого является Чугунный К.А/ KyberPrizrak /. Весь код доступен на GiHub. На стороне C++ работа с HTML, модель галереи. На стороне QtQuick визуализация.

В этот раз решил поковырять:

и его использование в Qml;
есть ли жизнь без Qt WebKit;

поковырять Qt Labs Controls.

Под катом будет рассмотрено:

• скриншоты;
• как получить HTML без Qt WebKit;
• как сделать кроссворд без Canvas.

Обходимся без Qt WebKit

Сайт отдает кроссворд в виде матрицы:

Дальше JS скрипы создают html код кроссворда. Модуль WebKit был помечен как deprecated. В замен него предлагается использовать модуль Web Engine основанный на проекте Chrome.

Тут сразу ждет небольшое разочарование. Web Engine не имеет API для работы с DOM на странице. Для разбора HTML кода пришлось воспользоваться сторонними средствами(Парсим HTML на C++ и Gumbo).
А вот загрузить страницу, отрендерить и получить нужный HTML мы можем.

QTimer::singleShot здесь используется для ожидания когда страница достроится. Метод toHtml асинхронный и принимает в качестве входного параметра функцию обратного вызова, для получения результата.

Построение кроссворда

Кроссворд решил представить как множество столбцов и строчек. Наверху красным обведено 10 столбцов, каждый размера 3. Слева обведены 10 строк, каждая размером 3. Далее код будет оперировать этими величинами.

Кроссворд можно сделать несколькими способами:

• рисовать на C++;
• рисовать на JS и Canvas;
• построить из базовых элементов(Item, Rectangle, MouseArea и т.д.)

Я выбрал последний вариант.

Основа представлена Item, размер которого вычисляется из размера crossGrid и размера отступа(margin)

Элемент crossGrid

topLeftItm прямоугольник заполняющий пространство. cGrid и rGrid описывают сетку с числами. playingField поле для решения кроссворда.

Построение сетки

Если написать так:

то получим удвоение линии

Что бы убрать удвоение линии используем трюк с размерами Item и Rectangle. Размер Item фиксирован, для того что бы в повторителе(Repeater) все элементы располагались ровно. Rectangle шире и выше на единицу, в зависимости от необходимости двойной линии.

Тут на основе индекса вычисляется строка(rw) и колонка(cn), увеличиваются на единицу, берется остаток от деления на 5. Т.е. через каждые 5 клеток ширина или высота Rectangle и Item совпадают, что дает удвоение линии.

Поле кроссворда

От поля нам нужна сетка и обработка щелчка мыши. Введем состояние ячейки сетки:

• неактивная(default);
• закрашенная(SHADED);
• помеченная пустой(CLEAR).

Начинать будем c неактивного состояния и менять по клику мыши в следующей последовательности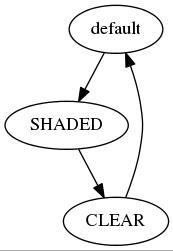

Код рисования ячейки:

itmTxt элемент добавляющий крестик на ячейку, отображая её как помеченную пустой. Тут вовсю используется возможность описывать различные состояния через states.
MouseArea осуществляет переход. То из-за чего все затевалось. Никаких расчетов(преобразования координаты мыши в ячейку сетки), никаких ручных перерисовок.

Рисовать японские кроссворды теперь можно не только с помощью встроенного редактора, но и путем загрузки изображений подготовленных в любой программе для создания и редактирования графики. Подробнее я расскажу об этом в видео.

     Все методы, связанные с заполнением отдельной строки или отдельного столбца, я буду описывать в применении к строкам. Это проще не только для набора текста, но и для восприятия. Для перенесения метода со строки на столбец достаточно мысленно повернуть японский кроссворд на 90 градусов против часовой стрелки.

     I. Базовый метод намёток

     1. Находим незаполненную строку.
     — Если в поле чисел этой строки вообще нет чисел, заполняем строку знаками · (точками). Строка заполнена. Переходим к другой строке.
     — Если есть хотя бы одно — переходим к п. 2.
     2. Находим сумму чисел, соответствующую данной строке в поле чисел, и прибавляем к ней число промежутков. Число промежутков равно количеству чисел минус один.
     3. Вычитаем получившееся число из длины строки.
     — Если разность равна нулю, все полосы в строке определены. Заполняем строку слева направо, делая промежутки между полосами длиной в единицу. Клетки полос заполняем знаками ×, клетки промежутков — знаками ·. В поле чисел зачёркиваем все числа, соответствующие данной строке. Строка заполнена. Переходим к другой строке.
     — Если разность больше нуля, переходим к пункту 4.
     4. Сравниваем получившуюся разность с каждым из чисел в строке. Каждое число, которое больше разности, соответствует полосе, которую можно наметить.
     — Если таких чисел нет, строку на данном этапе наметить невозможно. Переходим к другой строке.
     — Если есть хотя бы одно такое число, переходим к пункту 5.
     5. Осуществляем намётку. С помощью знаков < и > размечаем строку так, как будто первая полоса начинается от её левого края, а все промежутки между полосами равны единицам. Затем размечаем её повторно так, как будто последняя полоса начинается от её правого края, а все промежутки между полосами равны единицам.
     Для простоты можно ставить рядом с каждой из уголковых скобок порядковый номер, означающий то, какую по счёту из полос мы намечаем. Лучшее, что можно сделать — держать эти порядковые номера в оперативной памяти, чтобы не загромождать клетки японского кроссворда, а тренировать клетки мозга.
     6. Левый и правый варианты некоторых полос (тех, чья длина больше разности из п. 3) пересекутся. В клетках пересечения ставим знаки ×.
     7. Обводим кружками числа, соответствующие намеченным полосам. Намётка завершена. Переходим к другой строке.
     Для примера — строка с ходом расстановки намёток.
     1. Нашли незаполненную строку. Её длина — 16 единиц.

1 3 4 3

     2. 1+3+4+3=11. 11+3=14
     3. 16-14=2. 2>0, так что переходим к п.4
     4. 1<2; 3>2; 4>2; 3>2. Таким образом, три из четырёх полос в строке можно наметить (и уж хотя бы одну — точно). Переходим к п. 5.
     5. Сперва наметим полосы с «левым выравниванием». Обратите внимание: цифры означают не длину полосы, а её порядковый номер слева! Обратите также внимание на то, что открывающие угловые скобки имеют внутри клетки левое выравнивание, а закрывающие — правое.

1 3 4 3

<1 1>

<2

2>

<3

3>

<4

4>

     Теперь — с “правым выравниванием” (для отличия — здесь красным цветом)

1 3 4 3

<1 1>

<2 <1 1>

<2 2>

<3 2>

<3

3>

<4 3>

<4 4>

4>

     Теперь находим такие пары угловых скобок, чтобы:
     а. Они были помечены одинаковыми порядковыми номерами.
     б. Они имели разный цвет: открывающая скобка — красный, а закрывающая — чёрный (не наоборот).
     в. Слева стояла открывающая угловая скобка <, а справа закрывающая >
     Таких пар насчитывается три — пара №2 (открывающая и закрывающая скобки в одной клетке), пара № 3 и пара №4.
     6. Расставляем крестики в клетках, содержащих такие парные угловые скобки, и во всех клетках между ними. Угловые скобки в моём примере стёрты, чтобы не перегружать клетки (в настоящих японских кроссвордах желательно делать угловые скобки едва заметными). Для сравнения здесь же дана строка в предыдущем состоянии.

1 3 4 3

<1 1>

<2 <1 1>

<2 2>

<3 2>

<3

3>

<4 3>

<4 4>

4>

1 3 4 3

×

×

×

×

     7. Обводим кругами числа, соответствующие намеченным полосам (здесь — числа заключены в рамки).

1 3 4 3

×

×

×

×

     Намётка завершена.

     II. Метод определения полос.

     1. В случае, если мы точно можем утверждать, что какая-то из полос определена и полностью отмечена в строке знаками рисунка (×), слева и справа от неё ставятся знаки фона (·). В случае, если одной из сторон полоса примыкает к краю (началу или концу) строки, знак фона ставится только с другой её стороны.
     Пример:

5 1

×

×

×

×

×

     Можно видеть, что числу 5 в поле чисел соответствует каким-то (неважно, каким, лишь бы правильным) образом полученная полоса длиной в 5 единиц. Замыкаем её слева и справа точками.

5 1

·

×

×

×

×

×

·

     Теперь зачёркиваем пятёрку как соответствующую определённой полосе:

5 1

·

×

×

×

×

×

·

     2. В случае, если определена первая (последняя) в строке полоса, и она находится не в самом начале (не в самом конце) строки, заполняем пространство между левым краем полосы и началом строки (правым краем полосы и концом строки) знаками фона — ведь раньше первой и позже последней полосы никаких полос быть не может.
     Продолжая предыдущий пример (новые точки — красным цветом):

5 1

·

·

×

×

×

×

×

·

     III. Метод определения строки

     В случае, если все полосы в строке определены, все клетки, оставшиеся свободными, заполняем знаками фона.
     Пример:

4 2

·

×

×

×

×

·

·

×

×

·

     Перед нами строка, все полосы которой определены. Прежде всего мы могли бы, согласно п. 2 раздела II, заполнить все клетки левее первой и правее последней полосы. Но мы можем сразу поступить иначе — заполнить все свободные клетки знаками фона (здесь для наглядности красным).

4 2

·

·

·

×

×

×

×

·

·

·

×

×

·

·

·

     Строка определена полностью; больше к ней не возвращаемся, если только не окажется, что в ней содержатся ошибки.

     IV. Метод непустой строки

     Метод применяется в том случае, когда в строке в результате каких-то предыдущих действий со столбцами (или в столбце — в результате действий со строками) уже есть знаки × и/или ·, но она определена не полностью.
     1. Если в строке есть знаки фона (·), намечаем полосы в строке с их учётом. Учитывать наличие этих знаков можно следующим образом:
     а. Точка отсекает в начале строки число клеток, меньшее, чем длина первой полосы (либо, соответственно, в конце строки — число клеток, меньшее, чем длина последней полосы). В таком случае промежуток между этой точкой и началом (соответственно, концом) строки заполняется точками.
     Пример:

4 1 1 2

·

     Точка отсекает от строки участок длиной в три единицы. Между тем, первая полоса имеет длину в четыре единицы. Заполняем левый отсечённый кусок точками.

4 1 1 2

·

·

·

·

     Как можно понять, ознакомившись с п.3 этого раздела, данная строка определена полностью.
     б. Если знаки фона (·) стоят друг от друга на расстоянии, меньшем длины любой полосы в строке, заполняем промежуток между ними знаками фона.
     Пример:

3 3 3 3

·

·

     Два знака фона стоят так, что свободное пространство между ними составляет две единицы. Ни одна из полос сюда не влезет. Поэтому заполняем пространство между ними знаками фона (для отличия от старых знаков — красным цветом).

3 3 3 3

·

·

·

·

     в. Любая стоящая в строке точка разбивает строку на две области, каждую из которых можно воспринимать как отдельную строку с собственной длиной. Как действовать с учётом этого обстоятельства, см. п. 3.
     2. Если в строке есть знаки рисунка (×), действуем базовым методом намёток (I), а затем смотрим, нет ли среди крестов, бывших до заполнения базовым методом намёток, таких, которые лежат вплотную к намёткам. В ряде случаев дополнение намёток этими клетками с крестами даёт определённую полосу.
     Пример:

7 1 1 2

×

     Делаем намётку по базовому методу намёток. Получаем картину (для отличия от заранее стоявшего креста — красным цветом)

7 1 1 2

×

×

×

×

×

×

×

×

     Видно, что первая полоса полностью определена — все семь крестов расставлены. Что делать с полностью определённой полосой, см. в разделе II. Мы же зачёркиваем число, соответствующее определённой полосе, и обводим в кружок (здесь — заключаем в рамку) число, соответствующее намеченной полосе.

7 1 1 2

×

×

×

×

×

×

×

×

     3. Строка отчасти определена. Это может означать, что в ней есть определённые полосы и определённые клетки фона. В этом случае мы действуем согласно генеральному правилу: то, что можно разбить на меньшие области, разбей на меньшие области. Затем работаем с каждой областью отдельно — так, как будто это целая строка.
     Пример 1:

3 2 5

·

×

×

·

     Полоса длиной в две единицы явно разбивает строку на две области. В одной из них, левой, находится полоса длиной 3 единицы, в другой, правой — полоса в 5 единиц. Сперва зачёркиваем число, соответствующее определённой полосе.

3 2 5

·

×

×

·

     Теперь действуем так, как будто у нас две отдельных строки, соответствующие двум свободным областям (мысленно действуем, разумеется):

3

5

     Обрабатываем первую область по базовому методу намёток. 7 клеток, 7-3=4, 3<4, значит, область незаполняема (здесь изложены основные пункты рассуждения, лучше проделать его полностью самостоятельно).
     Обрабатываем вторую область тем же методом. 9 клеток, 9-5=4, 5>4, значит, в области можно произвести намётку. Выполняя её строго в соответствии с методом, получаем:

5

×

     Целая строка (которую, напомню, мы разбивали на области только мысленно) будет выглядеть следующим образом:

3 2 5

·

×

×

·

×

     Остаётся обвести число, соответствующее намеченной полосе:

3 2 5

·

×

×

·

×

     Пример 2 (из п.1б раздела IV):

3 3 3 3

·

·

·

·

     Строка разбита на две области, но неизвестно, какие полосы в каких областях содержатся. В этом случае исследуем каждую из областей так, как будто она могла бы содержать все полосы. Наша задача — убедиться либо разубедиться в том, что это не так.
     Левая область:

3 3 3 3

     В ней пять клеток. Она может содержать одну или ни одной полосы длиной в три единицы.
     Правая область

3 3 3 3

     В ней 11 клеток. Она может содержать не более трёх полос длиной в три единицы, причём все три будут определёнными.
     Рассуждаем следующим образом. Если левая область не содержит ни одной полосы, правая вынуждена содержать четыре (поскольку всего в строке их четыре). Если правая содержит меньше трёх полос, левая вынуждена содержать больше одной. Ни то, ни другое невозможно. Значит, левая область содержит одну полосу, а правая — три.
     Действуем с каждой из областей по базовому методу намёток, дополненному методом определения полос. Получаем:

3

×

     и

3 3 3

×

×

×

·

×

×

×

·

×

×

×

     Объединяя, получаем:

3 3 3 3

×

·

·

·

·

×

×

×

·

×

×

×

·

×

×

×

     Пример 3:

1 3 3 4

·

·

     Строка разбита на две области. В левой может уместиться только одна полоса длиной в 1 единицу (о полосе длиной в 3 и тем более в 4 единицы речь не идёт, т.к. начинаем счёт с первой полосы). В правой области могут уместиться все четыре полосы, в т.ч. и длиной в единицу, но может оказаться, что в ней три полосы. При таком уровне неопределённости работаем с той областью, в которой обязательно находится хотя бы одна полоса — в нашем случае это правая область.
     Для работы с областью используем базовый метод намёток в следующей модификации. Считаем, что в области, содержащей хотя бы одну полосу, содержится минимальное возможное их число (в нашем случае это три полосы длиной в 3, 3 и 4 единицы). Получаем следующее:

3 3 4

×

×

×

×

     Объединяем области и получаем:

1 3 3 4

·

·

×

×

×

×

(продолжение см. http://alchutoff.livejournal.com/160253.html)