Непозиционная система счисления


4.3
Средняя оценка: 4.3
Всего получено оценок: 106.
4.3
Средняя оценка: 4.3
Всего получено оценок: 106.
Набор символов для обозначения чисел и правила их использования составляют систему счисления. Системы счисления принято делить на позиционные и непозиционные. Описание и примеры непозиционных систем счисления приведены в данной статье.
Что такое непозиционная система счисления
В непозиционной системе счисления изменение положения символа в числе не влияет на значение самого числа.
Отличие позиционных и непозиционных систем хорошо видно при сравнении арабских и римских чисел. Числа, записанные арабскими цифрами, составляются в позиционной системе. И здесь важно учитывать понятие разрядности. Одна и та же цифра, в зависимости от того, в каком разряде числа она записывается, обозначает разную числовую величину. Например, в числе 234 цифра 2 обозначает величину двести, а в числе 324 – соответствует двадцати.
В римской системе счисления, цифра, в какое положение ее не помещай, всегда означает одно и то же. Например, с помощью римских цифр V и I, эквивалентных арабским 5 и 1, можно составить числа VI и IV, что соответствует 6 и 4. В непозиционной системе расположение цифры никак не влияет на ее значение.
История возникновения непозиционных систем счисления уходит корнями в глубокую древность. Жители древних государств: Вавилона, Майя, Древнего Египта, Греции и Рима, пользовались непозиционным принципом в составлении чисел. Некоторые из таких систем, например, римские цифры, используются и по сей день.
Римская система счисления
В римской системе ключевые числа записываются латинскими буквами I, V, X, L, C, D, M, а все остальные числовые значения получаются путем комбинирования этих знаков с использованием принципов сложения и вычитания.
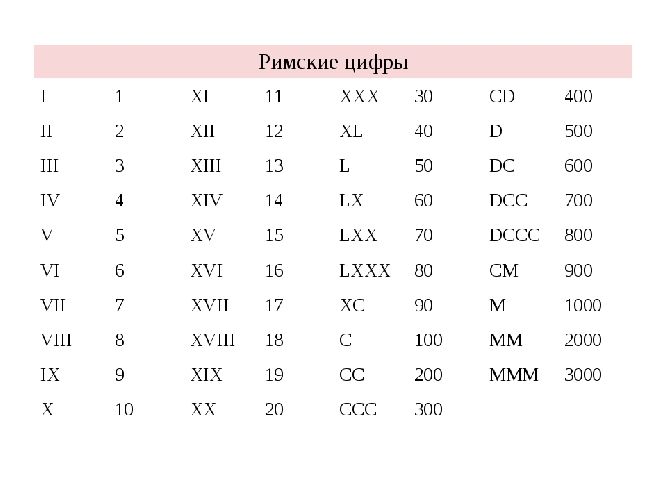
Римская система получила название от места своего возникновения. Она начала использоваться еще в Древнем Риме, более двух тысяч лет назад. В римской системе есть одна особенность – в ней не используется цифра ноль.
Числа в римской системе следует записывать слева направо от большего к меньшему. Если в числе перед большей цифрой стоит меньшая, то ее следует вычесть из следующей за ней цифрой, исходя из принципа вычитания. Меньшие цифры, стоящие после больших, соответственно прибавляются.
Например, арабское число 1978 в римской системе будет записано так: MCMLXXVIII.
Римская система, в настоящее время используется для записи дат, обозначения валентности химических элементов.
Древние непозиционные системы счисления
Исторической науке известны древние системы счисления, использующие различные знаки, символы и рисунки для обозначения числовых значений. Самыми известными являются:
- Древнеегипетская система счисления
- Вавилонская система счисления
- Система счисления майя
Древнеегипетская система счисления
В древнеегипетской системе счисления специальные символы заменяли числа 1, 10, 100, 1000, 1000, и так далее, кратные десяти.
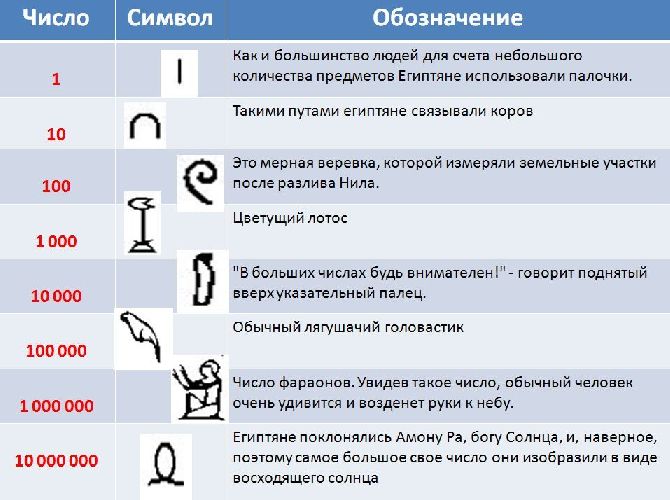
Числа записывались в виде комбинации таких символов, повторяющихся в зависимости от значения конкретного разряда не более девяти раз. Например, в числе 45 символ для обозначения 10 записывается четыре раза, а символ единицы, повторяется пять раз.
Вавилонская система счисления
Вавилонская система представления чисел использует для обозначения чисел знаки в виде вертикальных и горизонтальных насечек – клиньев. Такую систему написания знаков называют клинописью.
Единицы в древнем Вавилоне обозначали прямыми клиньями, десятки – лежащими, то есть горизонтальными. Прямым клином обозначается также число шестьдесят.
Вавилонскую систему записи числовых значений называют также шестидесятеричной. Принцип разделения числового пространства на группы по 60 единиц используется и в настоящее время для определения временных отрезков. Один час состоит из 60 минут, одна минута – из 60 секунд.
Вавилонская система представляет собой комбинированный вариант системы счисления, так как представление чисел от 1 до 60 подчинено непозиционному принципу, а числа свыше шестидесяти представляются с использованием позиционного подхода.
Например, число 34 в вавилонской системе записывается как последовательность из трех горизонтальных клиньев, за которыми следует четыре прямых клина. А число 84 будет начинаться с прямого клина, обозначающего 60, за которым следуют два лежащих клина и затем четыре прямых.
Система счисления майя
Для обозначения чисел в различных бытовых ситуациях Майя использовали непозиционную систему представления чисел, в которой записывались числа от 0 до 19 с помощью знаков, представляющих собой комбинации точек и горизонтально расположенных отрезков.
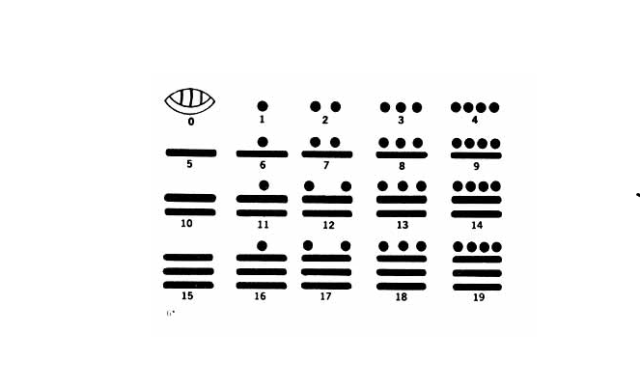
Например, цифра для обозначения числа 17 выглядит как две точки, расположенные над тремя горизонтальными черточками.

Что мы узнали?
Для представления чисел используются позиционные и непозиционные системы счисления. В непозиционных системах расположение знаков, составляющих числа не влияет на их числовые значения. Самой известной непозиционной системой является система римских цифр. Известные исторической науке системы записи чисел древних народов Египта, Вавилона, цивилизации Майя применяли непозиционный принцип представления чисел, используя различные знаки для обозначения числовых эквивалентов.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Николай Шалак
10/10
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 106.
А какая ваша оценка?
Основы систем счисления
Время на прочтение
11 мин
Количество просмотров 502K
Изучая кодировки, я понял, что недостаточно хорошо понимаю системы счислений. Тем не менее, часто использовал 2-, 8-, 10-, 16-ю системы, переводил одну в другую, но делалось все на “автомате”. Прочитав множество публикаций, я был удивлен отсутствием единой, написанной простым языком, статьи по столь базовому материалу. Именно поэтому решил написать свою, в которой постарался доступно и по порядку изложить основы систем счисления.
Введение
Система счисления — это способ записи (представления) чисел.
Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палецзарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки
Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.
Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.
Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.
Непозиционные системы
Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.
Единичная система счисления
Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.
Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Древнеегипетская десятичная система
В Древнем Египте использовались специальные символы (цифры) для обозначения чисел 1, 10, 102, 103, 104, 105, 106, 107. Вот некоторые из них:
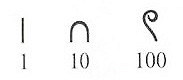
Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.
Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:

Вавилонская шестидесятеричная система
В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32:

Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92:

Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа:
Теперь число 3632 следует записывать, как:

Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.
Римская система
Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.
Методы определения значения числа:
- Значение числа равно сумме значений его цифр. Например, число 32 в римской системе счисления имеет вид XXXII=(X+X+X)+(I+I)=30+2=32
- Если слева от большей цифры стоит меньшая, то значение равно разности между большей и меньшей цифрами. При этом, левая цифра может быть меньше правой максимум на один порядок: так, перед L(50) и С(100) из «младших» может стоять только X(10), перед D(500) и M(1000) — только C(100), перед V(5) — только I(1); число 444 в рассматриваемой системе счисления будет записано в виде CDXLIV = (D-C)+(L-X)+(V-I) = 400+40+4=444.
- Значение равно сумме значений групп и цифр, не подходящих под 1 и 2 пункты.
Помимо цифирных, существуют и буквенные (алфавитные) системы счисления, вот некоторые из них:
1) Славянская
2) Греческая (ионийская)
Позиционные системы счисления
Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.
Десятичная система счисления
Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.
Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*102 + 0*101 + 3*100 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 50310.
Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.
Двоичная система счисления
Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.
Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.
Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 1012 = 1*22 + 0*21 + 1*20 = 4+0+1 = 510.
Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?
Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 1011002. В восьмеричной — это 101 100 = 548, а в шестнадцатеричной — 0010 1100 = 2С16. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.
Восьмеричная система счисления
8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.
Пример восьмеричного числа: 254. Для перевода в 10-ю систему необходимо каждый разряд исходного числа умножить на 8n, где n — это номер разряда. Получается, что 2548 = 2*82 + 5*81 + 4*80 = 128+40+4 = 17210.
Шестнадцатеричная система счисления
Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.
В качестве примера возьмем число 4F516. Для перевода в восьмеричную систему — сначала преобразуем шестнадцатеричное число в двоичное, а затем, разбив на группы по 3 разряда, в восьмеричное. Чтобы преобразовать число в 2-е необходимо каждую цифру представить в виде 4-х разрядного двоичного числа. 4F516 = (100 1111 101)2. Но в 1 и 3 группах не достает разряда, поэтому заполним каждый ведущими нулями: 0100 1111 0101. Теперь необходимо разделить полученное число на группы по 3 цифры справа налево: 0100 1111 0101 = 010 011 110 101. Переведем каждую двоичную группу в восьмеричную систему, умножив каждый разряд на 2n, где n — номер разряда: (0*22+1*21+0*20) (0*22+1*21+1*20) (1*22+1*21+0*20) (1*22+0*21+1*20) = 23658.
Помимо рассмотренных позиционных систем счисления, существуют и другие, например:
1) Троичная
2) Четверичная
3) Двенадцатеричная
Позиционные системы подразделяются на однородные и смешанные.
Однородные позиционные системы счисления
Определение, данное в начале статьи, достаточно полно описывает однородные системы, поэтому уточнение — излишне.
Смешанные системы счисления
К уже приведенному определению можно добавить теорему: “если P=Qn (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”
Опираясь на теорему, можно сформулировать правила перевода из P-й в Q-ю системы и наоборот:
- Для перевода из Q-й в P-ю, необходимо число в Q-й системе, разбить на группы по n цифр, начиная с правой цифры, и каждую группу заменить одной цифрой в P-й системе.
- Для перевода из P-й в Q-ю, необходимо каждую цифру числа в P-й системе перевести в Q-ю и заполнить недостающие разряды ведущими нулями, за исключением левого, так, чтобы каждое число в системе с основанием Q состояло из n цифр.
Яркий пример — перевод из двоичной системы счисления в восьмеричную. Возьмем двоичное число 100111102, для перевода в восьмеричное — разобьем его справа налево на группы по 3 цифры: 010 011 110, теперь умножим каждый разряд на 2n, где n — номер разряда, 010 011 110 = (0*22+1*21+0*20) (0*22+1*21+1*20) (1*22+1*21+0*20) = 2368. Получается, что 100111102 = 2368. Для однозначности изображения двоично-восьмеричного числа его разбивают на тройки: 2368 = (10 011 110)2-8.
Смешанными системами счисления также являются, например:
1) Факториальная
2) Фибоначчиева
Перевод из одной системы счисления в другую
Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.
Преобразование в десятичную систему счисления
Имеется число a1a2a3 в системе счисления с основанием b. Для перевода в 10-ю систему необходимо каждый разряд числа умножить на bn, где n — номер разряда. Таким образом, (a1a2a3)b = (a1*b2 + a2*b1 + a3*b0)10.
Пример: 1012 = 1*22 + 0*21 + 1*20 = 4+0+1 = 510
Преобразование из десятичной системы счисления в другие
Целая часть:
- Последовательно делим целую часть десятичного числа на основание системы, в которую переводим, пока десятичное число не станет равно нулю.
- Полученные при делении остатки являются цифрами искомого числа. Число в новой системе записывают, начиная с последнего остатка.
Дробная часть:
- Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.
- Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.
Пример: переведем 1510 в восьмеричную:
158 = 1, остаток 7
18 = 0, остаток 1
Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 1510 = 178.
Преобразование из двоичной в восьмеричную и шестнадцатеричную системы
Для перевода в восьмеричную — разбиваем двоичное число на группы по 3 цифры справа налево, а недостающие крайние разряды заполняем ведущими нулями. Далее преобразуем каждую группу, умножая последовательно разряды на 2n, где n — номер разряда.
В качестве примера возьмем число 10012: 10012 = 001 001 = (0*22 + 0*21 + 1*20) (0*22 + 0*21 + 1*20) = (0+0+1) (0+0+1) = 118
Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.
Преобразование из восьмеричной и шестнадцатеричной систем в двоичную
Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.
Для примера рассмотрим число 458: 45 = (100) (101) = 1001012
Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.
Преобразование дробной части любой системы счисления в десятичную
Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.
Пример: 101,0112 = (1*22 + 0*21 + 1*20), (0*2-1 + 1*2-2 + 1*2-3) = (5), (0 + 0,25 + 0,125) = 5,37510
Преобразование дробной части двоичной системы в 8- и 16-ую
Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.
Пример: 1001,012 = 001 001, 010 = (0*22 + 0*21 + 1*20) (0*22 + 0*21 + 1*20), (0*22 + 1*21 + 0*20) = (0+0+1) (0+0+1), (0+2+0) = 11,28
Преобразование дробной части десятичной системы в любую другую
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.
Для примера переведем 10,62510 в двоичную систему:
0,625*2 = 1,25
0,250*2 = 0,5
0,5*2 = 1,0
Записав все остатки сверху вниз, получаем 10,62510 = (1010), (101) = 1010,1012
Здравствуйте, на этой странице рассмотрим одну из важных тем в информатике – а именно непозиционные системы счисления. Здесь вы узнаете, что является непозиционными системами, и познакомитесь с основными определениями, которые относятся к этой теме. Также затронем их отличия от позиционных нумераций и приведем достоинства и недостатки.
Определение непозиционной системы счисления
Непозиционными являются нумерации, где положение цифры в числе (разряд) не влияет на её значение.
Чтобы разобраться конкретно в том, что здесь написано, выберем самое популярное исчисление, которое называется десятичным. Вы все с ним знакомы. Им пользуются люди в большинстве стран мира. Алфавит десятичной нумерации состоит из арабских знаков – чисел от 0 до 9. Данный вид записи является позиционным. Почему, спросите вы? Всё просто. В качестве примера приведем два числа – 1000 и 10. Смотрите на цифру один – в зависимости от того, какое место она занимает в числе, меняется значение, которое она обозначает. В числе 1000 – тысячи, а 10 – десятки.
В непозиционных представлениях все обстоит совсем иначе. Давайте приведем в пример Римскую нотацию. Её вы тоже видели и с ней знакомы. Вспомните – в книгах по истории с помощью неё представляются века и номера монархов. Как пример, Петр I или Иван IV Грозный. Обратите внимание на I и IV, которые в арабском виде запишутся как 1 и 4. Здесь значение единицы не изменяется от того, какое место она занимает. На первом месте она стоит или на втором – неважно.
Историками считается, что исчисления, которые называются непозиционными, ведут свои корни от глубокой древности – это первые формы для счета, которые использовал человек. Поговорим дальше про их виды и разберем недостатки.
Примеры непозиционных систем счисления
Унарная непозиционная
Еще называется непозиционной единичной. Скорее всего, вы уже догадались, почему она так называется. Дело в том, что в этой форме записи используется только один знак. Это представление применяли древнейшие люди. Для записи значений использовались насечки на костях животных или стенах пещеры. Также в обиходе были зарубки на дереве. Используется до сих пор. Вспомните сериалы, где заключенные отсчитывают свои дни в неволе. Также применяется для обучения детей счету – так называемый пальцевый метод.

Унарная сс – отметки на кости
Римская непозиционная
Её мы уже привели выше. Используется до сих пор. В качестве алфавита здесь применяются латинские буквы, такие как V, I, D, M, C, X, L. Всё остальное же получается с помощью различного написания этих символов – здесь используются принципы вычитания и сложения. Так если младший разряд записывается перед старшим, то он вычитается. Если же наоборот, то складывается. Есть у неё и еще одна особенность – нет 0, который является отсутствием числа. Ниже приведена небольшая табличка с расшифровкой римских цифр.
Римское непозиционное счисление появилось в Риме на самом пике процветания империи. Однако и после того как империя распалась этим счислением пользовались еще очень долго. Она использовалась в Европе до 1200х годов, пока великий математик Леонардо Фибоначчи не издал трактат – “Книга Абака”. В нем ученый показывал превосходство позиционных систем над непозиционными.
Египетская непозиционная
Возникла в третьем тысячелетии до нашей эры. Все значения записывались здесь с помощью иероглифов. Каких-то особых правил здесь не существовало – все числовые значения просто складывались. Также не было и правил, которые относятся к записи – последовательность могла быть записана, как слева на право, так и справа налево. Иероглифы могли занимать любой разряд. Ниже приведена табличка со значениями некоторых из них.

Алфавитные системы счисления
Стоит отметить эти формы записи. Здесь все очень просто – каждой букве алфавита сопоставлялась цифра. Стоит отметить, что эти непозиционные системы являются более совершенными, чем все предыдущие, поскольку имелись обозначения десятков и сотен. К недостаткам можно отнести их сложность. Здесь можно выбрать два популярных примера.
Славянская
Использовалась нашими предками во времена древней Руси. Первые записи о ней в летописи временных лет появляются с начала десятого века. Каждой букве глаголицы соответствовало некоторое число. Полностью вышла из использования во времена Российской Империи в восемнадцатом веке, её место заняло десятичное исчисление. Пользуемся мы им, и посей день.

Греческая
Она же называется непозиционной новогреческой или ионийской. Упоминания о ней датируются третьим веком до нашей эры. Здесь счет велся буквами, которые употреблялись в римской письменности. Пришла на смену старогреческому формату. По сути, непозиционное кириллическое представление является её копией.
Достоинства и недостатки. Возможность использования в информатике и других науках.
К достоинствам можно отнести только их простоту. Как мы уже говорили выше, та же унарная непозиционная система применяется для обучения детей. Однако недостатков у них гораздо больше и они очень существенные:
- Регулярно нужно выбирать и вводить новые знаки;
- Недостаток в представлении больших числовых значений и громоздкая запись;
- Также возникают большие сложности выполнения арифметических операций из-за малого или полного отсутствия правил по отображению величин;
- Главным же минусом является отсутствие средств для представления дробных и отрицательных чисел.
Всё эти недостатки делают их использование в математике и информатике непрактичным.
Заключение
В качестве итогов можно сказать, что после прочтения этого материала вы имеете полное представление о том, что называется непозиционными системами счисления, овладели нужным определением. Знаете виды, которые использовали разные народы в различных частях земного шара. Теперь вы имеете представление о том, как считали люди в Риме, Египте, Греции и древней Руси. Знаете их плюсы и минусы. Понимаете, почему нельзя использовать их в информатике. Как по мне тема достаточно легкая, но очень интересная. При возникновении вопросов задайте их в комментариях к этой записи. Буду рад на них ответить. Также вы можете почитать другие материалы, которые затрагивают информатику на нашем сайте.
андрей орлов
Мыслитель
(7085)
8 лет назад
можно придумать систему состоящую из трех цифр A,B,C, В которой А=45, В=769, С=1001.
новекровчоУченик (21)
8 лет назад
Привет можешь написать как делать а то я вовще не понимаю как делать отмечю как лучший пжл
новекровчоУченик (21)
8 лет назад
пжл
новекровчоУченик (21)
8 лет назад
напиши как делать умаляю
андрей орлов
Мыслитель
(7085)
Позиционная, иероглифическая, третьей системы нет. это кидалово.
Какие системы счисления называются непозиционными
Содержание:
- Что таоке непозиционная система счисления в информатике
-
Разновидности непозиционных систем счисления с примерами
- Биномиальная
- Греческая
- Римская
- Древнеегипетская
- Вавилонская
- Система счисления майя
Что таоке непозиционная система счисления в информатике
В информатике используют позиционный и непозиционный метод записи чисел. Позиционный способ предполагает представление числовых обозначений в определенной последовательности для сохранения величины числа.
Определение
Непозиционная система счисления – это способ записи числа с помощью символов, в котором изменение положения знаков не влияет на значение величины числа.
Разновидности непозиционных систем счисления с примерами
Существует несколько видов непозиционной системы исчисления.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Биномиальная
В данном методе для записи чисел применяются биноминальные коэффициенты.
Определение
Биноминальные коэффициенты – это объединение количества сочетаний, определенное лишь для неотрицательных целых чисел. Такие обобщения зачастую возникают в задачах, требующих перебора всех возможных вариантов ответов, а также в теории вероятности.
Число x в рассматриваемой системе представляет собой сумму биноминальных коэффициентов:
где, 0 <= c1 < c2 < … < cn.
Биноминальные числа бывают:
- линейные – в виде последовательности 0 и 1. Эта форма предполагает наличие двух чисел: количество столбцов в матрице и сумму числа столбцов и строк в матрице;
- матричные – в виде матрицы, элементами которой являются единицы и нули. При этом в одном столбце матрицы возможно наличие только одной 1.
Пример преобразования матричной формы в линейную:
Каждой составляющей матрицы соответствует один биноминальный коэффициент. При сложении коэффициентов, соответствующих единицам в матрице, получится количественный эквивалент.
Применение биноминальных чисел:
- действия с комбинаторных кодом – их получение, перебор и нумерация;
- шифрование информации и сжатие данных благодаря двоичному алфавиту данной системы счисления;
- представление решений генетических алгоритмов.
Греческая
Определение
Греческая система счисления – это метод представления числа с помощью букв греческого алфавита и некоторых знаков доклассического периода. Другие названия данного способа – ионийская, новогреческая.
В Греции рассматриваемый алфавитный способ записи чисел стал применяться в III веке до н.э. Буквы греческого алфавита соответствуют следующим числам:
С помощью ионийской системы можно записать лишь числа от 1 до 999.
Римская
Определение
Римская система исчисления – это метод числовой записи посредством использования символов латинского алфавита.
Соответствие букв латиницы числовому значению:
- I — один;
- V — пять;
- X — десять;
- L — пятьдесят;
- C — сто;
- D — пятьсот;
- M — тысяча.
Для представления чисел десятичной системы счисления в виде римских букв работают следующие правила:
- Стоящий слева от большего меньший символ вычитается из большего.
- Стоящий справа от большего меньший символ прибавляется к большему.
Пример
При переводе числа 67 в римскую систему счисления получаем следующий набор латинских букв: LXVII = (50 + 10) + (5 + 2) = 60 + 7.
545 имеет вид DXLV = 500 + (50 – 10) +5.
Применение данной системы исчисления:
- обозначение знаменательных дат;
- разделов и глав книг;
- обозначение порядкового номера.
Древнеегипетская
Способ записи чисел, используемый в Древнем Египте, основывался на иероглифах. С помощью этих символов записывались основные числа 1, 10, 100 и т.д. Другие числовые значения получались с помощью сложения ключевых чисел.
Действие производилось в следующей последовательности:
- Первым записывали число высшего порядка, после него – низшего.
- Умножение и деление осуществлялось путем последовательного удвоения числовых значений.
- Повторение каждой цифры допускалось до девяти раз.
Пример
Вавилонская
Определение
Вавилонская система исчисления – это позиционный метод записи чисел с основанием 60, применявшийся в Древнем Вавилоне. Это первая известная шестидесятеричная система.
В данной системе счисления числа записываются справа налево в порядке убывания: сотни, десятки, единицы. Досчитав до 60, отмечают новый числовой ряд, запись чисел вновь начинается с 1.
Цифрами вавилонского числового метода считались клинья, разные для записи единиц, десятков и нуля.
Пример
Примечание
В измерении времени: час состоит из 60 минут, а минуты – из 60 секунд.
В измерении углов: градус равен 60 минутам, а минута – 60 секундам.
Система счисления майя
Определение
Цифры майя – это позиционная запись чисел с основанием 20, используемая племенами майя.
Рассматриваемый способ исчисления состоял из нуля и 19 сложных цифр. Ноль имел обозначение пустой ракушки. Цифры составлялись из точки и горизонтальной черточки. Точка означала единицу, черта – пятерку.
Цифры майя применялась в календарных расчетах. В бытовых целях использовали непозиционный метод записи. Об этом свидетельствует то, что в позиционной системе счисления цивилизации майя имеется больше чисел, чем необходимые 12.
Насколько полезной была для вас статья?
Рейтинг: 4.13 (Голосов: 8)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так

