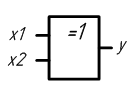Дешифраторы
выпускаются в виде отдельных микросхем
или используются в составе более сложных
микросхем. В настоящее время десятичные
или восьмеричные дешифраторы используются
в основном как составная
часть других микросхем, таких как
мультиплексоры,
демультиплексоры,
ПЗУ
или ОЗУ.
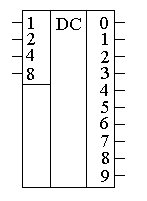
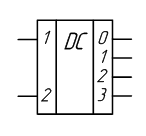
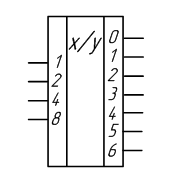
Условно-графическое
обозначение микросхемы дешифратора на
принципиальных схемах приведено на
рисунке 2. На этом рисунке приведено
обозначение двоично-десятичного
дешифратора, полная внутренняя
принципиальная принципиальная схема
которого изображена на рисунке 1.
Рисунок 1
– Условно-графическое
обозначение
двоично-десятичного дешифратора
Точно таким же
образом можно получить принципиальную
схему и для любого другого декодера
(дешифратора). Наиболее распространены
схемы восьмеричных и шестнадцатеричных
дешифраторов. Для индикации такие
дешифраторы в настоящее время практически
не используются. В основном такие
дешифраторы используются как составная
часть более сложных цифровых модулей.
Семисегментный дешифратор
Для
отображения десятичных и шестнадцатеричных
цифр часто используется семисегментный
индикатор.
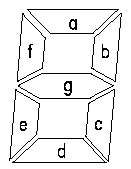
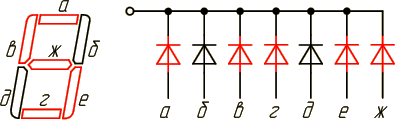
Изображение семисегментного индикатора
и название его сегментов приведено на
рисунке 3.
Рисунок 2
– Изображение семисегментного индикатора
и название его сегментов
Для изображения
на таком индикаторе цифры 0 достаточно
зажечь сегменты a, b, c, d, e, f. Для изображения
цифры ‘1’ зажигают сегменты b и c. Точно
таким же образом можно получить
изображения всех остальных десятичных
или шестнадцатеричных цифр. Все комбинации
таких изображений получили название
семисегментного кода.
Составим
таблицу истинности дешифратора, который
позволит преобразовывать двоичный код
в семисегментный. Пусть сегменты
зажигаются нулевым потенциалом. Тогда
таблица истинности семисегментного
дешифратора примет вид, приведенный в
таблице 1. Конкретное значение сигналов
на выходе дешифратора зависит от схемы
подключения сегментов индикатора к
выходу микросхемы. Эти схемы мы рассмотрим
позднее, в главе, посвящённой отображению
различных видов информации.
Таблица 1
– Таблица истинности
|
Входы |
Выходы |
|||||||||
|
8 |
4 |
2 |
1 |
a |
b |
c |
d |
e |
f |
g |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
В
соответствии с принципами построения
произвольной таблицы истинности по
произвольной таблице истинности получим
принципиальную
схему семисегментного дешифратора,
реализующего таблицу истинности,
приведённую в таблице 1. На этот раз
не будем подробно расписывать процесс
разработки схемы. Полученная принципиальная
схема семисегментного дешифратора
приведена на рисунке 4.
Рисунок 4
– Принципиальная схема семисегментного
дешифратора
Для облегчения
понимания принципов работы схемы на
выходе логических элементов “И”
показаны номера строк таблицы истинности,
реализуемые ими.
Например, на выходе
сегмента ‘a’ логическая единица появится
только при подаче на вход комбинации
двоичных сигналов 0001 (1) и 0100 (4). Это
осуществляется объединением соответствующий
цепей элементом “2ИЛИ”. На выходе
сегмента ‘b’ логическая единица появится
только при подаче на вход комбинации
двоичных сигналов 0101 (5) и 0110 (6), и так
далее.
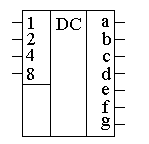
В настоящее время
семисегментные дешифраторы выпускаются
в виде отдельных микросхем или используются
в виде готовых блоков составе других
микросхем. Условно-графическое обозначение
микросхемы семисегментного дешифратора
приведено на рисунке 5.
Рисунок 5
– Условно-графическое обозначение
семисегментного дешифратора.
В качестве примера
семисегментных дешифраторов можно
назвать такие микросхемы отечественного
производства как К176ИД3. В современных
цифровых схемах семисегментные
дешифраторы обычно входят в состав
больших интегральных схем.
Соседние файлы в папке курсовой проект
- #
02.04.2017110.44 Кб27КР_дешифратор_10_принципиальная схема И2Л_01.ms11 (Security copy)
- #
02.04.2017183.85 Кб31КР_дешифратор_11_принципиальная схема И2Л_Х1.ms11
- #
02.04.2017185.38 Кб33КР_дешифратор_11_принципиальная схема И2Л_Х1.ms11 (Security copy)
- #
02.04.2017149.94 Кб32КР_дешифратор_12_делаем красивее.ms11
- #
02.04.201789.99 Кб22КР_дешифратор_12_делаем красивее.ms11 (Security copy)
- #
- #
- #
Лабораторная работа выполняется с помощью учебного лабораторного стенда LESO2.
1 Цель работы
Целью работы является изучение принципов действия комбинационных схем: дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
2 Краткие теоретические сведения
2.1 Дешифратор (декодер)
Дешифратор (декодер) служит для преобразования n-разрядного позиционного двоичного кода в единичный выходной сигнал на одном из 2n выходов. При каждой входной комбинации сигналов на одном из выходов появляется 1. Таким образом, по единичному сигналу на одном из выходов можно судить о входной кодовой комбинации. Таблица истинности для декодера с двумя входами изображена в таблице 2.1.
Таблица 2.1 – Таблица истинности двухразрядного дешифратора
| x1 | x2 | y0 | y1 | y2 | y3 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
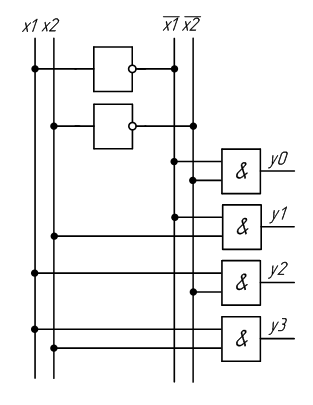
Для построения схемы декодера по таблице истинности воспользуемся методикой, изложенной в лабораторной работе №1, выполняемой на стенде LESO2. Например, устройство должно иметь 4 выхода. Для каждого выхода записываем логическое выражение. На основе СДНФ:
y0 = x1·x2
y1 = x1·x2
y2 = x1·x2
y3 = x1·x2
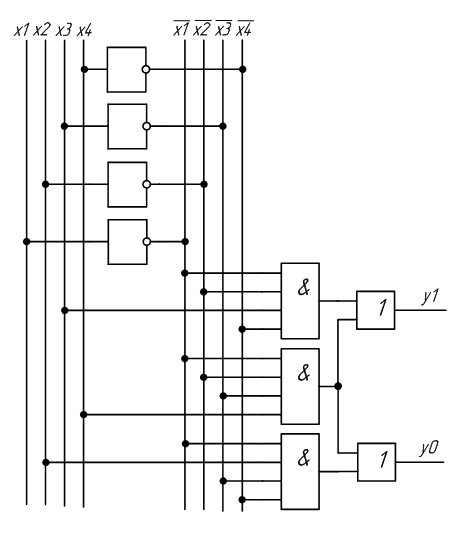
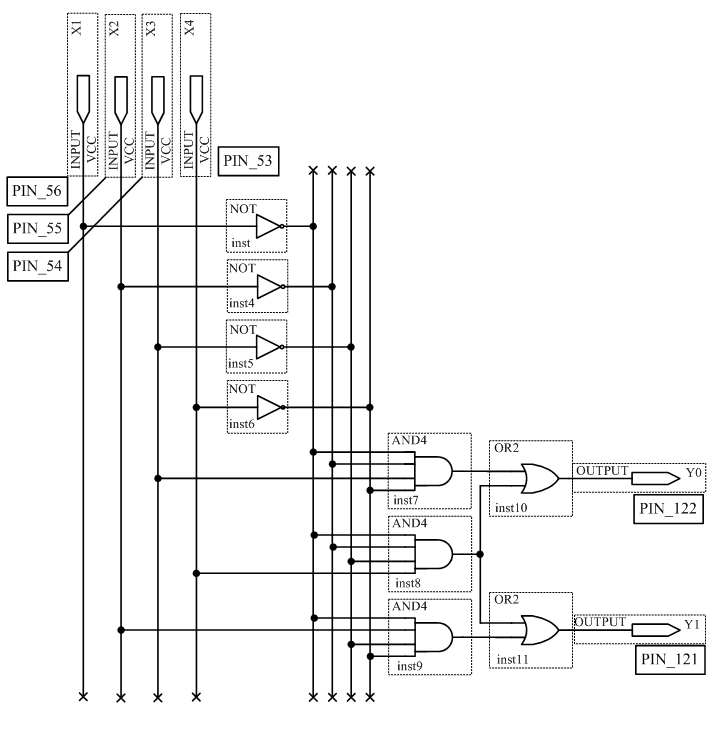
По этой системе выражений несложно построить схему требуемого дешифратора (рисунок 2.1).
Рисунок 2.1 – Схема дешифратора
Условное графическое обозначение такого дешифратора изображено на рисунке 2.2.
Рисунок 2.2 – Условное графическое обозначение дешифратора
2.2 Шифратор (кодер)
Шифратор выполняет функцию, обратную декодеру (дешифратору), то есть преобразует непозиционный (унитарный) двоичный 2n разрядный код в n разрядный позиционный код. При подаче на один из входов единичного сигнала на выходе формируется соответствующий двоичный код. Составим таблицу истинности шифратора при n = 2.
Таблица 2.2 – Таблица истинности шифратора при n = 2
| x1 | x2 | x3 | x4 | y1 | y0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
Синтезируем шифратор. Для этого запишем систему его собственных функций:
y1 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4
y0 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4
Рисунок 2.3 – Схема шифратора
Рисунок 2.4 – Условное графическое обозначение шифратора
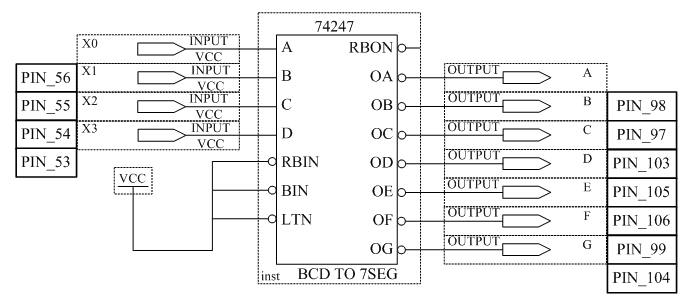
2.3 Преобразователь кода для семисегментного индикатора
Наиболее широко преобразователи кодов известны применительно к цифровым индикаторам. Например, преобразователь 4-х разрядного позиционного двоичного кода в десятичные цифры. Имеется семи сегментный индикатор и с его помощью требуется высветить десять цифр.
Рисунок 2.5 – Семи сегментный индикатор
Очевидно, что двоичный код должен иметь не менее 4 – х разрядов (2^4 = 16, что больше 10). Составим таблицу истинности работы такого преобразователя.
Таблица 2.3 – Таблица истинности преобразователя
| Цифра | Двоичный код 8-4-2-1 | a | б | в | г | д | е | ж | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 7 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
По ТИ несложно составить систему собственных функций для всех выходов, т.е. СДНФ, минимизировать её и составить принципиальную схему.
Рисунок 2.6 – Условное графическое обозначение преобразователя кода
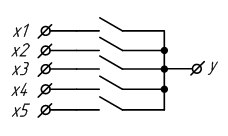
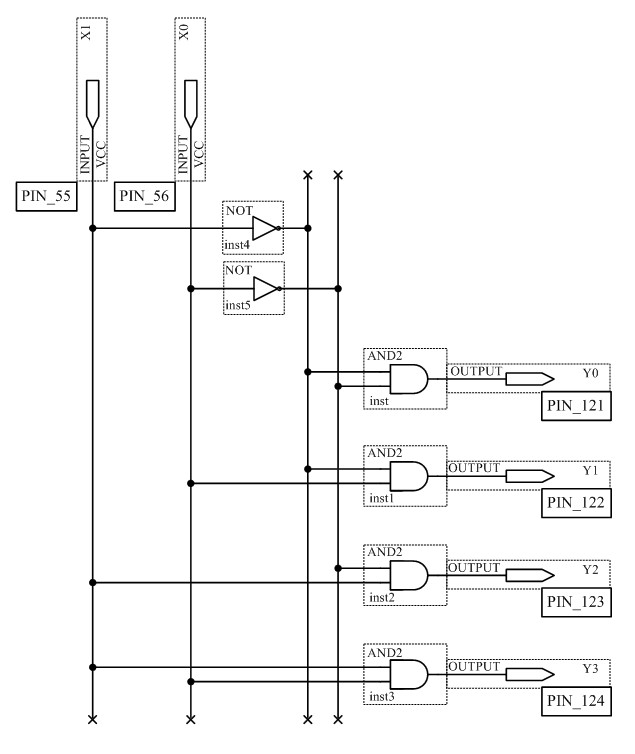
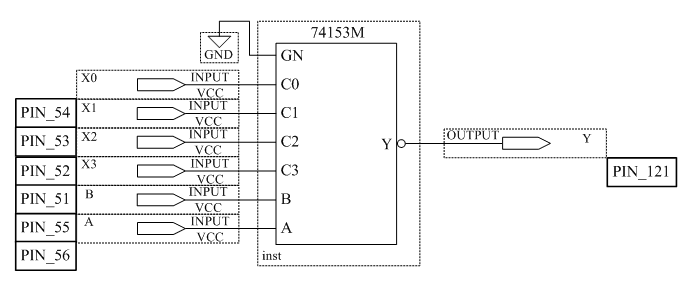
2.4 Мультиплексор
Мультиплексор – устройство, которое позволяет коммутировать один из 2^n информационных входов X на один выход Y под действием n управляющих (адресных) сигналов. На рисунке. 2.7 изображена упрощенная функциональная схема мультиплексора на идеализированных электронных ключах.
Рисунок 2.7 – Схема мультиплексора на идеализированных электронных ключах
В цифровых схемах требуется управлять ключами при помощи логических уровней. Поэтому желательно подобрать устройство, которое могло бы выполнять функции электронного ключа с управлением цифровым сигналом. Попробуем «заставить» работать в качестве электронного ключа уже знакомые нам логические элементы. Рассмотрим ТИ логического элемента «И». При этом один из входов логического элемента «И» будем рассматривать как информационный вход электронного ключа, а другой вход – как управляющий. Так как оба входа логического элемента «И» эквивалентны, то не важно какой из них будет управляющим входом. Пусть вход X будет управляющим, а Y – информационным. Для простоты рассуждений, разделим ТИ на две части в зависимости от уровня логического сигнала на управляющем входе X.
Таблица 2.4 – Таблица истинности
| y | x | Out |
| 0 0 |
0 1 |
0 0 |
| 1 1 |
0 1 |
0 1 |
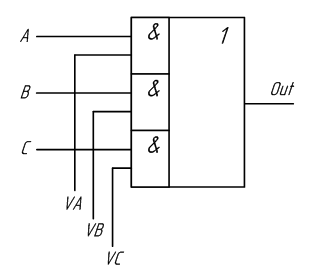
По таблице истинности отчётливо видно, что если на управляющий вход X подан нулевой логический уровень, сигнал, поданный на вход Y, на выход Out не проходит. При подаче на управляющий вход X логической единицы, сигнал, поступающий на вход Y, появляется на выходе Out. Это означает, что логический элемент «И» можно использовать в качестве электронного ключа. При этом не важно, какой из входов элемента “И” будет использоваться в качестве управляющего входа, а какой – в качестве информационного. Остается только объединить выходы элементов «И» на один общий выход. Это делается при помощи логического элемента «ИЛИ» точно так же как и при построении схемы по произвольной таблице истинности. Получившийся вариант схемы коммутатора с управлением логическими уровнями приведён на рисунке 2.8.
Рисунок 2.8 – Принципиальная схема мультиплексора, выполненная на логических элементах
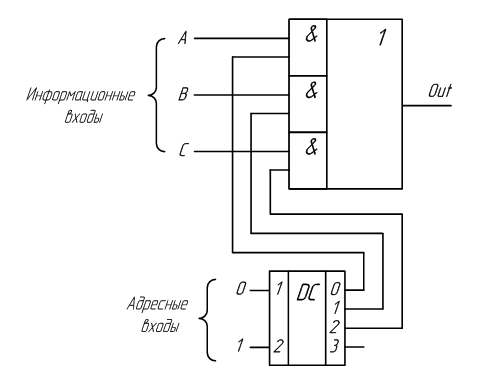
В схемах, приведенных на рисунках 2.7 и 2.8, можно одновременно включать несколько входов на один выход. Однако обычно это приводит к непредсказуемым последствиям. Кроме того, для управления таким коммутатором требуется много входов, поэтому в состав мультиплексора обычно включают двоичный дешифратор, как показано на рисунке 2.9. Такая схема позволяет управлять переключением информационных входов мультиплексора при помощи двоичных кодов, подаваемых на его управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.
Рисунок 2.9 – Принципиальная схема мультиплексора, управляемого двоичным кодом
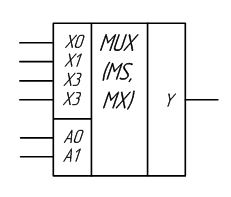
Условное графическое обозначение 4–х входового мультиплексора с управлением двоичным кодом приведено на рисунке 2.10. Входы A0 и A1 являются управляющими входами мультиплексора, определяющими адрес информационного входного сигнала, который будет соединён с выходным выводом мультиплексора Y. Информационные входные сигналы обозначены: X0, X1, X2 и X3.
Рисунок 2.10 – Условное графическое обозначение 4-х входового мультиплексора
В условном графическом обозначении названия информационных входов A, B, C и D заменены названиями X0, X1, X2 и X3, а название выхода Out заменено на название Y. Такое обозначение входов и выходов мультиплексора более распространено в отечественной литературе. Адресные входы обозначены как A0 и A1.
Об особенностях реализации мультиплесоров на языке Verilog можно почитать в статье:
Архитектура ПЛИС. Часть 2. Мультиплексор
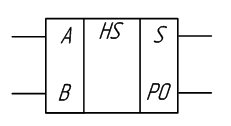
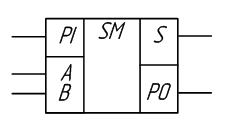
2.5 Сумматор
Сумматор – узел компьютера, предназначенный для сложения двоичных чисел. Построение двоичных сумматоров обычно начинается с сумматора по модулю 2.
Сумматор по модулю 2
Схема сумматора по модулю 2 совпадает со схемой исключающее «ИЛИ».
Таблица 2.5 – Таблица истинности сумматора по модулю 2
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
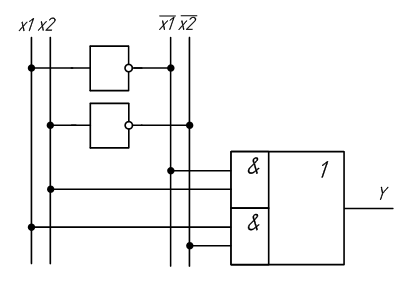
Логическое выражение, описывающее сумматор по модулю 2:
y = x1 · x2 + x1 · x2
Рисунок 2.11 – Условное графическое обозначение сумматора по модулю 2
На основе логического уравнения, описывающего этот элемент можно синтезировать схему:
Рисунок 2.12 – Схема сумматора по модулю 2
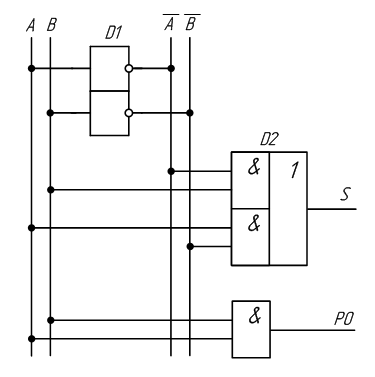
Сумматор по модулю 2 выполняет суммирование без учёта переноса. В обычном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена в таблице 2.6.
Таблица 2.6 – Таблица истинности полусумматора
| A | B | S | P0 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Здесь A и B – слагаемые;
S – сумма;
P0 – перенос в старший разряд (выход переноса Pout).
Запишем систему собственных функций для полусумматора:
S = A · B + A · B
P0 = A · B
Рисунок 2.13 – Принципиальная схема, реализующая таблицу истинности полусумматора
Рисунок 2.14 – Изображение полусумматора на схемах
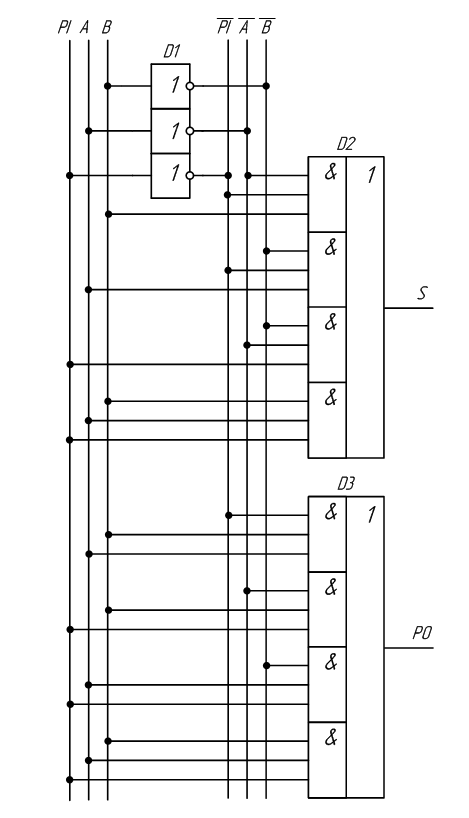
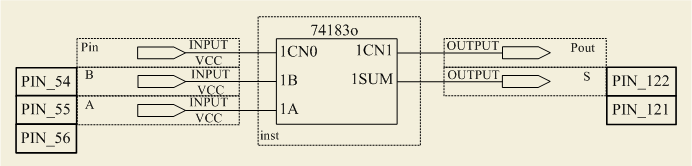
Полный сумматор.
Схема полусумматора формирует перенос в старший разряд, но не может учитывать перенос из младшего разряда. При сложении многоразрядных двоичных чисел необходимо складывать три цифры в каждом разряде – 2 слагаемых и единицу переноса из предыдущего разряда PI.
Таблица 2.7 – Таблица истинности полного сумматора
| PI | A | B | S | PO |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
PI – вход 1 переноса из предыдущего разряда,
PO – выход 1 переноса в старший разряд.
На основании таблицы истинности запишем систему собственных функций для каждого выхода:
S = A · B · PI + A · B · PI + A · B · PI + A · B · PI
PO = A · B · PI + A · B · PI + A · B · PI + A · B · PI
В результате получим схему полного сумматора (рисунок 2.15).
Рисунок 2.15 – Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора
Рисунок 2.16 – Изображение полного двоичного одноразрядного сумматора на схемах
3 Задание к работе
3.1 Исследовать принцип работы дешифратора 2 x 4
Сконфигурировать ПЛИС в соответствии с рисунком 3.1. Подключить к входам X0 и X1 переключатели S7 и S8, а к выходам Y0, Y1, Y2, Y3 светодиодные индикаторы LED5, LED6, LED7, LED8. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС.
Рисунок 3.1 – Схема дешифратора
Подавая все возможные комбинации логических уровней на входы X0, X1 с помощью ключей S7, S8 и наблюдая за состояниями светодиодных индикаторов LED5, LED6, LED7, LED8, заполните таблицу истинности дешифратора.
Таблица 3.1 – Таблица дешифратора
| x1 | x2 | y0 | y1 | y2 | y3 |
| 0 | 0 | ||||
| 0 | 1 | ||||
| 1 | 0 | ||||
| 1 | 1 |
3.2 Исследовать принцип работы шифратора 4×2
Сконфигурировать ПЛИС в соответствии с рисунком 3.2.
Рисунок 3.2 – Схема шифратора 4×2
Подключить к входам X1, X2, X3, X4 переключатели S8, S7, S6, S5, а к выходам Y0, Y1 светодиодные индикаторы LED8, LED7. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС. Подавая все возможные комбинации логических уровней на входы X1, X2, X3, X4 с помощью ключей S8, S7, S6, S5 и наблюдая за состояниями светодиодных индикаторов LED7, LED8, заполните таблицу истинности шифратора.
Таблица 3.2 – Таблица истинности шифратора
| x1 | x2 | x3 | x4 | y1 | y0 |
| 1 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 1 |
3.3 Исследовать работу преобразователя кода для семисегментного индикатора.
Составить таблицу истинности преобразователя кода (таблица. 3.3).
Собрать схему, изображенную на рисунке 3.3.
Таблица 3.3 – Таблица истинности преобразователя
| x3 | x2 | x1 | x0 | A | B | C | D | E | F | G |
| 0 | 0 | 0 | 0 | |||||||
| 0 | 0 | 0 | 1 | |||||||
| 0 | 0 | 1 | 0 | |||||||
| 0 | 0 | 1 | 1 | |||||||
| 0 | 1 | 0 | 0 | |||||||
| 0 | 1 | 0 | 1 | |||||||
| 0 | 1 | 1 | 0 | |||||||
| 0 | 1 | 1 | 1 | |||||||
| 1 | 0 | 0 | 0 | |||||||
| 1 | 0 | 0 | 1 |
Рисунок 3.3 – Схема преобразователя кода для семисегментного индикатора
Подавая с помощью ключей S8, S7, S6, S5 различные кодовые комбинации на входы X0, X1, X2, X3 определить цифры, высвечиваемые на индикаторе. По результатам эксперимента заполнить таблицу 3.4.
Таблица 3.4 – Таблица, описывающая работу преобразователя кода для семисегментного индикатора
| x3 | x2 | x1 | x0 | Показание индикатора |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 |
3.4 Исследовать работу мультиплексора 4×1
Сконфигурировать ПЛИС в соответствии с рисунком 3.4.
Рисунок 3.4 – Схема мультиплексора 4×1
Поочередно устанавливая все возможные кодовые комбинации на адресных входах A и B, определите номера коммутируемых каналов. Номер коммутируемого канала определяется путем поочерёдного подключения к входам X0, X2, X3, X4 уровня логической единицы и наблюдения за выходом Y. Заполните таблицу 3.5.
Таблица 3.5 – Таблица, описывающая работу мультиплексора
| B | A | Номер коммутируемого канала |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
3.5 Исследовать схему сумматора
Сконфигурировать ПЛИС в соответствии с рисунком 3.5. Здесь Pin, Pout соответственно вход и выход единицы переноса, A и B – слагаемые, S – сумма.
Рисунок 3.5 – Схема сумматора
Заполнить таблицу истинности сумматора (таблица 3.6).
Таблица 2.7 – Таблица истинности полного сумматора
| Pin | B | A | Pout |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 |
4 Содержание отчета
- Цель работы.
- Схемы исследования дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
- Таблицы истинности для каждой схемы.
- Выводы по каждому заданию.
5 Контрольные вопросы
- Принцип работы дешифратора?
- Как синтезировать дешифратор с произвольной разрядностью?
- Как работает шифратор?
- Изобразите таблицу истинности шифратора.
- Как работает преобразователь кода для семисегментного индикатора?
- Как устроен семи сегментный индикатор?
- Как работает мультиплексор?
- Как в лабораторной работе проводилось исследование мультиплексора?
- Как работает сумматор?
- Изобразите таблицу истинности шифратора.
- Что такое единица переноса?
Семисегментный индикатор: программирование работы
Перевод двоичного кода десятичного числа в код семисегментного индикатора
Программирование одноразрядного семисегментного индикатора
В первой части статьи о семисегментных светодиодных индикаторах было дано описание индикатора и способов его подключения к микроконтроллеру. Во второй и третьей части мы последовательно пройдем все этапы организации работы микроконтроллера с индикатором и создание программы, результатом которых станет реально работающая конструкция.
Перевод двоичного кода десятичного числа в код семисегментного индикатора
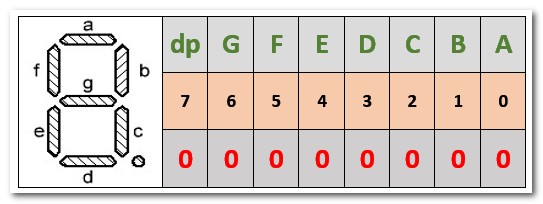
Давайте еще раз посмотрим на схему подключения семисегментного индикатора к микроконтроллеру:
На этой схеме выводы порта PB0…..PB7 подключены к выводам индикатора в определенной последовательности. Выводу PB0 соответствует сегмент “А” и далее соответственно по порядковому номеру вывода порта и по алфавиту выводов индикатора, при этом десятичная точка “dp” подсоединена к выводу порта PB7. Сейчас и далее мы будем рассматривать схемы подключения для индикаторов с общим катодом, а при необходимости я буду вставлять дополнения для индикатора с общим анодом.
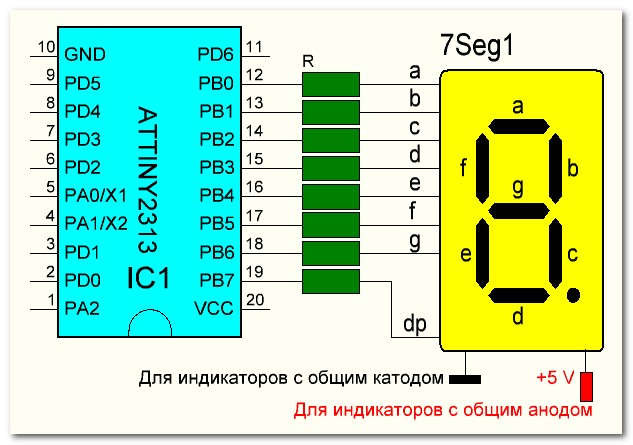
Для того, чтобы высветить определенную цифру на индикаторе, необходимо на соответствующих выводах порта микроконтроллера установить логическую единицу
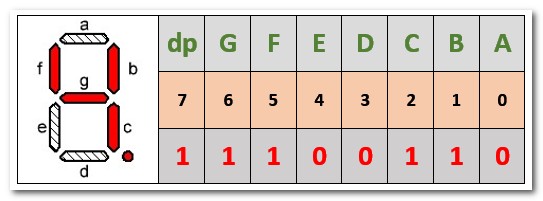
На рисунке выше, черные цифры от 0 до 7 – выводы порта, зеленные латинские буквы – выводы светодиодного индикатора, красные нули – логические уровни на выходах порта (в данном случае логический уровень “0”). Для того, чтобы, к примеру, высветить на индикаторе цифру “4” и зажечь десятичную точку нам необходимо подать логическую 1 на выводы индикатора B, C, F, G и dp, что соответствует подачи логической единицы на выводы порта 1,2,5,6 и 7:
Поэтому, первое что нам необходимо сделать, это определить соответствие каждой десятичной цифре двоичного числа, которое надо выдавать на выход порта микроконтроллера для зажигания соответствующих сегментов индикатора.
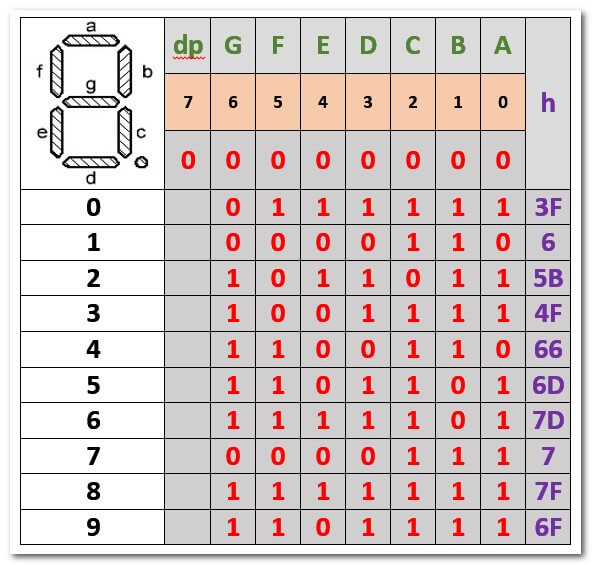
Для “четверки” мы уже определили такую комбинацию = 1110 0110, что соответствует шестнадцатиричному числу 66h, определяем и для остальных цифр:
Операция, которую мы проделали, называется переводом двоичного кода десятичного числа в код семисегментного индикатора.
Данная таблица дана для семисегментных индикаторов с общим катодом (сегмент индикатора зажигается логическим уровнем “1”). Для индикаторов с общим анодом (сегмент индикатора зажигается логическим уровнем “0”) двоичные коды необходимо проинвертировать (поменять 0 на 1, и наоборот) и заново вычислить соответствующие значения в шестнадцатиричной системе.
Программирование одноразрядного семисегментного индикатора
Использование в конструкции одноразрядного индикатора может потребоваться в разных случаях. К примеру, собираем кодовый замок и есть необходимость высвечивать цифру соответствующую нажатой кнопки, или в охранной сигнализации высвечивать номер сработавшего датчика. Так что сфера применения одноразрядных индикаторов приличная.
Организацию вывода цифр на одноразрядный индикатор мы оформим в виде подпрограммы: “Вывод информации на одноразрядный семисегментный светодиодный индикатор”, так, чтобы затем эту подпрограмму с минимальными изменениями можно было использовать в любой программе.
Алгоритм подпрограммы:
1. Инициализация индикатора (подпрограмма)
– настройка порта, к которому подключен индикатор на вывод информации
– запись кодов семисегментного индикатора, соответствующих десятичным цифрам в определенные ячейки памяти
Данная подпрограмма должна вызываться отдельно из основной программы
2. Вход в основную подпрограмму
3. Основная часть
– считываем текущую цифру
– определяем какой код семисегментного индикатора соответствует текущей десятичной цифре
– записываем определенный код индикатора в порт микроконтроллера
4. Выход из подпрограммы
Для оформления программы в виде подпрограммы нам необходимо проделать ряд действий:
1. Присваиваем имя подпрограмме инициализации индикатора – Ini_Indiкator_1 (к примеру)
2. Присваиваем имя основной подпрограмме – Indicator_1
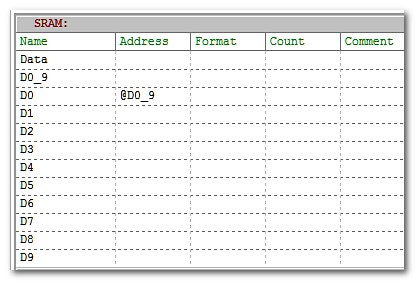
3. Присваиваем имена переменным SRAM в которых будут храниться коды семисегментного индикатора, к примеру:
– D0 (для цифры 0, и так далее), D1, D2, D3, D4, D5, D6, D7, D8, D9
– присваиваем имя переменной в которой будет хранится адрес ячейки памяти (D0) с кодом первой цифры (0) – D0_9
4. Присваиваем имя переменной, в которой будет хранится текущая цифра, которую необходимо вывести на индикатор. В эту переменную основная программа будет записывать вычисленные данные (цифры), которые мы выводим на индикатор – Data (к примеру).
Вот как, к примеру, в Algorithm Builder (остальные примеры тоже для этой программы), объявляются имена переменных в памяти программ (ОЗУ, SRAM):
В графе “Name” перечислены все имена переменных. В графе “Adress” запись “@D0_9” означает, что в переменной D0_9 хранится адрес первой переменной (D0)
Подпрограмма инициализации индикатора (подпрограмма вызывается из основной программы до обращения к подпрограмме вывода информации на индикатор):
А теперь давайте посмотрим основную часть программы и расшифруем ее:
Основная программа записала в назначенную нами переменную Data текущую цифру (для примера – цифра 6) и для вывода ее на индикатор вызвала подпрограмму Indikator_1.
Работа подпрограммы:
– Содержимое переменной Data записывается в рабочий регистр R20, теперь в регистре число 6 (рабочий регистр может быть любой)
– Допустим, первая переменная с кодом цифры 0 у нас находится в ячейки памяти по адресу 100. На самом деле мы не знаем адреса ячеек памяти где хранятся значения D0…D9, но они точно следуют друг за другом. Поэтому была назначена переменная D0_9, в которой, как мы назначили, хранится адрес ячейки памяти D0 (в данный момент адрес =100).
– Следующей командой:
@D0_9 –> Y мы загружаем в двойной регистр Y адрес переменной D0 и получаем, что в регистре Y записалось число – 100.
– Следующей командой:
Y + R20 мы складываем число 100 с числом 6, результат = 106 при этом сохраняется в двойном регистре Y.
– Следующей командой:
[Y] –> R20 мы записываем содержимое ячейки памяти, расположенной по адресу, который записан в двойном регистре Y (106), а по этому адресу у нас расположена ячейка памяти переменной D6. Теперь в рабочем регистре R20 записано число 7Dh – код семисегментного индикатора для вывода цифры 6.
– Следующей командой:
R20 –> PortB мы выводим содержимое R20 в порт PB – высвечиваем цифру 6
– Возвращаемся из подпрограммы
Надеюсь, что материал изложен доступно, если что-то не понятно, спрашивайте.
Предыдущая статья:
Часть 1: Семисегментный светодиодный индикатор: описание, подключение к микроконтроллеру
Следующая статья:
Часть 3: Многоразрядный семисегментный индикатор: организация динамической индикации, алгоритм работы, программа индикации
(16 голосов, оценка: 4,94 из 5)
Загрузка…
Семисегментный индикатор: программирование
Семисегментный индикатор: подключение, программирование, перевод двоичного кода числа в код семисегментного индикатора
Published by: Мир микроконтроллеров
Date Published: 10/02/2015
