Дисперсионный анализ
Назначение сервиса . С помощью сервиса проводится дисперсионный анализ линейной и нелинейной зависимости f(x).
- Шаг №1
- Шаг №2
- Видеоинструкция
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
∑(yi – ycp) 2 = ∑(y(x) – ycp) 2 + ∑(y – y(x)) 2
где
∑(yi – ycp) 2 – общая сумма квадратов отклонений;
∑(y(x) – ycp) 2 – сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
∑(y – y(x)) 2 – остаточная сумма квадратов отклонений.
Таблица дисперсионного анализа
Для модели множественной регрессии существуют две формы записи таблицы дисперсионного анализа: краткая и полная. В краткой форме таблица дисперсионного анализа характеризует уравнение (4.1) в целом (табл. 4.1) и отличается от соответствующей таблицы для парной регрессии (см. табл. 3.1) только степенями свободы сумм квадратов.
Таблица дисперсионного анализа
Полная форма таблицы дисперсионного анализа характеризует не только уравнение целиком, но и каждый регрессор в отдельности. Построение этой таблицы основано на более подробном разложении суммы квадратов [9, 68], которое имеет место при полном отсутствии корреляции между регрессорами (ортогональности регрессоров):
где RSS.-сумма квадратов, обусловленная влиянием независимой переменной (регрессором) X-,j =1,2. к. Вычисление RSSj производится следующим образом:
где RSS(j) — объясненная сумма квадратов соответствующей вспомогательной регрессионной модели. Вспомогательная регрессионная модель отличается от исходной только отсутствием в ней независимой переменной X. и записывается в виде
Другой способ вычисления суммы квадратов, обусловленной воздействием одного регрессора, заключается в использовании остаточных сумм квадратов
где ESS(j) — остаточная сумма квадратов модели (4.27).
С использованием сумм квадратов RSSj можно проверять значимость регрессоров. При этом гипотеза (4.19) уже
Полная таблица дисперсионного анализа
Построить таблицу дисперсионного анализа для оценки значимости уравнения в целом
Постройте таблицу дисперсионного анализа для оценки значимости уравнения регрессии в целом. [c.35]
Составить таблицу дисперсионного анализа для проверки при уровне значимости а = 0,05 статистической значимости уравнения множественной регрессии и его показателя тесноты связи. [c.61]
По данным таблиц дисперсионного анализа, представленным на рис. 2.9 и 2.10, факт =151,65. Вероятность случайно получить [c.76]
Согласно данным таблицы дисперсионного анализа см. рис. 4.21), полученные значения -критерия Фишера и коэффициента детерминации Л2 показывают высокий уровень аппроксимации исходных данных. [c.163]
Оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа (табл. 2.2). [c.53]
Расчет F-критерия можно вести и в таблице дисперсионного анализа результатов регрессии, как это было показано для линейной функции (см. табл. 2.2). [c.85]
Чтобы получить частный. F-критерий для факторах,, необходимо рассмотреть другую таблицу дисперсионного анализа, в которой оценивается дополнительный вклад фактора х, после включения в модель фактора х2 (табл. 3.3). [c.135]
Если уравнение содержит больше двух факторов, то соответствующая программа P дает таблицу дисперсионного анализа, показывая значимость последовательного добавления к уравнению регрессии соответствующего фактора. Так, если рассматривается уравнение [c.136]
Таблица дисперсионного анализа [c.340]
ТАБЛИЦА 10.6. ТАБЛИЦА ДИСПЕРСИОННОГО АНАЛИЗА [c.173]
Таблица дисперсионный анализ [c.615]
| Таблица 7.9 Схема однофакторного дисперсионного анализа |
| Таблица 7.10 Схема двухфакторного дисперсионного анализа |
| Таблица 6.9. Дисперсионный анализ |
Первичный анализ может быть описательным и представлять табличные данные, на основе которых выводят или рассчитывают такие показатели, как средние уровни, стандартные отклонения и частости, либо сравнительным, то есть содержать, например, сопоставительные таблицы. В более сложных случаях используют методы поиска корреляции, например регрессионный анализ. Для установления причинно-следственных соотношений применяют, например, дисперсионный анализ экспериментальных данных. [c.68]
Составьте таблицу результатов дисперсионного анализа. [c.81]
Постройте таблицу результатов дисперсионного анализа. Оцените значимость построенной модели. [c.159]
| Таблица 3.2 Дисперсионный анализ для оценки существенности фактора хг |
Табл. 3.2 отличается от таблиц результатов дисперсионного анализа, рассматриваемых ранее (см., например, табл.3.1). В ней источник вариации регрессия раскладывается на две составляющие 1) обусловленная влиянием фактора j ( 2) обусловленная дополнительным включением в регрессионную модель фактора х2. Соответственно в нашем примере число степеней свободы за счет регрессии, равное 2, также раскладывается на число степеней свободы для каждого фактора, т. е. 1 для фактора х, и 1 для фактора х2. Сумма квадратов за счет регрессии [c.134]
| Таблица 3.3 Дисперсионный анализ для оценки существенности фактора ж, |
| Таблица 5.5. Дисперсионный анализ для ц |
| Таблица 11.2. Дисперсионный анализ на основе аккумуляционного |
| Таблица 14.3. Результаты дисперсионного анализа дисперсионных |
| Таблица 14.4. Результаты дисперсионного анализа для эффектов |
Особое значение информационной статистики заключается в том, что для таблиц с многосторонней группировкой она может быть разложена на аддитивные составляющие, соответствующие различным гипотезам. При этом может быть построена теория, во многом параллельная дисперсионному анализу (см. гл. 13). [c.129]
Методы статистического исследования зависимостей, в особенности регрессионный анализ, анализ временных рядов, дисперсионный анализ, анализ таблиц сопряженности, планирование эксперимента, наиболее употребительны среди методов обработки данных в различных областях науки и техники. Соответственно к настоящему времени существует и продолжает разрабатываться обширное программное обеспечение, связанное с исследованием зависимостей. Ниже кратко рассмотрены программные средства — пакеты и библиотеки программ, доступные пользователям в СССР, а также наиболее интересные, на наш взгляд, для обеспечения статистического исследования зависимостей зарубежные пакеты и библиотеки. Основные сведения о пакетах и библиотеках программ приведены в табл. 15.1. [c.425]
В факторных планах используются методы дисперсионного анализа. Эти планы позволяют измерять влияние взаимодействий, но методика в достаточной мере сложна. Она заключается в построении таблицы, содержащей всевозможные комбинации различных факторов. Например, для четырех факторов, каждый из которых может находиться на 3, 2, 5 и 3 уровнях, соответственно существует 3X2, [c.192]
| Таблица 3 Дисперсионный анализ для одного фактора с / наблюдениями в ячейке |
В VI.9 мы рассмотрим несколько методов отыскания важных факторов, т. е. таких факторов, которые приводят к потере работоспособности ММР. Показано, что первый метод, который использует таблицы сопряженности признаков, неприемлем. Второй метод заключается в применении биномиального критерия вероятности того, что в отброшенных комбинациях фактор, имеющий один и тот же уровень, тем не менее не важен. Показано, что эти критерии, однако, имеют малую мощность. Третий метод—это регрессионный анализ. Будут исследованы обычные предпосылки регрессионного и дисперсионного анализа и будет показано, почему простой метод наименьших квадратов предпочтительнее обобщенного метода. Мы оценим коэффициенты регрессии или эффекты , проверим адекватность уравнения регрессии (если Р 0,90, будет провозглашена адекватность), значимость отличия коэффициентов регрессии от нуля (фактор 1 даст нулевой эффект, фактор 5, может быть, тоже имеет нулевой эффект). [c.270]
Верхняя строка корректированный / -квадрат = 0,872390 вторая строка / -квадрат = 0,897912 третья строка множественный R = 0,947582. Затем приводится таблица дисперсионного анализа, в которой указываются источники вариации объясненная сумма квадратов отклонений значений, рассчитанных по уравнению регрессии, от среднего значения DlfnM il = Z(p/ – у)2 = 662 772,98 при числе степеней свободы, равном числу объясняющих переменных dfk = 3 остаточная – отклонения фактических значений от расчетных Dwm Z(y/ – у)2 = 75353,96 при числе степеней свободы, равном df=n-k-, df= 2 общая – ZO/ – У = 738 126,94, при числе степеней свободы df = п – 1, df = 15. Затем приводится средний квадрат отклонений s = Д , с//)6ы, , = 662772,98 3 = 220924,3 s г = D,Km dfwm, = 75353,96 12 = 6279,5. Далее указано их отношение, т. е. 5, /г2 = F-критерию. Наконец, указывается вероятность ошибочного решения, т. е. нулевого / 2, равная 0,000003171. [c.277]
Припишем численные значения оценкам vl — хорошо, v2 — удовлетворительно, v3 — неудовлетворительно. Тогда набранные лабораториями оценки можно представить в виде односторонней таблицы дисперсионного анализа (см. гл. 13), в которой СКП — полная сумма квадратов отклонений, СКМ — сумма квадратов отклонений между лабораториями и СКВИ — сумма квадратов отклонений внутри лабораторий (табл. 3.3) [c.133]
Вопрос 4. При проведении эксперимента, используя сырье, поставленное тремя фирмами A , AZ, А8, измерили предел прочности при растяжении в условиях Bj, когда предварительная обработка не проводилась, в условиях Ва, когда предварительная обработка проводилась, и с применением соответствующих способов работы GI, Са. При этом 12 раз рандомизированно осуществлялись испытания. В результате были получены значения, приведенные в таблице. Проведите дисперсионный анализ. [c.189]
Проверка значимости регрессии с помощью дисперсионного анализа (F-тест)
history 26 января 2019 г.
-
Группы статей
- Статистический анализ
Проведем проверку значимости простой линейной регрессии с помощью процедуры F -тест.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Проверку значимости взаимосвязи переменных в рамках модели простой линейной регрессии можно провести разными, но эквивалентными между собой, способами:
Проверку значимости взаимосвязи переменных в рамках модели простой линейной регрессии можно провести разными, но эквивалентными между собой, способами:
Процедуру F -теста рассмотрим на примере простой линейной регрессии , когда прогнозируемая переменная Y зависит только от одной переменной Х.
Чтобы определить может ли предложенная модель линейной регрессии быть использована для адекватного описания значений переменной Y, дисперсию наблюдаемых данных анализируют методом Дисперсионного анализа (ANOVA for Simple Regression) . Дисперсия данных разбивается на компоненты, которые затем используются в F -тесте для определения значимости регрессии.
F -тест для проверки значимости регрессии НЕ относится к простым и интуитивно понятным процедурам. Вероятно, это связано с тем, что для проведения F -теста требуется быть знакомым с определенным количеством статистических понятий и нужно неплохо разбираться в связанных с ними статистических методах. Нам потребуются понятия из следующих разделов статистики:
Можно, конечно, рассмотреть F -тест формально:
- вычислить на основании выборки значение тестовойFстатистики;
- сравнить полученное значение со значением, соответствующему заданному уровню значимости ;
- в зависимости от соотношения этих величин принять решение о значимости вычисленной линейной регрессии
В этой статье ставится более амбициозная задача – разобраться в самом подходе, на котором основан F -тест . Сначала введем несколько определений, которые используются в процедуре F -теста , затем рассмотрим саму процедуру.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части .
Определения, необходимые для F -теста
Согласно определению дисперсии , дисперсия выборки прогнозируемой переменной Y определяется формулой:
В формуле используется ряд сокращений:
- SST (Total Sum of Squares) – это просто компактное обозначение Суммы Квадратов отклонений от среднего (такое сокращение часто используется в зарубежной литературе).
- MST (Total Mean Square) – Среднее Суммы Квадратов отклонений (еще одно общеупотребительное сокращение).
Примечание : Необходимо иметь в виду, что с одной стороны величины MST и SST являются случайными величинами, вычисленными на основании выборки, т.е. статистиками . Однако с другой стороны, при проведении регрессионного анализа по данным имеющейся выборки вычисляются их конкретные значения. В этом случае величины MST и SST являются просто числами.
Значение n-1 в вышеуказанной формуле равно числу степеней свободы ( DF ) , которое относится к дисперсии выборки (одна степень свободы у n величин yi потеряна в результате наличия ограничения , связывающего все значения выборки). Число степеней свободы у величины SST также имеет специальное обозначение: DFT (DF Total).
Как видно из формулы, отношение величин SST и DFT обозначается как MST. Эти 3 величины обычно выдаются в таблице результатов дисперсионного анализа в различных прикладных статистических программах (в том числе и в надстройке Пакет анализа, инструмент Регрессия ).
Значение SST, характеризующую общую изменчивость переменной Y, можно разбить на 2 компоненты:
- Изменчивость объясненную моделью (Explained variation), обозначается SSR
- Необъясненную изменчивость (Unexplained variation), обозначается SSЕ
Известно , что справедливо равенство:
Величинам SSR и SSE также сопоставлены степени свободы . У SSR одна степень свободы , т.к. она однозначно определяется одним параметром – наклоном линии регрессии a (напомним, что мы рассматриваем простую линейную регрессию ). Это очевидно из формулы:
Примечание: Очевидность наличия только одной степени свободы проистекает из факта, что переменная Х – контролируемая (не является случайной величиной).
Число степеней свободы величины SSR имеет специальное обозначение: DFR (для простой регрессии DFR=1, т.к. число независимых переменных Х равно 1) . По аналогии с MST, отношение этих величин также часто обозначают MSR = SSR / DFR .
У SSE число степеней свободы равно n -2 , которое обозначается как DFE (или DFRES – residual degrees of freedom). Двойка вычитается, т.к. изменчивость переменной yi имеет 2 ограничения, связанные с оценкой 2-х параметров линейной модели ( а и b ): ŷi=a*xi+b
Отношение этих величин также часто обозначают MSE = SSE / DFE .
MSR и MSE имеют размерность дисперсий, хотя корректней их называть средними значениями квадратов отклонений. Тем не менее, ниже мы их будем «дисперсиями», т.к. они отображают меру разброса: MSE – меру разброса точек наблюдений относительно линии регрессии, MSR показывает насколько линия регрессии совпадает с горизонтальной линией среднего значения Y.
Примечание : Напомним, что MSE (Mean Square of Errors) является оценкой дисперсии s 2 ошибки, подробнее см. статью про линейную регрессию , раздел Стандартная ошибка регрессии .
Число степеней свободы обладает свойством аддитивности: DFT = DFR + DFE . В этом можно убедиться, составив соответствующее равенство n -1=1+( n -2)
Наконец, определившись с определениями, переходим к рассмотрению самой процедуры F -тест .
Процедура F -теста
Сущность F -теста при проверке значимости регрессии заключается в том, чтобы сравнить 2 дисперсии : объясненную моделью (MSR) и необъясненную (MSE). Если эти дисперсии «примерно равны», то регрессия незначима (построенная модель не позволяет объяснить поведение прогнозируемой Y в зависимости от значений переменной Х). Если дисперсия, объясненная моделью (MSR) «существенно больше», чем необъясненная, то регрессия значимая .
Примечание : Чтобы быстрее разобраться с процедурой F -теста рекомендуется вспомнить процедуру проверки статистических гипотез о равенстве дисперсий 2-х нормальных распределений (т.е. двухвыборочный F-тест для дисперсий ).
Чтобы пояснить вышесказанное изобразим на диаграммах рассеяния 2 случая:
- регрессия значима (в этом случае имеем значительный наклон прямой) и
- регрессия незначима (линия регрессии близка к горизонтальной прямой).
На первой диаграмме показан случай, когда регрессия значима:
- Зеленым цветом выделены расстояния от среднего значения до линии регрессии , вычисленные для каждого хi. Сумма квадратов этих расстояний равна SSR;
- Красным цветом выделены расстояния от линии регрессии до соответствующих точек наблюдений . Сумма квадратов этих расстояний равна SSЕ.
Из диаграммы видно, что в случае значимой регрессии, сумма квадратов «зеленых» расстояний, гораздо больше суммы квадратов «красных». Понятно, что их отношение будет гораздо больше 1. Следовательно, и отношение дисперсий MSR и MSE будет гораздо больше 1 (не забываем, что SSE нужно разделить еще на соответствующее количество степеней свободы n-2).
В случае значимой регрессии точки наблюдений будут находиться вдоль линии регрессии. Их разброс вокруг этой линии описываются ошибками регрессии, которые были минимизированы посредством процедуры МНК . Очевидно, что разброс точек относительно линии регрессии значительно меньше, чем относительно горизонтальной линии, соответствующей среднему значению Y.
Совершенно другую картину мы можем наблюдать в случае незначимой регрессии.
Очевидно, что в этом случае, сумма квадратов «зеленых» расстояний, примерно соответствует сумме квадратов «красных». Это означает, что объясненная дисперсия примерно соответствует величине необъясненной дисперсии (MSR/MSE будет близко к 1).
Если ответ о значимости регрессии практически очевиден для 2-х вышеуказанных крайних ситуаций, то как сделать правильное заключение для промежуточных углов наклона линии регрессии?
Понятно, что если вычисленное на основании выборки значение MSR/MSE будет существенно больше некоторого критического значения, то регрессия значима, если нет, то не значима. Очевидно, что это значение должно быть больше 1, но как определить это критическое значение статистически обоснованным методом ?
Вспомним, что для формулирования статистического вывода (т.е. значима регрессия или нет) используют проверку гипотез . Для этого формулируют 2 гипотезы: нулевую Н 0 и альтернативную Н 1 . Для проверки значимости регрессии в качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. наклон прямой a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
Примечание : Даже если связи между переменными нет (a=0), то вычисленная на основании данных выборки оценка наклона – величина а , из-за случайности выборки будет близка, но все же отлична от 0.
По умолчанию принимается, что нулевая гипотеза верна – связи между переменными нет. Если это так, то:
- MSR/MSE будет близко к 1;
- Случайная величина F = MSR/MSE будет иметь F-распределениесо степенями свободы 1 (в числителе) и n-2 (знаменателе). F является тестовой статистикой для проверки значимости регрессии.
Примечание : MSR и MSE являются случайными величинами (т.к. они получены на основе случайной выборки). Соответственно, выражение F=MSR/MSE, также является случайной величиной, которая имеет свое распределение, среднее значение и дисперсию .
Ниже приведен график плотности вероятности F-распределения со степенями свободы 1 (в числителе) и 59 (знаменателе). 59=61-2, 61 наблюдение минус 2 степени свободы.
Если нулевая гипотеза верна, то значение F 0 =MSR/MSE, вычисленное на основании выборки, должно быть около ее среднего значения (т.е. около 1,04). Если F 0 будет существенно больше 1 (чем больше F0 отклоняется в сторону больших значений, тем это маловероятней), то это будет означать, что F не имеет F-распределение , а, следовательно, нулевую гипотезу нужно отклонить и принять альтернативную, утверждающую, что связь между переменными есть (значима).
Обычно предполагают, что если вероятность, того что F -статистика приняла значение F0 составляет менее 5%, то это событие маловероятно и нулевую гипотезу необходимо отклонить. 5% – это заданный исследователем уровень значимости , который может быть, например, 1% или 10%.
Значение статистики F0 может быть вычислено на основании выборки:
Вычисления в MS EXCEL
В MS EXCEL критическое значение для заданного уровня значимости F1-альфа, 1, n-2 можно вычислить по формуле = F.ОБР(1- альфа;1; n-2) или = F.ОБР.ПХ(альфа;1; n-2) . Другими словами требуется вычислить верхний альфа-квантиль F-распределения с соответствующими степенями свободы .
Таким образом, при значении статистики F0> F1-альфа, 1, n-2 мы имеем основание для отклонения нулевой гипотезы.
Значение F 0 можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции ЛИНЕЙН() :
В случае простой регрессии значение F0 также равно квадрату t-статистики, которую мы использовали при проверке двусторонней гипотезе о равенстве 0 коэффициента регрессии .
Проверку значимости регрессии можно также осуществить через вычисление p-значения. В этом случае вычисляют вероятность того, что случайная величина F примет значение F0 (это и есть p-значение), затем сравнивают p-значение с заданным уровнем значимости . Если p-значение больше уровня значимости, то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
В MS EXCEL для проверки гипотезы используя p -значение используйте формулу = F.РАСП.ПХ(F0;1;n-2) файл примера , где показано эквивалентность всех подходов проверки значимости регрессии).
В программах статистики результаты процедуры F -теста выводят с помощью стандартной таблицы дисперсионного анализа . В файле примера такая таблица приведена на листе Таблица, которая построена на основе результатов, возвращаемых инструментом Регрессия надстройки Пакета анализа MS EXCEL .
[spoiler title=”источники:”]
http://studme.org/179660/matematika_himiya_fizik/tablitsa_dispersionnogo_analiza
http://economy-ru.info/info/15309/
http://excel2.ru/articles/proverka-znachimosti-regressii-s-pomoshchyu-dispersionnogo-analiza-f-test
[/spoiler]
Однофакторный дисперсионный анализ используется для определения того, существует ли статистически значимое различие между средними значениями трех или более независимых групп.
Этот тип теста называется односторонним дисперсионным анализом, потому что мы анализируем, как одна предикторная переменная влияет на переменную отклика.
Если бы вместо этого нас интересовало, как две переменные-предикторы влияют на переменную отклика, мы могли бы провести двусторонний дисперсионный анализ .
В этом учебном пособии объясняется, как провести однофакторный дисперсионный анализ в SPSS.
Пример. Однофакторный дисперсионный анализ в SPSS
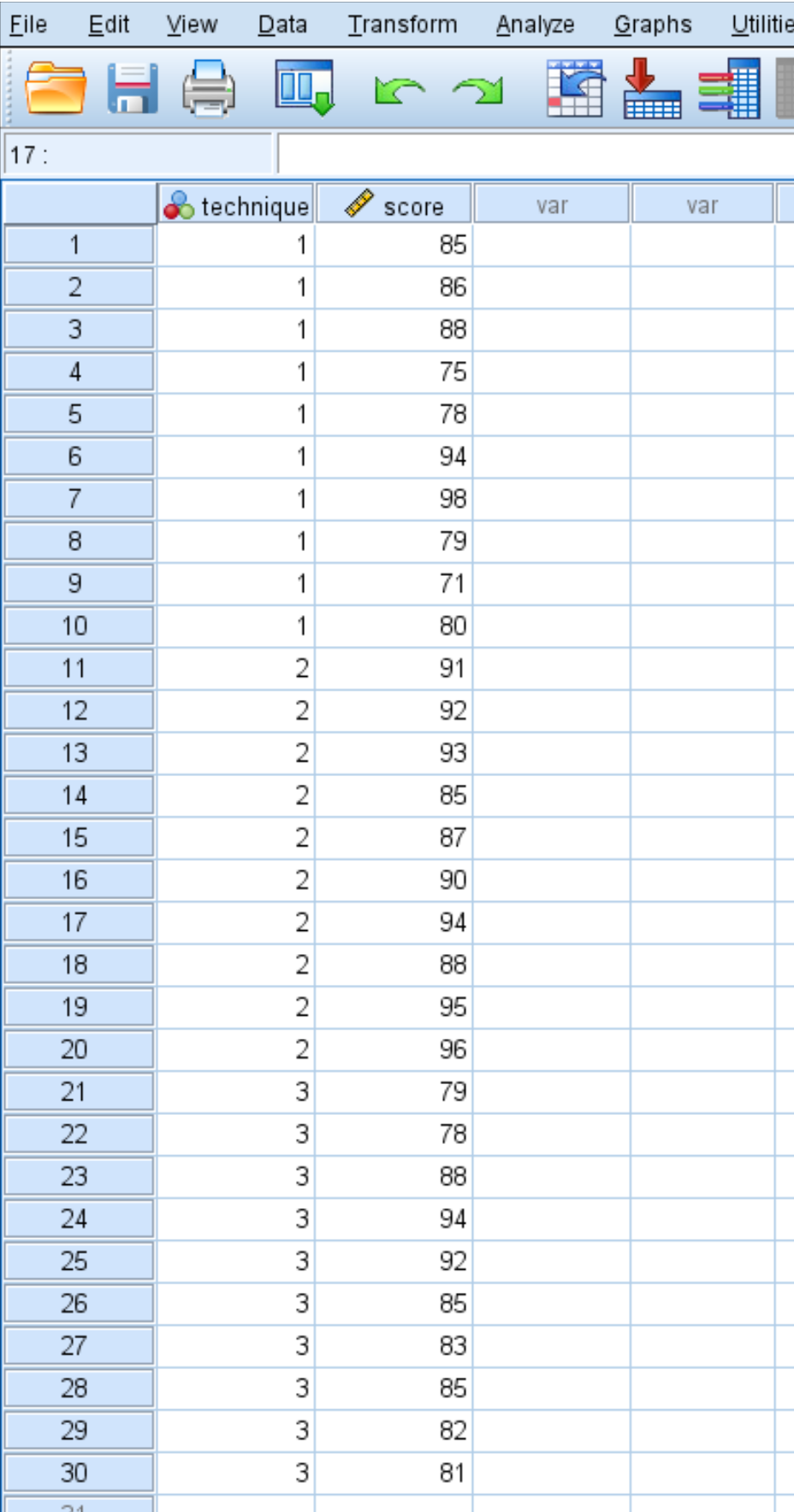
Предположим, исследователь набирает 30 студентов для участия в исследовании. Студентам случайным образом назначают использовать один из трех методов обучения в течение следующего месяца для подготовки к экзамену. В конце месяца все студенты сдают одинаковый тест.
Ниже представлены результаты тестов учащихся:
Используйте следующие шаги, чтобы выполнить однофакторный дисперсионный анализ, чтобы определить, одинаковы ли средние баллы для всех трех групп.
Шаг 1: Визуализируйте данные.
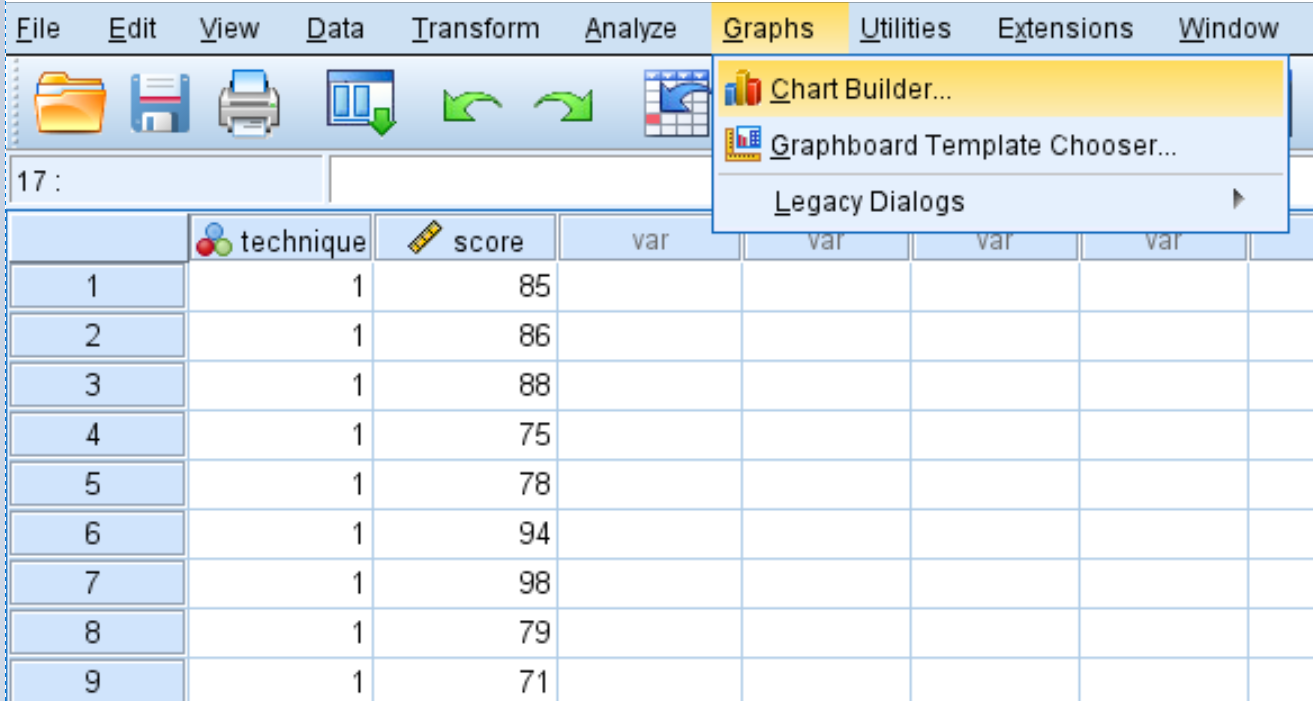
Во-первых, мы создадим диаграммы , чтобы визуализировать распределение результатов тестов для каждого из трех методов обучения. Перейдите на вкладку « Графики », затем щелкните « Построитель диаграмм ».
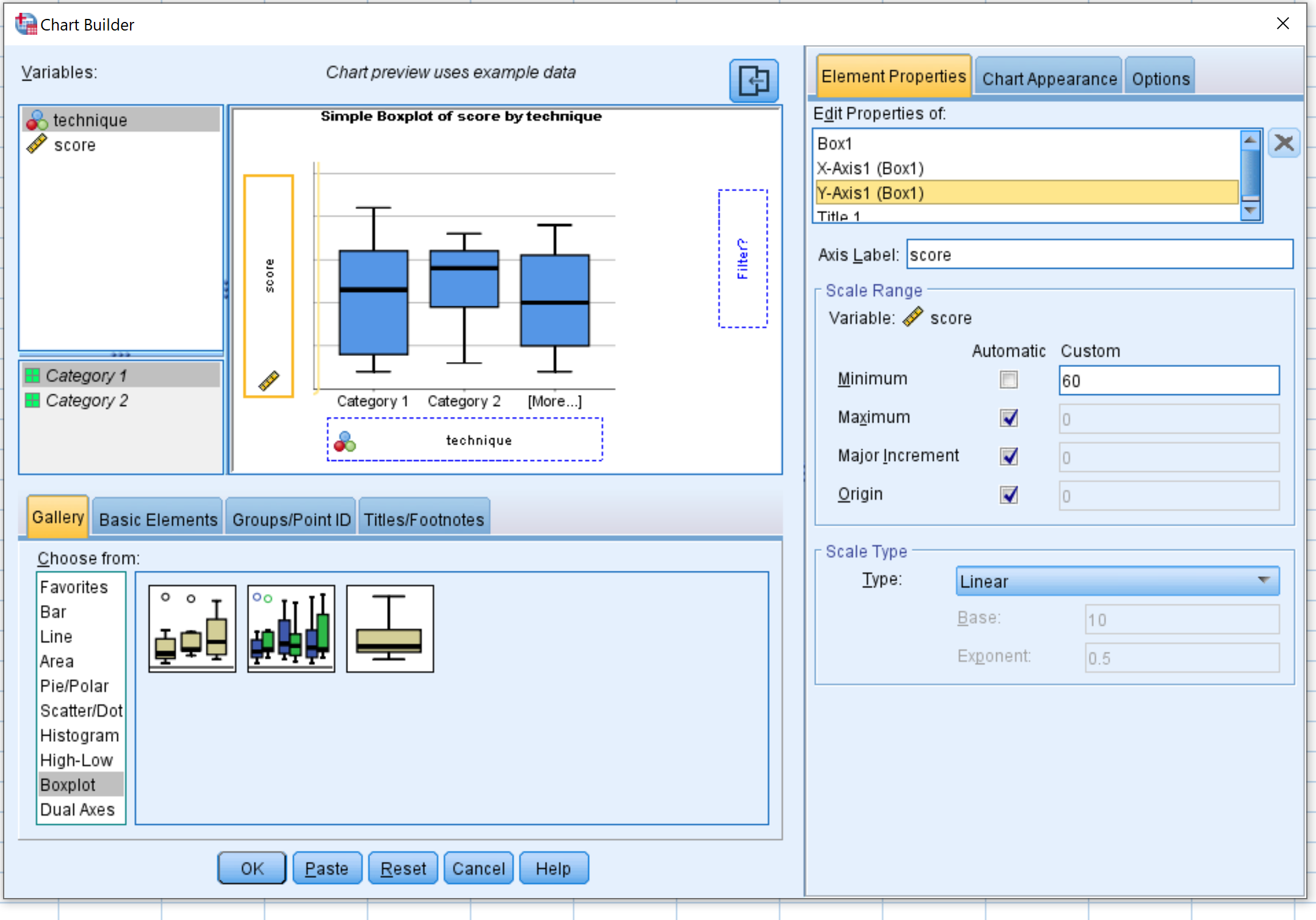
Выберите Boxplot в окне Choose from:. Затем перетащите первую диаграмму с названием Simple boxplot в главное окно редактирования. Перетащите вариативную технику на ось X, а оценку — на ось Y.
Затем нажмите « Свойства элемента» , затем «Ось Y1».Измените минимальное значение на 60. Затем нажмите OK .
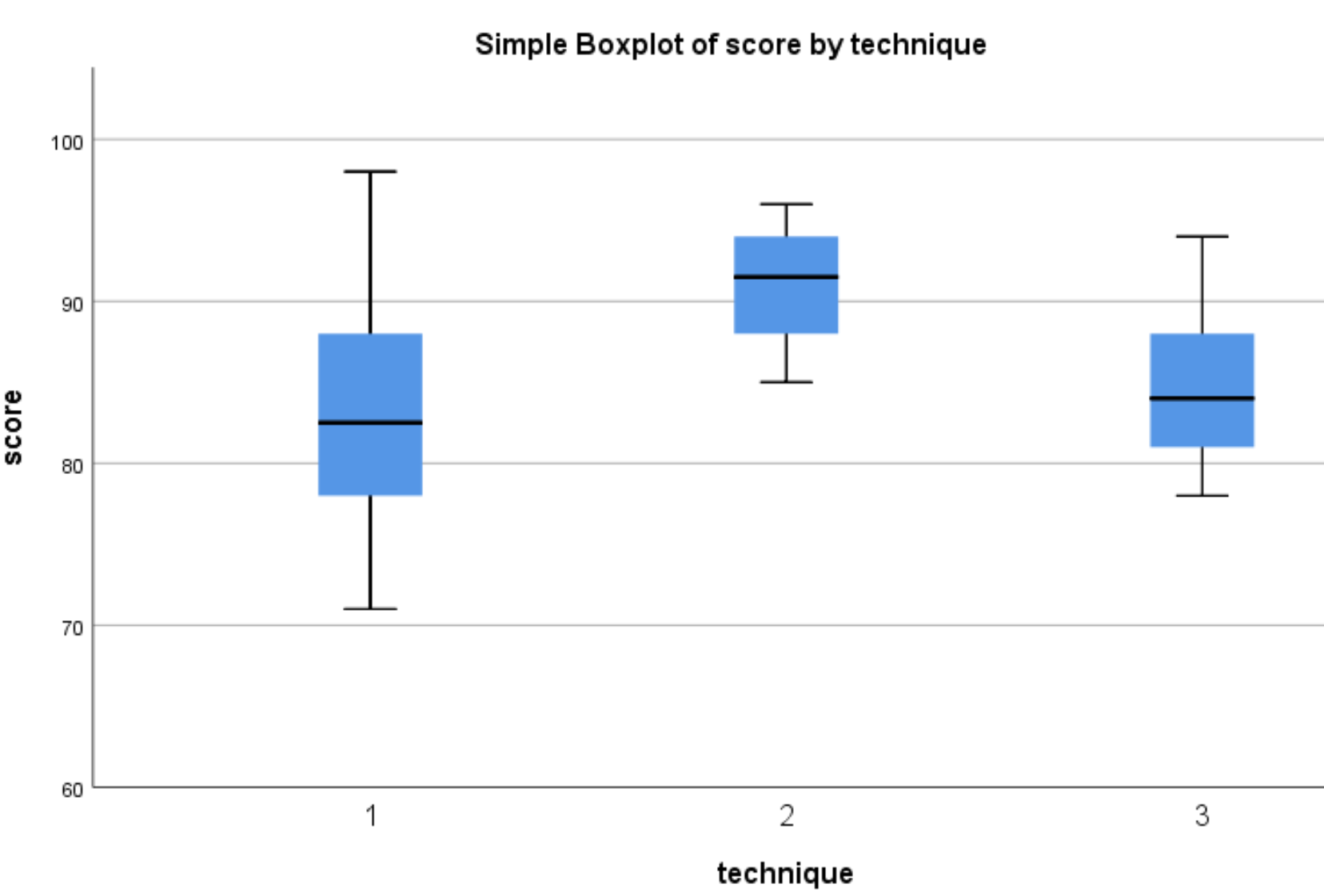
Появятся следующие диаграммы:
Мы можем видеть, что распределение результатов тестов, как правило, выше для учащихся, которые использовали метод 2, по сравнению со студентами, которые использовали методы 1 и 3. Чтобы определить, являются ли эти различия в баллах статистически значимыми, мы выполним однофакторный дисперсионный анализ.
Шаг 2: Выполните односторонний ANOVA.
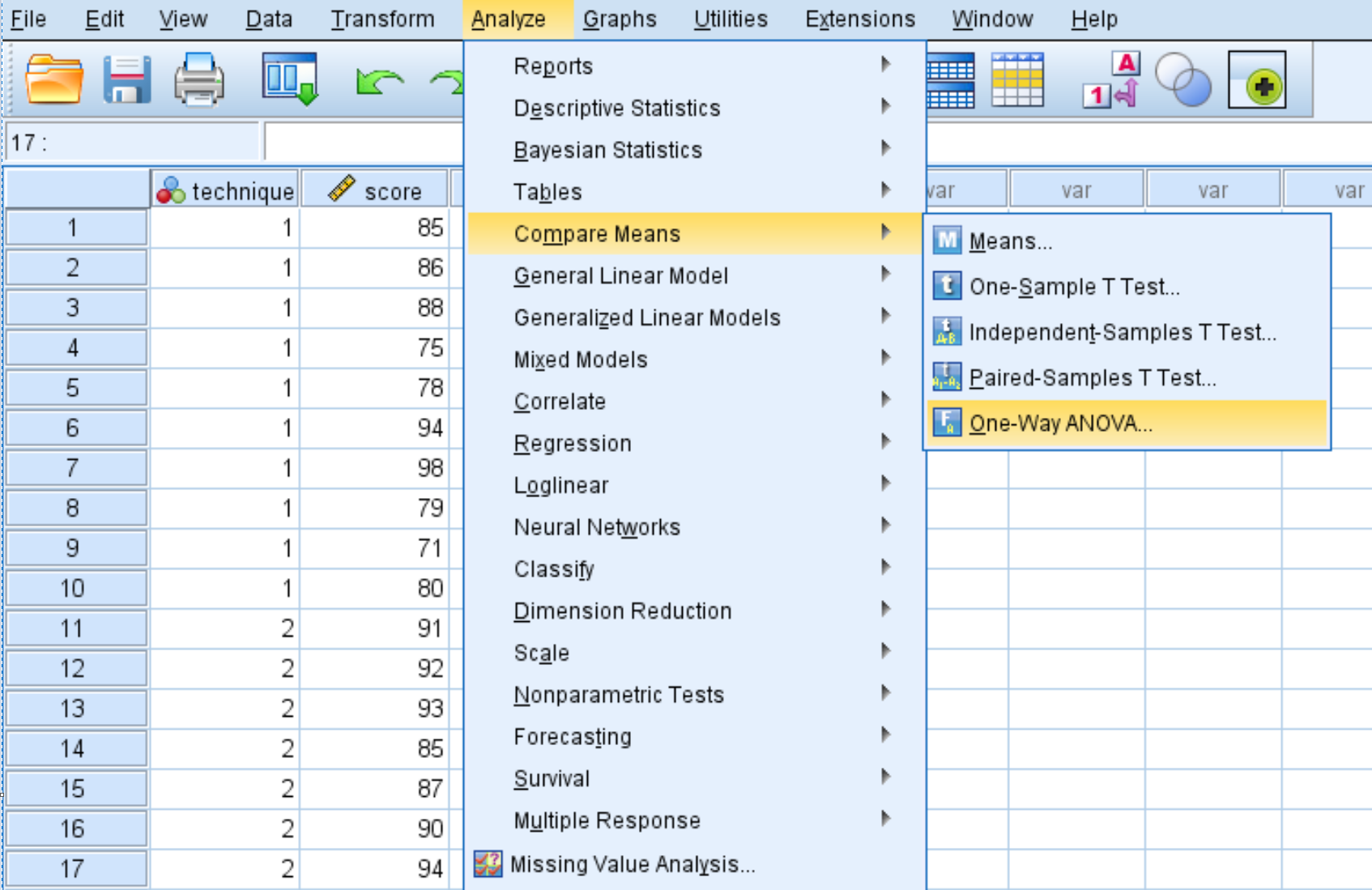
Перейдите на вкладку « Анализ », затем « Сравнить средние » и «Однофакторный дисперсионный анализ ».
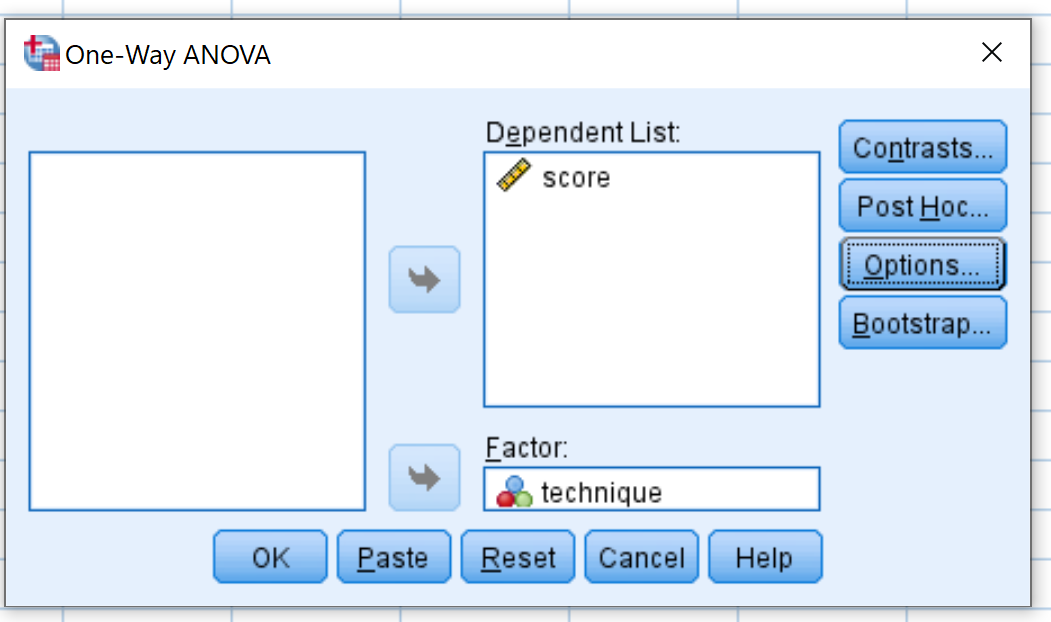
В новом всплывающем окне поместите переменную оценку в поле с надписью Зависимый список, а переменную технику — в поле с надписью Фактор.
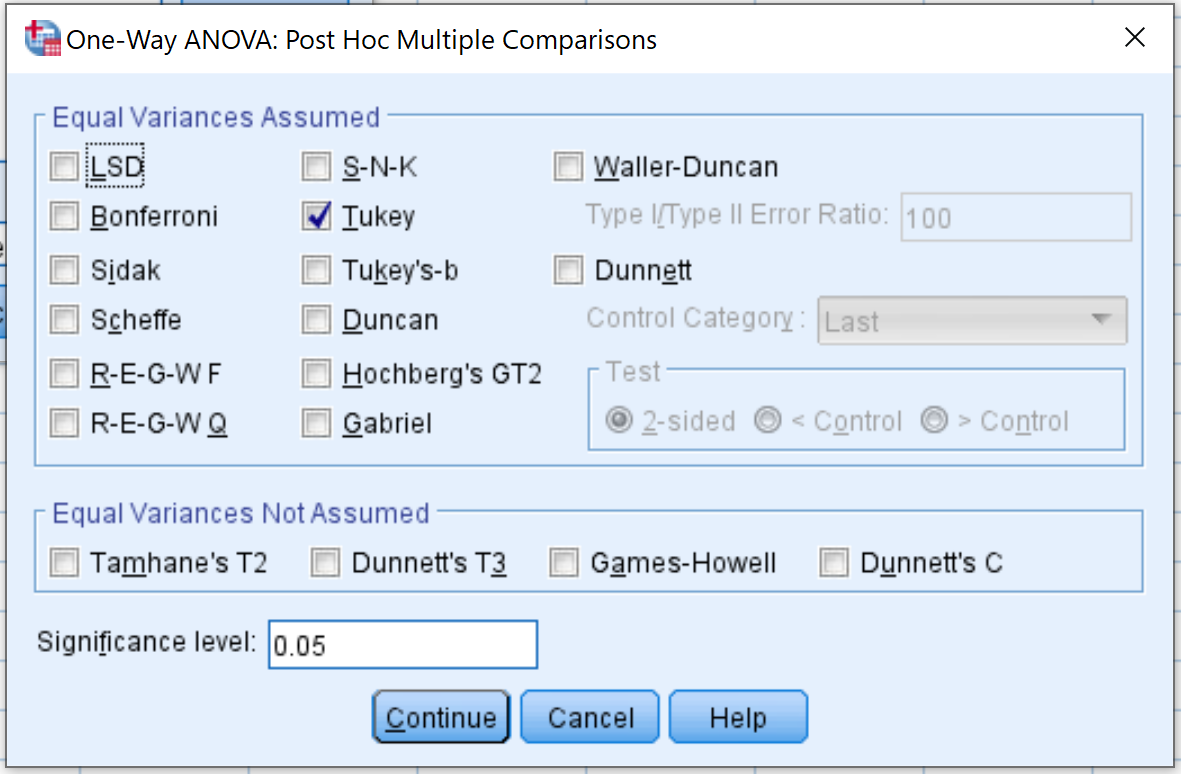
Затем щелкните Post Hoc и установите флажок рядом с Tukey.Затем нажмите «Продолжить» .
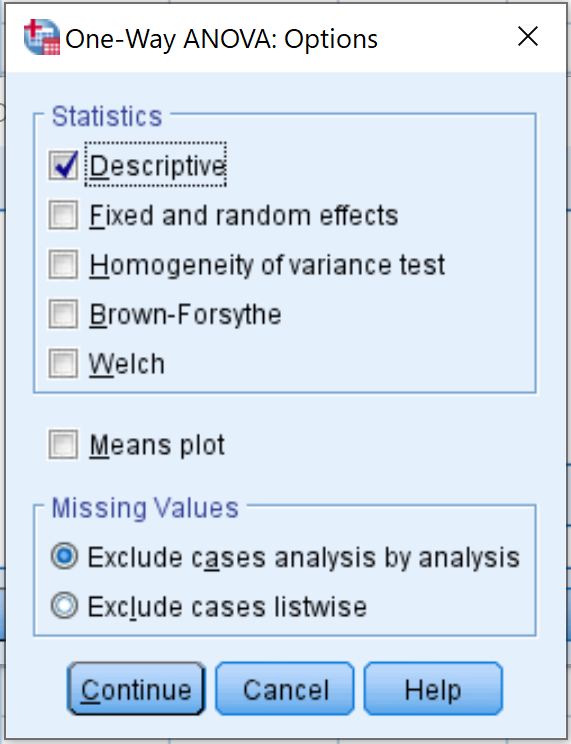
Затем нажмите « Параметры » и установите флажок « Описательный ». Затем нажмите «Продолжить» .
Наконец, нажмите ОК .
Шаг 3: Интерпретируйте вывод.
Как только вы нажмете OK , появятся результаты однофакторного дисперсионного анализа. Вот как интерпретировать вывод:
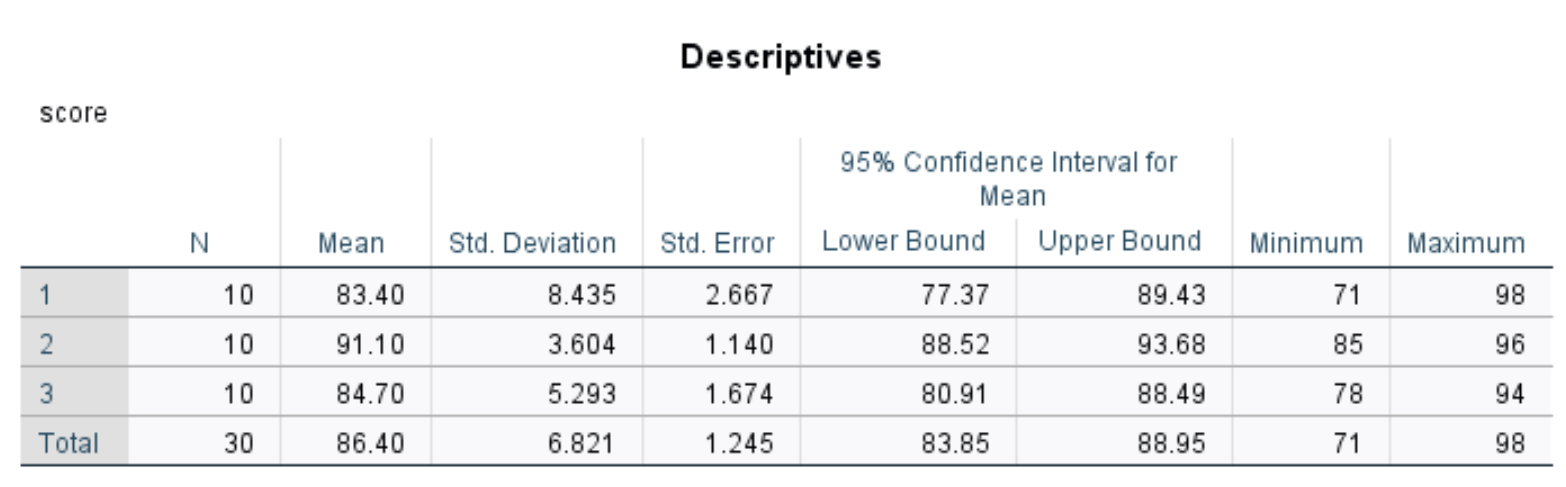
Описательная таблица
Эта таблица отображает описательную статистику для каждой из трех групп в нашем наборе данных.
Наиболее актуальные цифры включают в себя:
- N: количество студентов в каждой группе.
- Среднее значение: средний балл теста для каждой группы.
- стандарт Отклонение: стандартное отклонение результатов теста для каждой группы.
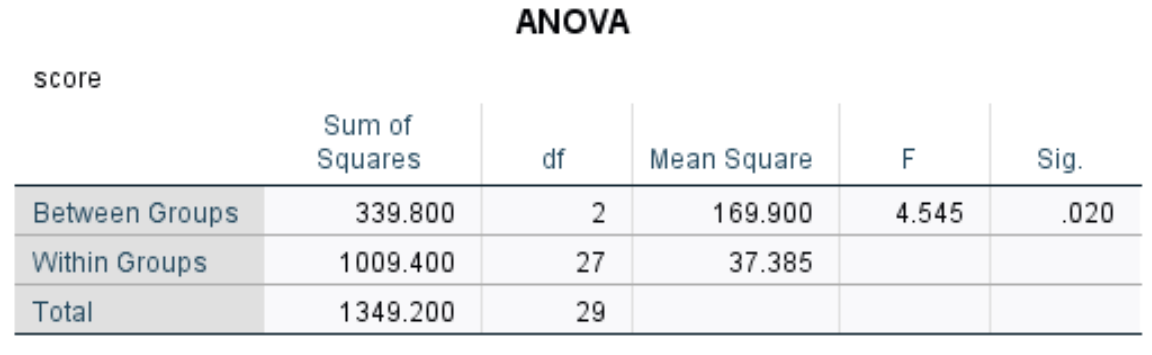
Таблица дисперсионного анализа
В этой таблице показаны результаты однофакторного дисперсионного анализа:
Наиболее актуальные цифры включают в себя:
- F: Общая F-статистика.
- Sig: значение p, соответствующее F-статистике (4,545) с числителем df (2) и знаменателем df (27). В этом случае p-значение оказывается равным 0,020 .
Напомним, что однофакторный дисперсионный анализ использует следующие нулевую и альтернативную гипотезы:
- H 0 (нулевая гипотеза): µ 1 = µ 2 = µ 3 = … = µ k (все средние значения совокупности равны)
- H A (альтернативная гипотеза): по крайней мере одно среднее значение по совокупности отличаетсяот остальных
Поскольку p-значение из таблицы ANOVA меньше 0,05, у нас есть достаточно доказательств, чтобы отклонить нулевую гипотезу и сделать вывод, что по крайней мере одно из средних значений группы отличается от остальных.
Чтобы узнать, какие именно групповые средние отличаются друг от друга, мы можем обратиться к последней таблице в выходных данных ANOVA.
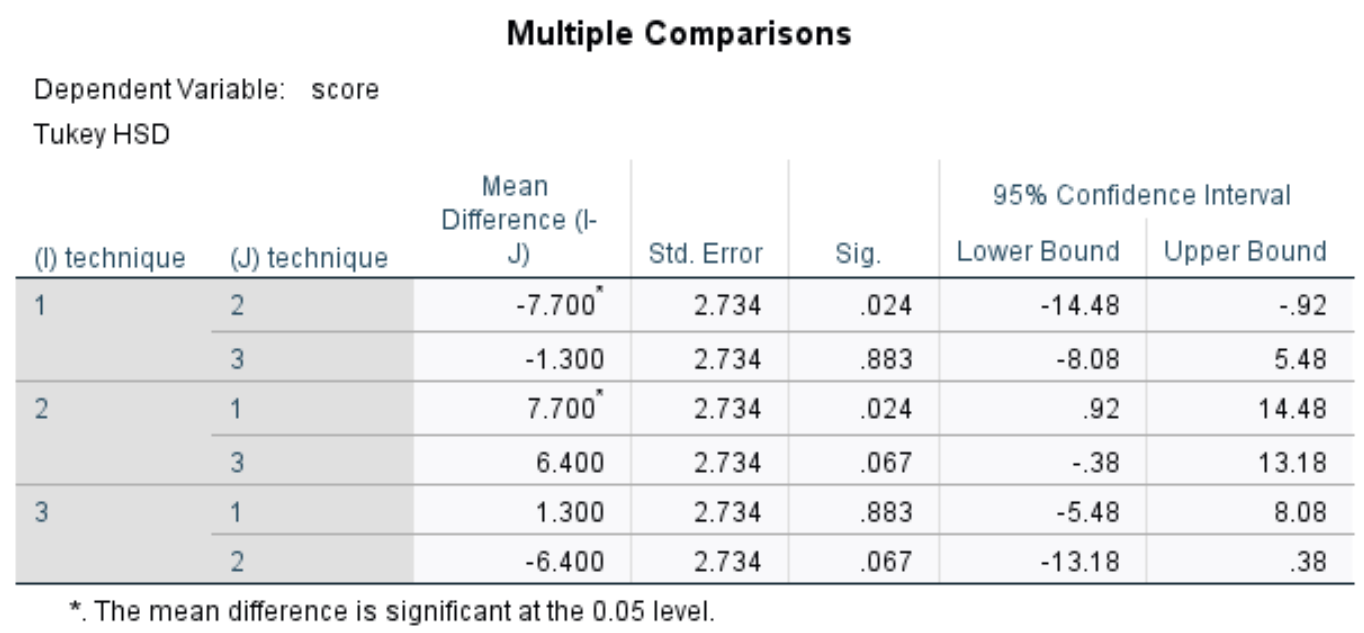
Таблица множественных сравнений
В этой таблице показаны апостериорные множественные сравнения Тьюки между каждой из трех групп. Нас больше всего интересует Sig. столбец, в котором отображаются p-значения для различий в средних значениях между каждой группой:
Из таблицы мы можем увидеть p-значения для следующих сравнений:
- Техника 1 против 2: | р-значение = 0,024
- Техника 1 против 3 | р-значение = 0,883
- Техника 2 против 3 | р-значение = 0,067
Единственное групповое сравнение, имеющее p-значение менее 0,05, проводится между методами 1 и 2.
Это говорит нам о том, что существует статистически значимая разница в средних результатах тестов между учащимися, использовавшими методику 1, и учащимися, использовавшими методику 2.
Однако статистически значимой разницы между методами 1 и 3 или между методами 2 и 3 нет.
Шаг 4: Сообщите о результатах.
Наконец, мы можем сообщить о результатах однофакторного дисперсионного анализа. Вот пример того, как это сделать:
Был выполнен однофакторный дисперсионный анализ, чтобы определить, приводят ли три разных метода обучения к разным результатам теста.
В общей сложности 10 студентов использовали каждый из трех методов обучения в течение одного месяца, прежде чем сдать один и тот же тест.
Однофакторный дисперсионный анализ показал, что существует статистически значимая разница в результатах тестов как минимум между двумя группами (F (2, 27) = 4,545, p = 0,020).
Тест Тьюки для множественных сравнений показал, что средние результаты теста значительно различались между учащимися, которые использовали метод 1 и метод 2 (p = 0,024, 95% ДИ = [-14,48, -0,92]).
Статистически значимой разницы между баллами по методам 1 и 3 (p = 0,883) или между баллами по методам 2 и 3 (p = 0,067) не было.
В программе MS Excel
для статистического анализа данных
имеется надстройка “Пакет анализа”,
которая позволяет проводить дисперсионный
анализ следующих видов:
-
однофакторный
дисперсионный анализ, -
двухфакторный
дисперсионный анализ без повторений, -
двухфакторный
дисперсионный анализ с повторениями.
Последний вид
двухфакторного анализа используется
в том случае, когда в каждой группе
данных имеется более одной выборки.
3. Расчет однофакторного комплекса.
Рассмотрим задачу
проверки влияния дозы мерказолила на
время Y (в сутках) устранения тиреотоксикоза
у больных диффузным токсическим зобом.
При этом исследуемый фактор A имеет три
уровня:
A1
– 30 мг/сутки
A2
– 25 мг/сутки
A3
– 20 мг/сутки.
Статистический
комплекс представлен на рисунке 2. Он
включает 3 группы и в каждой группе
имеется по 2 наблюдения, т.е. n = 2, к =3.
|
ВАРИАНТЫ |
||
|
Уровень |
Уровень |
Уровень |
|
фактора |
фактора |
фактора |
|
54 |
67 |
73 |
|
57 |
63 |
70 |
Рисунок
2
Для выполнения
расчетов в MS Excel:
1. Сформируйте
таблицу с исходными данными (Рисунок
3):
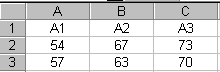
Рисунок 3
2.Выполните
команду Анализ
данных
из меню Сервис.
3.Выберите в
появившемся диалоговом окне метод
“Однофакторный дисперсионный анализ”
и нажмите кнопку [OK].
4.В окне “Однофакторный
дисперсионный анализ” (Рисунок 4)
установите для входных данных следующие
параметры:
-
входной
интервал равен $A$1:$C$3, -
входной
диапазон содержит метки в первой строке, -
альфа
(уровень значимости) равен
0,05.
Рисунок 4
5.Для параметров
вывода установите переключатель в
положение “Новый рабочий лист”.
6.После завершения
настройки параметров нажмите кнопку
[OK].
Результаты
дисперсионного анализа будут представлены
на новом листе и состоять из двух таблиц
(Рисунок 5). В первой таблице для каждой
строки и каждого столбца исходной
таблицы приведены числовые параметры:
количество чисел, сумма, среднее и
дисперсия.
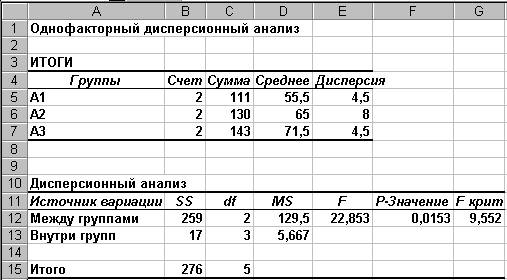
Рисунок 5
Вторая часть –
это результаты дисперсионного анализа.
В таблице результатов Excel использует
следующие обозначения:
В таблице результатов
MS Excel использует следующие обозначения:
-
SS
– сумма квадратов, -
df
– степени свободы, -
MS
– средний квадрат (дисперсия), -
F
– наблюдаемое значение F-статистики
Фишера, -
p-значение
– значимость критерия Фишера, -
F-критическое
– критическое значение F-статистики при
p=0,05.
Проанализируем
полученные результаты. В соответствии
с рисунком 5 имеем F = 22,85 и Fкр.
= 9,55, т.е. F > Fкр.
Следовательно влияние фактора на
результативный признак можно считать
достоверным, что и подтверждается
величиной значимости (p=0.0153), которая
меньше 0.05.
Итак,
конкурирующая гипотеза о достоверности
влияния фактора А может быть принята с
вероятностью 0.95. При этом сила влияния
мерказолила на устранение тиреотоксикоза
оценивается в
соответствии с формулой (10) величиной:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #