- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Образцы оформления задачи
В разделе “Задачи” мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
1. Задачи на нахождение суммы
В вопросе задач такого типа всегда есть “Сколько всего?”
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
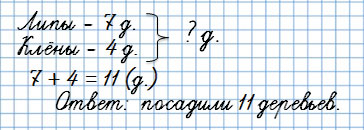
2. Задачи на нахождение остатка
В вопросе “Сколько … осталось?”
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
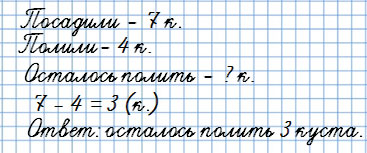
3. Задачи на увеличение или уменьшение числа на несколько единиц
В условии “на … больше”
Папа с Володей собирали грибы. Папа нашёл 8 грибов, а Володя на 3 гриба больше.
Сколько грибов нашёл Володя?
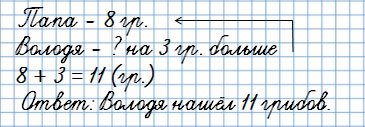
В условии “на … меньше”
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
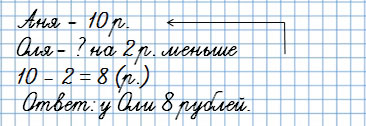
4. Задачи на разностное сравнение
В вопросе “На сколько больше…?”
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
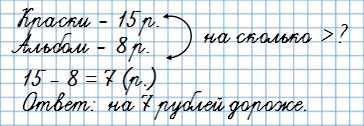
“На сколько меньше…?”
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
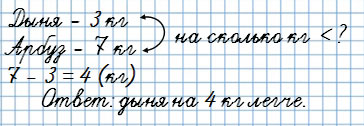
5. Задачи на нахождение неизвестного слагаемого
В условии “Было…Стало…”
В вопросе “Сколько добавили?”
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?

6. Задачи на нахождение неизвестного вычитаемого
В условии “Было… Осталось…”
В вопросе “Сколько уехало?”
“Сколько человек вышло?”
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?

7. Задачи на нахождение неизвестного уменьшаемого
В условии “Убрали… Осталось…”
В вопросе “Сколько было сначала?”
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?

Задачи в 2 и 3 действия
Первый вид
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
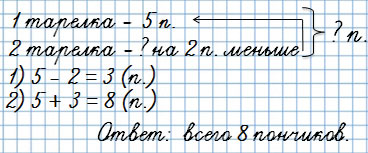
Второй вид
В классе два маленьких аквариума. В первом аквариуме 4 рыбки, а во втором – на 2 рыбки больше.
Сколько рыбок в двух аквариумах?
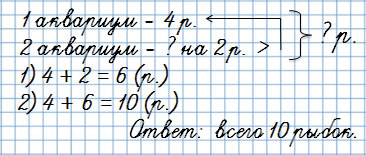
Третий вид
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?

Четвёртый вид
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
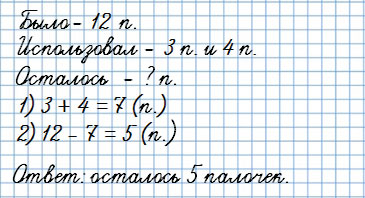
или
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
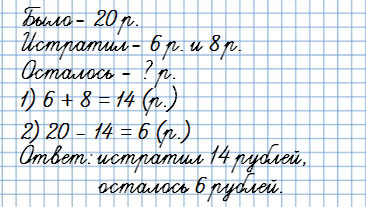
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?

II тип:
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?

Задачи с составлением рисунка по условию:
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
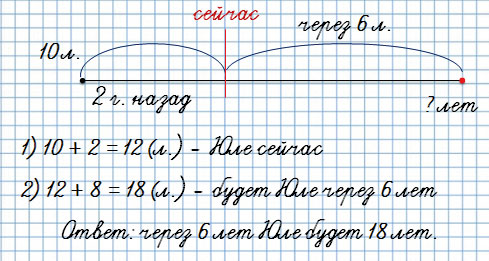
Советуем посмотреть:
Обратные задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 15,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 23,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 24,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 27,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 28,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 35,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 44,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 5,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
2 класс
Страница 54. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 41,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 60,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 50,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 73,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 75,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 34. ПР 3. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 8,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 71,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 72,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 63,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 15,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 18,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 41,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 46,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 49. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 402,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 410,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 137,
Мерзляк, Полонский, Якир, Учебник
Номер 164,
Мерзляк, Полонский, Якир, Учебник
Номер 249,
Мерзляк, Полонский, Якир, Учебник
Номер 499,
Мерзляк, Полонский, Якир, Учебник
Номер 501,
Мерзляк, Полонский, Якир, Учебник
Номер 503,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 370,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 372,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 405,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 412,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 419,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 420,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 421,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 452,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 453,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Автор: Наталья Александровна Катан
Использование таблиц для решения текстовых задач по математике в основной школе.
«Скажи мне, и я забуду.
Покажи мне, – я смогу запомнить.
Позволь мне это сделать самому,
и я научусь».
Конфуций
В традиционной методике обучения математике обучение решению текстовых задач занимает значительное место. Методы и приемы работы с задачей общеизвестны и не поддаются сомнению. Однако, именно текстовые задачи зачастую служат камнем преткновения на пути к успеху в изучении математики. А значит, нам учителям математики есть над чем задуматься.
К сожалению, в учебниках математики, нет целостной системы обучения решению текстовых задач. Оформление решения задач алгебраическим способом ведется путем описания. Вводится переменная, все остальные величины выражаются через неё. Такой способ не всегда является доступным и понятным учащимся. Многие виды задач можно решить с помощью составления таблиц.
ТЕМА: «РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ»
6 класс
1. На одной полке в 5 раз больше книг, чем на второй. После того как с первой полки переложили на вторую 12 книг, на полках книг стало поровну. Сколько книг было первоначально на каждой полке?
Указания:
а) обозначь через х число книг, находящихся первоначально на второй полке;
б) заполни следующую таблицу:
|
Число книг |
Было |
Стало |
|
на полке I |
||
|
на полке II |
х |
в) составь уравнение;
г) реши уравнение;
д) дай ответ на вопрос задачи.
I этап. Составление математической модели.
Пусть х книг было на второй полке.
|
Число книг |
Было |
Стало |
|
на полке I |
5х |
5х — 12 |
|
на полке II |
х |
х + 12 |
Вопросы по ходу решения и заполнения таблицы:
1. Сколько было книг на I полке? (в 5 раз больше, чем на второй)
2. Каким выражением можно это показать? (5х)
3. Что означает выражение 5х? (то, что на I полке было в 5 раз больше книг, чем на II)
4. Сколько книг переложили с I полки? (12)
5. Сколько стало на I полке? (на 12 меньше)
6. Каким выражением можно это показать? (5х – 12)
7. Куда переложили эти 12 книг? (на II полку)
8. Сколько стало книг на II полке? (на 12 больше)
9. Каким выражением можно это показать? ( х + 12)
10. После выполнения всех действий с книгами, какое количество книг стало на I и II полках? (равное)
11. Как составить уравнение?
Составим и решим уравнение: 5х – 12 = х + 12
II этап. Работа с математической моделью.
5х – х = 12 + 12
4х = 24
х = 6
III этап. Ответ на вопрос задачи.
6 книг было на II полке.
6*5= 30 (книг) – было на I полке.
Ответ: 30 книг, 6 книг.
2.Используя указания к предыдущей задаче, реши следующую:
В первой корзине было в 5 раз больше яблок, чем во второй. После того как из первой корзины взяли 8 кг яблок и переложили их во вторую корзину, яблок в корзинах стало поровну. Сколько яблок было первоначально в каждой корзине?
Указания:
а) обозначь через х число яблок, находящихся первоначально во второй корзине;
б) заполни следующую таблицу:
|
Число яблок |
Было |
Стало |
|
в корзине I |
||
|
в корзине II |
x |
в) составь уравнение;
г) реши уравнение;
д) дай ответ на вопрос задачи.
3. На путь от поселка до города велосипедист затрачивает 2 часа, а пешеход — 6 часов. Скорость велосипедиста на 12 км/ч больше скорости пешехода. С какой скоростью идет пешеход? Используй при решении таблицу.
|
Движение |
V (км/ч) |
t (ч) |
S (км) |
|
пешехода |
x |
||
|
велосипедисттата |
I этап. Составление математической модели.
|
Движение |
V (км/ч) |
t (ч) |
S (км) |
|
пешехода |
x |
6 |
6х |
|
велосипедиста |
х + 12 |
2 |
2*(х + 12) |
Вопросы по ходу решения и заполнения таблицы:
1. Как найти расстояние, зная время и скорость движения? (S = V* t)
2. Что означают выражения: 6х, х + 12, 2*(х + 12).
3. Есть ли среди этих выражений равные? Какие?
Составим и решим уравнение: 6х = 2*(х + 12).
II этап. Работа с математической моделью.
6х = 2х + 24
4х = 24
х = 6.
III этап. Ответ на вопрос задачи.
6 км/ч – скорость пешехода.
Ответ: 6 км/ч.
4. Используя указания к предыдущей задаче, реши следующую:
Туристы шли по дороге со скоростью 4 км/ч, а по шоссе — со скоростью 6 км/ч. На путь по шоссе они затратили на 3 часа меньше, чем на путь по дороге. Сколько времени туристы шли по шоссе, если пути по дороге и по шоссе равны? Используй при решении таблицу.
|
Движение |
V (км/ч) |
t (ч) |
S (км) |
|
по дороге |
|||
|
по шоссе |
6 класс.Одна бригада может выполнить работу за 6 дней, а другая – за 12 дней. За сколько дней две бригады выполнят ту же работу вместе?
Что такое производительность труда? Как в дробях обозначается целое?
Заполним таблицу. Примем всю работу за 1.
|
Производительность труда |
Время (д) |
Вся работа |
|
|
I |
? |
6 |
1 |
|
II |
? |
12 |
1 |
|
Вместе |
? |
? |
1 |
Как найти производительность труда, если известны вся работа и время?
1)1:6=1/6 (ч/д) – производительность 1 бригады.
2)1:12=1/12(ч/д) – производительность 2 бригады.
3)1/6+1/12=1/4(ч/д) – за 1 день 1 и 2 бригада вместе.
4)1:1/4=4 (д)
Ответ: за 4 дня.
Выводы
1. Описанный здесь способ решения помимо формальной стороны (заполнение таблицы определенным образом) имеет неформальную составляющую: медленное прочтение текста задачи, разбитого на части, и его осмысление. Неформальный момент затрудняет освоение метода.
2. С другой стороны, наличие не только алгоритмики в приеме решения, но и размышления, осознания представленной в тексте информации, способствует формированию чрезвычайно важного сегодня навыка осмысленного чтения, понимания слова, умения выразить словом свою мысль.
3. Помимо прямой цели – решить задачу – в этой учебной деятельности присутствует еще одна цель, неявная, но от этого не менее значимая: научиться медленно и осмысленно читать слова текста.
4. Следует отметить, что учиться разбивать текст на смысловые части – это отдельная учебная задача, которую удобно решать при работе в группах.
5. Отметим, что не любой способ заполнения таблицы становится эффективным при дальнейшем составлении уравнения. Именно пошаговое алгоритмизированное заполнение таблицы помогает четко выделить ту величину, вариация которой будет записана как уравнение. Исключается возможность приравнивания разноименных величин, например, часов к километрам.
6. Обратим внимание на то, что большинство детей, освоивших предлагаемый прием работы с текстовыми задачами, используют его и при самостоятельном поиске решения задачи.
7. Освоение представленного алгоритма развивает в ученике навык работы с письменным текстом, учит анализировать данные, логически структурировать информацию, выбирать главное. Данный подход способствует не только научению решать задачи, но и повышает качество учебной деятельности в целом.
Статьи
Начальное общее образование
Линия УМК Г. К. Муравина, О. В. Муравиной. Математика (1-4)
Математика
Урок математики в начальной школе: учимся работать с таблицей
Работа с таблицами — это работа с информацией, без чего в наше время не обойтись. Поэтому авторы курса «Математика» для 1-4 классов Георгий Муравин и Ольга Муравина уделили таблицам большое внимание в своих учебниках. Рассмотрим подробнее, с примерами, какие виды таблиц и задания к ним предлагают авторы учебников, как выстроено постепенное освоение важного метапредметного умения на уроках математики (с первого класса и до ВПР).
13 мая 2019
1. Информационные таблицы
Информационные таблицы содержат данные, которые ученику нужно использовать при выполнении задания. Могут быть указаны площади стран, сведения из биологии, другие показатели. Дети получают задания: «найди информацию», «классифицируй», «расположи по уменьшению» (и возрастанию), «сделай вычисления», «составь вопросы по таблице» и др. Вычисления производятся отдельно.
Примеры заданий
1 класс
(Из проверочных работ. Задание «со звездочкой»)
На даче собрали урожай ягод. Их количество записали в таблицу

Укажите верные утверждения, составленные по таблице.
- Крыжовника больше, чем малины.
- Черники меньше, чем крыжовника.
- Малины столько же, сколько черники.
- Крыжовника больше, чем черники, но меньше, чем клубники.
2 класс
(Из проверочных работ)
В таблице указано расписание движения поездов
|
Направление |
Номер поезда |
Время отправления |
|
Москва — Сочи |
083С |
20 ч 10 мин |
|
Москва — Уфа |
116Й |
12 ч 26 мин |
|
Москва — Анапа |
109В |
23 ч |
Запиши ответ на вопросы.
- Какой номер поезда Москва — Анапа?
- В какое время отправляется поезд Москва — Сочи?
- В какой город поезд отправляется раньше всех?
3 класс
«Моя телефонная книга»
Составь свою телефонную книгу. Расположи абонентов в алфавитном порядке. Какие телефоны экстренных служб обязательно должны быть занесены в книгу?
|
№ |
Список абонентов |
Телефон |
|
|
|
|
4 класс
Ответьте на вопросы по таблице, в которой записана длина корней некоторых растений.
|
Пшеница |
Фасоль |
Горох |
Лен |
Рожь |
|
150 см |
70 см |
90 см |
80 см |
130 см |

- Какое растение имеет: а) самые длинные корни; б) самые короткие корни?
- Расставь растения в порядке уменьшения длины корней.
- На сколько сантиметров корни пшеницы длиннее, чем корни льна?
- На сколько сантиметров корни гороха короче, чем корни ржи?

Занимательная математика. 1 класс. Рабочая тетрадь
Пособие может быть использовано в начальной школе при проведении занятий математического факультатива, кружка, олимпиады, клуба «Эрудит», интеллектуального марафона и других форм организации внешкольной деятельности учащихся. Задания, включенные в рабочую тетрадь, способствуют формированию у детей самостоятельности, наблюдательности, геометрической зоркости и умения рассуждать, а также создают условия для развития интереса к математике, математического кругозора и эрудиции учащихся.
Купить
2. Справочные таблицы
Справочные таблицы в первом классе показывают числа в пределах 20 с разных точек зрения. И далее, они помогают познакомить учеников с названиями чисел, видами вычислений, разрядами чисел, единицами измерения.
Примеры заданий
1 класс
Назови состав числа 5 по рисунку. Заполни домик.
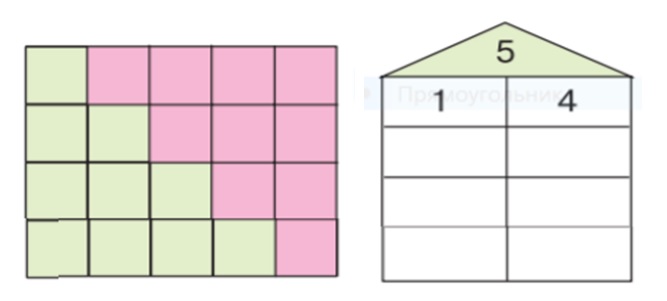
Найди значение выражений, пользуясь составом числа 5.
|
4 + 1 |
3 + 2 |
5 – 1 |
5 – 2 |
|
2 + 3 |
5 – 3 |
1 + 4 |
5 – 4 |
2 класс
Рассмотри таблицу чисел от 1 до 100. Назови числа, которые ты знаешь. По какому правилу составлена таблица? Какие числа пропущены?
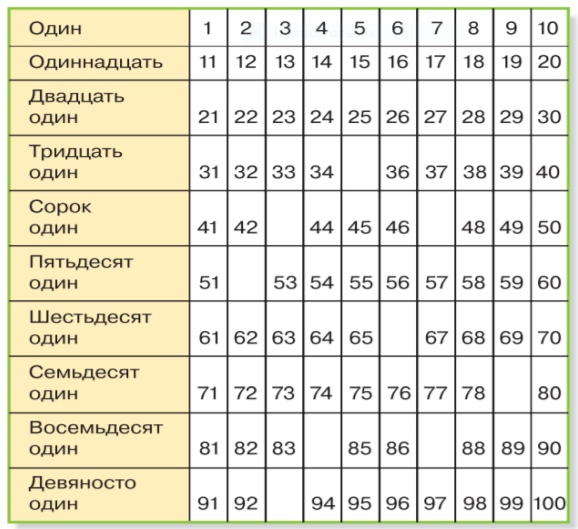
- Сколько двузначных чисел начинаются с цифры 7? Назови их.
- Сколько в таблице круглых чисел? Назови их.
- Сколько однозначных чисел? Назови их.
- Сколько двузначных чисел оканчивается цифрой 2? Назови их.
3 класс
Найди значения выражений и запиши их римскими цифрами.
| L – X | CCC + D | LX – XX |
| D + C | XL + X | DC – CD |
| XXX – V | CD – C |
|
Арабская нумерация |
1 |
5 |
10 |
50 |
100 |
500 |
|
Римская нумерация |
I |
V |
X |
L |
C |
D |
4 класс
Выполни задание по таблице.
Таблица разрядов и классов
|
Класс миллионов |
Класс тысяч |
Класс единиц |
||||||
|
Сот. |
Дес. |
Ед. |
Сот. |
Дес. |
Ед. |
Сот. |
Дес. |
Ед. |
|
0 |
0 |
0 |
4 |
6 |
5 |
9 |
0 |
7 |
|
3 |
2 |
8 |
0 |
0 |
0 |
6 |
5 |
0 |
|
1 |
7 |
9 |
4 |
5 |
6 |
2 |
0 |
3 |
- Сколько классов в таблице? Сколько разрядов?
- Назови разряды каждого класса.
- Какие цифры записаны в разряде десятков миллионов?
- Какие цифры записаны в разряде: единиц, единиц тысяч, единиц миллионов?
- В каких разрядах записана цифра 3?
- Назови старший разряд каждого числа.
- Прочитай второе число. Какой класс не назван?
3. Логические таблицы
Логические таблицы ставят перед учениками логические задачи: проанализировать данные, найти закономерности. Например: «дополни таблицу нужными элементами» (фигурами/числами), «продолжи запись», «сопоставь числа и формулы», «вставь подходящее число из предложенных и сделай вычисление» и т.д.
Примеры заданий
1 класс
Кто быстрее (ты или твой сосед по парте) нарисует фигуру, которую нужно поставить на свободное девятое место?
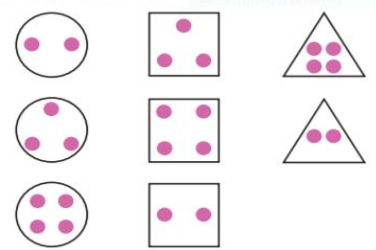
3 класс
Какие числа пропущены в таблице, если r — радиус окружности, а d — диаметр этой же окружности?
|
r |
24 м |
|
125 мм |
|
|
d |
|
24 дм |
|
125 см |
4 класс
Какие высказывания о таблице верные?
|
10 |
12 |
74 |
48 |
|
300 |
303 |
330 |
333 |
|
900 |
927 |
956 |
903 |
- В первом столбце записаны круглые числа.
- В первой строке записаны четные двузначные числа.
- В третьей строке записаны трехзначные числа, которые содержат 9 десятков.
- В четвертом столбце записаны числа, которые делятся на 3 без остатка.
- Сумма чисел в первой строке равна 144.
4. Вычислительные таблицы
Вычислительные таблицы являются формой вычислительного задания, то есть ученики производят вычисления непосредственно в таблице. Так школьники повторяют компоненты действий и составы чисел, работают с множителями, делимыми, разностями, остатками и т.д.
Примеры заданий
1 класс
Какие числа пропущены?
|
Уменьшаемое |
8 |
|
6 |
8 |
|
7 |
|
Вычитаемое |
|
3 |
4 |
|
4 |
|
|
Разность |
1 |
4 |
|
6 |
4 |
1 |
2 класс
Назовите числа, которые пропущены в каждой таблице.
|
Множитель |
2 |
|
2 |
8 |
|
Множитель |
9 |
2 |
3 |
|
|
Произведение |
18 |
10 |
|
16 |
|
Делимое |
12 |
8 |
18 |
|
|
Делитель |
6 |
|
9 |
2 |
|
Частное |
|
4 |
|
7 |
Закончи предложения.
- Если произведение двух чисел разделить на один из множителей, то получится … .
- Если делитель умножить на частное, то получится … .
- Если делимое разделить на частное, то получится … .
- Если делимое разделить на делитель, то получится … .
3 класс
Какие числа пропущены в таблице?
|
Делимое |
19 |
61 |
52 |
|
90 |
236 |
629 |
|
Делитель |
2 |
13 |
|
8 |
|
10 |
100 |
|
Частное |
9 |
|
3 |
100 |
3 |
|
6 |
|
Остаток |
|
9 |
10 |
13 |
12 |
6 |
|
4 класс
Вычисли устно и расшифруй название науки. Что она изучает?


Математика. 4 класс. Итоговая аттестация. Базовый и повышенный уровни сложности.
Рабочая тетрадь предназначена для оценки результатов деятельности выпускников начальной школы по освоению курса математики. В нее включены 10 вариантов заданий на двух уровнях трудности. В основе многих заданий лежат ситуации из реальной жизни. Пособие окажет учителям начальной школы помощь в организации диагностических процедур.
Купить
5. Таблицы для решения задач
Таблицы для решения задач подобны вычислительным таблицам, однако используются в заданиях с текстовыми задачами, сопровождаются иллюстрациями, схемами. Такие таблицы часто предусматривают работу с формулами и с пропорциями.
Примеры заданий
1 класс
Составь задачу и реши ее.

2 класс
На пошив спального мешка требуется 4 м ткани. Сколько метров ткани потребуется для 7 спальных мешков? Составь две обратные задачи, используя таблицу.
|
Расход ткани на 1 мешок |
Число мешков |
Расход ткани на все мешки |
|
|
|
|
3 класс
За 5 ластиков Оля заплатила 30 р., а Марина за такие же ластики заплатила 54 р. Сколько ластиков купила Марина?
|
|
Цена (а) |
Количество (n) |
Стоимость (c) |
|
О. |
Одинаковая |
5 шт. |
30 р. |
|
М. |
? шт. |
54 р. |
План решения.
- Найти цену ластика.
- Найти количество ластиков, купленных Мариной.
4 класс
Реши задачу, используя таблицу или схему. Машина в первый день за 8 ч проехала 464 км. Во второй день она была в пути 6 часов и двигалась с той же скоростью. Сколько всего километров проехала машина за два дня?
|
|
V |
t |
S |
|
I |
Одинаковая |
8 ч |
464 км |
|
II |
6 ч |
? км |
|
|
I + II |
(8 + 6) ч |
? км |

Задание с таблицей из демоверсии ВПР по математике (4 класс)
Проверяемые умения в соответствии с ФГОС:
- Умение работать с таблицами, схемами, графиками диаграммами, анализировать и интерпретировать данные.
- Сравнивать и обобщать информацию, представленную в строках и столбцах несложных таблиц и диаграмм.
Задание:
В спортивных соревнованиях по нескольким видам спорта приняли участие 4 команды. Количество медалей, полученных командами, представлено в таблице. Используя эти данные, ответь на вопросы.
|
Команда |
Золотые |
Серебряные |
Бронзовые |
|
«Сириус» |
7 |
8 |
3 |
|
«Орион» |
6 |
4 |
5 |
|
«Заря» |
4 |
6 |
7 |
|
«Весна» |
3 |
2 |
5 |
1) Сколько серебряных медалей завоевала команда «Сириус»? 2) Какая команда заняла 3-е место по сумме всех медалей?
Решение: 1) 7 + 8 + 3 = 18 (м.) — «Сириус»; 2) 6 + 4 + 5 = 15 (м.) — «Орион»; 3) 4 + 6 + 7 = 17 (м.) — «Заря»; 4) 3 + 2 + 5 = 10 (м.) — «Весна».
Ответ: 1) 8; 2) Орион.
Вы можете апробировать учебники «Математика» авторства Г. К. Муравина и О. В. Муравиной. Для этого воспользуйтесь акцией «5 учебников бесплатно».
#ADVERTISING_INSERT#
Использование
таблиц для решения текстовых задач по математике в основной школе
“Скажи мне, и я забуду.
Покажи
мне, – я смогу запомнить.
Позволь
мне это сделать самому,
и
я научусь”.
Конфуций
В традиционной методике обучения математике
обучение решению текстовых задач занимает значительное место. Методы и приемы
работы с задачей общеизвестны и не поддаются сомнению. Однако, именно текстовые
задачи зачастую служат камнем преткновения на пути к успеху в изучении
математики. А значит, нам учителям математики, есть над чем задуматься.
К сожалению, в учебниках
математики, нет целостной системы обучения решению текстовых задач. Оформление
решения задач алгебраическим способом ведется путем описания. Вводится
переменная, все остальные величины выражаются через неё. Такой способ не всегда
является доступным и понятным учащимся. Многие виды задач можно решить с
помощью составления таблиц.
В поиске новых приемов мы часто
забываем то, что было годами наработано и многократно проверено. Формируя УУД,
в т.ч. познавательные универсальные действия, мы должны научить каждого
ученика выполнять знаково-символические
действия:
• моделирование
— преобразование объекта из чувственной формы в модель, где выделены существенные
характеристики объекта (пространственно-графическая или знаково –
символическая);
• преобразование
модели с целью выявления общих законов,
определяющих данную предметную область.
Построение, либо
предъявление модели задачи, с последующим анализом, активизирует познавательную
деятельность учащихся. Поиск опорных слов, выполнение чертежей и схематических
рисунков, составление таблиц, т.е. наглядное оформление задачи, может
существенно определять ход мыслительного процесса.
Работа с таблицей
позволяет ученикам яснее увидеть зависимости между данными и искомыми
величинами и оценить задачу в целом.
В статьях о
моделировании при обучении решению текстовых задач мы можем ни слова не найти
о таблицах. В современной методике математики «таблица представляет собой
структуризацию информации, представленной в задаче. Благодаря таблице, сюжетный
текст превращается в информационную структуру со связями заданного вида, что
помогает вплотную подойти к составлению уравнения и поиску окончательного
решения». Традиционно таблицы составляют при решении задач на движение,
стоимость. Я считаю, что спектр их использования намного шире. Правильно
составленные таблицы являются незаменимым инструментом в построении
математических моделей. Следует отметить, что многие учителя используют таблицы
при решении текстовых задач, один и тот же прием, используя по-разному.
Основные принципы работы с таблицей
1.Таблица должна
быть «живой», действенной, создаваться самим учеником.
2.Принцип
единообразия.
Величины,
занесенные в первый и третий столбики таблицы, должны находиться в
прямопропорциональной зависимости.
3.Таблица должна
помогать анализу данных, не обременять решение.
4. Принцип
преемственности. Обучение составлению таблиц должно начинаться в период
обучения решению арифметических задач в начальных классах и продолжаться в 5-6
классах.
Рассмотрим
несколько примеров использования таблиц для составления математических моделей.
7 класс №403 а)
В 12 ящиков
можно разложить такое же количество яблок, что и в 18 корзин. Определите,
сколько килограммов яблок вмещает ящик и сколько корзина, если известно, что в
ящик вмещается на 3 кг яблок больше, чем в корзину.
|
Масса 1 |
Количество |
Масса |
|
|
Я. |
|||
|
К. |
Заполните
таблицу.
Пусть х кг – масса
яблок в 1 корзине.
|
Масса 1 |
Количество |
Масса |
|
|
Я. |
х+3 |
12 |
12(х+3) |
|
К. |
х |
18 |
18х |
Т.к. масса яблок
в 12 ящиках и 18 корзинах одинаковая, то
12(х+3) = 18х
Сборник Кузнецовой 2014 г.
№8.12
1)Николай
рассчитал, что он сможет хорошо приготовиться к экзамену, если будет решать по
12 задач в день. Однако ежедневно он перевыполнял свою норму на 8 задач и уже
за 5 дней до экзамена решил на 20 задач больше, чем планировал первоначально.
Сколько задач решил Николай?
|
Число |
Время |
Всего |
|
|
Планировал |
12 |
х/12 |
х |
|
Решил |
12+8 |
х+20/20 меньше |
х+20 |
Пусть х – число
задач, которые Николай планировал решить, готовясь к экзамену.
Т.к. Николай,
решая за 1 день на 8 задач больше, чем планировал, решил за 5 дней до экзамена
на 20 задач больше задуманного, то
х/12=х+20/20 + 5
Задачи
на концентрацию
8 класс №183
Сколько граммов
воды надо добавить к 80 г раствора, содержащего 15% соли, чтобы получить
12%-ный раствор?
Пусть х г – масса
воды, которую нужно добавить к 80 г 15%-го раствора соли, чтобы получить 12%-й
раствор соли. Заполните таблицу и решите уравнение.
|
Концентрация |
Масса |
Масса |
|
|
Было |
15% |
||
|
Стало |
12% |
Т.к.
масса соли в растворе остается постоянной, то
0,15*80 =
0,12(80+х)
Задачи
на работу, в т.ч. на совместную работу
Обучение решению
задач на совместную работу начинается в 5 классе арифметическим способом. Нужно
сразу же учить детей правильно составлять таблицу, чтобы избежать в дальнейшем
сложностей при решении задач алгебраическим способом (при составлении
уравнений).
5
класс №1078
Одна бригада может
выполнить работу за 6 дней, а другая – за 12 дней. За сколько дней две бригады
выполнят ту же работу вместе?
Что такое
производительность труда? Как в дробях обозначается целое?
Заполним таблицу.
Примем всю работу за 1.
|
Производительность |
Время |
Вся |
|
|
I |
? |
6 |
1 |
|
II |
? |
12 |
1 |
|
Вместе |
? |
? |
1 |
Как найти
производительность труда, если известны вся работа и время?
1)1:6=1/6 (ч/д) –
производительность 1 бригады.
2)1:12=1/12(ч/д) –
производительность 2 бригады.
3)1/6+1/12=1/4(ч/д)
– за 1 день 1 и 2 бригада вместе.
4)1:1/4=4 (д)
Ответ: за 4 дня.
№1089
Старинная задача. Китай II
в.н.э.
Дикая утка от
южного до северного моря летит 7 дней. Дикий гусь от северного моря до южного
моря летит 9 дней. Теперь дикая утка и дикий гусь вылетают одновременно. Через
сколько дней они встретятся?
|
Часть |
Время |
Расстояние |
|
|
Утка |
? |
7 |
1 |
|
Гусь |
? |
9 |
1 |
|
Вместе |
? |
? |
1 |
9
класс №435
Заказ на пошив
сумок был распределен между мастером и его учеником. Мастер выполнил 75%
заказа, сшив 90 сумок. Количество сумок, которое шил в день ученик, составило
30% количества сумок, изготовляемых в день мастером, и он работал на 1 день
дольше мастера. Сколько сумок в день шил мастер и сколько ученик?
Известно, что
мастер выполнил 75% заказа, сшив 90 сумок.
Каков весь заказ?
Сколько сумок сшил
ученик?
1)90:0,75=120(с)-
весь заказ.
2)120-90=30(с)-
сшил ученик.
Примем за х –
производительность труда мастера.
Заполним таблицу,
составим и решим уравнение.
|
Производительность |
Время |
Вся |
|
|
Мастер |
х |
? |
90 |
|
Ученик |
0,3 |
? |
30 |
Как
найти время, затраченное на работу?
|
Производительность |
Время |
Вся |
|
|
Мастер |
х |
90/х |
90 |
|
Ученик |
0,3х |
30/0,3х |
30 |
Т.к.
ученик работал на 1 день дольше, чем мастер, то можем составить уравнение:
30/0,3х –
90/х = 1
9
класс № 436
Электротехник и
его ученик вместе выполнили работу за 8 часов. За сколько часов эту работу мог
бы выполнить электротехник, работая один, если известно, что его ученик
работает в 2 раза медленнее?
Пусть
электротехник может выполнить эту работу за х ч. Тогда ученик за 2х ч.
Заполните таблицу и составьте уравнение
|
Производительность |
Время |
Вся |
|
|
Электротехник |
1/х |
х |
1 |
|
Ученик |
1/2х |
2х |
1 |
|
Вместе |
1/х+1/2х |
8 |
1 |
Т.к. за 8 ч,
работая вместе, они выполнили всю работу, то
8(1/х+1/2х) = 1
9 класс №438
Для ремонта
участка дороги выделили две бригады, одна из которых могла бы выполнить весь
ремонт на 7 дней быстрее другой. Работу начали одновременно с двух концов
участка и через 9 дней выполнили 75% всей работы. Сколько дней потребовалось бы
каждой бригаде на выполнение ремонта всей дороги?
|
Производительность |
Время |
Вся |
|
|
I |
1/х |
х |
1 |
|
II |
1/х+7 |
х+7 |
1 |
|
Вместе |
1/х+ |
9 |
0,75 |
Т.к., выполняя
работу одновременно, через 9 дней бригады сделали 0,75 всей работы, то
9(1/х +
1/х+7)=0,75
Сборник Кузнецовой 2014г.
№
8.13
1)На двух
копировальных машинах, работающих одновременно, можно сделать копию пакета
документов за 10 мин. За какое время можно выполнить эту работу на каждой
машине в отдельности, если известно, что на первой машине её можно сделать на
15 мин быстрее, чем на второй?
Пусть х мин –
время, за которое можно выполнить эту работу на I
машине,
у мин – на II
машине.
Заполним таблицу
и составим систему уравнений.
|
Скорость |
Время |
Вся |
|
|
I |
1/х |
х |
1 |
|
II |
1/у |
у |
1 |
|
Вместе |
1/х |
1 |

Использование
таблиц при решении задач помогает правильно проанализировать данные и верно
составить уравнение. Универсальные таблицы формируют общий способ действия,
учащиеся не испытывают страха и растерянности, решая задачу. Составление таблиц
является эффективным приемом обучения решению текстовых задач.
Литература:
1.Алгебра 9 класс.
Учебник для общеобразовательных учреждений.
Под редакцией
Г.В.Дорофеева. Москва «Просвещение» 2014
2.Математика.
Сборник заданий для подготовки к ГИА в 9 классе.
Л.В.Кузнецова и
др. Москва
«Просвещение»
2014
3. «Моделирование
при обучении решению текстовых задач»
И.И. Целищева Журнал «Математика в школе» 2008 №5
4. «Задачи в обучении
математике»
Выпускная
квалификационная работа
А.Р. Валиуллина 2014 г
Министерство
образования и науки РФ
Федеральное
государственное автономное образовательное учреждение высшего профессионального
образования «Казанский (Приволжский) федеральный университет»
Институт математики и
механики Н.И.Лобачевского
Кафедра теории и
технологий преподавания Математики и информатики
Активные приёмы работы с текстом на уроке математики.
Главная особенность работы с текстом на уроке математики в том, что ученикам приходится работать с нехудожественными текстами, которые характеризуются установкой на однозначность восприятия.
На уроках математики встречаются и сплошные тексты (статья в учебнике) и, чаще всего, несплошные. К несплошным текстам относятся таблицы, графики, схемы, диаграммы.
Одной из самых эффективных форм подачи, систематизации и моделирования информации являются таблицы.
Умение использовать различные способы кодирования информации в знаково-символической или графической форме – это метапредметное (познавательное) умение. Однако в курсе изучения математики в 1- 4 классах умение работать с таблицами является и предметным результатом. Данные планируемые результаты формируются при работе с информацией и решении задач (слайд )
Виды таблиц на уроках математики в начальной школе (слайды):
Информационные таблицы содержат данные, которые ученику нужно использовать при выполнении задания. Могут быть указаны площади стран, количество попаданий… и другие показатели. Дети получают задания: «найди информацию», «классифицируй», «расположи по уменьшению» (и возрастанию), «сделай вычисления», «составь вопросы по таблице» и т.д.
К информационным таблицам можно отнести таблицы, заполняемые по результатам выполнения практической работы;
Справочные таблицы в первом классе показывают числа в пределах 20 с разных точек зрения. И далее, они помогают познакомить учеников с названиями чисел, видами вычислений, разрядами чисел и т.д.
Логические таблицы ставят перед учениками логические задачи: проанализировать данные, найти закономерности. Например: «дополни таблицу нужными элементами» (фигурами/числами), «продолжи запись», «сопоставь числа и формулы», «вставь подходящее число из предложенных и сделай вычисление» и т.д.
Вычислительные таблицы являются формой вычислительного задания, то есть ученики производят вычисления непосредственно в таблице. Так школьники повторяют компоненты действий и составы чисел, работают с множителями, делимыми, разностями, остатками и т.д.
Таблицы для решения задач подобны вычислительным таблицам, однако используются в заданиях с текстовыми задачами, сопровождаются иллюстрациями, схемами. Такие таблицы часто предусматривают работу с формулами и с пропорциями.
Традиционно в начальной школе таблицы составляют при решении задач:
-) на расчёт стоимости (цена, количество, стоимость);
-) задач, в которых рассматриваются процессы движения (скорость, время, расстояние);
-) на нахождение работы (производительность труда, время, объём работы);
-) на нахождение массы (масса 1 предмета, количество, общая масса / масса всех предметов);
-) логических задач.
Система заданий, направленных на формирование умений работы с таблицами, должна включать задания, развивающие умения извлекать и анализировать информацию, представленную в таблице (умение читать), а также умение представлять необходимую информацию в виде таблицы.
Использование табличной формы позволяет расположить данные компактно, наглядно и рационально. За счёт чего облегчается их анализ, вскрываются те или иные характерные особенности изучаемых явлений: сходство и различие, взаимосвязь признаков и т. п. Это достигается тем, что внутри таблицы сведения располагаются рядами и столбцами, что дает возможность охватить их взглядом и сравнить между собой.
Традиционно выделяют три этапа, по которым следует проводить работу учащихся с текстом на уроках математики:
1 этап – работа до чтения;
2 этап – работа с текстом задачи непосредственно и решение;
3 этап- работа после чтения и решения.
Этапы обучения работе с таблицами при решении задач:
1.Начальный этап: понимание элементов таблицы и чертёж (слайд).
При работе с таблицами в начальной школе следует объяснить ученикам, что в самом простом случае таблица делится на строки и столбцы. Обычно каждый столбец имеет название, которое указывается в первой строке таблицы. До выполнения заданий, в которых информация представлена в таблице, необходимо отработать умение ее читать.
Это можно сделать при помощи вопросов:
– какую информацию из нее можно извлечь;
– зачем таблица в задании;
– какая информация представлена в столбцах, в строках;
-назовите, сколько строк в таблице; сколько столбцов;
– что представлено в столбцах, в строка;
какое значение у ячейки…; какие данные в ней представлены и др.
2. Методика работы с текстом задачи на уроке.
1) Поиск информации и понимание прочитанного- подготовительная работа к решению задачи.
Стратегии работы с текстом во время чтения:
– чтение с остановками (беседа),
– чтение про себя с пометками – выделение ключевых/опорных слов (ставим перед учениками задачу: представьте себя авторами учебника, какие слова вы бы выделили для облегчения понимания задачи) или выделение цветом (например, зеленой ручкой подчёркиваем, что дано; красной – что надо найти).
2) Преобразование и интерпретация информации.
Стратегия моделирования — преобразование объекта в модель, где выделены существенные характеристики объекта.
Построение модели задачи, с последующим анализом, активизирует познавательную деятельность учащихся. Правильно составленные таблицы являются математическими моделями.
Таблица удовлетворяет главному требованию модели: она отражает как количественные отношения, так и структуру связей между данными величинами и искомыми.
Работа над любым видом задач начинается с простых задач ( в 1 действие). (слайд)
Большое внимание обычно уделяется задачам на нахождение цены/ количества/ стоимости и задачам на движение. Поэтому я буду использовать фрагменты уроков при решении задач на нахождение массы.
– Читаем задачу. Масса пакета с мукой – 2 кг. Узнай массу 4 таких пакетов. Заносим данные в таблицу: (.)
|
Масса 1 пакета |
Количество |
Общая масса |
|
2 кг |
4п. |
? |
Устанавливаем взаимосвязь между понятиями «масса 1 пакета», «количество пакетов» и «масса всех пакетов» (общая масса). Рассуждаем и делаем вывод: чтобы найти массу всех предметов, нужно массу одного предмета умножить на количество предметов.
Стрелками обозначаю связь компонентов задачи (движение слева направо- умножаю) и выбор действия.
– Прочитаем вторую задачу. Масса 4 одинаковых пакетов с мукой – 8 кг. Узнай массу одного пакета. (:)
|
Масса 1 пакета |
Количество |
Общая масса |
|
? |
4п. |
8 кг |
Сделаем вывод: чтобы найти массу одного предмета, нужно массу всех предметов разделить на количество предметов. Стрелками обозначаю связь компонентов задачи (движение справа налево- делю) и выбор действия.
Аналогично работаем с третьей задачей.
Фрагменты уроков в 3 классе: решение составных задач на нахождение массы. (слайды).
Я планирую решение таких задач на серии уроков с последующим усложнением работы
1 день- первоначально в рабочем листе (экономим время на чертёж) дана готовая таблица. Учащиеся дополняют её из условия задачи. Работа с моделью позволяет ученикам яснее увидеть зависимости между данными и искомыми величинами и оценить задачу в целом.
2 день- теперь предлагаем учащимся самостоятельно заполнить ячейки готовой таблицы.
3 день- учащиеся самостоятельно озаглавливают и вносят данные в таблицу. Обращаем внимание учеников, если речь идёт о разных объектах, добавляем столбец наименование.
После заполнения таблицы (до решения) ученики самостоятельно проверяют заполнение таблицы по ключу. Анализируют и корректируют ошибки (в паре). Обсуждают план решения задачи и выполняют решение.
Каждый раз при решении задач с помощью таблицы обучающийся должен провести цепочку рассуждений (разбор задачи), которые приведут его к составлению плана решения задачи.
Благодаря таблице текст превращается в информационную структуру со связями заданного вида.
3) Следующий этап- проверка решения задачи- оценка информации.
Составление и решение обратной задачи.
При проверке решения задачи этим способом учащиеся, должны выполнить ряд действий: 1) подставить в текст задачи найденное число; 2) выбрать новое искомое; 3) сформулировать новую задачу; 4) решить составную задачу; 5) сравнить полученное число с тем данным первой задачи, которое было выбрано в качестве искомого, и на основе этого сравнения со ставить соответствующее умозаключения о правильности решения задачи.
Важно чтобы обучающиеся записывали полный ответ к задаче. Это приучает перед тем, как написать ответ, еще раз прочитать вопрос задачи и спросить: «На все ли вопросы задачи я ответил?».
3. Организация дополнительной работы с решенной задачей.
Также для развития читательской грамотности и умения решать текстовые задачи важно организовать дополнительную работу с решенной задачей.
Ученик научится решать задачи конкретного вида, когда пройдёт все этапы. Умение перейдёт в навык, когда ученик не только будет произвольно воспроизводить усвоенное, но и применять. На этом этапе я провожу работу по изменению условия задачи, составление своей задачи по аналогии. (Обучающие самостоятельно меняют условия задачи. Работа может быть организована в группах, парах или по рядам).
Данная таблица наглядно показывает, на каком этапе математическая и читательская грамотность соединяются – когда учащиеся начинают действовать.
|
Прием смыслового чтения (читательская грамотность) |
Этап решения задач (математическая грамотность) |
Умения учащихся (читательская грамотность) |
Действия учащихся (читательская и математическая грамотность) |
|
Поиск информации и понимание прочитанного |
Анализ содержания задачи. Поиск пути решения задачи и составление плана ее решения |
Ориентироваться в содержании текста и понимать его целостный смысл, находить в тексте требуемую информацию. |
Читают задачу. Находят и подчеркивают ключевые слова. По ключевым словам, пересказывают текст задачи. |
|
Преобразование и интерпретация |
Осуществление плана решения задачи. |
Преобразовывать текст, используя новые формы представления информации. |
Составляют краткую запись в виде таблицы и решают задачу. |
|
Оценка информации |
Проверка решения задачи. |
Подвергать сомнению достоверность получаемой информации, обнаруживать её. |
Подставляют полученный результат в текст вопроса. |
Сделаю вывод: Успешное обучение в начальной и основной школе невозможно без сформированности у обучающихся читательской грамотности. На уроках математики активным приёмом работы с текстом является таблица. Она как модель помогает анализировать текст задачи, определить ход мыслительного процесса (верно выбрать действие) и, соответственно, решить задачу. Таблица будет помогать в обучении, если соблюдены основные принципы работы с ней.
- Таблица должна быть «живой», действенной моделью, создаваться самим учеником (совместно с учителем).
- Принцип единообразия. Величины, занесенные в первый и третий столбики таблицы, должны находиться в прямопропорциональной зависимости.
- Таблица должна помогать анализу данных, не обременять решение.
- Принцип преемственности. Обучение составлению таблиц должно начинаться в период обучения решению арифметических задач в начальных классах и продолжаться в 5 – 6 классах.
