Построение таблиц истинности
Екатерина Андреевна Гапонько
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Определение 2
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
Определение 3
Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:
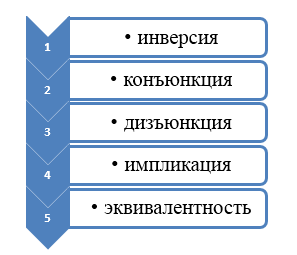
Рисунок 1.
Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
-
Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
-
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
-
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
«Построение таблиц истинности» 👇
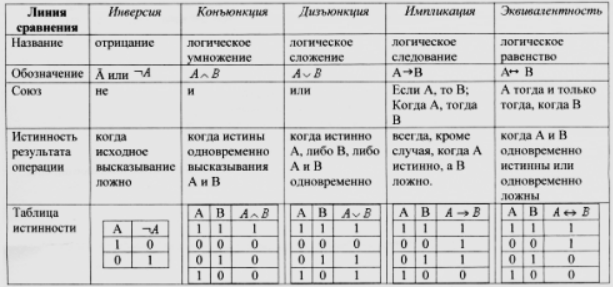
Рисунок 2.
Пример 1
Составить таблицу истинности логического выражения $D=bar{A} vee (B vee C)$.
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- инверсия ($bar{A}$);
- дизъюнкция, т.к. она находится в скобках ($B vee C$);
-
дизъюнкция ($overline{A}vee left(Bvee Cright)$) – искомое логическое выражение.
Кол-во столбцов = $3 + 3=6$.
-
Заполним таблицу, учитывая таблицы истинности логических операций.
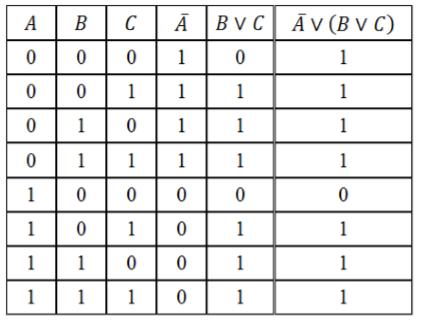
Рисунок 3.
Пример 2
По данному логическому выражению построить таблицу истинности:
[F=overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}]
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- отрицание ($bar{C}$);
- дизъюнкция, т.к. она находится в скобках ($A vee B$);
- конъюнкция ($(Avee B)bigwedge overline{C}$);
- отрицание, которое обозначим $F_1$ ($overline{(Avee B)bigwedge overline{C}}$);
- дизъюнкция ($A vee C$);
- конъюнкция ($(Avee C)bigwedge B$);
- отрицание, которое обозначим $F_2$ ($overline{(Avee C)bigwedge B}$);
-
дизъюнкция – искомая логическая функция ($overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}$).
Кол-во столбцов = $3 + 8 = 11$.
-
Заполним таблицу, учитывая таблицу истинности логических операций.
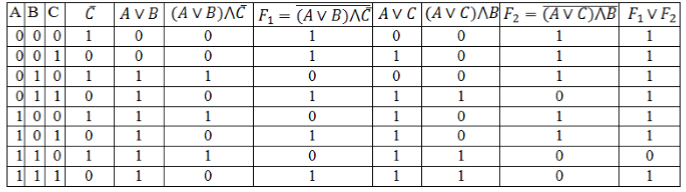
Рисунок 4.
Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
Пример 3
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.
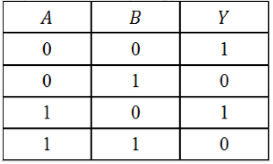
Рисунок 5.
Решение:
- Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
- Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:
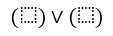
Рисунок 6.
- Каждое логическое выражение в этой дизъюнкции запишем как конъюнкцию аргументов функции $A$ и $B$: $left(Awedge Bright)vee left(Awedge Bright)$
- В случае, когда значение в соответствующей строке таблицы равно $0$, запишем этот аргумент с отрицанием, получим искомую функцию:[Yleft(A,Bright)=left(overline{A}wedge overline{B}right)vee left(Awedge overline{B}right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 12.04.2016
Время выполнения
4 часа
Цель работы
Изучить основы алгебры логики.
Задачи лабораторной работы
В результате прохождения занятия студент должен:
1. знать:
- определения основных понятий (простое и сложное высказывания, логические операции, логические выражения, логическая функция);
- порядок выполнения логических операций;
- алгоритм построения таблиц истинности;
- схемы базовых логических элементов;
- законы логики и правила преобразования логических выражений;
2. уметь:
- применять загоны логики для упрощения логических выражений;
- строить таблицы истинности;
- строить логические схемы сложных выражений.
Общие теоретические сведения
Основные понятия алгебры логики
Логической основой компьютера является алгебра логики, которая рассматривает логические операции над высказываниями.
Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Пример. «3 – простое число» является высказыванием, поскольку оно истинно.
Не всякое предложение является логическим высказыванием.
Пример. предложение «Давайте пойдем в кино» не является высказыванием. Вопросительные и побудительные предложения высказываниями не являются.
Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Пример. «x+2>5» – высказывательная форма, которая при x>3 является истинной, иначе ложной.
Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным. Слова и словосочетания «не», «и», «или», «если…, то», «тогда и только тогда» и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Высказывания, образованные из других высказываний с помощью логических связок, называются составными (сложными). Высказывания, которые не являются составными, называются элементарными (простыми).
Пример. высказывание «Число 6 делится на 2» – простое высказывание. Высказывание «Число 6 делится на 2, и число 6 делится на 3» – составное высказывание, образованное из двух простых с помощью логической связки «и».
Истинность или ложность составных высказываний зависит от истинности или ложности элементарных высказываний, из которых они состоят.
Чтобы обращаться к логическим высказываниям, им назначают имена.
Пример. Обозначим через А простое высказывание «число 6 делится на 2», а через В простое высказывание «число 6 делится на 3». Тогда составное высказывание «Число 6 делится на 2, и число 6 делится на 3» можно записать как «А и В». Здесь «и» – логическая связка, А, В – логические переменные, которые могут принимать только два значения – «истина» или «ложь», обозначаемые, соответственно, «1» и «0».
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение (табл. 1).
Таблица 1. Основные логические операции
| Обозначение операции | Читается | Название операции | Альтернативные обозначения |
| ¬ | НЕ | Отрицание (инверсия) | Черта сверху |
|
|
И | Конъюнкция (логическое умножение) | ∙ & |
|
|
ИЛИ | Дизъюнкция (логическое сложение) | + |
| → | Если … то | Импликация |
|
| ↔ | Тогда и только тогда | Эквиваленция | ~ |
| XOR | Либо …либо | Исключающее ИЛИ (сложение по модулю 2) |
|
НЕ Операция, выражаемая словом «не», называется отрицанием и обозначается чертой над высказыванием (или знаком ¬). Высказывание ¬А истинно, когда A ложно, и ложно, когда A истинно.
Пример. Пусть А=«Сегодня пасмурно», тогда ¬А=«Сегодня не пасмурно».
И Операция, выражаемая связкой «и», называется конъюнкцией (лат. conjunctio – соединение) или логическим умножением и обозначается точкой « • » (может также обозначаться знаками  или &). Высказывание А • В истинно тогда и только тогда, когда оба высказывания А и В истинны.
или &). Высказывание А • В истинно тогда и только тогда, когда оба высказывания А и В истинны.
Пример. Высказывание «Число 6 делится на 2, и число 6 делится на 3» – истинно, а высказывание «Число 6 делится на 2, и число 6 больше 10» – ложно.
ИЛИ Операция, выражаемая связкой «или» (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio – разделение) или логическим сложением и обозначается знаком 
(или плюсом). Высказывание А В ложно тогда и только тогда, когда оба высказывания А и В ложны.
В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Пример: Высказывание «Число 6 делится на 2 или число 6 больше 10» – истинно, а высказывание «Число 6 делится на 5 или число 6 больше 10» – ложно.
ЕСЛИ … ТО Операция, выражаемая связками «если …, то», «из … следует», «… влечет …», называется импликацией (лат. implico – тесно связаны) и обозначается знаком → . Высказывание А→В ложно тогда и только тогда, когда А истинно, а В ложно.
Пример. Высказывание «если студент сдал все экзамены на «отлично», то он получит стипендию». Очевидно, эту импликацию следует признать ложной лишь в том случае, когда студент сдал на «отлично» все экзамены, но стипендии не получил. В остальных случаях, когда не все экзамены сданы на «отлично» и стипендия получена (например, в силу того, что студент проживает в малообеспеченной семье) либо когда экзамены вообще не сданы и о стипендии не может быть и речи, импликацию можно признать истинной.
РАВНОСИЛЬНО Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «… равносильно …», называется эквиваленцией или двойной импликацией и обозначается знаком ↔ или ~ . Высказывание А↔В истинно тогда и только тогда, когда значения А и В совпадают.
Пример: Высказывание «Число является четным тогда и только тогда, когда оно делится без остатка на 2» является истинным, а высказывание «Число является нечетным тогда и только тогда, когда оно делится без остатка на 2» – ложно.
ЛИБО … ЛИБО Операция, выражаемая связками «Либо … либо», называется исключающее ИЛИ или сложением по модулю 2 и обозначается XOR или  . Высказывание А
. Высказывание А В истинно тогда и только тогда, когда значения А и В не совпадают.
В истинно тогда и только тогда, когда значения А и В не совпадают.
Пример. Высказывание «Число 6 либо нечетно либо делится без остатка на 2» является истинным, а высказывание «Либо число 6 четно либо число 6 делится на 3» – ложно, так как истинны оба высказывания входящие в него.
Замечание. Импликацию можно выразить через дизъюнкцию и отрицание:
 .
.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
 .
.
Исключающее ИЛИ можно выразить через отрицание, дизъюнкцию и конъюнкцию:
 .
.
Вывод. Операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания («не»), затем конъюнкция («и»), после конъюнкции – дизъюнкция («или») и исключающего или и в последнюю очередь – импликация и эквиваленция.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Логическая формула – это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).
Логическая функция – это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.
Пример.  – логическая функция двух переменных A и B.
– логическая функция двух переменных A и B.
Значения логической функции для разных сочетаний значений входных переменных – или, как это иначе называют, наборов входных переменных – обычно задаются специальной таблицей. Такая таблица называется таблицей истинности.
Приведем таблицу истинности основных логических операций (табл. 2)
Таблица 2
| A | B |  |
 |
 |
 |
 |
 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Опираясь на данные таблицы истинности основных логических операций можно составлять таблицы истинности для более сложных формул.
Алгоритм построения таблиц истинности для сложных выражений:
1. Определить количество строк:
- количество строк = 2n + строка для заголовка,
- n – количество простых высказываний.
2. Определить количество столбцов:
- количество столбцов = количество переменных + количество логических операций;
- определить количество переменных (простых выражений);
- определить количество логических операций и последовательность их выполнения.
Пример 1. Составить таблицу истинности для формулы И–НЕ, которую можно записать так: .
.
1. Определить количество строк:
На входе два простых высказывания: А и В, поэтому n=2 и количество строк =22+1=5.
2. Определить количество столбцов:
Выражение состоит из двух простых выражений (A и B) и двух логических операций (1 инверсия, 1 конъюнкция), т.е. количество столбцов таблицы истинности = 4.
3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 3).
Таблица 3. Таблица истинности для логической операции
| A | B |  |
 |
| 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 |
Подобным образом можно составить таблицу истинности для формулы ИЛИ–НЕ, которую можно записать так:
 .
.
Таблица 4. Таблица истинности для логической операции
| A | B |  |
 |
| 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 |
Примечание: И–НЕ называют также «штрих Шеффера» (обозначают | ) или «антиконъюнкция»; ИЛИ–НЕ называют также «стрелка Пирса» (обозначают ↓) или «антидизъюнкция».
Пример 2. Составить таблицу истинности логического выражения  .
.
Решение:
1. Определить количество строк:
На входе два простых высказывания: А и В, поэтому n=2 и количество строк=22+1= 5.
2. Определить количество столбцов:
Выражение состоит из двух простых выражений (A и B) и пяти логических операций (2 инверсии, 2 конъюнкции, 1 дизъюнкция), т.е. количество столбцов таблицы истинности = 7.
Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции.
3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 5).
Таблица 5. Таблица истинности для логической операции 
| A | B |  |
 |
 |
 |
C |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
Логические формулы можно также представлять с помощью языка логических схем.
Существует три базовых логических элемента, которые реализуют три основные логические операции:
- логический элемент «И» – логическое умножение – конъюнктор;
- логический элемент «ИЛИ» – логическое сложение – дизъюнктор;
- логический элемент «НЕ» – инверсию – инвертор.

Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из “кирпичиков”.
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояний, которая фактически является таблицей истинности, соответствующей логической функции, только представлена в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисления.
Алгоритм построения логических схем.
- Определить число логических переменных.
- Определить количество логических операций и их порядок.
- Изобразить для каждой логической операции соответствующий ей логический элемент.
- Соединить логические элементы в порядке выполнения логических операций.
Пример. По заданной логической функции  построить логическую схему.
построить логическую схему.
Решение.
- Число логических переменных = 2 (A и B).
- Количество операций = 5 (2 инверсии, 2 конъюнкции, 1 дизъюнкция). Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции.
- Схема будет содержать 2 инвертора, 2 конъюнктора и 1 дизъюнктор.
- Построение надо начинать с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые, в свою очередь, подаются один входной сигнал нормальный и один инвертированный (с инверторов).

Логические законы и правила преобразования логических выражений
Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений.
1. Закон двойного отрицания:  ;
;
2. Переместительный (коммутативный) закон:
3. Сочетательный (ассоциативный) закон:
4. Распределительный (дистрибутивный) закон:
5. Законы де Моргана:
6. Закон идемпотентности:
7. Законы исключения констант:
8. Закон противоречия: ;
;
9. Закон исключения третьего:  ;
;
11. Правило исключения импликации:  ;
;
12. Правило исключения эквиваленции:  .
.
Справедливость этих законов можно доказать составив таблицу истинности выражений в правой и левой части и сравнив соответствующие значения.
Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.
Пример. Упростить логическое выражение  .
.
Решение:
Согласно закону де Моргана:
 .
.
Согласно сочетательному закону:
 .
.
Согласно закону противоречия и закону идемпотентности:
 .
.
Согласно закону исключения 0:

Окончательно получаем
 /
/
Видеоурок по выполнению заданий лабораторной работы
- Текст задания (с данными своего варианта).
- Представление по каждому пункту задания подробного решения.
Технология выполнения работы
В данной работе необходимо составить таблицу истинности логического выражения, построить схему логической функции и упростить логическое выражение заданные каждому студенту в соответствии с его вариантом, записать ход рассуждений и полученные результаты.
Вопросы для защиты работы
- Что такое высказывание (приведите пример)?
- Что такое составное высказывание (приведите пример)?
- Как называются и как обозначаются (в языке математики) следующие операции: ИЛИ, НЕ, И, ЕСЛИ … ТО, ТОГДА И ТОЛЬКО ТОГДА, ЛИБО …ЛИБО?
- Укажите приоритеты выполнения логических операций.
- Составьте таблицу истинности для следующих операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.
- Изобразите функциональные элементы: конъюнктор, дизъюнктор, инвертор.
- Какие логические выражения называются равносильными?
- Записать основные законы алгебры логики.
Исследование логических элементов и синтез логических схем
Цель работы.
Ознакомление с основными функциями и
законами алгебры логики, характеристиками
логических микросхем, основами анализа
и синтеза простых и сложных логических
схем.
Краткие
теоретические сведения.
Анализ работы
цифровых устройств и синтез логических
цепей производится на основе
математического аппарата алгебры
логики или «булевой» алгебры, оперирующей
только двумя понятиями: истинным
(логическая «1») и ложным (логический
«0»). Функции, отображающие такую
информацию, а также устройства,
формирующие функции алгебры логики,
называются логическими. Логические
функции нескольких переменных определяют
характер логических операций, в
результате которых набору входных
переменных
x0,
x1,…,
xn-1
ставится в соответствие выходная
переменная F
F
= f(x0,
x1,…,
xn-1).
Функция преобразования
характеризуется таблицей, в которой
каждой комбинации входных переменных
соответствует значение выходной
переменной F.
Ее называют таблицей истинности.
Основными функциями
алгебры логики, с помощью которых можно
осуществлять любые логические
преобразования, являются логическое
умножение (конъюнкция), логическое
сложение (дизъюнкция) и логическое
отрицание (инверсия).
Алгебра логики
позволяет преобразовывать формулы,
описывающие сложные логические
зависимости, с целью их упрощения. Это
помогает в конечном итоге определять
оптимальную структуру того или иного
цифрового автомата, реализующего любую
сложную функцию. Под оптимальной
структурой принято понимать такое
построение автомата, при котором число
входящих в его состав элементов
минимально.
Основные законы
алгебры логики.
Переместительный
закон:
a
+ b
= b
+ а; ab
= ba.
Сочетательный
закон:
(a + b)
+ c = a + (b + c); (ab)c = a(bc).
Распределительный
закон:
a(b + c) = ab + ac; a + bc
= (a + b)(a +c).
Закон поглощения:
a + ab = a(1 + b) = a; a(a
+ b) = a + ab = a.
Закон
склеивания:
ab
+ a![]()
= a;
(a
+ b)(a
+![]() )
)
= a.
Закон отрицания:
![]() или
или
![]() .
.
Логические
элементы.
Логические элементы используют в
качестве значений входных и выходных
напряжений лишь два уровня: «высокий»
и «низкий». Если логическому «0»
соответствует напряжение низкого
уровня, а логической «1» – высокого, то
такую логику называют положительной,
и наоборот, если за логический «0»
принимают напряжение высокого уровня,
а за логическую «1» – напряжение низкого
уровня, то такую логику называют
отрицательной. В транзисторно-транзисторной
логике (ТТЛ) напряжение логического
«0» – U0
составляет десятые доли вольт
(менее 0,4 В), а напряжение логической
«1» – U1
>2,4 В. Логические элементы реализуют
простейшие функции или систему функций
алгебры логики.
|
Таблица |
|
|
|
|
|
0 |
1 |
|
1 |
0 |
П
 ростейшей
ростейшей
функцией алгебры логики является
функция НЕ. Она реализуется с помощью
инвертора, условное графическое
обозначение которого приведено на рис.
1. На вход инвертора подается величинаX,
которая может принимать два значения:
«0» и «1». Выходная величина Y,
при этом тоже принимает два значения:
«1» и «0». Взаимно однозначное соответствие
X
и Y
дается таблицей истинности (табл. 1),
причем значение выходной величины Y
зависит не от предыдущих значений, а
лишь от текущего значения входной
величины X:
Y
=
![]() .
.
Это справедливо
для всех логических элементов, не
имеющих памяти, у которых в таблице
истинности значение Y
не зависит от порядка строк.
|
Таблица |
||
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Л
 огическими
огическими
элементами, реализующими функции
логического сложения и логического
умножения, являются элементы ИЛИ и И.
Таблицы истинности для этих элементов
однозначно связывают значение выходной
величиныY
со значениями двух (или более) входных
величин хl,
х2,
… xn.
Условные графические обозначения
логических элементов ИЛИ и И приведены
соответственно на рис. 2 и 3, а их таблицы
истинности – в таблицах 2 и 3. Например,
для логического элемента 2-ИЛИ,
реализующего дизъюнкцию
Y
= хl
+ х2
или Y
= хl
х2,
а для элемента
2-И, реализующего конъюнкцию
Y
= хl
х2
или Y
= хl
х2.
|
Таблица |
||
|
|
|
|
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Н
 а
а
наборе логических элементов И,
ИЛИ, НЕ можно реализовать любую сколь
угодно сложную логическую функцию,
поэтому данный набор элементов
называют функционально полным.
На практике часто
используется расширенный набор
логических элементов, позволяющих
также составлять функционально полные
системы. К ним относятся элементы:
ИЛИ-НЕ (элемент
Пирса), реализующий функцию
![]() ;
;
И-НЕ (элемент
Шеффера), реализующий функцию
![]() .
.
Их обозначения и
таблицы истинности приведены на рис.
4 и в табл. 4.
|
Таблица |
|||
|
|
|
|
|
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |

Рис. 4
В частности
функционально полные системы могут
состоять из элементов только
одного типа, например, реализующих
функцию И-НЕ либо ИЛИ-НЕ.
Комбинационные
логические цепи – это такие цепи,
выходные сигналы которых однозначно
определяются сигналами, присутствующими
на их входах в рассматриваемый момент
времени и не зависят от предыдущего
состояния.
Набор логических
элементов, входящих в состав учебного
стенда по основам цифровой техники не
содержит элементов, реализующих функцию
ИЛИ-НЕ, что ограничивает число вариантов
построения логических схем при их
синтезе и позволяет составлять схемы
только в базисе элементов И-НЕ.
Прежде чем перейти
к вопросам анализа и синтеза логических
устройств в заданном базисе элементов
(И-НЕ), необходимо составить таблицу, в
которую будут сведены все возможные
формы представления выходных сигналов
указанных элементов при условии, что
на их входы поданы логические переменные
хl
и х2.
При синтезе схем можно использовать
два технических приема: двойное
инвертирование входного исходного
выражения или его части и применение
теорем Де-Моргана. При этом функция
преобразуется к виду, содержащему
только операции логического умножения
и инверсии, и переписывается через
условные обозначения операции И-НЕ и
НЕ.
Последовательность
проведения анализа и синтеза комбинационных
логических цепей:
-
Составление
таблицы функционирования логической
цепи (таблицы истинности). -
Запись логической
функции. -
Минимизация
логической функции и преобразование
ее к виду, удобному для реализации в
заданном базисе логических элементов
(И-НЕ, НЕ).
Пример проведения
анализа и синтеза логических цепей
[1].
Пусть необходимо
построить мажоритарную ячейку (ячейку
голосования) на три входа, т.е. такую
ячейку, у которой сигнал на выходе равен
единице тогда, когда на двух или трех
входах цепи присутствует сигнал единицы,
в противном случае выходной сигнал
должен быть равен нулю.
Вначале заполним
таблицу истинности (табл. 5). Поскольку
в данном случае имеются три входных
сигнала х1,
х2,
х3,
каждый из которых может принимать одно
из двух возможных значений (0 или 1), то
всего может быть восемь различных
комбинаций этих сигналов. Четырем из
этих комбинаций будет соответствовать
выходной сигнал F,
равный единице.
Таблица
5
|
N |
x1 |
x2 |
x3 |
F |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
1 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
Пользуясь данными табл.
5, можно записать логическую функцию,
которую должна реализовать
синтезируемая цепь. Для этого нужно
представить эту функцию в виде суммы
логических произведений, соответствующих
тем строкам табл. 5 (3, 5-7), для которых
функция F
равна единице. Аргументы записываются
без инверсии, если они равны единице и
с инверсией, если равны нулю.
Если в синтезируемой
таблице истинности выходная величина
чаще принимает значение «1», то
синтезируются строки, в которых выходная
величина равна «0».
При выполнении
заданной процедуры получим функцию
F=![]() . (1)
. (1)
Для минимизации
(упрощения) данной функции нужно
применить основные законы алгебры
логики. Возможна следующая последовательность
преобразований, например, с применением
закона склеивания (теоремы Де-Моргана):
F
=
![]() =
=
![]()
+![]()
=![]() . (2)
. (2)
Как видно, полученное
конечное выражение гораздо проще
исходного.
Аналогично
проводится анализ (составление таблиц
истинности) и более сложных логических
схем.
Для выполнения
задания предлагается набор наиболее
распространенных логических элементов
(рис. 5).
 Рис.
Рис.
5. Набор логических элементов для
выполнения задания
Задание к
лабораторной работе
1. Составить таблицы
истинности для всех логических элементов,
приведенных на рис. 5.
2. Для каждого
логического элемента из набора
представленных на рис. 5. составить
логические выражения, реализующие их
функции в базисе логических элементов
НЕ и И-НЕ и начертить полученные
тождественные схемы.
3. Собрать
рассмотренные схемы на стенде и, путем
перебора комбинаций входных сигналов,
составить их таблицы истинности.
4. Используя законы
отрицания (теоремы Де-Моргана) произвести
преобразование минимизированной
функции (2) для реализации ее в базисе
логических элементов НЕ и И-НЕ и начертить
полученную тождественную схему.
5. Собрать
представленную схему на стенде и, путем
перебора комбинаций входных сигналов,
проверить соответствие ее работы
таблице истинности (табл. 5).
Контрольные
вопросы
-
Что
такое функционально полная система и
базис логических элементов? -
В чем
особенности синтеза логических
устройств? -
В чем
заключаются принципы минимизации
логических устройств? -
Назовите основные
операции булевой алгебры. -
Что
отражают теоремы булевой алгебры?
Сформулировать теоремы Де-Моргана:
поглощения и склеивания. -
Какие
цифровые устройства называются
комбинационными?
ЛАБОРАТОРНАЯ
РАБОТА № 6
Соседние файлы в предмете Электроника
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ЛАБОРАТОРНАЯ РАБОТА
АЛГЕБРА ЛОГИКИ
Время
выполнения – 4 часа.
Цель
работы
Изучить
основы алгебры логики.
Задачи лабораторной работы
В
результате прохождения занятия
студент должен:
1)
знать:
–
определения основных понятий (простое и сложное высказывания,
логические
операции, логические выражения, логическая функция);
–
порядок выполнения логических операций;
–
алгоритм построения таблиц истинности;
–
схемы базовых логических элементов;
–
законы логики и правила преобразования логических выражений;
2)
уметь:
–
применять загоны логики для упрощения логических выражений;
–
строить таблицы истинности;
–
строить логические схемы сложных выражений.
Общие теоретические сведения
Основные
понятия алгебры логики
Логической
основой компьютера является алгебра логики, которая
рассматривает
логические операции над высказываниями.
Алгебра логики –
это раздел математики, изучающий высказывания, рассматриваемые
со стороны их логических значений (истинности или ложности) и логических операций
над ними.
Логическое
высказывание – это любое
повествовательное предложение,
в
отношении которого
можно однозначно сказать, истинно оно или ложно. Пример: «3 – простое число»
является высказыванием, поскольку оно
истинно.
Не
всякое предложение является логическим высказыванием.
Пример: предложение «Давайте пойдем в кино» не
является высказыванием. Вопросительные и побудительные предложения
высказываниями не являются.
Высказывательная форма – это повествовательное предложение, которое
прямо или косвенно содержит хотя бы одну переменную и становится
высказыванием, когда все переменные замещаются своими значениями.
Пример: «x+2>5» – высказывательная
форма, которая при x>3 является истинной, иначе
ложной.
Алгебра
логики рассматривает любое высказывание только с одной точки зрения – является
ли оно истинным или ложным. Слова и словосочетания «не»,
25
«и», «или», «если…,
то», «тогда и только тогда» и другие позволяют из уже заданных высказываний
строить новые высказывания. Такие слова и словосочетания называются логическими
связками.
Высказывания, образованные из других
высказываний с помощью логических связок, называются составными (сложными).
Высказывания, которые не являются составными, называются элементарными (простыми).
Пример:
высказывание «Число 6 делится на 2» – простое высказывание. Высказывание «Число
6 делится на 2, и число 6 делится на 3» – составное высказывание, образованное
из двух простых с помощью логической связки «и».
Истинность или ложность составных
высказываний зависит от истинности или ложности элементарных высказываний, из
которых они состоят.
Чтобы обращаться к логическим
высказываниям, им назначают имена. Пример: Обозначим через А простое
высказывание «число 6 делится на 2»,
а
через В простое высказывание
«число 6 делится на 3». Тогда составное высказывание «Число 6 делится на 2, и
число 6 делится на 3» можно записать как «А и В». Здесь «и» – логическая
связка, А, В – логические переменные, которые могут принимать только два
значения – «истина» или «ложь», обозначаемые, соответственно, «1» и «0».
Каждая логическая связка рассматривается как операция
над логическими высказываниями и имеет свое название и обозначение (табл. 1).
Таблица 1. Основные логические
операции
|
Обозначение |
Читается |
Название операции |
Альтернативные |
|
|
операции |
обозначения |
|||
|
¬ |
НЕ |
Отрицание (инверсия) |
Черта сверху |
|
|
∧ |
И |
Конъюнкция (логическое |
· & |
|
|
умножение) |
||||
|
∨ |
ИЛИ |
Дизъюнкция (логическое |
+ |
|
|
сложение) |
||||
|
→ |
Если … то |
Импликация |
⊃ |
|
|
Тогда и |
||||
|
↔ |
только |
Эквиваленция |
~ |
|
|
тогда |
||||
|
XOR |
Либо |
Исключающее ИЛИ |
⊕ |
|
|
…либо |
(сложение по модулю 2) |
|||
НЕ Операция, выражаемая словом
«не», называется отрицанием и обозначается чертой над
высказыванием (или знаком ¬). Высказывание ¬А истинно, когда A ложно, и ложно,
когда A истинно.
Пример.
Пусть А=«Сегодня пасмурно», тогда ¬А=«Сегодня не пасмурно».
И Операция, выражаемая связкой «и»,
называется конъюнкцией (лат. conjunctio – соединение) или логическим
умножением и обозначается точкой
«
· » (может также обозначаться знаками ∧ или &).
Высказывание А · В истинно тогда и только тогда, когда
оба высказывания А и В истинны.
26
Пример. Высказывание
«Число 6 делится на 2, и число 6 делится на 3» – истинно, а высказывание «Число
6 делится на 2, и число 6 больше 10» – ложно.
ИЛИ Операция, выражаемая связкой «или» (в
неисключающем смысле этого слова), называется дизъюнкцией (лат.
disjunctio – разделение) или логическим сложением и обозначается знаком ∨ (или плюсом). Высказывание А∨В ложно тогда и только тогда, когда оба высказывания А
и В ложны.
Пример. Высказывание «Число 6 делится на 2 или число 6
больше 10» – истинно, а высказывание «Число 6 делится на 5 или число 6 больше
10» – ложно.
ЕСЛИ … ТО Операция, выражаемая связками
«если …, то», «из … следует», «… влечет …»,
называется импликацией ( лат. implico – тесно связаны) и обозначается
знаком → . Высказывание А→В ложно тогда и только тогда, когда А
истинно, а В ложно.
Пример. Высказывание «если
студент сдал все экзамены на «отлично», то он получит стипендию». Очевидно, эту
импликацию следует признать ложной лишь в том случае, когда студент сдал на
«отлично» все экзамены, но стипендии не получил. В остальных случаях, когда не
все экзамены сданы на «отлично» и стипендия получена (например, в силу того,
что студент проживает в малообеспеченной семье) либо когда экзамены вообще не
сданы и о стипендии не может быть и речи, импликацию можно признать истинной.
РАВНОСИЛЬНО Операция, выражаемая связками
«тогда и только тогда», «необходимо и достаточно», «… равносильно
…», называется эквиваленцией или двойной импликацией и обозначается
знаком ↔ или ~ . Высказывание А↔В истинно тогда и только тогда,
когда значения А и В совпадают.
Пример. Высказывание «Число
является четным тогда и только тогда, когда оно делится без остатка на 2»
является истинным, а высказывание «Число является нечетным тогда и только
тогда, когда оно делится без остатка на 2» – ложно.
ЛИБО … ЛИБО Операция, выражаемая связками «Либо …
либо», называется исключающее ИЛИ или сложением по модулю 2 и
обозначается XOR или ⊕. Высказывание А⊕В истинно тогда и только тогда, когда значения А и В
не совпадают.
Пример . Высказывание «Число 6 либо нечетно либо
делится без остатка на 2» является истинным, а высказывание «Либо число 6 четно
либо число 6 делится на3» – ложно, так как истинны оба высказывания входящие в
него.
Замечание.
Импликацию можно выразить через
дизъюнкцию и отрицание:
A→B=¬A∨B.
Эквиваленцию можно выразить через
отрицание, дизъюнкцию и конъюнкцию:
A ↔
B=(¬A∨ B)∧(¬B∨ A).
Исключающее ИЛИ можно выразить через
отрицание, дизъюнкцию и конъюнкцию:
A XOR B=(¬A∧ B)∨(¬B&A)
27
Вывод. Операций отрицания, дизъюнкции
и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения
логических операций задается круглыми скобками. Но для уменьшения числа скобок
договорились считать, что сначала выполняется операция отрицания («не»), затем
конъюнкция («и»), после конъюнкции – дизъюнкция («или») и исключающего или и в
последнюю очередь – импликация и эквиваленция.
С
помощью логических переменных и
символов логических операций любое высказывание можно формализовать, то есть
заменить логической формулой (логическим выражением).
Логическая формула – это символическая запись высказывания, состоящая из
логических величин (констант или переменных), объединенных логическими
операциями (связками).
Логическая функция – это функция логических переменных, которая может
принимать только два значения: 0 или 1. В свою очередь, сама логическая
переменная (аргумент логической функции) тоже может принимать только два
значения: 0 или 1.
Пример. F( A, B ) = A & B ∨ A –
логическая функция двух переменных A и B.
Значения логической
функции для разных сочетаний значений входных переменных – или, как это иначе
называют, наборов входных переменных – обычно задаются специальной таблицей.
Такая таблица называется таблицей истинности.
Приведем таблицу
истинности основных логических операций (табл. 2) Таблица 2.
|
A |
B |
¬A |
A & B |
A ∨ B |
A → B |
A ↔ B |
AXOR B |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
Опираясь на данные таблицы истинности
основных логических операций можно составлять таблицы истинности для более
сложных формул.
Алгоритм
построения таблиц истинности для сложных выражений:
1.
Определить
количество строк:
– количество строк = 2n + строка для заголовка,
–
n – количество простых высказываний.
2.
Определить количество столбцов:
количество столбцов = количество
переменных + количество логических операций;
–
определить количество переменных (простых выражений);
– определить количество логических
операций и последовательность их выполнения.
28
3. Заполнить столбцы результатами
выполнения логических операций в обозначенной последовательности с учетом
таблиц истинности основных логических операций.
Пример 1. Составить
таблицу истинности для формулы И–НЕ, которую можно записать так: ¬( A & B ) .
1.
Определить количество строк:
На входе два простых высказывания: А и
В, поэтому n=2 и количество строк =22+1=5.
2.
Определить количество столбцов:
Выражение состоит из двух простых
выражений (A и B) и двух логических операций (1 инверсия, 1 конъюнкция), т.е.
количество столбцов таблицы истинности = 4.
3.
Заполнить столбцы с учетом таблиц
истинности логических операций
(табл.
3).
Таблица
3. Таблица истинности для логической операции ¬( A & B )
|
A |
B |
A & B |
¬(A&B) |
|
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
0 |
0 |
1 |
Подобным образом
можно составить таблицу истинности для формулы ИЛИ–НЕ, которую можно записать
так: ¬(A ∨ B) .
Таблица 4. Таблица истинности для логической операции ¬(A ∨ B)
|
A |
B |
A ∨ B |
¬(A ∨ B) |
|
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
Примечание:
И–НЕ называют
также «штрих Шеффера» (обозначают | ) или
«антиконъюнкция»; ИЛИ–НЕ называют также «стрелка Пирса» (обозначают ↓)
или «антидизъюнкция».
Пример 2. Составить таблицу истинности
логического выражения C=¬A&B∨A&¬B.
Решение:
1.
Определить количество строк:
На входе два простых высказывания: А и
В, поэтому n=2 и количество строк=22+1=
5.
2.
Определить количество столбцов:
Выражение состоит из двух простых
выражений (A и B) и пяти логических операций (2 инверсии, 2 конъюнкции, 1
дизъюнкция), т.е. количество столбцов таблицы истинности = 7.
Сначала
выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция
дизъюнкции.
29
3.
Заполнить столбцы с учетом таблиц
истинности логических операций
(табл.
5).
Таблица 5. Таблица истинности для логической операции C = ¬A &
B ∨ A & ¬B
|
A |
B |
¬A |
¬B |
¬A&B |
A &¬B |
C |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
Логические формулы можно
также представлять с помощью языка логических схем.
Существует три базовых логических элемента, которые
реализуют три основные логические операции:
логический элемент «И» – логическое
умножение – конъюнктор; логический элемент «ИЛИ» – логическое сложение –
дизъюнктор; логический элемент «НЕ» – инверсию – инвертор.
|
конъюнктор |
дизъюнктор |
инвертор |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Поскольку
любая логическая операция может быть представлена в виде комбинации трех
основных, любые устройства компьютера, производящие обработку или хранение
информации, могут быть собраны из базовых логических элементов, как из
“кирпичиков”.
Логические
элементы компьютера оперируют с сигналами, представляющими собой электрические
импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На
входы логического элемента поступают сигналы-значения аргументов, на выходе
появляется сигнал-значение функции.
Преобразование сигнала логическим
элементом задается таблицей состояний, которая фактически является таблицей
истинности, соответствующей логической функции, только представлена в форме
логических схем. В такой форме удобно изображать цепочки логических операций и
производить их вычисления.
Алгоритм
построения логических схем.
1.
Определить число логических
переменных.
2.
Определить количество логических
операций и их порядок.
3.
Изобразить для
каждой логической операции соответствующий ей логический элемент.
30
4.
Соединить
логические элементы в порядке выполнения логических операций.
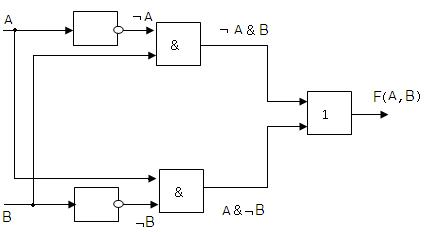
Пример. По заданной логической функции F( A, B ) = ¬A &
B ∨ A & ¬B построить логическую схему.
Решение.
1.
Число логических переменных = 2 (A
и B).
2.
Количество операций = 5 (2
инверсии, 2 конъюнкции, 1 дизъюнкция). Сначала выполняются операции инверсии,
затем конъюнкции, в последнюю очередь операция дизъюнкции.
3.
Схема будет содержать 2 инвертора,
2 конъюнктора и 1 дизъюнктор.
4.
Построение надо
начинать с логической операции, которая должна выполняться последней. В данном
случае такой операцией является логическое сложение, следовательно, на выходе
должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на
которые, в свою очередь, подаются один входной сигнал нормальный и один
инвертированный (с инверторов).
Логические законы и правила
преобразования логических выражений Если две формулы А и В одновременно, то есть при одинаковых
наборах значений входящих в них переменных, принимают одинаковые значения, то
они
называются равносильными.
В
алгебре логики
имеется ряд законов, позволяющих производить равносильные преобразования
логических выражений.
1)
Закон двойного отрицания:
A
= ¬(¬A);
2)
Переместительный (коммутативный)
закон:
– для логического сложения: A ∨ B = B ∨ A ;
– для логического умножения: A ∧ B = B ∧ A ;
3)
Сочетательный (ассоциативный)
закон:
– для логического сложения: (A ∨ B) ∨ C = A ∨ (B ∨ C) ;
– для логического умножения: (A ∧ B) ∧ C = A ∧ (B ∧ C) ;
4)
Распределительный (дистрибутивный)
закон:
– для логического сложения: (A ∨ B) ∧ C = ( A & C ) ∨ ( B & C ) ;
31
– для логического умножения: (A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C) ;
5)
Законы де Моргана:
– для логического сложения: ¬(A ∨ B) = ¬A & ¬B ;
– для логического умножения: ¬(A ∧ B) = ¬A ∨ ¬B ;
6)
Закон идемпотентности:
– для логического сложения: A ∨ A = A ;
– для логического умножения: A ∧ A = A ;
7)
Законы исключения констант:
– для логического сложения: A ∨1= 1, A ∨ 0 = A ;
– для логического умножения: A ∧ 1= A , A ∧ 0 = 0 ;
8)
Закон противоречия:
9)
Закон исключения третьего:
10) Закон поглощения:
– для логического сложения: A ∨ (A ∧ B) = A ;
– для логического умножения: A ∧ (A ∨ B) = A ;
11)
Правило исключения импликации:
12) Правило исключения эквиваленции:
A↔
B=(A→ B)∧(B→
A).
Справедливость этих
законов можно доказать составив таблицу истинности выражений в правой и левой
части и сравнив соответствующие значения.
Основываясь на законах, можно выполнять упрощение
сложных логических выражений. Такой процесс замены сложной логической функции
более простой, но равносильной ей, называется минимизацией функции.
Пример: Упростить
логическое выражение ¬(A ∨
B) ∧
( A & ¬B) .
Решение:
Согласно
закону де Моргана:
¬(A∨ B)∧(A &¬B)∨ A=¬A &¬B&(A &¬B)∨ A.
Согласно
сочетательному закону:
¬A &¬B&(A
&¬B)∨ A=¬A &A
&¬B&¬B ∨
A.
Согласно
закону противоречия и закону идемпотентности:
¬A&A&¬B&¬B∨ A=0∧¬B&¬B=0&¬B∨ A.
Согласно
закону исключения 0:
0&¬B=0
Окончательно получаем ¬(A ∨ B) ∧ ( A & ¬B) ∨ A = 0 ∨ A = A
С
дополнительным
теоретическим материалом можно ознакомиться в литературе [2, 7].
32
Задания
1.
Составить таблицу истинности
логического выражения C.
Варианты
задания:
|
№ варианта |
C |
|
1 |
(¬(A&B))↔ (A∨¬B)XOR |
|
2 |
(A&B)↔ (¬A&B)XOR |
|
3 |
(A&B)↔ (¬B→¬A)XOR |
|
4 |
¬(A ∨ B) ↔ (¬A & |
|
5 |
(A∨ B) ↔ ¬(A&¬B) |
|
6 |
¬(A&B)↔ (¬A∨ B)XOR A |
|
7 |
¬(A → B) ↔ (¬A∨ B) XOR |
|
8 |
(¬A&B)↔ (¬B→ A)XOR |
|
9 |
(A∨¬B)↔ ¬(B&A)XOR |
|
10 |
(¬B&A)↔ (A→¬B)XORB |
|
11 |
(¬A∨¬B)↔ (¬B&A) |
|
12 |
(¬B →¬A)↔ (A∨ B) XOR B |
|
13 |
¬(B∨ A)↔ (¬A→ B)XOR |
|
14 |
(¬(A&B))↔ (¬A→ B)XOR |
|
15 |
(¬A→¬B)↔ (B&A)XOR |
|
16 |
(¬A ∨ ¬B) ↔ (B ∨ ¬A) XOR |
2.
Построить логическую схему функции
F(A,B).
Варианты
задания:
|
№ варианта |
F(A,B) |
|
1 |
¬(A&B)∨(¬(B∨ A)) |
|
2 |
¬(A∨ B)∧(A &¬B) |
|
3 |
¬(A∨ B)∧(A∨¬B) |
|
4 |
¬((¬A ∨ B) ∧ (¬B ∨ A)) |
|
5 |
(¬A ∨ B) ∧ (¬B ∨ ¬A) |
|
6 |
(¬A ∨ B) ∧ ¬(A ∨ ¬B) |
|
7 |
¬(¬A & |
|
8 |
(¬A∨ B)∨¬(A&B) |
|
9 |
(A&B)∨((A∨ B)∧¬A) |
|
10 |
¬((¬A∨ B)& A)∧¬B |
|
11 |
¬(A ∨ ¬B) ∨ ¬(A ∨ B) |
|
12 |
¬A &¬B |
|
13 |
¬A∨ B∨¬(¬B∨ A) |
|
14 |
(¬A &¬B)∨(¬A & |
|
15 |
(¬A&B)∨(A&¬B) |
|
16 |
¬(A &(B |
|
33 |
3.
Упростить
логическое выражение D. Варианты задания:
|
№ варианта |
D |
|
1 |
(¬A&B)∨(A&¬B)∨(A&B) |
|
2 |
(¬A &¬B)∨(¬A &B)∨(A &B) |
|
3 |
¬(A&B)∨(¬(B∨C)) |
|
4 |
¬(¬A |
|
5 |
¬A∨ B∨¬(¬B∨ A)∨A&B |
|
6 |
¬A&B∨¬(A∨ B)∨ A |
|
7 |
¬(A∨¬B)∨¬(A∨ B)∨ A & B |
|
8 |
(A&B)∨((A∨ B)∧(¬A∨¬B)) |
|
9 |
¬((¬A∨ B)& A |
|
10 |
(¬A∨ B)∨(B∨C)∨(A&C) |
|
11 |
¬(¬A &¬B)∨((¬A∨ B)& A |
|
12 |
(¬A∨ B)∧(A∨¬B)∧(B ∨ A) |
|
13 |
(¬A∨ B)∧(¬B∨¬A)∧(¬C ∨ A) |
|
14 |
¬((¬A ∨ B) ∧ (¬B ∨ A)) ∨ (A ∨ B) |
|
15 |
¬(A∨ B)∧(A∨¬B) |
|
16 |
¬(A∨ B)∧(A &¬B) |
Содержание отчета
1.
Текст задания (с данными своего
варианта).
2.
Представление по каждому пункту
задания подробного решения.
Технология выполнения работы
В данной работе необходимо составить
таблицу истинности логического выражения, построить схему логической функции и
упростить логическое выражение заданные каждому студенту в соответствии с его
вариантом, записать ход рассуждений и полученные результаты.
Вопросы для защиты работы
1.
Что такое высказывание (приведите
пример)?
2.
Что такое составное высказывание
(приведите пример)?
3.
Как называются и как обозначаются
(в языке математики) следующие операции: ИЛИ, НЕ, И, ЕСЛИ … ТО, ТОГДА И ТОЛЬКО
ТОГДА, ЛИБО …ЛИБО?
4.
Укажите приоритеты выполнения
логических операций.
5.
Составьте таблицу
истинности для следующих операций: отрицание, конъюнкция, дизъюнкция,
импликация, эквиваленция.
6.
Изобразите функциональные
элементы: конъюнктор, дизъюнктор, инвертор.
7.
Какие логические выражения
называются равносильными?
8.
Записать основные законы алгебры
логики.
Описание презентации по отдельным слайдам:
-

1 слайд
Логика высказываний
Алгоритм построения
таблиц истинности -

2 слайд
Таблицы истинности
Решение логических выражений принято оформлять в виде таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных -

3 слайд
Для составления таблицы истинности необходимо:
Выяснить количество строк (2n, где n – количество переменных)
Выяснить количество столбцов (количество переменных + количество логических операций)
Построить таблицу, указывая названия столбцов и возможные наборы значений переменных
Заполнить таблицу истинности по столбцам -

4 слайд
Пример 1.
Построим таблицу истинности для функции
F = (А В) (¬A ¬B)
Переменных: две (А и В), т.е. N = 2 количество строк: 2n=22=4.
С заголовком: 5
Количество столбцов:
2 переменные + 5 операций (,,¬, и ¬).
Итого 7
Порядок операций:
1 5 2 4 3
F = (А В) (¬A ¬B) -

5 слайд
Пример 1. Таблица
0
1
1
1
1
1
0
0
F = (А В) (¬A ¬B)
1
0
1
0
1
1
1
0
0
1
1
0 -

6 слайд
Пример 2.
Построим таблицу истинности для функции
F = X Y ¬Z
Переменных:
три (X, Y и Z), т.е. n = 3 количество строк: 2n=23=8.
С заголовком: 9
Количество столбцов:
3 переменные + 3 операции (,,¬).
Итого 6
Порядок операций:3 2 1
F = X Y ¬Z -

7 слайд
Пример. Таблица
0
0
0
0
1
1
1
1
F = X Y ¬Z
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
0
1
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1
1


