Построение таблиц истинности
Екатерина Андреевна Гапонько
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Определение 2
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
Определение 3
Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:
Рисунок 1.
Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
-
Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
-
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
-
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
«Построение таблиц истинности» 👇
Рисунок 2.
Пример 1
Составить таблицу истинности логического выражения $D=bar{A} vee (B vee C)$.
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- инверсия ($bar{A}$);
- дизъюнкция, т.к. она находится в скобках ($B vee C$);
-
дизъюнкция ($overline{A}vee left(Bvee Cright)$) – искомое логическое выражение.
Кол-во столбцов = $3 + 3=6$.
-
Заполним таблицу, учитывая таблицы истинности логических операций.
Рисунок 3.
Пример 2
По данному логическому выражению построить таблицу истинности:
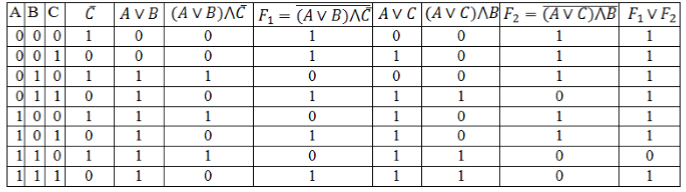
[F=overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}]
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- отрицание ($bar{C}$);
- дизъюнкция, т.к. она находится в скобках ($A vee B$);
- конъюнкция ($(Avee B)bigwedge overline{C}$);
- отрицание, которое обозначим $F_1$ ($overline{(Avee B)bigwedge overline{C}}$);
- дизъюнкция ($A vee C$);
- конъюнкция ($(Avee C)bigwedge B$);
- отрицание, которое обозначим $F_2$ ($overline{(Avee C)bigwedge B}$);
-
дизъюнкция – искомая логическая функция ($overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}$).
Кол-во столбцов = $3 + 8 = 11$.
-
Заполним таблицу, учитывая таблицу истинности логических операций.
Рисунок 4.
Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
Пример 3
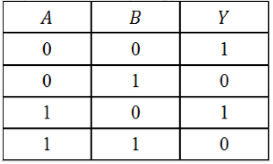
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.
Рисунок 5.
Решение:
- Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
- Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:
Рисунок 6.
- Каждое логическое выражение в этой дизъюнкции запишем как конъюнкцию аргументов функции $A$ и $B$: $left(Awedge Bright)vee left(Awedge Bright)$
- В случае, когда значение в соответствующей строке таблицы равно $0$, запишем этот аргумент с отрицанием, получим искомую функцию:[Yleft(A,Bright)=left(overline{A}wedge overline{B}right)vee left(Awedge overline{B}right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 12.04.2016
Описание презентации по отдельным слайдам:
-
1 слайд
Логика высказываний
Алгоритм построения
таблиц истинности -
2 слайд
Таблицы истинности
Решение логических выражений принято оформлять в виде таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных -
3 слайд
Для составления таблицы истинности необходимо:
Выяснить количество строк (2n, где n – количество переменных)
Выяснить количество столбцов (количество переменных + количество логических операций)
Построить таблицу, указывая названия столбцов и возможные наборы значений переменных
Заполнить таблицу истинности по столбцам -
4 слайд
Пример 1.
Построим таблицу истинности для функции
F = (А В) (¬A ¬B)
Переменных: две (А и В), т.е. N = 2 количество строк: 2n=22=4.
С заголовком: 5
Количество столбцов:
2 переменные + 5 операций (,,¬, и ¬).
Итого 7
Порядок операций:
1 5 2 4 3
F = (А В) (¬A ¬B) -
5 слайд
Пример 1. Таблица
0
1
1
1
1
1
0
0
F = (А В) (¬A ¬B)
1
0
1
0
1
1
1
0
0
1
1
0 -
6 слайд
Пример 2.
Построим таблицу истинности для функции
F = X Y ¬Z
Переменных:
три (X, Y и Z), т.е. n = 3 количество строк: 2n=23=8.
С заголовком: 9
Количество столбцов:
3 переменные + 3 операции (,,¬).
Итого 6
Порядок операций:3 2 1
F = X Y ¬Z -
7 слайд
Пример. Таблица
0
0
0
0
1
1
1
1
F = X Y ¬Z
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
0
1
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1
1
(курс 68 ч.) §11. Логические выражения
Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, углубленный уровень)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, углубленный уровень) | §11. Логические выражения
Содержание урока
Формализация
Таблицы истинности
Составление условий
Логические схемы
Выводы
Вопросы и задания
Любую логическую функцию можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Построим таблицу истинности для выражения
X = А и не В или не А и B,
которое можно также записать в виде
X = А • B + А • В.
Сколько строк в таблице истинности выражения с двумя переменными?
Будем вычислять выражение по частям: добавим в таблицу истинности дополнительные столбцы А • B и А • В, а потом выполним операцию ИЛИ с этими значениями (рис. 2.18).
Рис. 2.18
Из этой таблицы истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.
Высказывание «Вася — школьник или он не учится в школе» всегда истинно (для любого Васи). Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.
Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение всегда ложно, оно называется тождественно ложным или противоречием.
Выполните формализацию высказываний, о которых шла речь в последних двух абзацах. Запишите формулы для упрощения каждого из них.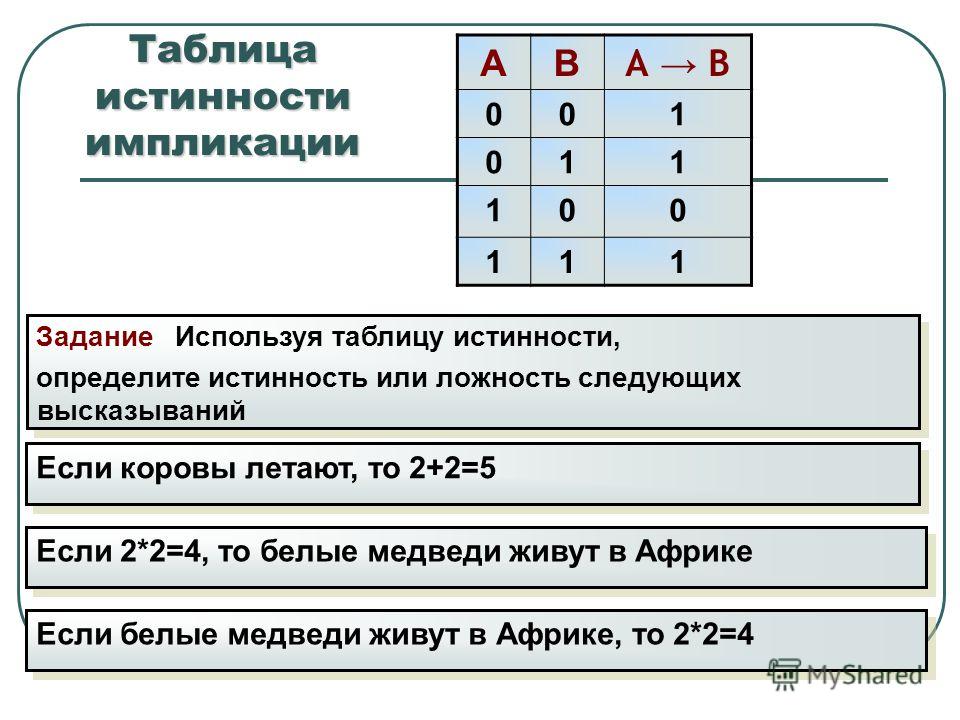
Постройте самостоятельна таблицу истинности логического выражения X = (А + В) • (A + B). Сравните её с таблицей на рис. 2.18. Истинно ли высказывание «Разные логические выражения могут определять одну и ту же логическую функцию»?
Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.
Сколько строк в таблице истинности выражения с тремя переменными?
Постройте таблицу истинности логического выражения
Х = А • В + А • С + В • С.
Предположим, что нам известна только часть таблицы истинности для функции трёх переменных (рис. 2.19).
Рис. 2.19
Как вы думаете, можно ли по такой части таблицы истинности определить логическую функцию? Почему?
Всего в таблице истинности функции от трёх переменных 23 = 8 строк, для каждой из них нужно знать, чему равно значение функции.
В нашем примере пять значений функции неизвестны, причём каждое из них может быть равно 0 или 1, т. е. у нас есть 5 свободных бит.
Сколько различных значений можно закодировать с помощью 5 бит?
Как вы нашли это значение?
Итак, таблице на рис. 2.19 могут соответствовать 32 различные логические функции. Проверим, подходят ли следующие варианты:
а) А + В + C;
б) A • С + В;
в) А + B • С;
г) А • В • C;
д) A • B + C.
Прежде всего, заметим, что в столбце значений функции два нуля и одна единица. Следовательно, вариант а) не подходит, потому что цепочка операций ИЛИ со всеми переменными (или их инверсиями, обратными значениями) даст только один ноль — в случае, когда все слагаемые равны нулю.
Проверяем вариант б), подставляя значения переменных А, В и С сначала из первой строки таблицы, потом из второй и третьей. В первой строке получаем A • С + В = 1 • 1 + 0 = 1, этот результат совпадает со значением функции в этой строке.
Для второй строки A • С + В = 1 • 1 + 1 = 1, значит, эта функция тоже не подходит.
Проверьте самостоятельно, подходят ли остальные варианты.
Скажите без вычислений, сколько нулей и сколько единиц должно быть в последнем столбце таблицы истинности функций с тремя переменными:
а) А + B + C;
б) A • С • В;
в) А • B • C;
г) A + В + С;
д) A + B + C.
Теперь предположим, что нам известна часть таблицы какой-то логической функции, причём с пропусками (рис. 2.20).
Рис. 2.20
Выясним, какие из следующих функций могут соответствовать этой таблице:
а) A + В + C;
б) A • С • В;
в) А + B + C;
г) А • B • С;
д) А + В + C.
Во-первых, обратим внимание, что в столбце значений функции две единицы, поэтому сразу делаем вывод, что это не могут быть цепочки двух операций И (ответы б) и г) неверные).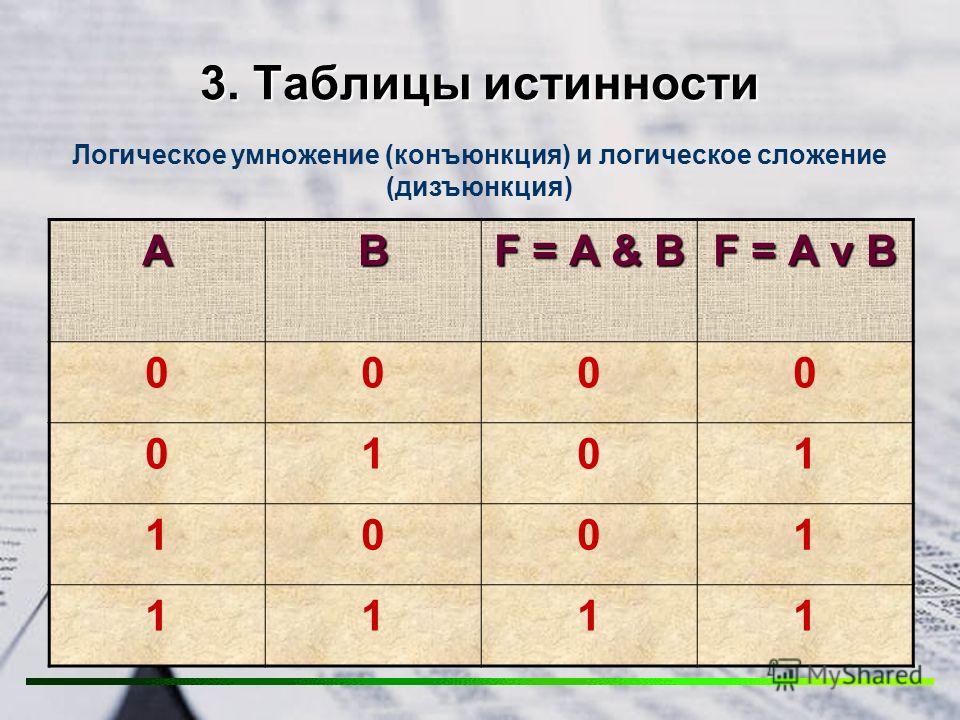
а) 1 + В + 0;
в) 0 + B + 0;
д) 0 + В + 0.
Видим, что в случае а) сумма не может быть равна нулю, это неверный ответ. А варианты в) и д) подходят: в первом из них нужно в первой строке поставить в пустую ячейку 1, а во втором — 0.
Кратко решение можно записать так:
1) поскольку в столбце значений функции один ноль, это не может быть цепочка операций И; остаются только цепочки операций ИЛИ;
2) для того чтобы получить нулевое значение функции в первой строке таблицы, нужно, чтобы переменная А (равная 0 в этой строке) входила в логическую сумму без инверсии (к ней не должна применяться операция НЕ) а переменная С (равная 1) — с инверсией;
3) этим условиям удовлетворяют функции в) и д).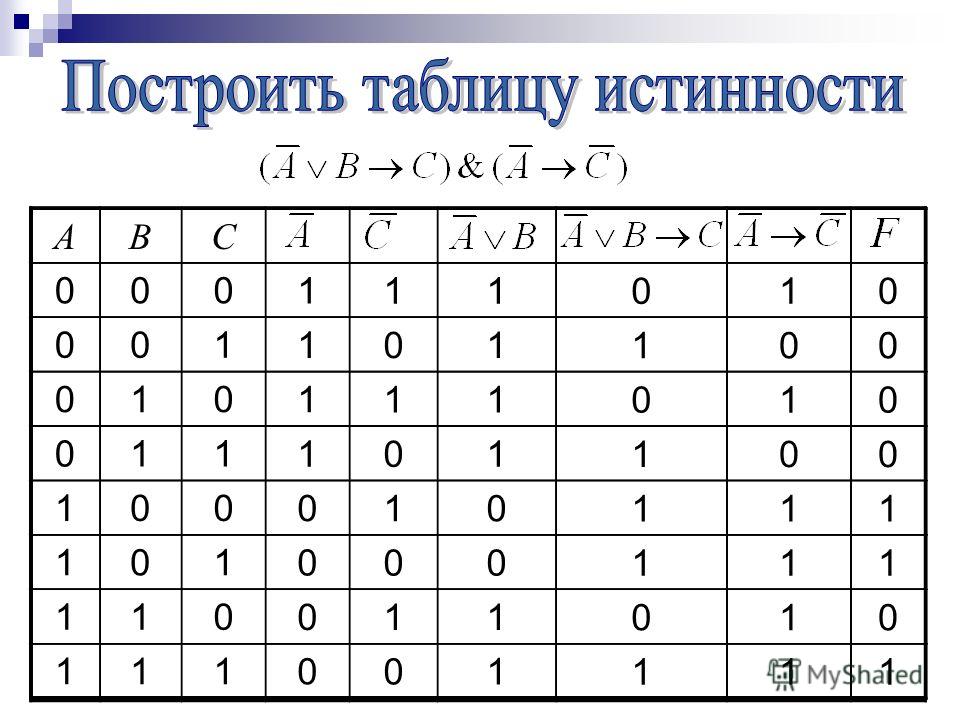
Известна часть таблицы какой-то логической функции с пропусками (рис. 2.21).
Рис. 2.21
Выясните, какие из следующих функций могут соответствовать этой таблице:
а) А • B + C;
б) A • С • В;
в) А + B + C;
г) А • B • С;
д) А + B + C.
Следующая страница Составление условий
Cкачать материалы урока
Таблица истинности логических выражений с примерами решения
Содержание:
- Свойства логических операций
- Законы алгебры логики могут быть доказаны с помощью таблиц истинности
- Примеры с решением
Построение таблиц истинности для логических выражений
Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных.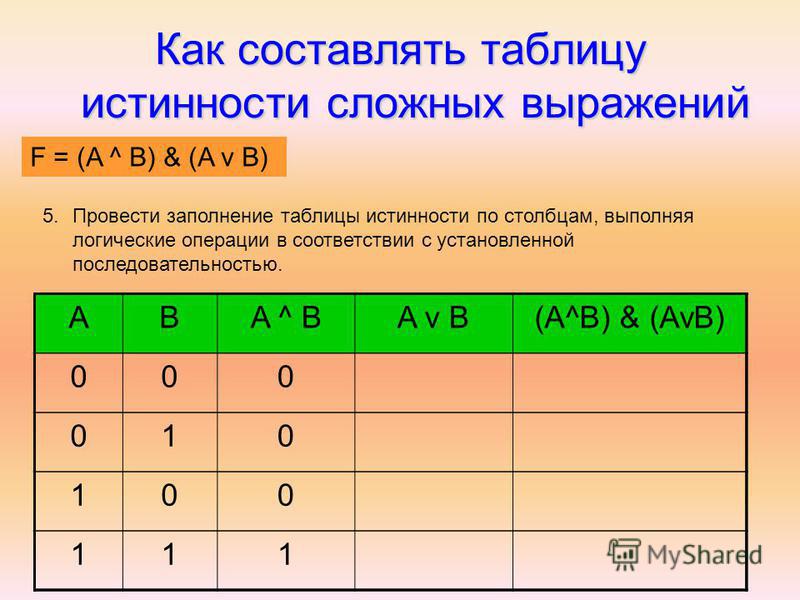
- подсчитать п — число переменных в выражении;
- подсчитать общее число логических операций в выражении;
- установить последовательность выполнения логических операций с учётом скобок и приоритетов;
- определить число столбцов в таблице: число переменных + число операций;
- заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в п. 3;
- определить число строк в таблице (не считая шапки таблицы): ;
- выписать наборы входных переменных с учётом того, что они представляют собой ряд целых п-разрядных двоичных чисел от 0 до ;
- провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
Построим таблицу истинности для логического выражения нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре столбца:
- Наборы входных переменных — это целые числа от 0 до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Высшая математика: лекции, формулы, теоремы, примеры задач с решением
Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение равносильно логической переменной А.
Возможно вам будут полезны данные страницы:
|
Интервал сходимости степенного ряда |
|
Примеры решений пределов с корнями |
|
Найти производную функции |
|
Уравнения касательной и нормали |
Свойства логических операций
Рассмотрим основные свойства логических операций, называемые также законами алгебры логики.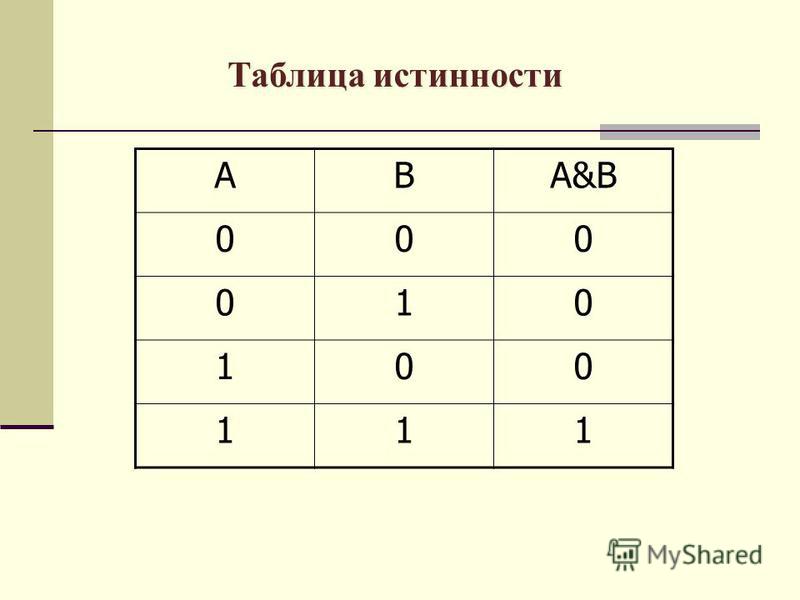
1. Переместительный (коммутативный) закон:
• для логического умножения:
• для логического сложения:
2. Сочетательный (ассоциативный) закон:
• для логического умножения:
• для логического сложения:
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
3. Распределительный (дистрибутивный) закон:
• для логического умножения:
• для логического сложения:
4. Закон двойного отрицания:
Двойное отрицание исключает отрицание.
5. Закон исключённого третьего:
• для логического умножения:
• для логического сложения:
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
6. Закон повторения:
• для логического умножения:
• для логического сложения:
7. Законы операций с 0 и 1:
• для логического умножения:
• для логического сложения:
8.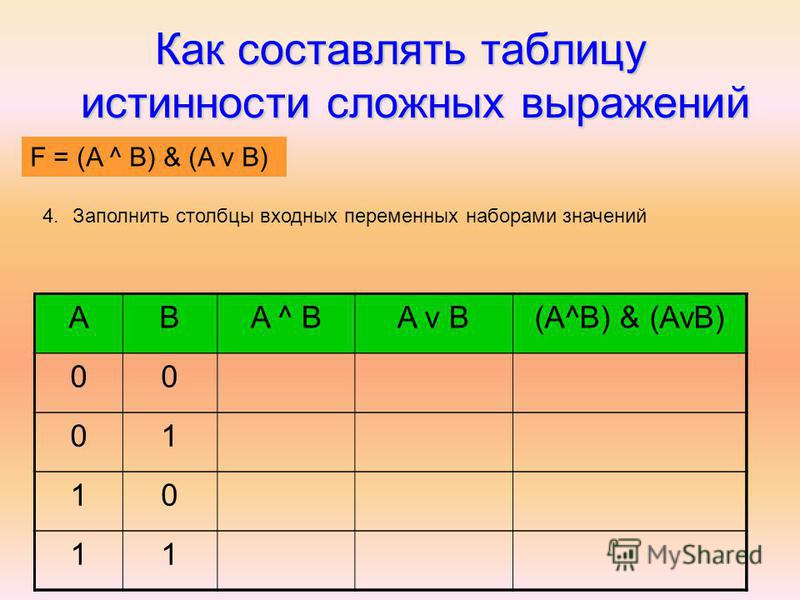
• для логического умножения:
• для логического сложения:
Законы алгебры логики могут быть доказаны с помощью таблиц истинности
Докажем распределительный закон для логического сложения:
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Примеры с решением
Пример 1.
Найдём значение логического выражения для числа X = 0.
Решение:
При X = 0 получаем следующее логическое выражение: . Так как логические выражения 0 < 3, 0 < 2 истинны, то, подставив их значения в логическое выражение, получаем:
Для решения задач вам понадобится знание таблиц истинности логических операций:
А также, вы должны знать:
Порядок выполнения логических операций задается круглыми скобками
Сначала выполняется операция отрицания НЕ
затем И
после И выполняется ИЛИ
затем следование
и в последнюю очередь — эквивалентность.
Задача 1
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
Решение:
Чтобы определить верное выражение, надо значения А,В,С каждой из строк таблицы подставить в очередное выражение, определить его результат выполнения и сравнить со значением F соответствующей строки.
То выражение, значения которого совпадут со значениями столбца F, и будет искомым. Решение:
Ответ: 4
Задача 2
Дан фрагмент таблицы истинности выражения F:
Каким выражением может быть F?
Решение:
Обратите внимание:
1) В каждом из приведенных выражений логические переменные связывает только один тип логической операции. В 1 и 3 вариантах это операция И (), во 2 и 4 вариантах это операция ИЛИ ().
2) По столбцу F видно, что выражение для двух комбинаций данных истинно, а для одной — ложно. Следовательно, выражение не может быть логическим умножением (И), так как логическое умножение истинно только для одной комбинации данных, а в таблице две истины.
Поэтому, в качестве ответа может быть 2 или 4 вариант. Рассмотрим их.
1) 2-й вариант: В первой строке таблицы истинности отображены только значения х1, хЗ, х5, и все они равны 0. Но в формуле 2го варианта у нас х5 отрицается, то есть значение х5 будет изменено на 1, и в результате всё выражение должно быть истинным. Что не соответствует заданной таблице. Остаётся 4-й вариант.
2) Как мы видим, переменные х1, хЗ и х5 в 4-м варианте ответа не отрицаются, что соответствует первой строке заданной таблицы.
Ответ: 4
Задача 4
Какое из приведенных имен сказочных героев удовлетворяет логическому условию:
1) АРТЕМОН
2) БАЗИЛИО
3) БУРАТИНО
4) МАЛЬВИНА
Решение:
Составим для каждого из предложенных ответов схему соответственно заданной логической формуле. Ищем истинное значение.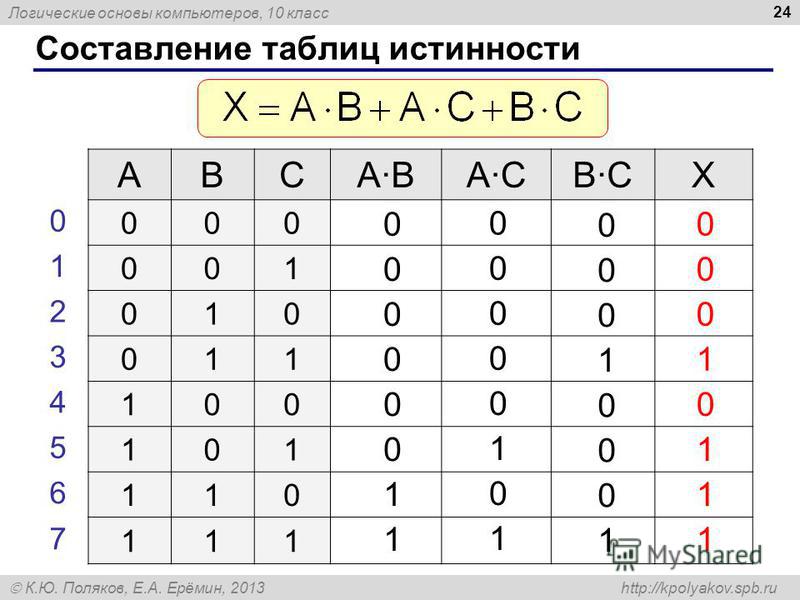
1) АРТЕМОН
Первая буква согласная — НЕТ (0)
Вторая буква не А — ДА (1)
Последняя буква гласная — НЕТ (0) / у
Предпоследняя буква гласная — ДА (1) X» ‘»X X»
Подставляем полученные значения в формулу и решаем ее: н 0 ->1 ) л 0 -> 1 ),= О
И так с каждым вариантом ответа, пока не найдете истину.
Задача 5
Логическая функция F задаётся выражением
Определите, какому столбцу таблицы истинности функции F соответствует каждая из
переменных X, Y, Z
Решение 1:
Последней операцией выполнения является операция . Поэтому выражение имеет значение ИСТИНА, когда
Рассмотрим все случаи, когда F = 1 (это значения в строках 1 и 3): — не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.
Рассматриваем только 1 и 3 строки таблицы:
- две единицы в 3-м столбце => это значения X
- два нуля в 1-м столбце => это значения Y
- ноль единица во 2-м столбце => это значения Z
Ответ: YZX
Решение 2:
Последней операцией выполнения является операция .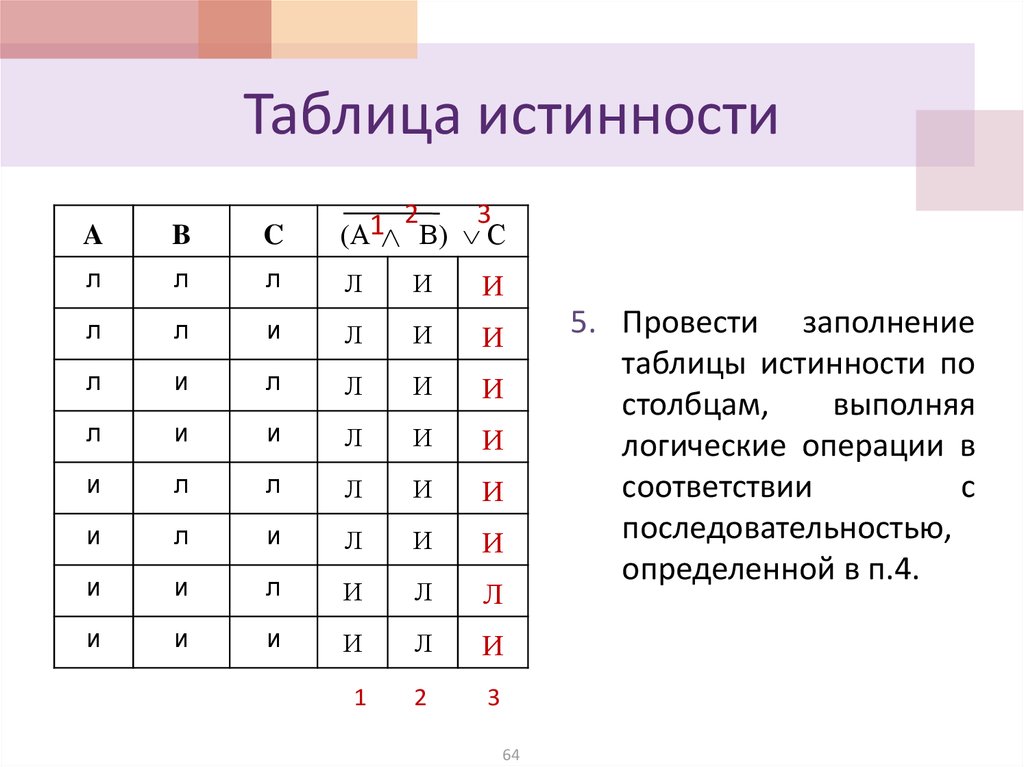
имеет значение ИСТИНА, когда
Выражение F равно 1 в 1й и Зй строках, в этих же строках только “Перем.3”=1, следовательно, значение X находится в 3-м столбце.
Теперь рассмотрим построчно значения 1-х двух столбцов:
(помним, что 1 -> 0 = 0, в остальных комбинациях =1)
1 строка: 0 и О, Y = Z. Поэтому Y и Z для столбцов не определить.
2 строка: 0 и 1. Независимо будет ли Y=0 Z=1 или Y=1 Z=0, функция F=0 т.к. уже
Х=0. Поэтому Y и Z для столбцов не определить.
3 строка: 0 и 1. В этой строке функция F=1, значит Комбинация
невозможна, иначе F будет = 0. Комбинация то, что надо. Следовательно, значение Y находится в 1-м столбце а значение Z во 2-м.
Ответ: YZX
Алгоритм построения таблицы истинности
|
Заглавная страница КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 11Следующая ⇒ При построении таблицы истинности целесообразно руководствоваться определенной последовательностью действий. 1. Определите количество строк в таблице. Если количество логических переменных равно n, то количество строк = 2n. 2. Определите количество столбцов, которое будет равно количеству переменных + количество логических операций. 3. Постройте таблицу, заполните шапку и внесите возможные наборы значений исходных логических переменных. 4. Заполните таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности. Пример 1. Для формулы A & (B V C) построить таблицу истинности. Количество логических переменных 3, следовательно, количество строк – 23 = 8. Количество логических операций в формуле – 2. Количество столбцов равно 2 + 3 = 5. Далее строим таблицу истинности по заданному алгоритму. Таблица 13 -Таблица истинности
Исходные данные 1. Таблица 14 -Фрагмент таблицы истинности выражения F
Какое выражение соответствует F: a) X V Y V Z; b) X & Y & Z; c) X & Y & Z; d) X V Y V Z. Для того чтобы определить, какое выражение соответствует F, необходимо составить фрагменты таблиц истинности для всех приведенных вариантов. 2. По заданному преподавателем варианту из таблицы 15 составить таблицу истинности для заданной формулы. При каких значениях A, B. Таблица 15- Выбор исходных данных
Содержание отчета 1. Номер, название темы практического занятия. 2. Цель практического занятия. 3. Результаты выполнения работы: построение таблиц истинности. 4. Выводы по работе. Контрольные вопросы 1. Перечислите основные логические операции. 2. Заполните таблицы истинности для следующих логических операций: логического отрицания, дизъюнкции, конъюнкции. 3. Поясните, в каком случае строится таблица истинности. 4. Скажите, чему равно количество строк в таблице истинности. 5. Скажите, чему равно количество столбцов в таблице истинности. 6. Сформулируйте алгоритм заполнения таблицы истинности для сложной логической формулы. Практическая работа 4 «Построение логических схем по заданным выражениям» Цель: изучить основные логические элементы, научиться строить логические схемы по заданным логическим выражениям. Теоретические сведения Основой всех компьютерных устройств, построенных по цифровому принципу, являются логические элементы – преобразователи. Логические элементы (преобразователи) могут, получая сигналы об истинности отдельных простых высказываний, обработать их и в результате выдать значение логического произведения или логической суммы, или отрицания. Из логических элементов (вентилей) составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом), становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе. Логический элемент И реализует конъюнкцию двух или более логических значений (табл. 16). Таблица 16 -Логический элемент И
Логический элемент ИЛИ реализует дизъюнкцию двух или более логических значений (табл. Таблица 17-Логический элемент ИЛИ
Логический элемент НЕ реализует логическую функцию «инверсия» (табл. 18). Таблица 18 -Логический элемент НЕ
|
Как составить таблицу истинности
Как составить таблицу истинности
|
Домашняя страница |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Философия 103: Введение в логику Как составить таблицу истинности Аннотация: Объясняются и иллюстрируются общие принципы построения таблиц истинности.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Отправляйте исправления или предложения по адресу [email protected] |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Аргументы | |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.
|
[произошла ошибка при обработке этой директивы]
Как составить таблицу истинности за девять простых шагов
Как составить таблицу истинности за девять простых шагов
Философия 4: Логика и Критика
Думая
Сьерра-колледж
Осень 2004 г.
Инструктор: Аль Чинелли
Шаг 1. Выясните, сколько отдельных
переменные утверждения находятся в аргументе или составном утверждении, которое вы будете анализировать, т.е.
сколько человек письма, представляющие пункты формулы .
Пример 1.
Вот аргумент: A -> (B v C)
~B
~C
/ ~А
Аргумент содержит три
переменные индивидуального требования : A, B, C.
Шаг 2. Каждая переменная утверждения имеет две истины
значения: Истина
или Ложь.
Вот полезная формула
чтобы узнать, сколько строк вам понадобится для таблицы истинности:
Возьмите общее количество независимых
переменные претензии, которые вам нужно построить, и сделать это показателем степени 2. Значение
для этого показателя — количество необходимых строк.
Один
переменная требования: P = две строки, 2 1 .
Два
переменные: P, Q = четыре строки, 2 2 .
Три
переменные: P, Q, R = восемь строк, 2 3 .
Четыре
переменные: P, Q, R, S = шестнадцать строк, 2 4 и так далее.
Пример 2. Аргумент в примере
1 имеет три отдельные переменные заявки.
Следовательно
его таблица истинности будет состоять из восьми строк.
Шаг 3.
утверждение и составное утверждение в утверждении или аргументе, который вы анализируете.
Сделать отдельные столбцы для:
i) отдельные требования, представленные буквами переменных требований, ii)
скобочные претензии (претензии внутри претензии), iii) все помещения и iv)
заключение рассуждения.
Пример 3. Аргумент в примере
у одного есть восемь отдельных утверждений: A, B, C, (B v C), A -> (B v C), ~ B, ~ C и
~А.
Шаг 4. Ваша таблица истинности должна содержать
полные возможности истинности для всех утверждений. Для этого нужно перечислить
возможности истинности для каждой переменной утверждения.
Возьмите первую переменную претензии, назначьте
это значение T для верхней половины строк и F для нижней половины.
Затем возьмите вторую переменную претензии
и присвойте ему значение T для первой и третьей четвертей строк.
Для третьей переменной претензии присвоить
Значения T и F для чередующихся восьмых строк и чередующихся шестнадцатых
для четвертой переменной, чередуя тридцать секунд и шестьдесят четвертых для
переменные пятого и шестого индивидуальных требований.
Продолжайте назначать значения истинности попеременно
соответствующими показателями двух для каждой дополнительной индивидуальной переменной претензии.
Пример 4.
Присвоения значений истинности для отдельных переменных утверждения для аргумента в
пример 1.
|
А |
Б |
С |
Б против С |
А -> (Б против С) |
~Б |
~С |
~А |
|
Т |
Т |
Т |
|||||
|
Т |
Т |
Ф |
|||||
|
Т |
Ф |
Т |
|||||
|
Т |
Ф |
Ф |
|||||
|
Ф |
Т |
Т |
|||||
|
Ф |
Т |
Ф |
|||||
|
Ф |
Ф |
Т |
|||||
|
Ф |
Ф |
Ф |
Шаг 5. Назначьте соответствующие значения истинности
к составным утверждениям, основанным на: а) значениях истинности отдельного утверждения
переменные и б) логическая связь между более простыми утверждениями в
Претензия к компонентам. Работайте от самых простых составных утверждений к самым сложным.
Пример 5. Присвоение значения истинности
для всех переменных утверждений для аргумента в примере 1.
|
А |
Б |
С |
Б против С |
А -> (Б против С) |
~Б |
~С |
~А |
|
Т |
Т |
Т |
Т |
Т |
Ф |
Ф |
Ф |
|
Т |
Т |
Ф |
Т |
Т |
Ф |
Т |
Ф |
|
Т |
Ф |
Т |
Т |
Т |
Т |
Ф |
Ф |
|
Т |
Ф |
Ф |
Ф |
Ф |
Т |
Т |
Ф |
|
Ф |
Т |
Т |
Т |
Т |
Ф |
Ф |
Т |
|
Ф |
Т |
Ф |
Т |
Т |
Ф |
Т |
Т |
|
Ф |
Ф |
Т |
Т |
Т |
Т |
Ф |
Т |
|
Ф |
Ф |
Ф |
Ф |
Т |
Т |
Т |
Т |
Шаг 6. Если вы строите график одного соединения
утверждение в таблице истинности, сравните его с другими утверждениями, которые вы построили. Если
значения истинности утверждения эквивалентны для одних и тех же назначений истинности
переменные индивидуального утверждения, то два составных утверждения эквивалентны.
Шаг 7. Чтобы определить действительность
аргумент, установить возможные значения истинности для всех отдельных аргументов
переменные претензии, составные претензии, предпосылки и вывод. Вычеркнуть все строки
в котором вывод верен. Затем вычеркните все строки, в которых есть какие-либо или
все посылки ложны. Если строк не осталось, то аргумент
является действительным. Если есть одна или несколько строк, содержащих все назначенные помещения
значение T, в то время как заключение ложно, аргумент недействителен.
Пример 7а. Удалите строки, в которых
вывод верный.
|
А |
Б |
С |
Б против С |
P1: А -> (Б против С) |
Ч2: ~В |
Р3: ~С |
Конц. |
|
Т |
Т |
Т |
Т |
Т |
Ф |
Ф |
Ф |
|
Т |
Т |
Ф |
Т |
Т |
Ф |
Т |
Ф |
|
Т |
Ф |
Т |
Т |
Т |
Т |
Ф |
Ф |
|
Т |
Ф |
Ф |
Ф |
Ф |
Т |
Т |
Ф |
Пример 7б.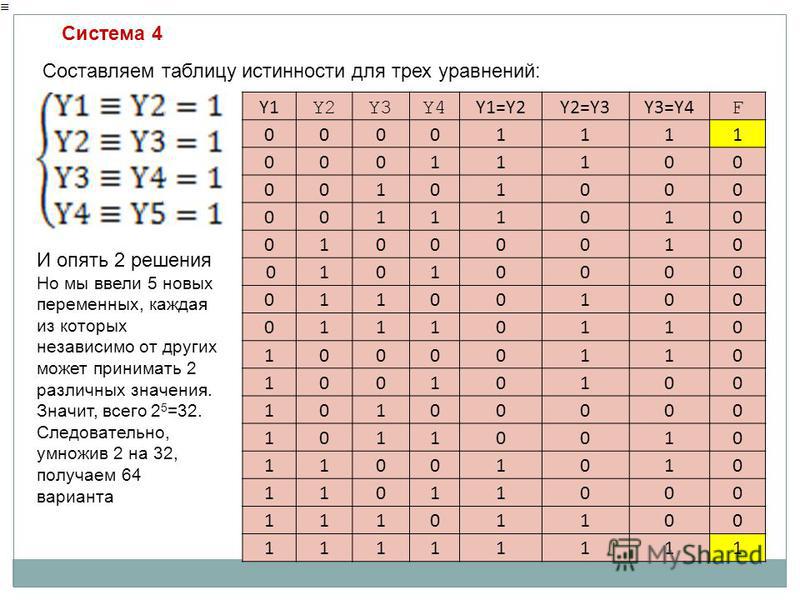
являются ложными.
|
P1: А -> (Б против С) |
Р2: ~В |
Р3: ~С |
Конц.: ~A |
|
|
х |
Т |
Ф |
Ф |
Ф |
|
х |
Т |
Ф |
Т |
Ф |
|
х |
Т |
Т |
Ф |
Ф |
|
х |
Ф |
Т |
Т |
Ф |
Все остальные строки
содержат хотя бы одну ложную посылку, следовательно, аргумент верен.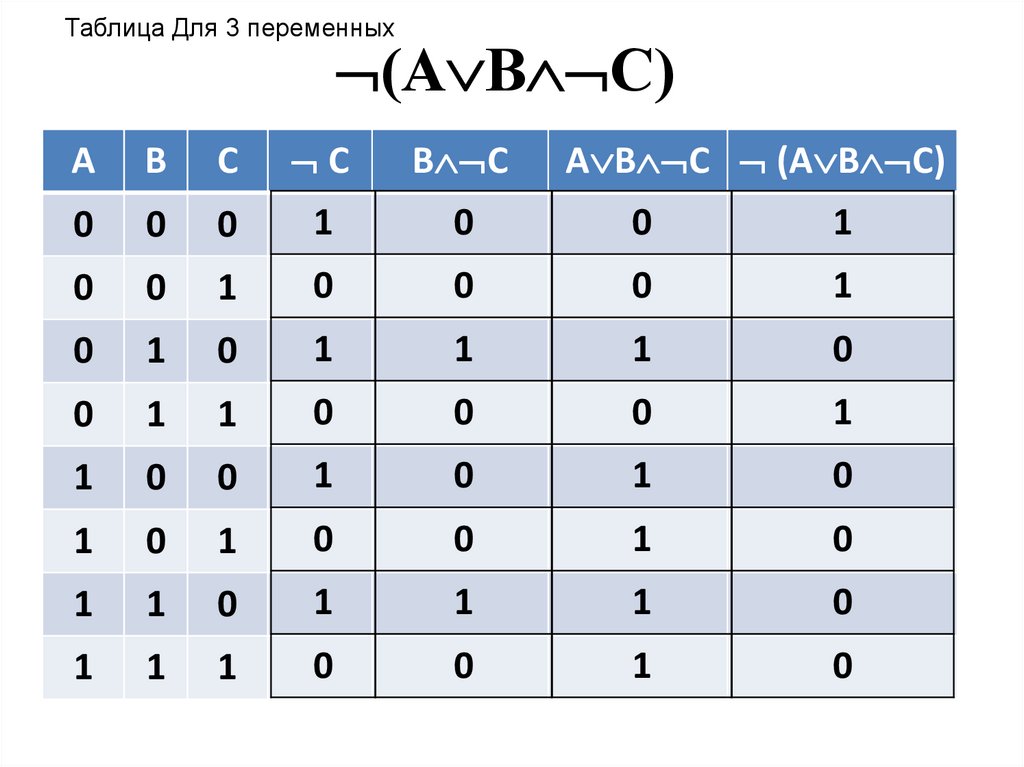
Шаг 8. Для определения достоверности с помощью
Версия таблиц истинности с «короткой таблицей», отображающая все столбцы обычной истины.
таблицу, затем создайте одну или две строки, где вы назначаете вывод об истине
значение F и присвоить всем посылкам значение T.
Пример 8. Два
ряды с ложным выводом.
|
А |
Б |
С |
Б против С |
P1: А -> (Б против С) |
Ч2: ~В |
Р3: ~С |
Конц.: ~A |
|
Т |
Т |
Т |
Ф |
Шаг 9.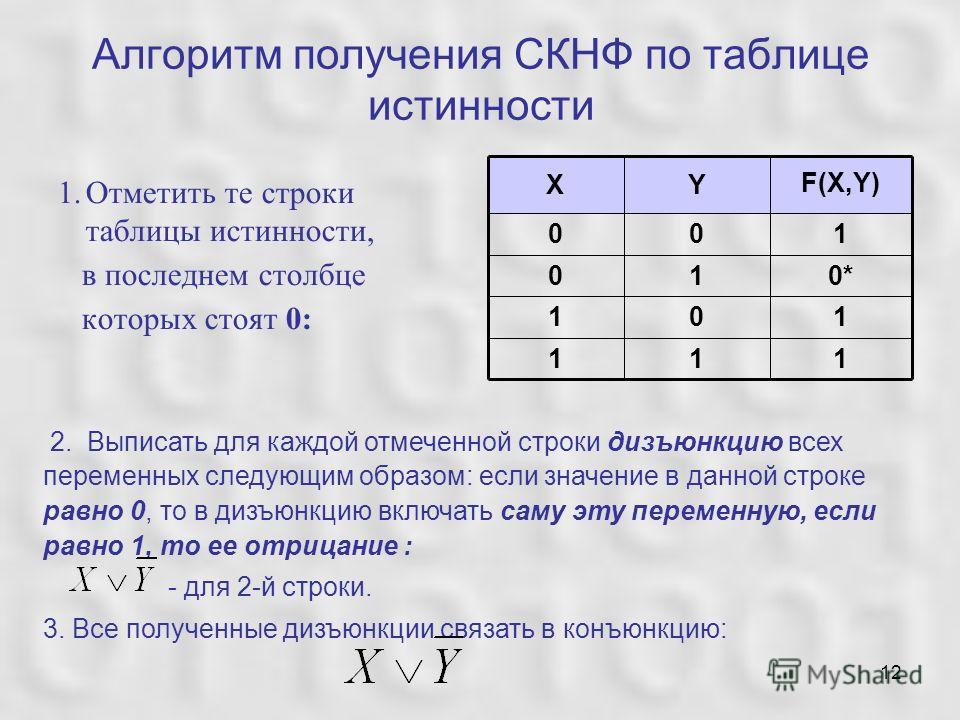
Можете ли вы присвоить значения истинности
составные претензии и переменные индивидуальных претензий, которые согласуются с
значения истинности, присвоенные посылкам и заключению?
Если сможете, продемонстрируйте, что
аргумент неверный. Если вы не можете, это означает, что аргумент действителен.
Некоторые пробы и ошибки
здесь может понадобиться.
Пример 9. Если вы знаете, что ~A
неверно, что еще можно вывести? Присвойте истинностное значение T помещениям. Будут
эта работа?
|
А |
Б |
С |
Б против С |
P1: А -> (Б против С) |
Р2: ~В |
Р3: ~С |
Конц. |
|
Т |
Ф |
Ф |
хххх |
Т |
Т |
Т |
Ф |
(B v C) должно быть правдой
чтобы P:1 было правдой. (B v C) не может быть истинным, если B и C оба ложны.
2.8: Таблицы истинности — K12 LibreTexts
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2146
Пока мы знаем эти символы для логики:
- (sim) не (отрицание)
- (стрелка вправо) если-то
- (поэтому) поэтому
Еще два символа:
- (клин) и
- (лор) или
Мы бы написали «(p) и (q)» как (pклин q) и «(p) или (q)» как (plor q) .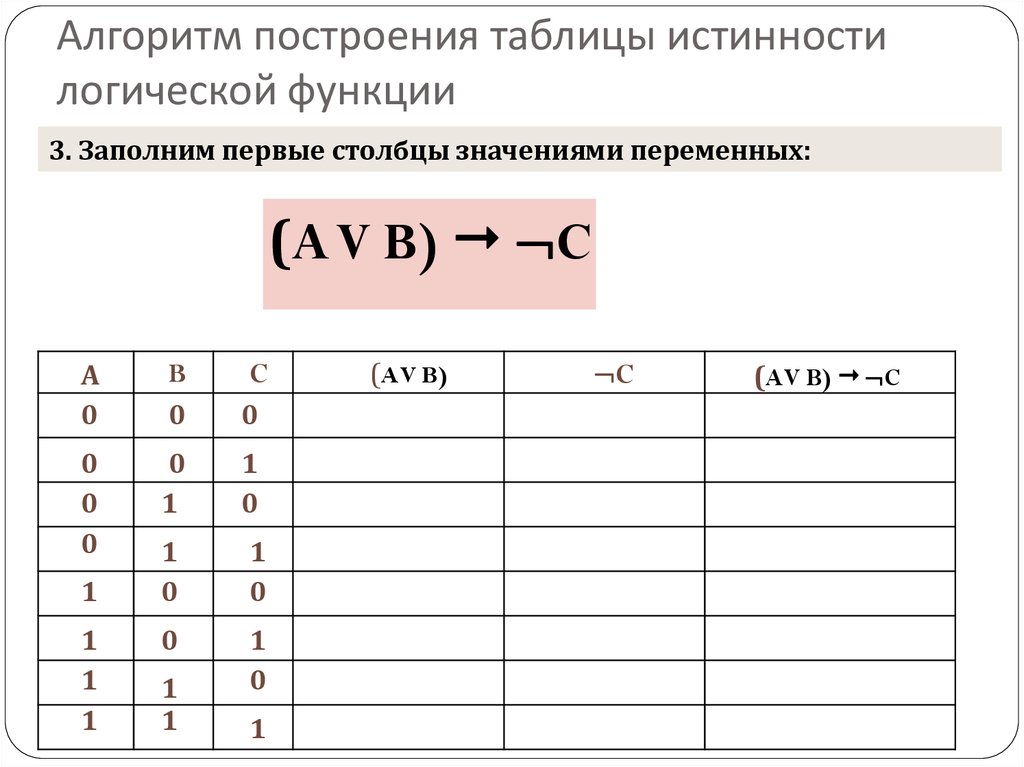
Таблицы истинности используют эти символы и представляют собой еще один способ анализа логики. Во-первых, давайте свяжем p и sim p. Чтобы было проще, установите p как: Четное число. Следовательно, sim p равно Нечетное число . Составьте таблицу истинности, чтобы узнать, верны ли они оба. Начните со всех «истин» p, истинных (T) или ложных (F).
Далее мы записываем соответствующие значения истинности для (sim p). (sim p) имеет значения истинности, противоположные (p). Итак, если (p) истинно, то (sim p) ложно, и наоборот.
| стр | sim p |
|---|---|
| Т | Ф |
| Ф | Т |
Резюме:
- Начать таблицы истинности со всеми возможными комбинациями истин.
Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом.
- Выполните отрицание любой из переменных.
- Любые комбинации в скобках.
- Завершите выполнение того, о чем просила проблема.
Составление таблицы истинности
1. Нарисуйте таблицу истинности для (p), (q) и (p клин q).
Сначала создайте столбцы для p и q. Заполните столбцы всеми возможными истинными и ложными комбинациями для этих двух.
| р | к | |
|---|---|---|
| Т | Т | |
| Т | Ф | |
| Ф | Т | |
| Ф | Ф |
Обратите внимание на все комбинации p и q.
Далее нам нужно выяснить, когда (pwedge q) истинно, основываясь на первых двух столбцах. p wedge q может быть истинным только в том случае, если ОБА p и q истинны. Итак, заполненная таблица выглядит так:
Рисунок (PageIndex{1})
Так всегда заполняется таблица истинности с двумя переменными и их столбцом «и».
2. Нарисуйте таблицу истинности для (p), (q) и (p lor q).
Сначала создайте столбцы для (p lor q) и (q), как в примере A.
| стр | к | |
|---|---|---|
| Т | Т | |
| Т | Ф | |
| Ф | Т | |
| Ф | Ф |
Далее нам нужно выяснить, когда (p или q) истинно, основываясь на первых двух столбцах.
Рисунок (PageIndex{2})
Разница между (p wedge q) и (p lor q) во второй и третьей строках. Для «и» оба (p) и (q) должны быть истинными, но для «или» только одно должно быть истинным.
Определение истинности переменных
Определите истинность для (p клин(sim q lor r)).
Во-первых, есть три переменных, поэтому нам понадобятся все комбинации их истинности. Для трех переменных всегда есть 8 возможных комбинаций.
| (р) | (к) | (р) | |||
|---|---|---|---|---|---|
| Т | Т | Т | |||
| Т | Т | Ф | |||
| Т | Ф | Т | |||
| Т | Ф | Ф | |||
| Ф | Т | Т | |||
| Ф | Т | Ф | |||
| Ф | Ф | Т | |||
| Ф | Ф | Ф |
Далее адрес (sim q).
| (р) | (к) | (р) | (sim q) | ||
|---|---|---|---|---|---|
| Т | Т | Т | Ф | ||
| Т | Т | Ф | Ф | ||
| Т | Ф | Т | Т | ||
| Т | Ф | Ф | Т | ||
| Ф | Т | Т | Ф | ||
| Ф | Т | Ф | Ф | ||
| Ф | Ф | Т | Т | ||
| Ф | Ф | Ф | Т |
Теперь давайте сделаем то, что указано в скобках, (sim qlor r).
| (р) | (к) | (р) | (sim q) | (sim qlor r) | |
|---|---|---|---|---|---|
| Т | Т | Т | Ф | Т | |
| Т | Т | Ф | Ф | Ф | |
| Т | Ф | Т | Т | Т | |
| Т | Ф | Ф | Т | Т | |
| Ф | Т | Т | Ф | Т | |
| Ф | Т | Ф | Ф | Ф | |
| Ф | Ф | Т | Т | Т | |
| Ф | Ф | Ф | Т | Т |
Наконец, мы можем решить всю проблему, (p wedge(sim q lor r)).
| (р) | (к) | (р) | (sim q) | (sim qlor r) | (p клин(sim q lor r)) |
|---|---|---|---|---|---|
| Т | Т | Т | Ф | Т | Т |
| Т | Т | Ф | Ф | Ф | Ф |
| Т | Ф | Т | Т | Т | Т |
| Т | Ф | Ф | Т | Т | Т |
| Ф | Т | Т | Ф | Т | Ф |
| Ф | Т | Ф | Ф | Ф | Ф |
| Ф | Ф | Т | Т | Т | Ф |
| Ф | Ф | Ф | Т | Т | Ф |
Построение таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.
Онлайн калькулятор позволяет быстро строить таблицу истинности для произвольной булевой функции или её вектора, рассчитывать совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы, находить представление функции в виде полинома Жегалкина, строить карту Карно и классифицировать функцию по классам Поста.
Калькулятор таблицы истинности, СКНФ, СДНФ, полинома Жегалкина
введите функцию или её вектор
Скрыть клавиатуру
∨
∧
¬
⊕
→
≡
↓
↑
0
1
a
b
c
x
y
z
(
)
X1
X2
X3
X4
X5
X6
Показать настройки
Таблица истинности
СКНФ
СДНФ
Полином Жегалкина
Классификация Поста
Минимизация, карта Карно
Фиктивные переменные
С решением
Построить
Построено таблиц, форм:
Как пользоваться калькулятором
- Введите в поле логическую функцию (например, x1 ∨ x2) или её вектор (например, 10110101)
- Укажите действия, которые необходимо выполнить с помощью переключателей
- Укажите, требуется ли вывод решения переключателем “С решением”
- Нажмите на кнопку “Построить”
Видеоинструкция к калькулятору
Используемые символы
В качестве переменных используются буквы латинского и русского алфавитов (большие и маленькие), а также цифры, написанные после буквы (индекс переменной). Таким образом, именами переменных будут: a, x, a1, B, X, X1, Y1, A123 и так далее.
Для записи логических операций можно использовать
как обычные символы клавиатуры (*, +, !, ^, ->, =), так и символы, устоявшиеся в литературе (∧, ∨, ¬, ⊕, →, ≡). Если на вашей клавиатуре отсутствует нужный символ операции, то используйте клавиатуру калькулятора (если она не видна, нажмите “Показать клавиатуру”), в которой доступны как все логические операции, так и набор наиболее часто используемых переменных.
Для смены порядка выполнения операций используются круглые скобки ().
Обозначения логических операций
- И (AND):
&•∧* - ИЛИ (OR):
∨+ - НЕ (NOT):
¬! - Исключающее ИЛИ (XOR):
⊕^ - Импликация:
->→=> - Эквивалентность:
=~≡<=> - Штрих Шеффера:
↑| - Стрелка Пирса:
↓
Что умеет калькулятор
- Строить таблицу истинности по функции
- Строить таблицу истинности по двоичному вектору
- Строить совершенную конъюнктивную нормальную форму (СКНФ)
- Строить совершенную дизъюнктивную нормальную форму (СДНФ)
- Строить полином Жегалкина (методами Паскаля, треугольника, неопределённых коэффициентов)
- Определять принадлежность функции к каждому из пяти классов Поста
- Строить карту Карно
- Минимизировать ДНФ и КНФ
- Искать фиктивные переменные
Что такое булева функция
Булева функция f(x1, x2, ... xn) — это любая функция от n переменных x1, x2, … xn, в которой её аргументы принимают одно из двух значений: либо 0, либо 1, и сама функция принимает значения 0 или 1. То есть это правило, по которому произвольному набору нулей и единиц ставится в соответствие значение 0 или 1. Подробнее про булевы функции можно посмотреть на Википедии.
Что такое таблица истинности?
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов. Таблица состоит из n+1 столбцов и 2n строк, где n – число используемых переменных. В первых n столбцах записываются всевозможные значения аргументов (переменных) функции, а в n+1-ом столбце записываются значения функции, которые она принимает на данном наборе аргументов.
Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.
Логические операции
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых. В качестве основных операций обычно называют конъюнкцию (∧ или &), дизъюнкцию (∨ или |), импликацию (→), отрицание (¬), эквивалентность (=), исключающее ИЛИ (⊕).
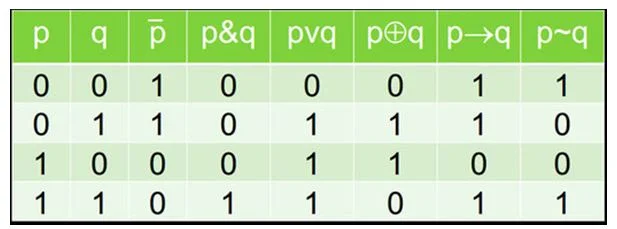
Таблица истинности логических операций
Как задать логическую функцию
Есть множество способов задать булеву функцию:
- таблица истинности
- характеристические множества
- вектор значений
- матрица Грея
- формулы
Рассмотрим некоторые из них:
Чтобы задать функцию через вектор значений необходимо записать вектор из 2n нулей и единиц, где n – число аргументов, от которых зависит функция. Например, функцию двух аргументов можно задать так: 0001 (операция И), 0111 (операция ИЛИ).
Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c
Способы представления булевой функции
С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:
- Совершенная дизъюнктивная нормальная форма (СДНФ)
- Совершенная конъюнктивная нормальная форма (СКНФ)
- Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Совершенная дизъюнктивная нормальная форма (ДНФ)
Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.
Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.
Например, ДНФ является функция ¬abc ∨ ¬a¬bc ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.
Совершенная конъюнктивная нормальная форма (КНФ)
Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.
Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.
Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.
Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.
Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.
Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1
Алгоритм построения СДНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 1
- Выписать простые конъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 0, то она входит в конъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые конъюнкции с помощью дизъюнкции
Алгоритм построения СКНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 0
- Выписать простые дизъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 1, то она входит в дизъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые дизъюнкции с помощью конъюнкции
Алгоритм построения полинома Жегалкина булевой функции
Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.
- Построить таблицу истинности для функции
- Добавить новый столбец к таблице истинности и записать в 1, 3, 5… ячейки значения из тех же строк предыдущего столбца таблицы истинности, а к значениям в строках 2, 4, 6… прибавить по модулю два значения из соответственно 1, 3, 5… строк.
- Добавить новый столбец к таблице истинности и переписать в новый столбец значения 1, 2, 5, 6, 9, 10… строк, а к 3, 4, 7, 8, 11, 12… строкам аналогично предыдущему пункту прибавить переписанные значения.
- Повторить действия каждый раз увеличивая в два раза количество переносимых и складываемых элементов до тех пор, пока длина не станет равна числу строк таблицы.
- Выписать булевы наборы, на которых значение последнего столбца равно единице
- Записать вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора записать единицу) и объединить их с помощью операции исключающего ИЛИ.
Примеры построения различных представлений логических функций
Построим совершенные дизъюнктивную и дизъюнктивную нормальные формы, а также полином Жегалкина для функции трёх переменных F = ¬ab∨¬bc∨ca
1. Построим таблицу истинности для функции
Построение совершенной дизъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает истинное значение: { 0, 0, 1 } { 0, 1, 0 } { 0, 1, 1 } { 1, 0, 1 } { 1, 1, 1 }
В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:
K1: { 0, 0, 1 } — ¬a¬bc
K2: { 0, 1, 0 } — ¬ab¬c
K3: { 0, 1, 1 } — ¬abc
K4: { 1, 0, 1 } — a¬bc
K5: { 1, 1, 1 } — abc
Объединим конъюнкции с помощью дизъюнкции и получим совершенную дизъюнктивную нормальную форму:
K1 ∨ K2 ∨ K3 ∨ K4 ∨ K5 = ¬a¬bc ∨ ¬ab¬c ∨ ¬abc ∨ a¬bc ∨ abc
Построение совершенной конъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает ложное значение: { 0, 0, 0 } { 1, 0, 0 } { 1, 1, 0 }
В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:
D1: { 0, 0, 0 } — a∨b∨c
D2: { 1, 0, 0 } — ¬a∨b∨c
D3: { 1, 1, 0 } — ¬a∨¬b∨c
Объединим дизъюнкции с помощью конъюнкции и получим совершенную конъюнктивную нормальную форму:
D1 ∧ D2 ∧ D3 = (a∨b∨c) ∧ (¬a∨b∨c) ∧ (¬a∨¬b∨c)
Построение полинома Жегалкина:
Добавим новый столбец к таблице истинности и запишем в 1, 3, 5 и 7 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 2, 4, 6 и 8 сложим по модулю два со значениями из соответственно 1, 3, 5 и 7 строк:
Добавим новый столбец к таблице истинности и запишем в 1 и 2, 5 и 6 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 3 и 4, 7 и 8 сложим по модулю два со значениями из соответственно 1 и 2, 5 и 6 строк:
Добавим новый столбец к таблице истинности и запишем в 1 2, 3 и 4 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 5, 6, 7 и 8 сложим по модулю два со значениями из соответственно 1, 2, 3 и 4 строк:
Окончательно получим такую таблицу:
Выпишем наборы, на которых получившийся вектор принимает единичное значение и запишем вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора следует записать единицу):
{ 0, 0, 1 } — c, { 0, 1, 0 } — b, { 0, 1, 1 } — bc, { 1, 1, 0 } — ab, { 1, 1, 1 } — abc
Объединяя полученные конъюнкции с помощью операции исключающего или, получим полином Жегалкина: c⊕b⊕bc⊕ab⊕abc
План урока:
Способы решению задач по логике
Табличный способ – этапы, особенности
Сравнение методов решения
Построение таблиц истинности для различных типов задач
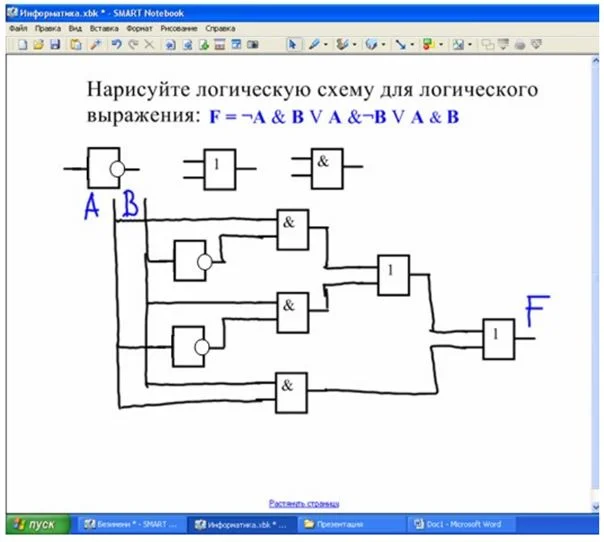
Построение электрических схем, реализующих логические операции
Способы решения задач по логике
Многие задачи можно решить, используя инструменты алгебры логики. Чтобы получить результат, можно пойти 3 путями:
- рассуждая над условием;
- решая логические операции;
- используя таблицы истинности.
Логический подход подразумевает перевод условия из естественного языка на язык символов, схем и формул. Для такой формализации высказываний нужно выполнить ряд шагов.
Этапы решения логических задач:
- Разобраться с условием на естественном языке, выделив простые высказывания, и дать им символьные обозначения (латиница).
- Записать условие в виде формулы. Решить ее поэтапно, упрощая, учитывая приоритеты (( ), ¬, &, V).
- Просчитать формулы строчно или при помощи таблиц истинности, учитывая законы алгебры логики.
- Проверить, соответствует ли полученный результат условию задачи.
Табличный способ – этапы, особенности
Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.
Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи.
Метод таблиц
Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.
Существует общий алгоритм построения таблиц:
- Определить число логических значений/переменных (n) в примере.
- Установить вид, число и тип операций. Важно заранее определить очередность действий, выразить это при помощи скобок.
- Полученные данные позволяют рассчитать сколько нужно столбцов – это сумма числа переменных и операций.
- Нарисовать таблицу, заполнить шапку, записав обозначение переменных и выбранные действия.
- Определить, сколько существует наборов логических переменных (т.е. число строчек) по формуле m = 2n+ 1 (шапка).
- Заполнить столбцы, вписав наборы значений логических переменных (0 или 1).
- Записать результаты логических операций, указанных в шапке для каждой совокупности значений.
- Сделать выводы на основании полученных результатов.
Если необходимо перебрать все значения простых выражений, то для задач:
- с 2-мя переменными может быть только 4 набора логических переменных;
Если словесно описывать все эти комбинаций, на каждый из примеров понадобится десятки строк текста.
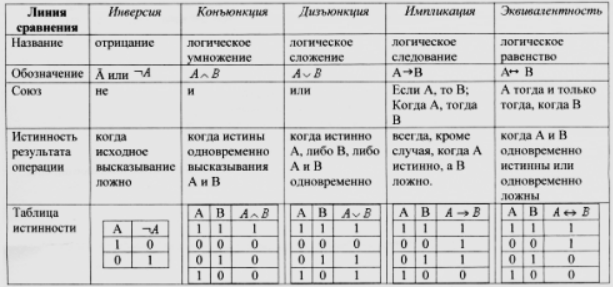
Обязательно учитывают приоритет операций:
- Указанные в скобках.
- Отрицание.
- Логическая конъюнкция чисел.
- Дизъюнкция.
- Строгая дизъюнкция.
- Импликация.
- Эквивалентность.
Обозначение логических операций:
Сравнение методов решения
Метод рассуждений
Он заключается в пошаговом анализе условий с промежуточными выводами на каждом этапе. Выполняется анализ таблицы истинности каждого логического выражения.
Пример №1.
Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по таким специальностям: гитарист, плотник, егерь и стоматолог.
Известно, что:
- дом плотника правее егеря;
- стоматолог проживает левее егеря;
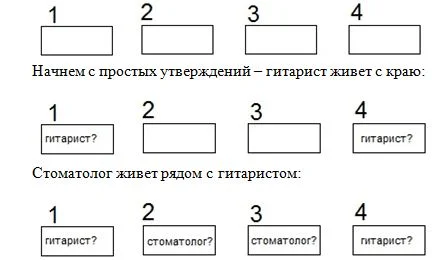
- дом гитариста с самого краю;
- стоматолог живет рядом с гитаристом;
- Владимир не гитарист, и его дом не соседствует с гитаристом;
- дома Дмитрия и егеря соседние;
- здание, в котором прописан Андрей, правее стоматолога;
- между домами Андрея и Дмитрия один дом.
Чтобы рассуждать было проще, добавим изображение зданий, присвоим им номера:
Но стоматолог живет левее егеря, а правее егеря – плотник. Получается, что дом гитариста не может быть последним, а дом стоматолога не может быть предпоследними. То есть, егерь живет в предпоследнем доме:
Между домами Андрея и Дмитрия стоит один дом, значит, дом Андрея не может быть предпоследним, получается номер – 4, что автоматом исключает проживание там Дмитрия и Владимира.
Условие задачи заняло 2 предложения, а рассуждений получилось на 2 страницы.
Такой подход лучше не использовать, если условие сложное или много данных.
Табличный метод
Более удачным подходом к решению задач с большим количеством данных (несколько множеств), считается табличный, или графический (диаграммы).
Чтобы построить таблицу истинности логических выражений, следует:
- Разбить задачу на простейшие утверждения, которые обозначить символами (большие буквы латинского алфавита).
- Записать условие задачи, как составное выражение из символов логических операций.
- Нарисовать таблицу истинности для полученных данных.
- Выбрать такой вариант, при котором полученные значения подходят под условие.
- Проверить соответствие выбранного варианта и условия задачи.
Чтобы преобразовывать условие задачи в логические выражения и операции, удобно пользоваться такой сводной таблицей истинности логических операций:
Рассмотрим тот же пример.
Определяем, что только гитарист может жить в первом доме, далее смотрим на заметки и условия и получаем таких жителей:
Метод компактнее, для некоторых задач нагляднее.
Построение таблиц истинности для различных типов задач
Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.
Пример 2.
Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.
Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:
А — «Первый студент летал в Англию»;
В — «Второй студент летал в Англию»;
С — «Третий студент летал в Англию».
Запишем выясненные данные при помощи логических операций:
Пример 3.
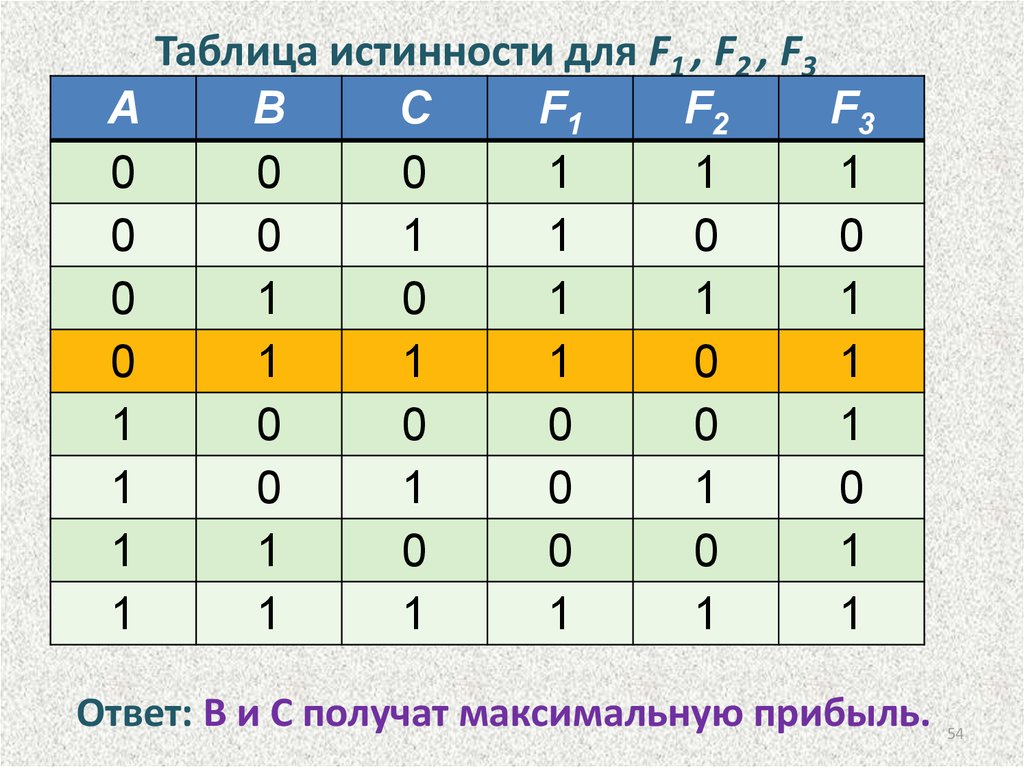
Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:
- Если А получит максимальный бал, то максимальный бал получат Ви С.
- А и С получат или не получат максимальный бал одновременно.
- Необходимым условием получения высшего бала С класса является получение высшего бала В классом.
По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.
Выясним, какие же классы добились высшего бала.
Разбиваем условие задачи на элементарные высказывания:
А – «А добьется высшего бала»;
В – «В добьется высшего бала»;
С – «С добьется высшего бала».
Запишем логические операции, описанные в примере:
Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.
Пример 4.
Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:
- последняя – гласная (Х1);
- или первая буква согласная (Х2)
- вторая – согласная (Х3).
¬(Х1→Х2)VХ3
Предложенные имена: Арина, Артур, Кэтрин, София.
Решим задачу, используя таблицу.
Сначала решим пошагово, выполняя операции по приоритету:
Указанному условию соответствует первое имя.
Пример 5.
Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.
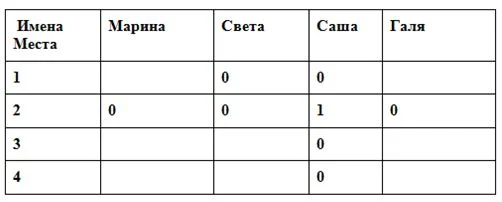
Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.
Маша Марина: «Саша заняла второе место, а Света – первое».
Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».
Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».
Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».
Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».
Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.
Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.
Построение электронных схем, реализующих логические операции
Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.
Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.
Электросхема с конъюнктором
Рассмотрим все варианты:
- Все контакты включены, тогда источник света горит.
- Первый контакт в положении «выключено» – свет не горит.
- Второй контакт выключен – лампа не светит.
- Все контакты отключены – свет не горит.
Заключение – эта электрическая цепь реализует операцию «И».
Дизъюнктор, схема электропитания
Рассмотрим этот вид электрической цепочки:
- Все контакты включены – лампа горит.
- Первый контакт включен, второй выключен – свет горит.
- Обратная ситуация – выключен первый, включен второй – лампа светится.
- Все контакты выключены – света нет.
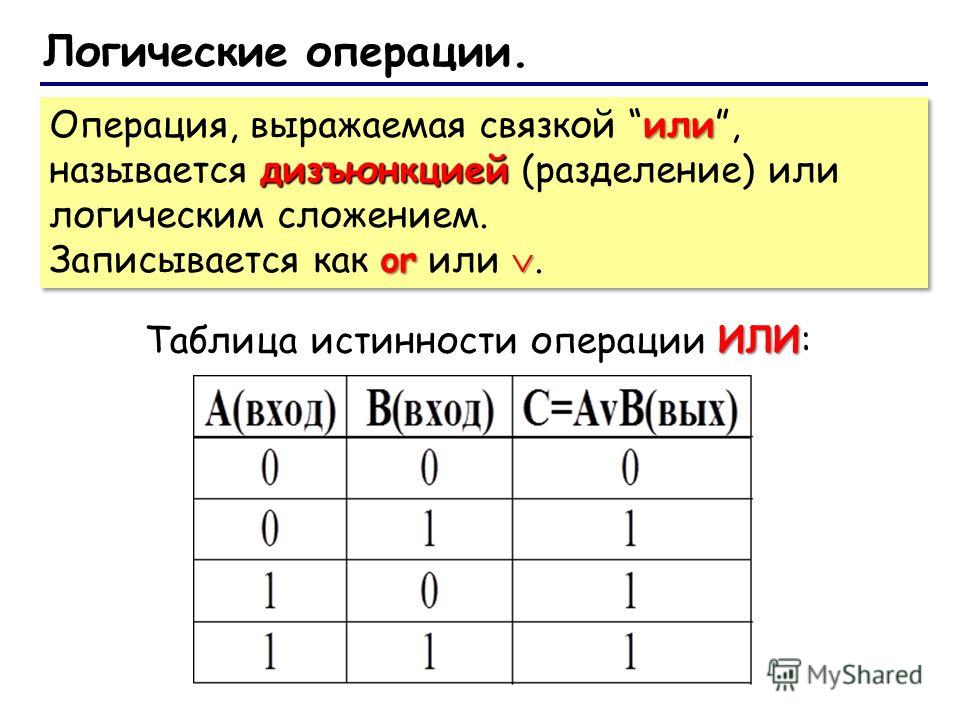
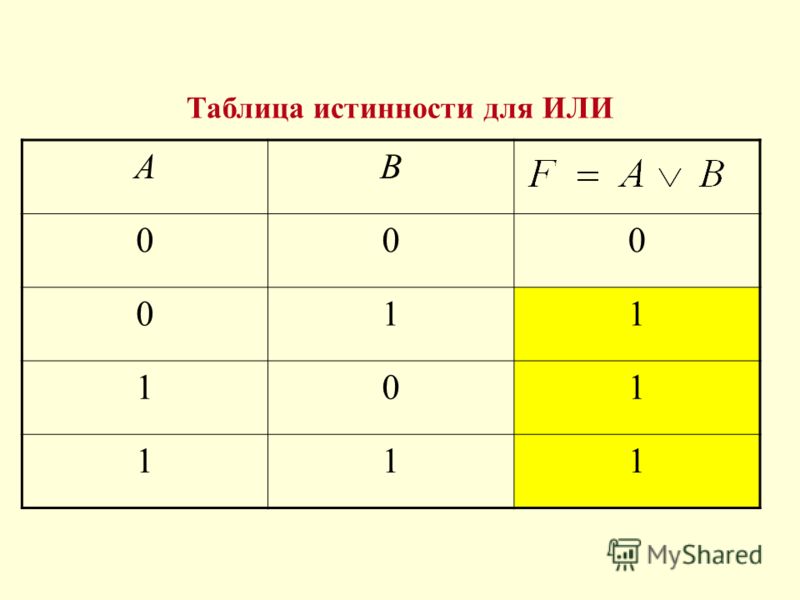
Заключение – такой вид электросхем соответствует логической операции «ИЛИ».
Инвертор в электросхемах
В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.
Заключение: схема соответствует логической операции «НЕ».
Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.
Обозначение логических элементов
Удобно создавать электросхемы в ПО SmartNotebook, которое используется с интерактивной доской.
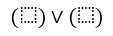









 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
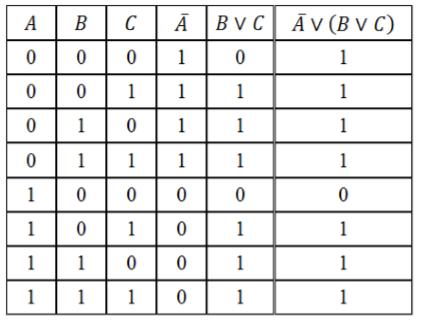
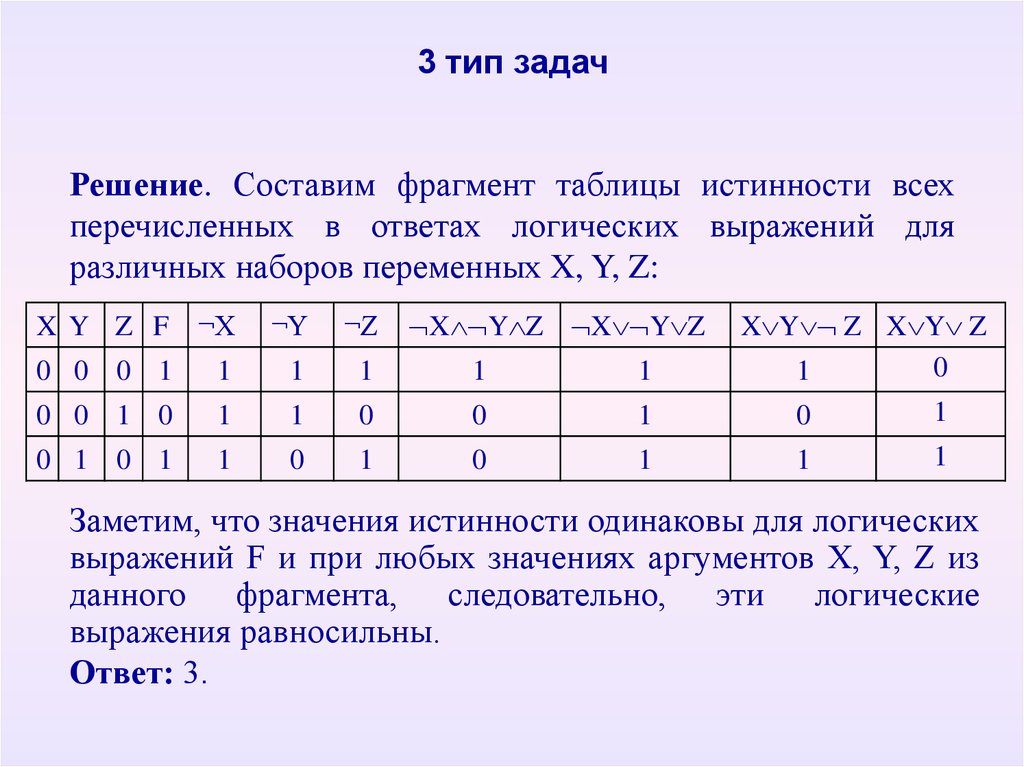
 Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (табл. 14).
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (табл. 14).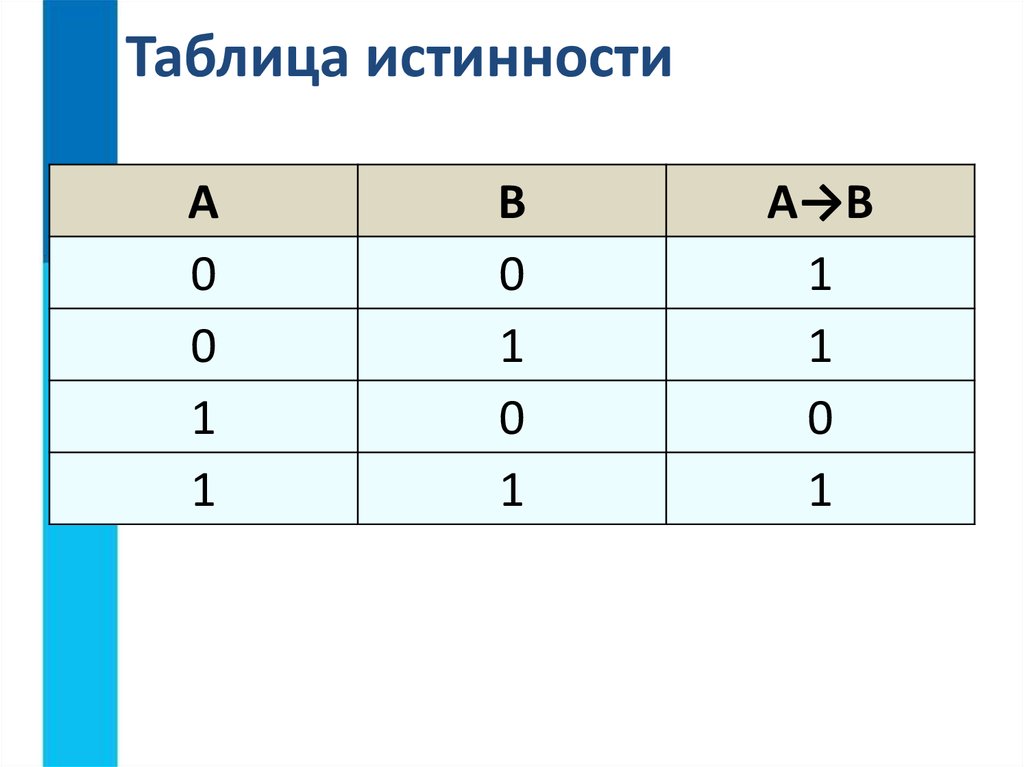 C логическое выражение будет истинным?
C логическое выражение будет истинным?
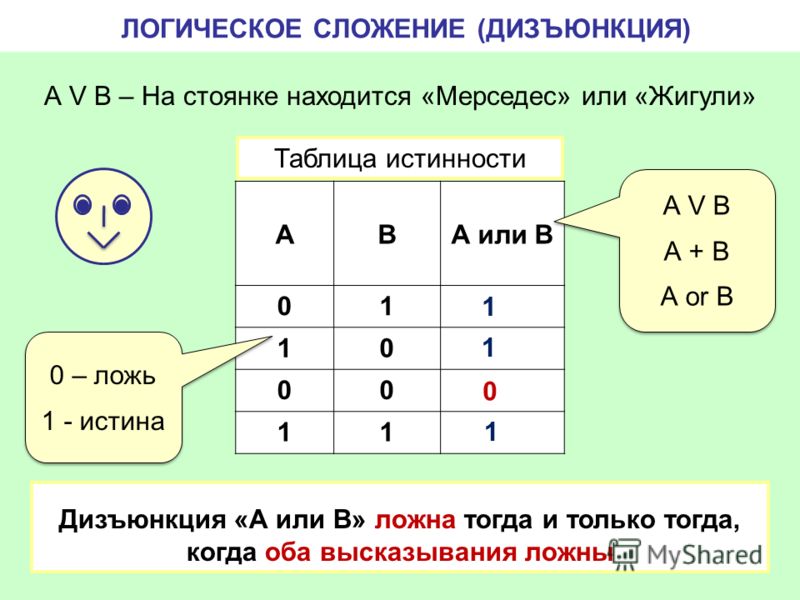 Логический элемент – это электронное устройство, выполняющее соответствующую логическую функцию.
Логический элемент – это электронное устройство, выполняющее соответствующую логическую функцию.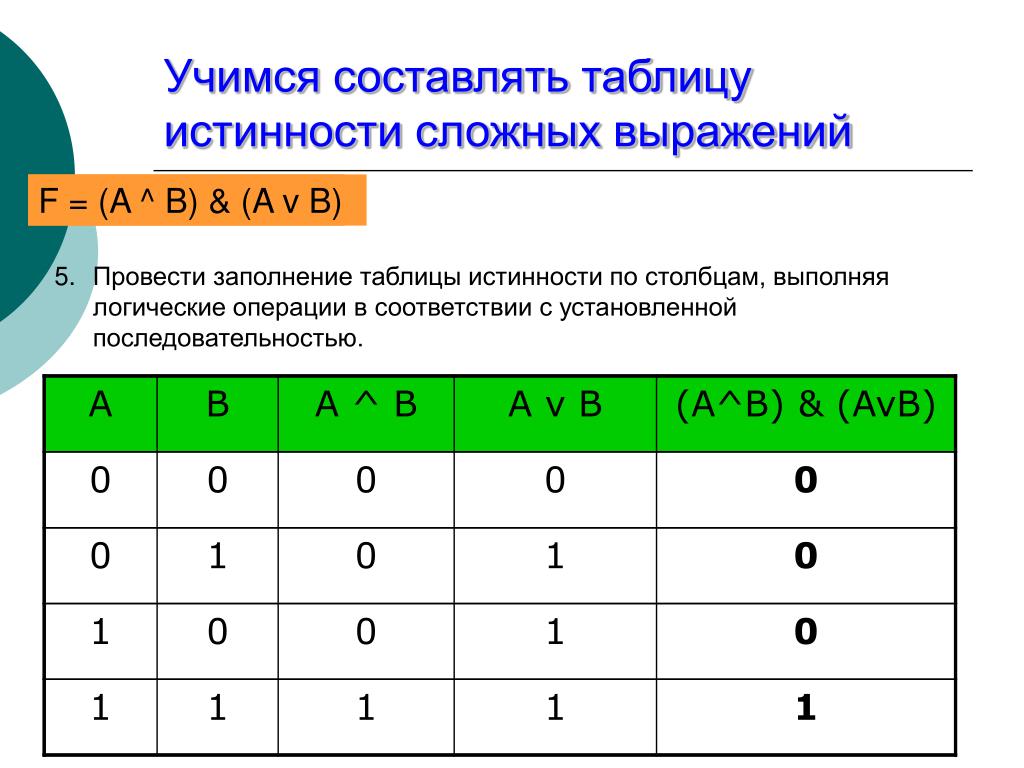 17).
17). su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.) 
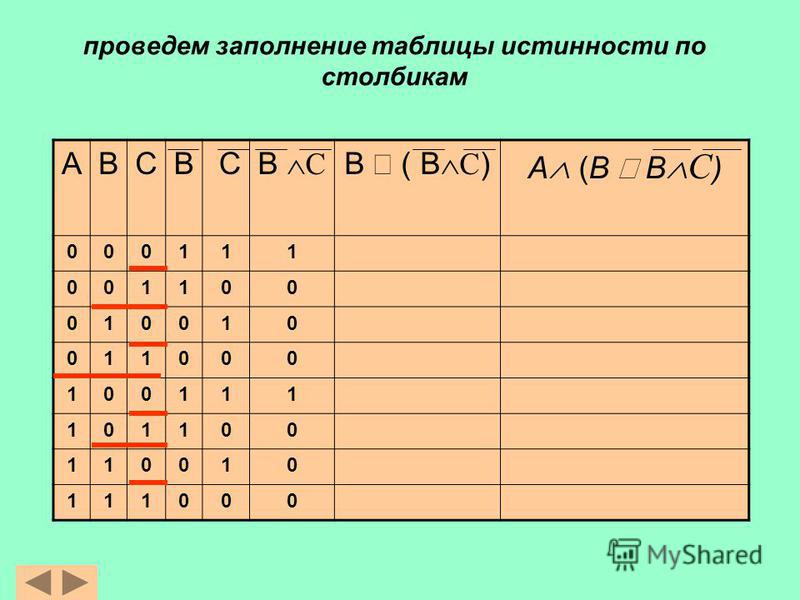
 : ~A
: ~A  Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом.
Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом.