Как составить таблицу истинности сумматора в лабораторной работе

Исследование параллельного и
последовательного регистра и параллельного
сумматора.

Цель работы:Изучение работы регистров
и полного сумматора

Основные теоретические сведения

Регистры– цифровые устройства,
предназначенные для хранения двоичной
информации. Различают последовательные
и параллельные регистры.

Последовательный регистр.

Рассмотрим последовательный 4-разрядный
регистр сдвига на основе Dтриггеров Рис.1.

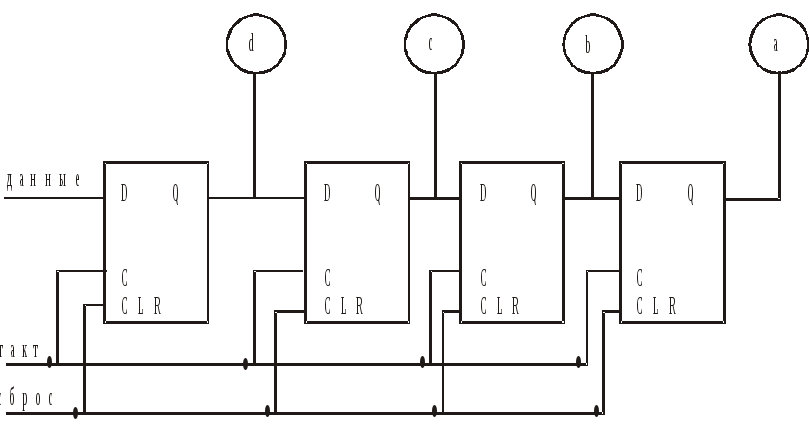
Рис1 . 4 –разрядный последовательный
регистр сдвига.

Позволяет хранить 4 бита информации (по
одному в каждом триггере). Загрузка
регистра осуществляется последовательной
подачей битов информации на вход данных.
Каждый бит информации загружается при
помощи тактового импульсатакт. Вход
сброс предназначен для установки
всех триггеров регистра в 0.

При подаче такта данные с входа данных
передаются в первый регистр (на выход
d). Данные из первого
регистра передаются во второй (d>>c),
из второго в третий (c>>b)
и из третьего в четвертый (b>>a).
Передачу данных иллюстрирует таблица
1.

Таблица .1. Загрузка числа 0011 в
последовательный регистр сдвига

Данные	Такт	сброс	d	c	b	a
0	0	1	0	0	0	0
1	0	0	0	0	0	0
1		0	1	0	0	0
1		0	1	1	0	0
0		0	0	1	1	0
0		0	0	0	1	1

Параллельный регистр.

В отличие от последовательного регистра
в параллельном загрузка данных в регистр
осуществляется параллельно (одновременно
во все триггеры).

Рассмотрим 4-разрядный кольцевой регистр
сдвига с параллельной загрузкой данных
на основе JK
триггеров Рис.2.

Данный регистр имеет 4 входа (предварительной
установки) данных d_i,
с_i,b_i,a_i, и
4 выходаd₀, с₀,b₀,a₀,
вход сброса и вход тактовых импульсов.
Данные в регистр можно записать
параллельно при помощи подачи сигналов
на входыd_i,
с_i,b_i,a_i
Это иллюстрирует строка 2 таблицы
2, а в дальнейшем при помощи подачи
синхроимпульсов на входтакт происходит
сдвиг регистра.

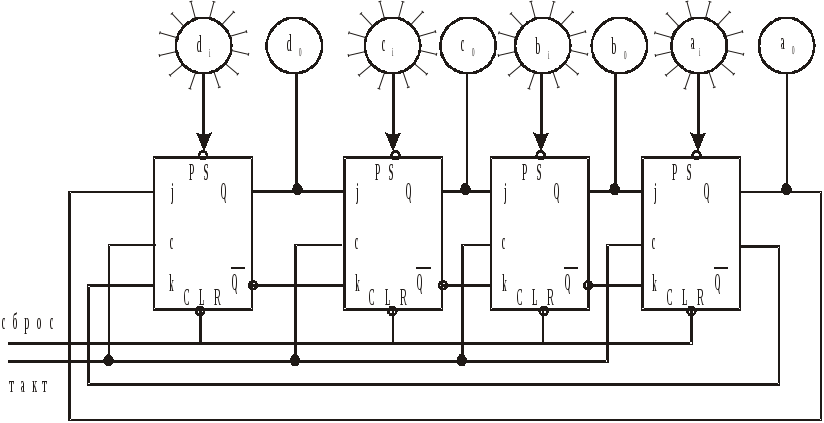
Рис.2. 4-Разрядный параллельный регистр
сдвига

Работу регистра иллюстрирует таблица
истинности.

Таблица 2. Работа параллельного регистра
сдвига

Такт	сброс	di	ci	bi	ai	d0	c0	b0	a0
0	0	0	0	0	0	0	0	0	0
0	0	0	1	1	0	0	1	1	0
0	0	0	0	0	0	0	1	1	0
1	0	0	0	0	0	0	0	1	1
2	0	0	0	0	0	1	0	0	1
3	0	0	0	0	0	1	1	0	0

Мы рассмотрели типичные примеры
последовательного и параллельного
регистров. В настоящее время промышленностью
выпускается большое количество
разнообразных регистров сдвига. В
лабораторной работе Вам необходимо
изучить работу регистров и составить
их таблицы истинности. (Примечание:
Работа регистров на карточках не
соответствует приведенной в методичке)

Арифметические устройства выполняющие операцию сложения Полусумматор

Полусумматор реализует сложение 2х бит
информации

Обозначим: А – 1 слагаемое, В – 2 слагаемое,
–
сумма, С₀– перенос в старший разряд.
Рассмотрим правила сложения двух
одноразрыдных чиселAиBРис.3..

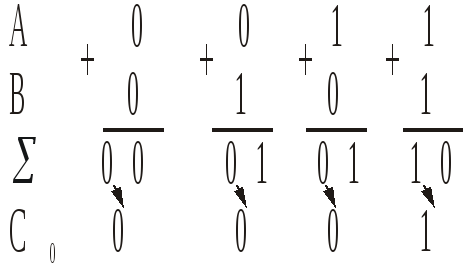
Рис.3. Правила сложения одноразрядных
чисел

Электрическая принципиальная схема
полусумматора реализующего эти правила
приведена на рис.4.

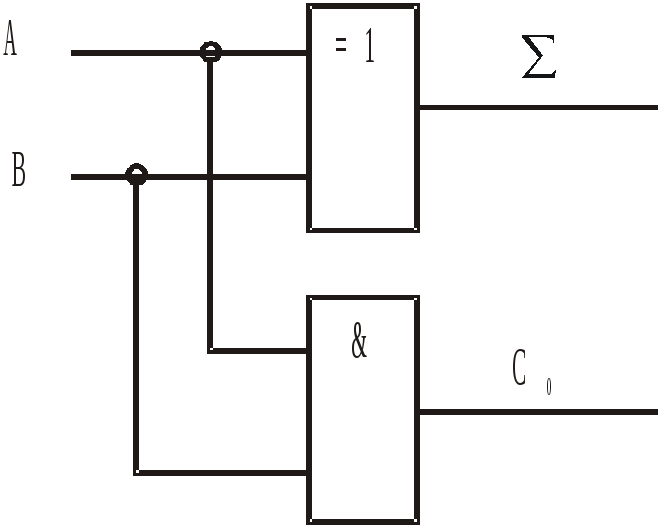
Рис.4. Полусумматор

Полный сумматор

Полный Сумматор – устройство для
сложения двух бит информации с учетом
возможного переноса из младшего разряда,
то есть
где С_in– перенос из
младшего разряда

Электрическая принципиальная схема
полного сумматора приведена на рис.5. и
таблица 3 иллюстрирует принцип работы

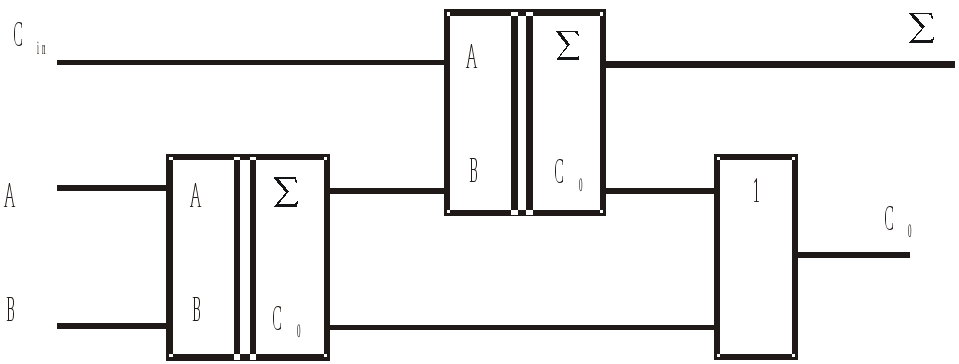
Рис. 5. Полный Сумматор

Таблица
3.Таблица истинности полного сумматора

Cin	A	B		C0
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Многоразрядный
сумматор

Многоразрядный
сумматор предназначен для сложения
многоразрядных двоичных чисел. Рассмотрим
трехразрядный сумматор. Он предназначен
для сложения 3х разрядных двоичных чисел
и состоит из 1 полусумматора и 2 полных
сумматоров.

Пример
сложения трехразрядных чисел

А

+

0 1 1

В 1 0 1

∑ 1 0 0 0

Схема
трехразрядного сумматора реализующего
данный пример представлена на рис.3.

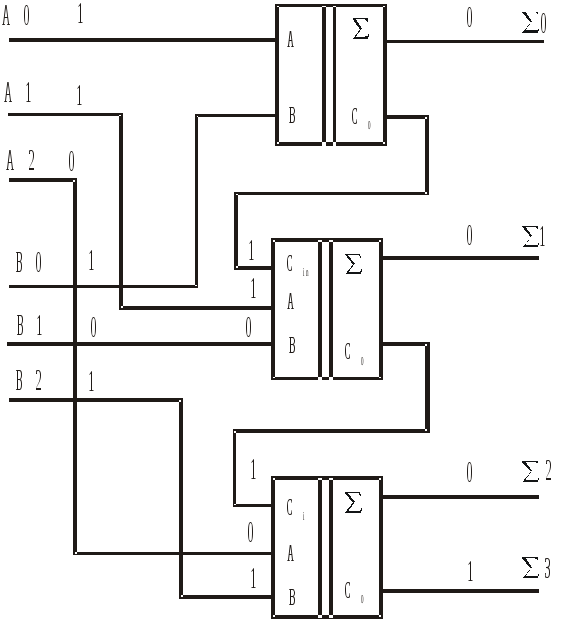
Рис. 6. 3-разрядный сумматор

Порядок выполнения работы:

1. Зарисовать схемы на карточках III-1,III-3

2. Продумать и составить таблицу истинности
по каждой карточке и заполнить ее при
помощи стенда ОАВТ

3. Для карточки III-3 составить
таблицу с примерами сложения двух чисел
согласно варианта

№ варианта	1 слагаемое (16-ричный код)	2 слагаемое (16-ричный код)	Состояние кнопки SB3 (при нажатой кнопке считается, что есть перенос из младшего разряда)
1	3	5	Без нажатия кнопки SB3
1	7	6	Без нажатия кнопки SB3
1	A	8	Без нажатия кнопки SB3
2	7	2	Без нажатия кнопки SB3
2	A	4	Без нажатия кнопки SB3
2	B	9	Без нажатия кнопки SB3
3	2	3	Без нажатия кнопки SB3
3	B	2	Без нажатия кнопки SB3
3	C	A	Без нажатия кнопки SB3
4	4	3	Без нажатия кнопки SB3
4	5	6	Без нажатия кнопки SB3
4	D	8	Без нажатия кнопки SB3
1	3	5	C нажатием кнопкиSB3
1	7	6	C нажатием кнопкиSB3
1	A	8	C нажатием кнопкиSB3
2	7	2	C нажатием кнопкиSB3
2	A	4	C нажатием кнопкиSB3
2	B	9	C нажатием кнопкиSB3
3	2	3	C нажатием кнопкиSB3
3	B	2	C нажатием кнопкиSB3
3	C	A	C нажатием кнопкиSB3
4	4	3	C нажатием кнопкиSB3
4	5	6	C нажатием кнопкиSB3
4	D	8	C нажатием кнопкиSB3

Содержание отчета:

1. Название и цель работы.

2. Исследуемые схемы

3. Таблицы истинности

4. Выводы по работе.

Контрольные вопросы:

1. Параллельный регистр. Назначение,
   Область применения, электрическая
   принципиальная схема, УГО параллельного
   регистра.

2. Последовательный регистр. Назначение,
   Область применения, электрическая
   принципиальная схема, УГО последовательного
   регистра..

1. Операции двоичного сложения, вычитания
   и умножения.

2. Полусумматор. Электрическая принципиальная
   схема, принцип работы, таблица истинности.

3. Полный сумматор. Электрическая
   принципиальная схема, принцип работы,
   таблица истинности.

4. Полувычитатель. Электрическая
   принципиальная схема, принцип работы,
   таблица истинности.

5. Полный вычитатель. Электрическая
   принципиальная схема, принцип работы,
   таблица истинности.

6. Многоразрядные сумматоры. Назначение.
   Электрическая принципиальная схема,
   принцип работы, таблица истинности.

7. Многоразрядные вычитатели. Назначение.
   Электрическая принципиальная схема,
   принцип работы, таблица истинности.

8. Многотактный умножитель. Привести
   структурную схему умножителя
   разрядности(5*3). Объяснить принцип и
   порядок работы.

9. Матричный умножитель. Привести
   структурную схему умножителя (4*4).
   Объяснить принцип и порядок работы.

10. Устройство и назначение семисегментного
    индикатора.

11. Принцип работы дешифратора.

12. Приведите часть электрической
    принципиальной схемы дешифратора для
    какого либо одного сегмента.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Лабораторная
работа 2.1

Сумматоры

Основные
теоретические положения

Сумматором
называется комбинационное логическое устройство, предназначенное для выполнения
операции арифметического сложения чисел, представленных в виде двоичных кодов.
Операция вычитания заменяется сложением чисел в обратном или дополнительном
кодах. Операции умножения и деления сводятся к реализации многократных сложений
и сдвигов.

Сумматор
складывает числа поразрядно, учитывая перенос из младшего разряда и формируя
результат сложения и перенос в старший разряд. По числу входов различают: полусумматоры,
полные сумматоры. Файлы для моделирования этих элементов расположены в папке Lab_2_1Модели,
в них используются индикаторы, которые отражают происходящие операции с
логическими функциями. В описании иногда приведены рисунки без части
индикаторов, имеющихся в моделях, для экономии места.

1 Полусумматор

Полусумматор (HS) складывает два двоичных числа одного, самого младшего
разряда A₀,
B₀
без учета переноса в этот разряд (младше разрядов нет). Выходные значения:
результат сложения S₀ и перенос в старший разряд P₀ представлены в таблице истинности
(табл. 1).

Таблица истинности
полусумматора          Таблица 1

A0	B0	S0	P0
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Из таблицы 1
следуют аналитические выражения выходных сигналов:

 

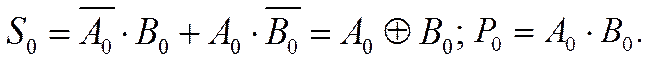(1)

Для
арифметического сложения в одном разряде двоичной системы счисления
используется логическая операция «Исключающее ИЛИ», для получения переноса –
логическая операция «Умножение».

Задание 1. С помощью комбинаций
входных логических сигналов, изучить работу полусумматора, и его таблицу
истинности.

Полусумматор Half Adder (файл L2_add_01.ewb) и его таблица истинности представлена на рисунках 1,
2, где используются следующие обозначения:

– A₀, B₀ –
слагаемые двоичные числа разряда 0;

– Sum₀ – результат
сложения в разряде 0;

– carry 0 (carry out)–
перенос результата сложения из разряда 0 в старший разряд 1.

Перенос возможен в том случае,
если A₁A₀ + B₁B₀ = 01+01=10, где carry out =1,
Sum₀ =0.

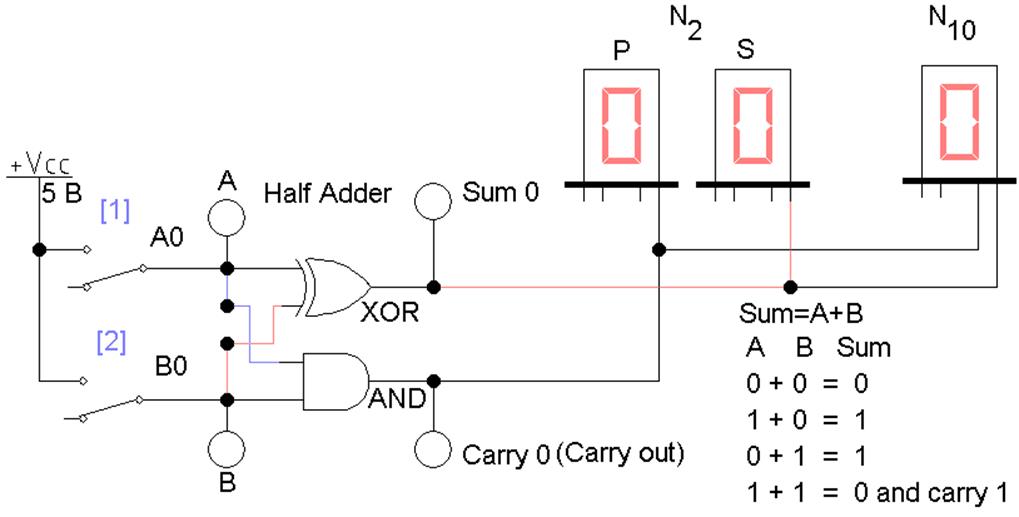
Рис. 1 Схема полусумматора
на логических элементах

L2_add_02.ewb – полусумматор из поля компонентов Digital и его таблица истинности
(рис. 2).

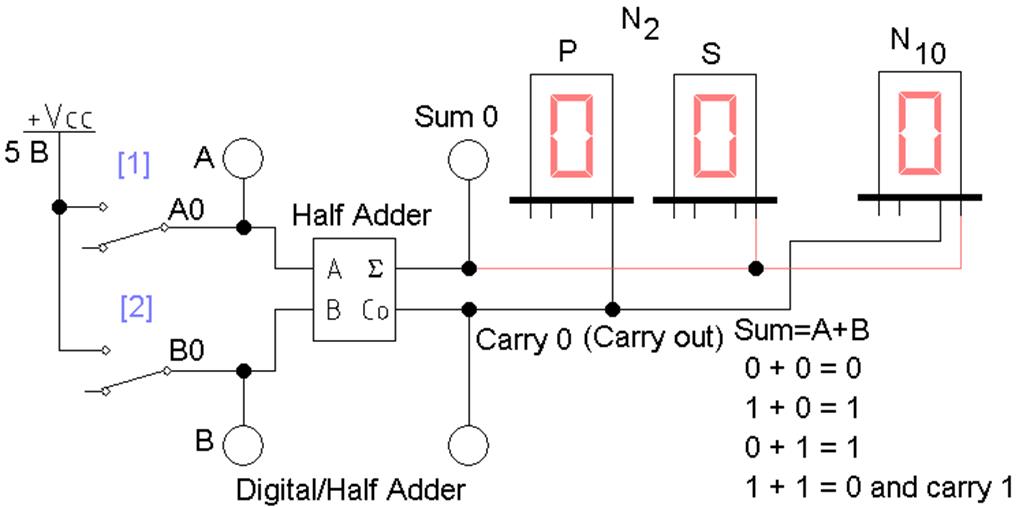
Рис. 2 Схема
полусумматора

2 Полный сумматор

Одноразрядный
полный сумматор (рис. 3) складывает три двоичных числа и имеет соответствующие
им входы: для разряда слагаемого A_n, разряда слагаемого B_n,
входного сигнала переноса из младшего разряда carry in.

Результат
сложения: Sum _n и
перенос в старший разряд carry out.

Полный
сумматор состоит из трех полусумматоров (рис. 3).

Следовательно,
суммирование осуществляется аналогично сложению «в столбик».

Задание 2

С помощью комбинаций
входных логических сигналов изучить работу полного сумматора (файлы L2_add_03.ewb– L2_add_03.ewb_07), и его
таблицу истинности.

Полный сумматор
Full Adder (файл L2_add_03.ewb) и его таблица
истинности (рис. 3, 4). Полусумматор для получения переноса можно заменить
элементом ИЛИ.

На первом
полусумматоре складываются переменные, на втором к результату добавляется
перенос из младшего разряда, третий используется для расчета переноса.

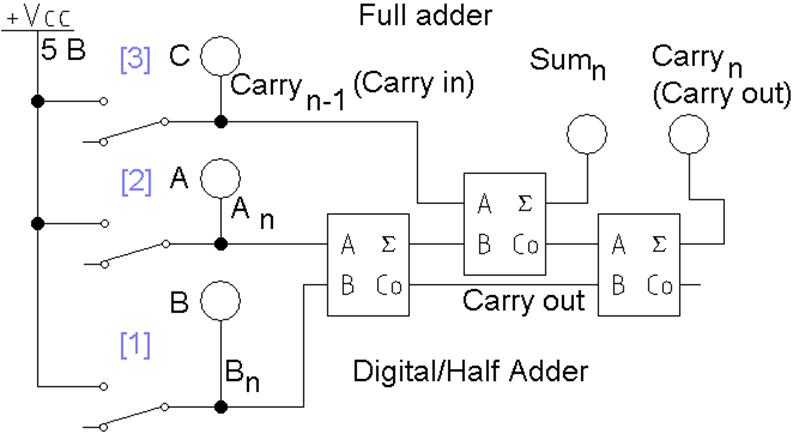
Рис. 3 Схема
одноразрядного полного сумматора на полусумматорах (без части индикаторов)

L2_add_04.ewb – полный сумматор из поля компонентов Digital и его таблица истинности
(рис. 4).

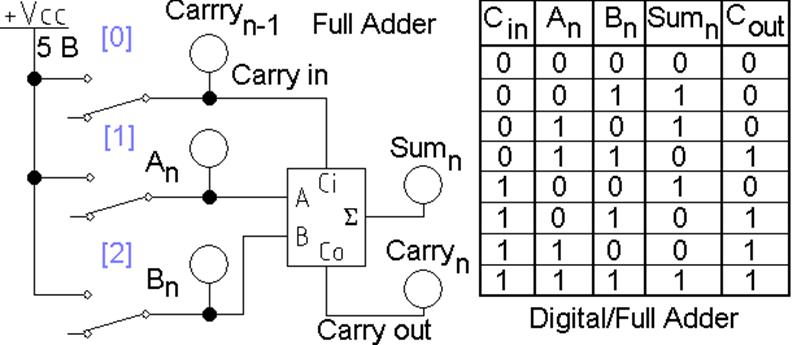
Рис. 4 Схема
одноразрядного полного сумматора (без части индикаторов) и таблица истинности

Модель в файле
L2_add_05.ewb – полный двухразрядный сумматор сложения двоичных
чисел A₁, A₀
и B₁, B₀
и его таблица истинности (рис. 5).

Обозначения на
рисунках:

A₁A₀, B₁B₀ –
слагаемые двухразрядные двоичные числа разрядов 1 и 0;

– Sum₀ – результат
сложения в младшем разряде 0;

– Sum₁ – результат
сложения в старшем разряде 1;

– carry 0
– перенос внутри сумматора из разряда 0, как результат сложения A₀ и B₀,
 в старший разряд 1, на выходе сумматора его нет;

– carry out
– перенос из разряда 1 в следующий старший разряд 2.

В данном
примере не учитывается перенос из разряда, младше 0, считается, что его нет.
Поэтому при суммировании в разряде 0 использован полусумматор. В файле
приводится пример сложения Example.

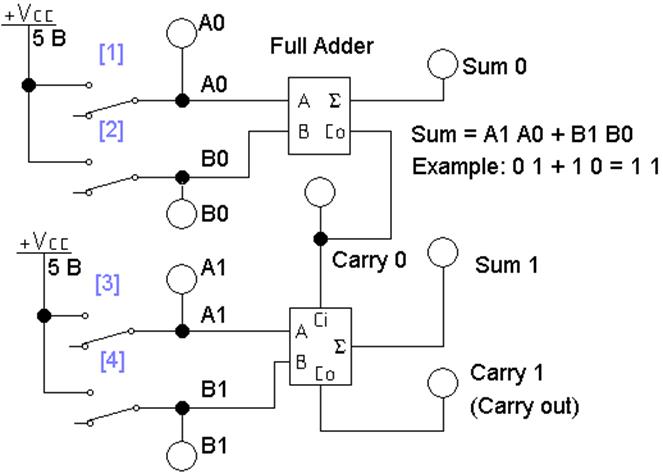
Рис. 5 Схема полного
двухразрядного сумматора (без части индикаторов)

3
Вычитатели

Операция вычитания осуществляется путем изменения знака вычитаемого и
сложения с уменьшаемой величиной. Изменение знака осуществляется переводом
вычитаемого в дополнительный код.

Для
распознавания знака числа используется старший разряд (знаковый разряд). У
положительных чисел он равен нулю, у отрицательных чисел равен единице.

При выполнении
операций сложения и вычитания возможны ошибки, если количество разрядов
результата вычислений превышает разрядность вычислительных устройств.

Например,
результат сложения чисел на калькуляторе превышает его возможности отображения,
при этом старший разряд может быть утрачен.

Пример: вычислить: 4 +(– 3),
результат представить в четырехразрядном двоичном коде. Пятый разряд
использовать как знаковый. Ответ в табл. 2.

Последовательность
операции вычитания                                                  Таблица
2

Двоичное число	Десятичное число	Комментарий
знак	модуль	знак	модуль
0	0100	+	4	Первое слагаемое (4 разряда)
0	0011	+	3	Вычитаемое в полном формате (4 разряда)
1	1100	–		Поразрядная инверсия вычитаемого
0	0001	+	1	Добавление единицы младшего разряда
1	1101	–	3	Второе слагаемое в дополнительном коде
0	0001	+	1	Результат вычитания

Если при
добавлении дополнения в n
– разрядном представлении есть перенос в n +1 разряд (второе слагаемое в
дополнительном коде табл. 2), то результат является положительным числом.

3.1 Одноразрядный
полувычитатель

Данное
устройство определяет разницу двух одноразрядных двоичных чисел без учета займа
в младший разряд. Результат вычитания D₀
и займ из старшего разряда E₀
представлены в таблице истинности (табл. 3).

Лабораторная работа 2

Тема: Исследование
двоичных сумматоров

Цель работы

Исследование внутренней структуры и логики
функционирования сумматоров и полусумматоров; проверка правильности их
функционирования.

Краткая теория к заданию

По числу входов различают полусумматоры,
одноразрядные сумматоры (ОС) и многоразрядные сумматоры.

Полусумматорами
называются устройства с двумя входами и двумя
выходами, на которых вырабатываются сигналы суммы и переноса. Полусумматор
реализует лишь часть задачи суммирования, так как не учитывает входной величины
– переноса из соседнего младшего разряда в данных. В таблице 1 приведена
таблица истинности полусумматора.

Таблица 1 – Таблица
истинности полусумматора

Ai	Bi	Si	Pi
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Одноразрядный двоичный сумматор состоит из двух комбинационных схем: одна – для формирования S_i, вторая – для определения P_i.

Многоразрядный сумматор строится на основе одноразрядных в соответствии с правилами сложения.
В зависимости от характера ввода-вывода кодов и организации переносов
многоразрядные сумматоры бывают последовательного и параллельного принципа
действия.

Одноразрядные сумматоры имеют три входа и
обеспечивают сложение разрядов слагаемых с переносом из предыдущего разряда. В
таблице 2 приведена таблица истинности сумматора.

Таблица 2 – Таблица истинности сумматора

Ai	Bi	Пi-1	Сi	Пi
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Обозначения в таблице 2:

·       
A_i, B_i – слагаемые i-го разряда;

·       
С_i – сумма
слагаемых  i-го разряда;

·       
П_i-1, П_i – переносы из (i‑1)-го и i-го
разрядов.

Арифметические сумматоры являются составной
частью так называемых арифметико-логических устройств (АЛУ) микропроцессоров
(МП). Они используют­ся также для формирования физического адреса ячеек памяти
в МП с сегментной ор­ганизацией памяти.

В программе ЕWВ арифметические
сумматоры представлены в двумя базовыми устройствами, показанными на рис. 1: полу­сумматором (слева) и полным сумматором (справа).

Рисунок 1 – Устройства полусумматора и сумматора

Они имеют следующие назначения
выводов:

А, В – входы слагаемых,

∑ – результат суммирования,

Со – выход переноса,

С_i – вход переноса.

Многоразрядный сумматор создается
на базе одного полусумматора и n полных сумматоров.

В качестве примера на рис. 2
приведена структура трех­разрядного сумматора. На входы А1, А2, АЗ и В1, В2, ВЗ
подаются первое и вто­рое слагаемые соответственно, а с выходов S1, S2, S3
снимается результат суммирования.

Рисунок 2 – Трёхразрядный сумматор

Для исследования внутренней структуры и логики
функционирования сумматоров как нельзя лучше подходит логический
преобразователь.

Схема подключения полусумматора  к логическому
преобразователю приведена на рис. 3.

Рисунок 3 – Подключение полусумматора к
логическому конвертеру

После подключения полусумматора к преобразователю
последовательно нажимаем кнопки (рис. 4) и в результате получаем таблицу истинности и логическое
выражение.

Рисунок 4 – Кнопки логического конвертера

Из полученной таблицы истинности
можно видеть, что при подключении вывода ∑ полусумматора к зажиму ОUТ преобразователя он выполняет функции элемента «Исключающее
ИЛИ». Подключив клемму ОUT преобразователя к выходу Со
полусумматора и проделав аналогичные действия, приходим к выводу, что в таком
включении полусумматор выполняет функции эле­мента И. Следовательно, эквивалентная схема полусумматора имеет вид, показан­ный на рис. 5.

Рисунок 5 – Эквивалентная
схема полусумматора

Практическая часть

1.    
Подключим полный сумматор к
логическому преобразователю, как указано на рис. 6, и выясним его внутреннюю
структуру, принимая во внима­ние методику решения аналогичной задачи для полусумматора.

Рисунок 6 – Исследование полного сумматора

2.    
Используя опыт работы со
схемой на рис. 8, подключим ко входам трехраз­рядного сумматора на рис. 2
генератор слова, а к выходам алфавитно-цифровой индикатор с дешифратором и
проверим правильность его функционирования.

Рисунок 7 – Подключение семисегментного
индикатора с дешифратором

В каталоге программы ЕWВ
имеется схема включения четырехразрядного АЛУ на базе серийной микросхемы 74181
(отечественный аналог К155ИПЗ.

Проверим работу ИМС
74181 (рис. 8) в режиме сумматора с переносом (на вход Сn подаём сигнал логического нуля).

ИМС74181 обеспечивает 32 режима работы АЛУ в
зависимости от состояния управляющих сигналов на входах М, S0…S3, а также допускает наращивание разрядности (вход СN
и выход СN<4 для
переносов).

Показанная
на рис. 8 схема включения ИМС соответствует режиму сумматора без переноса. Значения четырехразрядных операндов А и В на входе задаются с помощью
генератора слова и в шестнадцатеричном коде отображаются одноимёнными
алфавитно-цифровыми индикаторами. На выходах F0…F3 результат
суммирования отображается индикатором F. Изменяя
со­стояния сигналов на управляющих входах, можно
промоделировать большинство функций АЛУ, используемых в микропроцессорах.

Рисунок 8 – Подключение микросхемы ИМС74181 в
режиме сумматора без переноса

4.В соответствии с
рис. 8 соберем ИМС
74181. В генераторе слов вводим любые комбинации десятичного системы счисления.
(рис. 9).

Рисунок 9 – Ввод комбинаций

Вывод: При выполнении лабораторной работы мы изучили
принцип работы, внутреннюю структуру и логику функционирования  сумматоров и
полусумматоров, удостоверились в правильности функционировании  ИМС 74181  в
режиме сумматора с переносом (на вход Сn по­дали сигнал логического нуля).

Контрольные
вопросы и задания

1.     Чем отличается полусумматор от одноразрядного сумматора?

2.    
Сколько входов имеет полный сумматор? Сколько
выходов?

3.     Запишите функцию алгебры логики, которая реализует арифметическое
суммирование одноразрядных двоичных чисел.

Лабораторная работа выполняется с помощью учебного лабораторного стенда LESO2.

1 Цель работы

Целью работы является изучение принципов действия комбинационных схем: дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.

2 Краткие теоретические сведения

2.1 Дешифратор (декодер)

Дешифратор (декодер) служит для преобразования n-разрядного позиционного двоичного кода в единичный выходной сигнал на одном из 2n выходов. При каждой входной комбинации сигналов на одном из выходов появляется 1. Таким образом, по единичному сигналу на одном из выходов можно судить о входной кодовой комбинации. Таблица истинности для декодера с двумя входами изображена в таблице 2.1.

Таблица 2.1 – Таблица истинности двухразрядного дешифратора

x1	x2	y0	y1	y2	y3
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

Для построения схемы декодера по таблице истинности воспользуемся методикой, изложенной в лабораторной работе №1, выполняемой на стенде LESO2. Например, устройство должно иметь 4 выхода. Для каждого выхода записываем логическое выражение. На основе СДНФ:

y0 = x1·x2

y1 = x1·x2

y2 = x1·x2

y3 = x1·x2

По этой системе выражений несложно построить схему требуемого дешифратора (рисунок 2.1).

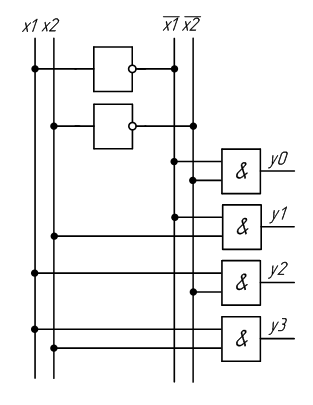
Рисунок 2.1 – Схема дешифратора

Условное графическое обозначение такого дешифратора изображено на рисунке 2.2.

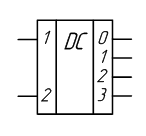
Рисунок 2.2 – Условное графическое обозначение дешифратора

2.2 Шифратор (кодер)

Шифратор выполняет функцию, обратную декодеру (дешифратору), то есть преобразует непозиционный (унитарный) двоичный 2n разрядный код в n разрядный позиционный код. При подаче на один из входов единичного сигнала на выходе формируется соответствующий двоичный код. Составим таблицу истинности шифратора при n = 2.

Таблица 2.2 – Таблица истинности шифратора при n = 2

x1	x2	x3	x4	y1	y0
1	0	0	0	0	0
0	1	0	0	0	1
0	0	1	0	1	0
0	0	0	1	1	1

Синтезируем шифратор. Для этого запишем систему его собственных функций:

y1 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4

y0 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4

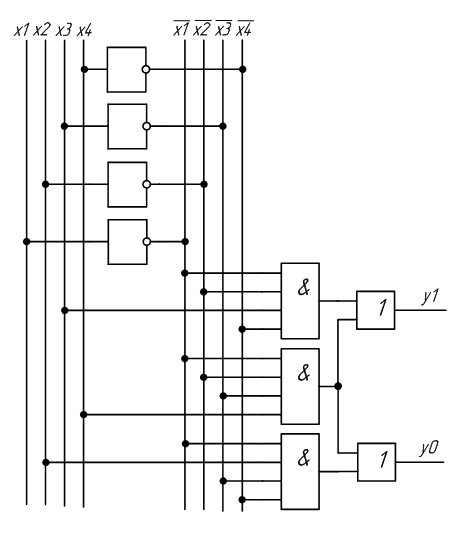
Рисунок 2.3 – Схема шифратора

 

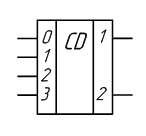
Рисунок 2.4 – Условное графическое обозначение шифратора

2.3 Преобразователь кода для семисегментного индикатора

Наиболее широко преобразователи кодов известны применительно к цифровым индикаторам. Например, преобразователь 4-х разрядного позиционного двоичного кода в десятичные цифры. Имеется семи сегментный индикатор и с его помощью требуется высветить десять цифр.

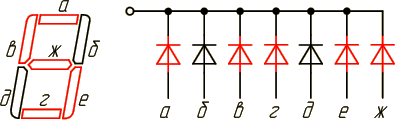
Рисунок 2.5 – Семи сегментный индикатор

Очевидно, что двоичный код должен иметь не менее 4 – х разрядов (2^4 = 16, что больше 10). Составим таблицу истинности работы такого преобразователя.

Таблица 2.3 – Таблица истинности преобразователя

Цифра	Двоичный код 8-4-2-1	a	б	в	г	д	е	ж
0	0	0	0	0	1	1	1	1	1	1	0
1	0	0	0	1	0	1	1	0	0	0	0
2	0	0	1	0	1	1	0	1	1	0	1
3	0	0	1	1	1	1	1	1	0	0	1
4	0	1	0	0	0	1	1	0	0	1	1
5	0	1	0	1	1	0	1	1	0	1	1
6	0	1	1	0	1	0	1	1	1	1	1
7	0	1	1	1	1	1	1	0	0	0	0
8	1	0	0	0	1	1	1	1	1	1	1
9	1	0	0	1	1	1	1	1	0	1	1

По ТИ несложно составить систему собственных функций для всех выходов, т.е. СДНФ, минимизировать её и составить принципиальную схему.

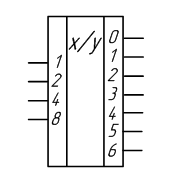
Рисунок 2.6 – Условное графическое обозначение преобразователя кода

2.4 Мультиплексор

Мультиплексор – устройство, которое позволяет коммутировать один из 2^n информационных входов X на один выход Y под действием n управляющих (адресных) сигналов. На рисунке. 2.7 изображена упрощенная функциональная схема мультиплексора на идеализированных электронных ключах.

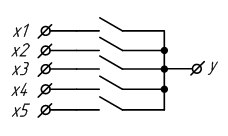
Рисунок 2.7 – Схема мультиплексора на идеализированных электронных ключах

В цифровых схемах требуется управлять ключами при помощи логических уровней. Поэтому желательно подобрать устройство, которое могло бы выполнять функции электронного ключа с управлением цифровым сигналом. Попробуем «заставить» работать в качестве электронного ключа уже знакомые нам логические элементы. Рассмотрим ТИ логического элемента «И». При этом один из входов логического элемента «И» будем рассматривать как информационный вход электронного ключа, а другой вход – как управляющий. Так как оба входа логического элемента «И» эквивалентны, то не важно какой из них будет управляющим входом. Пусть вход X будет управляющим, а Y – информационным. Для простоты рассуждений, разделим ТИ на две части в зависимости от уровня логического сигнала на управляющем входе X.

Таблица 2.4 – Таблица истинности

y	x	Out
0 0	0 1	0 0
1 1	0 1	0 1

По таблице истинности отчётливо видно, что если на управляющий вход X подан нулевой логический уровень, сигнал, поданный на вход Y, на выход Out не проходит. При подаче на управляющий вход X логической единицы, сигнал, поступающий на вход Y, появляется на выходе Out. Это означает, что логический элемент «И» можно использовать в качестве электронного ключа. При этом не важно, какой из входов элемента “И” будет использоваться в качестве управляющего входа, а какой – в качестве информационного. Остается только объединить выходы элементов «И» на один общий выход. Это делается при помощи логического элемента «ИЛИ» точно так же как и при построении схемы по произвольной таблице истинности. Получившийся вариант схемы коммутатора с управлением логическими уровнями приведён на рисунке 2.8.

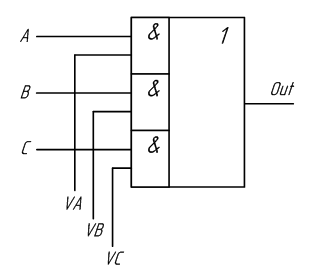
Рисунок 2.8 – Принципиальная схема мультиплексора, выполненная на логических элементах

В схемах, приведенных на рисунках 2.7 и 2.8, можно одновременно включать несколько входов на один выход. Однако обычно это приводит к непредсказуемым последствиям. Кроме того, для управления таким коммутатором требуется много входов, поэтому в состав мультиплексора обычно включают двоичный дешифратор, как показано на рисунке 2.9. Такая схема позволяет управлять переключением информационных входов мультиплексора при помощи двоичных кодов, подаваемых на его управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.

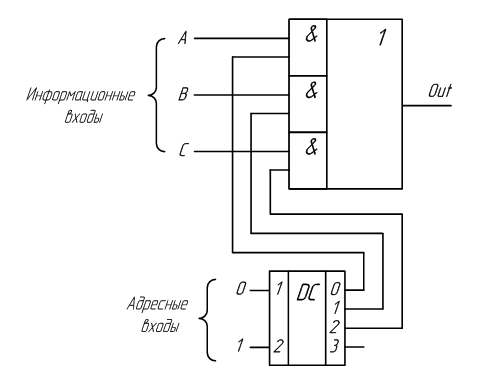
Рисунок 2.9 – Принципиальная схема мультиплексора, управляемого двоичным кодом

Условное графическое обозначение 4–х входового мультиплексора с управлением двоичным кодом приведено на рисунке 2.10. Входы A0 и A1 являются управляющими входами мультиплексора, определяющими адрес информационного входного сигнала, который будет соединён с выходным выводом мультиплексора Y. Информационные входные сигналы обозначены: X0, X1, X2 и X3.

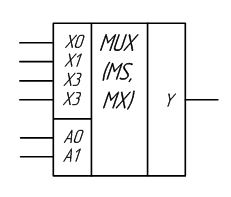
Рисунок 2.10 – Условное графическое обозначение 4-х входового мультиплексора

В условном графическом обозначении названия информационных входов A, B, C и D заменены названиями X0, X1, X2 и X3, а название выхода Out заменено на название Y. Такое обозначение входов и выходов мультиплексора более распространено в отечественной литературе. Адресные входы обозначены как A0 и A1.

Об особенностях реализации мультиплесоров на языке Verilog можно почитать в статье:
Архитектура ПЛИС. Часть 2. Мультиплексор

2.5 Сумматор

Сумматор – узел компьютера, предназначенный для сложения двоичных чисел. Построение двоичных сумматоров обычно начинается с сумматора по модулю 2.

Сумматор по модулю 2

Схема сумматора по модулю 2 совпадает со схемой исключающее «ИЛИ».

Таблица 2.5 – Таблица истинности сумматора по модулю 2

x1	x2	y
0	0	0
0	1	1
1	0	1
1	1	0

Логическое выражение, описывающее сумматор по модулю 2:

y = x1 · x2 + x1 · x2

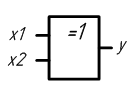
Рисунок 2.11 – Условное графическое обозначение сумматора по модулю 2

На основе логического уравнения, описывающего этот элемент можно синтезировать схему:

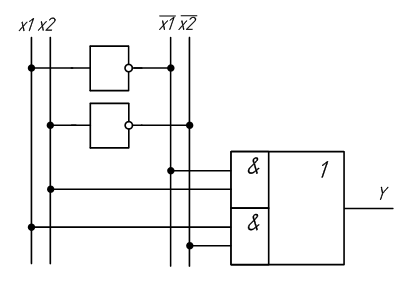
Рисунок 2.12 – Схема сумматора по модулю 2

Сумматор по модулю 2 выполняет суммирование без учёта переноса. В обычном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена в таблице 2.6.

Таблица 2.6 – Таблица истинности полусумматора

A	B	S	P0
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Здесь A и B – слагаемые;
S – сумма;
P0 – перенос в старший разряд (выход переноса Pout).
Запишем систему собственных функций для полусумматора:

S = A · B + A · B
P0 = A · B

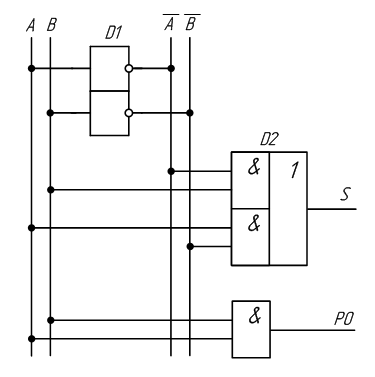
Рисунок 2.13 – Принципиальная схема, реализующая таблицу истинности полусумматора

 

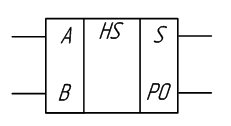
Рисунок 2.14 – Изображение полусумматора на схемах

Полный сумматор.

Схема полусумматора формирует перенос в старший разряд, но не может учитывать перенос из младшего разряда. При сложении многоразрядных двоичных чисел необходимо складывать три цифры в каждом разряде – 2 слагаемых и единицу переноса из предыдущего разряда PI.

Таблица 2.7 – Таблица истинности полного сумматора

PI	A	B	S	PO
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

 
PI – вход 1 переноса из предыдущего разряда,
PO – выход 1 переноса в старший разряд.

На основании таблицы истинности запишем систему собственных функций для каждого выхода:

S = A · B · PI + A · B · PI + A · B · PI + A · B · PI

PO = A · B · PI + A · B · PI + A · B · PI + A · B · PI

В результате получим схему полного сумматора (рисунок 2.15).

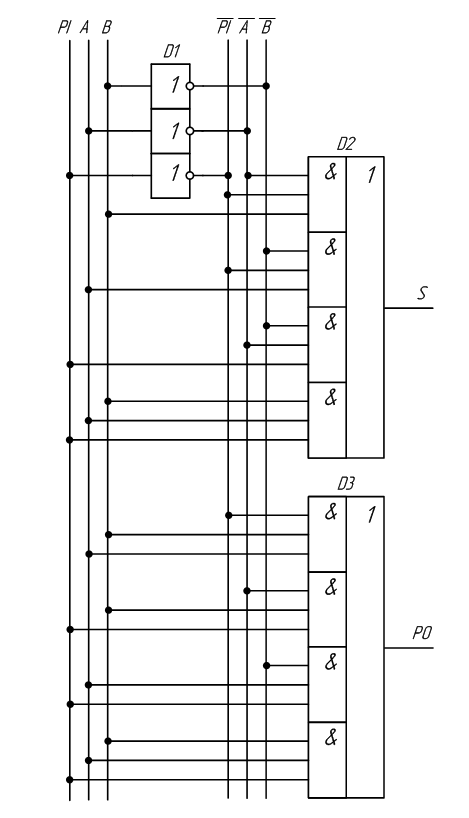
Рисунок 2.15 – Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора

 

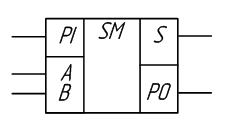
Рисунок 2.16 – Изображение полного двоичного одноразрядного сумматора на схемах

3 Задание к работе

3.1 Исследовать принцип работы дешифратора 2 x 4

Сконфигурировать ПЛИС в соответствии с рисунком 3.1. Подключить к входам X0 и X1 переключатели S7 и S8, а к выходам Y0, Y1, Y2, Y3 светодиодные индикаторы LED5, LED6, LED7, LED8. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС.

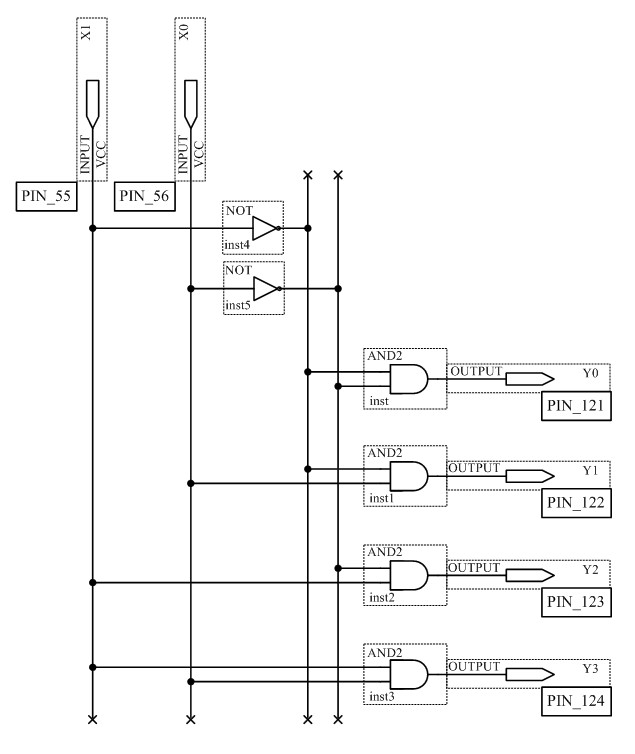
Рисунок 3.1 – Схема дешифратора

Подавая все возможные комбинации логических уровней на входы X0, X1 с помощью ключей S7, S8 и наблюдая за состояниями светодиодных индикаторов LED5, LED6, LED7, LED8, заполните таблицу истинности дешифратора.

Таблица 3.1 – Таблица дешифратора

x1	x2	y0	y1	y2	y3
0	0
0	1
1	0
1	1

3.2 Исследовать принцип работы шифратора 4×2
Сконфигурировать ПЛИС в соответствии с рисунком 3.2.

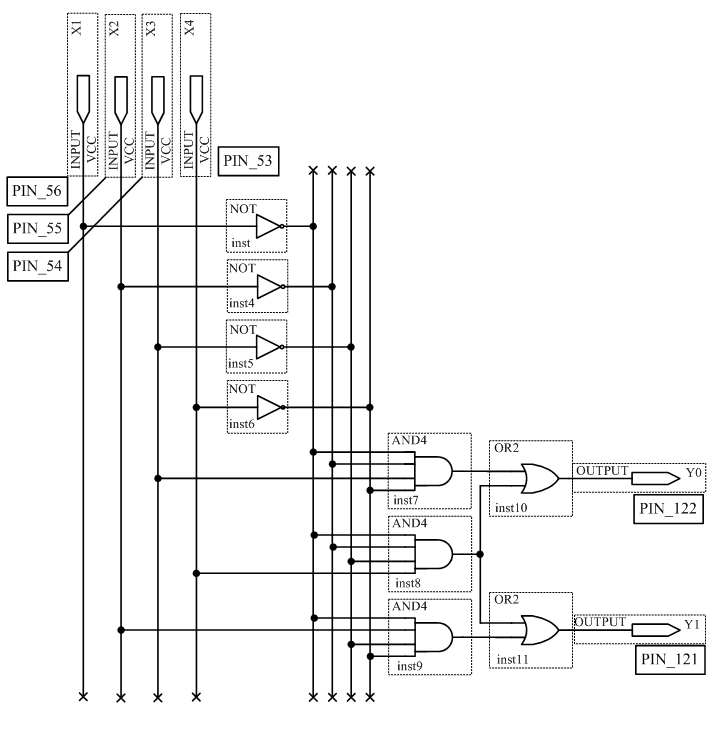
Рисунок 3.2 – Схема шифратора 4×2

Подключить к входам X1, X2, X3, X4 переключатели S8, S7, S6, S5, а к выходам Y0, Y1 светодиодные индикаторы LED8, LED7. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС. Подавая все возможные комбинации логических уровней на входы X1, X2, X3, X4 с помощью ключей S8, S7, S6, S5 и наблюдая за состояниями светодиодных индикаторов LED7, LED8, заполните таблицу истинности шифратора.

Таблица 3.2 – Таблица истинности шифратора

x1	x2	x3	x4	y1	y0
1	0	0	0
0	1	0	0
0	0	1	0
0	0	0	1

3.3 Исследовать работу преобразователя кода для семисегментного индикатора.

Составить таблицу истинности преобразователя кода (таблица. 3.3).
Собрать схему, изображенную на рисунке 3.3.

Таблица 3.3 – Таблица истинности преобразователя

x3	x2	x1	x0	A	B	C	D	E	F	G
0	0	0	0
0	0	0	1
0	0	1	0
0	0	1	1
0	1	0	0
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
1	0	0	1

 

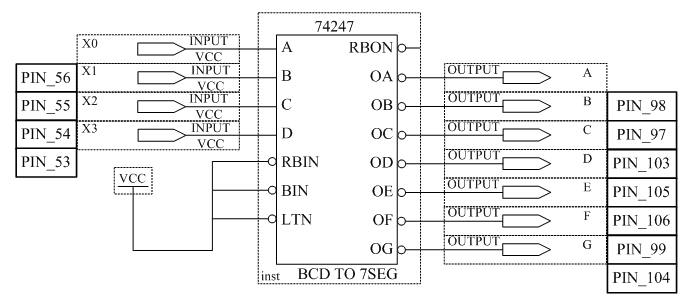
Рисунок 3.3 – Схема преобразователя кода для семисегментного индикатора

Подавая с помощью ключей S8, S7, S6, S5 различные кодовые комбинации на входы X0, X1, X2, X3 определить цифры, высвечиваемые на индикаторе. По результатам эксперимента заполнить таблицу 3.4.

Таблица 3.4 – Таблица, описывающая работу преобразователя кода для семисегментного индикатора

x3	x2	x1	x0	Показание индикатора
0	0	0	0
0	0	0	1
0	0	1	0
0	0	1	1
0	1	0	0
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
1	0	0	1

3.4 Исследовать работу мультиплексора 4×1

Сконфигурировать ПЛИС в соответствии с рисунком 3.4.

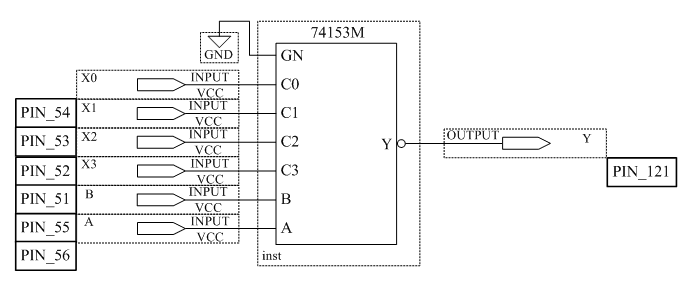
Рисунок 3.4 – Схема мультиплексора 4×1

Поочередно устанавливая все возможные кодовые комбинации на адресных входах A и B, определите номера коммутируемых каналов. Номер коммутируемого канала определяется путем поочерёдного подключения к входам X0, X2, X3, X4 уровня логической единицы и наблюдения за выходом Y. Заполните таблицу 3.5.

Таблица 3.5 – Таблица, описывающая работу мультиплексора

B	A	Номер коммутируемого канала
0	0
0	1
1	0
1	1

3.5 Исследовать схему сумматора

Сконфигурировать ПЛИС в соответствии с рисунком 3.5. Здесь Pin, Pout соответственно вход и выход единицы переноса, A и B – слагаемые, S – сумма.

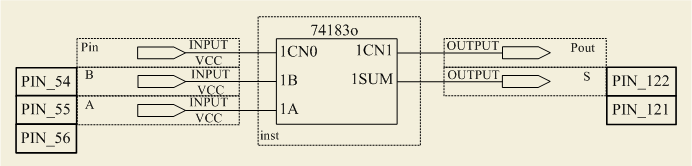
Рисунок 3.5 – Схема сумматора

Заполнить таблицу истинности сумматора (таблица 3.6).

Таблица 2.7 – Таблица истинности полного сумматора

Pin	B	A	Pout
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

4 Содержание отчета

1. Цель работы.
2. Схемы исследования дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
3. Таблицы истинности для каждой схемы.
4. Выводы по каждому заданию.

5 Контрольные вопросы

1. Принцип работы дешифратора?
2. Как синтезировать дешифратор с произвольной разрядностью?
3. Как работает шифратор?
4. Изобразите таблицу истинности шифратора.
5. Как работает преобразователь кода для семисегментного индикатора?
6. Как устроен семи сегментный индикатор?
7. Как работает мультиплексор?
8. Как в лабораторной работе проводилось исследование мультиплексора?
9. Как работает сумматор?
10. Изобразите таблицу истинности шифратора.
11. Что такое единица переноса?

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)