Как составить таблицу к задаче на количество

Как составить таблицу к задаче на количество

  1. Главная
  2. Справочники
  3. Справочник по математике для начальной школы
  4. Задачи
  5. Цена. Количество. Стоимость

В этом разделе научимся решать задачи и составлять таблицы по теме “Цена. Количество. Стоимость” и научимся находись зависимость между этими величинами.

Цена. Количество. Стоимость.

Стоимость – это то, что мы заплатили за всю покупку. 

Задача 1: Наташа купила 5 открыток по 3 р. за каждую. Сколько стоила вся покупка?

Количество Цена Стоимость
5 шт. 3 р. ?

3 • 5 = 15 (р.)

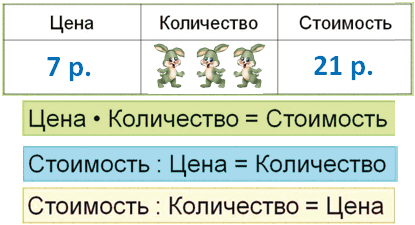
Чтобы узнать стоимость, нужно цену умножить на количество.

Цена. Количество. Стоимость. 

Цена показывает сколько стоит один предмет.

Задача 2: Наташа купила 5 открыток и заплатила за них 15 р. Сколько стоила одна открытка?

Количество Цена Стоимость
5 шт. ? 15 р.

15 : 5 = 3 (р.)

Чтобы найти цену, нужно стоимость разделить на количество.

Цена. Количество. Стоимость. 

Количество показывает сколько предметов мы купили.

Задача 3: Наташа купила несколько открыток по 3 р. за каждую и отдала за покупку 15 р. Сколько открыток купила Наташа?

Количество Цена Стоимость
? 3 р. 15 р.

15 : 3 = 5 (шт.)

Чтобы найти количество, нужно стоимость разделить на цену.

Запомни!

Советуем посмотреть:

Образцы оформления задачи

Обратные задачи

Скорость, время, расстояние

Задачи


Правило встречается в следующих упражнениях:

3 класс

Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 26,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 43,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 50. ПР 3. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 51. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 102,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 43. Урок 20,
Петерсон, Учебник, часть 3

Страница 74. Повторение,
Петерсон, Учебник, часть 3

Страница 75. Повторение,
Петерсон, Учебник, часть 3

4 класс

Страница 44,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 86,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 59. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 71. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 52,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 80,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 23. Урок 8,
Петерсон, Учебник, часть 1

5 класс

Задание 458,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 478,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1454,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1477,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 140,
Мерзляк, Полонский, Якир, Учебник

Номер 440,
Мерзляк, Полонский, Якир, Учебник

Номер 441,
Мерзляк, Полонский, Якир, Учебник

Номер 460,
Мерзляк, Полонский, Якир, Учебник

Номер 463,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 345,
Мерзляк, Полонский, Якир, Учебник

Номер 346,
Мерзляк, Полонский, Якир, Учебник

Номер 368,
Мерзляк, Полонский, Якир, Учебник

Номер 663,
Мерзляк, Полонский, Якир, Учебник

Номер 1331,
Мерзляк, Полонский, Якир, Учебник

Номер 5,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Задание 739,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 782,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 11,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 10,
Мерзляк, Полонский, Якир, Учебник

Источник

Использование таблиц для решения текстовых задач по математике в основной школе

Автор: Сокольникова Елена Васильевна

“Скажи мне, и я забуду.
Покажи мне, – я смогу запомнить.
Позволь мне это сделать самому,
и я научусь”.

Конфуций

В традиционной методике обучения математике обучение решению текстовых задач занимает значительное место. Методы и приемы работы с задачей общеизвестны и не поддаются сомнению. Однако, именно текстовые задачи зачастую служат камнем преткновения на пути к успеху в изучении математики. А значит, нам учителям математики есть над чем задуматься.

К сожалению, в учебниках математики, нет целостной системы обучения решению текстовых задач. Оформление решения задач алгебраическим способом ведется путем описания. Вводится переменная, все остальные величины выражаются через неё. Такой способ не всегда является доступным и понятным учащимся. Многие виды задач можно решить с помощью составления таблиц.  

В поиске новых приемов мы часто забываем то, что было годами наработано и многократно проверено. Формируя УУД, в т.ч. познавательные  универсальные действия, мы должны научить каждого ученика выполнять знаково-символические действия:

  • моделирование — преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическая или знаково – символическая);
  • преобразование модели с целью выявления общих законов, определяющих данную предметную область.

Построение, либо предъявление модели задачи, с последующим анализом, активизирует познавательную деятельность учащихся. Поиск опорных слов, выполнение чертежей и схематических рисунков, составление таблиц, т.е. наглядное оформление задачи, может существенно определять ход мыслительного процесса.

Работа с моделью позволяет ученикам яснее увидеть зависимости между данными и искомыми величинами и оценить задачу в целом.

В статьях о моделировании при обучении решению текстовых задач мы можем ни слова  не найти о таблицах. В современной методике математики «таблица представляет собой структуризацию информации, представленной в задаче. Благодаря таблице сюжетный текст превращается в информационную структуру со связями заданного вида, что помогает вплотную подойти к  составлению уравнения и поиску окончательного решения». Традиционно таблицы составляют при решении задач на движение, стоимость. Я считаю, что спектр их использования намного шире. Правильно составленные таблицы являются математическими моделями. Следует отметить, что многие учителя используют таблицы при решении текстовых задач. Один и тот же прием, используя по- разному.    

Основные принципы работы с таблицей

  1. Таблица  должна быть «живой», действенной моделью, создаваться самим учеником.
  2. Принцип единообразия.  Величины, занесенные в первый и третий столбики таблицы, должны находиться в прямопропорциональной зависимости.
  3. Таблица должна помогать анализу данных, не обременять решение.
  4. Принцип преемственности. Обучение составлению таблиц должно начинаться в период обучения решению арифметических задач в начальных классах и продолжаться в 5 – 6 классах.

7 класс №403 а)

В 12 ящиков можно разложить такое же количество яблок, что и в 18  корзин. Определите, сколько килограммов яблок вмещает ящик и сколько корзина, если известно, что в ящик вмещается на 3 кг яблок больше, чем в корзину.

Масса 1 ящика/корзины (кг)

Количество ящиков /корзин (шт)

Масса всех яблок (кг)

Я.

К.

Заполните таблицу.

Пусть х кг – масса яблок в 1 корзине.

Масса 1 ящика/корзины (кг)

Количество ящиков /корзин (шт)

Масса всех яблок (кг)

Я.

К.

Т.к. масса яблок в 12 ящиках и 18 корзинах одинаковая, то 

12(х+3) = 18х

Сборник Кузнецовой 2014 г. №8.12

1) Николай рассчитал, что он сможет хорошо приготовиться к экзамену, если будет решать по 12 задач в день. Однако ежедневно он перевыполнял свою норму на 8 задач и уже за 5 дней  до экзамена решил на 20 задач больше, чем планировал первоначально. Сколько задач решил Николай?

Число задач,  решенных за 1 д.(з/д)

Время (д.)

Всего задач

Планировал

Решил

Т.к. Николай, решая за 1 день на 8 задач больше, чем планировал, решил за  5 дней до экзамена на 20 задач больше задуманного, то

х/12=х+20/20 + 5

Задачи на концентрацию 8 класс №183

Сколько граммов воды надо добавить к 80 г раствора, содержащего 15% соли, чтобы получить 12%-ный раствор?

Концентрация соли в растворе

Масса раствора (г)

Масса соли в растворе (г)

Было

Стало

Т.к. масса соли в растворе остается постоянной, то

0,15*80 = 0,12(80+х)

Задачи на работу, в т.ч. на совместную работу

Обучение решению задач на совместную работу начинается в 5 классе арифметическим способом. Нужно сразу же учить детей правильно составлять таблицу, чтобы избежать в дальнейшем сложностей при решении задач алгебраическим способом.(при составлении уравнений)  

5 класс №1078

Одна бригада может выполнить работу за 6 дней, а другая – за 12 дней. За сколько дней две бригады выполнят ту же работу вместе?

Что такое производительность труда? Как в дробях обозначается целое?

Заполним таблицу. Примем всю работу за 1.

Производительность труда

Время (д)

Вся работа

I

?

6

1

II

?

12

1

Вместе

?

?

1

Как найти производительность труда, если известны вся работа и время?

1) 1:6=1/6 (ч/д) – производительность 1 бригады.

2) 1:12=1/12(ч/д) – производительность 2 бригады.

3) 1/6+1/12=1/4(ч/д) – за 1 день 1 и 2 бригада вместе.

4) 1:1/4=4 (д)

Ответ: за 4 дня.

№1089 Старинная задача. Китай II в.н.э.

Дикая утка  от южного до северного моря летит 7 дней. Дикий гусь от северного моря до южного моря летит 9 дней. Теперь дикая утка и дикий гусь вылетают одновременно. Через сколько дней они встретятся?

Часть пути за 1 час

Время (д)

Расстояние

Утка

?

7

1

Гусь

?

9

1

Вместе

?

?

1

9 класс №435

Заказ на пошив сумок был распределен между мастером и его учеником. Мастер выполнил 75% заказа, сшив 90 сумок. Количество сумок, которое шил в день ученик, составило 30% количества сумок, изготовляемых в день мастером, и он работал на 1 день дольше мастера. Сколько сумок в день шил мастер и сколько ученик?

Известно, что мастер выполнил 75% заказа, сшив 90 сумок.

Каков весь заказ?

Сколько сумок сшил ученик?

1) 90:0,75=120(с)- весь заказ.

2) 120-90=30(с)- сшил ученик.

Примем за х – производительность труда мастера.

Заполним таблицу и составим уравнение.

Производительность труда (с/д)

Время (д)

Вся работа (с)

Мастер

х

?

90

Ученик

0,3 х

?

30

Как найти время, затраченное на работу?

Производительность труда (с/д)

Время (д)

Вся работа (с)

Мастер

х

90/х

90

Ученик

0,3х

30/0,3х

30

Т.к. ученик работал на 1 день дольше, чем мастер, то можем составить уравнение:

30/0,3х – 90/х = 1

9 класс № 436

Электротехник и его ученик вместе выполнили работу за 8 часов. За сколько часов эту работу мог бы выполнить электротехник, работая один, если известно, что его ученик работает в 2 раза медленнее?

Пусть электротехник может выполнить эту работу за х ч. Тогда ученик за 2х ч. Заполните таблицу и составьте уравнение

Производительность труда

Время (ч)

Вся работа

Электротехник

1/х

х

1

Ученик

1/2х

2х

1

Вместе

1/х+1/2х

8

1

Т.к. за 8 ч, работая вместе, они выполнили всю работу, то

8(1/х+1/2х) = 1

9 класс №438

Для ремонта участка дороги выделили две бригады, одна из которых могла бы выполнить весь ремонт на 7 дней быстрее другой. Работу начали одновременно с двух концов участка и через 9 дней выполнили 75% всей работы. Сколько дней потребовалось бы каждой бригаде на выполнение ремонта всей дороги?

Производительность труда

Время (ч)

Вся работа

I

1/х

х

1

II

1/х+7

х+7

1

Вместе

1/х+ 1/х+7

9

0,75

Т.к., выполняя работу одновременно, через 9 дней  бригады сделали 0,75 всей работы, то

9(1/х + 1/х+7)=0,75

Сборник Кузнецовой 2014г.  № 8.13

1) На двух копировальных машинах, работающих одновременно, можно сделать копию пакета документов за 10 мин. За какое время можно выполнить эту работу на каждой машине в отдельности, если известно, что на первой машине её можно сделать на 15 мин быстрее, чем на второй?

Пусть х мин – время, за которое можно выполнить эту работу на I машине, у мин – на  II машине.

Заполним таблицу и составим систему уравнений.

Скорость работы копировальной машины

Время

Вся работа

I

1/х

х на 15 мин меньше

1

II

1/у

у

1

Вместе

1/х +1/у

1

Использование таблиц при решении задач помогает правильно проанализировать данные и верно составить уравнение. Универсальные таблицы формируют общий способ действия, учащиеся не испытывают страха и растерянности, решая задачу. Составление таблиц является эффективным приемом обучения решению текстовых задач.

Литература:

  1. Алгебра 9 класс. Учебник для общеобразовательных учреждений. Под редакцией Г.В.Дорофеева. Москва «Просвещение» 2012
  2. Математика. Сборник заданий для подготовки к ГИА в 9 классе. Л.В.Кузнецова и др. Москва  «Просвещение» 2014
  3. «Моделирование при обучении решению текстовых задач» И.И. Целищева  Ж-л «Математика в школе» 2008  №5
  4. «ЗАДАЧИ В ОБУЧЕНИИ МАТЕМАТИКЕ»  ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА  А.Р. Валиуллина  2014 г

Свидетельство о публикации статьи

В помощь учителю

Уважаемые коллеги! Опубликуйте свою педагогическую статью или сценарий мероприятия на Учительском портале и получите свидетельство о публикации методического материала в международном СМИ.

Для добавления статьи на портал необходимо зарегистрироваться.

Конкурсы

Конкурсы для учителей

Диплом и справка о публикации каждому участнику!

Маркер СМИ

© 2007 – 2023 Сообщество учителей-предметников “Учительский портал”
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

Источник

По теме: методические разработки, презентации и конспекты

Обобщение и закрепление знаний по теме : «Таблица умножения и деления» 3 класс

Урок совершенствования и закрепления навыков. Работа происходит в группах.
Все задания подобраны на развитие  логического и экономического мышления; умение делать выводы, обобщать….

Таблицы требований по предметам. 2 класс.

Мониторинг образовательных достижений учащихся по основным линиям развития….

демонстрационные таблицы по математике 1-4 класс

Данный дидактический мптериал поможет учащимся начальной школы  лучше усваивать изучаемый материал….

Технология работы над проектной задачей. Урок – проектная задача. Математика 3 класс. Симметрия.

Статья и пример конспекта урока в технологии работы над проектной задачей. Урок математики. 3 класс. Симметрия….

Урок математики. “Повторение таблицы сложения,решение примеров и задач.”1-ый класс.

Урок математики по теме “Повторение таблицы сложения,решение примеров и задач” составлен к празднику  8 Марта. 1-ый класс. Программа “Школа России.”…

Таблица проектной задачи для начальной школы

Эта таблица пригодится для предметов начальной школы. Она также содержит примеры заданий….

4 кл. (2022 год) Интерактивный плакат «Коллекция таблиц к задачам» (технологический прием «Инфографика»)

laquo;Коллекция таблиц для решения задач». Интерактивное пособие к урокам математики в начальной школе. Презентация выполнена с применением технологического приёма «Инфографика»…

Источник

Рядом данных называют результаты измерения, перечисленные в порядке их получения. Каждый из результатов называется вариантой измерения.
Например, результаты написания контрольной работы по математике для класса из 20 человек можно представить в виде следующего ряда данных: 3, 4, 4, 5, 3, 4, 3, 3, 3, 5, 5, 4, 5, 4, 5, 3, 3, 3, 4, 3. Эту же информацию можно представить в
виде таблицы:
text_zad_014
Кратность варианты — количество её повторений в ряду данных. В нашем ряду оценка «3» появилась 9 раз, поэтому её кратность равна 9.
Понятно, что таблица распределения отображает данные более наглядно и компактно.
Числовые характеристики данных
Объём измерения — количество всех данных этого измерения. Одна из наиболее важных характеристик варианты — это её частота. Частота варианты показывает долю этой
варианты в ряду распределения. Она вычисляется по формуле:

частота =кратность варианты/объём измерения

В нашем примере частота варианты «4» равна displaystyle frac{6}{20}=0,3.
Это означает, что оценка 4 составляет 0,3 всех полученных оценок.
Размах измерения — разность между максимальной и минимальной вариантами этого измерения. В нашем примере максимальная варианта равна 5, минимальная — 3, значит, размах равен 5-3=2.
Мода измерения — варианта, которая в измерении встретилась чаще других. В приведённом выше примере чаще всех встретилась оценка 3, значит, она и будет модой этого распределения.
Медиана распределения — это центральное число в упорядоченном ряду данных, если в ряду нечётное количество чисел, или полусумма двух центральных, если в ряду чётное количество чисел.
Например, для ряда распределения 1, 2, 3, 6, 9, объём измерения которого равен 5, медианой распределения будет третье число этого ряда, то есть 3.
Для ряда распределения 7, 3, 2, 1 с объёмом измерения, равным 4, медианой будет полусумма двух центральных чисел данного ряда, то есть число, равное displaystyle frac{2+3}{2}=2,5.
Для нахождения медианы распределения необходимо
1. Упорядочить ряд распределения по возрастанию или по убыванию: a_{1},a_{2},... .
2. Если объём измерения нечётный, то есть 2n+1, то получим следующую ситуацию:
text_zad_016
В этом случае медианой является число a_{n+1}.
3. Если объём измерения чётный, то есть 2n, то имеем
text_zad_018
В этом случае медианой является число — displaystyle frac{a_{n}+a_{n+1}}{2}.
Среднее ряда (среднее арифметическое) — сумма всех чисел ряда, делённая на их количество. Если имеется таблица распределения, то можно
1) умножить каждую варианту на её кратность;
2) просуммировать полученные значения;
3) разделить результат на объём измерения. Например, для ряда распределения 2, 4, б, 8, у которого объём измерения равен 4, среднее значение равно displaystyle frac{2+4+6+8}{4}=frac{20}{4}=5.
Задача 1. Даны результаты измерения веса школьников 9 класса: 55, 53, 56, 48, 45, 56, 49, 52, 53, 49, 50, 56, 45, 52, 56, 45, 45, 48, 55, 52, 43, 48, 52, 49, 50, 45, 48, 45, 50, 53.
а) Постройте таблицу распределения данных.
б) Найдите объём измерения.
в) Найдите размах ряда.
г) Найдите частоту появления каждого веса в указанном ряду.
д) Найдите медиану, моду и среднее указанного ряда.
Решение.
а) Наименьшее число в ряду — 43, оно встречается в ряду один раз, значит, его кратность равна 1. Следующее по величине — число 45, оно встречается шесть раз, значит, его кратность равна 6. Далее 48, оно встречалось 4 раза, значит, его кратность равна 4.
Продолжая аналогично, заполним таблицу:
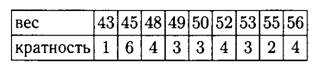
text_zad_020
б) Найти объём измерения можем несколькими способами.
1- й способ.
Посчитаем количество чисел в ряду, получим 30.
2- й способ.
Сложим кратности всех вариант: 1+6+4+3+3+4+3+2+4=30.
Ответ: 30.
в) Наибольшее значение в ряду 56, наименьшее — 43, значит, размах равен 56-43=13.
Ответ: 13.
г) Для каждой варианты делим её кратность на объём измерения (на 30), результаты пишем в таблицу.
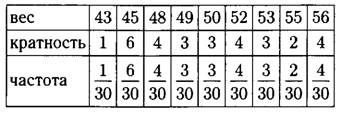
text_zad_022
д) В данном ряду 30 чисел, значит, медиана равна полусумме 15-го и 16-го чисел в упорядоченном ряду.
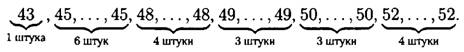
text_zad_024
Как видно из такой записи чисел, от 43 до 49 — 14 чисел, значит, 15-ое и 16-ое числа равны 50, и значит, медиана равна displaystyle frac{50+50}{2}=50.
Мода — то значение, которое встречается чаще всех, то есть то, у которого больше кратность. Из таблицы распределения находим, что наибольшую кратность имеет число 45, значит, мода равна 45.
Для нахождения среднего необходимо найти сумму всех чисел ряда и разделить ее на количество этих чисел. Сумму можно найти просто складывая подряд все числа ряда. А можно поступить иначе: каждую варианту умножить на её кратность и сложить полученные результаты. Имеем:
3cdot 1+45cdot 6+48cdot 4+49cdot 3+50cdot 3+52cdot 4+53cdot 3+55cdot 2+56cdot 4=1503.
Осталось разделить полученную сумму на количество всех чисел: displaystyle frac{1503}{30}=50,1.
Ответ: медиана: 50; мода: 45; среднее: 50,1.
Задача 2. Пятерых учеников попросили подсчитать, сколько времени (в минутах) они тратят на дорогу от дома до школы. Получили следующие результаты: 5,15,10,15,20.
1) На сколько среднее значение этого ряда меньше его размаха?
2) На сколько мода этого ряда больше медианы?
3) Найдите процентную частоту значения 10.
Решение.
1) Среднее ряда: displaystyle frac{5+15+10+15+20}{5}=13, размах: 20-5=15. Искомое значение равно 15-13=2.
Ответ: 2.
2) Найдём медиану. Расположим числа в порядке возрастания: 5, 10, 15, 15, 20. Медианой этого набора будет третье число в упорядоченном ряду, то есть 15.
В данном ряду число 15 встретилось 2 раза, остальные — по одному разу. Мода ряда равна 15. Мода и медиана этого ряда равны, значит, ответ 0.
Ответ: 0.
3) Кратность значения 10 равна 1, объём измерения равен 5 (всего 5 чисел). Частота значения 10 равна displaystyle frac{1}{5}=0,2, процентная частота равна displaystyle 0,2cdot 100%=20%.
Ответ: 20.
Задача 3. Имеется 4 группы породистых котов. Для некоторого соревнования отбирают котов с длиной шерсти не менее 8 см.
Известно следующее:
1) в первой группе наибольшая длина шерсти равна 10 см;
2) во второй группе средняя длина шерсти равна 8 см;
3) в третьей группе мода длины шерсти равна 8 см;
4) в четвёртой группе медиана длины шерсти равна 9 см.
В какой из групп хотя бы половина котов гарантированно подходит по длине шерсти?
Решение.
1) Из того, что наибольшая длина шерсти равна 10 см, не следует никакой другой информации, то есть ничего не можем сказать про остальных котов этой группы.
2) Рассмотрим для примера группу котов с длиной шерсти 7 см, 7 см и 10 см. Среднее равно displaystyle frac{7+7+10}{3}=8, но в этой группе нет половины котов, удовлетворяющих требованиям.
3) Рассмотрим для примера группу котов с шерстью длиной 8 см, 8 см, 7 см, б см, 5 см. Мода равна 8, но опять же нет половины котов, удовлетворяющих требованиям.
4) Если медиана равна 9 см, то есть половина котов с шерстью меньшей или равной длины и половина — с большей или равной длины. Значит, в этой группе найдётся половина котов с шерстью длиной не менее 8 см.
Ответ: 4.
Задача 4. По статистике автозавода из 1000 машин в среднем 20 бракованных. Сколько бракованных машин следует ожидать, если завод собирается выпустить 300 500 машин?
Решение.
Если из 1000 машин 20 бракованных, то частота появления бракованной машины равна displaystyle frac{20}{1000}=0,02. То есть доля бракованных машин будет равна 0,02, тогда из 300 500 машин будет displaystyle 300500cdot 0,02=6010 бракованных.
Ответ: 6010.

Источник

Математика, 3 класс

Урок №9. Связь между величинами: масса одного предмета, количество предметов, масса всех предметов

Перечень вопросов, рассматриваемых в теме:

– Что такое масса?

– Как найти массу одного предмета?

– Как найти общую массу?

Глоссарий по теме:

Масса предмета – величина, характеризующая вес предмета.

Чтобы найти массу одного предмета, нужно массу всех предметов разделить на количество предметов.

Чтобы найти массу всех предметов, нужно массу одного предмета умножить на количество предметов.

Основная и дополнительная литература по теме урока:

  1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с.23.
  2. Волкова С. И. Математика. Проверочные работы 3 класс. М.; Просвещение, 2014. – с.20.

Теоретический материал для самостоятельного изучения.

Рассмотрим задачу в картинках.

В задаче нужно определить массу каждого животного, т.е. вес.

Слово масса пришло к нам из латинского языка. Обозначает большое количество чего-нибудь или кого-нибудь. Измеряется масса килограммами, граммами. Вес очень больших предметов (машин, вагонов) измеряют тоннами. Прибор, с помощью которого измеряют массу – весы. Существуют разного вида и типа весы.

Решим задачу.

Масса пакета с мукой 2 кг. Узнай массу 4 таких пакетов.
К задаче можно составить схему, но удобнее будет заполнить таблицу.

В таблицу записываем названия величины и числовые данные.

Чтобы узнать массу 4 пакетов, мы должны 2 кг взять 4 раза. Массу всех пакетов узнаем действием умножением.

2 ∙ 4 = 8 (кг)

Вывод: Чтобы узнать массу всех предметов (пакетов, мешков, ящиков), нужно массу одного предмета умножить на количество.

Составим обратную задачу.

Масса 4 одинаковых пакетов с мукой 8 кг. Узнай массу одного пакета.

Заполняем таблицу.

Массу всех пакетов поровну распределим на 4 пакета.

8 : 4 = 2 (кг) – масса одного пакета.

Вывод: Чтобы узнать массу одного пакета, нужно массу всех пакетов разделить на количество.

Составим и решим следующую обратную задачу.

Масса одного пакета с мукой 2 кг. Сколько пакетов понадобится для 8 кг муки?

Заполняем таблицу.

Чтобы узнать количество пакетов, общую массу будем поровну раскладывать по 2 кг.

8 : 2 = 4 (п.)

Вывод: Чтобы узнать количество (пакетов, мешков, ящиков), нужно массу всех предметов разделить на массу одного предмета.

Тренировочные задания:

1. Выберите правильный ответ к задаче.

В одном пакете 2 кг яблок. Сколько килограммов в пяти пакетах?

7 кг; 10 кг; 5кг;

Правильный вариант: 10 кг.

2. Вставьте в таблицу пропущенные числа.

Правильный вариант:

Источник

Добавить комментарий