Время на прочтение
5 мин
Количество просмотров 110K
Статья написана, собрана и сверстана Brotherofken. Спасибо ему огромное.
В предыдущей статье я попытался изложить все основные определения и принципы, чтобы сделать эту статью максимально понятной. Все не уместилось, так что я настоятельно советую ознакомиться с этими файлами:
Базис, Базис2, Минимизация. Далее в этой статье я оставил несколько разъясняющих пометок курсивом.
В этой статье я попробую объяснить доступным языком что такое абстрактный автомат, способы его представления. Так как теория автоматов полна математики и сложна, постараюсь писать человеческим языком, чтобы неподготовленный читатель смог понять о чём идёт речь.
Электронные цифровые схемы формально можно разделить на 2 класса:
- Комбинационные Схемы (КС) – не обладают памятью. Выходной сигнал формируется в зависимости от комбинации входных данных в фиксированный момент времени (учитывая задержку на преобразования сигналов).Комбинационные схемы, их типы и принципы построения могут быть темой для отдельной статьи, а в качестве примеров можно привести: Управляемые шины, мультиплексоры и демультиплексоры, дешифраторы и шифраторы, преобразователи кодов, комбинационные счетчики и сумматоры и т. д.
- Схемы с памятью – алгоритм их работы зависит от состояния входов и памяти (того, что было в предыдущие моменты времени). Эти схемы описываются с применением теории конечных автоматов. Речь о них и пойдёт далее.
Другими словами первый класс — логические устройства, обрабатывающие входной сигнал. Второй элементы обладающие памятью и реагирующие на сигнал в зависимости от введенных в них данных.
Абстрактный автомат
Автомат должен будет реализовывать некоторые функции, которые заданы разработчиком. Он может быть простым сумматором, может реализовывать какую-либо микрокоманду процессора, выбирать слова из оперативной памяти или заниматься синтаксическим анализом выражения.
В общем виде, не вдаваясь в подробности, абстрактный автомат можно представить следующим образом:
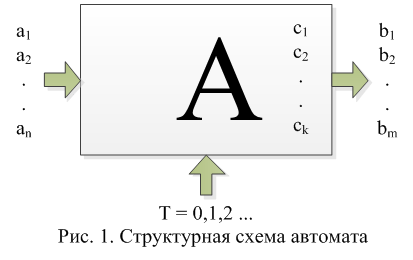
Или, если перейти от иллюстрации к математическому описанию:
A = <A, B, C, δ, λ>
Обозначения:
- Множество {A} – представляет собой множество значений на физических входах автомата. На входе в нашем случае будет какая-то последовательность высоких и низких уровней напряжения, которые будут кодировать логические нули и единицы.
- Множество {B} – представляет собой множество значений на физических выходах автомата.
- Множество {C} – а множество, которое представляет внутреннее состояние автомата – память. На будущее C0 будем обозначать начальное состояние автомата.
- δ = X × Z → Z – это функции переходов автомата, они однозначно определяют состояние ai в которое переходит автомат из состояния aj.
- λ = X × Z → Y – функции выходов, они определяют что находится на выходе автомата в зависимости от входов и внутреннего состояния.
δ и λ не показаны на схеме для визуального упрощения.
Такой автомат функционирует дискретно по времени, то есть значения входов, выходов и внутреннее состояние автомата изменяются в дискретные моменты времени.
Итак мы в общем виде описали что есть Абстрактный автомат. Примером такого автомата может быть триггер, регистр ЭВМ или сумматор.
Выделяют 2 типа автоматов:
- Автоматы Мили. Описывается системой уравнений:
c(t) = δ( a(t), c(t-1) );
b(t) = λ( a(t), c(t-1) ). - Автоматы Мура. Описывается уравнениями:
c(t) = δ( a(t), c(t-1) );
b(t) = λ( a(t), c(t) ).
Как видно
состояние автомата c(t) в текущий момент времени является функцией его состояния в предыдущий момент времени и входного сигнала
.
Отличаются автоматы видом функции выхода. В автомате Мили выходной сигнал определяется входным сигналом a(t) и состоянием автомата в предыдущий момент времени c(t-1). Выходной сигнал автомата Мура определяется парой входного сигнала a(t) и состояния в данный момент c(t).
Так же можно отметить, что от одного типа можно перейти ко второму и наоборот, причем при переходе от автомата Мили к автомату Мура число внутренних состояний автомата останется прежним, а при обратном переходе число внутренних состояний может возрасти. На этом останавливаться подробно не будем, считая, что синтезировали(нарисовали граф) автомат того типа, который надо.
Итак, на этом с матчастью окончено. Попробуем описать автоматы.
Т.е. автомат типа Мили вырабатывает выходной сигнал когда у него меняется входной, в зависимости от его предыдущего состояния. При этом длительность выходного сигнала не зависит от длительности входного, а только от его присутствия. В автоматах типа Мура выходной сигнал зависит от состояния автомата в текущий момент времени т.е. автомат будет вырабатывать определенный выходной сигнал пока не изменит свое состояние.
Способы задания автоматов
Как мы выяснили в первой части — автомат представляет собой совокупность входного и выходного алфавитов, множества внутренних состояний и функций, определяющих переходы и выходы. Однако, обычно функции δ и λ не заданы, и поведение автомата приходится описывать по-другому.
Есть два основных способа задания автомата:
- При помощи графов.
- При помощи таблиц переходов и выходов.
Графы
Граф автомата – это ориентированный связный граф, вершины которого символизируют внутренние состояния автомата, а дуги – переходы из одного состояния в другое.
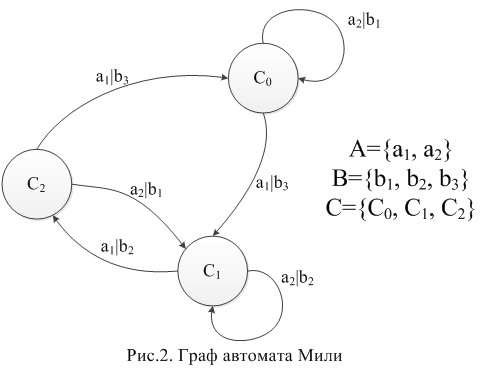
Для графа Мили на дугах указываются сходные и выходные буквы. Выходные буквы пишутся над дугами, символизируя то, что выходное состояние зависит от состояния автомата в предыдущий момент времени.

Для графа автомата Мура на дугах записываются только входные буквы, выходные же указываются около вершин.
Важный момент: Если из каждой вершины выходит столько дуг, сколько есть входных букв, то автомат называется
полным
. Другими словами – если из каждой вершины определены переходы для каждой входной буквы. В наших примерах автомат
Мили является полным
, а автомат
Мура – частичным
.
И ещё: Если из одной вершины выходит дуг больше, чем входных букв (то есть 2 и более дуг с одинаковыми входными буквами), то такой автомат называется
недетерминированным
. Такое может произойти при построении формализованного описания и тогда надо будет произвести переход к
детерминированному
автомату, но это не всегда можно выполнить. Описание этого процесса я тоже упускаю, сразу нарисовав детерминированный автомат.
На этом о графах всё.
Таблицы переходов и выходов.
Графы нагляднее для человека, а таблицы — для машины. Любой автомат можно представить в виде таблицы переходов и выходов (ТПВ). В ТПВ строками являются внутренние состояния автомата, а столбцами – входные буквы.
Построим ТПВ для наших графов Мили и Мура. Если не определена какая-либо входная или выходная буква, то вместо неё ставится прочерк. Если не определено состояние, то действует это же простое правило.
ТПВ графа Мили
В ТПВ Мили в каждой клетке записаны переходы и выходы. Например, если автомат находится в состоянии С0 и на вход приходит буква a1, то он перейдёт в состояние С1 и на выходе появится буква b3.
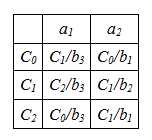
ТПВ графа Мура
Для графа Мура строят отмеченную таблицу переходов. Выделяется дополнительный столбец для выходных букв.
В клетке под входной буквой пишется в какое состояние автомат переходит, в крайней правой клетке — какую выходную букву возвращает.
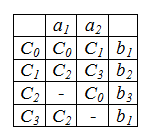
Пример синтеза автомата
При помощи абстрактных автоматов можно описать практически что угодно. Можно описать работу цифровой схемы, а можно – синтаксический или лексический анализатор. Попробуем описать триггер – чем не автомат?
Чтобы задать граф нужно словесное описание алгоритма работы триггера. Читаем:
Кодируем входной и выходной алфавиты:
A = {a0, a1}, где a0 – логическая 1 на входе R, a1 – логическая единица на входе S.
B = {b0, b1}, где b0 – логический 0 на выходе Q, b1 – логическая единица на выходе Q.
Строим граф автомата Мили:

Вот такая забавная чебурашка получилась :-). Теперь можно построить таблицу переходов и выходов:

Если расписать эту таблицу преобразовав условные обозначения в фактические, то получим таблицу которая представляет из себя таблицу переходов триггера. Затем её можно упростить:
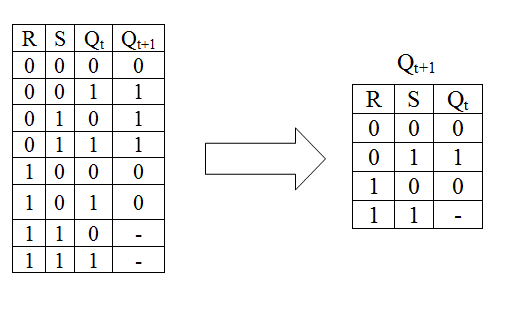
Нанесём полученную функцию на карту Вейча и минимизируем:
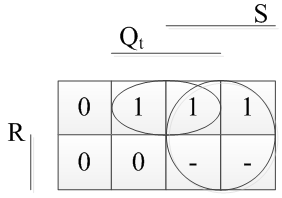
Выпишем, что получилось:

Строим по функции схему (Выполняли домашнее задание?):
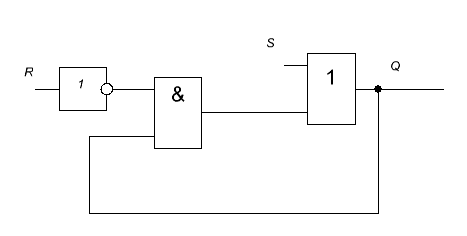
Немного непривычно видеть триггер в булевом базисе, поэтому переведём функцию в базис И-НЕ и нарисуем схему в нём:
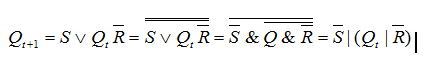

А на схеме асинхронный RS триггер обозначается вот так:
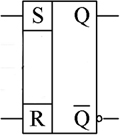
Теперь если приложить немного старания, то можно самостоятельно синтезировать простую новогоднюю гирлянду.
Поскольку
функции
и
определены на конечных множествах, их
можно задавать таблицами. Обычно две
таблицы сводят в одну таблицу :
 и называют таблицей переходов-выходов
и называют таблицей переходов-выходов
или просто таблицей переходов (автоматной
таблицей). При задании автомата
ориентированным графом (орграфом), его
вершины сопоставляют с внутренними
состояниями, и дуги – с условиями
перехода из состояния в состояние. Дуги
помечают входными символами автомата.
Дуги также помечают и соответствующими
выходными символами, если это автомат
Мили.
Рассмотрим
граф переходов некоторого автомата
Мили (рис. 52), Х={x1,x2},
Y={y1,y2,y3},
Z={z1,z2,z3}.
На
графе автомата Мили (рис. 52) дуги помечаются
дробью, где в числителе – входной символ,
в знаменателе – выходной символ.
Представим
этот же автомат Мили таблицей переходов
(табл. 50).

Рис.
52. Граф некоторого автомата Мили
Таблица
50
Таблица
переходов выходов автомата Мили,
заданного графом рис. 52
|
Внутреннее состояние |
Входной символ |
||
|
y(t) |
х1 |
х2 |
|
|
y1 |
|
|
|
|
y2 |
|
|
|
|
y3 |
|
– |
|
В
клетках табл. 50 записывается дробь, в
числителе которой указывается последующее
внутреннее состояние y(t+1),
а в знаменателе – выходной символ z(t).
Это указано в специальной выноске
таблицы (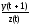 ).
).
Видно, что автомат не полностью
определенный (клеткаy3х2
не заполнена).
Рассмотрим
граф некоторого автомата Мура (рис. 53),
Х={x1,x2},
Y={y1,y2,y3},
Z={z1,z2,z3}:

Рис.
53. Граф некоторого автомата Мура
Выходные
символы в автомате Мура сопоставляются
с конкретными внутренними состояниями
и записываются в знаменателе дроби,
помечающей внутренние состояния. Само
внутреннее состояние указывается в
числителе. Дуги графа автомата Мура
помечаются только входными символами.
Соответствующая этому автомату Мура
таблица переходов представлена табл.
51.
Таблица
51
Таблица
переходов-выходов автомата Мура,
заданного графом рис. 53
|
Внутреннее состояние |
Входной символ |
Выходной символ |
|
|
y(t) |
х1 |
х2 |
|
|
y1 |
y3 |
y1 |
z2 |
|
y2 |
y1 |
y3 |
z1 |
|
y3 |
y1 |
– |
z3 |
|
y(t+1) |
В
клетках табл. 51, соответствующих входным
символам, записывается только последующее
внутреннее состояние y(t+1),
что указано в специальной сноске
(y(t+1)).
Комбинационный
автомат задается таблицей истинности
(соответствия), уже известной нам, так
как граф переходов такого автомата
имеет одну вершину и m
петель, где m
– число входных символов. Пример таблицы
истинности, задающей некоторый
комбинационный автомат, приведен табл.
52.
Таблица
52
Таблица
истинности комбинационного автомата:
Х={x1,x2,х3,х4},
Z={z1,z2,z3,z4}
|
Входной символ х |
Выходной символ z |
|
x1 |
z2 |
|
x2 |
z4 |
|
x3 |
z1 |
|
x4 |
z3 |
В
отличие от комбинационного конечного
автомата, имеющего одно внутреннее
состояние, конечные автоматы, имеющие
больше, чем одно внутреннее состояние,
называются последовательностными
конечными автоматами или просто
последовательностными автоматами.
Рассмотрим
последовательностный автомат, заданный
табл. 53. Зафиксируем начальное состояние
y1
и каждому входному слову (последовательности
входных символов) =xj1xj2…xjr
поставим в соответствие слово
в выходном алфавите:
=(xj1,y1)(xj1,xj2,y1)…
(xj1,…,xjr,y1).
Это
соответствие, отображающее входные
слова в выходные, называется автоматным
отображением.
Таблица
53
Таблица
переходов-выходов некоторого автомата
Мили

Зададим
входное слово =x1х2х3х4.
Тогда
выходное слово =z1z1z1z3.
Рассмотрим
подробнее процесс формирования выходного
слова:

В
этой последовательности указаны так
называемые переходы из состояния в
состояние, обведенные линией. То есть,
например, при поступлении х2
автомат сначала находится в состоянии
y1,
а затем автомат переходит в состояние
y2.
Указанные выше последовательности
иногда изображают стрелками в таблице
переходов-выходов.
Состояния
yj
называют достижимыми из состояния yi,
если существует входное слово ,
такое, что (,yi)=yj.
Состояния
называются эквивалентными, если они
соответствуют одинаковым последовательностям
«входное слово – выходное слово»; причем
длина такой последовательности может
быть любая 1.
Например, в последовательности:

состояния
y1
и y9
эквивалентны (длина последовательности
=1), состояния y3
и y7
неэквивалентны, поскольку последовательность
длиной 2: в первом случае
![]() ,
,
а во втором –![]() .
.
Таким
образом, состояние y9
заменяется на состояние y1.
В
последовательности:

состояния
y1,у5,y9
также эквивалентны. Эквивалентны
состояния y3
и y7,
а также состояния y4,y8.
Одинаковые последовательности обведены.
В
этих примерах предполагается, что далее
последовательности повторяются, т.е.
после y9
следует y2,y3
и т.д.
Таким
образом, вторую последовательность
можно представить в виде:
x1
x2
x3
x2
x1
x4
x3
x2
x1
y1
y2
y3
y4
y1
y5
y3
y4
y1
z1
z1
z2
z3
z1
z2
z2
z3
z1
где
y9
заменено на y1,
y7
на y3,
y8
на y4.
Автомат,
реализующий эту последовательность,
эквивалентен автомату, реализующему
исходную последовательность, но имеет
меньше состояний.
Автомат
называется сильно связанным, если из
любого его состояния достижимо любое
другое состояние.
Автомат
называется автономным, если его входной
алфавит состоит из одной буквы X={х}.
Все входные слова автономного автомата
имеют вид хх…х.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Занятие 14. Граф автомата, таблица переходов и выходов
Цель занятия. Изучение еще одного класса дискретных автоматов – автоматов с памятью, познакомится со способами описания работы этих устройств.
Теоретические положения и примеры. До сих пор мы изучали т. н. комбинационные схемы – дискретные устройства без памяти, т. е. устройства выходные сигналы которых однозначно определялись каждой комбинацией входных наборов. Теперь настала пора приступить к изучению дискретных устройств с памятью – последовательностных автоматов, т. е. устройств, реагирующих на последовательность входных наборов.
Работа последовательностного автомата определяется не только входным набором, но и собственным состоянием автомата. В свою очередь состояние Si автомата зависит от начального S0 его состояния и последовательности входных наборов, приведших его в это состояние(рис. 1).

Рисунок 58. Дискретное устройство с памятью (yi = F(x1,…,xn, Si)
Si {S0,S1,…,SL}, 2< L < m).
Мы рассматриваем дискретные устройства с конечным числом L состояний S. Рассмотрим представление автомата с памятью графом автомата. Начнем с представления триггера – автомата с 2 состояниями. Состояния представим вершинами, а связи между ними – стрелками. Стрелки снабдим условиями переходов.

Рисунок 59. D – триггер (задержка – сигнал х задерживается на один такт T).

Рисунок 60. Изображение D-триггера на схемах

Рисунок 61. С синхросигнал с периодом Т.
Сигнал D запоминается в момент, когда С=1 и хранится весь оставшийся период Т.
Теперь выполним проектирование так называемого “Секретного замка” – последовательного автомата запирающего дверь и открывающего ее, или поднимающего сигнал тревоги в зависимости от последовательностей входных воздействий.

Рисунок 62. “х1, х2”- входные переменные, “y1,y2” – выходные переменные.
1,дверь открывается,
y1=
0, дверь закрывается;
1, тревога звучит,
y2=
0, тревога не звучит.
Задана всего одна открывающая последовательность входных наборов. Еще один набор – нейтральный (х1х2 = 00), автомат остается в том же состоянии. На всех остальных последовательностях звучит сигнал тревоги.
Для нашего автомата открывающая входная последовательность пусть будет такой – х1х2= 01 11 10. Последовательности, например, начинающиеся с наборов 11 иди 10, вызовут сигнал тревоги автомата. Если дверь открыта, то она остается в этом состоянии при нейтральном входном наборе(00), любое нажатие входных кнопок вызовет закрытие двери. Наконец, если нечаянно сам владелец замка нажал неверную входную последовательность, то он может вывести автомат из тревоги, набрав единственную верную последовательность выхода из тревоги, например, х1х2 = 11 10.
Построим граф автомата “секретный замок” для уже сформулированных данных. Вначале автомат находится в некотором начальном состоянии( S0, x1x2=00, y1y2 = 00). Набираем первый набор открывающей последовательности. Автомат переходит в следующее состояние(S1, y1y2=00), но в этом состоянии автомат ждет уже второй набор открывающей последовательности. Поучив его (х1х2 =11), автомат переходит в следующее состояние(S2, y1y2 =00), в котором автомат ждет третий правильный входной набор. Получив его автомат переходит в состояние S3. Но в этом состоянии автомат, уже получив всю правильную открывающую входную последовательность, должен открыть дверь (S3, y1y2= 10). При входном нейтральном наборе (00) дверь остается открытой, после нажатия любого набора (01, или 11, или 10), дверь закрывается (S0, y1y2 =00).

Рисунок 63. Описание работы по открытию замка.
Остается реализовать режимы входа в тревогу и выхода из нее. В состоянии S1 наборы 00 и 01 уже задействованы, остаются наборы 10 и 11, при них нужно реализовать переход в тревогу – состояние (S4 y1y2 =01). В состоянии S1 нейтральный набор возвращает в то же состояние S1, наборы 01 и 10 переводят автомат в состояние тревоги S4. Аналогично в состоянии S2 нейтральный набор 00 возвращает автомат в состояние S2, наборы 11 и 01 – в состояние тревоги S4.

Рисунок 64. Описание работы по правильной последовательности и формированию сигнала тревоги.
Остается реализовать поведение автомата при выходе из тревоги. В состоянии S4 набор 11 переводит автомат в состояние S5 (y! y2 = 01). Из состояния S5 набор 10 сбрасывает тревогу (S0, y1y2 =00). При остальных наборах – возврат в состояние тревоги.

Рисунок 65. Полное описание графа автомата ”Секретный замок”.
Граф автомата полностью описывает его повеление. Но в некоторых случаях (когда число входных переменных не велико) используют другую форму задания алгоритма работы последовательностного автомата – таблица переходов и выходов автомата (ТПиВ). Таблица переходов и выходов автомата является прямоугольной матрицей, строки которой сопоставлены входным наборам и столбцы – состояниям.

Рисунок 66. Таблица переходов и выходов автомата “Секретный замок”.
Полученная таблица переходов и выходов еще представлена на так называемом абстрактном уровне. Чтобы перейти к комбинационным схемам необходимо заменить абстрактные символы состояний комбинациями наборов двоичных переменных, т. е. произвести кодирование состояний автомата. Необходимое условие правильного кодирования состояний – каждому состоянию нужно поставить свой, отличный от других состояний код. Отсюда число к внутренних переменных z1z2…zk, кодирующих состояния, вычисляется по следующей формуле k=]log2(L +1)[.Состояния переменных zi представляются состояниями памяти автомата, отсюда схема последовательностного автомата выглядит следующим образом.
Первоначально проведем так называемое тривиальное кодирование состояний, состояние Si закодируем k-разрядным двоичным кодом числа i. k=]log2(5+1)[=3.
|
z3 |
z2 |
z1 |
|
|
S0 |
0 |
0 |
0 |
|
S1 |
0 |
0 |
1 |
|
S2 |
0 |
1 |
0 |
|
S3 |
0 |
1 |
1 |
|
S4 |
1 |
0 |
0 |
|
S5 |
1 |
0 |
1 |

Рисунок 67. Кодированная таблица переходов и выходов.
Прежде всего обратим внимание на расстановку состояний по столбцам кодированной таблицы переходов и выходов. Они расставлены согласно их кодированию. Состояния Sx обозначают не использованные коды 110 и 111.
Итак, мы перешли от абстрактного представления автомата к системе булевых функций: первый столбец кодированной таблицы переходов и выходов представляет булеву функцию z1(t+1), второй столбец – булеву функцию z2(t+1), третий столбец – булеву функцию z3(t+1).
Чтобы построить выходные функции автомата, поступим следующим образом. Разместим состояния автомата на матрице трех переменных – z1z2z3:

Рисунок 68. Размещение состояний автомата “Секретный замок” на матричной форме переменных z1, z2, z3.
Функция у1 принимает единичное значение на единственном наборе, соответствующему состоянию S3 – это набор 011. И кроме того она не определена на наборах, соответствующих состояниям Sx. Функция у2 Принимает единичное значение на наборах, соответствующих состояниям S4, S5 и не определена на наборах для состояний Sx.

Рисунок 69. Выходные функции автомата “Секретного замка”.
Домашнее задание. Построить граф автомата “Секретный замок” по заданию[3, стр. 12], номер варианта определяется по i, младшая цифра задает открывающую последовательность, старшая – последовательность сброса тревоги. Построить таблицу переходов и выходов автомата, провести кодирование состояний и построить кодированную таблицу переходов и выходов. Построить функции z1,z2,z3,у1 и y2.
| Определение: |
Абстрактный автомат (англ. Abstract Machine) является математической моделью дискретного устройства и описывается шестикомпонентным набором , где
|
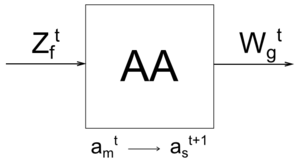
Работа Абстрактного автомата
Выходные сигналы АА зависят от того, что поступало на его вход раньше.
В каждый момент времени АА, будучи в состоянии , способен воспринимать одну из букв входного алфавита . В соответствии с функцией , АА перейдет в состояние с выдачей выходного сигнала, который вырабатывается в соответствии с функцией выходов .
Рассмотрим функционирование автоматов Мура и Мили.
|
Автомат Мили |
Автомат Мура |
В автоматах Мура выходные воздействия записаны на состояниях, а в автомате Мили — на переходах.
Содержание
- 1 Применение автоматов Мура и Мили
- 1.1 Автомат, регулирующий пешеходный переход
- 1.2 Торговый автомат
- 2 Способы задания автоматов
- 2.1 Табличный способ задания автомата Мили
- 2.2 Графический способ задания автомата Мили
- 2.3 Табличный способ задания автомата Мура
- 2.4 Графический способ задания автомата Мура
- 3 Реакция автоматов на входное слово
- 3.1 Автомат Мили
- 3.2 Автомат Мура
- 4 Эквивалентность автоматов Мили и Мура
- 4.1 Переход от автомата Мура к автомату Мили
- 4.2 Переход от автомата Мили к автомату Мура
- 5 См. также
- 6 Примечания
- 7 Источники информации
Применение автоматов Мура и Мили
Автоматы Мура и Мили широко применяются при проектировании цифровых устройств на основе программируемых логических интегральных схем (ПЛИС).
Основное преимущество использования автомата Мили заключается в возможности реакции автомата в течение текущего такта, что обусловлено зависимостью текущей выходной комбинации от текущей входной комбинации .
Наличие минимальной выходной задержки, связанной с переключением выходного регистра, отсутствие нестабильности переходного процесса на выходе автомата, отсутствие сквозного распространения сигнала через комбинационную схему от входа до выхода автомата, простота описания на языках описания аппаратуры HDL делает автомат Мура практически незаменимым.
Также автоматы Мура и взаимодействующие автоматы Мили используются в генетическом программировании (например, для решения задачи об “Умном муравье”
[1]).
Автомат, регулирующий пешеходный переход
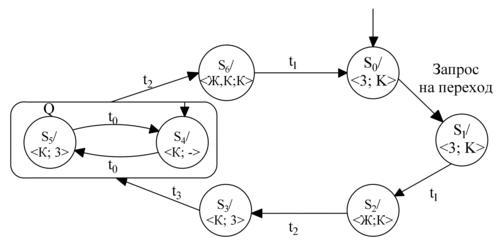
Рассмотрим автомат, регулирующий пешеходный переход по запросу пешеходов. Внешние события автомата — это события нажатия пешеходами кнопки-запроса на тротуаре и исчерпание тайм-аута. Автомат строится как автомат Мура, в котором выход — регулирование светофора и разрешающий сигнал на переход — это потенциальные сигналы, являющиеся функциями состояния.
Выход автомата в каждом состоянии определяется парой Светофор транспорта; светофор пешехода. Например, в состоянии управляющий автомат устанавливает З; К, то есть включёнными зеленый свет транспорту и красный — пешеходам. В состоянии установлен Ж, К; К, то есть желтый и красный свет транспорту (приготовиться) и красный — пешеходам. В начальном состоянии разрешен проезд транспорту, а пешеходам движение запрещено.
В состояниях , при запрещающем сигнале транспорту зеленый сигнал пешеходам мигает каждые секунд в течение секунд. Запрос на переход принимается только в состоянии , в остальных состояниях он игнорируется. Задержки (тайм-ауты — ) устанавливаются в момент перехода автомата в данное состояние, по исчерпании тайм-аута автомат переходит в следующее состояние. В гиперсостоянии , объединяющему пару состояний и , автомат находится ровно секунд: внутренние переходы не срывают тайм-аута.
Именно для этого удобно использовать гиперсостояние .
Торговый автомат
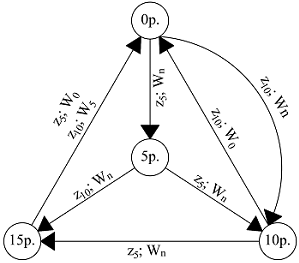
В качестве примера применения автомата Мили рассмотрим автомат по продаже шоколадок стоимостью рублей, принимающий монеты номиналом в и рублей и возвращающий сдачу, если это необходимо.
Состояний автомата всего четыре: , , и рублей.
Входных сигналов два: — рублей и — рублей.
Выходных сигналов три: — ничего не выдавать, — выдать шоколадку и рублей сдачи, — выдать шоколадку и рублей сдачи.
Например, если у человека есть одна монета номиналом в рублей и две монеты номиналом в рублей и монеты забрасываются в порядке , и рублей, то происходит следующее:
-
- Автомат переходит в состояние р. и ничего не выдает;
- Автомат переходит в состояние р. и ничего не выдает;
- Автомат переходит в состояние р., выдает шоколадку и не возвращает сдачу.
Способы задания автоматов
Табличный способ задания автомата Мили
Автомат Мили может быть задан таблицей переходов и таблицей выходов.
В таблице переходов АА Мили на пересечении столбца и строки записывается состояние , которое есть функция от и
В таблице выходов на пересечении столбца и строки записывается выходной сигнал, который есть функция от и .
Пример: Задание автомата Мили табличным способом (автомат имеет два входных сигнала, два выходных сигнала и три состояния).
|
Таблица переходов |
Таблица выходов |
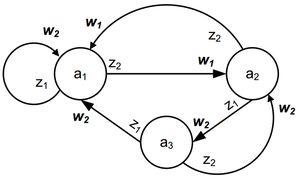
Графический способ задания автомата Мили
На рисунке приведен граф автомата Мили на 3 состояния, имеющий 2 входных сигнала и 2 выходных сигнала (см. предыдущий пример).
Табличный способ задания автомата Мура
В автомате Мура выходной сигнал зависит только от состояния автомата и не зависит от входного сигнала.
Поэтому достаточно для задания автомата Мура в таблице переходов добавить одну строку.
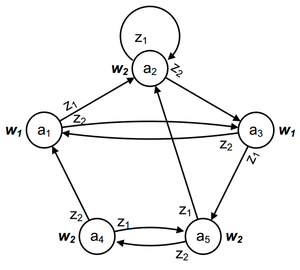
Графический способ задания автомата Мура
На рисунке приведен граф автомата Мура на 5 состояний, имеющий 2 входных сигнала и 2 выходных сигнала.
Реакция автоматов на входное слово
Автомат Мили
Допустим, входное слово поступает на вход автомата буква за буквой.
Выходное слово называется реакцией автомата Мили на входное слово в состоянии строится по таблице переходов и выходов).
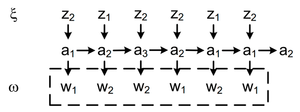
Реакцию автомата на входное слово можно заменить обходом графа.
Автомат Мура
Выходное слово называется реакцией автомата Мура на входное слово в состоянии .
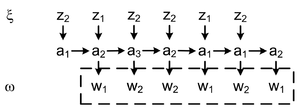
В рассматриваемом примере для автоматов Мили и Мура реакции автоматов на одинаковое входное слово совпадают, но они сдвинуты на один такт. Автоматы Мили и Мура дающие одинаковые реакции на одинаковые входные слова называются эквивалентными. Данное замечание приводит к задаче построения эквивалентных автоматов, дающих одинаковые реакции на одинаковые входные слова.
Эквивалентность автоматов Мили и Мура
Автомат Мура переходит в автомат Мили, если всем переходам в состояние поставить выходные воздействия этого состояния. После таких преобразований получим эквивалентный автомат Мили.
Однако, чтобы преобразовать автомат Мили в автомат Мура такой алгоритм не подходит, т.к. в одно состояние могут вести разные переходы. Но можно просто добавить новых состояний, устанавливая необходимые соответствия.
Далее будет приведено формальное доказательство факта эквивалентности с явным предъявлением конструкции.
| Теорема (Эквивалентность автоматов Мура и Мили): |
|
Для каждого автомата Мили может быть построен эквивалентный ему автомат Мура, и обратно — для каждого автомата Мура может быть построен эквивалентный ему автомат Мили. |
| Доказательство: |
| Для доказательства опишем алгоритмы взаимной трансформации моделей Мили и Мура и покажем эквивалентность получающихся автоматов. При этом в автоматах Мура будем пренебрегать выходным сигналом , связанным с начальным состоянием. |
Переход от автомата Мура к автомату Мили
Шестикомпонентным набором с индексом А будем обозначать автомат Мура, а с индексом В — автомат Мили.
Пусть задан автомат Мура.
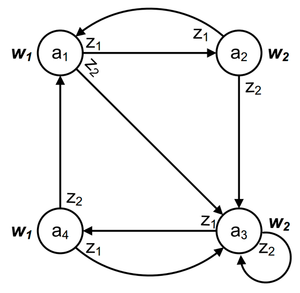
Требуется перейти к автомату Мили
),
у которого , , т.е. входные и выходные алфавиты совпадают.
Рассмотрим пример, в котором , , , алфавит состояний автомата Мура содержит четыре элемента.
При переходе от автомата Мура к автомату Мили алфавиты состояний также совпадают, т.е. .
Для определения соответствия между функциями переходов выходов автоматов Мура и Мили воспользуемся следующей вспомогательной таблицей.
При переходе от автомата Мура к автомату Мили функции переходов также совпадают, а для определения функции выходов выходные сигналы с вершин опускается на входные дуги.
Проделав такие преобразования мы должны доказать, что получили автомат Мили, эквивалентный автомату Мура, т.е. что реакции автоматов на одинаковые входные воздействия совпадают.
При таком переходе (Мура к Мили) число состояний совпадает.
| Утверждение: |
|
Полученный автомат эквивалентен исходному |
|
Пусть символ поступает на вход автомата Мура , который находится в состоянии . Следовательно, перейдет в состояние и выдаст сигнал . Соответствующий автомат Мили из состояния также перейдет в состояние и выдаст тот же сигнал . Таким образом, для выходной последовательности длины 1 поведение автоматов и полностью совпадает. Далее по индукции получаем эквивалентность автоматов. |
Переход от автомата Мили к автомату Мура
Пусть задан автомат Мили .
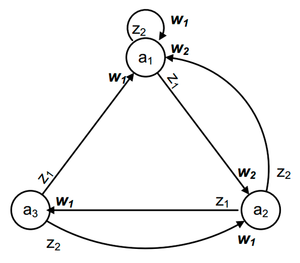
Требуется перейти к автомату Мура
,
у которого ; , т.е. входные и выходные алфавиты совпадают.
Рассмотрим пример, в котором , , алфавит состояний автомата Мили содержит три элемента.
Для определения алфавита состояний, функций переходов и выходов автомата Мура воспользуемся следующей вспомогательной таблицей.
В данном случае .
При таком переходе (Мили к Мура) каждому состоянию автомата Мили ставится в соответствие множество всевозможных пар , где есть функция от состояния и входного сигнала, функция от состояния и входного сигнала.
Пример:
| Мура | Мили |
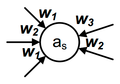
|
Для состояния:
В качестве начального состояния результирующего автомата может быть выбрано любое состояние Мура, порожденное начальным состоянием автомата Мили, т.е. состояния или .
При определении функции переходов результирующего автомата Мура из всех состояний, порожденных одним состоянием автомата Мили, должны быть переходы под воздействием одинаковых входных сигналов.
Поскольку в автомате Мура выходной сигнал зависит только от состояния автомата, то в примере рядом с состояниями проставим соответствующие выходные сигналы.
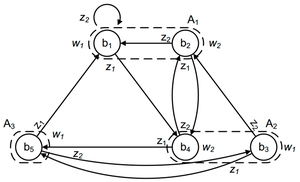
И так если осуществить следующие преобразования, то получим:
| Мили | Мура | Мили |
| 3 состояния | 5 состояний | 5 состояний |
Можно утверждать, что если эквивалентно , а эквивалентно , то эквивалентно (т.е. эквивалентность обладает свойством транзитивности).
| Утверждение: |
|
Полученный автомат эквивалентен исходному |
| Доказательство эквивалентности автоматов и аналогично предыдущему случаю. |
Методы взаимной транспозиции автоматов Мили и Мура показывают, что при переходе от автомата Мили к автомату Мура число состояний принципиально не меняется. В то время как при обратном переходе в автомат Мура число состояний, как правило, увеличивается. Вследствие транзитивности отношения эквивалентности два автомата Мили, первый из которых получен из автомата Мура, так же будут эквивалентны, но у второго автомата число состояний будет больше. Таким образом эквивалентные между собой автоматы могут иметь различное число состояний. В связи с чем и возникает задача нахождения минимального автомата в классе эквивалентных между собой автоматов. Существование для любого абстрактного автомата эквивалентного ему абстрактного автомата с минимальным числом внутренних состояний впервые было доказано Муром.
См. также
- Локальные автоматы
- Двусторонний детерминированный конечный автомат
- Квантовый конечный автомат
Примечания
- ↑ Применение генетических алгоритмов для генерации автоматов Мура и систем взаимодействующих автоматов Мили в задаче об “Умном муравье”
Источники информации
- Ожиганов А.А. Теория автоматов: Учебное пособие. СПб.: НИУ ИТМО, 2013 — С. 84.
- Богаченко Н.Ф., Файзуллин Р.Т. Синтез дискретных автоматов: Учебное пособие. Омск: Издательство Наследие. Диалог-Сибирь, 2006.
- Википедия — Автомат Мура
- Ofap.ulstu.ru — Абстрактные автоматы
- Николай Борисенко — Технические аспекты построения управляющих автоматов при проектировании цифровых устройств на основе современных ПЛИС







