Как составить таблицу по математике 4 класс в задаче на движение

Чтобы быстро решить задачи на движение, в том числе сложные и запутанные, нужно составить к ней схему или таблицу данных.

• Схемы задач на движение помогают представить наглядно условие задачи и найти верное решение.
• Таблица к задачам на движение позволяет структурировать данные, чтобы наглядно видеть исходные данные и неизвестные величины.

Поэтому, чтобы решить сложные задачи на движение, нужно нарисовать схему, а в дополнение к схеме рекомендуется нарисовать таблицу, где в шапке параметры скорости, времени и расстояния. При этом везде применяется основная формула:

Рассмотрим решение следующих типов задач:

• простые задачи на скорость, время и расстояние;
• задачи на движение в разных направлениях: сближение и удаление;
• задачи на движение в одном направлении: сближение и удаление;
• решение задач на движение по реке.

Решить простые задачи на движение

Для решения простых задач на движение, как правило, схема или таблица не требуется, в них применяется формула нахождения скорости, времени или расстояния. Но иногда, чтобы не запутаться в решении, лучше воспользоваться каким-либо методом. Рассмотрим схему и таблицу, чтобы вы смогли выбрать наиболее удобный для себя способ разобраться в задаче.

Задача 1. Средняя скорость

Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)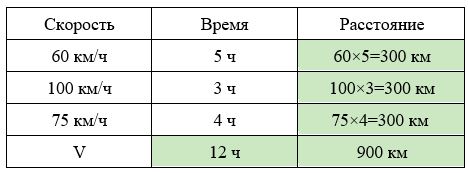 

Средняя скорость — это отношение пройденного пути ко времени, за который пройден этот путь.

• Найдем общее расстояние: 900 км.
• Найдем время в пути: 5 + 3 + 4 = 12 часов.
• Найдем среднюю скорость автомобиля: 900:12 = 75 км/ч.

Задача 2. Движение с остановкой

В 9:00 велосипедист выехал из пункта А в пункт Б. Доехав до пункта Б, он сделал остановку на полчаса, а в 11:30 выехал обратно с прежней скоростью. В 13:00 ему оставалось проехать 8 км до пункта А. Найдите расстояние между пунктами А и Б.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности.

• Найдем скорость: 8 : 0,5 = 16 км/ч
• Найдем расстояние: 16×2=32 км.

Задача 3. Уровень ЕГЭ.

Лыжник планировал проехать 10 км с горы за 20 минут с постоянной скоростью v. Вместо этого первые несколько километров он проехал в два раза быстрее, чем планировал, а оставшиеся километры он проехал в два раза медленнее, чем планировал. В итоге весь путь занял у него 34 минуты. Сколько километров лыжник проехал в два раза быстрее, чем планировал?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)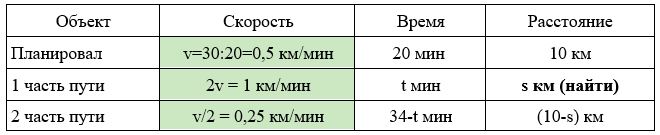

• Найдем скорость, с которой лыжник планировал скатиться: 10 : 20 = 0,5км/мин
• Найдем скорости, с которыми лыжник скатывался: 3км/мин и 0,25км/мин.
• Составим систему уравнений:
  1) 1×t=s  → t=s
  2) 0,25×(34-t)=10-s → 0,25×(34-s)=10-s → s=2 км.

Решить задачи на движение в разных направлениях: сближение и удаление

Задача 4. Скорость удаления

Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля  100  км/ч, скорость второго —  70  км/ч. Какое расстояние будет между автомобилями через  4  часа?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) /

Способ 1.
1) 100× 4 = 400 (км)  — проехал первый автомобиль,
2) 70 × 4 = 280 (км)  — проехал второй автомобиль.
3) 400 + 280 = 680 (км).

Способ 2.
1)  (100 + 70),  170  км/ч — это скорость удаления автомобилей.
2) 170× 4 = 680 км.

Задача 5. Скорость сближения

Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?

Решение.
Нарисуем схему движения.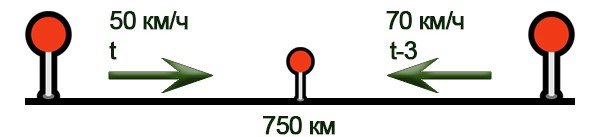

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)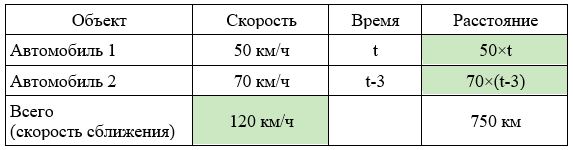

Способ 1.

• Составим уравнение: 50×t + 70×(t-3) =750
• Решим уравнение: 120t=960; t=8 часов.
• По условиям задачи нужно найти расстояние от пункта А, то есть расстояние для первого автомобиля: 50×8=400км.

Способ 2.

• За первые три часа пути автомобиль, выехавший из города А, проехал 150 километров и расстояние от него до города В стало равным 600 км.
• Скорость сближения двух автомобилей равна 120 км/ч, значит, они встретятся через 5 часов после выезда второго автомобиля: 600:120=5 часов.
• Таким образом, первый автомобиль всего ехал  8 часов: 50×8=400км.

Задача 6. Скорость сближения

Расстояние между пунктами А и В равно 135 км. Из пункта А в пункт В выехал легковой автомобиль. Одновременно с ним из пункта В в пункт А выехал грузовой автомобиль, скорость которого на 15 км/ч меньше скорости легкового. Через час после начала движения они встретились. Через сколько минут после встречи грузовой автомобиль прибыл в пункт А?

Решение.
Нарисуем схему движения.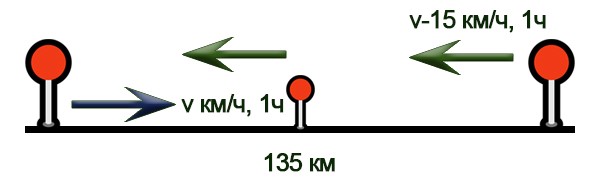

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)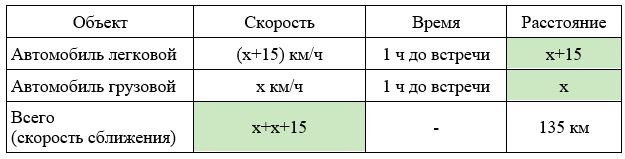

• Пусть x км/ч — скорость грузового автомобиля, тогда (x + 15) км/ч — скорость легкового автомобиля. Получаем уравнение: x+x+15=135; x=60км/ч. 
• Найдем сколько времени грузовой автомобиль затратил на весь путь: 135:60=2,25 часов.
• Найдем сколько времени грузовой автомобиль затратил на путь после встречи: 2,25-1=1,25 часов или 75 минут (1,25*60).
• Ответ: 75 мин.

Задача 7. Уровень ЕГЭ.

Два поезда движутся навстречу друг другу – один со скоростью 70 км/ч, другой со скоростью 80 км/ч. Пассажир, сидящий во втором поезде, заметим, что первый поезд прошел мимо него за 12 секунд. Какова длина первого поезда? Ответ дайте в метрах.

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)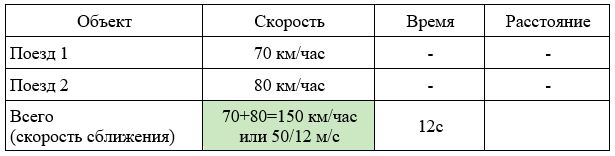

• Найдем скорость сближения: 70+80=150км/ч.
• Переведем ее в другие единицы измерения: 150 км/ч = 150000/3600 = 50/12 м/с
• Заметим, что фраза “первый поезд прошел мимо пассажира за 12с” означает, что с того момента, как пассажир увидел голову поезда, до того момента, как он увидел хвост поезда, прошло 12с.
  
• Найдем расстояние 50/12 × 12 =50 метров.

Решить задачи на движение в одном направлении: сближение и удаление

Задача 8. Скорость сближения

Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 3 км/ч пешехода за 57 секунд. Найдите длину поезда в метрах.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)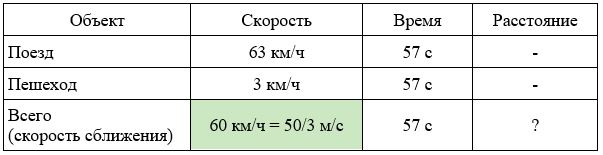

• Найдем скорость поезда относительно пешехода: 63 − 3 = 60 км/ч
• Переведем скорость сближения в другие единицы измерения: 60 км/ч = 60000/3600=50/3 м/с.
• Найдем длину поезда (расстояние, которое проехал поезд): (50/3)*57=950 м.

Задача 9. Скорость сближения

Два туриста одновременно вышли в одном направлении в город N. При этом вышли они из разных городов, расстояние между которыми 9 км. Известно, что турист, изначально находившийся дальше от города N, шёл со скоростью, в два раза превышающей скорость другого туриста. В город N они прибыли одновременно, через 3 часа после начала движения. Найдите скорость туриста, который шёл быстрее. Ответ дайте в км/ч.

Решение.
Нарисуем схему движения.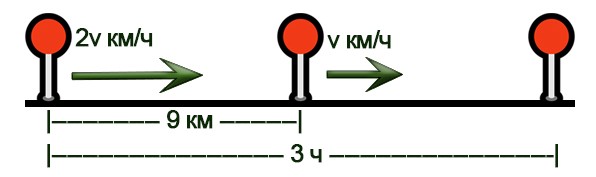

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость сближения туристов: 9:3=3 км/ч.
• По формуле сближения получаем: 2v-v=3  → v=3 →2v=6 км/ч.
• Ответ: 6

Задача 10. Скорость удаления

Два велосипедиста выехали из одного места в одном направлении. Скорость первого – 10 км/ч, а второго – 18 км/ч. Через сколько часов расстояние между велосипедистами будет равно 104 км?

Решение.
Нарисуем схему движения.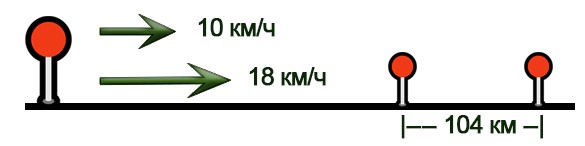

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)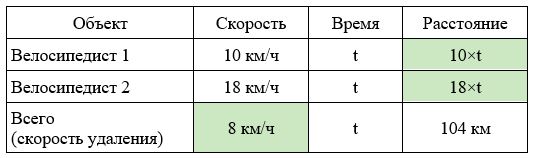

• Найдем скорость удаления: 18-10=8 км/ч
• Найдем время в пути: 108:8=13 часов.
• Ответ: 13

Задача 11. Скорость удаления

Два велосипедиста выехали в одном направлении из мест, находящихся на расстоянии 13 км друг от друга. Скорость первого – 12 км/ч, а второго – 17 км/ч, причем второй находился в начале движения впереди. Через сколько часов расстояние между велосипедистами будет равно 58 км?

Решение.
Нарисуем схему движения.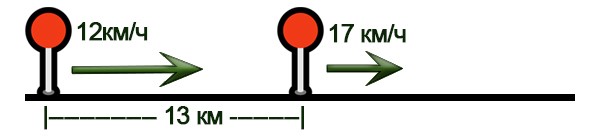

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)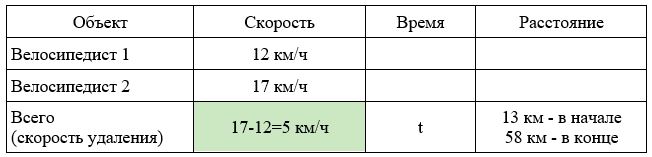

• Найдем скорость удаления: 17-12=5 км/ч
• Найдем расстояние, на которое они удались друг от друга: 58-13=45 км.
• Найдем время: 45:5=9 часов. 

Задача 12. Уровень ЕГЭ

Два кота одновременно выбегают в одном направлении из одного и того же подъезда. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между котами станет равным 200 метрам?

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)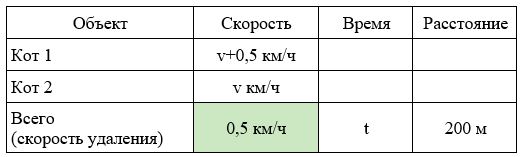

• Скорость удаления будет 0,5 км/ч — это скорость, с которой первый кот бежит быстрее второго.
• Найдем время: 0,2 : 0,5 = 0,4 часа
• Переведем время в другие единицы измерения: 0,4 ч = 0,4*60 = 24 мин.

Решить задачи на движение по реке

Задача 13.

Яхта движется по стоячей воде, ее собственная скорость равна 30 км/ч. Встречный ветер каждую минуту сносит яхту на 20 метров. За сколько часов яхта пройдет 259200 метров?

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Переведем скорость яхты в другие единицы измерения: 30 км/ч = 500 м/с.
• Найдем скорость удаления: 500-20=480 м/с.
• Найдем время: 259200 :480=540 минут = 9 часов.

Задача 14.

Расстояние от пристани А до пристани Б по течению реки катер прошёл за 5 часов, а на обратный путь он затратил на 1 час больше. Найдите скорость катера в неподвижной воде (собственную скорость), если скорость течения реки 2 км/ч. 

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)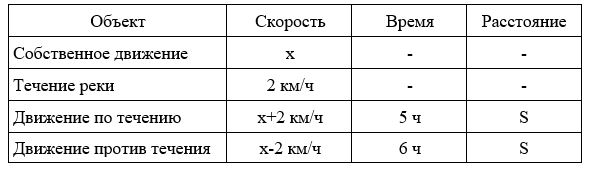

• Пусть скорость катера в неподвижной воде равна x км/ч.
• Составим уравнение: 5×(x+2)=6×(x-2); x=22 км/ч.

Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.

Советы для решения задач на движения

• В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который  будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
• Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.

Памятка «Учимся решать задач на движение»

В задачах на движение  рассматриваются три взаимосвязанные величины:

S – расстояние (пройденный путь),

t – время движения и

V – скорость – расстояние, пройденное за единицу времени.

Расстояние – это произведение скорости на время движения

S = V ● t

Скорость  – это частное от деления расстояния на время движения

V = S : t

Время – это частное от деления расстояния на скорость движения

t = S : V

Задачи на встречное движение

Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V

 Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?

Схема к задаче:

 

Решение:

S = V ● t

V сближ. = 1V + 2V

1 способ:

1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи

2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи

3) 36 + 42 = 78 (км)

2 способ:

1) 12 + 14 = 26 (км/ч) – скорость сближения

2) 26 • 3 = 78 (км)

Ответ: расстояние между посёлками 78 км.

 Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?

Схема к задаче:

 

Решение:

V сближ. = 1V + 2V

t = S : V

1) 80 + 60 = 140 (км/ч) – скорость сближения

2) 280 : 140 = 2 (ч)

Ответ: машины встретятся через  2 часа.

 Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?

Схема к задаче:

 

Решение:

V = S : t

2V = V сближ. – 1V

1) 340 : 2 = 170 (км/ч) – скорость сближения

2) 170 – 80 = 90 (км/ч)

Ответ: 90 км/ч. скорость второй машины

Задачи на движение в противоположных направлениях

Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях. 

V удал. = 1V + 2V

 Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?

Схема к задаче:

 Решение:

S = V ● t

1 способ

1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч

2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч

3)36 + 42 = 78 (км) 

2 способ

V удал. = 1V + 2V

S = V ● t

1)12 + 14 = 26 (км/ч) – скорость удаления

2)26 • 3 = 78 (км)

Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.

 Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?

Схема к задаче:

 

Решение:

V удал. = 1V + 2V

t = S : V

1) 80 + 60 = 140 (км/ч) – скорость удаления

2) 280 : 140 = 2 (ч)

Ответ: через 2 часа расстояние между машинами будет 280 км

Пример 3. Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?

Схема к задаче:

  

Решение:

V = S : t

2V = V удал. – 1V

1) 340 : 2 = 170 (км/ч) – скорость удаления машин

2) 170 – 80 = 90 (км/ч)

Ответ: скорость второй машины 90 км/ч.

Схемы задач на движение очень просто нарисовать. Они помогают представить наглядно условие задачи и найти верное решение. В дополнение к схеме в сложных случаях или когда ученик затрудняется с решением рекомендуется рисовать таблицу, где в шапке параметры скорости, времени и расстояния. Об этом подробнее ниже.

Узнайте также, как составить схемы к задачам по математике для 2 класса

Простые задачи на движение

Простые задачи про путников, лыжников, мотоциклистов и другие движущиеся объекты (встречаются даже задачки про черепах) начинают решать еще в начальных классах. Именно на этих примерах удобно разбирать составление схем.  

Задача 1. Пешеход вышел из пункта А в пункт Б со скоростью 5 км/ч. Через 3 часа он добрался до пункта Б. Какое расстояние между этими двумя пунктами?

Рисуем схему к задаче: прямая линия, соединяющая точки А и Б — это весь путь. Стрелкой обозначаем направление движения путника. Над стрелкой отмечаем скорость, если известна. Время или расстояние отмечаем под (или над) отрезком:

Если со схемой вы не смогли решить задачу, то предлагаю вам воспользоваться таблицей:

скорость	время	расстояние
5 км/ч	3 ч	? км

Чтобы решать с помощью таблицы, запомните правила:

• Чтобы найти расстояние, нужно скорость умножить на время: S = V x t
• Чтобы найти скорость, нужно расстояние разделить на время, (это производное из первой формулы:
  V = S : t )
• чтобы найти время, необходимо расстояние разделить на скорость. (также просто вывести из первой формулы:
  t = S : t

Решение

5 х 3 = 15 км — расстояние между пунктами А и Б

Обратные задачи на движение

Как найти скорость, если известно время и расстояние

Чтобы не путать вас разными условиями задачи состав задачу, обратную первому примеру:

Задача 2. Расстояние между пунктами А и Б равно 15 км. Путник преодолел это расстояние за 3 часа. С какой скоростью шел пешеход?

скорость	время	расстояние
? км/ч	3 ч	15 км

Решение

15 : 3 = 5 км/ч

Как найти время, когда известны скорость и расстояние

Задача 3. Расстояние между пунктами 15 км. Пешеход шел со скоростью 5 км/ч. За какое время пешеход преодолеет весь путь?

Скорость	время	расстояние
5 км/ч	? ч	15 км

Решение

15 : 5 = 3 часа

Схемы задач на встречное движение

Чтобы начертить встречное движение, мы рисуем стрелочки из двух пунктов навстречу. Флажком обозначаем место встречи

Когда задачи со встречным или удаляющимся движением — это задачи на общую скорость. Скоро будет подробный урок о них на моем сайте. 

Задача 4. Два пешехода вышли одновременно из пунктов А и Б навстречу друг другу. Скорость одного — 5 км/ч, другого — 3 км/ч. Через какое время они встретятся, если известно, что расстояние между пунктами 24 км?

Решение

1 способ:

5 + 3 =8 км/ч — общая скорость

24 : 8 = 3 часа

Задачи на движение в одном направлении

Задача 5. Два пешехода вышли из пунктов А и Б одновременно в одном направлении. Пешеход, который шел впереди, двигался со скоростью 3 км/ч, а второй — со скоростью 5 км/ч. Через какое время второй пешеход догонит первого, если расстояние между пунктами 2 км?

Здесь нужно выяснить скорость сближения. Так как один пешеход шел быстрее второго, то расстояние между ними сокращалось на 2 км/ч (мы посчитали так: 5 — 3 = 2 км/ч). Так как первоначальное расстояние между пунктами 2 км, то найдем время:

2км : 2 км/ч = 1 час.

Через 1 час пешеходы встретятся. 

Шпаргалка по решению задач на скорость, время и расстояние

Вы можете воспользоваться данной памяткой при решении этого типа задач. Кликните для просмотра в полном размере и распечатайте, нажав на клавиатуре клавиши CTRL + P.

Математика, 4 класс

Урок № 36. Связь между скоростью, временем и расстоянием

Перечень вопросов, рассматриваемых в теме:

– как скорость взаимосвязана с величинами время, расстояние?

– как определить скорость по известному расстоянию и времени движения?

– как определить расстояние по известной скорости и времени движения?

– как определить время движения по известному расстоянию и скорости?

Глоссарий по теме:

Скорость — это расстояние, пройденное за единицу времени.

Скорость, расстояние и время можно измерять и сравнивать, значит это величины.

Чтобы узнать скорость движения, нужно расстояние разделить на время.

Чтобы узнать расстояние, нужно скорость умножить на время.

Чтобы найти время, нужно расстояние разделить на скорость.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 – М.; Просвещение, 2017. – с.6-8.

2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.15.

3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.54.

Теоретический материал для самостоятельного изучения

В таблицах даны скорости вороны и комара, льва и кенгуру. Определи, какое расстояние пролетит ворона за 2 мин, а комар за 3 с. Какой путь преодолеет лев за 4 ч, а кенгуру за 30 мин?

Мотоциклист едет со скоростью 41 км/ч. Какое расстояние он преодолеет за 5 ч, если будет двигаться с той же скоростью?

Для того чтобы узнать расстояние, необходимо скорость, 41 км в час умножить на время, 5 часов. Таким образом, расстояние, которое преодолел мотоциклист равно 205 км.

41 · 5 = 205 км

Чтобы найти расстояние, нужно скорость умножить на время.

Будем учиться записывать задачи в таблицу и решать их.

Задача 1.

Черепаха двигалась со скоростью 5 м/ мин. Какое расстояние прошла она за 3 минуты?

Задача 2.

Слон двигался со скоростью 100 м/мин. Какое расстояние он прошёл за 10 мин?

Составим таблицу и рассмотрим, как можно найти расстояние, зная скорость и время движения.

Составим таблицу и рассмотрим, как можно найти расстояние, зная скорость и время движения. Расстояние, которое прошли черепаха и расстояние, которое прошёл слон, нам неизвестны. Поставим в таблице знаки «вопрос».

5 м/мин – это скорость черепахи, 100 м/мин – это скорость слона. Запишем данные в колонку «Скорость». 3 минуты это время движения черепахи, 10 минут – время, которое находился в пути слон. Запишем эти данные в третью колонку.

	Скорость	Время	Расстояние
Черепаха	5 м/мин	3 мин	?
Слон	100 м/мин	10 мин	?

Мы теперь знаем, чтобы найти расстояние, нужно скорость умножить на время. Запишем решение и ответ.

Скорость 5 м/мин умножим на время 3 мин, получится 15 метров. Это расстояние, которое прошла черепаха.

Скорость 100 м/мин умножим на время 10 мин, получится 1000 метров. Это расстояние, которое прошёл слон.

5 · 3 = 15 (м)

100 · 10 = 1000 (м)

Ответ: черепаха за 3мин прошла 15 м, а слон за 10 мин прошёл 1000 м.

Итак, чтобы найти расстояние, нужно скорость умножить на время.

А теперь рассмотрим задачу на нахождение времени.

Расстояние от города до посёлка 20 км. Из города вышел пешеход со скоростью 5 км/ч. Сколько времени потребуется пешеходу, чтобы пройти весь путь?

Это задача на движение, значит, речь идет о величинах скорость, время, расстояние. Заполним таблицу.

В задаче нужно узнать время движения пешехода. Оно нам неизвестно, поставим знак вопроса. Известно, что расстояние, которое нужно пешеходу равно 20 км.5 км/ч это скорость движения.

Скорость	Время	Расстояние
5 км/ч	?	20 км

Правило: чтобы найти время, нужно расстояние разделить на скорость. Запишем решение:

20 : 5 = 4 (ч)

Ответ: пешеход будет в пути 4 часа.

Запоминаем правило нахождения времени: чтобы узнать время, расстояние разделить на скорость.

Задания тренировочного модуля:

1. Заполните кроссворд.

Решите кроссворд.

По горизонтали:

2. Плот проплыл 630 м со скоростью 90 м/мин. Чему равно время движения плота?

3. Анника за 6 мин проехала на велосипеде 600 м. Чему равно время движения Анники?

По вертикали:

1. За 7 мин улитка проползла 7 дм. Чему равна скорость движения улитки?

Правильные ответы:

По горизонтали: 2.семь. 3. сто.

По вертикали: 1. десять.

2. Распределите единицы измерения величин по группам. Перенесите данные в соответствующие столбики.

Варианты ответа:

1. 85 см/мин

2. 120 с

3. 548 км

4. 12 мин

5. 850 м/с

6. 600 км/ч

7. 10 ч

8. 2500 м

9. 41 дм

Правильный вариант:

Скорость	Время	Расстояние
85 см/мин 850 м/с 600 км/ч	120 с 12 мин 10 ч	548 км 2500 м 41 дм

3. Вставьте пропущенное слово, выбирая из списка правильный ответ.

Как пройденный путь зависит от скорости?

Если скорость движения увеличить в несколько раз, то пройденный путь_______ во столько же раз.

Варианты ответа: уменьшится, увеличится.

Правильный вариант: увеличится.

В 4 классе дети начинают решать задачи на скорость сближения и скорость удаления. Ребята начинают путаться. Часто они не могут определить вид задачи или просто не знают формулы. Однако понять эту тему легко. В этой статье Я расскажу, как учу своих учеников не путаться в задачах данного вида.

Ситуация 1

Представь, что вы с мамой вышли из дома и пошли в разные стороны. Вы будете приближаться друг к другу или удаляться друг от друга? Удаляться. Расстояние между вами будет увеличиваться или уменьшаться? Увеличиваться. Для того, чтобы найти скорость удаления в данной ситуации, нужно две скорости сложить. 

Задача

Из города одновременно в разных направлениях выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Какое расстояние будет между автомобилями через 4 часа? 

1) 90 + 70 = 160 (км/ч) – скорость удаления. 

2) 160 × 4 = 640 (км) 

Ответ: 640 км будет расстояние между автомобилями через 4 часа.

Ситуация 2

Представь, что вы с мамой идете навстречу друг другу. 

В каждой из обсуждаемых ситуаций я задаю одни и те же вопросы, как в первой ситуации. Поэтому дальше я буду писать только результат наших рассуждений.

Когда мы идем навстречу друг другу, мы приближаемся друг к другу. Поэтому ищем скорость сближения. Расстояние между нами будет становиться меньше. Для того, чтобы найти скорость сближения в данной ситуации, нужно скорости сложить. 

Задача

Расстояние между двумя городами 640 км. Из каждой из них одновременно навстречу друг другу выехали два автомобиля. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Через сколько часов автомобили встретятся? 

1) 90 + 70 = 160 (км/ч) – скорость сближения

2) 640 : 160 = 4 (ч)

Ответ: автомобили встретятся через 4 часа.

Ситуация 3

Представь, что ты идешь по улице и видишь, что впереди  идет мама. Ты решаешь ее догнать. Твоя скорость больше, чем скорость мамы. Ты догонишь маму? Да. Вы будете приближаться к друг другу или удаляться?Расстояние между вами будет увеличиваться или уменьшаться? Уменьшаться. (приближаться, т. к. ребенок сокращает расстояние). В этой ситуации мы находим скорость  сближения. 

Задача

Из города в посёлок выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Через сколько часов второй автомобиль догонит первый, если расстояние между ними равно 120 км?

1) 90 – 70 = 20 (км/ч) – скорость сближения

2) 120 : 20 = 6 ( ч)

Ответ: второй автомобиль догонит первый через 6 часов.

Ситуация 4

Представь ту же ситуацию, но теперь скорость больше у мамы. Ты догонишь маму? Нет. Почему? Она будет постоянно удаляться. Находим скорость удаления. Для этого из большей скорости вычитаем меньшую. 

Задача

Одновременно из города выехали два автомобиля и поехали в одном направлении. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Какое расстояние будет между автомобилями через 4 часа? 

1) 90 – 70 = 20 (км/ч) – скорость удаления

2) 20 × 4 = 80 (км)

Ответ: 80 км будет расстояние между автомобилями через 4 часа.

Делитесь своим мнением в комментариях, подписывайтесь на мой канал