Пусть
требуется изучить статистическую
совокупность относительно некоторого
количественного признака X.
Числовые значения признака будем
обозначать через хi.
Из
генеральной совокупности извлекается
выборка объёма п.
-
Количественный
признак Х
– дискретная
случайная величина.
Наблюдаемые
значения хi
называют вариантами,
а последовательность вариантов,
записанных в возрастающем
порядке, –
вариационным
рядом.
Пусть
x1
наблюдалось n1
раз,
x2
наблюдалось n2
раз,
xk
наблюдалось nk
раз,
причем
.
Числа ni
называют
частотами,
а их отношение к объёму выборки, т.е.
,
–
относительными
частотами (или
частостями), причем
.
Значение
вариант и соответствующие им частоты
или относительные
частоты можно записать в виде таблиц 1
и 2.
Таблица
1
|
Варианта |
x1 |
x2 |
… |
xk |
|
Частота |
n1 |
n2 |
… |
nk |
Таблицу
1 называют дискретным
статистическим
рядом распределения (ДСР) частот, или
таблицей частот.
Таблица
2
|
Варианта |
x1 |
x2 |
… |
xk |
|
Относительная |
w1 |
w2 |
… |
wk |
Таблица
2
ДСР
относительных частот, или
таблица относительных частот.
Определение.
Модой
называется наиболее часто встречающийся
вариант, т.е. вариант с наибольшей
частотой. Обозначается xмод.
Определение.
Медианой
называется
такое значение признака, которое делит
всю статистическую совокупность,
представленную в виде вариационного
ряда, на две равных по числу части.
Обозначается
.
Если
n
нечетно, т.е. n
= 2m
+ 1,
то
=
xm+1.
Если
n
четно, т.е. n
= 2m,
то
.
Пример
3.
По результатам наблюдений: 1, 7, 7, 2, 3, 2,
5, 5, 4, 6, 3, 4, 3, 5, 6, 6, 5, 5, 4, 4 построить ДСР
относительных частот. Найти моду и
медиану.
Решение.
Объем выборки n
= 20. Составим ранжированный ряд элементов
выборки: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6,
7, 7. Выделим варианты и подсчитаем их
частоты (в скобках): 1 (1), 2 (2), 3 (3),
4 (4),
5 (5), 6 (3), 7 (2). Строим таблицу:
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
wi |
1/20 |
2/20 |
3/20 |
4/20 |
5/20 |
3/20 |
2/20 |
Наиболее
часто встречающийся вариант xi
=
5. Следовательно, xмод
=
5. Так
как объем выборки n
– четное число, то
Если
на плоскости нанести точки
и соединить их отрезками прямых, то
получим полигон
частот.
Если
на плоскости нанести точки
,
то получим полигон
относительных частот.
Пример 4.
Построить полигон частот и полигон
относительных частот по данному
распределению выборки:
|
xi |
4 |
7 |
8 |
12 |
17 |
|
ni |
2 |
4 |
5 |
6 |
3 |
|
wi |
2/20 |
4/20 |
5/20 |
6/20 |
3/20 |
Решение.
На рисунке 2 показан полигон частот и
на рисунке 3 – полигон относительных
частот.

Рис.
2 Рис.
3
Замечание.
Чем круче полигон, тем равномернее
процесс.
-
Пусть
количественный признак X
– непрерывная
случайная величина,
принимающая значения из интервала
(а,b).
Весь диапазон наблюдаемых данных делят
на частичные
интервалы
[хi;
xi+1),
которые берут обычно одинаковыми по
длине:
=
xi+1
–
xi
(i
= 0, 1, …, k).
Для определения величины интерваламожно использовать формулу
Стерджеса:
где
(xmax
–
xmin)
разность между наибольшим и наименьшим
значениями признака, k
= 1 + log2
n
число интервалов (log2
n
3,322
lg
n).
Если окажется, что h
дробное число, то за длину частичного
интервала следует брать либо ближайшее
целое число, либо ближайшую простую
дробь. За начало первого интервала
рекомендуется брать величину xнач
=
xmin
–
.
В каждом
из частичных интервалов подсчитывают
число наблюдаемых значений, т.е. частоту
ni.
По частотам находят относительные
частоты
.
Полученные интервалы и соответствующие
им частоты (или относительные частоты)
записывают в виде таблицы 3. При этом
правая граница последнего интервала
тоже включается.
Таблица
3
|
Частичный |
[x0, |
[x1, |
… |
[xk-1, |
|
Относительная |
w1 |
w2 |
… |
wk |
Таблица
3 называется интервальным
статистическим рядом распределения
(ИСР) относительных частот,
который задаёт распределение
выборки. Аналогично
составляется ИСР
частот.
Пример
5.
Измерили рост (с точностью до см) 30
наудачу отобранных студентов. Результаты
измерений таковы:
178,
160, 154, 183, 155, 153, 167, 186, 163, 155, 157, 175, 170, 166, 159,
173,
182, 167, 171, 169, 179, 165, 156, 179, 158, 171, 175, 173, 164, 172.
Построить
интервальный статистический ряд
относительных частот.
Решение.
Для
удобства проранжируем полученные
данные:
153,
154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167,
169,
170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 179, 182, 183, 186.
Отметим,
что Х
рост студента
непрерывная случайная величина. Как
видим, xmin
=
153, хmax
=
186; по формуле Стерджеса, при n
= 30, находим длину частичного интервала
Примем
= 6. Тогда хнач
= 153 –
=150.
Исходные данные разбиваем на шесть (k
=
1 + log230
= 5,907
6) интервалов:
[150,
156), [156, 162), [162, 168), [168, 174), [174, 180), [180, 186].
Подсчитав
число студентов ni,
попавших в каждый из полученных
промежутков, получим ИСР:
|
[xi,xi+1) |
[150, |
[156, |
[162, |
[168, |
[174,180) |
[180,186] |
|
ni |
4 |
5 |
6 |
7 |
5 |
3 |
|
wi |
4/30 |
5/30 |
6/30 |
7/30 |
5/30 |
3/30 |
Первая
и третья строчка таблицы образует ИСР
относительных частот.
Замечание.
При
решении учебных задач на построение
ИСР можно пользоваться следующими
правилами.
-
Назначаются нижняя
граница а
и верхняя граница b
для вариант так, чтобы отрезок [a;
b]
вместил всю выборку; часто полагают
,
,
но иногда a
и b
назначают из соображений удобства, но
не слишком далеко от
и
. -
Находится число
k
равных по длине частичных интервалов
варьирования, которое зависит от объема
выборки и обычно 6
k
20;
рассчитывается длина интервалов
группирования
.
Интервальный
статистический ряд распределения,
представленный графически, называется
гистограммой.
Гистограмма
относительных частот
строится следующим образом: по оси
абсцисс откладываются
интервалы (хi;
хi+1)
и на каждом из них строится прямоугольник
высотой
где
;
.
Площадь
i–го
прямоугольника
.
Площадь
всей гистограммы
.
З
амечание:
гистограмма на рисунке 4 – гистограмма
относительных частот.
x3
Рис.
4
Можно
построить гистограмму
частот,
высоты прямоугольников которых равны
.
Пример 6.
Построить гистограмму частот по данному
ИСР частот:
|
[xi; |
[100; |
[120; |
[140; |
[160; |
[180; |
|
ni |
20 |
50 |
80 |
40 |
10 |
Решение.
По ИСР частот находим длину частичных
интервалов
= 20 и высоты прямоугольников hi
=
.
Результаты занесем в таблицу:
|
[xi; |
[100; |
[120; |
[140; |
[160; |
[180; |
|
ni |
20 |
50 |
80 |
40 |
10 |
|
hi |
1 |
2,5 |
4 |
2 |
0,5 |
Искомая
гистограмма частот изображена на рис.
5.
hi
xi
xi
Рис.
5
В
теории вероятностей гистограмме
относительных частот соответствует
график плотности распределения
вероятностей. Распределение выборки,
задаваемое интервальным статистическим
рядом (табл. 3) или таблицей относительных
частот (табл. 2), называется эмпирическим
распределением случайной величины.
По
теореме Бернулли относительная частота
wi,
появление события в п
независимых
испытаниях
сходится
по вероятности к вероятности рi
этого события
.
Значит во второй строке таблицы 3 и
таблицы 2 стоят
приближённые значения вероятностей рi
следующих событий
и
,
поэтому
распределение выборки называют
эмпирическим распределением случайной
величины X.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Статистическое распределение выборки
Содержание:
- Примеры использования формул и таблиц для решения практических задач
- Статистический интервальный ряд распределения
Предположим случай, когда из генеральной совокупности извлекается некоторая выборка, при этом каждому значению соответствует некоторый параметр, означающий количество раз, когда появлялось данное значение. Здесь $x_1$ было зафиксировано $n_1$ раз, $x_2$ было обнаружено $n_2$$x_k$ выявлено $n_k$. При этом
$sum_{i=1}^{k}n_i=n$
Где n — объём рассматриваемой выборки.
Определение 1
Используется следующая терминология: $x_k$ носят наименование вариантов, а последовательность таких вариантов, зафиксированный по возрастанию именуется вариационным рядом. Количество наблюдений каждого из вариантов носят название частот. При этом частное частот и выборки называют относительными частотами.
Определение 2
Статистическое распределение —это название всего набора вариантов и частот, которые с ними соотносятся. Чаще всего задаётся с помощью специальной таблицы, где представлены частоты, а также интервалы им соответствующие.
| $x_1$ | $x_2$ | … | $x_k$ |
| $n_1$ | $n_2$ | … | $n_k$ |
| $frac{n_1}{n}$ | $frac{n_2}{n}$ | $frac{n_k}{n}$ |
Здесь в первой строке представлены варианты, во второй частоты, в третьеq взяты относительные частоты.
Для определения размера интервала используется следующее выражение:
$d=frac{x_{max}- x_{min}}{1+3,332cdot lg n}$
Здесь $x_{max}$, $x_{min}$ наибольшее и наименьшее значения ряда вариантов, а n характеризуем объём выборки.
Примеры использования формул и таблиц для решения практических задач
Пример 1
В ходе проведения измерений в однородных группах, были определены следующие значения выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74. Необходимо использовать данные значения, что определить ряд распределения частот и ряд распределения относительных частот.
Решение.
1) Составим статистический ряд распределения частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| ni | 2 | 4 | 8 | 2 | 4 |
2) Рассчитаем суммарный размер выборки: n=2+4+8+2+4=20. Определим относительные частоты, для этого используем формулы: ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Теперь зафиксируем в таблице распределение относительных частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| wi | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
Контрольная сумма должна равняться единице: 0,1+0,2+0,4+0,1+0,2=1.
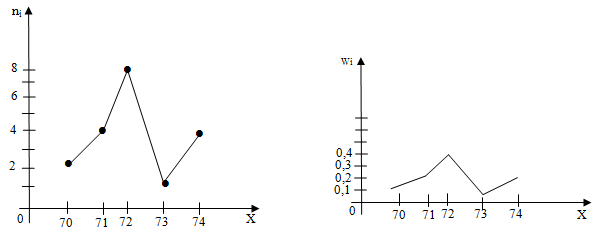
Полигон частот
Название «полигоном частот» применяют для обозначения ломаной линии, каждый отрезок, которой соединяют точки $(х_1,n_1),(х_2,n_2),…,(х_k,n_k)$. Для построения на графике полигона частот по оси абсцисс отмечают варианты $х_2$, при этом на оси ординат отсчитывают– соответствующие частоты $n_i$. Когда полученные точки $(х_i,n_i)$ соединяются с помощью отрезков, то автоматически получают полигон частот.
Статистический интервальный ряд распределения.
Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются, если число различающихся вариант в полученной выборке не слишком большое. Также применение возможно, когда дискретность имеет важное значение для экспериментатора. В тех случаях, когда важный для задачи признак генеральной совокупности Х распределяется непрерывным образом, либо его дискретность нет возможности учесть, то варианты предпочтительнее всего группировать, чтобы получить интервалы.
Статистическое распределение допустимо задавать в том числе в качестве последовательности интервалов и частот, соответствующих этим интервалам. При это за частоту какого-либо интервала принимается сумма всех частот, вошедших в данный интервал.
Особенно следует отметить ,что $h_i-h_{i-1}=h$ при всех i, т.е. группировка проводится с равным шагом h. Также в вопросе группировки можно ориентироваться на ряд полученных опытным путём рекомендацийу, касающихся таких параметров, как а, k и $h_i$:
1. $Rраз_{мах}=X_{max}-X_{min}$
2. $h=R/k$; k-число групп
3.$ kgeq 1+3.321lgn$ (формула Стерджеса)
4. $a=x_{min}, b=x_{max}$
5.$ h=a+h_i, i=0,1…k$
Определённую в ходе решения задачи группировку удобнее всего скомпоновать и перевести в вид специальной таблицы, которая также может именоваться — «статистический интервальный ряд распределения»:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Частоты | n1 | n2 | … | nk-1 | nk |
Таблицу подобного вида можно сделать, поменяв частоты $n_i$ на относительные частоты:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Отн. частоты | w1 | w2 | … | wk-1 | wk |

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример 2
На склад пришла крупная партия деталей. Из них методом случайного отбора взято 50 экземпляров. Рассматривая изделия по одному, особенно интересующему признаку — размеру, определённому с точностью до 1 см, получим следующий вариационный ряд: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Требуется произвести расчёт и определить статистический интервальный ряд распределения.
Решение
Найдём параметры выборки используя сведения из условия задачи.
$k geq1+3,321cdot lg50=1+3.32lg(5cdot10)=1+3.32(lg5+lg10)=6.6$
Получили a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.
| Интервалы группировки | 22-26 | 26-30 | 30-34 | 34-38 | 38-42 | 42-46 | 46-50 |
| Частоты | 1 | 4 | 10 | 18 | 9 | 5 | 3 |
| Отн. частоты | 0.02 | 0.08 | 0.2 | 0.36 | 0.18 | 0.1 | 0.06 |
Десятичные логарифмы от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| lnn≈ | 0 | 0.3 | 0.48 | 0.6 | 0.7 | 0.78 | 0.85 | 0.9 | 0.95 | 1 |
Не получается написать работу самому?
Доверь это кандидату наук!
Содержание
- Типы частот
- Шаги по составлению таблицы распределения частот
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
- Шаг 5
- Шаг 6
- Шаг 7
- Шаг 8
- Шаг 9
- Шаг 10
- Пример построения стола
- Упражнение решено
- Ссылки
А Распределение частоты В статистике это относится к тенденции, за которой следуют данные, организованные в группы, категории или классы, когда каждому присваивается номер, называемый частотой, который указывает, сколько данных находится в каждой группе.
Как правило, наблюдается, что эти частоты распределяются вокруг центральной группы: группы с наибольшим количеством данных.
Группы, которые находятся выше или ниже этой центральной категории, постепенно уменьшают свою частоту, становясь очень маленькими или незначительными для категорий, наиболее удаленных от категории с более высокой частотой.
Чтобы узнать частотное распределение набора данных, сначала создайте категории, а затем составьте таблицу частот. Визуальное представление частотной таблицы называется гистограммой.
Типы частот
Есть несколько типов частот:
1.- Абсолютная частота: он самый простой, и из него строятся остальные. Он просто состоит из общего количества данных, соответствующих категории.
2.- Относительная частота: абсолютная частота каждой категории, деленная на общее количество данных.
3.- Частота в процентах: это та же относительная частота, но умноженная на сто, указывающая процент появления значений в каждой категории.
4.- Накопленная частота: это сумма абсолютных частот категорий ниже или равных рассматриваемой категории.
5.- Кумулятивная частота в процентах: это сумма процентных частот категорий ниже или равных наблюдаемой категории.
Шаги по составлению таблицы распределения частот
Чтобы построить таблицу частотного распределения, необходимо выполнить несколько шагов.
Прежде всего, должны быть доступны данные, которые могут быть разного типа: возраст детей в школе, количество правильных ответов в тесте, рост сотрудников компании, длина листов. дерева и др.
Шаг 1
Определите минимальное значение xmin и максимальное значение xmax в наборе данных Икс.
Шаг 2
Рассчитайте диапазон R, который определяется как разница между максимальным значением минус минимальное значение: R = xmax – xmin.
Шаг 3
Определить количество k интервалов или классов, которые можно задать заранее. Номер k определит количество строк в частотной таблице.
Шаг 4
Если количество интервалов k ранее не указывалось, то оно должно быть установлено в соответствии со следующими руководящими принципами: наименьшее количество рекомендуемых категорий – 5, но оно может быть больше, и в этом случае предпочтительнее выбрать нечетное число.
Шаг 5
Есть формула, которая называется правило осетров что дает нам количество интервалов k рекомендуется для набора, состоящего из N данные:
k = [1 + 3,322⋅Log N]
Поскольку результат внутри скобки обязательно будет действительным числом, скобка говорит нам, что его необходимо округлить до ближайшего нечетного целого числа, чтобы получить целое значение k.
Шаг 6
Амплитуда рассчитывается К каждого интервала (классов или категорий), беря частное между диапазоном р и количество интервалов k: А = R / k. Если исходные данные являются целыми числами, то A округляется до ближайшего целого числа, в противном случае его реальное значение остается.
Шаг 7
Определите нижние пределы Li и верхние пределы Ls для каждого интервала или класса. Первый интервал или самый низкий класс имеет нижний предел Li наименьшего из исходных данных, то есть Li = xmin, а верхний предел – минимальное значение плюс ширина интервала, то есть Ls = xmin + A.
Шаг 8
Последовательные интервалы:
[xmin, xmin + A), [ xmin + A, xmin + 2⋅A), …, [ xmin + (k-1) A, xmin + k⋅A).
Шаг 9
Оценка класса Xc определяется для каждого интервала по следующей формуле: Xc = (Ls – Li) / 2 + Li.
Шаг 10
Размещается заголовок таблицы частот, который состоит из строки со следующими метками: классы, метка класса Xc, частота f, относительная частота fr (или процентная частота f%) и накопленная частота F (или накопленная частота в процентах). F%).
У нас будет следующее:
Первый столбец частотной таблицы– Содержит интервалы или классы, на которые были разделены данные.
Второй столбец: содержит метку класса (или среднюю точку) каждого подынтервала.
Третий столбец: содержит абсолютную частоту f каждого класса или категории.
Четвертая и пятая колонки: помещаются значения, соответствующие относительной частоте (или проценту) и накопленной частоте F (или накопленному проценту).
Пример построения стола
Следующие данные соответствуют правильным ответам анкеты из 100 вопросов, примененной к группе из 52 студентов:
65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.
Мы будем следовать шагам, чтобы построить таблицу частот:
1.- Минимальное и максимальное значения Xmin = 1, Xmax = 89.
2.- Диапазон: R = 89 – 1 = 88
3.- Определение количества интервалов по правило осетров: k = [1 + 3,322⋅Журнал 52] = [6,70] = 7.
4.- Расчет ширины интервалов: A = R / k = 88/7 = 12,57 ≈ 13.
5.- Интервалы: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92 ».
6.- Определяются оценки классов каждого интервала: 8, 21, 34, 47, 60, 73 и 86.
7.- Таблица сделана:
График частот для различных интервалов или категорий показан на рисунке 1.
Упражнение решено
Учитель записывает процент достижений целей по курсу физики для каждого студента. Однако оценка для каждого студента, хотя и зависит от процента достигнутых целей, ограничена определенными категориями, ранее установленными в правилах обучения университета.
Давайте рассмотрим конкретный случай: в разделе физики у нас есть процент достижений целей для каждого из 52 студентов:
15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 65, 70, 89, 64, 54, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.
В этом примере категории или классы соответствуют итоговой оценке, которая выставляется в соответствии с процентной долей x достигнутых целей:
1.- Очень плохо: 1 ≤ x <30
2.- Недостаточно: 30 ≤ x <50
3.- Достаточно: 50 ≤ x <70
4.- Хорошо: 70 ≤ x <85
5.- Отлично: 85 ≤ x ≤ 100
Чтобы составить частотную таблицу, данные упорядочиваются от наименьшего к наибольшему, и подсчитывается количество данных, соответствующих каждой категории, что и будет оценкой, которую студент получит за курс физики:
1.- Очень плохо: 4 ученика.
2.- Плохо: 6 учеников.
3.- Достаточно: 20 учеников.
4.- Хорошо: 17 учеников.
5.- Отлично: 5 учеников.
Ниже представлена гистограмма оценок, построенная на основе приведенной выше таблицы:
Ссылки
- Беренсон, М. 1985. Статистика для управления и экономики. Interamericana S.A.
- Канавос, Г. 1988. Вероятность и статистика: приложения и методы. Макгроу Хилл.
- Деворе, Дж. 2012. Вероятность и статистика для техники и науки. 8-е. Издание. Cengage.
- Левин, Р. 1988. Статистика для администраторов. 2-й. Издание. Прентис Холл.
- Шпигель, М. 2009. Статистика. Серия Шаум. 4-й Издание. Макгроу Хилл.
- Уолпол, Р. 2007. Вероятность и статистика для инженерии и науки. Пирсон.
Составление таблиц распределения частот по данным выборки
В том виде, в каком данные представлены в таблице 1, они мало приспособлены для осуществления контроля производственного процесса. Гораздо больших результатов можно достичь при распределении частот наблюдаемого признака в порядке увеличения их численных значений (ранжирования данных).
Таблица 2
Распределение частот вариационного ряда по данным из таблицы 1
|
30 |
| |
50 |
|||| |
70 |
|||| |
|
31 |
51 |
|| |
71 |
||||| |
|
|
32 |
52 |
|||| |
72 |
||||| | |
|
|
33 |
| |
53 |
|||| |
73 |
||| |
|
34 |
54 |
||||| || |
74 |
|||| |
|
|
35 |
| |
55 |
|| |
75 |
| |
|
36 |
56 |
||||| || |
76 |
|| |
|
|
37 |
57 |
|||| |
77 |
| |
|
|
38 |
58 |
||||| | |
78 |
||
|
39 |
| |
59 |
|||| |
79 |
||| |
|
40 |
60 |
||||| |
80 |
| |
|
|
41 |
61 |
||||| | |
81 |
||
|
42 |
|| |
62 |
||||| | |
82 |
| |
|
43 |
63 |
||||| | |
83 |
| |
|
|
44 |
| |
64 |
||||| |||| |
84 |
| |
|
45 |
|| |
65 |
|| |
85 |
|
|
46 |
||| |
66 |
||| |
86 |
| |
|
47 |
||| |
67 |
||||| |
87 |
|
|
48 |
|| |
68 |
||||| || |
88 |
|
|
49 |
|| |
69 |
||| |
89 |
| |
Оцифровывая значения частот из таблицы 2 и заменяя пробелы нулями, получаем статистический ряд (см. таблицу 3).
Таблица 3
Статистический ряд по данным из таблицы 2
|
Хi |
mi |
Хi |
mi |
Хi |
mi |
|
30 |
1 |
50 |
4 |
70 |
4 |
|
31 |
0 |
51 |
2 |
71 |
5 |
|
32 |
0 |
52 |
4 |
72 |
6 |
|
33 |
1 |
53 |
4 |
73 |
3 |
|
34 |
0 |
54 |
7 |
74 |
4 |
|
35 |
1 |
55 |
2 |
75 |
1 |
|
36 |
0 |
56 |
7 |
76 |
2 |
|
37 |
0 |
57 |
4 |
77 |
1 |
|
38 |
0 |
58 |
6 |
78 |
0 |
|
39 |
1 |
59 |
4 |
79 |
3 |
|
40 |
0 |
60 |
5 |
80 |
1 |
|
41 |
0 |
61 |
6 |
81 |
0 |
|
42 |
2 |
62 |
6 |
82 |
1 |
|
43 |
0 |
63 |
6 |
83 |
1 |
|
44 |
1 |
64 |
9 |
84 |
1 |
|
45 |
2 |
65 |
2 |
85 |
0 |
|
46 |
3 |
66 |
3 |
86 |
1 |
|
47 |
3 |
67 |
5 |
87 |
0 |
|
48 |
2 |
68 |
7 |
88 |
0 |
|
49 |
2 |
69 |
3 |
89 |
1 |
Полученная картина остаётся всё ещё недостаточно наглядной и компактной для эффективного визуального анализа. Компактность может быть достигнута соответствующей группировкой данных, то есть разбиением всех значений Хi признака Х из таблицы 3 на интервалов длиной ?Х = (хmах – хmin)/S, где n – объём выборки.
Из таблицы десятичных логарифмов из Приложения 1, находим S = 8,229 ? 8.
?Х = 7,4 ? 8,
Таким образом, разбиваем все значения НСВ Х из таблицы 3 на восемь интервалов (групп) длиной 8 каждый, причём правая граница предыдущего интервала служит левой границей следующего. Получаем частичные интервалы по схеме:
Х1 ч Х1 + ?Х = Х2,
Х2 ч Х2 + ?Х = Х3,
…
Х8 ч Х8 + ?Х = Х9.
Таблица 4
Сгруппированное распределение частот по данным рассматриваемого примера
|
Группа |
Середина группы Хс |
Фактическая частота mi |
Накопленная частота nX |
|
26 ч 34 |
30 |
2 |
2 |
|
34 ч 42 |
38 |
4 |
6 |
|
42 ч 50 |
46 |
17 |
23 |
|
50 ч 58 |
54 |
37 |
60 |
|
58 ч 66 |
62 |
40 |
100 |
|
66 ч 74 |
70 |
37 |
137 |
|
74 ч 82 |
78 |
9 |
146 |
|
82 ч 90 |
86 |
4 |
150 |
|
150 |
При цитировании материалов в рефератах, курсовых, дипломных работах правильно указывайте источник цитирования, для удобства можете скопировать из поля ниже:
Комментарии к статье
Содержание
При систематизации данных выборочных обследований используются статистические дискретные и интервальные ряды распределения.
1. Статистическое дискретное распределение. Полигон.
Пусть из генеральной совокупности извлечена выборка, причем х1 наблюдалось n1 раз, х2 – n2 раз, хk – nk раз и ∑ni=n – объем выборки. Наблюдаемые значения х1 называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Число наблюдений варианты называют частотой, а ее отношение к объему выборки – относительной частотой ni/n=wi
ОПРЕДЕЛЕНИЕ. Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант хi и соответствующих им частот ni или относительных частот wi.
Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения:
| x1 | x2 | … | xm |
| n1 | n2 | … | nm |
(сумма всех частот равна объему выборки ∑ni=n)
или в виде таблицы распределения относительных частот:
| x1 | x2 | … | xm |
| w1 | w2 | … | wm |
(сумма всех относительных частот равна единице ∑wi=1)
Пример 1. При измерениях в однородных группах обследуемых получены следующие выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74 (частота пульса). Составить по этим результатам статистический ряд распределения частот и относительных частот.
Решение. 1) Статистический ряд распределения частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| ni | 2 | 4 | 8 | 2 | 4 |
2) Объем выборки: n=2+4+8+2+4=20. Найдем относительные частоты, для чего разделим частоты на объем выборки ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Напишем распределение относительных частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| wi | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
Контроль: 0,1+0,2+0,4+0,1+0,2=1.
Полигоном частот называют ломаную, отрезки, которой соединяют точки (х1,n1),(х2,n2),…,(хk,nk). Для построения полигона частот на оси абсцисс откладывают варианты х2, а на оси ординат – соответствующие им частоты ni. Точки (хi,ni) соединяют отрезками и получают полигон частот.
Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки (х1,w1),(х2,w2),…,(хk,wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты хi, а на оси ординат соответствующие им частоты wi. Точки (хi,wi) соединяют отрезками и получают полигон относительных частот.
Пример 2. Постройте полигон частот и относительных частот по данным примера 1.
Решение: Используя дискретный статистический ряд распределения, составленный в примере 1 построим полигон частот и полигон относительных частот:
2. Статистический интервальный ряд распределения. Гистограмма. Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются в том случае, когда отличных друг от друга вариант в выборке не слишком много, или тогда, когда дискретность по тем или иным причинам существенна для исследователя. Если же интересующий нас признак генеральной совокупности Х распределен непрерывно или его дискретность нецелесообразно ( или невозможно) учитывать, то варианты группируются в интервалы.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
Замечание. Часто hi-hi-1=h при всех i, т.е. группировку осуществляют с равным шагом h. В этой ситуации можно руководствоваться следующими эмперическими рекомендациями по выборке а, k и hi:
1. Rразмах=Xmax-Xmin
2. h=R/k; k-число групп
3. k≥1+3.321lgn (формула Стерджеса)
4. a=xmin, b=xmax
5. h=a+ih, i=0,1…k
Полученную группировку удобно представить в форме частотной таблицы, которая носит название статистический интервальный ряд распределения:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Частоты | n1 | n2 | … | nk-1 | nk |
Аналогическую таблицу можно образовать, заменяя частоты ni относительными частотами:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Отн. частоты | w1 | w2 | … | wk-1 | wk |
Пример 3. Из очень большой партии деталей извлечена случайная выборка объема 50 интересующий нас признак Х-размеры деталей, измеренные с точностью до 1см, представлен следующим вариоционным рядом: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Найти статистический интервальный ряд распределения.
Решение. Определим характеристики группировки с помощью замечания.
k≥1+3.321lg50=1+3.32lg(5•10)=1+3.32(lg5+lg10)=6.6
Имеем, a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.
| Интервалы группировки | 22-26 | 26-30 | 30-34 | 34-38 | 38-42 | 42-46 | 46-50 |
| Частоты ni | 1 | 4 | 10 | 18 | 9 | 5 | 3 |
| Отн.частоты wi | 0.02 | 0.08 | 0.2 | 0.36 | 0.18 | 0.1 | 0.06 |
Десятичные логарифмы от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| lnn≈ | 0 | 0.3 | 0.48 | 0.6 | 0.7 | 0.78 | 0.85 | 0.9 | 0.95 | 1 |
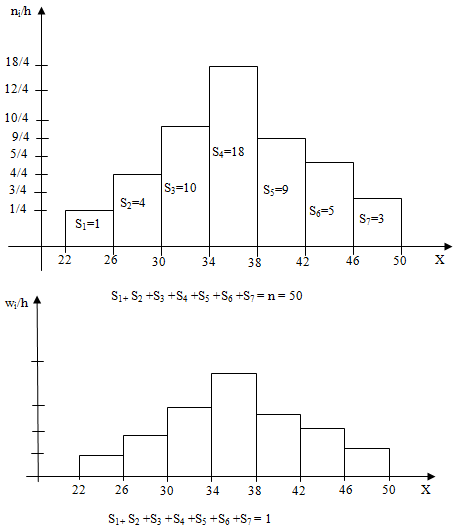
Наиболее информативной графической формой частот является специальный график, называемы гистограммой частот.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению ni/h (плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h. Площадь i-го частичного прямоугольника равна h•ni/h=ni – сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению wi/h (плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии wi/h. Площадь i-го частичного прямоугольника равна h•wi/h=wi – относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
Пример 4. Постройте гистограмму частот и относительных частот по данным примера 3.
Выборочная медиана – это середина вариационного ряда, значение, расположенное на одинаковом расстоянии от левой и правой границы выборки.
Выборочная мода – это наиболее вероятное, т.е. чаще всего встречающееся, значение в выборке.
Добавлять комментарии могут только зарегистрированные пользователи.
Регистрация Вход