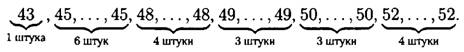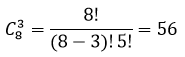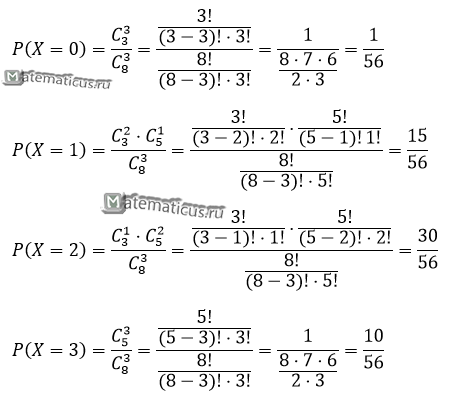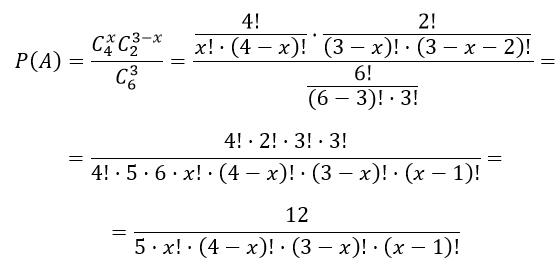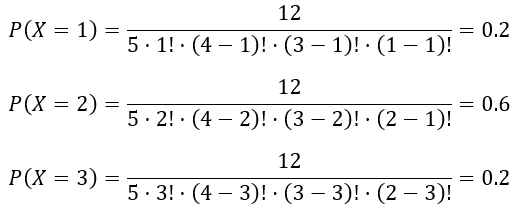Случайной величиной наЗЫвается переменная, которая может принимать в зависимости от исходов испытания те или иные случайные значения.
Если при этом переменная принимает последовательные различные значения и известны вероятности каждого из них; то она называется Дискретной случайной величиной. Дискретная случайная величина Х определена, если даны все ее возможные значения , число которых может быть как конечным, так и бесконечным, и соответствующие вероятности
Это задание представляется таблицей Распределения,
|
|
|
|
… |
|
|
|
|
|
… |
|
В котороЙ значения Х располагаются в строго возрастающем порядке. При этом сумма соответствующих этИМ значениям вероятностей равна 1, так как все возможные значения случайной величины представляют полную систему событий.
В случае конечного числа K возможных значений эта сумма запишется в виде
Для дискретной случайной величины с бесконечным множеством возможных значений эта сумма будет представлять собой ряд.
Представленная в виде таблицы совокупность всех значений случайной величины и соответственных вероятностей каждой из них или, что то же, функция Р(х), связывающая значения с соответствующими вероятностями, является Законом распределения случайной величины.
Примерами дискретных случайных величин являются:
1) число грузовых машин, проезжающих за один час через контрольный пункт автоинспекции;
2) сумма выигрыша, приходящегося на один билет денежно-вещевой лотереи;
3) число ничейных результатов в шахматном турнире;
4) число отличных оценок у студентов одной группы на экзамене.
Пример 1. Составить закон распределения случайной величины — числа появлений события А при П повторных независимых испытаниях, если вероятность появления этого события в отдельном испытании очень мала.
Решение. Вероятность появления события А M раз в испытаниях определяется формулой Пуассона
Соответствующая таблица распределения имеет такой вид:
|
Т |
0 |
1 |
2 |
… |
Т |
… |
|
|
|
|
|
… |
|
… |
Можно показать, что при неограниченном возрастании числа П сумма вероятностей в этом распределении представляет ряд, сходящийся к 1:
Пример 2. По мишени ведутся выстрелы до первого попадания или до Израсходования всех имеющихся патронов. Составить таблицу распределения случайной величины Х — Числа израсходованных патронов, если вероятность попадания при отдельНОм выстреле постоянна, Р=0,3, а число всех патронов .
Решение. Здесь случайная величина Х принимает значения: при попадании с одного выстрела,
— При попадании после одного промаха,
— При попадании после двух промахов и
— при четырех промахах или при попадании после трех промахов. Вероятности того, что случайная величина Х будет принимать указание значения, таковы:
и
Отсюда получаем искомую таблицу распределения
|
|
1 |
2 |
3 |
4 |
|
|
0.3 |
0.21 |
0.147 |
0.343 |
Условие выполнено.
График, соответствующий заданному распределению, называется Многоугольником распределения случайной величины. При этом по оси абсцисс откладываются значения х; случайной величины, а по оси ординат – их вероятности .
В качестве примера распределения случайной величины можно взять еще рассмотренное нами биномиальное распределение вероятностей числа пригодных деталей среди взятых наудачу 6 деталей
Здесь случайной величиной является число пригодных деталей со следующим законом распределения:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
0.0002 |
0.0041 |
0.033 |
0.132 |
0.297 |
0.3558 |
0.1779 |
Многоугольник распределения этой случайной величины графически совпадает с многоугольником, изображенным на рис. 2, с оговоркой, что по оси абсцисс откладываются значения случайной величины (количества пригодных деталей).
Помимо дискретных существуют еще Непрерывные случайные величины, которые могут принимать все значения в заданных границах (внутри некоторого отрезка) или на всей числовой оси. Приведем примеры непрерывных случайных величин:
1) расстояние точки падения диска от точки метания;
2) периметр перпендикулярного сечения ствола дерева;
3) расстояние от центра мишени до точки попадания пули при стрельбе.
Для непрерывной случайной величины нельзя составить таблицы, в которой были бы перечислены все ее значения даже в небольшом интервале. Поэтому закон ее распределения должен определять вероятность попадания ее значений в некоторый отрезок.
Пусть дана непрерывная случайная величина X. Тогда условие Х < Х для ее значений можно рассматривать как событие, вероятность наступления которого является некоторой функцией Х. Обозначив эту функцию через F(Х), будем иметь
F(X)=P(X<X).
F(Х) называют Функцией распределения вероятностей случайной величины, или интегральной функцией распределения1). Будем предполагать эту функциЮ непрерывной.
Отметим свойства функции F(X).
1°. Исходя из возможных значений вероятности, имеем
2°. При имеем
, так как
Отсюда F(X) — Функция неубывающая.
3°. Условие для значений случайной величины является достоверным событием, следовательно,
.
4°. Условие невозможно; поэтому
.
Выразим с помощью введенной функции вероятность того, что случайная величина Х удовлетворяет условию , т. е. найдем
.
Так как , то условие
означает, что или
, или
.
Отсюда на основании теоремы сложения вероятностей имеет место равенство
Здесь второе слагаемое
.
Но для непрерывной случайной величины вероятность того, что она примет какое-либо определенное значение, равна нулю и, в частности, .
Справедливость этого следует из непрерывности F(X). Действительно, если в равенстве
Принять и перейти к пределу, то найдем, что
Поэтому
И соответственно
.
Отсюда
.
Таким образом,
.
Этим определена вероятность того, что случайная величина принимает какое-то (безразлично какое) значение внутри отрезка в виде приращения функции F(Х) на всем этом отрезке.
Для дискретной случайной величины также можно определить функцию распределения. Ее значения легко находятся по таблице в виде суммы вероятностей тех значений случайной величины, которые удовлетворяют условию для каждого значения Х.
Пример 3. Составить функцию распределения для дискретной случайной величины Х — Числа появлений события А при 4 независимых испытаниях, если в каждом испытании .
Решение. Определив по формуле Бернулли значения вероятностей при I=0, 1, 2, 3 и 4, составим таблицу распределения
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
По данным этой таблицы определяем
Функция F(X) для дискретной случайной величины является кусочно-постоянной с точками разрыва при всех . График функции распределения для рассмотренного примера (рис. 5) наглядно отражает характер (ступенчатый) функции распределения дискретной случайной величины.
Рис. 5
Помимо рассмотренной функции распределения, представляющей интегральный закон, для характеристики непрерывной случайной величины применяется еще Дифференциальный закон распределения, Связанный с понятием ПлоТНости распределения вероятностей случайной величины.
Если с изменением длины отрезка вероятность попадания случайной величины Х в этот отрезок меняется пропорционально длине отрезка, т. Е.
, то говорят, что случайная величина Х равномерно распределена в промежутке
. При этом отношение
— величина постоянная.
Это отношение по аналогии со случаем равномерного распределения массы (в механике) называют Плотностью распределения вероятностей равномерно распределенной случайной величины.
Если при этом границы отрезка включают все возможные значения случайной величины X, то условие — событие достоверное. Тогда
,
И соответственно плотность вероятности
Если случайная величина не является равномерно распределенной, то приведенное отношение выражает среднюю плотность распределения вероятностей в данном промежутке, и тогда вводится понятие Плотности распределения вероятностей в точке.
Эта «плотность», как и в механике, определяется производной от функциИ F(Х) в точке Х:
Функция , выражающая плотность распределения вероятностей, называется Дифференциальной функцией распределения вероятностей и представляет дифференциальный закон распределения.
Переходя к дифференциалу как к главной части приращения функции, будем иметь
Это значит, что произведение приближенно определяет вероятность того, что случайная величина Х принимает некоторое значение в промежутке
.
Таким образом, установлено, что если функция Р(Х), выражающая интегральный закон распределения вероятностей, дает точное значение вероятности попадания случайной величины в промежуток, то плотность вероятности , выражающая дифференциальный закон распределения, дает здесь приближенное значение.
В теоретических исследованиях и при решении практических задач часто бывает удобней пользоваться дифференциальным законом распределения.
В порядке иллюстрации изложенных сведений о распределении непрерывной случайной величины можно, например, отметить, что при равномерном распределении случайной величины на отрезке Плотность ее вероятности
(рис. 6, а) изображается прямой, параллельной оси Ох, а функция распределения F(X) (рис. 6, б) — отрезком прямой, проходящей через точки
и
. ЗдесЬ
Рис. 6 а Рис. 6 б
Если непрерывная случайная величина задана плотностью , то график функции
называется Кривой распределения вероятностей этой случайной величины (рис. 7). При этом вероятность
определяется площаДью криволинейной трапеции, заключенной между кривой, осью абсцисс и прямыми
и
.
Если непрерывная случайная величина задана функцией распределения F(Х), то ее график называется Интегральной кривой расПределения (рис. 8). При этом вероятность Определяется приращением ординаты этой кривой
.

Рис. 7 Рис. 8
В рамках настоящего курса не рассматриваются различные виды распределения вероятностей, кроме нормального распределения, основные сведения о котором будут даны ниже.
| < Предыдущая | Следующая > |
|---|
Конспект урока алгебры
Таблицы
распределения
(9
класс)
Тип урока: комбинированный.
Цель урока:
познакомиться с основными понятиями математической статистики и узнать
способы описания окружающего нас мира с помощью числовых характеристик
Задачи: 1. Познакомиться с наглядным способом представления
(с помощью таблицы) распределения значений случайной величины по вероятностям,
по частотам и по относительным частотам.
2. Убедиться в применимости закона больших чисел
для решения прикладных задач, связанных с частотным распределением значений
случайной величины.
3.
Научиться составлять таблицы распределения по вероятностям, по частотам и по
относительным частотам.
Ход
урока
1. Организационный
момент:
Здравствуйте ребята! Сегодня у нас гости.
Тема нашего
сегодняшнего урока – «Таблицы распределения» (слайд 1).
Целями нашего
сегодняшнего урока являются: (слайд 2)
1. Познакомиться с
наглядным способом представления (с помощью таблицы) распределения значений
случайной величины по вероятностям, по частотам и по относительным частотам.
2. Убедиться в применимости
закона больших чисел для решения прикладных задач, связанных с частотным
распределением значений случайной величины.
3. Научиться составлять
таблицы распределения по вероятностям, по частотам и по относительным частотам.
Но прежде, чем мы приступим к реализации наших
целей, давайте повторим ранее пройденный нами материал.
Опрос: (слайд 3)
Мы с вами знаем, что нас окружает множество
явлений, о которых мы не можем с уверенностью сказать, как или когда они произойдут.
Например, когда будет извержение вулкана, как упадет подброшенная монета, когда
начнется эпидемия гриппа и т.д. Мы уже знаем, что такие явления называются
событиями. Давайте вспомним, какие бывают события.
- Что такое невозможное событие?
- Что такое достоверное событие?
- Что такое случайное событие?
- Какие события называют совместными и
несовместными? - Как вычислить вероятность наступления
события? - Что называют суммой событий?
- Что называют произведением событий?
- Что называют относительной частотой события?
Молодцы! Теперь для разминки рассмотрим
несколько задач из сборника типа В19
2. Подготовка
к ОГЭ
Устный счет: (слайд 4-5)
1.
В среднем на 50 карманных
фонариков приходится два неисправных. Найдите вероятность купить работающий
фонарик.
2.
В каждой пятой банке кофе,
согласно условиям акции есть приз. Призы распределены по банкам случайно. Галя
покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя
не найдет приз в своей банке.
3.
В среднем из каждых 80
аккумуляторов, поступивших в продажу 68 аккумуляторов заряжены. Найдите
вероятность того, что купленный аккумулятор не заряжен.
4.
Телевизор у Светы сломался и
показывает только один случайный канал. Света включает телевизор. В это время
по четырем каналам из двадцати показывают кинокомедии. Найдите вероятность
того, что Света попадет на канал, где комедия не идет.
5.
В фирме такси в данный момент
свободно 10 машин: 1 черная, 1 желтая и 8 зеленых. По вызову выехала одна из
машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того,
что к нему приедет желтое такси.
Молодцы! Ну а теперь
перейдем непосредственно к теме нашего сегодняшнего урока.
3. Объяснение
нового материала:
При изучении данной темы мы
с вами должны будем обратиться к математической статистике. Что же это за
наука? (слайд 6) Математическая статистика – это наука, которая
занимается изучением случайных величин и изучает способы обработки информации
об окружающем нас мире с помощью числовых характеристик. В этом определении нам
встретились незнакомые нам понятия. Это понятие случайной величины и способы обработки
информации об окружающем нас мире с помощью числовых характеристик. Давайте
разберемся с этими понятиями.
О том что такое случайная
величина нам расскажет _____________. Спасибо.
Теперь давайте разберемся,
как же обрабатывают информацию об окружающем нас мире? (слайд 7)
- Данные
измерений упорядочивают и группируют. - Составляют
таблицы распределений данных. - По
таблицам строят графики распределений. - В итоге
создается паспорт измерений, в котором собраны числовые характеристики
полученной информации.
Наша с
вами задача научиться составлять таблицы распределения случайной величины.
Давайте рассмотрим это на примерах.
Задача
1: (слайд 8)
После
проверки контрольной работы в 9 классе учитель составил таблицу, в которой
указаны оценки, полученные учащимися:
|
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
3 |
3 |
3 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
5 |
5 |
5 |
На основании этих данных
составить таблицы распределения по частотам (М), по относительным частотам (W) значений
случайной величины Х – оценок учащихся 9 класса.
Решим эту задачу. Итак, в
задаче случайной величиной Х являются оценки учащихся.
Составим таблицу
распределения случайной величины Х по частотам (М). Для этого подсчитаем число
случаев (М) получения каждой из оценок и внесем их в таблицу 1. Получим:
|
Х |
2 |
3 |
4 |
5 |
|
М |
3 |
15 |
9 |
3 |
|
|
|
|
|
|
Число
учащихся 9 класса N писавших контрольную работу,
равно сумме частот (М) всех выставленных оценок, т.е.
N = 3+15+9+3 = 30.
Зная, что
относительная частота находится по формуле ,
найдем относительную частоту для каждого значения величины Х и внесем в нашу
таблицу.
Наша
таблица распределения готова!
Вопросы?
Все ли было понятно? Хорошо.
Задача
2: (слайд 9)
Брошены
две игральные кости. Игроки делают ставки на выпавшую сумму очков на двух
костях. Есть ли сумма, на которую выгоднее всего делать ставку?
Решим эту
задачу. Итак, найдем вероятность появления каждой суммы очков. Общее число исходов
n – всевозможных пар очков, согласно
правилу произведения равно . Составим таблицу сумм
очков, выпавших на двух костях:
|
1-я кость |
2-я кость |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
С помощью
таблицы для каждой конкретной суммы определим число благоприятных исходов:
Вероятность
появления той или иной суммы в результате бросания двух костей можно
представить в виде таблицы распределения по вероятностям Р значений случайной величины Х – выпавших на костях сумм:
|
Сумма |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Вероятность |
|
|
|
|
|
|
|
|
|
|
|
Из
таблицы видно, что наибольшую вероятность появления имеет
сумма очков равная 7, таким образом на нее и выгоднее всего делать ставку.
Вопросы?
Все ли было понятно? Хорошо. А теперь перейдем к самостоятельной работе. Перед
вами задания.
4. Самостоятельная
работа: (слайд 10)
Задача 1.
В таблице записаны размеры
обуви 20 девочек 9 класса:
|
34 |
35 |
35 |
35 |
36 |
36 |
36 |
36 |
37 |
37 |
|
37 |
37 |
37 |
37 |
38 |
38 |
38 |
39 |
39 |
40 |
На основании этих данных
составить таблицы распределения по частотам (М), по относительным частотам (W) значений
случайной величины Х – размеров обуви девочек 9 класса.
Задача 2.
На стол бросают две
монеты. Исходу «орел» припишем условное числовое значение 0, а исходу «решка» –
1. Составить таблицу распределения по вероятностям Р значений случайной
величины Х – суммы выпавших на монетах чисел.
5. Подведение
итогов урока:
Подведем
итоги нашего урока. Достигли ли мы поставленной цели? Легко ли вы справляетесь
с заданиями такого типа, как мы разобрали? Все ли вам было понятно?
Вы сегодня
все молодцы! Домашнее задание: № 385, 387, тренировочные работы 9-12 задания
типа В19 (слайд 11)
Самостоятельная
работа:
Задача 1.
В таблице записаны размеры
обуви 20 девочек 9 класса:
|
34 |
35 |
35 |
35 |
36 |
36 |
36 |
36 |
37 |
37 |
|
37 |
37 |
37 |
37 |
38 |
38 |
38 |
39 |
39 |
40 |
На основании этих данных
составить таблицы распределения по частотам (М), по относительным частотам (W) значений
случайной величины Х – размеров обуви девочек 9 класса.
Решение:
|
Х |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
М |
|||||||
|
|
N =
Задача 2.
На стол бросают две
монеты. Исходу «орел» припишем условное числовое значение 0, а исходу «решка» –
1. Составить таблицу распределения по вероятностям Р значений случайной
величины Х – суммы выпавших на монетах чисел.
Решение:
|
1-я |
2-я |
|
|
0 |
1 |
|
|
0 |
||
|
1 |
|
Сумма чисел |
|||
|
Вероятность |
A probability distribution table is a table that displays the probability that a random variable takes on certain values.
For example, the following probability distribution table tells us the probability that a certain soccer team scores a certain number of goals in a given game:
The left-hand column shows the number of goals and the right-hand column tells us the probability that the team will score this number of goals.
For example:
- The probability that the team scores exactly 0 goals is 0.18.
- The probability that the team scores exactly 1 goal is 0.34.
- The probability that the team scores exactly 2 goals is 0.35.
And so on.
Properties of a Probability Distribution Table
A probability distribution table has the following properties:
1. All probabilities must add up to 1.
For a probability distribution table to be valid, all of the individual probabilities must add up to 1. We can verify that the previous probability distribution table is valid:
Sum of probabilities = 0.18 + 0.34 + 0.35 + 0.11 + 0.02 = 1.
2. The mean can be calculated.
The formula to calculate the mean of a given probability distribution table is:
μ = Σx * P(x)
where:
- x: Data value
- P(x): Probability of value
For example, consider our probability distribution table for the soccer team:
The mean number of goals for the soccer team would be calculated as:
μ = 0*0.18 + 1*0.34 + 2*0.35 + 3*0.11 + 4*0.02 = 1.45 goals.
3. The standard deviation can be calculated.
The formula to calculate the standard deviation of a given probability distribution table is:
σ = √Σ(xi-μ)2 * P(xi)
where:
- xi: The ith value
- μ: The mean of the distribution
- P(xi): The probability of the ith value
For example, here’s how to calculate the standard deviation of goals scored by the soccer team:
The standard deviation is the square root of the sum of the values in the third column:
Standard deviation = √(.3785 + .0689 + .1059 + .2643 + .1301) = 0.9734
How to Visualize a Probability Distribution Table
The easiest way to visualize the values in a probability distribution table is by using a histogram, which displays the values of the random variable along the x-axis and the probability of those values along the y-axis:
This lets us quickly visualize the probability values from the table.
In particular, we can see that there is a high probability that the team scores 2 goals or less while there is a tiny probability that the team scores as many as 4 goals.
Additional Resources
Probability Distribution Calculator
How to Find the Mean of a Probability Distribution
How to Find the Standard Deviation of a Probability Distribution
Рядом данных называют результаты измерения, перечисленные в порядке их получения. Каждый из результатов называется вариантой измерения.
Например, результаты написания контрольной работы по математике для класса из 20 человек можно представить в виде следующего ряда данных: 3, 4, 4, 5, 3, 4, 3, 3, 3, 5, 5, 4, 5, 4, 5, 3, 3, 3, 4, 3. Эту же информацию можно представить в
виде таблицы:
Кратность варианты — количество её повторений в ряду данных. В нашем ряду оценка «3» появилась 9 раз, поэтому её кратность равна 9.
Понятно, что таблица распределения отображает данные более наглядно и компактно.
Числовые характеристики данных
Объём измерения — количество всех данных этого измерения. Одна из наиболее важных характеристик варианты — это её частота. Частота варианты показывает долю этой
варианты в ряду распределения. Она вычисляется по формуле:
частота =кратность варианты/объём измерения
В нашем примере частота варианты «4» равна .
Это означает, что оценка 4 составляет 0,3 всех полученных оценок.
Размах измерения — разность между максимальной и минимальной вариантами этого измерения. В нашем примере максимальная варианта равна 5, минимальная — 3, значит, размах равен .
Мода измерения — варианта, которая в измерении встретилась чаще других. В приведённом выше примере чаще всех встретилась оценка 3, значит, она и будет модой этого распределения.
Медиана распределения — это центральное число в упорядоченном ряду данных, если в ряду нечётное количество чисел, или полусумма двух центральных, если в ряду чётное количество чисел.
Например, для ряда распределения 1, 2, 3, 6, 9, объём измерения которого равен 5, медианой распределения будет третье число этого ряда, то есть 3.
Для ряда распределения 7, 3, 2, 1 с объёмом измерения, равным 4, медианой будет полусумма двух центральных чисел данного ряда, то есть число, равное .
Для нахождения медианы распределения необходимо
1. Упорядочить ряд распределения по возрастанию или по убыванию: .
2. Если объём измерения нечётный, то есть , то получим следующую ситуацию:
В этом случае медианой является число .
3. Если объём измерения чётный, то есть , то имеем
В этом случае медианой является число — .
Среднее ряда (среднее арифметическое) — сумма всех чисел ряда, делённая на их количество. Если имеется таблица распределения, то можно
1) умножить каждую варианту на её кратность;
2) просуммировать полученные значения;
3) разделить результат на объём измерения. Например, для ряда распределения 2, 4, б, 8, у которого объём измерения равен 4, среднее значение равно
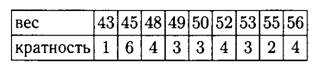
Задача 1. Даны результаты измерения веса школьников 9 класса: 55, 53, 56, 48, 45, 56, 49, 52, 53, 49, 50, 56, 45, 52, 56, 45, 45, 48, 55, 52, 43, 48, 52, 49, 50, 45, 48, 45, 50, 53.
а) Постройте таблицу распределения данных.
б) Найдите объём измерения.
в) Найдите размах ряда.
г) Найдите частоту появления каждого веса в указанном ряду.
д) Найдите медиану, моду и среднее указанного ряда.
Решение.
а) Наименьшее число в ряду — 43, оно встречается в ряду один раз, значит, его кратность равна 1. Следующее по величине — число 45, оно встречается шесть раз, значит, его кратность равна 6. Далее 48, оно встречалось 4 раза, значит, его кратность равна 4.
Продолжая аналогично, заполним таблицу:
б) Найти объём измерения можем несколькими способами.
1- й способ.
Посчитаем количество чисел в ряду, получим 30.
2- й способ.
Сложим кратности всех вариант:
Ответ: 30.
в) Наибольшее значение в ряду 56, наименьшее — 43, значит, размах равен
Ответ: 13.
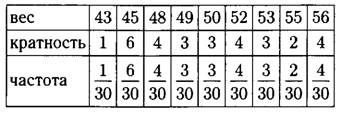
г) Для каждой варианты делим её кратность на объём измерения (на 30), результаты пишем в таблицу.
д) В данном ряду 30 чисел, значит, медиана равна полусумме 15-го и 16-го чисел в упорядоченном ряду.
Как видно из такой записи чисел, от 43 до 49 — 14 чисел, значит, 15-ое и 16-ое числа равны 50, и значит, медиана равна
Мода — то значение, которое встречается чаще всех, то есть то, у которого больше кратность. Из таблицы распределения находим, что наибольшую кратность имеет число 45, значит, мода равна 45.
Для нахождения среднего необходимо найти сумму всех чисел ряда и разделить ее на количество этих чисел. Сумму можно найти просто складывая подряд все числа ряда. А можно поступить иначе: каждую варианту умножить на её кратность и сложить полученные результаты. Имеем:
.
Осталось разделить полученную сумму на количество всех чисел: .
Ответ: медиана: 50; мода: 45; среднее: 50,1.
Задача 2. Пятерых учеников попросили подсчитать, сколько времени (в минутах) они тратят на дорогу от дома до школы. Получили следующие результаты: 5,15,10,15,20.
1) На сколько среднее значение этого ряда меньше его размаха?
2) На сколько мода этого ряда больше медианы?
3) Найдите процентную частоту значения 10.
Решение.
1) Среднее ряда: , размах:
. Искомое значение равно
.
Ответ: 2.
2) Найдём медиану. Расположим числа в порядке возрастания: 5, 10, 15, 15, 20. Медианой этого набора будет третье число в упорядоченном ряду, то есть 15.
В данном ряду число 15 встретилось 2 раза, остальные — по одному разу. Мода ряда равна 15. Мода и медиана этого ряда равны, значит, ответ 0.
Ответ: 0.
3) Кратность значения 10 равна 1, объём измерения равен 5 (всего 5 чисел). Частота значения 10 равна , процентная частота равна
.
Ответ: 20.
Задача 3. Имеется 4 группы породистых котов. Для некоторого соревнования отбирают котов с длиной шерсти не менее 8 см.
Известно следующее:
1) в первой группе наибольшая длина шерсти равна 10 см;
2) во второй группе средняя длина шерсти равна 8 см;
3) в третьей группе мода длины шерсти равна 8 см;
4) в четвёртой группе медиана длины шерсти равна 9 см.
В какой из групп хотя бы половина котов гарантированно подходит по длине шерсти?
Решение.
1) Из того, что наибольшая длина шерсти равна 10 см, не следует никакой другой информации, то есть ничего не можем сказать про остальных котов этой группы.
2) Рассмотрим для примера группу котов с длиной шерсти 7 см, 7 см и 10 см. Среднее равно , но в этой группе нет половины котов, удовлетворяющих требованиям.
3) Рассмотрим для примера группу котов с шерстью длиной 8 см, 8 см, 7 см, б см, 5 см. Мода равна 8, но опять же нет половины котов, удовлетворяющих требованиям.
4) Если медиана равна 9 см, то есть половина котов с шерстью меньшей или равной длины и половина — с большей или равной длины. Значит, в этой группе найдётся половина котов с шерстью длиной не менее 8 см.
Ответ: 4.
Задача 4. По статистике автозавода из 1000 машин в среднем 20 бракованных. Сколько бракованных машин следует ожидать, если завод собирается выпустить 300 500 машин?
Решение.
Если из 1000 машин 20 бракованных, то частота появления бракованной машины равна . То есть доля бракованных машин будет равна 0,02, тогда из 300 500 машин будет
бракованных.
Ответ: 6010.
Закон распределения дискретной случайной величины (ДСВ) представляет собой соответствие между значениями х1, х2,…,хn этой величины и их вероятностями p1, p2,…,pn
Может быть задан аналитически, графически или таблично.
Самый простой способ представления закона распределения дискретной случайной величины — в виде таблицы ряда распределения, то есть
| X | x1 | x2 | …… | xn |
| P | p1 | p2 | …… | pn |
х1, х2,…,хn — значения дискретной случайной величины;
p1, p2,…,pn — вероятности значений X дискретной случайной величина.
Также должно выполняться условия, что сумма вероятностей равна 1, то есть
∑p=p1+p2+ … +pn=1
Графически закон распределения ДСВ задается в виде многоугольника распределения см. здесь., а аналитически, например, с применением формулы Бернулли.Рассмотрим примеры
Пример 1
Монета подбрасывается 10 раз, герб выпал 6 раз, а орел — 4 раза. Составить закон распределения дискретной случайной величины.
Решение
Вероятности равны:
p1(6)=6/10=0,6;
p2(4)=4/10=0,4
Пример 2
Из корзины извлечено 4 белых шара, 6 черных, 8 синих и 2 красных шара. Найти закон распределения случайной величины X возможного выигрыша на один билет.
Решение
Объем выборки равен
n=4+6+8+2=20
X принимает следующие значения:
x1=4; x2=6; x3=8; x1=2
Найдем их вероятности:
p1(4)=4/20=0,2;
p2(6)=6/20=0,3;
p3(8)=8/20=0,4;
p4(2)=2/20=0,1
Получаем таблицу закона распределения дискретной случайной величины
| X | 4 | 6 | 8 | 2 |
| P | 0.2 | 0.3 | 0.4 | 0.1 |
Пример 3
По контрольной работе по математике школьники получили оценки:
удовлетворительно — 5 человек;
хорошо — 13 человек;
отлично — 7 человек.
Составьте таблицу закона распределения ДСВ
Решение
n=5+13+7=26
Вычислим вероятности:
p1(5)=5/25=0,2;
p2(13)=13/25=0,52;
p3(7)=7/25=0,28
Таблица имеет вид:
| X | 5 | 13 | 8 | 2 |
| P | 0.2 | 0.52 | 0.28 | 0.1 |
Пример 4
Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.
Решение
Для составления закона распределения воспользуемся формулой комбинаторики сочетание без повторений, то есть всего 8 изделия, а отобрать необходимо 3 изделия получаем:
при P(X=0) — вероятность того, что среди трех отобранных изделий не окажется ни одного стандартного;
при P(X=1) — вероятность того, что среди трех отобранных изделий окажется одно стандартное и два нестандартных изделия;
при P(X=2) — вероятность того, что среди трех отобранных изделий окажется два стандартных и одно нестандартное изделие;
при P(X=3) — вероятность того, что среди трех отобранных изделий все три изделия стандартные.
Составим таблицу распределения
| X | 0 | 1 | 2 | 3 |
| P | 0.018 | 0.268 | 0.536 | 0.178 |
Пример 5
В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных.
Решение
Возможные варианты значений СВ X: 1, 2, 3
$n=C_6^3$ — числу способов, которыми можно выбрать три детали из шести;
$C_4^x$ — число способов, которыми из четырех деталей выбирают х деталей.
$C_2^{3 — x}$ — общее число способов отбора нестандартных деталей
Тогда вероятности события A вычисляются по формуле
Закон распределения дискретной случайной величины X для составления ряда распределения:
Получаем таблицу ряда распределения ДСВ
| X | 0 | 1 | 2 | 3 |
| P | 0 | 0.2 | 0.6 | 0.2 |
17215