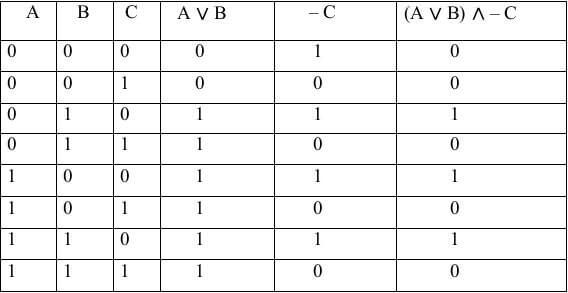
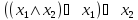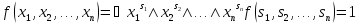Построение таблиц истинности
Екатерина Андреевна Гапонько
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Определение 2
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
Определение 3
Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:
Рисунок 1.
Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
-
Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
-
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
-
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
«Построение таблиц истинности» 👇
Рисунок 2.
Пример 1
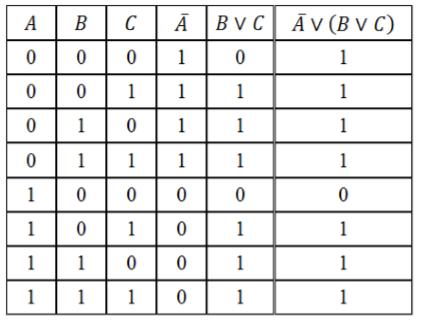
Составить таблицу истинности логического выражения $D=bar{A} vee (B vee C)$.
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- инверсия ($bar{A}$);
- дизъюнкция, т.к. она находится в скобках ($B vee C$);
-
дизъюнкция ($overline{A}vee left(Bvee Cright)$) – искомое логическое выражение.
Кол-во столбцов = $3 + 3=6$.
-
Заполним таблицу, учитывая таблицы истинности логических операций.
Рисунок 3.
Пример 2
По данному логическому выражению построить таблицу истинности:
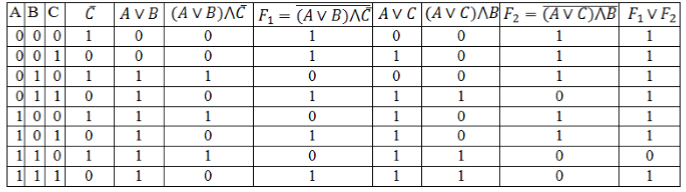
[F=overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}]
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- отрицание ($bar{C}$);
- дизъюнкция, т.к. она находится в скобках ($A vee B$);
- конъюнкция ($(Avee B)bigwedge overline{C}$);
- отрицание, которое обозначим $F_1$ ($overline{(Avee B)bigwedge overline{C}}$);
- дизъюнкция ($A vee C$);
- конъюнкция ($(Avee C)bigwedge B$);
- отрицание, которое обозначим $F_2$ ($overline{(Avee C)bigwedge B}$);
-
дизъюнкция – искомая логическая функция ($overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}$).
Кол-во столбцов = $3 + 8 = 11$.
-
Заполним таблицу, учитывая таблицу истинности логических операций.
Рисунок 4.
Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
Пример 3
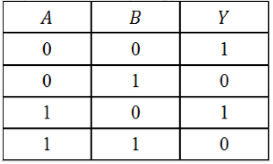
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.
Рисунок 5.
Решение:
- Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
- Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:
Рисунок 6.
- Каждое логическое выражение в этой дизъюнкции запишем как конъюнкцию аргументов функции $A$ и $B$: $left(Awedge Bright)vee left(Awedge Bright)$
- В случае, когда значение в соответствующей строке таблицы равно $0$, запишем этот аргумент с отрицанием, получим искомую функцию:[Yleft(A,Bright)=left(overline{A}wedge overline{B}right)vee left(Awedge overline{B}right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 12.04.2016
Теория:
Алгеброй
называется множество с определенными
на нем операциями. Обычно, алгебра
задается следующей парой: (Ω;M),
где M
– множество элементов алгебры; Ω –
сигнатура, включающая в себя множество
операций над элементами алгебры.
Алгеброй
логики называется алгебра, в которой М
– множество логических переменных и
функций, а Ω имеет следующий вид:
Ω={



/, ~,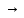

Функцией
алгебры логики (логической функцией
или булевой функцией) называется функция,
аргументы которой и ее значения могут
принимать значения из двух-элементарного
множества. (Чаще всего это множества,
содержащие 0 и 1)
Любая
логическая функция n-переменных
может быть задана в виде таблицы, в
которой в левой ее части перечислены
2n
наборов значений переменных, а в правой
части этой таблицы значение функций на
этих наборах. Такая таблица так же
называется таблицей истинности.
Наборы
переменных в левой части таблицы
расположены в соответствии с порядком
возрастания, причем сами эти наборы
рассматриваются как двоичные числа.
При
построении таблиц истинности заданных
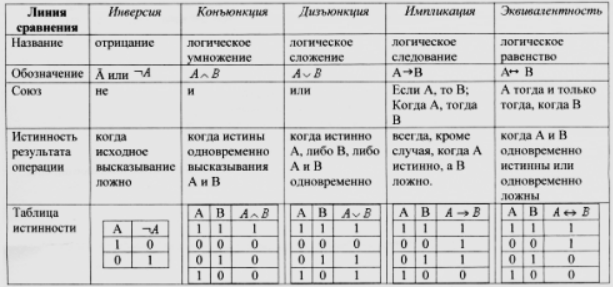
высказываний используются таблицы
истинности элементарных булевых функций.
Таблицы
истинностей булевых функций:
Конъюнкция:
|
X1 |
X2 |
X1 |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Конъюнкцию
называют также логическим умножением.
Конъюнкция
обозначается также A*B
или
A&B
.
Дизъюнкция:
|
X1 |
X2 |
X1 |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Дизъюнкция
обозначается также A+B
.
Сложение
по модулю два (неравнозначность):
|
X1 |
X2 |
X1 |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Неравнозначность
называют также суммой по модулю 2, суммой
Жегалкина, прямой суммой, строгой
дизъюнкцией.
Импликация
(следование):
|
X1 |
X2 |
X1 |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Импликацию
называют также следуемостью.
Импликация
обозначается также A
A
B
.
Эквиваленция:
|
X1 |
X2 |
X1~X2 |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Эквиваленцию
двух высказываний называют также
равнозначностью, равносильностью,
тождественностью.
Эквиваленция
обозначается также A
=
B
или
A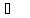
A~
B
.
Стрелка
Пирса:
|
X1 |
X2 |
X1 |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Штрих
Шеффера:
|
X1 |
X2 |
X1 |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Отрицание:
|
X |
|
|
0 |
1 |
|
1 |
0 |
Иерархия
булевых функций:
действия
в скобках,
отрицание,
конъюнкция,
дизъюнкция,
неравнозначеность,
эквиваленция,
импликация
(операции,
стоящие на одном уровне, при отсутствии
скобок выполняются в порядке их появления
в записи
формулы
слева направо).
Пример:
Составить таблицу истинности для функции

Выполняется
“по действиям”, как в 5м классе.
|
x1 |
x2 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
Приведение
функций к СДНФ и СКНФ.
Теория:
Полной
конъюнкцией
n
переменных называется конъюнкция,
состоящая из n
переменных или их отрицаний, в которых
каждая переменная встречается только
1 раз.
СДНФ
логической функции называется формула,
представляющая данную логическую
функцию и имеющая вид дизъюнкции полных
конъюнкций, которая формируется для
наборов переменных, для которых функция
f=1;
Полной
дизъюнкцией
n
переменных называется дизъюнкция,
состоящая из n
переменных или их отрицаний, в которых
каждая переменная встречается только
1 раз.
СКНФ
логической функции называется формула,
представляющая данную логическую
функцию и имеющая вид дизъюнкции полных
дизъюнкций, которая формируется для
наборов переменных, для которых функция
f=0;
Соседние файлы в папке Arkhiv_v_pomosch
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Логическая функция одно из основополагающих понятий математической логики. Она зависит от логических переменных и принимает значения из множества, от которого находится в зависимости. Логические функции булевых переменных могут принимать только два значения – 1 или 0.
Понятие таблиц истинности
Задаваться логическая функция может числовым способом, словесным описанием, картами Карно, аналитическим выражением и с помощью таблиц истинности. В последнем случае все аргументы функции следует записать в левой части таблицы, а значения, которые им соответствуют, в правой.
Определения 1 — 2
Таблица истинности – это таблица, просто и наглядно показывающая, какие значения будут у логического выражения при всевозможных наборах переменных функции.
Равносильными именуют те логические выражения с совпадающими последними столбцами таблицы истинности. Обозначают равносильные функции знаком «=».
Правила того, как следует проводить построение таблицы истинности
Несоблюдение хотя бы одного из них ведёт к очень грубой ошибке. Вот эти правила:
- Число строк таблицы должно совпадать с числом комбинаций всевозможных n логических переменных, то есть быть равным 2n;
- Количество столбцов таблицы должно равняться сумме числа логических переменных и числа логических операций;
- В построенный шаблон таблицы истинности должны вписываться все значения исходных переменных;
- Построение таблицы истинности выражения происходит по её столбцам, при этом обязательно учитываются правила логических операций.
Порядок действий при построении таблицы истинности для логических выражений
Порядок действий при построении таблицы истинности, какой бы ни была логическая функция, следующий:
- Определить, какое число строк и столбцов будет в будущей таблице. Делается подобное по формулам
X = n + m, Y = 2n+1.
Где n – число переменных, m – чило логических операций. - Заполнить самую верхнюю строку таблицы переменными и логическими операциями, идя слева направо. При этом приоритетность логических операций следует учитывать обязательно, иначе получится совсем не то, что нужно;
- В первых столбцах перечислить всевозможные комбинации входных значений;
- Выполняя заданные логические операции, заполнить все оставшиеся ячейки;
Ответом следует считать последний заполненный столбец таблицы.
О порядке логических операций
Лучше его представить списком. Логические операции выполняют в следующей последовательности: сначала идёт инверсия, затем конъюнкция, после этого дизъюнкция, после неё импликация, по её выполнении эквиваленция.
После них идут Штрих Шеффера и Стрелка Пирса. Первым может быть выполнено как то, так и другое.
Далее приведём несколько поучительных задач на построение таблиц истинности
Задачи 1 — 3
Сделать построение таблицы истинности для функции ((A→B) ∧ A) ↔ B
Решение:
-
- Определяем сколько будет у нас столбцов. Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.
- Определяем, сколько будет у на строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций. У нас будет 2n+1 = 22 + 1= 5;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В двух первых столбцах записываем возможные значения переменных;
- В далее идущих столбцах записываем, какие значения принимают промежуточные функции;
- В самом последнем из столбцов записываем итоговые значения функции.
В результате всего этого у нас должно получиться:
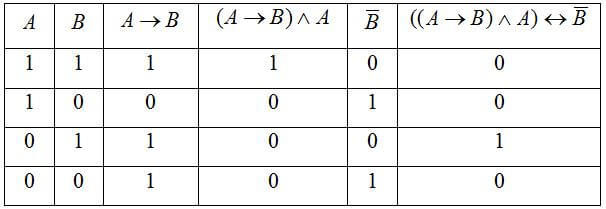
Провести построение таблицы истинности функции (A ∨ B) ∧ – C
Решение:
- Определяем сколько будет столбцов. Количество переменных у нас 3, количество логических операций 3. Складываем то и другое: 3+3 = 5.
- Определяем, количество строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций.В итоге будет 2n+1 = 23 + 1= 9;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В два первые столбца вносим возможные значения наших переменных;
- В далее следующие столбцы записываем, какие значения принимают промежуточные функции;
- В последнем столбце записываем итоговые значения функции.
В итоге получим таблицу:
Сделать таблицу истинности для
(A ∧ B ↔ B ∧ C) ∨ (C → A)
Функция посложнее и таблица получится значительно больше, чем предыдущая.
- Считаем столбцы. Количество переменных 3, количество логических операций 6. Значит столбцов будет 3+6=9;
- Считаем строки. Их количество будет 23+1= 9;
- Заполняем первую строку таблицы;
- В первых столбцах записываем все допустимые значения наших переменных;
- В остающихся столбцах пишем, какие наша функция принимает промежуточные значения
- В последний столбец пишем итоговые значения данной нам функции.
В итоге у нас получается таблица:
Нет времени решать самому?
Наши эксперты помогут!
Построения функции, если известна её таблица истинности
Совершенной дизъюнктивной нормальной формой считают такую нормальную форму, в которой отсутствуют одинаковые элементарные конъюкции и все конъюкции включают один и тот же набор переменных, куда каждая из них входит не более одного раза.
Алгоритм действий для получения СДНФ по таблице истинности:
- Отметьте в таблице строки, в которых значение функции равняется 1
- Выпишете для каждой отмеченной строки конъюкцию всех переменных. Если переменная равна 1, в конъюкцию следует включить саму эту переменную. Если переменная равняется 0, то её отрицание;
- Все полученные конъюкции свяжите в дизъюкцию.
Аналогичным образом определяется СКНФ
В строках, в последнем столбце которых функция равна 0, запишите дизъюкции всех переменных. Если значение переменной в данной строке будет 0, в дизъюкцию следует включить саму эту переменную. Если значение функции равно 1, то включить нужно её отрицание.
Правило + задача
СДНФ всегда равно СКНФ. СДНФ = СКНФ.
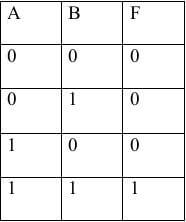
Дана таблица истинности:
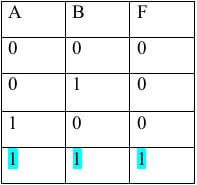
Выделяем в ней цветом строку
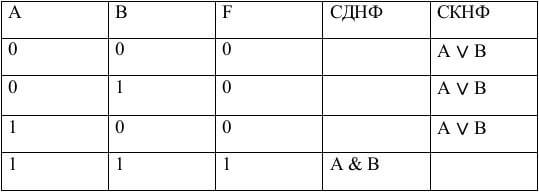
Заполняем столбцы с СДНФ и с СКНФ
Записываем СДНФ
СДНФ = A & B
Записываем СКНФ
СКНФ = (A ∨ B) & (A ∨ B) & (A ∨ B)
Как известно, все существующие логические функции обладают совершенной дизъюнктивной нормальной формой, а также совершенной конъюнктивной нормальной формой. Обозначаются они аббревиатурами СДНФ и СКНФ соответственно. Рассмотрим принципы их построения с использованием таблицы истинности, устанавливающей соответствие всех возможных вариаций логических переменных.
Основные правила при построении СДНФ
СДНФ является дизъюнкцией конституента единицы, соответствующей входящей совокупности логических переменных, при которых функция достигает показателя «1». Она удовлетворяет 3 условия:
- Включает разные элементарные конъюнкции.
- Конъюнкции включают разные переменные.
- Все из элементарных конъюнкций включают в одной и той же последовательности все имеющиеся логические переменные этой ДНФ.
Привести к СДНФ можно всякую булеву формулу за исключением той, что не выступает тождественно ложной. Получению СДНФ предшествует создание таблицы истинности. Чтобы построить СДНФ следует записать произведение для каждой совокупности присутствующих переменных. Важно учесть, что логические переменные со значением «0» нужно брать с отрицанием.
Не каждый студент может себе позволить за семестр в ВУЗе отдать 100 000 ₽. Но круто, что есть гранты на учебу. Грант-на-вуз.рф – это возможность учиться на желанной специальности. По ссылке каждый получит бонус от 300 ₽ до 100 000 ₽ – грант-на-вуз.рф
Принципы построения СКНФ
СКНФ является конъюнкцией конституента нуля, соответствующих входящих логических переменных, при которых функция достигает «0». Она удовлетворяет 3 условия:
- Включает разные элементарные дизъюнкции.
- Дизъюнкции включают разные переменные.
- Все из элементарных дизъюнкций включают каждую логическую переменную данной КНФ.
К такой форме возможно привести булеву формулу, за исключением той, которая не выступает тождественно истинной.
Чтобы получить СКНФ функции необходимо сначала построить таблицу истинности. При построении СКНФ по таблице следует записать сумму для каждого набора логических переменных. Обратите внимание, что переменные, имеющие значение «1» нужно брать с отрицанием.
Примеры нахождения СКНФ и СДНФ
Запишем логическую функцию по ее таблице истинности:
Решение:
Воспользуемся правилом построения СДНФ:
Получим СДНФ:
Воспользуемся правилом построения СКНФ:
Получим СКНФ:
Напоминаем про сервис грант-на-вуз.рф. Не упусти свой шанс изучать то, что тебе нравится. Ну или просто сэкономить на учебе. Ты точно получишь от 300 ₽ до 100 000 ₽, перейдя по ссылке грант-на-вуз.рф!
Описание презентации по отдельным слайдам:
-
1 слайд
Логика высказываний
Алгоритм построения
таблиц истинности -
2 слайд
Таблицы истинности
Решение логических выражений принято оформлять в виде таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных -
3 слайд
Для составления таблицы истинности необходимо:
Выяснить количество строк (2n, где n – количество переменных)
Выяснить количество столбцов (количество переменных + количество логических операций)
Построить таблицу, указывая названия столбцов и возможные наборы значений переменных
Заполнить таблицу истинности по столбцам -
4 слайд
Пример 1.
Построим таблицу истинности для функции
F = (А В) (¬A ¬B)
Переменных: две (А и В), т.е. N = 2 количество строк: 2n=22=4.
С заголовком: 5
Количество столбцов:
2 переменные + 5 операций (,,¬, и ¬).
Итого 7
Порядок операций:
1 5 2 4 3
F = (А В) (¬A ¬B) -
5 слайд
Пример 1. Таблица
0
1
1
1
1
1
0
0
F = (А В) (¬A ¬B)
1
0
1
0
1
1
1
0
0
1
1
0 -
6 слайд
Пример 2.
Построим таблицу истинности для функции
F = X Y ¬Z
Переменных:
три (X, Y и Z), т.е. n = 3 количество строк: 2n=23=8.
С заголовком: 9
Количество столбцов:
3 переменные + 3 операции (,,¬).
Итого 6
Порядок операций:3 2 1
F = X Y ¬Z -
7 слайд
Пример. Таблица
0
0
0
0
1
1
1
1
F = X Y ¬Z
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
0
1
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1
1

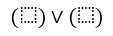
 X2
X2 X2
X2 X2
X2 X2
X2
 X2
X2 X2
X2