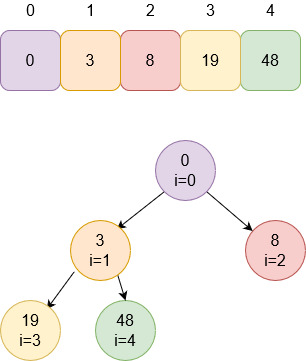
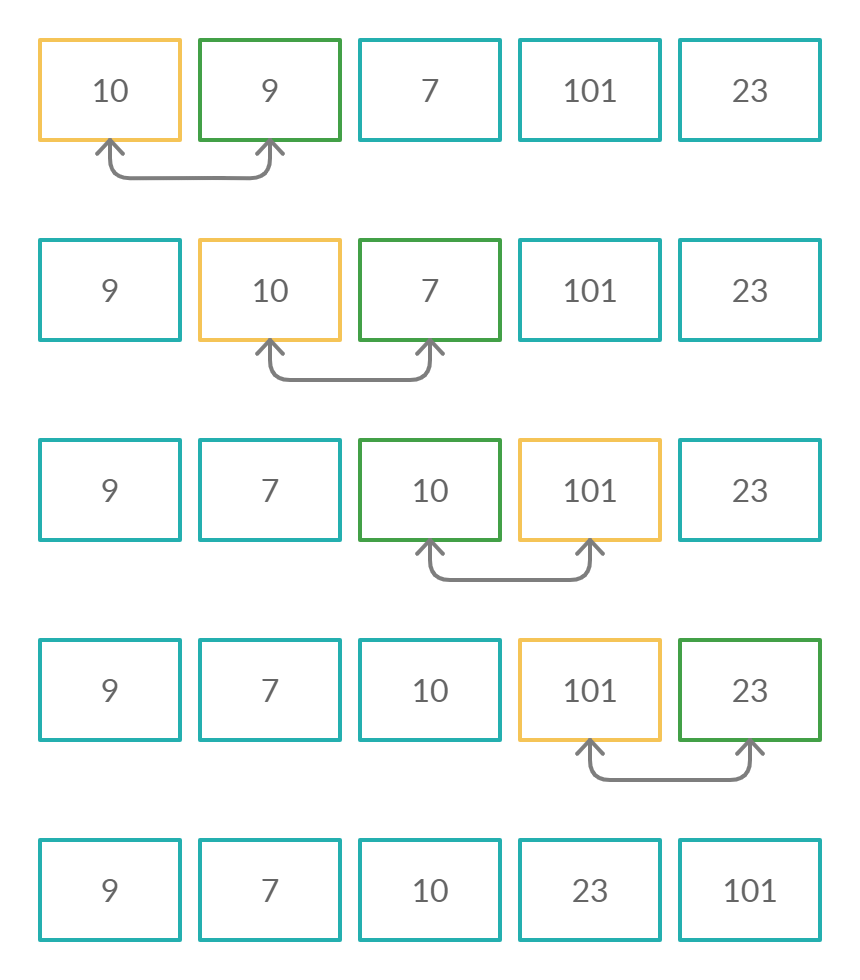
Описание алгоритмов сортировки и сравнение их производительности
Время на прочтение
24 мин
Количество просмотров 589K
Вступление
На эту тему написано уже немало статей. Однако я еще не видел статьи, в которой сравниваются все основные сортировки на большом числе тестов разного типа и размера. Кроме того, далеко не везде выложены реализации и описание набора тестов. Это приводит к тому, что могут возникнуть сомнения в правильности исследования. Однако цель моей работы состоит не только в том, чтобы определить, какие сортировки работают быстрее всего (в целом это и так известно). В первую очередь мне было интересно исследовать алгоритмы, оптимизировать их, чтобы они работали как можно быстрее. Работая над этим, мне удалось придумать эффективную формулу для сортировки Шелла.
Во многом статья посвящена тому, как написать все алгоритмы и протестировать их. Если говорить о самом программировании, то иногда могут возникнуть совершенно неожиданные трудности (во многом благодаря оптимизатору C++). Однако не менее трудно решить, какие именно тесты и в каких количествах нужно сделать. Коды всех алгоритмов, которые выложены в данной статье, написаны мной. Доступны и результаты запусков на всех тестах. Единственное, что я не могу показать — это сами тесты, поскольку они весят почти 140 ГБ. При малейшем подозрении я проверял и код, соответствующий тесту, и сам тест. Надеюсь, что статья Вам понравится.
Описание основных сортировок и их реализация
Я постараюсь кратко и понятно описать сортировки и указать асимптотику, хотя последнее в рамках данной статьи не очень важно (интересно же узнать реальное время работы). О потреблении памяти в дальнейшем ничего писать не буду, замечу только, что сортировки, использующие непростые структуры данных (как, например, сортировка деревом), обычно потребляют ее в больших количествах, а остальные сортировки в худшем случае только создают вспомогательный массив. Также существует понятие стабильности (устойчивости) сортировки. Это значит, что относительный порядок элементов при их равенстве не меняется. Это тоже в рамках данной статьи неважно (в конце концов, можно просто прицепить к элементу его индекс), однако в одном месте пригодится.
Сортировка пузырьком / Bubble sort
Будем идти по массиву слева направо. Если текущий элемент больше следующего, меняем их местами. Делаем так, пока массив не будет отсортирован. Заметим, что после первой итерации самый большой элемент будет находиться в конце массива, на правильном месте. После двух итераций на правильном месте будут стоять два наибольших элемента, и так далее. Очевидно, не более чем после n итераций массив будет отсортирован. Таким образом, асимптотика в худшем и среднем случае – O(n2), в лучшем случае – O(n).
Реализация:
void bubblesort(int* l, int* r) {
int sz = r - l;
if (sz <= 1) return;
bool b = true;
while (b) {
b = false;
for (int* i = l; i + 1 < r; i++) {
if (*i > *(i + 1)) {
swap(*i, *(i + 1));
b = true;
}
}
r--;
}
}Шейкерная сортировка / Shaker sort
(также известна как сортировка перемешиванием и коктейльная сортировка). Заметим, что сортировка пузырьком работает медленно на тестах, в которых маленькие элементы стоят в конце (их еще называют «черепахами»). Такой элемент на каждом шаге алгоритма будет сдвигаться всего на одну позицию влево. Поэтому будем идти не только слева направо, но и справа налево. Будем поддерживать два указателя begin и end, обозначающих, какой отрезок массива еще не отсортирован. На очередной итерации при достижении end вычитаем из него единицу и движемся справа налево, аналогично, при достижении begin прибавляем единицу и двигаемся слева направо. Асимптотика у алгоритма такая же, как и у сортировки пузырьком, однако реальное время работы лучше.
Реализация:
void shakersort(int* l, int* r) {
int sz = r - l;
if (sz <= 1) return;
bool b = true;
int* beg = l - 1;
int* end = r - 1;
while (b) {
b = false;
beg++;
for (int* i = beg; i < end; i++) {
if (*i > *(i + 1)) {
swap(*i, *(i + 1));
b = true;
}
}
if (!b) break;
end--;
for (int* i = end; i > beg; i--) {
if (*i < *(i - 1)) {
swap(*i, *(i - 1));
b = true;
}
}
}
}Сортировка расческой / Comb sort
Еще одна модификация сортировки пузырьком. Для того, чтобы избавиться от «черепах», будем переставлять элементы, стоящие на расстоянии. Зафиксируем его и будем идти слева направо, сравнивая элементы, стоящие на этом расстоянии, переставляя их, если необходимо. Очевидно, это позволит «черепахам» быстро добраться в начало массива. Оптимально изначально взять расстояние равным длине массива, а далее делить его на некоторый коэффициент, равный примерно 1.247. Когда расстояние станет равно единице, выполняется сортировка пузырьком. В лучшем случае асимптотика равна O(nlogn), в худшем – O(n2). Какая асимптотика в среднем мне не очень понятно, на практике похоже на O(nlogn).
Реализация:
void combsort(int* l, int* r) {
int sz = r - l;
if (sz <= 1) return;
double k = 1.2473309;
int step = sz - 1;
while (step > 1) {
for (int* i = l; i + step < r; i++) {
if (*i > *(i + step))
swap(*i, *(i + step));
}
step /= k;
}
bool b = true;
while (b) {
b = false;
for (int* i = l; i + 1 < r; i++) {
if (*i > *(i + 1)) {
swap(*i, *(i + 1));
b = true;
}
}
}
}Об этих сортировках (пузырьком, шейкерной и расческой) также можно почитать здесь.
Сортировка вставками / Insertion sort
Создадим массив, в котором после завершения алгоритма будет лежать ответ. Будем поочередно вставлять элементы из исходного массива так, чтобы элементы в массиве-ответе всегда были отсортированы. Асимптотика в среднем и худшем случае – O(n2), в лучшем – O(n). Реализовывать алгоритм удобнее по-другому (создавать новый массив и реально что-то вставлять в него относительно сложно): просто сделаем так, чтобы отсортирован был некоторый префикс исходного массива, вместо вставки будем менять текущий элемент с предыдущим, пока они стоят в неправильном порядке.
Реализация:
void insertionsort(int* l, int* r) {
for (int *i = l + 1; i < r; i++) {
int* j = i;
while (j > l && *(j - 1) > *j) {
swap(*(j - 1), *j);
j--;
}
}
}Сортировка Шелла / Shellsort
Используем ту же идею, что и сортировка с расческой, и применим к сортировке вставками. Зафиксируем некоторое расстояние. Тогда элементы массива разобьются на классы – в один класс попадают элементы, расстояние между которыми кратно зафиксированному расстоянию. Отсортируем сортировкой вставками каждый класс. В отличие от сортировки расческой, неизвестен оптимальный набор расстояний. Существует довольно много последовательностей с разными оценками. Последовательность Шелла – первый элемент равен длине массива, каждый следующий вдвое меньше предыдущего. Асимптотика в худшем случае – O(n2). Последовательность Хиббарда – 2n — 1, асимптотика в худшем случае – O(n1,5), последовательность Седжвика (формула нетривиальна, можете ее посмотреть по ссылке ниже) — O(n4/3), Пратта (все произведения степеней двойки и тройки) — O(nlog2n). Отмечу, что все эти последовательности нужно рассчитать только до размера массива и запускать от большего от меньшему (иначе получится просто сортировка вставками). Также я провел дополнительное исследование и протестировал разные последовательности вида si = a * si — 1 + k * si — 1 (отчасти это было навеяно эмпирической последовательностью Циура – одной из лучших последовательностей расстояний для небольшого количества элементов). Наилучшими оказались последовательности с коэффициентами a = 3, k = 1/3; a = 4, k = 1/4 и a = 4, k = -1/5.
Несколько полезных ссылок:
Сортировка Шелла в русскоязычной Википедии
Сортировка Шелла в англоязычной Википедии
Статья на Хабре
Реализации:
void shellsort(int* l, int* r) {
int sz = r - l;
int step = sz / 2;
while (step >= 1) {
for (int *i = l + step; i < r; i++) {
int *j = i;
int *diff = j - step;
while (diff >= l && *diff > *j) {
swap(*diff, *j);
j = diff;
diff = j - step;
}
}
step /= 2;
}
}
void shellsorthib(int* l, int* r) {
int sz = r - l;
if (sz <= 1) return;
int step = 1;
while (step < sz) step <<= 1;
step >>= 1;
step--;
while (step >= 1) {
for (int *i = l + step; i < r; i++) {
int *j = i;
int *diff = j - step;
while (diff >= l && *diff > *j) {
swap(*diff, *j);
j = diff;
diff = j - step;
}
}
step /= 2;
}
}
int steps[100];
void shellsortsedgwick(int* l, int* r) {
int sz = r - l;
steps[0] = 1;
int q = 1;
while (steps[q - 1] * 3 < sz) {
if (q % 2 == 0)
steps[q] = 9 * (1 << q) - 9 * (1 << (q / 2)) + 1;
else
steps[q] = 8 * (1 << q) - 6 * (1 << ((q + 1) / 2)) + 1;
q++;
}
q--;
for (; q >= 0; q--) {
int step = steps[q];
for (int *i = l + step; i < r; i++) {
int *j = i;
int *diff = j - step;
while (diff >= l && *diff > *j) {
swap(*diff, *j);
j = diff;
diff = j - step;
}
}
}
}
void shellsortpratt(int* l, int* r) {
int sz = r - l;
steps[0] = 1;
int cur = 1, q = 1;
for (int i = 1; i < sz; i++) {
int cur = 1 << i;
if (cur > sz / 2) break;
for (int j = 1; j < sz; j++) {
cur *= 3;
if (cur > sz / 2) break;
steps[q++] = cur;
}
}
insertionsort(steps, steps + q);
q--;
for (; q >= 0; q--) {
int step = steps[q];
for (int *i = l + step; i < r; i++) {
int *j = i;
int *diff = j - step;
while (diff >= l && *diff > *j) {
swap(*diff, *j);
j = diff;
diff = j - step;
}
}
}
}
void myshell1(int* l, int* r) {
int sz = r - l, q = 1;
steps[0] = 1;
while (steps[q - 1] < sz) {
int s = steps[q - 1];
steps[q++] = s * 4 + s / 4;
}
q--;
for (; q >= 0; q--) {
int step = steps[q];
for (int *i = l + step; i < r; i++) {
int *j = i;
int *diff = j - step;
while (diff >= l && *diff > *j) {
swap(*diff, *j);
j = diff;
diff = j - step;
}
}
}
}
void myshell2(int* l, int* r) {
int sz = r - l, q = 1;
steps[0] = 1;
while (steps[q - 1] < sz) {
int s = steps[q - 1];
steps[q++] = s * 3 + s / 3;
}
q--;
for (; q >= 0; q--) {
int step = steps[q];
for (int *i = l + step; i < r; i++) {
int *j = i;
int *diff = j - step;
while (diff >= l && *diff > *j) {
swap(*diff, *j);
j = diff;
diff = j - step;
}
}
}
}
void myshell3(int* l, int* r) {
int sz = r - l, q = 1;
steps[0] = 1;
while (steps[q - 1] < sz) {
int s = steps[q - 1];
steps[q++] = s * 4 - s / 5;
}
q--;
for (; q >= 0; q--) {
int step = steps[q];
for (int *i = l + step; i < r; i++) {
int *j = i;
int *diff = j - step;
while (diff >= l && *diff > *j) {
swap(*diff, *j);
j = diff;
diff = j - step;
}
}
}
}Сортировка деревом / Tree sort
Будем вставлять элементы в двоичное дерево поиска. После того, как все элементы вставлены достаточно обойти дерево в глубину и получить отсортированный массив. Если использовать сбалансированное дерево, например красно-черное, асимптотика будет равна O(nlogn) в худшем, среднем и лучшем случае. В реализации использован контейнер multiset.
Здесь можно почитать про деревья поиска:
Википедия
Статья на Хабре
И ещё статья на Хабре
Реализация:
void treesort(int* l, int* r) {
multiset<int> m;
for (int *i = l; i < r; i++)
m.insert(*i);
for (int q : m)
*l = q, l++;
}Гномья сортировка / Gnome sort
Алгоритм похож на сортировку вставками. Поддерживаем указатель на текущий элемент, если он больше предыдущего или он первый — смещаем указатель на позицию вправо, иначе меняем текущий и предыдущий элементы местами и смещаемся влево.
Реализация:
void gnomesort(int* l, int* r) {
int *i = l;
while (i < r) {
if (i == l || *(i - 1) <= *i) i++;
else swap(*(i - 1), *i), i--;
}
}Сортировка выбором / Selection sort
На очередной итерации будем находить минимум в массиве после текущего элемента и менять его с ним, если надо. Таким образом, после i-ой итерации первые i элементов будут стоять на своих местах. Асимптотика: O(n2) в лучшем, среднем и худшем случае. Нужно отметить, что эту сортировку можно реализовать двумя способами – сохраняя минимум и его индекс или просто переставляя текущий элемент с рассматриваемым, если они стоят в неправильном порядке. Первый способ оказался немного быстрее, поэтому он и реализован.
Реализация:
void selectionsort(int* l, int* r) {
for (int *i = l; i < r; i++) {
int minz = *i, *ind = i;
for (int *j = i + 1; j < r; j++) {
if (*j < minz) minz = *j, ind = j;
}
swap(*i, *ind);
}
}Пирамидальная сортировка / Heapsort
Развитие идеи сортировки выбором. Воспользуемся структурой данных «куча» (или «пирамида», откуда и название алгоритма). Она позволяет получать минимум за O(1), добавляя элементы и извлекая минимум за O(logn). Таким образом, асимптотика O(nlogn) в худшем, среднем и лучшем случае. Реализовывал кучу я сам, хотя в С++ и есть контейнер priority_queue, поскольку этот контейнер довольно медленный.
Почитать про кучу можно здесь:
Википедия
Статья на Хабре
Реализация:
template <class T>
class heap {
public:
int size() {
return n;
}
int top() {
return h[0];
}
bool empty() {
return n == 0;
}
void push(T a) {
h.push_back(a);
SiftUp(n);
n++;
}
void pop() {
n--;
swap(h[n], h[0]);
h.pop_back();
SiftDown(0);
}
void clear() {
h.clear();
n = 0;
}
T operator [] (int a) {
return h[a];
}
private:
vector<T> h;
int n = 0;
void SiftUp(int a) {
while (a) {
int p = (a - 1) / 2;
if (h[p] > h[a]) swap(h[p], h[a]);
else break;
a--; a /= 2;
}
}
void SiftDown(int a) {
while (2 * a + 1 < n) {
int l = 2 * a + 1, r = 2 * a + 2;
if (r == n) {
if (h[l] < h[a]) swap(h[l], h[a]);
break;
}
else if (h[l] <= h[r]) {
if (h[l] < h[a]) {
swap(h[l], h[a]);
a = l;
}
else break;
}
else if (h[r] < h[a]) {
swap(h[r], h[a]);
a = r;
}
else break;
}
}
};
void heapsort(int* l, int* r) {
heap<int> h;
for (int *i = l; i < r; i++) h.push(*i);
for (int *i = l; i < r; i++) {
*i = h.top();
h.pop();
}
}Быстрая сортировка / Quicksort
Выберем некоторый опорный элемент. После этого перекинем все элементы, меньшие его, налево, а большие – направо. Рекурсивно вызовемся от каждой из частей. В итоге получим отсортированный массив, так как каждый элемент меньше опорного стоял раньше каждого большего опорного. Асимптотика: O(nlogn) в среднем и лучшем случае, O(n2). Наихудшая оценка достигается при неудачном выборе опорного элемента. Моя реализация этого алгоритма совершенно стандартна, идем одновременно слева и справа, находим пару элементов, таких, что левый элемент больше опорного, а правый меньше, и меняем их местами. Помимо чистой быстрой сортировки, участвовала в сравнении и сортировка, переходящая при малом количестве элементов на сортировку вставками. Константа подобрана тестированием, а сортировка вставками — наилучшая сортировка, подходящая для этой задачи (хотя не стоит из-за этого думать, что она самая быстрая из квадратичных).
Реализация:
void quicksort(int* l, int* r) {
if (r - l <= 1) return;
int z = *(l + (r - l) / 2);
int* ll = l, *rr = r - 1;
while (ll <= rr) {
while (*ll < z) ll++;
while (*rr > z) rr--;
if (ll <= rr) {
swap(*ll, *rr);
ll++;
rr--;
}
}
if (l < rr) quicksort(l, rr + 1);
if (ll < r) quicksort(ll, r);
}
void quickinssort(int* l, int* r) {
if (r - l <= 32) {
insertionsort(l, r);
return;
}
int z = *(l + (r - l) / 2);
int* ll = l, *rr = r - 1;
while (ll <= rr) {
while (*ll < z) ll++;
while (*rr > z) rr--;
if (ll <= rr) {
swap(*ll, *rr);
ll++;
rr--;
}
}
if (l < rr) quickinssort(l, rr + 1);
if (ll < r) quickinssort(ll, r);
}Сортировка слиянием / Merge sort
Сортировка, основанная на парадигме «разделяй и властвуй». Разделим массив пополам, рекурсивно отсортируем части, после чего выполним процедуру слияния: поддерживаем два указателя, один на текущий элемент первой части, второй – на текущий элемент второй части. Из этих двух элементов выбираем минимальный, вставляем в ответ и сдвигаем указатель, соответствующий минимуму. Слияние работает за O(n), уровней всего logn, поэтому асимптотика O(nlogn). Эффективно заранее создать временный массив и передать его в качестве аргумента функции. Эта сортировка рекурсивна, как и быстрая, а потому возможен переход на квадратичную при небольшом числе элементов.
Реализация:
void merge(int* l, int* m, int* r, int* temp) {
int *cl = l, *cr = m, cur = 0;
while (cl < m && cr < r) {
if (*cl < *cr) temp[cur++] = *cl, cl++;
else temp[cur++] = *cr, cr++;
}
while (cl < m) temp[cur++] = *cl, cl++;
while (cr < r) temp[cur++] = *cr, cr++;
cur = 0;
for (int* i = l; i < r; i++)
*i = temp[cur++];
}
void _mergesort(int* l, int* r, int* temp) {
if (r - l <= 1) return;
int *m = l + (r - l) / 2;
_mergesort(l, m, temp);
_mergesort(m, r, temp);
merge(l, m, r, temp);
}
void mergesort(int* l, int* r) {
int* temp = new int[r - l];
_mergesort(l, r, temp);
delete temp;
}
void _mergeinssort(int* l, int* r, int* temp) {
if (r - l <= 32) {
insertionsort(l, r);
return;
}
int *m = l + (r - l) / 2;
_mergeinssort(l, m, temp);
_mergeinssort(m, r, temp);
merge(l, m, r, temp);
}
void mergeinssort(int* l, int* r) {
int* temp = new int[r - l];
_mergeinssort(l, r, temp);
delete temp;
}Сортировка подсчетом / Counting sort
Создадим массив размера r – l, где l – минимальный, а r – максимальный элемент массива. После этого пройдем по массиву и подсчитаем количество вхождений каждого элемента. Теперь можно пройти по массиву значений и выписать каждое число столько раз, сколько нужно. Асимптотика – O(n + r — l). Можно модифицировать этот алгоритм, чтобы он стал стабильным: для этого определим место, где должно стоять очередное число (это просто префиксные суммы в массиве значений) и будем идти по исходному массиву слева направо, ставя элемент на правильное место и увеличивая позицию на 1. Эта сортировка не тестировалась, поскольку большинство тестов содержало достаточно большие числа, не позволяющие создать массив требуемого размера. Однако она, тем не менее, пригодилась.
Блочная сортировка / Bucket sort
(также известна как корзинная и карманная сортировка). Пусть l – минимальный, а r – максимальный элемент массива. Разобьем элементы на блоки, в первом будут элементы от l до l + k, во втором – от l + k до l + 2k и т.д., где k = (r – l) / количество блоков. В общем-то, если количество блоков равно двум, то данный алгоритм превращается в разновидность быстрой сортировки. Асимптотика этого алгоритма неясна, время работы зависит и от входных данных, и от количества блоков. Утверждается, что на удачных данных время работы линейно. Реализация этого алгоритма оказалась одной из самых трудных задач. Можно сделать это так: просто создавать новые массивы, рекурсивно их сортировать и склеивать. Однако такой подход все же довольно медленный и меня не устроил. В эффективной реализации используется несколько идей:
1) Не будем создавать новых массивов. Для этого воспользуемся техникой сортировки подсчетом – подсчитаем количество элементов в каждом блоке, префиксные суммы и, таким образом, позицию каждого элемента в массиве.
2) Не будем запускаться из пустых блоков. Занесем индексы непустых блоков в отдельный массив и запустимся только от них.
3) Проверим, отсортирован ли массив. Это не ухудшит время работы, так как все равно нужно сделать проход с целью нахождения минимума и максимума, однако позволит алгоритму ускориться на частично отсортированных данных, ведь элементы вставляются в новые блоки в том же порядке, что и в исходном массиве.
4) Поскольку алгоритм получился довольно громоздким, при небольшом количестве элементов он крайне неэффективен. До такой степени, что переход на сортировку вставками ускоряет работу примерно в 10 раз.
Осталось только понять, какое количество блоков нужно выбрать. На рандомизированных тестах мне удалось получить следующую оценку: 1500 блоков для 107 элементов и 3000 для 108. Подобрать формулу не удалось – время работы ухудшалось в несколько раз.
Реализация:
void _newbucketsort(int* l, int* r, int* temp) {
if (r - l <= 64) {
insertionsort(l, r);
return;
}
int minz = *l, maxz = *l;
bool is_sorted = true;
for (int *i = l + 1; i < r; i++) {
minz = min(minz, *i);
maxz = max(maxz, *i);
if (*i < *(i - 1)) is_sorted = false;
}
if (is_sorted) return;
int diff = maxz - minz + 1;
int numbuckets;
if (r - l <= 1e7) numbuckets = 1500;
else numbuckets = 3000;
int range = (diff + numbuckets - 1) / numbuckets;
int* cnt = new int[numbuckets + 1];
for (int i = 0; i <= numbuckets; i++)
cnt[i] = 0;
int cur = 0;
for (int* i = l; i < r; i++) {
temp[cur++] = *i;
int ind = (*i - minz) / range;
cnt[ind + 1]++;
}
int sz = 0;
for (int i = 1; i <= numbuckets; i++)
if (cnt[i]) sz++;
int* run = new int[sz];
cur = 0;
for (int i = 1; i <= numbuckets; i++)
if (cnt[i]) run[cur++] = i - 1;
for (int i = 1; i <= numbuckets; i++)
cnt[i] += cnt[i - 1];
cur = 0;
for (int *i = l; i < r; i++) {
int ind = (temp[cur] - minz) / range;
*(l + cnt[ind]) = temp[cur];
cur++;
cnt[ind]++;
}
for (int i = 0; i < sz; i++) {
int r = run[i];
if (r != 0) _newbucketsort(l + cnt[r - 1], l + cnt[r], temp);
else _newbucketsort(l, l + cnt[r], temp);
}
delete run;
delete cnt;
}
void newbucketsort(int* l, int* r) {
int *temp = new int[r - l];
_newbucketsort(l, r, temp);
delete temp;
}Поразрядная сортировка / Radix sort
(также известна как цифровая сортировка). Существует две версии этой сортировки, в которых, на мой взгляд, мало общего, кроме идеи воспользоваться представлением числа в какой-либо системе счисления (например, двоичной).
LSD (least significant digit):
Представим каждое число в двоичном виде. На каждом шаге алгоритма будем сортировать числа таким образом, чтобы они были отсортированы по первым k * i битам, где k – некоторая константа. Из данного определения следует, что на каждом шаге достаточно стабильно сортировать элементы по новым k битам. Для этого идеально подходит сортировка подсчетом (необходимо 2k памяти и времени, что немного при удачном выборе константы). Асимптотика: O(n), если считать, что числа фиксированного размера (а в противном случае нельзя было бы считать, что сравнение двух чисел выполняется за единицу времени). Реализация довольно проста.
Реализация:
int digit(int n, int k, int N, int M) {
return (n >> (N * k) & (M - 1));
}
void _radixsort(int* l, int* r, int N) {
int k = (32 + N - 1) / N;
int M = 1 << N;
int sz = r - l;
int* b = new int[sz];
int* c = new int[M];
for (int i = 0; i < k; i++) {
for (int j = 0; j < M; j++)
c[j] = 0;
for (int* j = l; j < r; j++)
c[digit(*j, i, N, M)]++;
for (int j = 1; j < M; j++)
c[j] += c[j - 1];
for (int* j = r - 1; j >= l; j--)
b[--c[digit(*j, i, N, M)]] = *j;
int cur = 0;
for (int* j = l; j < r; j++)
*j = b[cur++];
}
delete b;
delete c;
}
void radixsort(int* l, int* r) {
_radixsort(l, r, 8);
}MSD (most significant digit):
На самом деле, некоторая разновидность блочной сортировки. В один блок будут попадать числа с равными k битами. Асимптотика такая же, как и у LSD версии. Реализация очень похожа на блочную сортировку, но проще. В ней используется функция digit, определенная в реализации LSD версии.
Реализация:
void _radixsortmsd(int* l, int* r, int N, int d, int* temp) {
if (d == -1) return;
if (r - l <= 32) {
insertionsort(l, r);
return;
}
int M = 1 << N;
int* cnt = new int[M + 1];
for (int i = 0; i <= M; i++)
cnt[i] = 0;
int cur = 0;
for (int* i = l; i < r; i++) {
temp[cur++] = *i;
cnt[digit(*i, d, N, M) + 1]++;
}
int sz = 0;
for (int i = 1; i <= M; i++)
if (cnt[i]) sz++;
int* run = new int[sz];
cur = 0;
for (int i = 1; i <= M; i++)
if (cnt[i]) run[cur++] = i - 1;
for (int i = 1; i <= M; i++)
cnt[i] += cnt[i - 1];
cur = 0;
for (int *i = l; i < r; i++) {
int ind = digit(temp[cur], d, N, M);
*(l + cnt[ind]) = temp[cur];
cur++;
cnt[ind]++;
}
for (int i = 0; i < sz; i++) {
int r = run[i];
if (r != 0) _radixsortmsd(l + cnt[r - 1], l + cnt[r], N, d - 1, temp);
else _radixsortmsd(l, l + cnt[r], N, d - 1, temp);
}
delete run;
delete cnt;
}
void radixsortmsd(int* l, int* r) {
int* temp = new int[r - l];
_radixsortmsd(l, r, 8, 3, temp);
delete temp;
}Битонная сортировка / Bitonic sort:
Идея данного алгоритма заключается в том, что исходный массив преобразуется в битонную последовательность – последовательность, которая сначала возрастает, а потом убывает. Ее можно эффективно отсортировать следующим образом: разобьем массив на две части, создадим два массива, в первый добавим все элементы, равные минимуму из соответственных элементов каждой из двух частей, а во второй – равные максимуму. Утверждается, что получатся две битонные последовательности, каждую из которых можно рекурсивно отсортировать тем же образом, после чего можно склеить два массива (так как любой элемент первого меньше или равен любого элемента второго). Для того, чтобы преобразовать исходный массив в битонную последовательность, сделаем следующее: если массив состоит из двух элементов, можно просто завершиться, иначе разделим массив пополам, рекурсивно вызовем от половинок алгоритм, после чего отсортируем первую часть по порядку, вторую в обратном порядке и склеим. Очевидно, получится битонная последовательность. Асимптотика: O(nlog2n), поскольку при построении битонной последовательности мы использовали сортировку, работающую за O(nlogn), а всего уровней было logn. Также заметим, что размер массива должен быть равен степени двойки, так что, возможно, придется его дополнять фиктивными элементами (что не влияет на асимптотику).
Реализация:
void bitseqsort(int* l, int* r, bool inv) {
if (r - l <= 1) return;
int *m = l + (r - l) / 2;
for (int *i = l, *j = m; i < m && j < r; i++, j++) {
if (inv ^ (*i > *j)) swap(*i, *j);
}
bitseqsort(l, m, inv);
bitseqsort(m, r, inv);
}
void makebitonic(int* l, int* r) {
if (r - l <= 1) return;
int *m = l + (r - l) / 2;
makebitonic(l, m);
bitseqsort(l, m, 0);
makebitonic(m, r);
bitseqsort(m, r, 1);
}
void bitonicsort(int* l, int* r) {
int n = 1;
int inf = *max_element(l, r) + 1;
while (n < r - l) n *= 2;
int* a = new int[n];
int cur = 0;
for (int *i = l; i < r; i++)
a[cur++] = *i;
while (cur < n) a[cur++] = inf;
makebitonic(a, a + n);
bitseqsort(a, a + n, 0);
cur = 0;
for (int *i = l; i < r; i++)
*i = a[cur++];
delete a;
}Timsort
Гибридная сортировка, совмещающая сортировку вставками и сортировку слиянием. Разобьем элементы массива на несколько подмассивов небольшого размера, при этом будем расширять подмассив, пока элементы в нем отсортированы. Отсортируем подмассивы сортировкой вставками, пользуясь тем, что она эффективно работает на отсортированных массивах. Далее будем сливать подмассивы как в сортировке слиянием, беря их примерно равного размера (иначе время работы приблизится к квадратичному). Для этого удобного хранить подмассивы в стеке, поддерживая инвариант — чем дальше от вершины, тем больше размер, и сливать подмассивы на верхушке только тогда, когда размер третьего по отдаленности от вершины подмассива больше или равен сумме их размеров. Асимптотика: O(n) в лучшем случае и O(nlogn) в среднем и худшем случае. Реализация нетривиальна, твердой уверенности в ней у меня нет, однако время работы она показала довольно неплохое и согласующееся с моими представлениями о том, как должна работать эта сортировка.
Подробнее timsort описан здесь:
Здесь
Здесь
Реализация:
void _timsort(int* l, int* r, int* temp) {
int sz = r - l;
if (sz <= 64) {
insertionsort(l, r);
return;
}
int minrun = sz, f = 0;
while (minrun >= 64) {
f |= minrun & 1;
minrun >>= 1;
}
minrun += f;
int* cur = l;
stack<pair<int, int*>> s;
while (cur < r) {
int* c1 = cur;
while (c1 < r - 1 && *c1 <= *(c1 + 1)) c1++;
int* c2 = cur;
while (c2 < r - 1 && *c2 >= *(c2 + 1)) c2++;
if (c1 >= c2) {
c1 = max(c1, cur + minrun - 1);
c1 = min(c1, r - 1);
insertionsort(cur, c1 + 1);
s.push({ c1 - cur + 1, cur });
cur = c1 + 1;
}
else {
c2 = max(c2, cur + minrun - 1);
c2 = min(c2, r - 1);
reverse(cur, c2 + 1);
insertionsort(cur, c2 + 1);
s.push({ c2 - cur + 1, cur });
cur = c2 + 1;
}
while (s.size() >= 3) {
pair<int, int*> x = s.top();
s.pop();
pair<int, int*> y = s.top();
s.pop();
pair<int, int*> z = s.top();
s.pop();
if (z.first >= x.first + y.first && y.first >= x.first) {
s.push(z);
s.push(y);
s.push(x);
break;
}
else if (z.first >= x.first + y.first) {
merge(y.second, x.second, x.second + x.first, temp);
s.push(z);
s.push({ x.first + y.first, y.second });
}
else {
merge(z.second, y.second, y.second + y.first, temp);
s.push({ z.first + y.first, z.second });
s.push(x);
}
}
}
while (s.size() != 1) {
pair<int, int*> x = s.top();
s.pop();
pair<int, int*> y = s.top();
s.pop();
if (x.second < y.second) swap(x, y);
merge(y.second, x.second, x.second + x.first, temp);
s.push({ y.first + x.first, y.second });
}
}
void timsort(int* l, int* r) {
int* temp = new int[r - l];
_timsort(l, r, temp);
delete temp;
}Тестирование
Железо и система
Процессор: Intel Core i7-3770 CPU 3.40 GHz
ОЗУ: 8 ГБ
Тестирование проводилось на почти чистой системе Windows 10 x64, установленной за несколько дней до запуска. Использованная IDE – Microsoft Visual Studio 2015.
Тесты
Все тесты поделены на четыре группы. Первая группа – массив случайных чисел по разным модулям (10, 1000, 105, 107 и 109). Вторая группа – массив, разбивающийся на несколько отсортированных подмассивов. Фактически брался массив случайных чисел по модулю 109, а далее отсортировывались подмассивы размера, равного минимуму из длины оставшегося суффикса и случайного числа по модулю некоторой константы. Последовательность констант – 10, 100, 1000 и т.д. вплоть до размера массива. Третья группа – изначально отсортированный массив случайных чисел с некоторым числом «свопов» — перестановок двух случайных элементов. Последовательность количеств свопов такая же, как и в предыдущей группе. Наконец, последняя группа состоит из нескольких тестов с полностью отсортированным массивом (в прямом и обратном порядке), нескольких тестов с исходным массивом натуральных чисел от 1 до n, в котором несколько чисел заменены на случайное, и тестов с большим количеством повторений одного элемента (10%, 25%, 50%, 75% и 90%). Таким образом, тесты позволяют посмотреть, как сортировки работают на случайных и частично отсортированных массивах, что выглядит наиболее существенным. Четвертая группа во многом направлена против сортировок с линейным временем работы, которые любят последовательности случайных чисел. В конце статьи есть ссылка на файл, в котором подробно описаны все тесты.
Размер входных данных
Было бы довольно глупо сравнивать, например, сортировку с линейным временем работы и квадратичную, и запускать их на тестах одного размера. Поэтому каждая из групп тестов делится еще на четыре группы, размера 105, 106, 107и 108 элементов. Сортировки были разбиты на три группы, в первой – квадратичные (сортировка пузырьком, вставками, выбором, шейкерная и гномья), во второй – нечто среднее между логарифмическим временем и квадратом, (битонная, несколько видов сортировки Шелла и сортировка деревом), в третьей все остальные. Кого-то, возможно, удивит, что сортировка деревом попала не в третью группу, хотя ее асимптотика и O(nlogn), но, к сожалению, ее константа очень велика. Сортировки первой группы тестировались на тестах с 105элементов, второй группы – на тестах с 106и 107, третьей – на тестах с 107и 108. Именно такие размеры данных позволяют как-то увидеть рост времени работы, при меньших размерах слишком велика погрешность, при больших алгоритм работает слишком долго (или же недостаток оперативной памяти). С первой группой я не стал заморачиваться, чтобы не нарушать десятикратное увеличение (104 элементов для квадратичных сортировок слишком мало), в конце концов, сами по себе они представляют мало интереса.
Как проводилось тестирование
На каждом тесте было производилось 20 запусков, итоговое время работы – среднее по получившимся значениям. Почти все результаты были получены после одного запуска программы, однако из-за нескольких ошибок в коде и системных глюков (все же тестирование продолжалось почти неделю чистого времени) некоторые сортировки и тесты пришлось впоследствии перетестировать.
Тонкости реализации
Возможно, кого-то удивит, что в реализации самого процесса тестирования я не использовал указатели на функции, что сильно сократило бы код. Оказалось, что это заметно замедляет работу алгоритма (примерно на 5-10%). Поэтому я использовал отдельный вызов каждой функции (это, конечно, не отразилось бы на относительной скорости, но… все же хочется улучшить и абсолютную). По той же причине были заменены векторы на обычные массивы, не были использованы шаблоны и функции-компараторы. Все это более актуально для промышленного использования алгоритма, нежели его тестирования.
Результаты
Все результаты доступны в нескольких видах – три диаграммы (гистограмма, на которой видно изменение скорости при переходе к следующему ограничению на одном типе тестов, график, изображающий то же самое, но иногда более наглядно, и гистограмма, на которой видно, какая сортировка лучше всего работает на каком-то типе тестов) и таблицы, на которых они основаны. Третья группа была разделена еще на три части, а то мало что было бы понятно. Впрочем, и так далеко не все диаграммы удачны (в полезности третьего типа диаграмм я вообще сильно сомневаюсь), но, надеюсь, каждый сможет найти наиболее подходящую для понимания.
Поскольку картинок очень много, они скрыты спойлерами. Немного комментариев по поводу обозначений. Сортировки названы так, как выше, если это сортировка Шелла, то в скобочках указан автор последовательности, к названиям сортировок, переходящих на сортировку вставками, приписано Ins (для компактности). В диаграммах у второй группы тестов обозначена возможная длина отсортированных подмассивов, у третьей группы — количество свопов, у четвертой — количество замен. Общий результат рассчитывался как среднее по четырем группам.
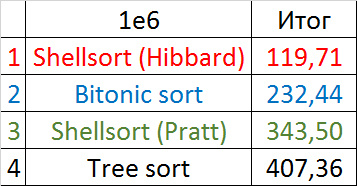
Первая группа сортировок
Массив случайных чисел
Совсем скучные результаты, даже частичная отсортированность при небольшом модуле почти незаметна.
Частично отсортированный массив
Уже гораздо интереснее. Обменные сортировки наиболее бурно отреагировали, шейкерная даже обогнала гномью. Сортировка вставками ускорилась только под самый конец. Сортировка выбором, конечно, работает совершенно также.
Свопы
Здесь наконец-то проявила себя сортировка вставками, хотя рост скорости у шейкерной примерно такой же. Здесь проявилась слабость сортировки пузырьком — достаточно одного свопа, перемещающего маленький элемент в конец, и она уже работает медленно. Сортировка выбором оказалась почти в конце.
Изменения в перестановке
Группа почти ничем не отличается от предыдущей, поэтому результаты похожи. Однако сортировка пузырьком вырывается вперед, так как случайный элемент, вставленный в массив, скорее всего будет больше всех остальных, то есть за одну итерацию переместится в конец. Сортировка выбором стала аутсайдером.
Повторы
Здесь все сортировки (кроме, конечно, сортировки выбором) работали почти одинаково, ускоряясь по мере увеличении количества повторов.
Итоговые результаты
За счет своего абсолютного безразличия к массиву, сортировка выбором, работавшая быстрее всех на случайных данных, все же проиграла сортировке вставками. Гномья сортировка оказалась заметно хуже последней, из-за чего ее практическое применение сомнительно. Шейкерная и пузырьковая сортировки оказались медленнее всех.
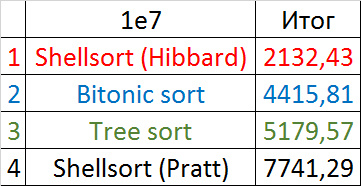
Вторая группа сортировок
Массив случайных чисел
Сортировка Шелла с последовательностью Пратта ведет себя совсем странно, остальные более менее ясно. Сортировка деревом любит частично отсортированные массивы, но не любит повторов, возможно, поэтому самое худшее время работы именно посередине.
Все как прежде, только Шелл с Праттом усилился на второй группе из-за отсортированности. Также становится заметным влияние асимптотики — сортировка деревом оказывается на втором месте, в отличие от группы с меньшим числом элементов.
Частично отсортированный массив
Здесь понятным образом ведут себя все сортировки, кроме Шелла с Хиббардом, который почему-то не сразу начинает ускоряться.
Здесь все, в общем, как и прежде. Даже асимптотика сортировки деревом не помогла ей вырваться с последнего места.
Свопы
Здесь заметно, что у сортировок Шелла большая зависимость от частичной отсортированности, так как они ведут себя практически линейно, а остальные две только сильно падают на последних группах.
Изменения в перестановке
Здесь все похоже на предыдущую группу.
Повторы
Опять все сортировки продемонстрировали удивительную сбалансированность, даже битонная, которая, казалось бы, почти не зависит от массива.
Ничего интересного.
Итоговые результаты
Убедительное первое место заняла сортировка Шелла по Хиббарду, не уступив ни в одной промежуточной группе. Возможно, стоило ее отправить в первую группу сортировок, но… она слишком слаба для этого, да и тогда почти никого не было бы в группе. Битонная сортировка довольно уверенно заняла второе место. Третье место при миллионе элементах заняла другая сортировка Шелла, а при десяти миллионах сортировка деревом (асимптотика сказалась). Стоит обратить внимание, что при десятикратном увеличении размера входных данных все алгоритмы, кроме древесной сортировки, замедлились почти в 20 раз, а последняя всего лишь в 13.
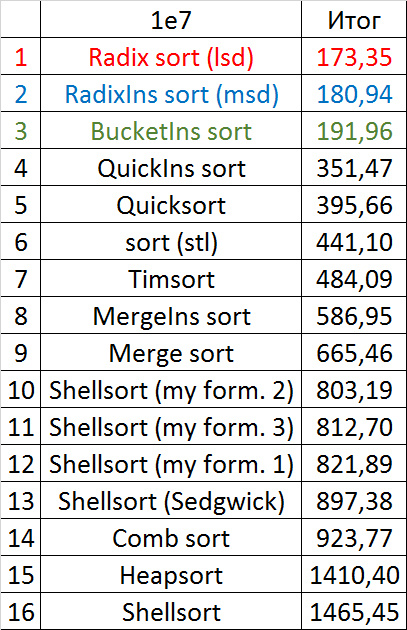
Третья группа сортировок
Массив случайных чисел
Почти все сортировки этой группы имеют почти одинаковую динамику. Почему же почти все сортировки ускоряются, когда массив частично отсортирован? Обменные сортировки работают быстрее потому, что надо делать меньше обменов, в сортировке Шелла выполняется сортировка вставками, которая сильно ускоряется на таких массивах, в пирамидальной сортировке при вставке элементов сразу завершается просеивание, в сортировке слиянием выполняется в лучшем случае вдвое меньше сравнений. Блочная сортировка работает тем лучше, чем меньше разность между минимальным и максимальным элементом. Принципиально отличается только поразрядная сортировка, которой все это безразлично. LSD-версия работает тем лучше, чем больший модуль. Динамика MSD-версия мне не ясна, то, что она сработала быстрее чем LSD удивило.
Частично отсортированный массив
Здесь все тоже довольно понятно. Стало заметен алгоритм Timsort, на него отсортированность действует сильнее, чем на остальные. Это позволило этому алгоритму почти сравняться с оптимизированной версией быстрой сортировки. Блочная сортировка, несмотря на улучшение времени работы при частичной отсортированности, не смогла обогнать поразрядную сортировку.
Свопы
Здесь очень хорошо сработали быстрые сортировки. Это, скорее всего, объясняется удачным выбором опорного элемента. Все остальное почти также, как и в предыдущей группе.
Изменения в перестановке
Мне удалось достичь желаемой цели — поразрядная сортировка упала даже ниже адаптированной быстрой. Блочная сортировка оказалась лучше остальных. Еще почему-то timsort обогнал встроенную сортировку C++, хотя в предыдущей группе был ниже.
Повторы
Здесь все довольно тоскливо, все сортировки работают с одинаковой динамикой (кроме линейных). Из необычного можно заметить, что сортировка слиянием упала ниже сортировки Шелла.
Итоговые результаты
Несмотря на мои старания, LSD-версия поразрядной сортировки все-таки заняла первое место и при 107, и при 108 элементов. Также она продемонстрировала почти линейный рост времени. Единственная ее замеченная мной слабость — плохая работа с перестановками. MSD-версия сработала немного хуже, в первую очередь из-за большого количества тестов, состоящих из случайных чисел по модулю 109. Реализацией блочной сортировки я остался доволен, несмотря на громоздкость, она показало неплохой результат. Кстати, я слишком поздно это заметил, она не до конца соптимизирована, можно еще отдельно создавать массивы run и cnt, чтобы не тратить время на их удаление. Далее уверенно заняли места различные версии быстрой сортировки. Timsort-у не удалось, на мой взгляд, оказать им серьезную конкуренцию, хотя он не сильно отстал. Далее по скорости идут сортировки слиянием, после них — мои версии сортировки Шелла. Лучше всего оказалась последовательность s * 3 + s / 3, где s — предыдущий элемент последовательности. Далее идет единственное расхождение в двух таблицах — сортировка расческой оказалась лучше при большем числе элементов, чем сортировка Шелла с последовательностью Седжвика. И за последнее место боролись пирамидальная сортировка и оригинальная сортировка Шелла.
Выиграла последняя. Кстати, сортировка Шелла, как я потом проверил, очень плохо работает на тестах размера 2n, так что ей просто повезло, что она попала в первую группу.
Если говорить о практическом применении, то хороша поразрядная сортировка (особенно lsd-версия), она стабильна, проста в реализации и очень быстра, однако не основана на сравнениях. Из основанных на сравнениях сортировок лучше всего смотрится быстрая сортировка. Ее недостатки — неустойчивость и квадратичное время работы на неудачных входных данных (пусть они и могут встретиться только при намеренном создании теста). Но с этим можно бороться, например, выбирая опорный элемент по какому-нибудь другому принципу, или же переходя на другую сортировку при неудаче (например, introsort, который, если не ошибаюсь, и реализован в С++). Timsort лишен этих недостатков, лучше работает на сильно отсортированных данных, но все же медленнее в целом и гораздо сложнее пишется. Остальные сортировки на данный момент, пожалуй, не очень практичны. Кроме, конечно, сортировки вставками, которую весьма удачно иногда можно вставить в алгоритм.
Заключение
Должен отметить, что не все известные сортировки приняли участие в тестировании, например, была пропущена плавная сортировка (мне просто не удалось ее адекватно реализовать). Впрочем, не думаю, что это большая потеря, эта сортировка очень громоздкая и медленная, как можно видеть, например, из этой статьи: habrahabr.ru/post/133996 Еще можно исследовать сортировки на распараллеливание, но, во-первых, у меня нет опыта, во-вторых, результаты, которые получались, крайне нестабильны, очень велико влияние системы.
Здесь можно посмотреть результаты всех запусков, а также некоторые вспомогательные тестирования: ссылка на документ.
Здесь можно посмотреть код всего проекта
Реализации алгоритмов с векторами остались, но их корректность и хорошую работу не гарантирую. Проще взять коды функций из статьи и переделать. Генераторы тестов тоже могут не соответствовать действительности, на самом деле такой вид они приняли уже после создания тестов, когда нужно было сделать программу более компактной.
В общем, я доволен проделанной работой, надеюсь, что Вам было интересно.
Что такое сортировка и зачем она нужна
Сортировка распределяет элементы в порядке, удобном для работы. Если отсортировать массив чисел в порядке убывания, то первый элемент всегда будет наибольшим, а последний наименьшим. Поэтому желательно хранить информацию упорядочено, чтобы было проще проводить над ней операции.
В данной статье вы научитесь разным техникам сортировок на языке С++. Мы затронем 7 видов:
- Пузырьковая сортировка (Bubble sort);
- Сортировка выбором (Selection sort);
- Сортировка вставками (Insertion sort);
- Быстрая сортировка (Quick sort);
- Сортировка слиянием (Merge sort);
- Сортировка Шелла (Shell sort);
- Сортировка кучей (Heap sort).
Знание этих техник поможет получить работу. На площадке LeetCode содержится более 200 задач, связанных с сортировками. 19 из них входят в топ частых вопросов на собеседованиях по алгоритмам.
1. Пузырьковая сортировка
В пузырьковой сортировке каждый элемент сравнивается со следующим. Если два таких элемента не стоят в нужном порядке, то они меняются между собой местами. В конце каждой итерации (далее называем их проходами) наибольший/наименьший элемент ставится в конец списка.
Прежде чем писать код, разберем сортировку визуально на примере массива из пяти элементов. Отсортируем его в порядке возрастания.
Проход №1
Оранжевым отмечаются элементы, которые нужно
поменять местами. Зеленые уже стоят в нужном порядке.
Наибольший элемент — число 48 — оказался в конце
списка.
Проход №2
Наибольший элемент уже занимает место в конце
массива. Чтобы поставить следующее число по убыванию, можно пройтись лишь до 4-й позиции, а не пятой.
Проход №3
Проход №4
После четвертого прохода получаем
отсортированный массив.
Функция сортировки в качестве параметров будет принимать указатель на массив и его размер. Функцией swap() элементы
меняются местами друг с другом:
#include <iostream>
using namespace std;
void bubbleSort(int list[], int listLength)
{
while(listLength--)
{
bool swapped = false;
for(int i = 0; i < listLength; i++)
{
if(list[i] > list[i + 1])
{
swap(list[i], list[i + 1]);
swapped = true;
}
}
if(swapped == false)
break;
}
}
int main()
{
int list[5] = {3,19,8,0,48};
cout << "Input array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
bubbleSort(list, 5);
cout << "Sorted array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность в лучшем случае: O(n).
Сложность в среднем случае: O(n2).
Сложность в худшем случае: O(n2).
2. Сортировка выбором
Ищем наименьшее значение в массиве и ставим
его на позицию, откуда начали проход. Потом двигаемся на следующую позицию.
Возьмем тот же массив из пяти элементов и отсортируем его.
Проход №1
Зеленым отмечается наименьший элемент в
подмассиве — он ставится в начало списка.
Проход №2
Число 4 — наименьшее в оставшейся части массива.
Перемещаем четверку на вторую позицию после числа 0.
Проход №3
Проход №4
Напишем функцию поиска наименьшего элемента и
используем ее в сортировке:
int findSmallestPosition(int list[], int startPosition, int listLength)
{
int smallestPosition = startPosition;
for(int i = startPosition; i < listLength; i++)
{
if(list[i] < list[smallestPosition])
smallestPosition = i;
}
return smallestPosition;
}
#include <iostream>
using namespace std;
int findSmallestPosition(int list[], int startPosition, int listLength)
{
int smallestPosition = startPosition;
for(int i = startPosition; i < listLength; i++)
{
if(list[i] < list[smallestPosition])
smallestPosition = i;
}
return smallestPosition;
}
void selectionSort(int list[], int listLength)
{
for(int i = 0; i < listLength; i++)
{
int smallestPosition = findSmallestPosition(list, i, listLength);
swap(list[i], list[smallestPosition]);
}
return;
}
int main ()
{
int list[5] = {12, 5, 48, 0, 4};
cout << "Input array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
selectionSort(list, 5);
cout << "Sorted array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность в любом случае: O(n2).
3. Сортировка вставками
В сортировке вставками начинаем со второго
элемента. Проверяем между собой второй элемент с первым и, если надо, меняем местами.
Сравниваем следующую пару элементов и проверяем все пары до нее.
Проход №1. Начинаем со второй позиции.
Число 12 больше 5 — элементы меняются местами.
Проход №2. Начинаем с третьей позиции.
Проверяем вторую и третью позиции. Затем
первую и вторую.
Проход №3. Начинаем с четвертой позиции.
Произошло три смены местами.
Проход №4. Начинаем с последней позиции.
Получаем отсортированный массив на выходе.
#include <iostream>
using namespace std;
void insertionSort(int list[], int listLength)
{
for(int i = 1; i < listLength; i++)
{
int j = i - 1;
while(j >= 0 && list[j] > list[j + 1])
{
swap(list[j], list[j + 1]);
cout<<"ndid";
j--;
}
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
insertionSort(list, 8);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
return 0;
}
Сложность в лучшем случае: O(n).
Сложность в худшем случае: O(n2).
4. Быстрая сортировка
В основе быстрой сортировки лежит стратегия
«разделяй и властвуй». Задача разделяется на более мелкие подзадачи. Подзадачи
решаются отдельно, а потом решения объединяют. Точно так же, массив разделяется
на подмассивы, которые сортируются и затем сливаются в один.
В первую очередь выбираем опорный элемент.
Отметим его синим. Все значения больше опорного элемента ставятся после него,
остальные — перед.
На иллюстрации массив разделяется по опорному
элементу. В полученных массивах также выбираем опорный элемент и разделяем по
нему.
Опорным может быть любой элемент. Мы выбираем
последний в списке.
Чтобы расположить элементы большие — справа от
опорного элемента, а меньшие — слева, будем двигаться от начала списка. Если
число будет больше опорного, то оно ставится на его место, а сам опорный на
место перед ним.
Напишем функцию разделения partition(),
которая возвращает индекс опорного элемента, и используем ее в сортировке.
int partition(int list[], int start, int pivot)
{
int i = start;
while(i < pivot)
{
if(list[i] > list[pivot] && i == pivot-1)
{
swap(list[i], list[pivot]);
pivot--;
}
else if(list[i] > list[pivot])
{
swap(list[pivot - 1], list[pivot]);
swap(list[i], list[pivot]);
pivot--;
}
else i++;
}
return pivot;
}
#include <iostream>
using namespace std;
int partition(int list[], int start, int pivot)
{
int i = start;
while(i < pivot)
{
if(list[i] > list[pivot] && i == pivot-1)
{
swap(list[i], list[pivot]);
pivot--;
}
else if(list[i] > list[pivot])
{
swap(list[pivot - 1], list[pivot]);
swap(list[i], list[pivot]);
pivot--;
}
else i++;
}
return pivot;
}
void quickSort(int list[], int start, int end)
{
if(start < end)
{
int pivot = partition(list, start, end);
quickSort(list, start, pivot - 1);
quickSort(list, pivot + 1, end);
}
}
int main()
{
int list[6]={2, 12, 5, 48, 0, 4};
cout<<"Input array ...n";
for (int i = 0; i < 6; i++)
{
cout<<list[i]<<"t";
}
quickSort(list, 0, 6);
cout<<"nnSorted array ... n";
for (int i = 0; i < 6; i++)
{
cout<<list[i]<<"t";
}
return 0;
}
Сложность в лучшем случае: O(n*logn).
Сложность в худшем случае: O(n2).
5. Сортировка слиянием
Сортировка слиянием также следует стратегии
«разделяй и властвуй». Разделяем исходный массив на два равных подмассива.
Повторяем сортировку слиянием для этих двух подмассивов и объединяем обратно.
Цикл деления повторяется, пока не останется по
одному элементу в массиве. Затем объединяем, пока не образуем полный список.
Алгоритм сортировки состоит из четырех этапов:
- Найти середину массива.
- Сортировать массив от
начала до середины. - Сортировать массив от
середины до конца. - Объединить массив.
void merge(int list[],int start, int end, int mid);
void mergeSort(int list[], int start, int end)
{
int mid;
if (start < end){
mid=(start+end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1, end);
merge(list,start,end,mid);
}
}
Для объединения напишем отдельную функцию
merge().
Алгоритм объединения массивов:
- Циклично проходим по
двум массивам.. - В объединяемый ставим тот элемент, что меньше.
- Двигаемся дальше, пока не дойдем до конца
обоих массивов.
#include <iostream>
using namespace std;
void merge(int list[],int start, int end, int mid);
void mergeSort(int list[], int start, int end)
{
int mid;
if (start < end){
mid=(start+end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1, end);
merge(list,start,end,mid);
}
}
void merge(int list[],int start, int end, int mid)
{
int mergedList[8];
int i, j, k;
i = start;
k = start;
j = mid + 1;
while (i <= mid && j <= end) {
if (list[i] < list[j]) {
mergedList[k] = list[i];
k++;
i++;
}
else {
mergedList[k] = list[j];
k++;
j++;
}
}
while (i <= mid) {
mergedList[k] = list[i];
k++;
i++;
}
while (j <= end) {
mergedList[k] = list[j];
k++;
j++;
}
for (i = start; i < k; i++) {
list[i] = mergedList[i];
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
mergeSort(list, 0, 7);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
}
Сложность в любом случае: O(n*logn).
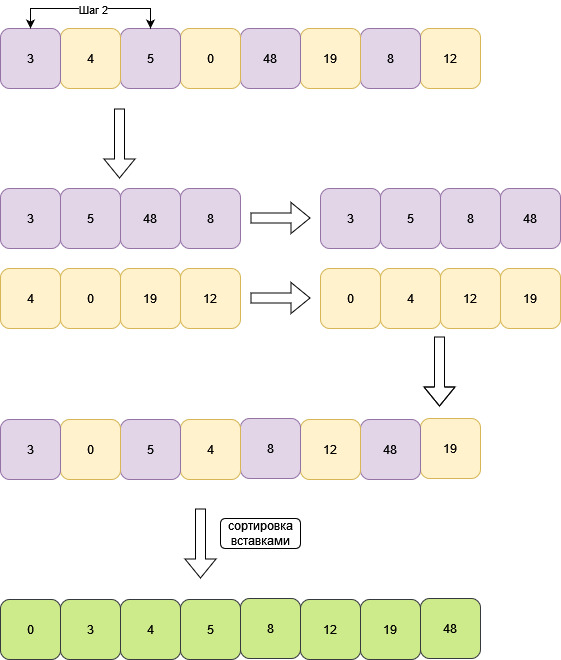
6. Сортировка Шелла
Алгоритм включает в себя сортировку вставками.
Исходный массив размером N разбивается на подмассивы с шагом N/2. Подмассивы
сортируются вставками. Затем вновь разбиваются, но уже с шагом равным N/4. Цикл
повторяется. Производим целочисленное деление шага на два каждую итерацию.
Когда шаг становится равен 1, массив просто сортируется вставками.
У массива размером с 8, первый шаг будет равен 4.
Уменьшаем шаг в два раза. Шаг равен 2.
#include <iostream>
using namespace std;
void shellSort(int list[], int listLength)
{
for(int step = listLength/2; step > 0; step /= 2)
{
for (int i = step; i < listLength; i += 1)
{
int j = i;
while(j >= step && list[j - step] > list[i])
{
swap(list[j], list[j - step]);
j-=step;
cout<<"ndid";
}
}
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
shellSort(list, 8);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
}
Сложность в лучшем и среднем случае:
O(n*logn).
Сложность в худшем случае: O(n2).
Исходный массив представляем в виде структуры
данных кучи. Куча – это один из
типов бинарного дерева.
У кучи есть следующие свойства:
- Родительский узел
всегда больше дочерних; - На i-ом слое 2i
узлов, начиная с нуля. То есть на нулевом слое 1 узел, на первом – 2 узла, на
втором – 4, и т. д. Правило для всех слоев, кроме последнего; - Слои заполняются слева направо.
После формирования кучи будем извлекать самый
старший узел и ставить на конец массива.
Алгоритм сортировки кучей:
- Формируем бинарное
дерево из массива. - Расставляем узлы в
дереве так, чтобы получилась куча (методheapify()). - Верхний элемент
помещаем в конец массива. - Возвращаемся на шаг 2, пока куча не опустеет.
Обращаться к дочерним узлам можно, зная, что
дочерние элементы i-го элемента находятся на позициях 2*i + 1 (левый узел) и
2*i + 2 (правый узел).
Изначальная куча:
Индекс с нижним левым узлом определим по
формуле n/2-1, где n – длина массива. Получается 5/2 – 1 = 2 – 1 = 1. С этого
индекса и начинаем операцию heapify(). Сравним дочерние узлы 1-й позиции.
Дочерний узел оказался больше. Меняем местами
с родителем.
Теперь проверяем родительский узел от позиции
1.
48 больше 3. Меняем местами.
После смены проверяем все дочерние узлы
элемента, который опустили. То есть для числа 3 проводим heapify(). Так как 3
меньше 19, меняем местами.
Наибольший элемент оказался наверху кучи.
Осталось поставить его в конце массива на позицию 4.
Теперь продолжаем сортировать кучу, но последний элемент игнорируем. Для
этого просто будем считать, что длина массива уменьшилась на 1.
Повторяем алгоритм сортировки, пока куча не
опустеет, и получаем отсортированный массив.
void heapify(int list[], int listLength, int root)
{
int largest = root;
int l = 2*root + 1;
int r = 2*root + 2;
if (l < listLength && list[l] > list[largest])
largest = l;
if (r < listLength && list[r] > list[largest])
largest = r;
if (largest != root)
{
swap(list[root], list[largest]);
heapify(list, listLength, largest);
}
}
#include <iostream>
using namespace std;
void heapify(int list[], int listLength, int root)
{
int largest = root;
int l = 2*root + 1;
int r = 2*root + 2;
if (l < listLength && list[l] > list[largest])
largest = l;
if (r < listLength && list[r] > list[largest])
largest = r;
if (largest != root)
{
swap(list[root], list[largest]);
heapify(list, listLength, largest);
}
}
void heapSort(int list[], int listLength)
{
for(int i = listLength / 2 - 1; i >= 0; i--)
heapify(list, listLength, i);
for(int i = listLength - 1; i >= 0; i--)
{
swap(list[0], list[i]);
heapify(list, i, 0);
}
}
int main()
{
int list[5] = {3,19,8,0,48};
cout<<"Input array ..."<<endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
heapSort(list, 5);
cout << "Sorted array"<<endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность алгоритма в любом случае: O(n*logn).
***
В этой статье мы познакомились с семью видами
сортировок, рассмотрели их выполнение и написание на С++. Попробуйте применить
новые знания в решении задачек на LeetCode или Codeforces. Понимание подобных
алгоритмов поможет в будущем пройти собеседование.
Источники:
- https://www.softwaretestinghelp.com/sorting-techniques-in-cpp/
- https://medium.com/@ssbothwell/sorting-algorithms-and-big-o-analysis-332ce7b8e3a1
- https://www.programiz.com/dsa/shell-sort
- https://www.happycoders.eu/algorithms/sorting-algorithms/
***
Материалы по теме
- Какая сортировка самая быстрая? Тестируем алгоритмы
- Пузырьковая сортировка на JavaScript
- Вводный курс по алгоритмам: от сортировок до машины Тьюринга
***
Мне сложно разобраться самостоятельно, что делать?
Алгоритмы и структуры данных действительно непростая тема для самостоятельного изучения: не у кого спросить и что-то уточнить. Поэтому мы запустили курс «Алгоритмы и структуры данных», на котором в формате еженедельных вебинаров вы:
- изучите сленг, на котором говорят все разработчики независимо от языка программирования: язык алгоритмов и структур данных;
- научитесь применять алгоритмы и структуры данных при разработке программ;
- подготовитесь к техническому собеседованию и продвинутой разработке.
Курс подходит как junior, так и middle-разработчикам.
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Задача сортировки массива заключается в том, чтобы расставить его элементы в определённом порядке (чаще всего — по неубыванию: каждый элемент должен быть больше или равен предыдущему).
Будет полезно вместе с описанем алгоритмов смотреть их визуализацию.
Сортировка пузырьком
Наш первый подход будет заключаться в следующем: обозначим за (n) длину массива и (n) раз пройдёмся раз пройдемся по нему, меняя два соседних элемента, если первый больше второго.
Как каждую итерацию максимальный элемент «всплывает» словно пузырек к концу массива — отсюда и название.
void bubble_sort(vector<int>& array) {
int n = (int) array.size();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - 1; j++) {
// сравниваем элемент со следующим
// и меняем местами, если следующий меньше
if (array[j] > arr[j + 1]) {
swap(array[j], array[j + 1]);
}
}
}
}
vector<int> a = {1, -3, 7, 88, 7};
bubble_sort(a);
for (auto elem : a) {
cout << elem << " ";
}
// -3 1 7 7 88После (i) шагов алгоритма сортировки пузырьком последние ((i + 1)) чисел всегда отсортированы, а значит алгоритм работает корректно.
Упражнение. Алгоритм можно немного ускорить. Подумайте, какие лишние элементы мы перебираем. Как нужно изменить границы в двух циклах for, чтобы не делать никаких бесполезных действий?
Сортировка выбором
Другим способом является сортировка выбором минимума (или максимума).
Чтобы отсортировать массив, просто (n) раз выберем минимум среди еще неотсортированных чисел и поставим его на свое место. На (i)-ом шаге будем искать минимум на отрезке ([i, n – 1]) и менять его местами с (i)-тым элементом, после чего отрезок ([0, i]) будет отсортирован.
Содержательная часть будет выглядеть так:
for (i = 0; i < n - 1; i++) {
for (j = i + 1; j < n; j++) {
if (a[i] > a[j]) {
swap(a[j], a[i]);
}
}
}Сортировка вставками
Определение. Префиксом длины (i) будем называть первые (i) элементов массива.
Тогда пусть на (i)-ом шаге у нас уже будет отсортирован префикс до (i)-го элемента. Чтобы этот префикс увеличить, нужно взять элемент, идущий после него, и менять с левым соседом, пока этот элемент наконец не окажется больше своего левого соседа. Если в конце он больше левого соседа, но меньше правого, то это будет означать, что мы правильно вставили этот элемент в отсортированную часть массива.
for (int i = 1; i < n; i++) {
for (int j = i; j > 0; j--) {
if (a[j - 1] < a[j]) {
break;
}
swap(a[j], a[j - 1]);
}
}Сортировка подсчетом
Предыдущие три алгоритма работали с массивами, в которых лежат абсолютно любые объекты, которые можно сравнивать: любые числа, строки, пары, другие массивы — почти все что угодно.
Но особых случаях, когда элементы принадлежат какому-то маленькому множеству, можно использовать другой алгоритм — сортировку подсчетом.
Пусть, например, нам гарантируется, что все числа натуральные и лежат в промежутке от (1) до (100). Тогда есть такой простой алгоритм:
-
Создадим массив размера (100), в котором будем хранить на (k)-ом месте, сколько раз число (k) встретилось в этом массиве.
-
Пройдемся по всем числам исходного массива и увеличим соответствующее значение массива на (1).
-
После того, как мы посчитали, сколько раз каждое число встретилось, можно просто пройтись по этому массиву и вывести (1) столько раз, сколько встретилась (1), вывести (2) столько раз, сколько встретилась (2), и так далее.
Время работы такого алгоритма составляет (O(M+N)), где (M) — число возможных значений, (N) — число элементов в массиве. Сейчас мы расскажем, что же это означает.
О-нотация
Часто требуется оценить, сколько времени работает алгоритм. Но тут возникают проблемы:
- на разных компьютерах время работы всегда будет слегка отличаться;
- чтобы измерить время, придётся запустить сам алгоритм, но иногда приходится оценивать алгоритмы, требующие часы или даже дни работы.
Зачастую основной задачей программиста становится оптимизировать алгоритм, выполнение которого займёт тысячи лет, до какого-нибудь адекватного времени работы. Поэтому хотелось бы уметь предсказывать, сколько времени займёт выполнение алгоритма ещё до того, как мы его запустим.
Для этого сначала попробуем оценить число операций в алгоритме. Возникает вопрос: какие именно операции считать. Как один из вариантов — учитывать любые элементарные операции:
- арифметические операции с числами:
+, -, *, / - сравнение чисел:
<, >, <=, >=, ==, != - присваивание:
a[0] = 3
При этом надо учитывать, как реализованы некоторые отдельные вещи в самом языке. Например, в питоне срезы массива (array[3:10]) копируют этот массив, то есть этот срез работает за 7 элементарных действий. А swap, например, может работать за 3 присваивания.
Упражнение. Попробуйте посчитать точное число сравнений и присваиваний в сортировках пузырьком, выбором, вставками и подсчетом в худшем случае (это должна быть какая формула, зависящая от (n) — длины массива).
Чтобы учесть вообще все элементарные операции, ещё надо посчитать, например, сколько раз прибавилась единичка внутри цикла for. А ещё, например, строчка n = len(array) — это тоже действие. Поэтому даже посчитав их, сразу очевидно, какой из этих алгоритмов работает быстрее — сравнивать формулы сложно. Хочется придумать способ упростить эти формулы так, чтобы:
- не нужно было учитывать много информации, не очень сильно влияющей на итоговое время;
- легко было оценивать время работы разных алгоритмов для больших чисел;
- легко было сравнивать алгоритмы на предмет того, какой из них лучше подходит для тех или иных входных данных.
Для этого придумали (O)-нотацию — асимптотическое время работы вместо точного (часто его ещё называют асимптотикой).
Определение. Пусть (f(n)) – это какая-то функция. Говорят, что алгоритм работает за (O(f(n))), если существует число (C), такое что алгоритм работает не более чем за (C cdot f(n)) операций.
В таких обозначениях можно сказать, что
- сортировка пузырьком работает за (O(n^2));
- сортировка выбором работает за (O(n^2));
- сортировка вставками работает за (O(n^2));
- сортировка подсчетом работает за (O(n + m)).
Это обозначение удобно тем, что оно короткое и понятное, а также оно не зависит от умножения на константу или прибавления константы. Например, если алгоритм работает за (O(n^2)), то это может значить, что он работает за (n^2), за (n^2 + 3), за (frac{n(n-1)}{2}) или даже за (1000 cdot n^2 + 1) действие. Главное — что функция ведет себя как (n^2), то есть при увеличении (n) (в данном случае это длина массива) он увеличивается как некоторая квадратичная функция. Например, если увеличить (n) в 10 раз, время работы программы увеличится приблизительно в 100 раз.
Все рассуждения про то, сколько операций в swap или считать ли отдельно присваивания, сравнения и циклы — отпадают. Каков бы ни был ответ на эти вопросы, они меняют ответ лишь на константу, а значит асимптотическое время работы алгоритма никак не меняется.
Первые три сортировки именно поэтому называют квадратичными — они работают за (O(n^2)). Сортировка подсчетом может работать намного быстрее — она работает за (O(n + m)), а если в задаче (M leq N), то это вообще линейная функция (O(n)).
Упражнение. Найдите асимптотику данных функций, маскимально упростив ответ (например, до (O(n)), (O(n^2)) и т. д.):
- (frac{N}{3})
- (frac{N(N-1)(N-2)}{6})
- (1 + 2 + 3 + ldots + N)
- (1^2 + 2^2 + 3^2 + ldots + N^2)
- (log{N} + 3)
- (179)
- (10^{100})
Упражнение. Найдите асимптотическое время работы данных функций:
def f(n):
s = 0
for i in range(n):
for j in range(n):
s += i * j
return sdef g(n):
s = 0
for i in range(n):
s += i
for i in range(n):
s += i * i
return sdef h(n):
if n == 0:
return 1
return h(n - 1) * nУпражнение. Найдите лучшее время работы алгоритмов, решающих данные задачи:
- Написать числа от (1) до (n).
- Написать все тройки чисел от (1) до (n).
- Найти разницу между максимумом и минимумом в массиве.
- Найти число единиц в бинарной записи числа (n).
Сортировки за (O(n log n))
Сортировка очень часто применяется как часть решения олимпиадных задач. В таких случаях обычно не пишут её заново, а используют встроенную.
Пример на Python:
a = [1, 5, 10, 5, -4]
a.sort()Пример на C++:
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
int main() {
vector<int> v = {1, 5, 10, 5, -4};
sort(v.begin(), v.end());
}В разных языках она может быть реализована по-разному, но везде она работает за (O(n log n)), и, обычно, неплохо оптимизирована. Далее мы опишем два подхода к её реализации.
Сортировка слиянием
Найти количество пар элементов (a) и (b) в отсортированном массиве, такие что (b – a > K).
Наивное решение: бинарный поиск. Будем считать, что массив уже отсортирован. Для каждого элемента (a) найдем первый справа элемент (b), который входит в ответ в паре с (a). Нетрудно заметить, что все элементы, большие (b), также входят в ответ. Итоговая асимптотика (O(nlog n)).
А можно ли быстрее?
Да, давайте перебирать два указателя — два индекса (first) и (second). Будем перебирать (first) просто слева направо и поддерживать для каждого (first) первый элемент справа от него, такой что (a[second] – a[first] > K) как (second). Тогда в пару к (a=a[first]) подходят ровно (n-second) элементов массив начиная с (second).
int second = 0, ans = 0;
for (int first = 0; first < n; ++first) {
while (second != n && a[second] - a[first] <= r) {
second++;
}
ans += n - second;
}За сколько же работает это решение? С виду может показаться, что за (O(n^2)), но давайте посмотрим сколько раз меняется значение переменной (second). Так как оно изначально равняется нулю, только увеличивается и не может превысить (n), то суммарно операций мы сделаем (O(n)).
Это называется метод двух указателей — так как мы двигаем два указателя first и second одновременно слева направо по каким-то правилам. Обычно его используют на одном отсортированном массиве.
Давайте разберем еще примеры.
Слияние
Еще пример двух указателей на нескольких массивах.
Пусть у нас есть два отсортированных по неубыванию массива размера (n) и (m). Хотим получить отсортированный массив размера (n + m) из исходных.
Пусть первый указатель будет указывать на начало первого массива, а второй, соответственно, на начало второго. Из двух текущих элементов, на которые указывают указатели, выберем наименьший и положим на соответствующую позицию в новом массиве, после чего сдвинем указатель. Продолжим этот процесс пока в обоих массивах не закончатся элементы. Тогда код будет выглядеть следующим образом:
int a[n + 1], b[m + 1], res[n + m];
a[n] = INF; // Создаем в конце массива фиктивный элемент, который заведомо больше остальных
b[m] = INF; // Чтобы избежать лишних случаев
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
for (int j = 0; j < m; ++j) {
cin >> a[j];
}
int i = 0, j = 0;
for (int k = 0; k < n + m; ++k) {
if (a[i] < b[j]) {
res[k] = a[i];
i++;
} else {
res[k] = b[j];
j++;
}
}Итоговая асимптотика: (O(n + m)).
Сортировка слиянием
Давайте подробно опишем как использовать операцию слияния для сортировки за (O(nlog n)).
Пусть у нас есть какой-то массив.
int a[8] = {7, 2, 5, 6, 1, 3, 4, 8};Сделаем такое предположение. Пусть мы уже умеем как-то сортировать массив размера (n). Тогда научимся сортировать массив размера (2n). Давайте разобьем наш массив на две половины, отсортируем каждую из них, а после это сделаем слияние двух массивов, которое мы научились делать за (O(n)) в данных условиях. Также заметим, что массив размера (1) уже отсортирован, тогда мы можем делать это процедуру рекурсивно. Тогда для данного массива (a) это будет выглядеть следующим образом:
// (7 2 5 6 1 3 4 8)
// (7 2 5 6)(1 3 4 8)
// (7 2)(5 6)(1 3)(4 8)
// (2 7)(5 6)(1 3)(4 8)
// (2 5 6 7)(1 3 4 8)
// (1 2 3 4 5 6 7 8)
#include // Воспользуемся встроенной функцией merge
void merge_sort(vector &v, int l, int r) { // v - вектор, который хотим отсортировать
if (r - l == 1) { // l и r - полуинтервал, который хотим отсортировать
return;
}
int mid = (l + r) / 2;
merge_sort(v, l, mid);
merge_sort(v, mid, r);
vector temp(r - l); // временный вектор
merge(v.begin() + l, v.begin() + mid, v.begin() + mid, v.begin() + r, c.begin());
for (int i = 0; i < r - l; ++i) {
v[i + l] = temp[i];
}
return;
}Так сколько же работает это решение?
Пускай (T(n)) — время сортировки массива длины (n), тогда для сортировки слиянием справедливо (T(n)=2T(n/2)+O(n)) (O(n)) — время, необходимое на то, чтобы слить два массива длины n. Распишем это соотношение:
(T(n)=2T(n/2)+O(n)=4T(n/4)+2O(n)=ldots=T(1)+log(n)O(n)=O(nlog(n)).)
Количество инверсий
Пусть у нас есть некоторая перестановка (a). Инверсией называется пара индексов (i) и (j) такая, что (i < j) и (a[i] > a[j]).
Найти количество инверсий в данной перестановке.
Очевидно, что эта задача легко решается обычным перебором двух индексов за (O(n^2)):
int a[n], ans = 0;
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
if (a[i] > a[j]) {
ans++;
}
}
}
cout << ans << endl;Внезапно эту задачу можно решить используя сортировку слиянием, слегка модифицируя её. Оставим ту же идею. Пусть мы умеем находить количество инверсий в массиве размера (n), научимся находить количество инверсий в массиве размера (2n).
Заметим, что мы уже знаем количество инверсий в левой половине и в правой половине массива. Осталось лишь посчитать число инверсий, где одно число лежит в левой половине, а второе в правой половине. Как же их посчитать?
Давайте подробнее рассмотрим операцию merge левой и правой половины (которую мы ранее заменили на вызов встроенной функции merge). Первый указатель указывает на элемент левой половины, второй указатель указывает на элемент второй половины, мы смотрим на минимум из них и этот указатель вдигаем вправо.
Рассмотрим число (A) в левой половине. В скольки инверсиях между половинами оно участвует? В стольки, сколько чисел в правой половине меньше, чем оно. Знаем ли мы это количество? Да! Ровно в тот момент, когда мы число (A) вносим в слитый массив, второй указатель указывает на первое число в правой половине, которое больше чем (A).
Значит в тот момент, когда мы добавляем число (A) из левой половины, к ответу достаточно прибавить индекс второго указателя (минус начало правой половины). Так мы учтем все инверсии между половинами.
Быстрая сортировка
Быстрая сортировка заключается в том, что на каждом шаге мы находим опорный элемент, все элементы, которые меньше его кидаем в левую часть, остальные в правую, а затем рекурсивно спускаемся в обе части.
void quicksort(int l, int r){
if (l < r){
int index = (l + r) / 2; /* index - индекс опорного элемента для
начала сделаем его равным середине отрезка*/
index = divide(l, r, index); /* divide - функция разбивающие элементы
на меньшие и больше/равные a[index],
при этом функция возвращает границу разбиения*/
quicksort(l, index);
quicksort(index + 1, r);
}
}Давайте оценим асимптотику данной сортировки. На случайных данных она работает за (O(NlogN)) , так как каждый раз мы будем делить массив на две примерно равные части, то есть суммарно размер рекурсии будет около логарифма и при этом на каждом этапе рекурсии мы просмотрим не более, чем размер массива. Однако можно легко найти две проблемы, одна – одинаковые числа, а вторая – если вдруг середина – минимум или максимум.
Существуют несколько выходов из этой ситуации :
-
Давайте если быстрая сортировка работает долго, то запустим любую другую сортировку за (NlogN).
-
Давайте делить массив не на две, а на три части(меньше, равны, больше).
-
Чтобы избавиться от проблемы с максимумом/минимумом в середине, давайте брать случайный элемент.
Поиск (k)-ой порядковой статистики за (O(N))
Пусть дан массив (A) длиной (N) и пусть дано число (K). Задача заключается в том, чтобы найти в этом массиве (K)-ое по величине число, т.е. (K)-ую порядковую статистику.
Давайте поймем, что в быстрой сортировке мы можем узнать, сколько элементов меньше данного, тогда рассмотрим три случая
-
количество чисел, меньше данного = (k – 1), тогда наше число – ответ.
-
количество чисел, меньше данного >= (k), тогда спускаемся рекурсивно в левую часть и ищем там ответ.
-
количество чисел, меньше данного < (k), спускаемся в правую ищем ((k) – левая – 1) – ое число.
За сколько же это работает, из быстрой сортировки мы имеем, что размер убывает приблизительно в 2 раза, то есть мы имеем сумму (sum_{k=1}^n {2 ^ k} = {2^{k+1}-1}) что в нашем случае это максимум равно (2 * N – 1), то есть (O(N)).
Также в C++ эта функция уже реализована и называется nth_element .
Алгоритм сортировки — это алгоритм для упорядочивания элементов в списке.
Виды алгоритмов сортировки
Сортировка пузырьком / Bubble sort
wiki
Сортировка пузырьком — это простейший и один из самых известных алгоритмов сортировки. Идея заключается в последовательном сравнении значений соседних элементов. Если текущий элемент больше следующего, меняем их местами. Алгоритм необходимо повторять до тех пор, пока массив не будет отсортирован.
Плюсы и минусы
Этот алгоритм считается учебным и почти не применяется на практике из-за низкой эффективности: он медленно работает на тестах, в которых маленькие элементы (их называют «черепахами») стоят в конце массива. Однако на нём основаны многие другие методы, например, шейкерная сортировка и сортировка расчёской.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
private fun bubbleSort(array: IntArray) {
if (array.isEmpty()) return
var swap = true
while (swap) {
swap = false
for (i in 1 until array.size) {
if (array[i] < array[i - 1]) {
val temp = array[i - 1]
array[i - 1] = array[i]
array[i] = temp
swap = true
}
}
}
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n) | O(n2) | O(n2) |
| Память | O(1) |
Сортировка перемешиванием / Shaker (cocktail, ripple, shuffle, shuttle) sort
wiki
Также известна как шейкерная или коктейльная сортировка.
Сортировка перемешиванием – это разновидность сортировки пузырьком. Отличие в том, что данная сортировка в рамках одной итерации проходит по массиву в обоих направлениях (слева направо и справа налево), тогда как сортировка пузырьком – только в одном направлении (слева направо).
Общая идея алгоритма:
- Обход массива слева направо, аналогично пузырьковой – сравнение соседних элементов, меняя их местами, если левое значение больше правого. В итоге наибольшее число будет перемещено в конец массива.
- Обход массива в обратном направлении (справа налево), начиная с элемента, который находится перед последним отсортированным. На этом этапе элементы также сравниваются между собой и меняются местами, чтобы наименьшее значение всегда было слева. В итоге наименьшее число будет перемещено в начало массива.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
fun cocktailSort(a: IntArray) {
fun swap(i: Int, j: Int) {
val temp = a[i]
a[i] = a[j]
a[j] = temp
}
do {
var swapped = false
for (i in 0 until a.size - 1)
if (a[i] > a[i + 1]) {
swap(i, i + 1)
swapped = true
}
if (!swapped) break
swapped = false
for (i in a.size - 2 downTo 0)
if (a[i] > a[i + 1]) {
swap(i, i + 1)
swapped = true
}
} while (swapped)
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n) | O(n2) | O(n2) |
| Память | O(1) |
Сложность у алгоритма такая же, как и у сортировки пузырьком, однако реальное время работы лучше (обычно менее чем в два раза быстрее).
Сортировка расчёской / Comb sort
wiki
Сортировка расчёской – еще одна разновидность сортировки пузырьком. Данная сортировка улучшает сортировку пузырьком за счет устранения маленьких значений в конце списка (черепах).
Достигается это тем, что вместо сравнения соседних элементов, сравниваются элементы на достаточно большом расстоянии друг от друга, постепенно уменьшая это расстояние. Сначала разрыв между элементами берётся максимальный, т.е. на единицу меньше, чем размер массива. Затем на каждой итерации расстояние уменьшается путём деления расстояния на фактор уменьшения. Так продолжается до тех пор, пока разность индексов сравниваемых элементов не достигнет единицы. Тогда сравниваются уже соседние элементы как и в сортировке пузырьком, но эта итерация будет последней.
Оптимальное значение фактора уменьшения – 1,247.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
fun combSort(input: Array<Int>) {
var gap = input.size
if (gap <= 1) return // если массив <= 1, то он считается отсортированным
var swaps = false
while (gap > 1 || swaps) {
gap = (gap / 1.247331).toInt()
if (gap < 1) gap = 1
var i = 0
swaps = false
while (i + gap < input.size) {
if (input[i] > input[i + gap]) {
val tmp = input[i]
input[i] = input[i + gap]
input[i + gap] = tmp
swaps = true
}
i++
}
}
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n log n) | Ω(n2/2p), где p – количество инкрементов | O(n2) |
| Память | O(1) |
Сортировка вставками / Insertion sort
wiki
Сортировка вставками – алгоритм, при котором каждый последующий элемент массива сравнивается с предыдущими элементами (отсортированными) и вставляется в нужную позицию.
Общая идея алгоритма:
- Сравниваем второй элемент с первым элементом массива и при необходимости меняем их местами. Условно эти элементы (первый и второй) будут являться отсортированным массивом, остальные элементы – неотсортированным.
- Сравниваем следующий элемент из неотсортированного массива с элементами отсортированного и вставляем в нужную позицию.
- Повторям шаг 2 до тех пор, пока в неотсортированном массиве не останется элементов.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
fun insertionsort(items:MutableList<Int>): List<Int> {
if (items.isEmpty() || items.size < 2){
return items
}
for (count in 1..items.count() - 1) {
val item = items[count]
var i = count
while (i > 0 && item < items[i - 1]) {
items[i] = items[i - 1]
i -= 1
}
items[i] = item
}
return items
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n) | O(n2) | O(n2) |
| Память | O(1) |
Сортировка Шелла / Shell sort
wiki
Сортировка Шелла – усовершенствованная разновидность сортировки вставками.
Сначала сравниваются и сортируются между собой значения, стоящие друг от друга на некотором расстоянии – d. После этого расстояние d уменьшается и процедура повторяется до тех пор, пока значение d не станет минимальным, т.е. d = 1. Это означает, что сортировка достигла последнего шага. А на последнем шага элементы сортируются обычной сортировкой вставками.
Первоначально было предложено расчитывать расстояние между сравниваемыми элементами следующим образом:
- первая итерация – d1 = N/2, где N – размер массива;
- последующие итерации – di = di-1/2;
- последняя итерация – dk = 1
Существуют и другие последовательности.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
fun sort(arr: IntArray): Int {
val n = arr.size
var gap = n / 2
while (gap > 0) {
var i = gap
while (i < n) {
val temp = arr[i]
var j = i
while (j >= gap && arr[j - gap] > temp) {
arr[j] = arr[j - gap]
j -= gap
}
arr[j] = temp
i += 1
}
gap /= 2
}
return 0
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n log n) | зависит от выбранных шагов (d) | O(n2) или O(n log2 n) (зависит от выбранных шагов) |
| Память | O(1) |
Сортировка выбором / Selection Sort
wiki
Сортировка выбором – это алгоритм, при котором многократно осуществляется поиск минимального элемента в неотсортированной части массива и его помещение в конец отсортированной части массива.
Общая идея алгоритма:
- Данный алгоритм условно делит массив на две части:
- подмассив, который уже отсортирован (находится в левой части массива),
- подмассив, который нужно отсортировать (находится в правой части массива).
- Поиск минимального значения в неотсортированном массиве. Найденное значение меняем местами с первым элементом в неотсортированном массиве.
- Повторяем предыдущий шаг до тех пор, пока массив не будет отсортирован.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
fun selectionSort(sampleArray: IntArray) {
var n = sampleArray.size
var temp: Int
for(i in 0..n-1) {
var indexOfMin = i
for(j in n-1 downTo i) {
if (sampleArray[j] < sampleArray[indexOfMin])
indexOfMin=j
}
if (i != indexOfMin) {
temp = sampleArray[i]
sampleArray[i] = sampleArray[indexOfMin]
sampleArray[indexOfMin] = temp
}
}
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n2) | O(n2) | O(n2) |
| Память | O(1) |
Быстрая сортировка / Quick Sort
wiki
Быстрая сортировка – это алгоритм типа “разделяй и властвуй”.
Общая идея алгоритма:
- Выбрать из массива элемент, который обычно называют опорным. Это может быть любой элемент из массива. От выбора опорного элемента не зависит корректность алгоритма, но в отдельных случаях может сильно зависеть его эффективность.
- Сравнить все остальные элементы с опорным и переставить их в массиве так, чтобы разбить массив на три непрерывных отрезка, следующих друг за другом: «элементы меньшие опорного», «равные» и «большие».
- Рекурсивно применить первые два шага к отрезкам, содержащим «меньшие» и «большие» значения. Не применять к массиву, в котором только один элемент или отсутствуют элементы.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
fun quicksort(items: List<Int>): List<Int> {
// если в массиве меньше 2х элементов, то он уже отсортирован
if (items.count() < 2) {
return items
}
// выбираем опорный элемент
val pivot = items[items.count()/2]
// сортируем элементы по 3м массивам - меньшие, равные и большие опорного
val equal = items.filter { it == pivot }
val less = items.filter { it < pivot }
val greater = items.filter { it > pivot }
// рекурсивно вызываем функцию для меньших и больших элементов
return quicksort(less) + equal + quicksort(greater)
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n) | O(n log n) | O(n2) |
| Память | O(n) |
Сортировка слиянием / Merge sort
wiki
Сортировка слиянием – это алгоритм типа “разделяй и властвуй”.
Общая идея алгоритма:
- Массив разбивается на две части примерно одинакового размера. Разбиение получившихся массивов повторяется до тех пор, пока размер каждого массива не достигнет единицы.
- Каждая из получившихся частей сортируется отдельно, после чего происходит слияние двух массивов следующим образом:
- На каждом шаге сравниваем первые элементы массивов, берём наименьшее значение и записываем в результирующий массив.
- Когда один из массив закончился, добавляем оставшиеся элементы второго массива в результирующий массив.
- Слияние подмассивов продолжается до тех пор, пока не получим один, отсортированный массив.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
fun mergeSort(list: List<Int>): List<Int> {
if (list.size <= 1) {
return list
}
val middle = list.size / 2
var left = list.subList(0, middle)
var right = list.subList(middle, list.size)
return merge(mergeSort(left), mergeSort(right))
}
fun merge(left: List<Int>, right: List<Int>): List<Int> {
var indexLeft = 0
var indexRight = 0
var newList: MutableList<Int> = mutableListOf()
while (indexLeft < left.count() && indexRight < right.count()) {
if (left[indexLeft] <= right[indexRight]) {
newList.add(left[indexLeft])
indexLeft++
} else {
newList.add(right[indexRight])
indexRight++
}
}
while (indexLeft < left.size) {
newList.add(left[indexLeft])
indexLeft++
}
while (indexRight < right.size) {
newList.add(right[indexRight])
indexRight++
}
return newList;
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n log n) | O(n log n) | O(n log n) |
| Память | O(n) |
Пирамидальная сортировка / Heap sort
wiki
Пирамидальная сортировка – это улучшенная сортировка выбором.
Для сортировки используется бинарное сортирующее дерево – дерево, у которого выполнены условия:
- Каждый лист имеет глубину либо d, либо d-1, d — максимальная глубина дерева.
- Значение в любой вершине не меньше значения её потомков.
Общая идея алгоритма:
- Выстраиваем массив в виде сортирующего дерева:
Array[i] >= Array[2i + 1]
Array[i] >= Array[2i + 2]
при 0 <= i < n/2 - Обмениваем элементы Array[0] и Array[n-1] местами. Array[0] является корнем сортирующего дерева, т.е. самым большим значением массива.
- Повторям шаги до тех пор, пока в сортирующем дереве не останется один элемент.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
fun heapSort(a: IntArray) {
heapify(a)
var end = a.size - 1
while (end > 0) {
val temp = a[end]
a[end] = a[0]
a[0] = temp
end--
siftDown(a, 0, end)
}
}
fun heapify(a: IntArray) {
var start = (a.size - 2) / 2
while (start >= 0) {
siftDown(a, start, a.size - 1)
start--
}
}
fun siftDown(a: IntArray, start: Int, end: Int) {
var root = start
while (root * 2 + 1 <= end) {
var child = root * 2 + 1
if (child + 1 <= end && a[child] < a[child + 1]) child++
if (a[root] < a[child]) {
val temp = a[root]
a[root] = a[child]
a[child] = temp
root = child
}
else return
}
}
fun main(args: Array<String>) {
val aa = arrayOf(
intArrayOf(100, 2, 56, 200, -52, 3, 99, 33, 177, -199),
intArrayOf(4, 65, 2, -31, 0, 99, 2, 83, 782, 1),
intArrayOf(12, 11, 15, 10, 9, 1, 2, 3, 13, 14, 4, 5, 6, 7, 8)
)
for (a in aa) {
heapSort(a)
println(a.joinToString(", "))
}
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n log n) | O(n log n) | O(n log n) или O(n) (при одинаковых ключах) |
| Память | O(1) |
Сортировка подсчётом / Counting sort
wiki
Сортировка подсчётом – это алгоритм, основанный на подсчёте повторяющихся элементов в массиве.
Общая идея алгоритма (простой вариант):
- Есть массив A длиной n элементов, который нужно отсортировать. Создаётся вспомогательный массив C с индексами от 0 до k (максимальное значение в массиве A) и заполняется нулями.
- Последовательно проходим по массиву A и записываем в C[i] количество чисел, равных i. Таким образом индексы в массиве C – это значения массива A, а значение в массиве C – это то, сколько раз это число повторяется в массиве A.
- Проходим по массиву C и переносим значения в массив A.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
fun countingSort(array: IntArray) {
if (array.isEmpty()) return
// вычисляем минимальное и максимальное значение в массиве
val min = array.min()!!
val max = array.max()!!
// создаём вспомогательный массив, все элементы которого == 0
val count = IntArray(max - min + 1)
// подсчитываем числа и записываем во вспомогательный массив
for (number in array) count[number - min]++
// переносим значения в первоначальный массив
var z = 0
for (i in min..max)
while (count[i - min] > 0) {
array[z++] = i
count[i - min]--
}
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | Ω(n+k) | θ(n+k) | O(n + k) |
| Память | O(k) |
- n – размер отсортированного массива, а k – размер вспомогательного массива
Блочная (карманная, корзинная) сортировка / Bucket sort
wiki
Блочная сортировка – это алгоритм, основанный на разделении входного массива на несколько частей – блоки/сегменты – и использовании другого алгоритма для их сортировки.
Общая идея алгоритма:
- Делим массив на блоки таким образом, чтобы элементы в каждом следующем блоке были всегда больше, чем в предыдущем.
- Сортируем каждый блок, используя какой-либо другой алгоритм сортировки, либо рекурсивно тем же методом разбиения на блоки.
- Объединяем все блоки в один массив.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
fun insertion_sort(arr: ArrayList<Double>) {
var n = arr.size
var i: Int
for (j in 1 until n) {
var key = arr[j]
i = j - 1
while (i >= 0 && arr[i] > key) {
arr[i + 1] = arr[i]
i--
}
arr[i + 1] = key
}
}
fun bucketSort(arr:Array<Double>) {
var n = arr.size
var bucket = Array<ArrayList<Double>>(n, {i-> ArrayList() } )
for(i in 0..arr.size-1) {
bucket[Math.floor(n * arr[i]).toInt()].add(arr[i])
}
for(i in 0..arr.size - 1) {
insertion_sort(bucket[i])
}
for (i in 1..arr.size - 1) {
bucket[0].addAll(bucket[i])
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | Ω(n+k) | θ(n+k) | O(n2) |
| Память | O(1) |
- k – количество блоков.
Поразрядная (цифровая) сортировка / Radix sort
wiki
Поразрядная сортировка – это алгоритм, который использует внутреннюю структуру сортируемых объектов.
Перед началом сортировки необходимо знать:
- length – максимальное количество разрядов в сортируемых величинах (например, при сортировке слов необходимо знать максимальное количество букв в слове);
- rang количество возможных значений одного разряда (при сортировке слов – количество букв в алфавите).
Общая идея алгоритма:
- Создаём пустые массивы, количество которых равно rang.
- Распределяем исходные значения по этим массивам. Распределение осуществляется по значению младшего (крайнего) разряда.
- Соединяем значения в той последовательности, в которой они находятся после распределения по спискам.
- Повторяем шаги 1-2 для оставшихся разрядов.
Пример реализации на Kotlin:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
fun radixSort(original: IntArray): IntArray {
var old = original
for (shift in 31 downTo 0) {
val tmp = IntArray(old.size)
var j = 0
for (i in 0 until old.size) {
val move = (old[i] shl shift) >= 0
val toBeMoved = if (shift == 0) !move else move
if (toBeMoved)
tmp[j++] = old[i]
else {
old[i - j] = old[i]
}
}
for (i in j until tmp.size) tmp[i] = old[i - j]
old = tmp
}
return old
}
|
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | Ω(n+w) | θ(nk) | O(w * n) |
| Память | O(n + w) |
- w – количество бит, требуемых для хранения каждого ключа.
Битонная сортировка / Bitonic sort
wiki
Битонная сортировка – алгоритм, основанный на понятии битонных последовательностей и операций над ними.
Битонная последовательность – последовательность, которая сначала возрастает, а потом убывает.
Общая идея алгоритма:
- Создаём битонную последовательность. В результате получаем два массива: первый отсортирован в порядке возрастания, второй – в порядке убывания.
- Последовательно сравниваем элементы первого и второго массивов (сначала первые элементы, потом вторые и т.д.). Если какой либо элемент из второго массива окажется меньше, то меняем его местами с элементом из первого массива. В результате в первом массиве окажутся наименьшие элементы из обоих массивов, а во втором – наибольшие. При этом каждый из массивов будет являться битонной последовательностью.
- Рекурсивно применяем второй шаг к отсортированным массивам, после чего массивы можно склеить.
Чтобы превратить произвольную последовательность в битонную, нужно:
- разделить последовательность пополам;
- первую часть отсортировать по возрастанию;
- вторую часть отсортировать по убыванию.
Пример реализации на Kotlin:
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(log2(n) | O(log2(n) | O(log2(n) |
| Память | O(log2(n) |
Timsort
wiki
Timsort – гибридный алгоритм, сочетающий в себе сортировку вставками и сортировку слиянием.
Общая идея алгоритма:
- По специальному алгоритму разделяем входной массив на подмассивы.
- Каждый подмассив сортируем при помощи сортировки вставками.
- Отсортированные массивы собираются в единый массив с помощью модифицированной сортировки слиянием.
Пример реализации на Kotlin:
| Сложность | Лучшее | Среднее | Худшее |
|---|---|---|---|
| Время | O(n) | O(n log n) | O(n log n) |
| Память | O(n) |
Полезные ссылки
Алгоритм сортировки – общая статья на wiki об алгоритмах сортировки.
Programming algorithms – сайт, посвящённый алгоритмам. Есть раздел с алгоритмами сортировки.
Описание алгоритмов сортировки и сравнение их производительности – статья, в которой сравниваются все основные сортировки на большом числе тестов разного типа и размера.
Sorting Algorithms – список статей на geeksforgeeks.org об алгоритмах сортировки.
Sorting Algorithms Visualized – радужная визуализация алгоритмов сортировки.
Kotlin Algorithms – примеры реализации алгоритмов на Kotlin.
Kotlin Algorithm Club – примеры реализации алгоритмов на Kotlin.
Просмотров 17.2к. Обновлено 23 ноября 2020
Урок из серии: «Программирование на языке Паскаль»
Процесс обработки и поиска информации при решении многих задач проходит быстрее и эффективнее, если данные расположены в определенном порядке. Например, различные списки студентов, учащихся, сотрудников — в алфавитном порядке, числовые данные от большего значения к меньшему (или наоборот) и т.д.
Существует довольно много различных методов сортировки массивов, отличающихся друг от друга степенью эффективности, под которой понимается количество сравнений и количество обменов, произведенных в процессе сортировки. Рассмотрим подробно некоторые из них.
Сортировка массива методом простого выбора
При сортировке массива методом выбора применяется базовый алгоритм поиска максимального (минимального) элемента и его номера.
Алгоритм сортировки массива методом выбора:
- Для исходного массива выбрать максимальный элемент.
- Поменять его местами с последним элементом (после этого самый большой элемент будет стоять на своем месте).
- Повторить п.п. 1-2 с оставшимися n-1 элементами, то есть рассмотреть часть массива, начиная с первого элемента до предпоследнего, найти в нем максимальный элемент и поменять его местамис предпоследним (n-1)- м элементом массива, затем с оставшиеся (n-2)-мя элементами и так далее, пока не останется один элемент, уже стоящий на своем месте.
Для упорядочения массива потребуется (n-1) просмотров массива. В процессе сортировки будет увеличиваться отсортированная часть массива, а неотсортированная, соответственно, уменьшаться.
При сортировке данных выполняется обмен содержимого переменных. Для обмена необходимо создавать временную переменную, в которой будет храниться содержимое одной из переменных. В противном случае ее содержимое окажется утерянным.
Задача 1. Массив из 10 элементов отсортировать по возрастанию методом простого перебора.
Решение
Напишем процедуру. Входным параметром для неё будет массив. Он же будет и выходным параметром. Поэтому описываем его как параметр-переменная (с ключевым словом var).
В процедуре внешний цикл по i — определяет длину рассматриваемой части массива. Она будет изменяться от n до 2.
Внутренний цикл по j используется для поиска максимального элемента и его номера. В качестве начального значения максимума разумно взять значение последнего элемента рассматриваемой части массива.
Программный код процедуры:
Procedure sorting1(var a:myarray);
{Сортировка по возрастанию методом простого выбора}
var i,j:integer;
k,m:integer; {номер и значение максимального элемента}
begin
for i:= n downto 2 do{задаем длину рассматриваемой части массива}
begin
{ищем максимальный элемент и его номер}
k:=i; m:=a[i]; for j:= 1 to i-1 do
if a[j] > m then begin k:=j; m:=a[k] end;
{меняем местами найденный элемент и последний}
if k <> i then
begin a[k]:=a[i]; a[i]:= m; end;
end;
end;
end;
Программный код основной программы:
program primer_1;
const n = 10;
type myarray = array[1..n] of integer;
var a:myarray;
Procedure sorting1(var a:myarray);
{Линейная сортировка (сортировка отбором)}
...
begin {main}
writeln('Введите исходный массив:');
for i:=1 to n do read(a[i]);
sorting1(a);
writeln('Отсортированный массив:');
for i:=1 to 10 do write(a[i],' ');
writeln;
end.
Процесс упорядочения элементов в массиве по возрастанию методом отбора:
| Номер элемента | 1 | 2 | 3 | 4 | 5 |
| Исходный массив | 8 | 7 | 5 | 4 | 2 |
| Первый просмотр | 2 | 7 | 5 | 4 | 8 |
| Второй просмотр | 2 | 4 | 5 | 7 | 8 |
| Третий просмотр | 2 | 4 | 5 | 7 | 8 |
| Четвертый просмотр | 2 | 4 | 5 | 7 | 8 |
При упорядочивании массива по убыванию необходимо перемещать минимальный элемент. Для чего в алгоритме нахождения максимального элемента достаточно знак «>» поменять на знак «<«.
Сортировка массива методом простого обмена (методом пузырька)
Наиболее известным методом сортировки является сортировка пузырьковым методом. Его популярность объясняется запоминающимся названием и простым алгоритмом.
Метод основан на том, что в процессе исполнения алгоритма более «легкие» элементы массива постепенно «всплывают».
Особенностью данного метода является сравнение не каждого элемента со всеми, а сравнение в парах соседних элементов. Выполняется несколько последовательных просмотров массива от начала к концу. Если соседние элементы расположены «неправильно», то они меняются местами.
Алгоритм сортировки массива по возрастанию методом простого обмена:
- Начнем просмотр с первой пары элементов ( a[1] и a[2] ). Если первый элемент этой пары больше второго, то меняем их местами, иначе оставляем без изменения. Затем берем вторую пару элементов ( a[2] и a[3] ), если второй больше третьего, то также меняем их, далее сравниваем третий и четвертый, и если третий больше четвертого, меняем их местами, и т.д. Последними сравниваем (n-1)-ый и n-ый элементы.При первом обходе массива будут просмотрены все пары элементов массива a[i] и a[i+1] для i от 1 до (n-1). В результате максимальный элемент массива переместится в конец массива.
- Поскольку самый большой элемент находится на своем месте, рассмотрим часть массива без него, то есть с первого до (n-1) — го элемента.Повторим предыдущие действия для этой части массива, в результате чего второй по величине элемент массива переместится на последнее место рассматриваемой части массива, то есть на ( n-1 ) — е место во всем массиве.
- Эти действия продолжают до тех пор, пока количество элементов в текущей части массива не уменьшится до двух. В этом случае необходимо выполнить последнее сравнение и упорядочить последние два элемента.
Нетрудно заметить, что для преобразования массива, состоящего из n элементов, необходимо просмотреть его n–1 раз, каждый раз уменьшая диапазон просмотра на один элемент.
Ниже приведен текст процедуры сортировки массива по возрастанию методом пузырька.
procedure sorting2(var a:myarray);
var k,i,t:integer;
begin
for k := 1 to n-1 do {цикл по номеру просмотра}
for i:=1 to n-k do
{Если текущий элемент больше следующего, поменять местами}
if a[i] > a[i+1] then
begin
t:=a[i];
a[i]:=a[i+1];
a[i+1]:=t;
end;
end;
Для упорядочения элементов массива по убыванию их значений необходимо при сравнении элементов массива знак «>» заменить на «<«.
Процесс упорядочения элементов в массиве по возрастанию методом обмена:
| Номер элемента | 1 | 2 | 3 | 4 | 5 |
| Исходный массив | 8 | 7 | 5 | 4 | 2 |
| Первый просмотр | 7 | 5 | 4 | 2 | 8 |
| Второй просмотр | 5 | 4 | 2 | 7 | 8 |
| Третий просмотр | 4 | 2 | 5 | 7 | 8 |
| Четвертый просмотр | 2 | 4 | 5 | 7 | 8 |