Умножение в разных системах счисления опять-таки очень похоже на привычное умножение в десятичной системе счисления. Чтобы уметь хорошо умножать и получать правильный ответ нужно иметь складывать числа. Без операции сложение невозможно посчитать умножение в столбик.
Для начала стоит повторить, как же происходит умножение в десятичной системе счисления, а потом уже разобраться с другими.
Сама по себе операция умножения проводится поразрядным умножением одного числа на каждый разряд другого. После чего полученные числа складываются между собой.
Если при сложении у нас переносится “десяток” в следующий разряд при десяти или более.
При умножении же пока первое произведение при расчёте больше основания системы счисления, то из него вычитается это основание. Количество “вычитаний” переносится в следующий разряд, а то что осталось, после вычитания, спускается вниз.
Умножение в десятичной системе счисления
Произведём умножение двух десятичных чисел: 67 и 54. Операцию будем производить в столбик.
Как можем увидеть в данном примере, сначала посчитали два произведения, а далее уже их суммируем.
Разберём действия поэтапно:
- 4 * 7 = 28 (28 – 10 – 10 = 8) → т.к. два вычитания, то двойка идёт в следующий разряд;
- 4 * 6 + 2 = 26 (26 – 10 – 10 = 6) → т.к. два вычитания, то двойка идёт в следующий разряд;
- Просто спускаем двойку;
- 5 * 7 = 35 (35 – 10 – 10 – 10 = 5) → т.к. три вычитания, то тройка идёт в следующий разряд;
- 5 * 6 + 3 = 33 (33 – 10 – 10 – 10 = 3) → т.к. три вычитания, то тройка идёт в следующий разряд;
- Спускаем тройку;
- Складываем полученные числа и получаем ответ.
Умножение в пятеричной системе счисления
Произведём умножение в пятеричной системе счисления. Возьмём два числа 33 и 44. Действия также будем проводить в столбик. Если в десятичной системе счисления переносили десяток по достижению десяти или больше, то здесь по достижению пяти и более.
Соответственно, вычитать будем уже не 10, а пять. До тех пор, пока не получим число меньше 5.
Разберём действия поэтапно:
- 4 * 3 = 12 (12 – 5 – 5 = 2) → т.к. два вычитания, то двойка идёт в следующий разряд;
- 4 * 3 + 2 = 14 (14 – 5 – 5 = 4) → т.к. два вычитания, то двойка идёт в следующий разряд;
- Двойку просто спускаем;
- 4 * 3 = 12 (12 – 5 – 5 = 2) → т.к. два вычитания, то двойка идёт в следующий разряд;
- 4 * 3 + 2 = 14 (14 – 5 – 5 = 4) → т.к. два вычитания, то двойка идёт в следующий разряд;
- Двойку просто спускаем;
- Складываем полученные числа и получаем ответ.
Умножение в шестнадцатеричной системе счисления
Особенным умножение будет в шестнадцатеричной системе счисления из-за “буквенных” цифр. Страшно в первый раз увидеть произведение букв из которого появляются числа. Но такова уж данная система.
Перемножим два шестнадцатеричных числа AB и CD.
Распишем действия поэтапно:
- D * B → 13 * 11 = 143 (143 – 16×8 = 15) → т.к. восемь вычитаний, то восьмёрка идёт в следующий разряд;
- D * A + 8 → 13 * 10 + 8 = 138 (130 – 16×8 = 10) → т.к. восемь вычитаний, то восьмёрка идёт в следующий разряд;
- Просто спускаем восьмёрку;
- C * B → 12 * 11 = 132 (132 – 16×8 = 4) → т.к. восемь вычитаний, то восьмёрка идёт в следующий разряд;
- C * A + 8 = 12 * 10 + 8 = 128 (128 – 16×8 = 0) → т.к. восемь вычитаний, то восьмёрка идёт в следующий разряд;
- Восьмёрку спускаем;
- Складываем полученные числа и получаем ответ.
С другими системами счисления операция умножения работает аналогично. Главное — помнить о правилах переноса в следующий разряд при умножении и сложении.
Понравилась статья? Хочешь разбираться в информатике, программировании и уметь работать в разных программах? Тогда ставь лайк, подпишись на канал и поделись статьей с друзьями!
Читайте также:
#информатика #системы счисления #школьная информатика #образование #арифметика #умножение
Презентация по дисциплине «Основы теории информации» на тему «Пятеричная система счисления»
Презентация по дисциплине«Основы теории информации»на тему«Пятеричная система счисления»
Выполнил:
Студент гр. Кс117
Корешков Никита Николаевич
Принял:
Ситова Анна Алексеевна
Департамент образования Владимирской области
Государственное автономное професиональное образовательное учреждение Владимирской области
«Гусь-Хрустальный технологический колледж» им. Г.Ф. Чехлова
Гусь- Хрустальный, 2019
Содержание Определение Применение
Содержание
Определение
Применение
Возможности перевода
Арифметические действия
Список источников
2
Определение Пятеричная система счисления – позиционная система счисления с основанием 5
1.Определение
Пятеричная система счисления – позиционная система счисления с основанием 5. Число в пятеричной системе изображается пятью цифрами: 0, 1, 2, 3, 4. В этой системе цифра 4 — наибольшая (как 9 — в десятичной), единица высшего разряда не в 10, а в 5 раз больше единицы низшего.
При изображении числа в пятеричной системе счисления, на первом месте справа стоят простые единицы (не свыше 4), на втором — не десятки, а пятерки, на третьем — не сотни, а «25» и т.д.
3
Применение Очевидна связь пятеричной системы со строением человеческой руки
2.Применение
Очевидна связь пятеричной системы со строением человеческой руки.
По свидетельству известного исследователя Африки Стэнли, у ряда африканских племен была распространена пятеричная система счисления. Долгое время пользовались этой системой счисления и в Китае. Также пятеричная система использовалась в Древнем Риме.
4
Применение в римской сисчтеме счисления 5
Применение в римской сисчтеме счисления
5
Возможность перевода Перевод из пятеричной
3.Возможность перевода
Перевод из пятеричной СС в десятеричную СС осуществляется по формуле:
Aq = an-1*qn-1 + an-2*qn-2 + … + a0*q0 + a-1*q-1+ a-2*q-2+ … +a-m*q-m
Где ai – цифры СС
n и m число целых и дробных разрядов
Пример:
4405 перевести в десятеричную СС
4405=0*50+4*51+4*52= 0+20+100=12010
Ответ: 4405= 12010
6
Возможность перевода Перевод из десятеричной
3.Возможность перевода
Перевод из десятеричной СС в пятеричную СС производиться с помощью алгоритма перевода из десятичной системы в пятеричную:
Выполнить деление исходного числа на 5. Если результат деления больше или равен 5, продолжать делить его на 5 до тех пор, пока результат деления не станет равен 1,2,3 или 4. Выписать результат последнего деления и все остатки от деления в обратном порядке в одну строку.
Пример:
4610 переведем в пятеричную СС
46:5=9(остаток 1)
9:5=1(ост. 4)
1:5=0(ост. 1)
Ответ: 4610= 1415
7
Арифметические действия Сложение и вычитание
4.Арифметические действияСложение и вычитание
Составим таблицу сложения для пятеричных цифр (будем использовать ее при сложении и вычитании чисел в «столбик»).
|
0 |
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
10 |
|
2 |
3 |
4 |
10 |
11 |
|
3 |
4 |
10 |
11 |
12 |
|
4 |
10 |
11 |
12 |
13 |
8
Арифметические действия Пример операции сложения:
4.Арифметические действия
Пример операции сложения:
Найдем 2345 + 3125. Складываем поразрядно в «столбик», используя таблицу сложения. Важно правильно записать числа друг под другом поразрядно справа налево.
Ответ:2345+3125=11025
9
Арифметические действия Пример операции вычитания:
4.Арифметические действия
Пример операции вычитания:
Найдем 2035 – 345. Вычитать будем поразрядно в «столбик», используя таблицу сложения. Важно правильно записать числа друг под другом поразрядно справа налево.
Ответ: 2035-345=1145
10
Арифметические действия Умножение
4.Арифметические действияУмножение
Составим таблицу умножения для пятеричной системы счисления (цифру 0 не включаем, т.к. умножение на 0 всегда равно 0).
|
0 |
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
|
2 |
2 |
4 |
11 |
13 |
|
3 |
3 |
11 |
14 |
22 |
|
4 |
4 |
13 |
22 |
31 |
Пример операции умножения:
135*245 . Умножать будем в «столбик», используя таблицу умножения. Важно правильно записать числа друг под другом поразрядно справа налево.
Ответ: 135*245 =4225
11
Арифметические действия Деление
4.Арифметические действияДеление
Рассмотрим так же пример деления:
Разделим 124215 на 325
Ответ:124215: 325=2135
12
Список источников Worksbase [электронный ресурс]
5.Список источников
Worksbase [электронный ресурс]. – Режим доступа: http://worksbase.ru. – Заглавие с экрана. – (Дата обращения: 4.02.2019)
Uzluga [электронный ресурс]. – Режим доступа: http://uzluga.ru Заглавие с экрана. – (Дата обращения: 4.02.2019)
Wikipedia [электронный ресурс]. – Режим доступа: https://ru.wikipedia.org – Заглавие с экрана. – (Дата обращения: 4.02.2019)
Studfiles [электронный ресурс]. – Режим доступа: https://studfiles.net – Заглавие с экрана. – (Дата обращения: 4.02.2019)
Yaklass [электронный ресурс]. – Режим доступа: https://www.yaklass.ru – Заглавие с экрана. – (Дата обращения: 4.02.2019)
13
Арифметические
операции в рассматриваемых позиционных
системах счисления выполняются по
законам, известным из десятичной
арифметики. Двоичная система счисления
имеет основание 2, и для записи чисел
используются всего две цифры 0 и 1 в
отличие от десяти цифр десятичной
системы счисления.
Рассмотрим
сложение одноразрядных чисел: 0+0=0, 0+1=1,
1+0=0. Эти равенства справедливы как для
двоичной системы, так и для десятичной
системы. Чему же равно 1+1? В десятичной
системе это 2. Но в двоичной системе нет
цифры 2! Известно, что при десятичном
сложении 9+1 происходит перенос 1 в старший
разряд, так как старше 9 цифры нет. То
есть 9+1=10. В двоичной системе старшей
цифрой является 1. Следовательно, в
двоичной системе 1+1=10, так как при сложении
двух единиц происходит переполнение
разряда и производится перенос в старший
разряд. Переполнение разряда наступает
тогда, когда значение числа в нем
становится равным или большим основания.
Для двоичной системы это число равно 2
(102=210).
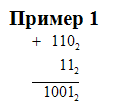
Продолжая
добавлять единицы, заметим: 102+1=112,
112+1=1002
– произошла “цепная реакция”, когда
перенос единицы в один разряд вызывает
перенос в следующий разряд.
Сложение
многоразрядных
чисел происходит по этим же правилам с
учетом возможности переносов из младших
разрядов в старшие.
Вычитание
многоразрядных
двоичных чисел производится с учетом
возможных заёмов
из старших разрядов.
Действия
умножения и деления чисел в двоичной
арифметике можно выполнять по общепринятым
для позиционных систем правилам.
В
основе правил арифметики любой позиционной
системы лежат таблицы
сложения и умножения одноразрядных
чисел.
Таблицы,
аналогичные таблицам арифметических
операций в двоичной системе счисления
(см. п.1.3), составляются для любой
позиционной системы счисления. Пользуясь
такими таблицами, можно выполнять
действия над многозначными числами.
Пример
4.Выполнить
действия в пятеричной системе счисления:
3425+235;
2135.55.
Решение:
Составим
таблицы сложения и умножения для
пятеричной системы счисления:
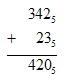
Рассуждаем
так: два плюс три равно 10 (по таблице); 0
пишем, 1 – в уме. Четыре плюс два равно 11
(по таблице), да еще один, 12. 2 пишем, 1 – в
уме. Три да один равно 4 (по таблице).
Результат – 420.
Рассуждаем
так: трижды три – 14 (по таблице); 4 пишем,
один – в уме. Трижды один дает 3, да плюс
один, – пишем 4. Дважды три (по таблице) –
11; 1 пишем, 1 переносим влево. Окончательный
результат – 1144.
Если
числа, участвующие в выражении,
представлены в разных системах, нужно
сначала привести их к одному основанию.
Пример
5.Сложить
два числа: 178
и 1716.
Решение:
Приведем
число 1716
к основанию 8 посредством двоичной
системы (пробелами условно обозначено
деление на тетрады и триады):
1716=101112=101112=278.
Выполним
сложение в восьмеричной системе:
Таким
образом, арифметические действия в
позиционных системах счисления
выполняются по общим правилам. Необходимо
только помнить, что перенос в следующий
разряд при сложении и заем из старшего
разряда при вычитании определяются
величиной основания системы счисления.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Получить развернутую форму числа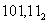 
.
Решение: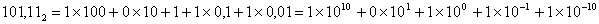 
.
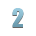Перевести число 
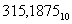в восьмеричную систему счисления.
Решение: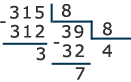 
– 
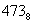целая часть числа; 
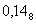– дробная часть числа.
.
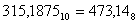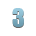Перевести числа 
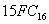в десятичную систему счисления.
Решение: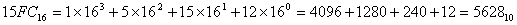 
;
.
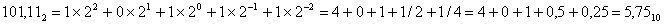Перевести число 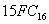в двоичную систему счисления.
Решение: для решения необходимо каждую цифру шестнадцатеричного числа заменить на соответствующую ей четверку двоичных знаков (там, где знаков меньше четырех, слева добавить нули).
; 
;
; 
.
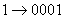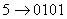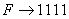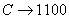
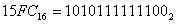Перевести число 
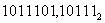в шестнадцатеричную систему счисления.
Решение: для решения необходимо разделить целую часть данного числа на группы по четыре цифры справа налево, а дробную часть числа аналогично по четыре двоичных знака от запятой слева направо (если в крайней левой или правой группе окажется меньше четырех цифр, то дополнить их нулями).
0101 1101, 1011 1000 ⇒ 5D,В816.
Сложить числа представленные в пятеричной системе счисления: 
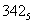и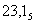 
.
Ответ: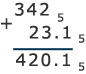 
Решение: для того, чтобы производить арифметические операции над пятеричными числами, надо знать таблицу сложения и умножения в пятеричной системе.
Таблицы сложения и умножения в пятеричной системе счисления выглядят так:
|
Таблица сложения |
Таблица умножения |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Умножить числа представленные в пятеричной системе счисления
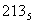и
.
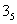Решение: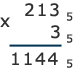 
.
