-
Составление таблицы значений функции с использованием Мастера функций
Построим
таблицу значений функции
с шагом 1.
а)
создание числовой последовательности
Вычисление
значений функции по точкам начинается,
как правило, с подготовки последовательности
чисел – значений аргумента функции. В
Ехсеl существует несколько
способов создания последовательности.
1-й
способ. Можно использовать операцию
заполнения. Если последовательность
представляет собой арифметическую
прогрессию, операция выполняется
следующим образом:
-
Введите
в первые две ячейки последовательности
числовые величины. -
Выделите
ячейки. -
Установите
указатель мыши на маркер заполнения +
и выделите весь диапазон, в котором
нужно разместить последовательность.
Программа автоматически определит шаг
прогрессии и заполнит ячейки данными.
2-й
способ. Задача
выполняется так:
-
Введите
в ячейку значение первого элемента
последовательности. -
Выберите
команду Правка>Заполнить>Прогрессия.
Откроется диалог Прогрессия. -
Задайте
в этом окне следующие параметры:
расположение последовательности (по
строкам или по столбцам), вид прогрессии,
величину шага прогрессии, конечное
(предельное) значение последовательности.
Нажмите ОК.
Этот
способ удобен тем, что границы диапазона,
в котором создается последовательность
чисел, могут уходить за пределы экрана.
Итак,
значения аргумента х будут -5, -4, -3,
-2, -1, 0, 1, 2, 3, 4, 5. Сначала создадим исходную
последовательность значений аргумента
одним из вышеприведенных способов и
разместим в диапазоне ячеек А1:К1, т.е. в
строке таблицы. Можно выбрать любой
другой шаг приращения аргумента,
соответственно при этом увеличится
число ячеек, где необходимо хранить
рассчитанные значения.
Последовательность
значений аргумента создана. Далее:
б)
расчет значений функции.
Теперь
можно построить последовательность
значений функции, вычисленных по формуле.
Для хранения расчетных значений функции
будем использовать ячейки с адресами
А2:К2, т.е. следующую строку.
Теперь
можно рассчитать значения функции у
для этого введем в предварительно
выделенную ячейку А2 формулу =-3*А1^2+5*А1-9
и нажмем на кнопку Ввод. Затем
установив указатель мыши на маркер
заполнения ячейки А2, выделить диапазон
В2:К2. В каждую ячейку диапазона запишется
указанная формула, а ссылки в формулах
будут настроены автоматически. Формулы
в ячейках примут вид соответственно:
для В2=-3*В1^2+5*В1-9,
для С2=-3*С1^2+5*С1-9,
и т. д.
Формула,
по которой производится вычисление,
может быть сколь угодно сложной.
Самостоятельная
работа.
Построить
таблицу расчетных значений функции
для значений аргумента х от 0 до 1 с
шагом 0,1. При решении задачи воспользуйтесь
приложением.
Подсказка:
подумайте почему формула для ячейки А2
будет иметь следующий вид: =EXP(-A1)*SIN(10*A1)
Построение
графиков и диаграмм.
Электронные
таблицы позволяют визуализировать
данные, размещенные на рабочем листе,
в виде графика или диаграммы. Графики
и диаграммы наглядно отображают
зависимости между данными, что облегчает
восприятие и помогает при анализе и
сравнении данных.
Построение
графиков. Графики выбирают в тех
случаях, когда хотят отобразить изменение
данных с течением времени. Графики
позволяют анализировать закономерности
изменения величин.
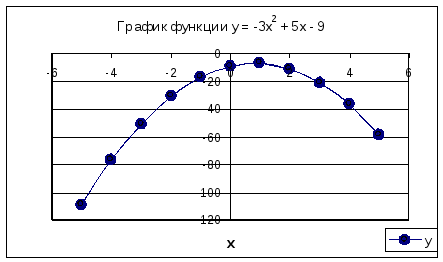
Мы
создали таблицу значений функции
с шагом 1.
|
x |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
y |
-109 |
-77 |
-51 |
-31 |
-17 |
-9 |
-7 |
-11 |
-21 |
-37 |
-59 |
Для
построения графика используется Мастер
диаграмм.
-
Выделить
диапазон ячеек A1:L2,
содержащих данные. Запустить Мастер
диаграмм с помощью команды
[Вставка-Диаграмма…] или кнопки
на панели инструментов Стандартная. -
На
первом шаге необходимо выбрать тип
диаграммы. В списке Тип: выбираем пункт
Точечная. В окне Вид: выбираем Точечная
диаграмма со значениями, соединенными
сглаживающими линиями. -
На
втором шаге мы увидим, как будет
выглядеть наша диаграмма. Справа от
диаграммы появляется Легенда, которая
содержит необходимые пояснения к
диаграмме. Окно Диапазон: содержит
диапазон адресов ячеек, содержащих
данные для диаграммы. Этот диапазон
можно изменить. -
На
третьем шаге мы можем уточнить детали
отображения диаграммы, изменить формат
диаграммы и легенды (размеры, шрифт,
цвета, подписи и так далее). -
На
четвертом шаге необходимо определить,
где разместить диаграмму: на отдельном
листе или на листе вместе с данными.
Наконец, в результате мы получим готовую
диаграмму (график).
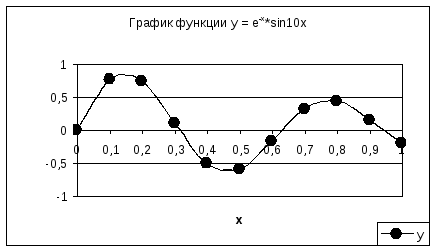
Далее
построим график функции
для значений аргумента х от 0 до 1 с
шагом 0,1. Сначала подготовим таблицу
данных значений аргумента и функции.
|
X |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
y |
0 |
0,76 |
0,74 |
0,10 |
-0,51 |
-0,58 |
-0,15 |
0,33 |
0,44 |
0,17 |
-0,20 |
Теперь
по вышеуказанному алгоритму построим
график функции.
Построение
столбцовой диаграммы. Диаграммы могут
быть различных типов и соответственно
представлять данные в различной форме.
Для каждого набора данных важно правильно
подобрать тип создаваемой диаграммы.
Для наглядного сравнения различных
величин используются линейчатые
диаграммы. Например, с помощью линейчатой
диаграммы можно наглядно представить
данные о численности населения различных
стран.
Для
отображения величин частей от целого
применяется круговая диаграмма. Диаграммы
могут располагаться как на листе с
данными (внедренные диаграммы), так и
на отдельных листах. Диаграммы связаны
с исходными данными на рабочем листе и
обновляются при обновлении данных на
рабочем листе.
Для
построения для построения диаграмм
используется Мастер диаграмм.
|
Объем за |
Всего за |
|||
|
1 |
2 |
3 |
4 |
|
|
50 |
100 |
400 |
200 |
750 |
|
70 |
140 |
450 |
270 |
930 |
-
Выделить
диапазон ячеек A4:D5,
содержащих данные только по кварталам
двух лет. Запустить Мастер диаграмм с
помощью команды [Вставка-Диаграмма…]
или кнопки
на панели инструментов Стандартная. -
На
первом шаге необходимо выбрать тип
диаграммы. На вкладке СТАНДАРТНЫЕ в
списке ТИП: выбираем пункт ДИАГРАММА.
В окне ВИД выбираем диаграмму, выбранную
по умолчанию (она отображается в
инверсном виде). Нажимаем кнопку ДАЛЕЕ.
Внимание! На вкладке НЕСТАНДАРТНЫЕ
можно выбрать и построить другие типы
диаграмм. Нажимаем кнопку ДАЛЕЕ. -
На
втором шаге на вкладке ДИАПАЗОН
ДАННЫХ мы увидим, как будет выглядеть
наша диаграмма. Окно ДИАПАЗОН содержит
диапазон адресов ячеек, содержащих
данные для диаграммы. При необходимости
этот диапазон можно изменить. Справа
от диаграммы появляется Легенда, которая
содержит необходимые пояснения к
диаграмме. Выберем вкладку РЯД и обратим
внимание на список РЯД и текстовое поле
ИМЯ. В списке РЯД по умолчанию выбран
Ряд1. Поскольку Ряд1 – данные за 2004г.,
то в текстовое поле ИМЯ введем 2004 г.,
затем выберем Ряд2 и в текстовое поле
ИМЯ введем 2005 г. Таким образом, содержание
легенды на диаграмме становится
понятным. В текстовом поле ПОДПИСИ ПО
ОСИ Х щелкнем курсором и введем номера
кварталов, т.е. адреса ячеек (A3:D3),
в которых содержатся эти данные. Проще
всего это делать выделением ячеек
методом протаскивания при нажатой
левой кнопке мыши. В результате в этом
окне появится формула, которую надо
было бы вводить вручную. Нажимаем кнопку
ДАЛЕЕ. -
На
третьем шаге можно уточнить детали
отображения диаграммы: заголовок
диаграммы, изменить формат диаграммы
и легенды, подписи осей и т.д. Итак,
выбираем вкладку ЗАГОЛОВКИ и в текстовое
окно НАЗВАНИЕ ДИАГРАММЫ вводим название
таблицы. Соответственно в текстовые
окна ОСЬ Х (КАТЕГОРИЙ) и ОСЬ Y
(ЗНАЧЕНИЙ) введем «кварталы» и «тыс.
руб.». Нажимаем кнопку ДАЛЕЕ. -
На
четвертом шаге необходимо определить,
где поместить диаграмму: на отдельном
листе или на листе вместе с данными.
Наконец, нажав на кнопку ГОТОВО, мы
получим построенную диаграмму.
Д
ля
форматирования различных параметров
диаграммы удобно пользоваться правой
кнопкой мыши и контекстным меню. Щелкнув
правой кнопкой на выделенном объекте,
в контекстном меню обеспечивается
доступ к системе диалоговых окон.
Основными являются:
-
ФОРМАТ
ОБЛАСТИ ДИАГРАММЫ…; -
ФОРМАТ
ОБЛАСТИ ПОСТРОЕНИЯ…; -
ФОРМАТ
РЯДОВ ДАННЫХ…; -
ФОРМАТ
ЗАГОЛОВКА ДИАГРАММЫ…; -
ФОРМАТ
ЛЕГЕНДЫ…; -
ФОРМАТ
НАЗВАНИЯ ОСИ…; -
ФОРМАТ
ОСИ…
Построение
круговой диаграммы. Для построения
этой диаграммы воспользуемся данными
предыдущей задачи. Возьмем для построения
круговой диаграммы, данные только за
2005 г. Для работы будем использовать
МАСТЕР ДИАГРАММ. Выполним упражнение
самостоятельно.
|
Объем за |
Всего за |
|||
|
1 |
2 |
3 |
4 |
|
|
70 |
140 |
450 |
270 |
930 |
Для
наглядности отображают процентное
значение каждого из секторов диаграммы.
В диалоговом окне ФОРМАТ РЯДОВ ДАННЫХ…,
перейдем на вкладку ПОДПИСИ ДАННЫХ и
на панели ВКЛЮЧИТЬ В ПОДПИСИ установим
флажок ДОЛИ. Должна получиться примерно
такая диаграмма.
Надстройки
в электронных таблицах
Возможности
электронных таблиц не ограничиваются
вычислениями по формулам и построением
диаграмм и графиков. С помощью надстроек
электронных таблиц можно приближенно
с заданной точностью решать уравнения
методом подбора параметра, решать задачи
оптимизационного моделирования методом
поиска решений и так далее.
Подбор
параметра.
Подбор
параметра является
одним из инструментов анализа «что,
если». Этот метод используется при
поиске значения аргумента функции,
который обеспечивает требуемое значение
функции. При подборе параметра изменяется
значение в ячейке аргумента функции до
тех пор, пока значение в ячейке самой
функции не будет возвращать нужный
результат.
В
качестве примера рассмотрим поиск корня
уравнения х3
– sin x – 0,5 = 0. Представим функцию в табличной
форме, построим ее график, который
позволит определить корень уравнения
грубо приближенно. Для поиска решения
с заданной точностью используем метод
Подбор
параметра. Точность
подбора зависит от заданной точности
представления чисел в ячейках таблицы.
Подбор
параметра
-
Представить
функцию в табличной форме. -
Построить
график функции. По графику грубо,
приближенно можно определить, что
уравнение имеет корень х = 1. Методом
подбора параметра необходимо определить
значение аргумента х, при котором
значение функции у равно нулю. -
Ввести
команду [Сервис-Подбор параметра…]. -
На
панели ПОДБОР ПАРАМЕТРА в текстовое
поле УСТАНОВИТЬ В ЯЧЕЙКЕ введем
абсолютный адрес значения функции
близкого к нулю. Сделать это можно
просто щелкнув левой кнопкой мыши на
требуемой ячейке. В поле ЗНАЧЕНИЕ ввести
требуемое значение функции (в данном
случае 0). В поле ИЗМЕНЯЯ ЗНАЧЕНИЕ ЯЧЕЙКИ
ввести соответствующий абсолютный
адрес ячейки (в ячейке хранится значение
аргумента), в которой будет изводиться
подбор значения аргумента. -
На
панели Результат подбора параметра
будет выведена информация о величине
подбираемого и подобранного значений. -
В
ячейке аргумента появится подобранное
значение 1, 1185.
Таким
образом, корень уравнения х = 1,1185 найден
с заданной точностью.
Практическое
задание. Методом
подбора параметра решить уравнение х2
– sin x + 0,1 = 0 с точностью четырех знаков
после запятой.
Логические
функции
В
первом семестре мы изучали логические
операции (умножения, сложения, отрицания)
и их таблицы истинности. В электронных
таблицах имеются соответствующие
логические функции, с помощью которых
достаточно просто построить таблицы
истинности логических операций.
Аргументами
логических функций являются логические
значения ИСТИНА и ЛОЖЬ. Логические
значения, в свою очередь, могут быть
получены как результат вычисления
значений логических выражений. Например,
для логического выражения 10>5 результатом
будет логическое значение ИСТИНА, а для
логического выражения А1<А2 (где в
ячейке А1 хранится число 10, а в ячейке
А2 – число 5) – значение ЛОЖЬ.
Логическая
функция «И» имеет в качестве аргументов
логические значения, которые могут быть
истинными или ложными, и задается
формулой =И(лог
знач1; лог знач2;…). Принимает
значение ИСТИНА тогда и только тогда,
когда все аргументы имеют значение
ИСТИНА.
Логическая
функция «ИЛИ» имеет в качестве аргументов
логические значения и задается формулой
= ИЛИ(лог знач1;
лог знач2; …). Принимает
значение ИСТИНА, если хотя бы один из
аргументов имеет значение ИСТИНА.
Логическая
функция «НЕ» имеет один аргумент и
задается формулой =НЕ(лог
знач). Принимает
значение ИСТИНА, если аргумент имеет
значение ЛОЖЬ, и наоборот. Например,
значение функции =НЕ(10>5) – ЛОЖЬ. Построим
с помощью электронных таблиц таблицу
истинности операции логического
умножения, используя логическую функцию
«И».
Построение
таблицы истинности операции логического
умножения.
-
В
пары ячеек (А1,В1), (А2,В2), (А3,В3), (А4,В4)
ввести пары значений аргументов
логической операции (ЛОЖЬ, ЛОЖЬ), (ИСТИНА,
ЛОЖЬ), (ЛОЖЬ, ИСТИНА) и (ИСТИНА, ИСТИНА). -
В
ячейку С1 ввести формулу логической
функции «И» =И(А1;В1). -
Скопировать
формулу в ячейки С2, С3 и С4. -
Значением
этой функции в трех случаях является
ЛОЖЬ и только в последнем – ИСТИНА. Мы
получили таблицу истинности операции
логического умножения.
Практические
задания
В
электронных таблицах получить таблицы
истинности операций логического сложения
и логического отрицания.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
10.02.2015120.83 Кб1038.doc
- #
- #
- #
- #
- #
13.11.2018151.55 Кб24.doc
- #
Подставляешь в функцию число и считаешь, потом число на 1 больше и считаешь, потом еще на 1 больше и так далее
Tseluevaolga_zn
22 Апр, 18
Функция задана формулой
y
=
4
−
x
2
, где −3 ⩽ x ⩽ 2.
1) Составьте таблицу значений функции с шагом 1.
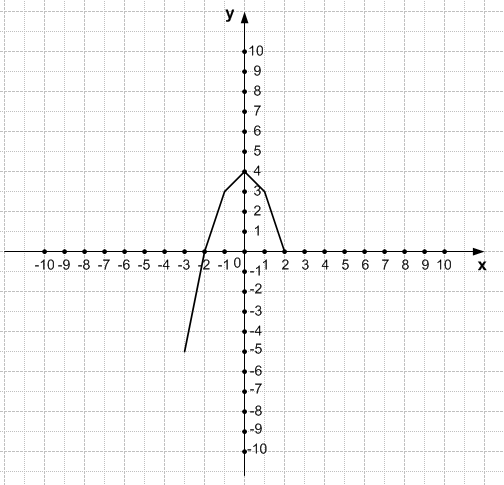
2) Постройте график функции, пользуясь составленной таблицей.
3) Пользуясь графиком, найдите, при каких значениях аргумента значения функции меньше нуля и при каких − больше нуля.
4) Пользуясь графиком функции, укажите область значений функции.
reshalka.com
Алгебре 7 класс Мерзляк. Номер №833
Решение 1

y
1
=
4
−
x
1
2
=
4
−
(
−
3
)
2
=
4
−
9
=
−
5
;
y
2
=
4
−
x
2
2
=
4
−
(
−
2
)
2
=
4
−
4
=
0
;
y
3
=
4
−
x
3
2
=
4
−
(
−
1
)
2
=
4
−
1
=
3
;
y
4
=
4
−
x
4
2
=
4
−
0
2
=
4
−
0
=
4
;
y
5
=
4
−
x
5
2
=
4
−
1
2
=
4
−
1
=
3
;
y
6
=
4
−
x
6
2
=
4
−
2
2
=
4
−
4
=
0
.
Решение 2
Решение 3
при −3 ⩽ x < −2 значения функции меньше нуля;
при −2 < x < 2 значения функции больше нуля.
Решение 4
Область значения функции: −5 ⩽ y ⩽ 4.
Задания к лабораторной работе
по Excel
Оглавление
Задание №1
Варианты заданий
Задание №2
Варианты заданий
Задание №3
Варианты заданий
Задание №4
Задание №1
1. Вычислить значение функции
для х=1 и у=2 двумя способами:
а) в ячейку А1 запишем 1 значение х, а в В1 запишем значение у 2 и тогда в ячейку С1 запишем вышеуказанную формулу, ввод формулы всегда начинается со знака = , значок ^- операция возведение в степень, *- операция умножение
б)
Для записи формулы по варианту б) необходимо ячейкам A2 и B2 присвоить имена соответственно х и у. Для этого:
Выделить ячейку, в которую будем записывать значение х и выполнить
Вставка-Имя-Присвоить(в Office-2003)
Формула- выбрать Присвоить (в Office-2007)
,откроется диалоговое окно, в котором подтвердить новое имя ячейки х, аналогично выполнить для у и записать формулу в ячейку С2, при нажатии Enter получим результат.
Перейти на Лист2.
2.а) составить таблицу, содержащую фамилии студентов ( не менее 5 фамилий),их рост и возраст;
б) найти средний рост и возраст;
в) построить вертикальную столбчатую диаграмму на одном листе с данными, содержащую рост и возраст каждого студента.
Среднее значение роста вычислить с помощью мастера функций ,используя функцию Срзнач, а среднее значение возраста вычислить с помощью автосуммы : вычислить сумму и разделить ее на количество
Перейти на Лист3.
3. а) составить таблицу значений функции y=sin(x), для х принадлежащего отрезку [20o,60o] c шагом h =3o;
б) построить по данным таблицы график функции y=sin(x)
Столбцы А и В заполнить ,используя автозаполнение: для этого поместить в ячейки В2 и В3 соответственно 20 и 23 ,выделить обе ячейки ,подвести указатель мыши к маленькому черному квадрату и нажать левую кнопку мыши и ,не отпуская ее ,провести по всем ячейкам данного столбца, таким же образом ,заполнить столбец А.Установить курсор в ячейку С2,поместить в нее знак = и вызвать мастер функций.
Вставка-Мастер функций (в Office-2003)
Формулы (в Office-2007)
Выбрать категорию функций Математическая в открывшемся диалоговом окне и в списке справа отыскать функцию радианы для перевода углов из градусов в радианы. Откроется другое диалоговое окно, в котором необходимо указать адрес ячейки для которой выполняется операция. Адрес ячейки указать с помощью мыши. За черный квадрат распространить формулу на остальные ячейки столбца С.Аналогичные действия выполнить со столбцом D.
Для построения графика выделить отдельно столбцы Х(радианы) и У, используя клавишу Ctrl.
Вызвать мастер диаграмм: Вставка-Мастер диаграмм (в Office-2003)
Вставка (в Office-2007 )
выбрать Точечная, просмотреть все открывающиеся диалоговые окна и задать имя графику и ответить на все вопросы мастера. График построить на листе с исходными данными.
4. Создание макроса.
Вернуться на Лист2.
Удалить диаграмму и записать макрос создания диаграммы.
Выполнить команду
Сервис-Макрос-Начатьзапись (вOffice-2003)
Вид-Макросы-Записьмакроса (в Office-2007)
Появится диалоговое окно, в котором будет предложено дать имя макросу, можно оставить предложенное имя.
Выделить данные для диаграммы и вызвать мастер диаграмм, построить диаграмму и выполнить команду
Сервис-Макрос-Остановитьзапись (в Office-2003)
Вид-Макросы-Остановитьзапись.(в Office-2007)
Макрос будет записан. Его можно просмотреть или выполнить.
Сервис–Макросы-Макрос (в Office-2003)
Вид-Макросы-Макросы(в Office-2007)
выбрать из предложенного списка имя макроса:
— для просмотра текста- войти
-для выполнения — выполнить.
Перейти на Лист3 удалить график и создать самостоятельно макрос создания графика. Пиктограммы работы с макросами также можно найти на ленте Разработчик
5. Настройка рабочей панели для запуска макросов
Сервис-Настройка-Панели инструментов-Создать-Настраиваемая1 (в Office—2003)
В окне документа появится пустая панель.
Выбрать из Сервис-Настройка–Команда-Макросы (в Office-2003)
Появится настраиваемая кнопка для запуска макроса. Перенести кнопку на настраиваемую панель и с помощью контекстного меню назначить имя макроса, который будет связан с этой кнопкой. С помощью контекстного меню можно изменить вид кнопки и назначить ей другой макрос.
Создать кнопки запуска макросов для построения диаграммы и графика.
В Office-2007 можно кнопки вызова макросов поместить в панель быстрого доступа.
Если панель быстрого доступа отсутствует, то на пиктограмме Макросы(Вид) через контекстное меню добавить панель быстрого доступа, а если она есть, то настроить ее:
Открывается окно Параметры Excel, в котором выбратьНастройка, затем команду
Макросы (В окне Настройка панели быстрого доступа) и добавитькнопку для запуска макросов
Варианты индивидуальных заданий
1.а) Составить таблицу значений функции y=2sin(x)cos(x), для х принадлежащего отрезку [0o,360o] c шагом h =45o.
б) Построить по данным таблицы график функции y=2sin(x)cos(x).
в) Создать макрос графика.
2.а) Составить таблицу значений функции y=tg(x), для х принадлежащего отрезку [0o,180o] c шагом h =30o.
б) Построить по данным таблицы график функции y=tg(x).
в) Создать макрос графика.
3.а) Составить таблицу значений функции y=ex, для х принадлежащего отрезку [1,5] c шагом h =1.
б) Построить по данным таблицы график функции y=ex.
в) Создать макрос графика.
4.a) Составить таблицу значений функции y=sin(x)+cos(x), для х принадлежащего отрезку
[-180o,=180o] c шагом h =30o.
б) Построить по данным таблицы график функции y=sin(x)+cos(x).
в) Создать макрос графика.
5.a) Составить таблицу значений функции y=ln(x), для х принадлежащего отрезку [1,10] c шагом h =1.
б) Построить по данным таблицы график функции y=ln(x).
в) Создать макрос графика.
6.a) Составить таблицу значений функции y=xsin(x), для х принадлежащего отрезку [0o,360o] c шагом h =30o.
б) Построить по данным таблицы график функции y=xsin(x).
в) Создать макрос графика.
7.a) Составить таблицу значений функции y=xcos(x), для х принадлежащего отрезку
[-180o,360o] c шагом h =30o.
б) Построить по данным таблицы график функции y=xcos(x).
в) Создать макрос графика.
8.a) Составить таблицу значений функции y=sin2(x), для х принадлежащего отрезку [30o,180o] c шагом h =10o.
б) Построить по данным таблицы график функции y=sin2(x).
в) Создать макрос графика.
9.a) Составить таблицу значений функции y=cos2(x)+x, для х принадлежащего отрезку [20o,90o] c шагом h =5o.
б) Построить по данным таблицы график функции y=cos2(x)+x.
в) Создать макрос графика.
10.a) Составить таблицу значений функции y=ctg(x), для х принадлежащего отрезку
[-180o,180o] c шагом h =60o.
б) Построить по данным таблицы график функции y=ctg(x).
в) Создать макрос графика.
11.a). Составить таблицу значений функции y=tg(x)+ctg(x), для х принадлежащего отрезку [0o,360o] c шагом h =45o.
б) Построить по данным таблицы график функции y=tg(x)+ctg(x).
в) Создать макрос графика.
) Составить таблицу значений функции y=x 2sin(x), для х принадлежащего отрезку [20o,90o] c шагом h =5o.
б) Построить по данным таблицы график функции y=x 2sin(x).
в) Создать макрос графика.
13.a) Составить таблицу значений функции y=xln(x), для х принадлежащего отрезку [1,6] c шагом h =1.
б) Построить по данным таблицы график функции y=xln(x).
в) Создать макрос графика.
14.a) Составить таблицу значений функции y=exln(x), для х принадлежащего отрезку [2,20] c шагом h =2.
б). Построить по данным таблицы график функции y=exln(x);.
в) Создать макрос графика.
Задание №2
Работа с матрицами
1. Умножить матрицу А2,з на В3,з и получить матрицу С2,з
- Задаем значения элементам матриц А и В
- Выделяем место для результирующей матрицы С |
- В строку формул записываем знак =
- С помощью мастера функций находим функцию МУМНОЖ.
- Задаем для нее исходные данные (параметры) с помощью мыши
- Активизируем строку формул
- Нажимаем одновременно 3 клавиши .ctrl+shift+enter.
- Результат появляется в результирующей матрице
2. Найти для матрицы A транспонированную матрицу, используя функцию ТРАНСП
3. Для матрицы В найти обратную матрицу с помощью функции МОБР
4. Решение системы уравнений методом обращения матриц.
Задана система линейных уравнений
x1+2x2+3x3 = 4
4x1+3x2+2x3=1 (1)
x1+3x2+2x3 = 4
В матричной форме система (1) имеет вид
А3,3 · Х3,1 =В3,1 (2), где А3,3-матрица коэффициентов при неизвестных
B3,1-вектор правых частей
Вектор неизвестных Х3,1 может быть найден по формуле
Х3,1=А3,3-1· В3,1 (5)
А3,3-1— обратная матрица
Решение задачи выполнить в таблице
1.Ввести в таблицу значения матрицы коэффициентов А3,3
2.Ввести в таблицу значения вектора В3,1
3.Выделить место для обратной матрицы А3,3-1
4.Вызвать мастер функций, отыскать функцию Мобр, которая вычисляет обратную матрицу.
5.Открывается диалоговое окно, в которое надо ввести адрес исходной матрицы коэффициентов. Нажать клавишу ctrl и обвести мышью исходную матрицу. Проверить записанный адрес. Если все нормально, щелкнуть мышью по строке формул (в ней появится курсор) и нажать 3 клавиши одновременно ctrl+shift+enter.
В выделенных ячейках появятся значения обратной матрицы.
6.Выделить место для результата (вектор неизвестных) Х3,1.
7.С помощью мастера функций найти функцию МУМНОЖ.
8.Откроется диалоговое окно, в которое надо ввести два адреса:
-адрес обратной матрицы (массив1)
-адрес вектора правых частей (массив2) .Выполнить выделение обязательно мышью
Активизировать строку формул , чтобы в ней появился курсор и нажать клавиши ctrl+shift+enter.
Варианты индивидуальных заданий
1. 2х1+х2-5х3+х4=8 2. 3х1-х2=5
х1-3х2-6х4=9 -2х1+х2+х3=0
2х2-х3+2х4=-5 2х1-х2+4х3=15
х1+4х2-7х3+6х4=0
3. 7,9х1+5,6х2+5,7х3-7,2х4=6,68 4. 6х1-х2-х3=11,33
8,5х1-4,8х2+0,8х3+3,5х4=9,95 -х1+6х2-х3=32
4,3х1+4,2х2-3,2х3+9,3х4=8,6 -х1-х2+6х3=42
3,2х1-1,4х2-8,9х3+3,3х4=1
5. 3х1+х2-х3+2х4=6 6. 10х1+х2+х3=12
-5х1+х2+3х3-4х4=-12 2х1+10х2+х3=13
2х1+х3-х4=1 2х1+2х2+10х3=14
х1-5х2+3х3-3х4=3
7. 2х1-х2-х3=-3 8. х1-0,2х2-0,2х3=0,6
3х1+5х2-2х3=1 -0,1х1+х2-0,2х3=0,7
х1-4х2+10х3=0 -0,1х1-0,1х2+х3=0,8
9. 3х1-х2= 5,2 10. 2х1+х2-5х3+х4=8
-2х1+х2+х3=0 х1-3х2-6х4=9
2х1-х2+4х3=15,4 2х2-х3+2х4=-5
х1+4х2-7х3+6х4=0
11. 6х1-х2-х3=11,33 12. х1+3х2-2х3-2х5=0,5
-х1+6х2-х3=32 3х1+4х2-5х3+х4-3х5=5,4
-х1-х2+6х3=42 -2х1-5х2+3х3-2х4+2х5=5,0
х2-2х3+5х4+3х5=7,5
-2х1-3х2+2х3+3х4+4х5=3,3
13. 3х1+х2-х3+2х4=6 14. 4х1+0,24х2-0,08х3=8
-5х1+х2+3х3-4х4=-12 0,09х1+3х2-0,15х3=9
2х1+х3-х4=1 0,04х1-0,08х2+4х3=20
х1-5х2+3х3-3х4=3
Задание №3
Логическая функция Если
Пример№1 -начисление премии в зависимости от должности
Ст. инспектор получает 2500 руб., инспектор-2000руб.
- Установить курсор в С2 ,с помощью мастера функций выбрать категорию Логические и функцию ЕСЛИ
- В диалоговом окне Аргументы функции задать необходимые параметры
В строке Логическое выражение необходимо указать адрес ячейки должности 1-ой записи(для этого щелкнуть мышкой по ячейке В2 и в строке логическое выражение появится адрес В2, дописать =”Ст.инспектор” т.е. логическое выражение будет иметь вид В2=”Ст.инспектор”
3. В строке значение, если истина записать 2500
4. В строке значение, если ложь записать 2000 и подтвердить ОК
- Скопировать формулу в другие ячейки
- Построить гистограмму
Пример №2
Если х>0 и x<y найти сумму чисел, иначе вычислить разность чисел
- Задать столбик значений х с шагом 5 от -50 до 50
- Вычислить столбик значений у по формуле у=х+5(адреса ячеек выбирать мышкой)
- Установить курсор в С2, с помощью мастера функций выбрать категорию Логические и функцию И
- В диалоговом окне Аргументы функции задать необходимые параметры
Логическое условие 1 для ячейки со значением -50 будет А2>0
Логическое условие 2 для ячейки со значением -50 будет А2<B2 и подтвердить ОК
- Скопировать формулу в другие ячейки столбца С
- Установить курсор в D2 , с помощью мастера функций выбрать категорию Логические и функцию Если
- В диалоговом окне Аргументы функции задать необходимые параметры
Логическое выражение-адрес C2 , в строке значение, если истина А2+В2,
В строке значение, если ложь А2-В2
8. Полученное значение скопировать в остальные ячейки столбца D
9. Построить график зависимости результирующего значения функции от х
Построение гистограммы и графика описано в задании №1
Варианты заданий
1.Если х>5 или х≤-20 вычислить у=1+tgx иначе вычислить у=х2.
Задать изменение х от -100 до 100 с шагом 10. Построить график зависимости у(х).
2.Если х принадлежит интервалу (4,20) вычислить значение функции по формуле y=х2+1 иначе вычислить значение функции по формуле y=sinх, задать изменение х от -60 до 60 с шагом 4. Построить график зависимости у(х).
3.Если х<-15 или х>10 вычислить у=x+5 иначе вычислить у=lnx.
Задать изменение х от -40 до 40 с шагом 5. Построить график зависимости у(х).
4.Если х принадлежит отрезку [5,8] вычислить значение функции по формуле y=cosx иначе вычислить значение функции по формуле y=x2+x , задать изменение х от -5 до 10 с шагом 1. Построить график зависимости у(х).
5.Если х<-1 или х<20 вычислить у=ex иначе вычислить у=sin(x+4)
Задать изменение х от -50 до 50 с шагом 5 Построить график зависимости у(х).
6.Если х>-10 и х<40 вычислить у=x+2 иначе вычислить у=cosx+x
Задать изменение х от -50 до 50 с шагом 5 Построить график зависимости у(х).
7.Если x>0 и y<-4 вычислить произведение чисел, иначе сумму.
Задать изменение х от -20 до 20 с шагом 5, а у вычислить по формуле х-2 Построить график зависимости у(х).
8.Если х<-5 или х>10 вычислить у=x3+5 иначе вычислить у=ln(x+2).
Задать изменение х от -40 до 40 с шагом 5. Построить график зависимости у(х).
9.Если х принадлежит отрезку [3,10] вычислить значение функции по формуле y=xcosx иначе вычислить значение функции по формуле y=x+4 , задать изменение х от -4 до 20 с шагом 2 Построить график зависимости у(х).
10.Если х>10 или х≤-20 вычислить у=sinx+cosx иначе вычислить у=х2.
Задать изменение х от -50 до 50 с шагом 10. Построить график зависимости у(х).
11. Если х принадлежит интервалу (8,30) вычислить значение функции по формуле y=х2+1 иначе вычислить значение функции по формуле y=2sin(х+2) , задать изменение х от -60 до 60 с шагом 10. Построить график зависимости у(х).
12.Если x>-6 и y<х вычислить произведение чисел, иначе разность.
Задать изменение х от -20 до 20 с шагом 5, а у вычислить по формуле х-2 Построить график зависимости у(х).
13. Если х принадлежит интервалу (-10,30) вычислить значение функции по формуле y=х2+1 иначе вычислить значение функции по формуле y=tgx+ctgx , задать изменение х от -60 до 60 с шагом 10. Построить график зависимости у(х).
14. Если х не принадлежит отрезку [-4,10] вычислить значение функции по формуле y=2cosx иначе вычислить значение функции по формуле y=x+2 , задать изменение х от -10 до 20 с шагом 2
Задание №4
Лабораторная работа по базам данных в ЭТ Excel.
- Создать БД в виде таблицы 1.
Таблица1
- Ввести 3 записи.
- Создать форму для ввода данных.
а)Для этого выделить все поля без 1-ой строки
б) В меню выбрать пункт Данные-Форма(2003) ВкладкаДанные(2007)
Появится форма для ввода данных.Поля Общий размер и Общая стоимость сделать вычисляемыми.Общий размер вычислить как сумму ячеек с адресами D3+E3+F3
Общая стоимость должна быть вычислена по формуле D3*G3+E3*H3+F3*I3
В форму ввести еще 5 записей.
4.Выполнить сортировку данных по номеру садового участка и ФИО.
Для этого выделить данные.
В пункте меню Данные выбрать сортировку
5. С помощью пункта меню Данные выбрать Автофильтр и отобрать данные о садовых участках, у которых самые неплодородные земли. Выделить данные без 1-ой строки и
выполнить команду Данные-Фильтр-Автофильтр
В строке заголовка таблицы появятся стрелки раскрывающегося списка. Щелкнуть на значок неплодородные земли и задать условие выбора. Условие задать таким образом, чтобы в списке осталось3-4 владельца садового участка. Условие задается в диалоговом окне. Показать преподавателю и восстановить базу данных.
6. Расширенный фильтр. Выдать на экран владельцев , у которых самые плодородные земли и больше всего строений. Для этого скопировать БД (базу данных) на новый лист и назвать лист Расширенный .Задать диапазон условий ниже БД. Для задания условий использовать операции отношения <,=,>,=,<>. Скопировать область заголовка на свободное место за БД и задать условия выбора в полях Плодородные земли и строения. Затем установить курсор в БД и выдать команду Данные–Фильтр-Расширенный фильтр откроется диалоговое окно , в котором необходимо задать
1). Скопировать результат на новое место
2). В строке исходный диапазон указать адрес БД.
3). В строке условие задать диапазон условий.
4). Для результата отвести место на свободном поле после диапазона условий
и закрыть диалоговое окно. Если такие записи есть в вашей БД, то они будут выведены на экран. Для задания условий использовать операции отношения <,>,<>,>=,<=,=
7.Выдать в мерию список владельцев садовых участков, у которых самые неплодородные земли и меньше всего строений, т.е. нуждающихся в материальной помощи. Скопировать БД на новый лист и выбрать таких владельцев с помощью расширенного фильтра. Скопировать список на новый лист, назвать его список. Оформить с заголовком Список, выдать дату с помощью функции Сегодня. Список должен содержать следующие столбцы: Имя владельца, номер садового участка, общий размер участка, размер неплодородной земли и количество строений, остальные столбцы скрыть Формат-Столбцы -Скрыть.
Цели урока:
- научить строить графики элементарных
математических функций с помощью табличного
процессора Excel; - показать возможности использования программы
Excel для решения задач по математике; - закрепить навыки работы с Мастером диаграмм.
Задачи урока:
- образовательная – знакомство учащихся с
основными приемами построения графиков функций
в программе Excel; - развивающие – формирование у учащихся
логического и алгоритмического мышления;
развитие познавательного интереса к предмету;
развитие умения оперировать ранее полученными
знаниями; развитие умения планировать свою
деятельность; - воспитательные – воспитание умения
самостоятельно мыслить, ответственности за
выполняемую работу, аккуратности при выполнении
работы.
Тип урока:
- комбинированный
Учебники:
Информатика. Базовый курс 2-е издание/Под ред.
С.В. Симоновича. – СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.
- Проектор
Раздаточный материал:
- Карточки с индивидуальными заданиями на
построение графиков функций.
План урока.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока. Домашнее задание – 7
мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка
отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный
опрос)
Вопросы для проверки
- Что представляет собой рабочая область
программы Excel? - Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она
задается? - Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как
изменить ориентацию бумаги? - Что такое функциональная зависимость у = f(х)?
Какая переменная является зависимой, а какая
независимой? - Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.
При объяснении нового материала может быть
использован файл Excel с шаблонами задач (Приложение 1), который
выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного
процессора Excel для графиков функций. На
предыдущих практических вы уже строили
диаграммы к различным задачам, используя Мастер
диаграмм. Графики функций, так же как и диаграммы
строятся с помощью Мастера диаграмм программы
Excel.
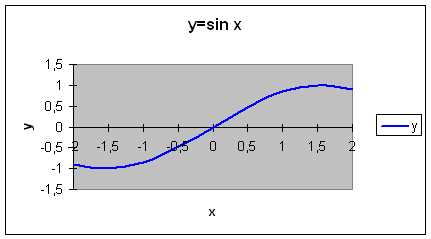
Рассмотрим построение графиков функций на
примере функции у = sin x.
Вид данного графика хорошо известен вам по
урокам математики, попробуем построить его
средствами Excel.
Программа будет строить график по точкам: точки
с известными значениями будут плавно
соединяться линией. Эти точки нужно указать
программе, поэтому, сначала создается таблица
значений функции у = f(х).
Чтобы создать таблицу, нужно определить
- отрезок оси ОХ, на котором будет строиться
график. - шаг переменной х, т.е. через какой промежуток
будут вычисляться значения функции.
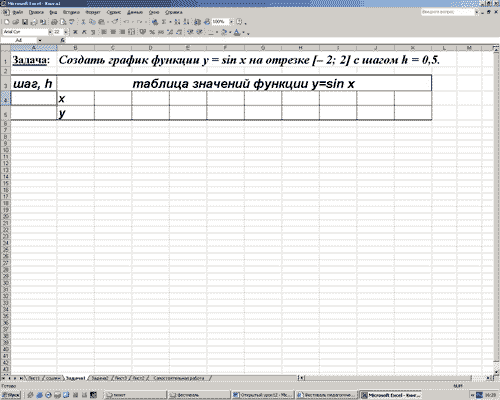
Задача 1.Построить график функции у = sin
x на отрезке [– 2; 2] с шагом h = 0,5.
1. Заполним таблицу значений функции. В ячейку С4
введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет
добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево
ячейки строки 4, до тех пор, пока получим значение
другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в
категории математические выберем функцию SIN, в
качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу
в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов
(х) и значений (у) функции у = sin x на отрезке [-2;2] с
шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,6816 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 | 0,9092 |
6. Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на
кнопку “Удалить” (график изменений х нам не
нужен. График функции – это график изменения
значений у)
В поле Подписи оси Х нажать на кнопку.
Выделить в таблице ячейки со значениями х и
нажмите на кнопку . Подписи по горизонтальной оси
станут такими, как у нас в таблице.
8. На третьем шаге заполним вкладку Заголовки.
9. Пример полученного графика.
На самом деле пока это мало похоже на график
функции в нашем привычном понимании.
Для форматирования графика:
- Вызовем контекстное меню оси ОУ. Затем, выберем
пункт Формат оси…. Во вкладке Шкала установим:
цена основного деления: 1. Во вкладке Шрифт
установим размер шрифта 8пт. - Вызовем контекстное меню оси ОХ. Выберем пункт
Формат оси….
Во вкладке Шкала установим: пересечение с осью
ОУ установите номер категории 5 (чтобы ось ОУ
пересекала ось ОХ в категории с подписью 0, а это
пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт.
Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на
построение графика функций. Эту задачу
попробуйте решить самостоятельно, сверяясь с
экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и
сформулировать следующую задачу.
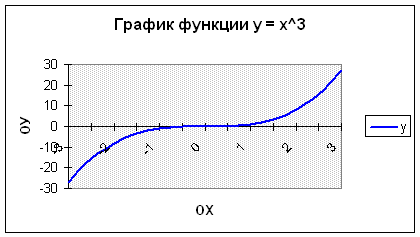
Задача 2. Построить график функции у = х3
на отрезке [– 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица
значений функции у = f(х).
2. В ячейку С4 ввести первое значение отрезка: –3
3. В ячейку D4 ввести формулу, которая будет
добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
4. Маркером заполнения ячейки D3 заполнить влево
ячейки строки 3, до тех пор, пока не будет получено
значение другого конца отрезка: 3.
5. В ячейку С5 ввести формулу вычисления значения
функции: = С4^3
6. Маркером заполнения скопировать формулу в
ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица
аргументов (х) и значений (у) функции у = х3 на
отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -1 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7. Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики.
8. На втором шаге во вкладке Ряд выполнить:
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры
диаграмм таким образом, что бы все поместилось на
одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (Вид
Колонтитулы…):
14. Верхний колонтитул слева: график функции у = x3
Сохранить документ своей папке под именем
График.
Самостоятельная работа.
Работа по карточкам с индивидуальными
заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде,
выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с
шагом h=c
2. Установить параметры страницы и размеры
графика таким образом, что бы все поместилось на
одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (Вид
Колонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный
график”
5. Вывести документ на печать.
После выполнения задания правильность каждого
варианта проверяется с помощью проектора.
Подведение итогов.
Домашнее задание.
Оценки за урок.