На прошлых уроках мы подробно рассмотрели частные случаи квадратичной функции: игрек равен а икс в квадрате, игрек равен а икс в квадрате плюс эн и игрек равен а умножить на квадрат икс минус эм. При этом последние два получаются параллельным переносом из первого случая. Игрек равен а икс в квадрате плюс эн сдвигом вдоль оси игрек на эн единиц вверх, если эн больше нуля, или на эн единиц вниз, если эн меньше нуля. Функция игрек равен а умножить на квадрат икс минус эм получается с помощью сдвига вдоль оси икс на эм единиц вправо, если эм больше нуля, или на эм единиц влево, если эм меньше нуля.
Так же мы получили график функции игрек равен а умножить на квадрат икс минус эм плюс эн с помощью двух параллельных переносов, который можно производить в любом порядке.
Известно, что графиком любой квадратичной функции является парабола. При изображении графика важно знать координаты вершины параболы.
Мы говорили, что парабола игрек равен а умножить на квадрат икс минус эм плюс эн имеет вершину с координатами эм, эн. Как же определить координаты вершины параболы, которая является графиком квадратичной функции, записанной формулой общего вида?
Так как мы умеем находить вершину параболы игрек равен а умножить на квадрат икс минус эм плюс эн, то попробуем привести квадратичную функцию к данному виду. Запишем правую часть и выделим из неё квадрат двучлена. Вынесем а за скобки. Второе слагаемое в скобках представим в виде удвоенного произведения. Тогда второе выражение равно бэ делённое на два а. Добавим и отнимем квадрат второго выражения. Выделим квадрат суммы. После упрощения получаем выражение.
Мы получили формулу вида а умножить на квадрат икс минус эм плюс эн. Значит можем записать следующие равенства: эм равно минус бэ делённое на два а. Эн равно минус дробь в числителе которой бэ в квадрате минус четыре а цэ, в знаменателе четыре а.
Значит, график квадратичной функции есть парабола, которую можно получить из графика функции игрек равен а икс в квадрате с помощью двух параллельных переносов – сдвига вдоль оси икс и сдвига вдоль оси игрек. Вершина параболы имеет координаты эм, эн. При этом эм равно минус бэ делённое на два а. Эн равно минус дробь в числителе которой бэ в квадрате минус четыре а цэ, в знаменателе четыре а.
Осью симметрии параболы служит прямая икс равен эм, параллельная оси игрек.
Найдём координаты вершины параболы игрек равен минус два икс в квадрате плюс пять икс минус три. Для удобства выпишем коэффициенты квадратного трёхчлена. Вычислим значение эм, подставляя соответствующие значения в формулу минус бэ делённое на два а. Получим эм равно одной целой одной четвёртой. Вычислим эн по формуле. Подставим значения коэффициентов и получим эн равно одной восьмой.
Таким образом, получили координаты вершины параболы: одна целая одна четвёртая, одна восьмая.
Так как прямая икс равен эм является осью симметрии параболы, то ординату вершины параболы можно вычислить без формулы для эн. Подставим значение эм в функцию. Получим, значение игрек равно одной восьмой. Оно совпадает со значением эн.
Значит для того, чтобы найти координаты вершины параболы надо вычислить эм по формуле минус бэ делённое на два а и подставить полученное значение в функцию. Получим значение ординаты вершины.
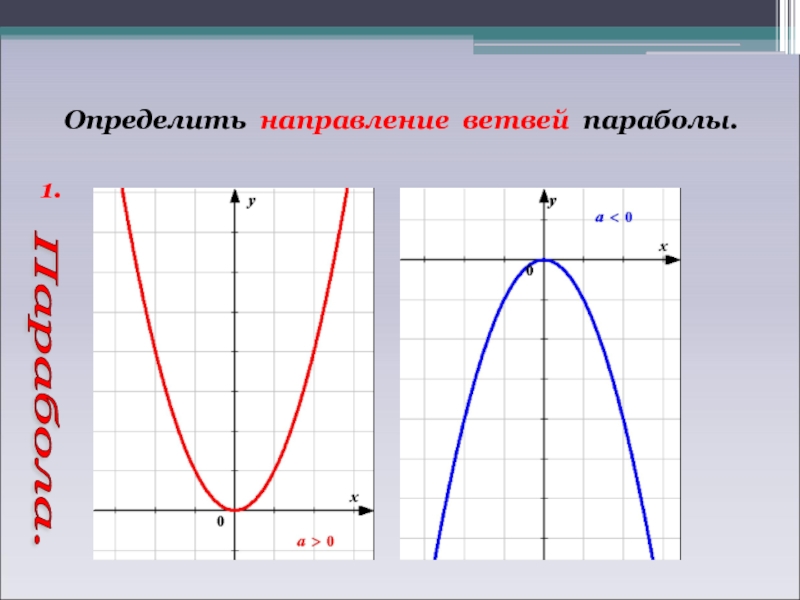
Запишем алгоритм построения графика квадратичной функции. Первый шаг – определить направление ветвей параболы. Ветви направлены вверх, если коэффициент а положительный. Ветви параболы направлены вниз, если коэффициент а отрицательный. Второй шаг – найти координаты вершины параболы и отметить её на координатной плоскости. Третьим шагом определить ось симметрии икс равен эм. Четвёртый шаг – построить ещё несколько точек, принадлежащих параболе. То есть составить таблицу значений функции с учётом оси симметрии. Последний пятый шаг – соединить полученные точки плавной линией.
Построим график квадратичной функции игрек равен икс в квадрате плюс шесть икс плюс один, придерживаясь полученного алгоритма. Сначала определим направление ветвей параболы. А равно единице, это больше нуля. Значит, ветви параболы направлены вверх. Найдём координаты вершины эм, эн. Вычислим эм по формуле минус бэ делённое на два а. Подставим коэффициенты квадратичной функции. Эм равно мину трём. Вычислим эн, подставив вместо икс в формулу полученное значение эм. Эн равно минус восьми. Отметим на координатной плоскости вершину с координатами минус три, минус восемь. Определим ось симметрии. Это прямая икс равен минус трём. Теперь составим таблицу значений, чтобы получить ещё несколько точек параболы. Возьмём значения икс минус шесть, минус пять, минус четыре, минус два, минус один, нуль. Выбранные значения симметричны относительно оси симметрии. Подставим их в формулу. Получим значения игрек один, минус четыре, минус семь, минус семь, минус четыре и один. Отметим полученные точки на координатной плоскости. Соединим их плавной линией. Получили параболу, которая является графиком функции игрек равен икс в квадрате плюс шесть икс плюс один.
Графиком
любой квадратичной функции является парабола.
У каждой параболы есть вершина, при изображении графика важно знать её
координаты. Вершина параболы имеет
координаты (m,n).
Определите
координаты вершин для парабол:
Определим
координаты вершины параболы, которая является графиком квадратичной функции
записанной в виде .
Преобразуем
квадратный трёхчлен, выделим из него квадрат двучлена:
Второе
слагаемое представим в виде удвоенного произведения:
Выделим
квадрат суммы:
После
сокращения получаем:
Отсюда
запишем, что:
Вывод.
Графиком функции
является
парабола, которую можно получить из
параболы с помощью двух параллельных переносов: сдвига относительно оси x и сдвига относительно оси y. Данная парабола имеет вершину с
координатами (m,n), где ,
.
Осью симметрии является прямая x=m.
Пример.
Найти
координаты вершины параболы .
Вершина
будет иметь координаты (m,n), каждую из которых можно получить
по формуле. Подставим коэффициенты квадратичной функции в формулу и найдём эти
значения:
Вершина
параболы имеет координаты (-2,-5).
Воспользуемся
наиболее простым способом: сначала найдём m вершины по формуле. И учитывая,
что вершина принадлежит графику функции, подставим m вместо
аргумента в функцию:
Получили
вершину, которая имеет координаты (-2,-5).
Алгоритм
построения графика квадратичной функции:
1.
Определить
направление ветвей парабола. Если a>0, то ветви
направлены вверх, если a<0,
то — вниз.
2.
Найти
координаты вершины параболы и отметить её на координатной плоскости. Применив
формулу ,
найдём абсциссу вершины параболы, и, подставив это значение в формулу, задающую
функцию, найдем ординату этой точки.
3.
Определить
ось симметрии x=m.
4.
Построить
ещё несколько точек принадлежащих параболе, составив таблицу значений функции с
учётом оси симметрии.
5.
Соединить
отмеченные точки плавной линией.
Пример.
Изобразить
график функции .
1.
Определим
направление ветвей параболы:
2.
Найдём
координаты вершины:
Получили
вершину с координатами (-2, -3).
3.
Определим
ось симметрии:
4.
Составим
таблицу значений:
Выбранные
значения симметричны относительно оси симметрии.
5.
Отметим
и соединим полученные точки на координатной плоскости:
Получили
параболу, которая является графиком функции.
Пример.
Изобразить
график функции и
описать её свойства.
Изобразим
график функции:
1.
Определим
направление ветвей параболы:
2.
Найдём
координаты вершины параболы:
Вершина
имеет координаты (-2,-4).
3.
Определим
ось симметрии:
4.
Составим
таблицу значения функции:
5.
Соединив
эти точки, получаем:
Определим
свойства функции.
Областью
определения и областью значений являются:
Определим
нули функции:
Перечислим
промежутки знакопостоянства функции:
Опишем
промежутки монотонности:
Описание презентации по отдельным слайдам:
-
1 слайд
Построение графика квадратичной функции
-
2 слайд
Y = x2
Y = x2
Y = 3×2
Y = 0,3×2
Y = -0,5×2y=ax2
Парабола -
3 слайд
Y = x2
Y = x2 – 4
Y = x2 + 3
y=ax2+n
Как получить графики функций Y = x2 – 4 и Y = x2 + 3 из графика функции Y = x2 -
4 слайд
y=a(x-m)2
Y = x2
Y = ( x – 6 )2
Y = (x + 3)2 -
5 слайд
y=a(x-m)2 + n
Y = (x – 6)2 + 4Как получить график функции y=a(x-m)2 + n из графика функции y=ax2
-
6 слайд
Найдите соответствия:
-
7 слайд
Параболу y = 5×2 cдвинули на 3 единицы вниз и на 6 единиц вправо. Графиком какой функции является полученная парабола? Составьте уравнение параболы
Параболу y = -2×2 cдвинули на 7 единицы вверх и на 4 единицы влево. Графиком какой функции является полученная парабола? -
8 слайд
Построение графика функции у = ах2 + bх +с.
1.
Определить направление ветвей параболы.
Парабола. -
9 слайд
Построение графика функции у = ах2 + bх +с.
2.
Найти координаты вершины параболы
(т; п).
3.
Провести ось
симметрии.О (т;п)
-
10 слайд
Построение графика функции у = ах2 + bх +с.
4.
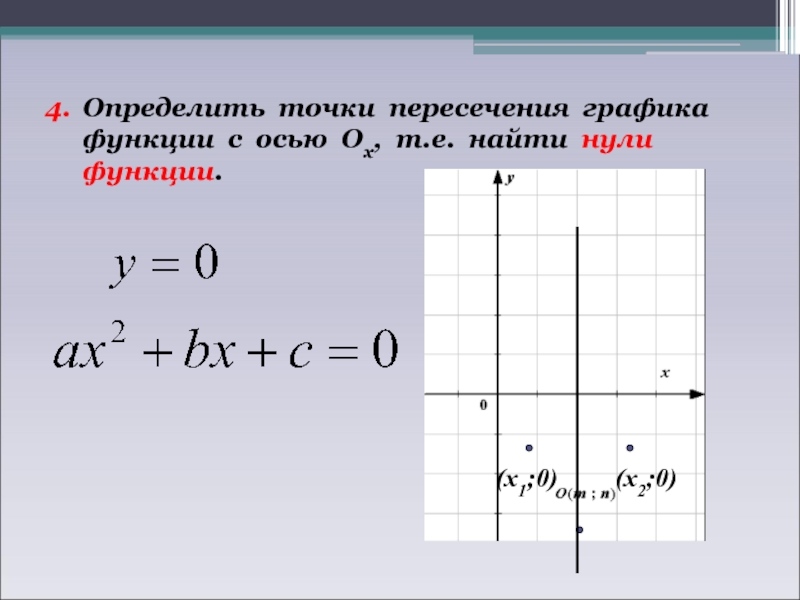
Определить точки пересечения графика
функции с осью Ох, т.е. найти нули
функции.
(х1;0)
(х2;0) -
11 слайд
Построение графика функции у = ах2 + bх +с.
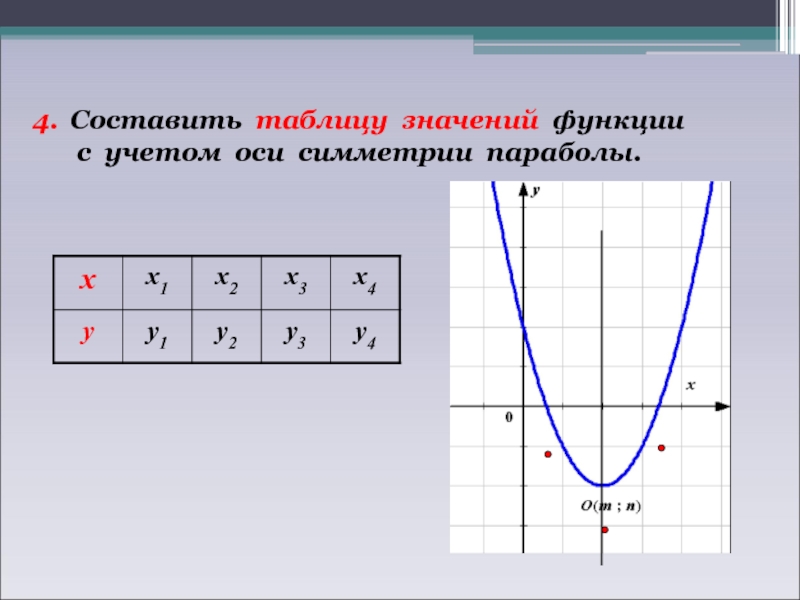
5.
Составить таблицу значений функции
с учетом оси симметрии параболы. -
12 слайд
Алгоритм построения графика функции у = ах2 + bх +с.
1.
Определить направление ветвей параболы.
2.
Найти координаты вершины параболы
(m; n).
3.
Провести ось симметрии.
4.
Определить точки пересечения графика
функции с осью Ох, т.е. найти нули
функции.
5.
Составить таблицу значений функции
с учетом оси симметрии параболы. -
13 слайд
Постройте график функции y = x2 – 2x – 3.
С помощью графика найдите:
Область определения функции;
Область значений функции;
Нули функции;
Промежутки, в которых у>0, y<0;
Промежутки возрастания и убывания функции;
Наибольшее (наименьшее) значение функции
Тест -
14 слайд
y = -x2 – 4x – 5
-
15 слайд
y = x2 – 4x – 7
Постройте график функции -
16 слайд
y = x2 – 2x – 3.
-
Слайд 1
Построение графика квадратичной функции
Слайд 2
Y = x 2 Y = x 2 Y = 3x 2 Y = 0,3x 2 Y = -0,5x 2 y=ax 2 Парабола.
Слайд 3
Y = x 2 Y = x 2 – 4 Y = x 2 + 3 y=ax 2 +n Как получить графики функций Y = x 2 – 4 и Y = x 2 + 3 из графика функции Y = x 2
Слайд 4
y=a(x-m) 2 Y = x 2 Y = ( x – 6 ) 2 Y = (x + 3) 2
Слайд 5
y=a(x-m) 2 + n Y = (x – 6) 2 + 4 Как получить график функции y=a(x-m) 2 + n из графика функции y=ax 2
Слайд 6
Найдите соответствия:
Слайд 7
Параболу y = 5x 2 c двинули на 3 единицы вниз и на 6 единиц вправо. Графиком какой функции является полученная парабола? Составьте уравнение параболы Параболу y = -2 x 2 c двинули на 7 единицы вверх и на 4 единицы влево. Графиком какой функции является полученная парабола? Y =5(x – 6) 2 – 3 Y = -2(x + 4) 2 + 7
Слайд 8
Построение графика функции у = ах 2 + b х +с. 1. Определить направление ветвей параболы. Парабола.
Слайд 9
Построение графика функции у = ах 2 + b х +с. 2. Найти координаты вершины параболы (т; п). 3. Провести ось симметрии. О (т;п)
Слайд 10
Построение графика функции у = ах 2 + b х +с. 4. Определить точки пересечения графика функции с осью О х , т.е. найти нули функции. (х 1 ;0) (х 2 ;0)
Слайд 11
Построение графика функции у = ах 2 + b х +с. 5. Составить таблицу значений функции с учетом оси симметрии параболы. х х 1 х 2 х 3 х 4 у у 1 у 2 у 3 у 4
Слайд 12
Алгоритм построения графика функции у = ах 2 + b х +с. 1. Определить направление ветвей параболы. 2. Найти координаты вершины параболы ( x в ; y в ). 3. Провести ось симметрии. 4. Определить точки пересечения графика функции с осью О х , т.е. найти нули функции. 5. Составить таблицу значений функции с учетом оси симметрии параболы.
Слайд 13
Постройте график функции y = x 2 – 2x – 3 . С помощью графика найдите : Область определения функции ; Область значений функции ; Нули функции ; Промежутки , в которых у >0, y<0; Промежутки возрастания и убывания функции ; Наибольшее (наименьшее) значение функции Тест
Слайд 14
y = -x 2 – 4x – 5
Слайд 15
Проверочная работа
Слайд 16
Спасибо за урок. Успехов!
Слайд 17
y = x 2 – 2x – 3 . y = x 2 – 2x – 3 .
Слайд 18
y = x 2 – 2x – 3 .
Слайд 1Квадратичная функция
МОУ лицей имени Д. А. Фурманова
Алгебра, 8 класс
Учитель Асланова Е. А.

Слайд 2Квадратичная функция
у = ах2 + bx +c, а=0
Повторение

Слайд 3у = х2 +2
у = (х +3) 2
у = х2 +6х
+9
у = х2
«Высшее назначение математики состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает» .
Н. Винер
2
у = ах2 + bx +c, а=0
у = а (х + n )² + m, а=0

Слайд 5у = 4х² у = – 0,5(х+3)²
у = 3(х-2)² – 1
Как построить графики функций :
Построить график функции
у = – 2х² + 4х – 1

Слайд 6
у = – 2х² + 4х – 1
…
у = – 2
(х – 1)² + 1
у = – 2х² у = – 2(х – 1)² у = – 2 (х – 1)² + 1

Слайд 7Построение графика функции
у = ах2 + bх +с.

Слайд 8Изучение нового материала.
Самостоятельная работа с учебником.
Стр. 94
Выделить квадрат двучлена:
ах²
+ вх + с = …
а (х + в/2а)² + (4ас- в²)/4а
m = – в/2а , n = (4ас- в²)/4а

Слайд 91.
Определить направление ветвей параболы.
Парабола.
Слайд 102.
Найти координаты вершины параболы
(т; п).
3.
Провести
ось симметрии.
О (т;п)

Слайд 114.
Определить точки пересечения графика
функции с осью Ох, т.е. найти нули
Слайд 124.
Составить таблицу значений функции
с учетом оси симметрии параболы.
Слайд 13Алгоритм построения графика функции у = ах2 + bх +с.
1.
Определить направление
ветвей параболы.
2.
Найти координаты вершины параболы
(т; п).
3.
Провести ось симметрии.
4.
Составить таблицу значений функции
с учетом оси симметрии параболы.
.

Слайд 14
…Мне мудрость не чужда была земная,
Разгадки тайн ища, не ведал сна я.
За семьдесят перевалило мне,
Что ж я узнал! –
Что ничего не знаю.
Омар Хайям

Слайд 15Домашнее задание:
1. Построить график функции
у = х² – 2х – 3.
Записать все свойства функции.
2. Найти наибольшее значение функции
у = -2х² + 4х – 3.


















