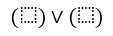Логические выражения и таблица истинности
Примеры задач с решениями по этой теме Пройти тестирование по теме Контрольная по теме
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2n, где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
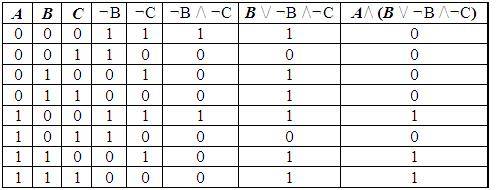
Пример 1. Для формулы A/ (B / ¬B /¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
Пример 2. Определите истинность логического выражения F(А, В) = (А/ В)/(¬А/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А/ В; 2) ¬А; 3) ¬В; 4) ¬А/¬В; 5) (А/ В)/(¬А/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
|
А |
В |
А/ В |
¬А |
¬В |
¬А/¬В |
F |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Пример 3. Построёте таблицу истинности для логического выражения
F = (A/ B) / ¬С
- В данной функции три логические переменные – А, В, С
- количество строк таблицы = 23 =8
- В формуле 3 логические операции.
- Расставляем порядок действий
1) А/ В; 2) ¬С; 3) (AVB) / ¬С .
- количество столбцов таблицы = 3 + 3 = 6
|
А |
В |
С |
A/B |
¬С |
(A/B) / ¬С |
|
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
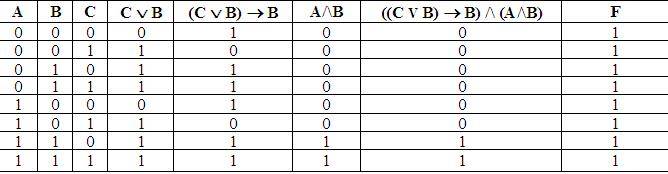
Пример 4. Определите истинность формулы: F = ((С /В) => В) / (А / В) => В.
Построим таблицу истинности этой формулы.
Ответ: формула является тождественно истинной.
Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
|
X |
Y |
Z |
F |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
Какое выражение соответствует F?
1) ¬X/¬Y/Z 2) ¬X/¬Y/Z 3) X/Y/¬Z 4) X/Y/Z
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
|
X |
Y |
Z |
F |
¬X |
¬Y |
¬Z |
¬X/¬Y/Z |
¬X/¬Y/Z |
X/Y/¬Z |
X/Y/Z |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
Очевидно, что значения заданной функции F совпадают со значениями выражения X/Y/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
1) первое заданное выражение ¬X/¬Y/Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2) второе заданное выражение ¬X/¬Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X/Y/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X/Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Ответ: 3
План урока:
Способы решению задач по логике
Табличный способ – этапы, особенности
Сравнение методов решения
Построение таблиц истинности для различных типов задач
Построение электрических схем, реализующих логические операции
Способы решения задач по логике
Многие задачи можно решить, используя инструменты алгебры логики. Чтобы получить результат, можно пойти 3 путями:
- рассуждая над условием;
- решая логические операции;
- используя таблицы истинности.
Логический подход подразумевает перевод условия из естественного языка на язык символов, схем и формул. Для такой формализации высказываний нужно выполнить ряд шагов.
Этапы решения логических задач:
- Разобраться с условием на естественном языке, выделив простые высказывания, и дать им символьные обозначения (латиница).
- Записать условие в виде формулы. Решить ее поэтапно, упрощая, учитывая приоритеты (( ), ¬, &, V).
- Просчитать формулы строчно или при помощи таблиц истинности, учитывая законы алгебры логики.
- Проверить, соответствует ли полученный результат условию задачи.
Табличный способ – этапы, особенности
Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.
Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи.
Метод таблиц
Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.
Существует общий алгоритм построения таблиц:
- Определить число логических значений/переменных (n) в примере.
- Установить вид, число и тип операций. Важно заранее определить очередность действий, выразить это при помощи скобок.
- Полученные данные позволяют рассчитать сколько нужно столбцов – это сумма числа переменных и операций.
- Нарисовать таблицу, заполнить шапку, записав обозначение переменных и выбранные действия.
- Определить, сколько существует наборов логических переменных (т.е. число строчек) по формуле m = 2n+ 1 (шапка).
- Заполнить столбцы, вписав наборы значений логических переменных (0 или 1).
- Записать результаты логических операций, указанных в шапке для каждой совокупности значений.
- Сделать выводы на основании полученных результатов.
Если необходимо перебрать все значения простых выражений, то для задач:
- с 2-мя переменными может быть только 4 набора логических переменных;
Если словесно описывать все эти комбинаций, на каждый из примеров понадобится десятки строк текста.
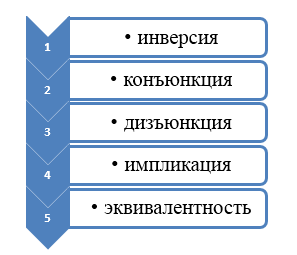
Обязательно учитывают приоритет операций:
- Указанные в скобках.
- Отрицание.
- Логическая конъюнкция чисел.
- Дизъюнкция.
- Строгая дизъюнкция.
- Импликация.
- Эквивалентность.
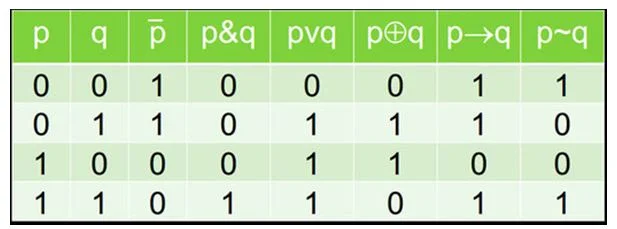
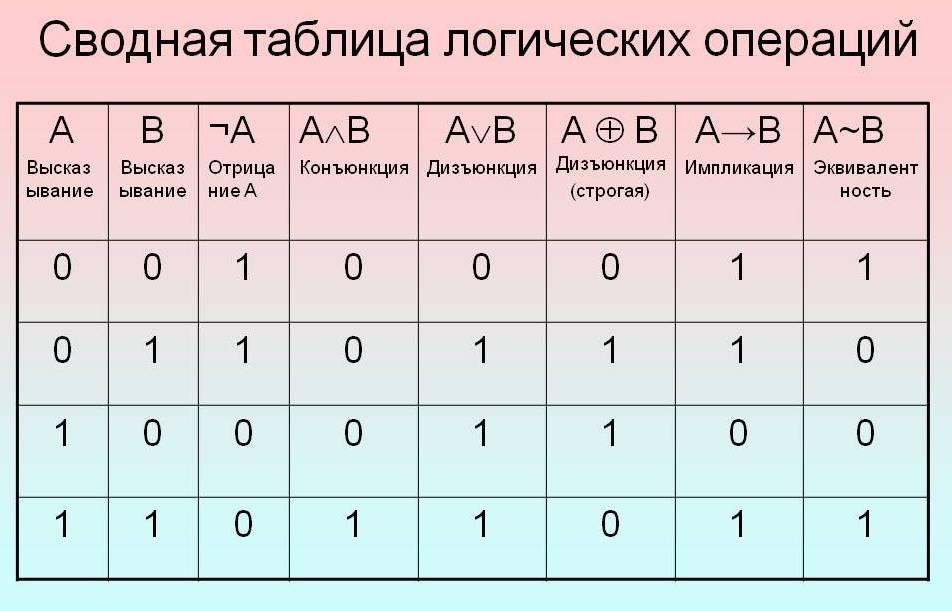
Обозначение логических операций:
Сравнение методов решения
Метод рассуждений
Он заключается в пошаговом анализе условий с промежуточными выводами на каждом этапе. Выполняется анализ таблицы истинности каждого логического выражения.
Пример №1.
Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по таким специальностям: гитарист, плотник, егерь и стоматолог.
Известно, что:
- дом плотника правее егеря;
- стоматолог проживает левее егеря;
- дом гитариста с самого краю;
- стоматолог живет рядом с гитаристом;
- Владимир не гитарист, и его дом не соседствует с гитаристом;
- дома Дмитрия и егеря соседние;
- здание, в котором прописан Андрей, правее стоматолога;
- между домами Андрея и Дмитрия один дом.
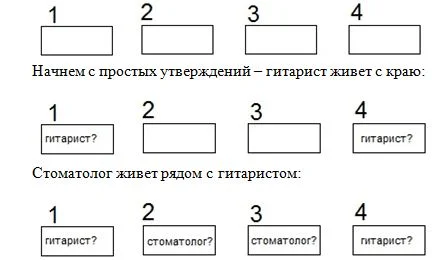
Чтобы рассуждать было проще, добавим изображение зданий, присвоим им номера:
Но стоматолог живет левее егеря, а правее егеря – плотник. Получается, что дом гитариста не может быть последним, а дом стоматолога не может быть предпоследними. То есть, егерь живет в предпоследнем доме:
Между домами Андрея и Дмитрия стоит один дом, значит, дом Андрея не может быть предпоследним, получается номер – 4, что автоматом исключает проживание там Дмитрия и Владимира.
Условие задачи заняло 2 предложения, а рассуждений получилось на 2 страницы.
Такой подход лучше не использовать, если условие сложное или много данных.
Табличный метод
Более удачным подходом к решению задач с большим количеством данных (несколько множеств), считается табличный, или графический (диаграммы).
Чтобы построить таблицу истинности логических выражений, следует:
- Разбить задачу на простейшие утверждения, которые обозначить символами (большие буквы латинского алфавита).
- Записать условие задачи, как составное выражение из символов логических операций.
- Нарисовать таблицу истинности для полученных данных.
- Выбрать такой вариант, при котором полученные значения подходят под условие.
- Проверить соответствие выбранного варианта и условия задачи.
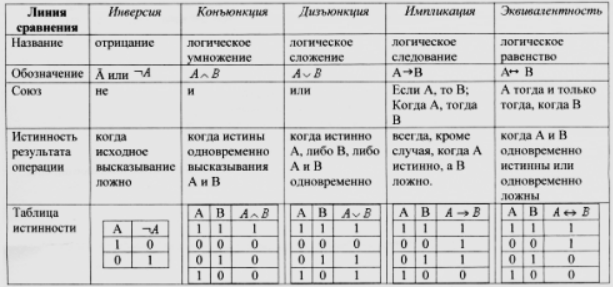
Чтобы преобразовывать условие задачи в логические выражения и операции, удобно пользоваться такой сводной таблицей истинности логических операций:
Рассмотрим тот же пример.
Определяем, что только гитарист может жить в первом доме, далее смотрим на заметки и условия и получаем таких жителей:
Метод компактнее, для некоторых задач нагляднее.
Построение таблиц истинности для различных типов задач
Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.
Пример 2.
Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.
Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:
А — «Первый студент летал в Англию»;
В — «Второй студент летал в Англию»;
С — «Третий студент летал в Англию».
Запишем выясненные данные при помощи логических операций:
Пример 3.
Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:
- Если А получит максимальный бал, то максимальный бал получат Ви С.
- А и С получат или не получат максимальный бал одновременно.
- Необходимым условием получения высшего бала С класса является получение высшего бала В классом.
По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.
Выясним, какие же классы добились высшего бала.
Разбиваем условие задачи на элементарные высказывания:
А – «А добьется высшего бала»;
В – «В добьется высшего бала»;
С – «С добьется высшего бала».
Запишем логические операции, описанные в примере:
Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.
Пример 4.
Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:
- последняя – гласная (Х1);
- или первая буква согласная (Х2)
- вторая – согласная (Х3).
¬(Х1→Х2)VХ3
Предложенные имена: Арина, Артур, Кэтрин, София.
Решим задачу, используя таблицу.
Сначала решим пошагово, выполняя операции по приоритету:
Указанному условию соответствует первое имя.
Пример 5.
Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.
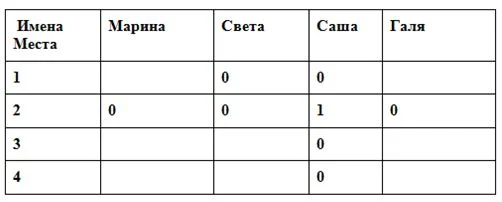
Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.
Маша Марина: «Саша заняла второе место, а Света – первое».
Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».
Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».
Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».
Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».
Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.
Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.
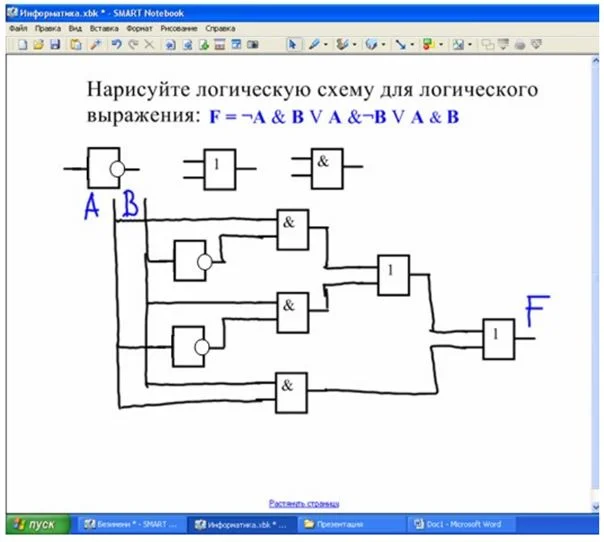
Построение электронных схем, реализующих логические операции
Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.
Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.
Электросхема с конъюнктором
Рассмотрим все варианты:
- Все контакты включены, тогда источник света горит.
- Первый контакт в положении «выключено» – свет не горит.
- Второй контакт выключен – лампа не светит.
- Все контакты отключены – свет не горит.
Заключение – эта электрическая цепь реализует операцию «И».
Дизъюнктор, схема электропитания
Рассмотрим этот вид электрической цепочки:
- Все контакты включены – лампа горит.
- Первый контакт включен, второй выключен – свет горит.
- Обратная ситуация – выключен первый, включен второй – лампа светится.
- Все контакты выключены – света нет.
Заключение – такой вид электросхем соответствует логической операции «ИЛИ».
Инвертор в электросхемах
В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.
Заключение: схема соответствует логической операции «НЕ».
Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.
Обозначение логических элементов
Удобно создавать электросхемы в ПО SmartNotebook, которое используется с интерактивной доской.
Построение таблиц истинности
Екатерина Андреевна Гапонько
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Определение 2
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
Определение 3
Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:
Рисунок 1.
Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
-
Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
-
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
-
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
«Построение таблиц истинности» 👇
Рисунок 2.
Пример 1
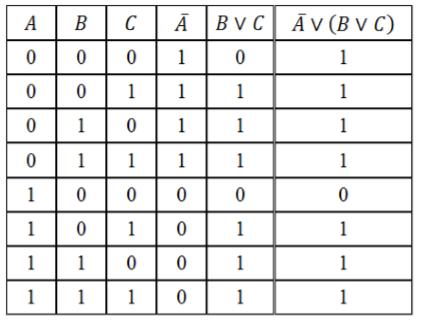
Составить таблицу истинности логического выражения $D=bar{A} vee (B vee C)$.
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- инверсия ($bar{A}$);
- дизъюнкция, т.к. она находится в скобках ($B vee C$);
-
дизъюнкция ($overline{A}vee left(Bvee Cright)$) – искомое логическое выражение.
Кол-во столбцов = $3 + 3=6$.
-
Заполним таблицу, учитывая таблицы истинности логических операций.
Рисунок 3.
Пример 2
По данному логическому выражению построить таблицу истинности:
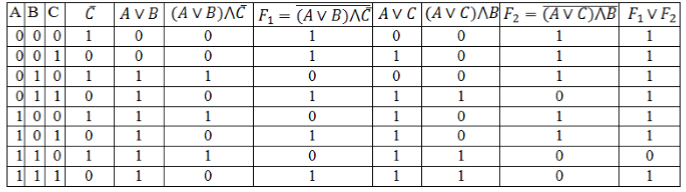
[F=overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}]
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- отрицание ($bar{C}$);
- дизъюнкция, т.к. она находится в скобках ($A vee B$);
- конъюнкция ($(Avee B)bigwedge overline{C}$);
- отрицание, которое обозначим $F_1$ ($overline{(Avee B)bigwedge overline{C}}$);
- дизъюнкция ($A vee C$);
- конъюнкция ($(Avee C)bigwedge B$);
- отрицание, которое обозначим $F_2$ ($overline{(Avee C)bigwedge B}$);
-
дизъюнкция – искомая логическая функция ($overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}$).
Кол-во столбцов = $3 + 8 = 11$.
-
Заполним таблицу, учитывая таблицу истинности логических операций.
Рисунок 4.
Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
Пример 3
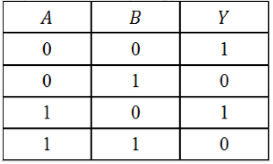
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.
Рисунок 5.
Решение:
- Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
- Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:
Рисунок 6.
- Каждое логическое выражение в этой дизъюнкции запишем как конъюнкцию аргументов функции $A$ и $B$: $left(Awedge Bright)vee left(Awedge Bright)$
- В случае, когда значение в соответствующей строке таблицы равно $0$, запишем этот аргумент с отрицанием, получим искомую функцию:[Yleft(A,Bright)=left(overline{A}wedge overline{B}right)vee left(Awedge overline{B}right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 12.04.2016
Таблица истинности — это мощный инструмент, который может помочь вам узнать итог логического выражения для возможных его переменных. Изучаете ли вы логику, математику, информатику или любую другую область, научиться создавать такие таблицы — необходимый навык. В этой статье мы расскажем как составить таблицу истинности.
Содержание
- Шаги по созданию таблицы истинности
- Полезные советы
- Расширенные концепции в таблицах истинности
Шаги по созданию таблицы истинности
- Перечислите все предложения в высказываниях.
Составление списков. Например, (A и B) или (не C) пропозициями являются A, B и C.
- Определите количество строк
Оно равно 2n, где n — количество предложений в выражении. В нашем примере есть три предложения (A, B и C), поэтому число строк будет равно 2 3 = 8.
- Перечислите все возможные итоги истинности
На этом этапе необходимо перечислить все исходы значений истинности для утверждений внутри выражения. Например, в нашем примере с тремя предложениями (A, B и C) бывает 8 исходов.
- Вычислите значения для всего
В промежутке узнать значение для каждого строкового данного. Для этого вам нужно подставить результаты для предложений в выражении и вычислить пример.
Полезные советы
Начните с простых выражений
Если вы новичок, рекомендуется начать с простых примеров, содержащих только одно или два предложения. Это поможет вам понять, как работают таблицы истинности, прежде чем переходить к более сложным примерам.
Используйте согласованный порядок для предложений
При перечислении предложений в таблице истинности важно использовать согласованный порядок. Это упростит отслеживание того, какое предложение соответствует какому столбцу в таблице.
Используйте таблицу истинности. Для упрощения
Одним из преимуществ является то, что их можно использовать для упрощения сложных логических выражений. Определяя строки в таблице истинности, в которых выражение имеет значение true или false, можно узнать шаблоны, которые можно использовать для упрощения выражения, что позволит вам правильно составить таблицу истинности.
Расширенные концепции в таблицах истинности
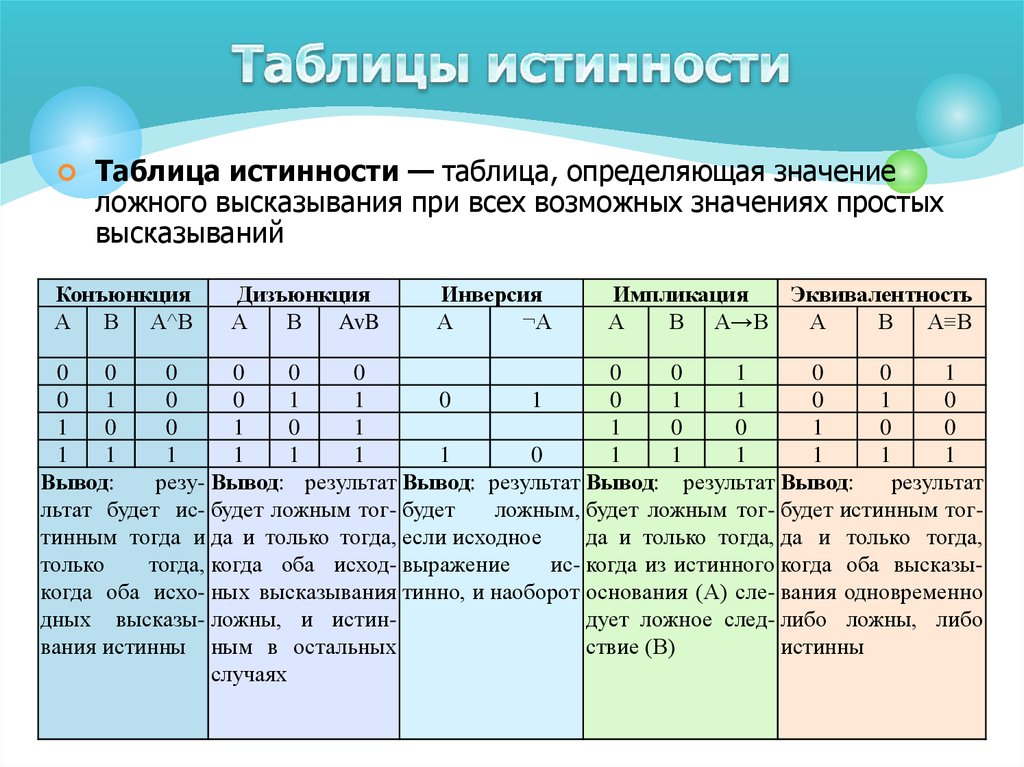
Как только вы освоите основы таблиц истинности, вы можете перейти к сложным концепциям. Вот несколько примеров:
- Отрицание (Инверсия)
Отрицание — это логический оператор, который изменяет смысл предложения на противоположное. В таблице истинности отрицание может быть представлено символом «не» (~).
- Конъюнкция
Это оператор, может быть представлен знаком «и» (&).
- Дизъюнкция
Это оператор, представляющий «или». Она может быть представлена символом «или» (|).
- Условный
Это оператор, который представляет «если-то». В таблице условное обозначение может быть представлено символом стрелки (->).
Следуя нашим советам, вы без труда сможете правильно составить таблицу истинности. А если у вас остались вопросы, задавайте их в комментариях.
Логическая функция одно из основополагающих понятий математической логики. Она зависит от логических переменных и принимает значения из множества, от которого находится в зависимости. Логические функции булевых переменных могут принимать только два значения – 1 или 0.
Понятие таблиц истинности
Задаваться логическая функция может числовым способом, словесным описанием, картами Карно, аналитическим выражением и с помощью таблиц истинности. В последнем случае все аргументы функции следует записать в левой части таблицы, а значения, которые им соответствуют, в правой.
Определения 1 — 2
Таблица истинности – это таблица, просто и наглядно показывающая, какие значения будут у логического выражения при всевозможных наборах переменных функции.
Равносильными именуют те логические выражения с совпадающими последними столбцами таблицы истинности. Обозначают равносильные функции знаком «=».
Правила того, как следует проводить построение таблицы истинности
Несоблюдение хотя бы одного из них ведёт к очень грубой ошибке. Вот эти правила:
- Число строк таблицы должно совпадать с числом комбинаций всевозможных n логических переменных, то есть быть равным 2n;
- Количество столбцов таблицы должно равняться сумме числа логических переменных и числа логических операций;
- В построенный шаблон таблицы истинности должны вписываться все значения исходных переменных;
- Построение таблицы истинности выражения происходит по её столбцам, при этом обязательно учитываются правила логических операций.
Порядок действий при построении таблицы истинности для логических выражений
Порядок действий при построении таблицы истинности, какой бы ни была логическая функция, следующий:
- Определить, какое число строк и столбцов будет в будущей таблице. Делается подобное по формулам
X = n + m, Y = 2n+1.
Где n – число переменных, m – чило логических операций. - Заполнить самую верхнюю строку таблицы переменными и логическими операциями, идя слева направо. При этом приоритетность логических операций следует учитывать обязательно, иначе получится совсем не то, что нужно;
- В первых столбцах перечислить всевозможные комбинации входных значений;
- Выполняя заданные логические операции, заполнить все оставшиеся ячейки;
Ответом следует считать последний заполненный столбец таблицы.
О порядке логических операций
Лучше его представить списком. Логические операции выполняют в следующей последовательности: сначала идёт инверсия, затем конъюнкция, после этого дизъюнкция, после неё импликация, по её выполнении эквиваленция.
После них идут Штрих Шеффера и Стрелка Пирса. Первым может быть выполнено как то, так и другое.
Далее приведём несколько поучительных задач на построение таблиц истинности
Задачи 1 — 3
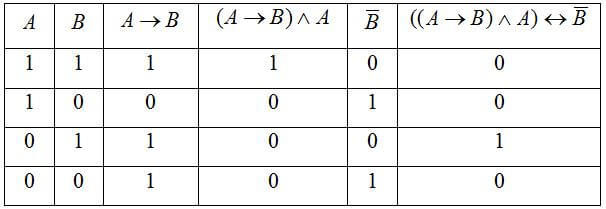
Сделать построение таблицы истинности для функции ((A→B) ∧ A) ↔ B
Решение:
-
- Определяем сколько будет у нас столбцов. Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.
- Определяем, сколько будет у на строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций. У нас будет 2n+1 = 22 + 1= 5;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В двух первых столбцах записываем возможные значения переменных;
- В далее идущих столбцах записываем, какие значения принимают промежуточные функции;
- В самом последнем из столбцов записываем итоговые значения функции.
В результате всего этого у нас должно получиться:
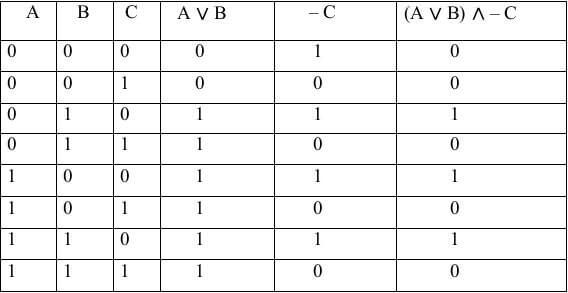
Провести построение таблицы истинности функции (A ∨ B) ∧ – C
Решение:
- Определяем сколько будет столбцов. Количество переменных у нас 3, количество логических операций 3. Складываем то и другое: 3+3 = 5.
- Определяем, количество строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций.В итоге будет 2n+1 = 23 + 1= 9;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В два первые столбца вносим возможные значения наших переменных;
- В далее следующие столбцы записываем, какие значения принимают промежуточные функции;
- В последнем столбце записываем итоговые значения функции.
В итоге получим таблицу:
Сделать таблицу истинности для
(A ∧ B ↔ B ∧ C) ∨ (C → A)
Функция посложнее и таблица получится значительно больше, чем предыдущая.
- Считаем столбцы. Количество переменных 3, количество логических операций 6. Значит столбцов будет 3+6=9;
- Считаем строки. Их количество будет 23+1= 9;
- Заполняем первую строку таблицы;
- В первых столбцах записываем все допустимые значения наших переменных;
- В остающихся столбцах пишем, какие наша функция принимает промежуточные значения
- В последний столбец пишем итоговые значения данной нам функции.
В итоге у нас получается таблица:
Нет времени решать самому?
Наши эксперты помогут!
Построения функции, если известна её таблица истинности
Совершенной дизъюнктивной нормальной формой считают такую нормальную форму, в которой отсутствуют одинаковые элементарные конъюкции и все конъюкции включают один и тот же набор переменных, куда каждая из них входит не более одного раза.
Алгоритм действий для получения СДНФ по таблице истинности:
- Отметьте в таблице строки, в которых значение функции равняется 1
- Выпишете для каждой отмеченной строки конъюкцию всех переменных. Если переменная равна 1, в конъюкцию следует включить саму эту переменную. Если переменная равняется 0, то её отрицание;
- Все полученные конъюкции свяжите в дизъюкцию.
Аналогичным образом определяется СКНФ
В строках, в последнем столбце которых функция равна 0, запишите дизъюкции всех переменных. Если значение переменной в данной строке будет 0, в дизъюкцию следует включить саму эту переменную. Если значение функции равно 1, то включить нужно её отрицание.
Правило + задача
СДНФ всегда равно СКНФ. СДНФ = СКНФ.
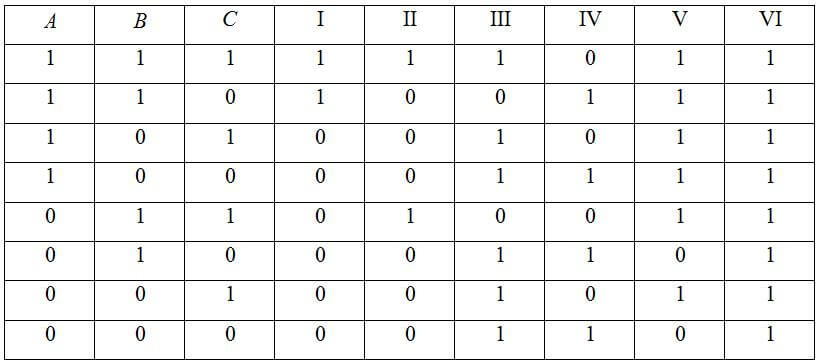
Дана таблица истинности:
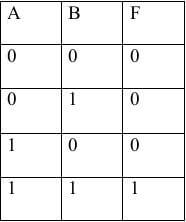
Выделяем в ней цветом строку
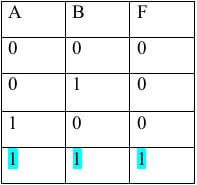
Заполняем столбцы с СДНФ и с СКНФ
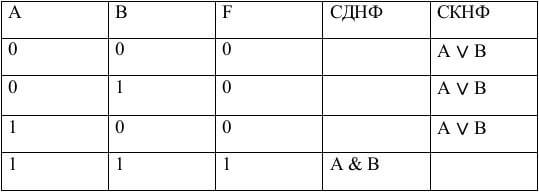
Записываем СДНФ
СДНФ = A & B
Записываем СКНФ
СКНФ = (A ∨ B) & (A ∨ B) & (A ∨ B)