Как составить таблицы распределения по частотам значений случайной величины

Лекция
16. Распределение данных по частотам.

На практике часто после проведения реальных испытаний
составляются таблицы распределения значений случайных величин по частотам (или
по относительным частотам), после чего для большей наглядности распределение
данных представляют либо в виде диаграммы, либо в виде полигона частот (полигона
относительных частот).

Гистограмма частот — это фигура,
состоящая из прямоугольников, опирающихся на интервалы группировки.

Полигон частот — один из способов
графического представления плотности вероятности случайной величины.
Представляет собой ломаную, соединяющую точки, соответствующие срединным
значениям интервалов группировки и частотам этих интервалов.

► Например,  имеются результаты 20 измерений
диаметра d болта (в миллиметрах с точностью до 0,1):

10,1     10,0     10,2  
  10,1     9,8     9,9     10,0  
  10,0     10,2     10,0

10,0     9,9     10,0  
  10,1     10,0     9,9     10,0  
  10,1     10,1     10,0

Представим эти данные с помощью: 1) таблицы распределения
по частотам M и относительным частотам W; 2) полигона частот.

1) Таблица частот и относительных частот
d	9,8	9,9	10,0	10,1	10,2
M	1	3	9	5	2
W = M/N	0,05	0,15	0,45	0,25	0,1

Отметим, что сумма всех значений частот (строка
значений M) равна N = 20, сумма всех значений относительных
частот (строка значений W) равна 1.

2) Полигон частот

Задания для
самостоятельной работы по теме:

1.                
Составить таблицу распределения по частотам
М значений случайной величины Х – цифр, встречающихся в выборке следующих
телефонных номеров:

1) 3965184, 6542913, 7902914, 2878858.

2) 1316573, 4336582, 2983412, 3941009.

2.  Построить полигон
частот и полигон относительных частот значений случайной величины Х ,
распределение которой представлено в таблице

Х	5	6	7	8	9
М	2	3	6	4	1

3.    
 таблице записаны результаты 20 взвешиваний (с точностью до 1 г)
одной и той же стальной отливки:

99	97	101	100	99	102	100	102	98	101
100	98	100	98	101	97	101	100	100	99

Составить таблицы распределения по частотам (М) и относительным
частотам (W), а также полигон частот значений случайной величины Х-
результата определения массы стальной отливки.

Сегодня на уроке мы вспомним, что называют относительной частотой
события.

Напомним, чем занимается статистика. Выясним, какие величины
называют случайными. Узнаем, какие величины называют дискретными, а какие –
непрерывными.

Прежде, чем приступить к рассмотрению новой темы, вспомним, что относительной
частотой события  в
данной серии испытаний называют отношение числа испытаний , в
которых это событие произошло, к числу всех проведённых испытаний . При
этом число  называют
частотой события . Относительную
частоту события  обозначают
.

Тогда по определению .

Сегодня на занятии мы перейдём к изучению раздела математики,
который называют статистикой.

Статистика – это наука, которая
занимается получением, обработкой и анализом количественных данных о
разнообразных массовых явлениях, происходящих в обществе и природе.

Можно сказать, что статистика занимается сбором, представлением (в
виде таблиц, графиков, диаграмм) и анализом информации о различных случайных
величинах.

Случайными величинами называют
такие величины, которые в ходе наблюдений или испытаний могут принимать
различные значения.

Можно говорить, что величину называют случайной, если она может
принимать заранее неизвестные числовые значения, зависящие от случайных
обстоятельств. Примерами являются число попаданий при трёх выстрелах; число
вызовов, поступающих на телефонную станцию за сутки; число выпавших решек при
бросании монеты.

Сумма чисел, выпадающая при бросании двух игральных костей, также
является случайной величиной. Обозначим её – .
Отметим, что, как правило, случайные величины обозначают , , .

Случайная величина  может
принимать значения: , , , …, . Каждое
из значений является суммой чисел, которые выпадают при бросании двух игральных
костей.

Сейчас вы видите таблицу, в которой указаны возможные суммы, выпадающие
при бросании двух игральных костей.

Ниже давайте составим таблицу, в которой покажем распределение
значений случайной величины X по их вероятностям P. Каждой из сумм (, , , …, )
поставим в соответствие вероятность, с которой она может появиться в результате
одного испытания, то есть одного бросания двух игральных костей.

Таким образом, мы показали распределение значений случайной
величины  по их
вероятностям. Иногда для наглядности это может быть изображено, например, в
виде линейной или столбчатой диаграммы.

Сумма вероятностей  всех
значений величины ,
которые записаны во второй строке таблицы равна 1, как сумма вероятностей всех
элементарных исходов испытания с нахождением суммы очков при одном бросании
двух игральных костей.

Посмотрите на знак, с помощью которого мы записали сумму значений
вероятностей.

Этот знак был введён Леонардом Эйлером. Он используется для записи
суммы значений некоторой величины.

Вообще, таблицы распределения значений случайной величины составляются
по результатам теоретических расчётов вероятностей. На практике часто после
проведения реальных испытаний составляются таблицы распределения значений
случайных величин по частотам (или относительным частотам). Для наглядности
распределение данных представляют в виде диаграммы или полигона частот
(полигона относительных частот).

С диаграммами вы уже знакомы. Вы знаете, что диаграмма – это
графическое изображение, наглядно показывающее соотношение между различными
величинами. Полигон (или его ещё называют графиком) также
используют для наглядного изображения распределения данных, полученных в
результате статистического исследования.

Давайте решим задачу. В результате эксперимента получены
следующие значения случайных величин:

.

Представьте эти данные с помощью таблицы распределения по частотам
и относительным частотам и с помощью полигона частот.

Решение. В первую очередь имеющиеся
данные (значения случайной величины) представим в виде таблицы распределения по
частотам и относительным частотам.

Теперь построим полигон частот. Для этого мы на координатной
плоскости на оси абсцисс отметим значения случайной величины, а на оси ординат
– значения частот. Отметим точки с соответствующими координатами. Затем
последовательно соединив эти точки отрезками, получим ломаную, которую является
полигоном частот.

Рассмотренные выше случайные величины принимали изолированные друг
от друга значения. Такие величины называют дискретными, что в переводе с
латинского означает «раздельный, прерывистый».

Если случайная величина принимает любое значение из некоторого
промежутка, то такую величину называют непрерывной. Например, расстояние
от точки попадания пули до центра мишени. Множество значений этой величины –
некоторый непрерывный отрезок числовой прямой.

 А сейчас выполним задание. Составьте таблицу распределения
по частотам значений случайной величины X – цифр, встречающихся в
выборке следующих телефонных номеров:

.

Решение.

И выполним ещё одно задание. Постройте полигон частот
значений случайной величины X, распределение которой представлено в следующей таблице.

Чтобы выполнить это задание, мы на координатной плоскости на оси
абсцисс отметим значения случайной величины, а на оси ординат – значения частот.
Отметим точки с соответствующими координатами. Затем, последовательно соединив
эти точки отрезками, получим ломаную, которую является полигоном частот.

Пусть
требуется изучить статистическую
совокупность относительно некоторого
количественного признака X.
Числовые значения признака будем
обозначать через х_i.

Из
генеральной совокупности извлекается
выборка объёма п.

1. Количественный
   признак Х
   – дискретная
   случайная величина.

Наблюдаемые
значения х_i
называют вариантами,
а последовательность вариантов,
записанных в возрастающем
порядке, –
вариационным
рядом.

Пусть
x₁
наблюдалось n₁
раз,

x₂
наблюдалось n₂
раз,

x_k
наблюдалось n_k
раз,

причем

.
Числа n_i
называют
частотами,
а их отношение к объёму выборки, т.е.

,
–
относительными
частотами (или
частостями), причем

.

Значение
вариант и соответствующие им частоты
или относительные
частоты можно записать в виде таблиц 1
и 2.

Таблица
1

Варианта xi	x1	x2	…	xk
Частота ni	n1	n2	…	nk

Таблицу
1 называют дискретным
статистическим
рядом распределения (ДСР) частот, или
таблицей частот.

Таблица
2

Варианта xi	x1	x2	…	xk
Относительная частота wi	w1	w2	…	wk

Таблица
2 
ДСР
относительных частот, или
таблица относительных частот.

 Определение.
Модой
называется наиболее часто встречающийся
вариант, т.е. вариант с наибольшей
частотой. Обозначается x_мод.

 Определение.
Медианой
называется
такое значение признака, которое делит
всю статистическую совокупность,
представленную в виде вариационного
ряда, на две равных по числу части.
Обозначается

.

Если
n
нечетно, т.е. n
= 2m
+ 1,
то

=
x_m+1.

Если
n
четно, т.е. n
= 2m,
то

.

Пример
3.
По результатам наблюдений: 1, 7, 7, 2, 3, 2,
5, 5, 4, 6, 3, 4, 3, 5, 6, 6, 5, 5, 4, 4 построить ДСР
относительных частот. Найти моду и
медиану.

Решение.
Объем выборки n
= 20. Составим ранжированный ряд элементов
выборки: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6,
7, 7. Выделим варианты и подсчитаем их
частоты (в скобках): 1 (1), 2 (2), 3 (3),

4 (4),
5 (5), 6 (3), 7 (2). Строим таблицу:

xi	1	2	3	4	5	6	7
wi	1/20	2/20	3/20	4/20	5/20	3/20	2/20

Наиболее
часто встречающийся вариант x_i
=
5. Следовательно, x_мод
=
5. Так
как объем выборки n
– четное число, то

Если
на плоскости нанести точки

и соединить их отрезками прямых, то
получим полигон
частот.

Если
на плоскости нанести точки

,
то получим полигон
относительных частот.

Пример 4.
Построить полигон частот и полигон
относительных частот по данному
распределению выборки:

xi	4	7	8	12	17
ni	2	4	5	6	3
wi	2/20	4/20	5/20	6/20	3/20

Решение.
На рисунке 2 показан полигон частот и
на рисунке 3 – полигон относительных
частот.

Рис.
2 Рис.
3

Замечание.
Чем круче полигон, тем равномернее
процесс.

1. Пусть
   количественный признак X
   – непрерывная
   случайная величина,
   принимающая значения из интервала
   (а,b).
   Весь диапазон наблюдаемых данных делят
   на частичные
   интервалы
   [х_i;
   x_i+1),
   которые берут обычно одинаковыми по
   длине:
   
   =
   x_i+1
   –
   x_i
   (i
   = 0, 1, …, k).
   Для определения величины интервала

   можно использовать формулу
   Стерджеса:

где
(x_max
–
x_min)
разность между наибольшим и наименьшим
значениями признака, k
= 1 + log₂
n

число интервалов (log₂
n

3,322
lg
n).
Если окажется, что h

дробное число, то за длину частичного
интервала следует брать либо ближайшее
целое число, либо ближайшую простую
дробь. За начало первого интервала
рекомендуется брать величину x_нач
=
x_min
–

.
В каждом
из частичных интервалов подсчитывают
число наблюдаемых значений, т.е. частоту
n_i.
По частотам находят относительные
частоты

.
Полученные интервалы и соответствующие
им частоты (или относительные частоты)
записывают в виде таблицы 3. При этом
правая граница последнего интервала
тоже включается.

Таблица
3

Частичный интервал [xi,xi+1)	[x0, x1)	[x1, x2)	…	[xk-1, xk]
Относительная частота wi	w1	w2	…	wk

Таблица
3 называется интервальным
статистическим рядом распределения
(ИСР) относительных частот,
который задаёт распределение
выборки. Аналогично
составляется ИСР
частот.

Пример
5.
Измерили рост (с точностью до см) 30
наудачу отобранных студентов. Результаты
измерений таковы:

178,
160, 154, 183, 155, 153, 167, 186, 163, 155, 157, 175, 170, 166, 159,

173,
182, 167, 171, 169, 179, 165, 156, 179, 158, 171, 175, 173, 164, 172.

Построить
интервальный статистический ряд
относительных частот.

Решение.
Для
удобства проранжируем полученные
данные:

153,
154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167,

169,
170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 179, 182, 183, 186.

Отметим,
что Х

рост студента 
непрерывная случайная величина. Как
видим, x_min
=
153, х_max
=
186; по формуле Стерджеса, при n
= 30, находим длину частичного интервала

Примем

= 6. Тогда х_нач
= 153 –

=150.
Исходные данные разбиваем на шесть (k
=
1 + log₂30
= 5,907 
6) интервалов:

[150,
156), [156, 162), [162, 168), [168, 174), [174, 180), [180, 186].

Подсчитав
число студентов n_i,
попавших в каждый из полученных
промежутков, получим ИСР:

[xi,xi+1)	[150, 156)	[156, 162)	[162, 168)	[168, 174)	[174,180)	[180,186]
ni	4	5	6	7	5	3
wi	4/30	5/30	6/30	7/30	5/30	3/30

Первая
и третья строчка таблицы образует ИСР
относительных частот.

Замечание.
При
решении учебных задач на построение
ИСР можно пользоваться следующими
правилами.

1. Назначаются нижняя
   граница а
   и верхняя граница b
   для вариант так, чтобы отрезок [a;
   b]
   вместил всю выборку; часто полагают
   
   ,
   
   ,
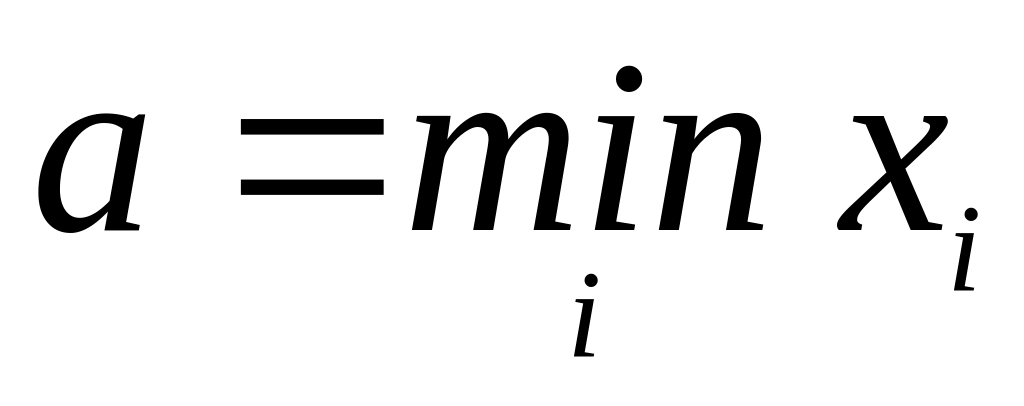
   но иногда a
   и b
   назначают из соображений удобства, но
   не слишком далеко от
   

   и
   
   .

2. Находится число
   k
   равных по длине частичных интервалов
   варьирования, которое зависит от объема
   выборки и обычно 6
   
   k
   
   20;
   рассчитывается длина интервалов
   группирования
   
   .

Интервальный
статистический ряд распределения,
представленный графически, называется
гистограммой.

Гистограмма
относительных частот
строится следующим образом: по оси
абсцисс откладываются
интервалы (х_i;
х_i+1)
и на каждом из них строится прямоугольник
высотой

где

;

.

Площадь
i–го
прямоугольника

.

Площадь
всей гистограммы

.

З
амечание:
гистограмма на рисунке 4 – гистограмма
относительных частот.

x₃

Рис.
4

Можно
построить гистограмму
частот,
высоты прямоугольников которых равны

.

Пример 6.
Построить гистограмму частот по данному
ИСР частот:

[xi; xi+1)	[100; 120)	[120; 140)	[140; 160)	[160; 180)	[180; 200]
ni	20	50	80	40	10

Решение.
По ИСР частот находим длину частичных
интервалов

= 20 и высоты прямоугольников h_i
=

.
Результаты занесем в таблицу:

[xi; xi+1)	[100; 120)	[120; 140)	[140; 160)	[160; 180)	[180; 200]
ni	20	50	80	40	10
hi	1	2,5	4	2	0,5

Искомая
гистограмма частот изображена на рис.
5.

h_i

x_i

x_i

Рис.
5

В
теории вероятностей гистограмме
относительных частот соответствует
график плотности распределения
вероятностей. Распределение выборки,
задаваемое интервальным статистическим
рядом (табл. 3) или таблицей относительных
частот (табл. 2), называется эмпирическим
распределением случайной величины.

По
теореме Бернулли относительная частота
w_i,
появление события в п
независимых
испытаниях
сходится
по вероятности к вероятности р_i
этого события

.
Значит во второй строке таблицы 3 и
таблицы 2 стоят
приближённые значения вероятностей р_i
следующих событий

и

,
поэтому
распределение выборки называют
эмпирическим распределением случайной
величины X.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Условие /
задание / 327

327. Составить таблицу распределения по частотам М, значений случайной величины X — цифр, встречающихся на ценниках товаров в некотором киоске: 73, 102, 225, 30, 44, 68, 76, 5, 90, 119, 86, 24, 37, 207, 8, 45, 51, 13, 201, 69.

решебник / задание / 327

Видеорешение / задание / 327

Другие номера из решебника