Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.
Что такое теплообмен и при каких условиях он происходит
Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.
Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.
Рассмотрим два тела, имеющие различные температуры (рис. 1).
Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.
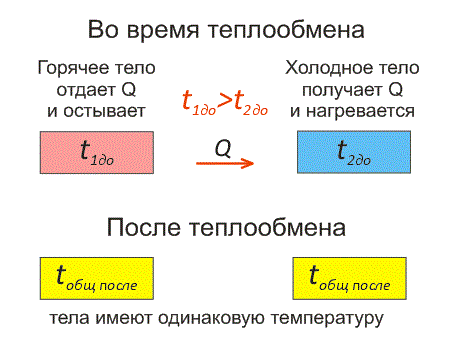
Рис.1. Два тела во время теплообмена и после
На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.
Когда температуры тел выравниваются, теплообмен прекращается.
Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.
Когда температура тел выравняется, теплообмен прекратится.
Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.
Уравнение теплового баланса и сохранение тепловой энергии
Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».
А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».
Эти факты отражены на рисунке 2.

Рис. 2. Полученное количество теплоты имеет знак «+», а отданное Q – знак «-»
Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.
Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.
Уравнение теплового баланса
Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.
Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:
[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]
(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.
(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.
В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.
Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.
В некоторых учебниках применяют сокращения:
[large Q_{1} + Q_{2} = 0 ]
Примечание: Складывая два числа мы получим ноль, когда эти числа будут:
- равными по модулю и
- имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).
Если несколько тел участвуют в процессе теплообмена
Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:
[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]
При этом:
- Q для каждого нагреваемого тела будет обладать знаком «+»,
- Q для каждого охлаждаемого тела — знаком «-».
Пример расчетов для теплообмена между холодным и горячим телом
К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.
Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
Решение:
В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.
Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.
1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:
[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]
2). Теперь запишем формулу для каждого количества теплоты:
[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]
[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]
Примечания:
- (large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
- Массу воды переводим в килограммы;
- Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
- Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;
3). Подставим выражения для каждого Q в уравнение баланса:
[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]
4). Для удобства, заменим символы числами:
[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]
Проведем упрощение:
[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]
Раскрыв скобки и решив это уравнение, получим ответ:
[large t_{text{общ}} = 58,33 ]
Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.
Задача для самостоятельного решения:
В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.
Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:
- (large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
- (large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
- (large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;
А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.
Выводы
- Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
- Когда тела будут иметь равную температуру, теплообмен прекратится;
- Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
- А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
- Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
- Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
- В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
- В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.

Общие сведения
Баланс в переводе на русский язык означает равновесие. Когда теплоизолированная система приходит в состояние теплового равновесия, то температура всех тел, образующих эту совокупность, становится одинаковой. Такую ситуацию называют законом теплового равновесия или нулевым уравнением термодинамики.
Впервые с уравнением теплового баланса знакомят в средней школе на уроке физики. Ученикам в седьмом классе предлагается решить несколько простых заданий, используя равенство. Формула и определение даётся без доказательства, так как для понимания процесса нужно знать понятия, которые разбираются в выпускных классах школы. Например, то, что теплоёмкость не является характеристикой вещества, при этом она может быть разной в зависимости от проходящих процессов.

Закон теплового баланса позволяет утверждать, что когда в изолированной системе физических тел происходит только теплообмен, то часть тепла, переданного телами, внутреннее состояние энергии которых уменьшается, численно равняется теплу, полученному объектами с возрастающей внутренней энергии. Математически уравнение записывается в виде следующей формулы: Q 1 + Q 2 + Q 3 + …+ Qn = 0, где:
- n — число тел, находящихся в теплоизолированной системе;
- Q — полученное количество теплоты.
Если предположить, что имеется совокупность, состоящая из двух тел, из которых одно отдаёт тепло, а другое принимает его, то справедливо будет записать: Q1 = Q2. Таким образом, теплоотдача всегда равняется теплоприёму. Поэтому этот закон и называют правилом сохранения энергии в тепловых процессах.
Когда тела два, то понять, какое из них отдаёт тепло, а какое получает, несложно. То, что имеет большее нагревание, — будет отдавать. Если же объектов три и более, и некоторые из них имеют промежуточную температуру, определить, какие из них принимают тепло, довольно сложно. Вот тут на помощь и приходит уравнение термодинамики.
Изменение внутренней энергии объясняется теплопередачей, то есть случаем, когда работа не совершается. Поэтому в физике уравнение теплового баланса используется при анализе процессов теплопередачи, нахождении КПД. Это равенство можно применять как при рассмотрении твёрдых тел, так и жидкости.
Суть уравнения
Следует рассмотреть процесс установления теплового равновесия в теплоизолированной системе. Это такая совокупность, в которой объекты взаимодействуют только друг с другом. Простейшая система будет состоять из двух тел. Например, в термос налит сок и в него вброшен лёд. В этом случае термос является изолятором от внешнего воздействия. Пусть первое тело имеет температуру t1, а второе t2. Допустим, что t1 больше t2. Это допущение не является принципиальным, поэтому его можно использовать.
В начальный момент времени тела находятся далеко друг от друга и теплообмен между ними не происходит. Как только, они соприкоснутся — начнётся взаимодействие. Так как температура первого тела больше, то оно начнёт остывать, а второе нагреваться. Происходит теплопередача. В какой-то момент времени она прекратится и наступит тепловое равновесие. То есть температура двух тел станет одинаковой: t1 = t2.
Получившаяся температура называется равновесной. Обозначается она греческой буквой тета — θ. Так как раньше первое тело имело большую температуру, то получается, что в процессе взаимодействия оно отдало тепло. Записать это можно как Q1– — количество теплоты, отданное первым телом. Второй же объект в процессе подогрелся — увеличил температуру. Обозначить это можно как +Q2 — количество теплоты, полученное вторым телом.
Получить тепло второй объект мог только от первого тела, так как рассматриваемая система изолированная. Соответственно, и отдать определённое количество теплоты первое тело могло только второму. Отсюда можно сделать вывод, что если система теплоизолированная, то эти два количества теплоты одинаковы: Q1– = +Q2. Фактически это есть уравнение баланса.
Такая запись даётся в школьных учебниках. Но профессиональные физики записывают его в другой форме. Для термодинамики неважно, какой объект отдаёт, а какой получает тепло. Наука изучает только количество теплоты, полученное в процессе. Взяв простую аналогию с весом, когда о похудевшем человеке на два килограмма можно сказать, что он поправился на минус два кило, будет верным записать: Q1– = -Q1 или -Q1 = Q2.

Если собрать два слагаемых таким образом, чтобы они находились с одной стороны знака равенства, то можно записать: Q1 + Q2 = 0.
Суммарное количество теплоты, образуемое при теплообмене тел в теплоизолированной системе, равно нулю. При этом это правило будет справедливо и для энного количества объектов.
Доказательство закона
Пусть имеется теплоизолированная система, состоящая из нескольких помещённых в неё объектов. Сами тела могут обмениваться теплом только друг с другом. Первый закон термодинамики для системы в целом можно записать как Q = А’ + Δ U. То есть количество теплоты, полученное всей системой, равняется суммарной работе, совершённой всеми телами в совокупности над внешним миром, складывающейся с изменением энергии всех тел внутри системы.
По условию задачи внутренняя энергия меняется не за счёт совершения работы. Поэтому А’ = 0. С другой же стороны, теплоизоляция обозначает, что Q = 0. Иными словами, количество энергии, поступающее из окружения Земли, равняется нулю. Следовательно, изменение внутренней энергии всех тел в системе будет нулевым: Δ U = 0.

Энергия системы состоит из внутренних энергий каждого из входящих в неё тел: U = U1 + U2 +…+ Un. Изменение же её Δ U = Δ U 1 + Δ U 2 + … + Δ Un. Отсюда следует, что если внутренняя энергия остаётся неизменной, то сумма Δ U будет нулевой: Δ U 1 + Δ U 2 + … + Δ Un = 0.
Первый закон термодинамики персонально для каждого из тел входящих в систему можно записать как следующую систему:
{Q1 = А 1′ + Δ U1;
{Q2 = А 2′ + Δ U2;
… ;
{Qn = А n’ + Δ Un.
Все уравнения, входящие в неё, можно сложить почленно. При этом распределив слагаемые для удобства дальнейшего анализирования: Q1 + Q2 +…+ Q n = (А n1′ + А n2′ + … + А n’) + (Δ U1 + Δ U2 + … + Δ Un). Из полученного выражения можно сделать вывод, что сумма дельт второго члена в правой части равняется нулю. В первом же члене с правой стороны каждое слагаемое также равняется нулю. Поэтому можно записать: Q1 + Q2 +…+ Q n = 0. Что и следовало доказать.
Для решения задач полезно вспомнить, на что может идти полученное тепло. К таким частным случаям относят:

- Процессы, при которых нет фазовых переходов. В таком случае полученное количество идёт на увеличение теплоты потенциальной и кинетической энергии: Q = c * m * ΔT (изохорная теплоёмкость).
- Плавление. Например, есть тающий лёд, к которому подводят тепло, при этом кинетическая энергия остаётся постоянной. Значит, изменяется только потенциальная мощность. В этом случае происходит превращение льда в воду. Это действие называют плавлением — переход кристаллического вещества из твёрдого состояния в жидкое: Q = λ * m.
- Парообразование. Выделение из жидкости пара: Q = L * m.
Типовое задание
Явление теплового баланса используется как в изучении процессов при переходе из одного агрегатного состояния в другое, так и для твёрдых или жидких тел, не изменяющих решётку. Существуют типовые задания, входящие в школьную программу. Ученик, решая их, научится находить удельные параметры и сможет понять всю важность выражения теплового баланса.

В латунный котёл массой 128 граммов, содержащий 240 граммов воды, при 8,4 градусах опущено металлическое тело массой 192 грамма, нагретое до 120 градусов Цельсия. Окончательная установившаяся температура составила 21,5 градус. Определить удельную теплоёмкость рассматриваемого тела. Для решения задачи необходимо из справочника взять значение энергетической теплоёмкости латуни. Она составляет 400 Дж/ кг *С0. При этом нужно учитывать, что котёл теплоизолирован.
Температуру, которая установилась через время, обозначают буквой θ. Решение подобных задач начинают с установления количества тел, участвующих в теплообмене. В этом примере их три: вода, котёл, испытываемое тело. Количество тепла, полученное всеми тремя объектами, согласно закону, будет равняться нулю: Qв + Qк +Qт = 0. Теперь следует каждое слагаемое расписать отдельно:
- Qв = mв * cв * Св (θ – Tв).
- Qк = mк * cл * (θ – Tв).
- Qт = mт * cт * (θ – Tк).
Полученные формулы нужно подставить в исходное уравнение. При этом следует обратить внимание, что при подстановке образуется общий множитель (θ – T в), который можно вынести за скобки: (m в * c в + m к * c л) * (θ – T в) + m т * c т * (θ – T к) = 0.
Из условия задачи известно, что у тела температура 100 градусов, а равновесная температура меньше. Поэтому последняя скобка будет отрицательной. Значит, есть смысл перенести это слагаемое вправо, поменяв местами вычитаемое и уменьшаемое: (m в * c в + m к * c л) * (θ – T в) = m т * c т * (T к — θ). Отсюда можно выразить удельную теплоёмкость массы тела. Она будет равняться: C т = (m в * c в + m к * c л) * (θ – T в) / m т * (T к — θ) .
Все данные, используемые в формуле, известны. Остаётся только провести расчёты, подставив значения: Cт = (0,24 кг * 4,2 кДж/кг*С + 0,128 кг * 0,4 кДж/кг*С *(21,5 — 8,4) С) / 0,192 кг * (100 — 21,5)С = 0,921 кДж/ кг *С0. Полученное вещество является алюминием.
Примеры высокого уровня
Эти задачи рассчитаны на подготовленных учащихся, понимающих суть процессов и знающих уравнение баланса. Например, электрическая установка с мощностью P = 350 Вт не может нагреть воду массой 0,6 кг до кипения. Убедившись в этом, её выключают. Нужно определить, каким останется конечный нагрев воды через 15 секунд.
Из условия можно утверждать, что мощность теплопотерь равняется мощности нагревателя: Pпот = P. По сути, мощность теплопотерь это количество тепла, отдаваемое телом в единицу времени. То есть: P пот = Q– / ΔT. С другой стороны, отданное тепло находится из формулы: Q – = c * m * (-ΔT). Отсюда можно записать: P = – c * m * ΔT / Δt. Из последнего выражения легко выразить искомый параметр: ΔT = -(P * Δt) / (c * m). Все необходимые данные есть в условии и их необходимо просто подставить: ΔT = – 350 Вт * 15 с / 4200 Дж * 0,6 кг = – 2,1 С0. Минус в ответе показывает, что температура понижается. Задача решена.

Вот ещё одна задача, для решения которой необходимо вначале исследовать ситуацию. В ёмкость поместили смесь, состоящую из пяти килограммов воды и трёх килограммов льда. Затем туда пустили 0,2 кг водяного пара при температуре 1000С. Нужно определить, что произойдёт.
По условию задачи даны три массы mв, mл, mп. Можно предположить, что при смешении в момент запуска пара температура в системе была нулевой. Это исходит из того, что в ёмкости одновременно находится лёд и вода. Поступающий пар конденсирует, и из него образуется вода. Через время она остывает до нуля. Поэтому в начальный момент выделившаяся энергия идёт только на таяние льда. Cуществует три варианта развития события:
- Лёд не растает ( θ =00С).
- Лёд полностью растает (0 < θ < 1000С).
- Вода начнёт кипеть ( θ = 1000С) .
Для того чтобы выяснить, какой вариант верный, нужно найти выделившуюся энергию: Qпл = λ * m = 330 * 3 = 990 кДж. Получается, чтобы растопить лёд, нужно 990 кДж теплоты. Пар, вступая в реакцию, отдаёт: Q- = L* m + cв * mв (Tпар – Tпл) = 2300 + 0,2 + 4,2 * 0,2 * 100 = 544 кДж. Учитывая два полученных результата, можно утверждать, что при конденсации основного пара выделившейся теплоты будет недостаточно для расплавления льда. Следовательно θ = 00С.
Содержание:
Тепловое равновесие:
Температура — мера средней кинетической энергии теплового движения частиц вещества
В повседневной жизни под температурой мы понимаем степень нагретости тела (холодное, тёплое, горячее). Такой подход является довольно субъективным, он зависит не только от состояния рассматриваемого тела, но и от наших ощущений. Чтобы избежать субъективной неопределённости, необходимо установить способ измерения температуры.
Тепловое равновесие
Если привести в соприкосновение два тела, то молекулы этих тел, взаимодействуя между собой, будут обмениваться энергией. При этом молекулы с большей кинетической энергией передают часть энергии молекулам с меньшей кинетической энергией. В результате средняя кинетическая энергия теплового движения молекул одного тела увеличивается, а другого — уменьшается. Отдающее энергию тело называют более нагретым, а тело, к которому энергия переходит, — менее нагретым. Как показывает опыт, такой переход энергии продолжается до тех пор, пока не установится некоторое состояние, в котором тела могут находиться сколь угодно долго. В этом состоянии степень нагретости тел становится и остаётся одинаковой, следовательно, у тел одинаковая температура. Это учитывают при измерении температуры тела. Термометр приводят в соприкосновение с телом, но отсчёт его показаний выполняют не сразу, а через некоторый промежуток времени. Это необходимо для того, чтобы между термометром и телом установилось тепловое равновесие.
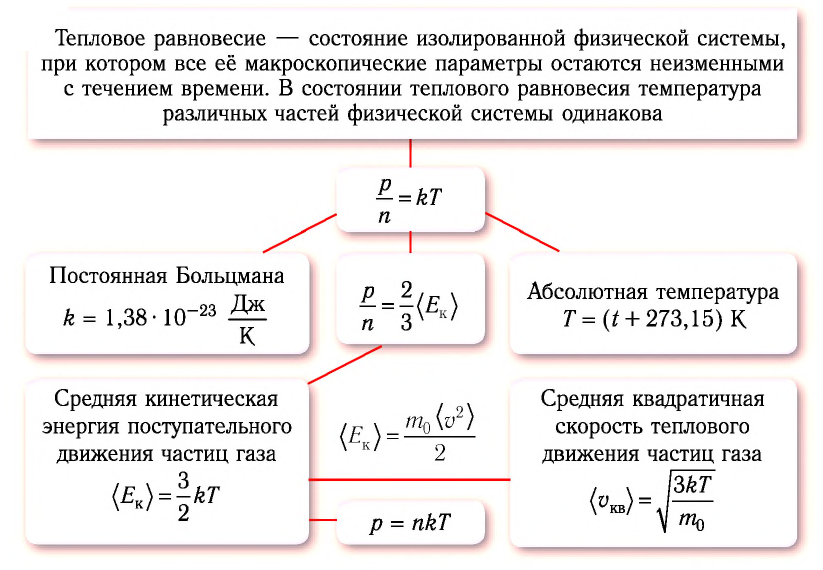
Тепловое равновесие — состояние изолированной физической системы, при котором все её макроскопические параметры остаются неизменными с течением времени.
Под изолированной, или замкнутой, системой понимают систему тел, которая не обменивается энергией с окружающими телами.
Отметим, что у тел, входящих в физическую систему, находящуюся в состоянии теплового равновесия, могут быть различные значения плотности, концентрации, давления и объёма. Однако температура всех тел, входящих в такую систему, всегда одинакова.
Интересно знать:
Понятия «градус» и «температура» появились задолго до изобретения термометра. Знаменитый древнеримский врач Гален (II в.) считал, что все лекарства следует различать по «градусам» (от лат. gradus — ступень) теплоты, холода, сухости и влажности. Гален учил, что одни лекарства оказывают охлаждающее действие, а другие — согревающее. При необходимости следовало смешивать лекарства, чтобы умерить излишнее тепло влажностью, а холод — сухостью. От латинского слова temperature (смешение) возник термин «температура».
Температура и средняя кинетическая энергия поступательного движения молекул газа
Определение температуры должно основываться на такой физической величине, которая характеризует состояние тел и является одинаковой для любых тел, находящихся в состоянии теплового равновесия. Необходимым свойством обладает средняя кинетическая энергия теплового движения частиц вещества. Тепловое движение частиц вещества существенно изменяется при изменении его агрегатного состояния. Максимально простым оно оказывается у одноатомного газа, атомы которого совершают только поступательное движение.
Возьмём несколько сосудов разной вместимости, снабжённых манометрами для измерения давления (рис. 16). Заполнив их различными газами, например аргоном, неоном и гелием, поместим сначала в сосуд с тающим льдом (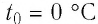
Опытным путём установлено, что в состоянии теплового равновесия, несмотря на различные значения давления 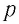 и концентрации
и концентрации 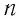 частиц, отношение давления к концентрации
частиц, отношение давления к концентрации 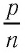 во всех сосудах оказалось практически одинаковым:
во всех сосудах оказалось практически одинаковым: 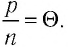 Это отношение для разреженных газов (удовлетворяющих требованиям модели «идеальный газ») зависит только от температуры, и эта зависимость является линейной, т. е.
Это отношение для разреженных газов (удовлетворяющих требованиям модели «идеальный газ») зависит только от температуры, и эта зависимость является линейной, т. е.
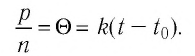
Здесь 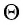 характеризует температуру газов в энергетических единицах (в СИ измеряют в джоулях*);
характеризует температуру газов в энергетических единицах (в СИ измеряют в джоулях*); 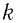 — коэффициент пропорциональности, зависящий от выбора температурной шкалы. В 1899 г. немецкий физик-теоретик Макс Планк (1858—1947) предложил назвать коэффициент
— коэффициент пропорциональности, зависящий от выбора температурной шкалы. В 1899 г. немецкий физик-теоретик Макс Планк (1858—1947) предложил назвать коэффициент 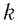 постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844 — 1906), одного из основателей молекулярно-кинетической теории газов:
постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844 — 1906), одного из основателей молекулярно-кинетической теории газов:
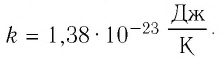
Если для измерения температуры использовать абсолютную температурную шкалу, то при определении числового значения температуры по этой шкале полагают:

Абсолютную (термодинамическую) шкалу температур предложил в 1848 г. выдающийся английский физик Уильям Томсон (1824—1907), удостоенный за работы в области физики в 1892 г. титула лорда Кельвина. Поэтому эту шкалу обычно называют шкалой Кельвина.
Шкала Кельвина совершенно не зависит от физических свойств каких бы то ни было веществ, поэтому её можно считать абсолютной и универсальной.
Нулевая точка по шкале Кельвина соответствует самой низкой теоретически возможной температуре (абсолютный нуль температуры). Температура тающего льда по этой шкале 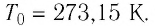 Связь между температурами по шкале Цельсия
Связь между температурами по шкале Цельсия 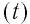 и по шкале Кельвина (Т) имеет вид:
и по шкале Кельвина (Т) имеет вид: 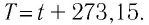
* Единица измерения температуры джоуль неудобна. Например, температура кипения воды, выраженная в джоулях: 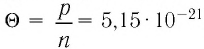 Дж.
Дж.
Единица температуры по абсолютной шкале один кельвин (1 К) является основной единицей температуры в СИ и совпадает с одним градусом (1 °С) по шкале Цельсия. Поэтому разность температур по шкале Кельвина и по шкале Цельсия одинакова, т. е. 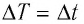 (рис. 17).
(рис. 17).

От теории к практике:
Выразите по шкале Кельвина температуру тела здорового человека.
Из основного уравнения молекулярно-кинетической теории идеального газа (3.2) следует: 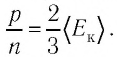 Таким образом, учитывая выражение (4.1), можно записать:
Таким образом, учитывая выражение (4.1), можно записать: 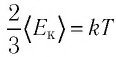 или
или

Соотношение (4.2) устанавливает связь между абсолютной температурой Т идеального газа и средней кинетической энергией 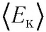 поступательного движения его частиц. Таким образом, из формулы (4.2) следует, что средняя кинетическая энергия поступательного движения частиц идеального газа пропорциональна его абсолютной температуре.
поступательного движения его частиц. Таким образом, из формулы (4.2) следует, что средняя кинетическая энергия поступательного движения частиц идеального газа пропорциональна его абсолютной температуре.
Средняя кинетическая энергия поступательного движения молекул газов, находящихся в состоянии теплового равновесия, одинакова для разных газов и не зависит от массы молекулы газа.
Этот вывод, основанный на экспериментах с разреженными газами, справедлив для жидкостей и твёрдых тел.
Уравнение (4.2) можно записать следующим образом: 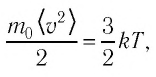 откуда
откуда
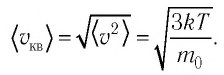
С учётом формулы (4.1) основное уравнение молекулярно-кинетической теории идеального газа может быть записано в виде:

Из уравнения (4.3) следует, что при одинаковых значениях абсолютной температуры Т и концентрации 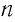 частиц давление любых газов одинаково, независимо от того, из каких частиц они состоят.
частиц давление любых газов одинаково, независимо от того, из каких частиц они состоят.
Пример №1
Сравните средние квадратичные скорости атомов гелия и молекул кислорода, если газы находятся в состоянии теплового равновесия.
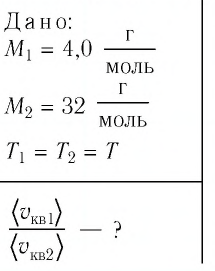
Решение. Средняя квадратичная скорость теплового движения частиц газа 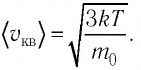 Поскольку масса одной молекулы вещества
Поскольку масса одной молекулы вещества 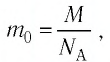 то
то
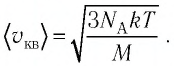 Так как газы находятся в состоянии теплового равновесия, т. е.
Так как газы находятся в состоянии теплового равновесия, т. е. 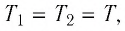 то средние квадратичные скорости атомов гелия
то средние квадратичные скорости атомов гелия
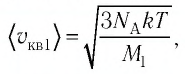
молекул кислорода 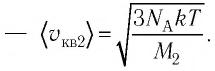
Тогда: 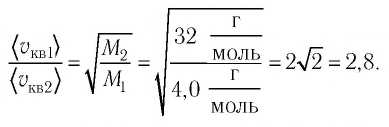
Ответ: в состоянии теплового равновесия средняя квадратичная скорость атомов гелия в 2,8 раза больше средней квадратичной скорости молекул кислорода.
Пример №2
В баллоне вместимостью 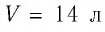 находился газ, абсолютная температура которого
находился газ, абсолютная температура которого 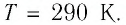 Расходуя газ, из баллона выпустили
Расходуя газ, из баллона выпустили 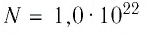 молекул. Определите, на сколько уменьшилось давление газа в баллоне, если через некоторый промежуток времени его температура увеличилась до первоначального значения.
молекул. Определите, на сколько уменьшилось давление газа в баллоне, если через некоторый промежуток времени его температура увеличилась до первоначального значения.
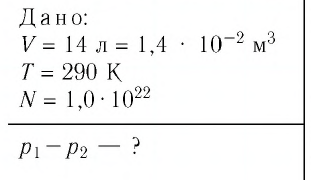
Решение. Начальное давление газа
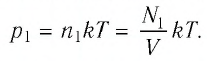
После того как израсходовали часть газа, а его температура увеличилась до первоначального значения Т, давление газа стало
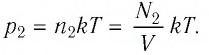
Тогда убыль давления газа:
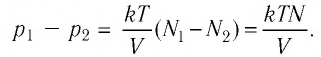
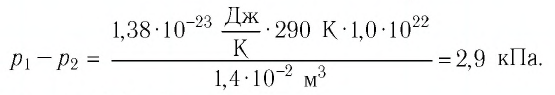
Ответ: 
Тепловое равновесие, температура
Понятие температуры занимает важное место в повседневной жизни. Так, говоря температура, мы обычно подразумеваем степень нагретости (горячее, теплое, холодное) тела. Такое рассмотрение в достаточной степени субъективно, потому что температура зависит не только от состояния рассматриваемого тела, но и от нашей чувствительности.
Тепловое равновесие:
Известно, что при соприкосновении двух тел с разными температурами между ними происходит теплообмен: тепло переходит от тела с высокой температурой к телу с более низкой температурой. Этот процесс продолжается до тех пор, пока температуры обоих тел не сравняются. Этот факт учитывается при измерении температуры тел — термометр приводится в соприкосновение с телом, но его показания снимаются не сразу, а через определенный промежуток времени, в течение которого между телом и термометром устанавливается тепловое, или так называемое термодинамическое равновесие. При термодинамическом равновесии макроскопические параметры системы остаются постоянными, то есть изменение агрегатного состояния вещества не происходит.
Тепловое или термодинамическое равновесие – это состояние системы, когда ее макроскопические параметры длительное время остаются неизменными.
Состояние теплового равновесия системы характеризуется температурой.
Температура – физическая величина, характеризующая состояние теплового равновесия макроскопической системы: в состоянии теплового равновесия температура всех частей системы одинакова.
Качественное и количественное определение температуры должно основываться на определении физической величины, которая, во-первых, должна характеризовать состояние тела, во-вторых, должна быть одинакова для всех тел, находящихся в тепловом равновесии. Такой величиной является средняя кинетическая энергия поступательного движения молекул вещества. Можно легко определить ее значения для поступательно движущихся молекул одноатомного идеального газа.
С этой целью был поставлен следующий интересный эксперимент: три баллона разного объема, снабженные манометрами (прибор для измерения давления), заполнены различными газами, например, аргоном, неоном и гелием. Баллоны помещаются сначала в тающий лед  а затем в кипящую воду
а затем в кипящую воду (b).
(b).
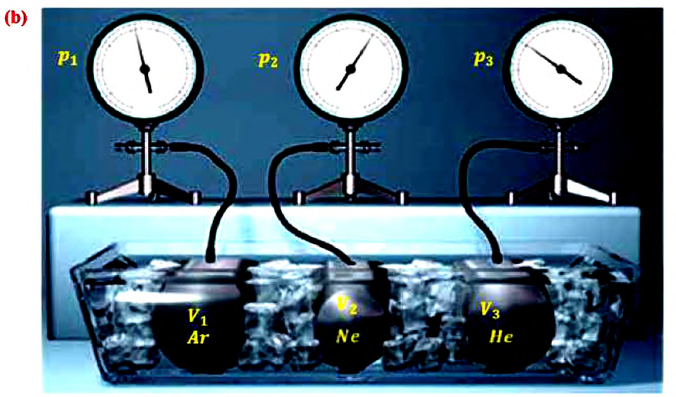
Произведенные вычисления показывают, что в обоих случаях (и при температуре 0°С, и при температуре 100°С) при достижении теплового равновесия, отношение 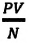 во всех баллонах остается постоянным, несмотря на то, что давление и концентрация газов разная:
во всех баллонах остается постоянным, несмотря на то, что давление и концентрация газов разная:
при 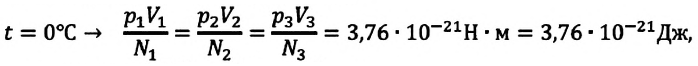
при 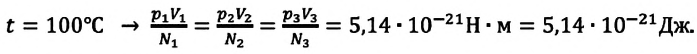
Если принять во внимание, что 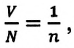 то получается, что при тепловом равновесии отношение давления газа к его концентрации равно постоянной величине, измеряемой в единицах энергии — джоулях:
то получается, что при тепловом равновесии отношение давления газа к его концентрации равно постоянной величине, измеряемой в единицах энергии — джоулях:

Здесь 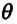 (тета) — является постоянной величиной, зависящей для всех разреженных газов, приближенных к идеальному газу, только от температуры:
(тета) — является постоянной величиной, зависящей для всех разреженных газов, приближенных к идеальному газу, только от температуры:

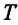 – абсолютная температура,
– абсолютная температура, 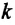 – является коэффициентом пропорциональности и называется постоянной Больцмана, в честь австрийского физика Людвига Больцмана (1844—1906). Опытным путем было определено, что постоянная Больцмана равна:
– является коэффициентом пропорциональности и называется постоянной Больцмана, в честь австрийского физика Людвига Больцмана (1844—1906). Опытным путем было определено, что постоянная Больцмана равна:
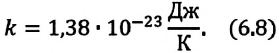
Постоянная Больцмана связывает температуру 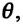 измеряемую в единицах энергии, с абсолютной температурой
измеряемую в единицах энергии, с абсолютной температурой 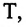 измеряемой в Кельвинах. Из выражений (6.6) и (6.7) получается выражение для давления идеального газа:
измеряемой в Кельвинах. Из выражений (6.6) и (6.7) получается выражение для давления идеального газа:

Выражение (6.9) может быть использовано для определения абсолютной температуры в Кельвинах:

Формула (6.10) дает возможность создания новой температурной шкалы. Такая температурная шкала, называемая шкалой абсолютных температур, была предложена в 1848 году английским физиком Уильямом Томсоном (1824-1907). За вклад в области физики в 1892 году он был награжден титулом лорда Кельвина.
Поэтому предложенная им шкала температур называется шкалой Кельвина. Нулевая точка шкалы Кельвина, то есть температура абсолютного нуля, это самая низкая температура, какая возможна теоретически и практически. Согласно этой шкале температура плавления льда равна 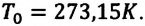 Соотношение между температурной шкалой Цельсия и шкалой Кельвина следующая:
Соотношение между температурной шкалой Цельсия и шкалой Кельвина следующая: 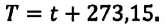 При вычислениях это соотношение можно записать в более простой форме:
При вычислениях это соотношение можно записать в более простой форме:

Единица измерения абсолютной температуры, являющейся основной в СИ – Кельвин 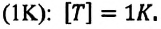 Эта температура соответствует температуре
Эта температура соответствует температуре 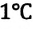 по шкале Цельсия. Поэтому, разность температур и по шкале Кельвина, и по шкале Цельсия одинакова:
по шкале Цельсия. Поэтому, разность температур и по шкале Кельвина, и по шкале Цельсия одинакова:
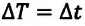 (с).
(с).

Температура – мера средней кинетической энергии молекул. На самом деле из сравнения выражений (6.4) и (6.9) получаем, что абсолютная температура, являющаяся макроскопическим параметром идеального газа (или разреженного газа), связана со средней кинетической энергией молекул, являющейся ее микроскопическим параметром:
• Средняя кинетическая энергия поступательного движения молекул газа прямо пропорциональна его абсолютной температуре:

Из формулы (6.12) ясно виден физический смысл температуры:
Температура – это мера средней кинетической энергии поступательного движения молекул тела. Это утверждение так же верно для жидкостей и твердых тел. Из формулы видно, что среднее значение кинетической энергии поступательного движения, а значит, и средняя квадратичная скорость молекул при абсолютном нуле равна нулю.
Средняя квадратичная скорость молекул
Из формул (6.1), (6.3) и (6.5) можно вычислить среднюю квадратичную скорость молекул:
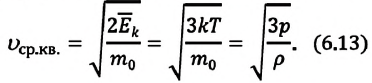
- Изопроцессы в физике
- Твердые тела и их свойства в физике
- Строение и свойства жидкостей в физике
- Испарение и конденсация в физике
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа
- Температура в физике
- Парообразование и конденсация

Содержание
- Что такое тепловое равновесие?
- Что такое тепловое равновесие?
- Формула теплового равновесия
- Нулевой закон термодинамики
- Примеры теплового равновесия
- Рекомендации:
Мы объясняем, что такое тепловое равновесие, из чего оно состоит и какова его формула. Также нулевой закон термодинамики и примеры.

Что такое тепловое равновесие?
В физике это называется тепловое равновесие в состояние, в котором два тела, соприкасающиеся или разделенные проводящей поверхностью, равны своим изначально разным температурам из-за передачи тепла от одного к другому.
Если мы имеем два соприкасающихся объекта, один из которых горячее другого, со временем оба будут стремиться к достижению одной и той же температуры и, если нет передачи тепла другим объектам, отныне они будут поддерживать тепловое равновесие, то есть постоянную температуру.
Что такое тепловое равновесие?

Это явление можно объяснить микроскопически, понимая, что температура объектов напрямую связана со средней кинетической энергией их частиц, будь то атомы, молекулы или те, которые следует учитывать. Это среднее значение обычно называют «внутренней энергией» в физике, поэтому чем выше кинетическая энергия, тем выше внутренняя энергия и выше температура системы..
Два тела в контакте обмениваются энергией с течением времени. Таким образом, точка теплового равновесия достигается, когда кинетическая энергия обоих тел равна, так что оба тела начинают работать как единая термодинамическая система, наделенная одинаковым количеством внутренней энергии и, следовательно, температуры.
Формула теплового равновесия
Выражение теплового равновесия включает в себя расчет разницы температур между двумя телами, поэтому необходимо определить количество тепла (Q), которым они обмениваются.
Этот Он определяется по формуле Q = m. Ce. Δt, где m – масса тела, Ce – его удельная теплоемкость, выраженная в кал / гр ° C, а Δt – изменение температуры, то есть: Δt = tf – ti, конечное время минус начальное время.
После того, как количество тепла Q для каждого тела будет вычислено, мы сможем сравнить их, зная, что тепловое равновесие происходит при равенстве температур между телом 1 и телом 2. Для достижения теплового равновесия, тепло, которое получает самое холодное тело, – это тепло, которое теряет более теплое тело, поэтому Q1 = Q2, то есть полученное тепло = потерянное тепло.
Нулевой закон термодинамики

Этот принцип выражен в так называемом нулевом законе термодинамики, который был озвучен в 1931 году Р. Х. Фаулером следующим образом: «Если две системы A и B находятся, каждая по отдельности, в тепловом равновесии с третьей системой, которую мы назовем C, то A и B также находятся в тепловом равновесии друг с другом».
То есть: если A = C и B = C, то A = B.
Благодаря этому принципу, основанному на математической формулировке термодинамики, известно, что Максвелл выразил словами следующим образом: «Все тепло однотипное».
Примеры теплового равновесия
Вот несколько простых примеров теплового равновесия:
- Когда мы входим в жаркую комнату, мы сразу ощущаем тепло воздуха, но с некоторой задержкой наше тело будет обмениваться теплом с воздухом и войдет в тепловое равновесие с ним, поэтому мы перестанем ощущать разницу в температуре.
- Если мы поместим стеклянный сосуд с холодной водой в сосуд большего размера с кипящей водой, тепловой поток между ними охладит горячую воду и нагреет холодную, пока не достигнет промежуточного уровня теплового равновесия.
- Продукты, которые у нас есть в морозильной камере на кухне, находятся в тепловом равновесии по отношению к замороженному воздуху между ними, так что все они имеют одинаковую температуру.
Рекомендации:
- «Тепловое равновесие» в Википедии.
- «Тепловое равновесие» (видео) в Католическом университете Сан-Пабло.
- «Тепловое равновесие» в Hyperphysics.phy.
- «Нулевой закон термодинамики: тепловое равновесие» (видео) в Dave Explains.
- «Тепловое равновесие» в Британской энциклопедии.
Остаток средствтермический состояние, в котором тело оказывается в одно и тожетемпература чем их окружение. Замечено, что все тела, температура которых выше, чем у их соседей, имеют тенденцию самопроизвольно отдавать им тепло, пока оба не начнут иметь одинаковую температуру.
Посмотритетакже:Основы термологии
Тепловое равновесие и нулевой закон термодинамики
Тепловое равновесие – центральная концепция нулевого закона термодинамики. Такой закон устанавливает, что в случае, когда две термодинамические системы, THE а также B, находятся в тепловом равновесии с третьей термодинамической системой, Ç, тогда, THE а также B они также будут находиться в тепловом равновесии.
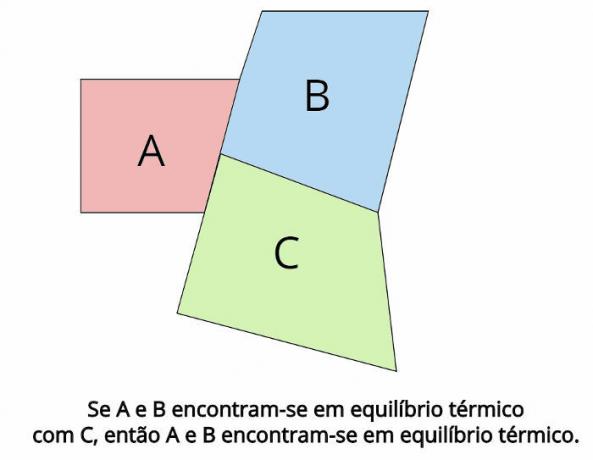
В тепловом равновесии конечные температуры каждого тела должны быть равны: TTHE = TB = TÇ
Посмотрите, что утверждает утверждение нулевого закона термодинамики:
“Если два тела находятся в тепловом равновесии с третьим телом, то эти тела будут находиться в тепловом равновесии друг с другом ».
Другой способ понять тепловой баланс основан на внутренней энергии тел. Внутренняя энергия или просто тепловая энергия – это физическая величина.
напрямуюпропорциональный à температура тела. Следовательно, если в одной термодинамической системе есть тела с разными температурами, они будут иметь разные модули внутренняя энергия и, следовательно, будет передавать часть этой энергии между ними до тех пор, пока не будет разницы между их энергиями. внутренний. Хотите узнать больше о том, что такое внутренняя энергия и каковы ее свойства? Доступ к статье: Внутренняя энергия.
Не останавливайся сейчас… После рекламы есть еще кое-что;)
тепло и тепловой баланс
Передача тепла всегда происходит спонтанно, от тела с самой высокой температурой к телу с самой низкой температурой. Эта передача энергии в виде тепла может происходить посредством таких процессов, как вождение, конвекция а также радиация.
-
Вождение: Это передача тепла между телами, особенно в твердых телах. При этом типе проводимости не происходит массопереноса. Этот тип теплопередачи объясняет, например, как происходит тепловое равновесие в металлах.
-
Конвекция: Это теплопередача, происходящая в жидкостях. В этом режиме теплопередачи происходит массообмен, когда нагретая жидкость движется, образуя конвекционные потоки, пока вся жидкость не достигнет теплового равновесия.
-
Радиация: Это передача тепла посредством электромагнитных волн, поэтому этот процесс происходит, даже если между телом и другим телом при разных температурах нет физической среды. Передаваемое тепло в этом случае эквивалентно электромагнитным волнам с меньшей энергией, чем видимый свет, то есть тепловое излучение, расположенный в области инфракрасный.
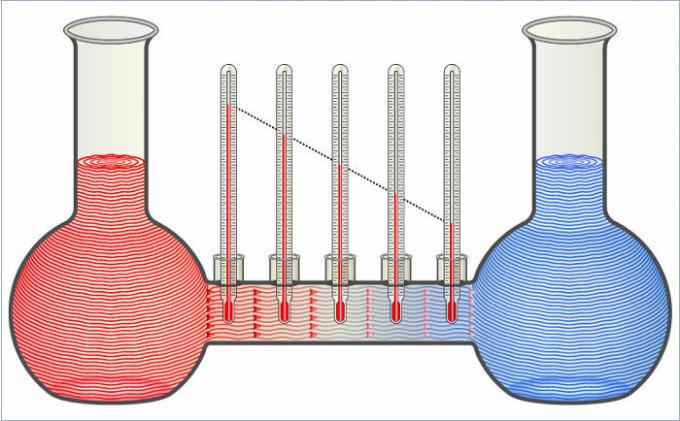
Две жидкости на рисунке передают тепло друг другу, пока их температуры не сравняются.
Хотите узнать больше о том, как протекает каждый из процессов теплопередачи? Доступ к статье: Процессы распространения тепла.
явное тепло
когда есть разницавтемпература между двумя телами или между телом и его окружением будет происходить самопроизвольный теплообмен между ними, так что тело с более высокой температурой охлаждается, а тела с более низкой температурой нагреваются, пока все не достигнут температуры в остаток средствтермический.
Количество тепла, которое обменивается между телами при разных температурах, называется явное тепло и эту сумму можно рассчитать по формуле, показанной на рисунке ниже:
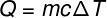
Q – тепло (лайм или Дж)
м – масса (г или кг)
ç – удельная теплоемкость (кал / гºC или Дж / кг. K)
ΔT – изменение температуры (° C или K)
В приведенной выше формуле важно подчеркнуть величие имени. удельная теплоемкость. такая величина измеряет количество энергии на массу, которое вещество должно отдавать или поглощать, чтобы его температура изменилась на 1 ° C. В случае чистой воды, например, и в условиях нормального давления, чтобы изменить ее температуру на 1ºC, требуется 1,0 калория на каждый грамм воды.
Таким образом, все вещества, установившие тепловой контакт друг с другом, стремятся достичь состояния остаток средствтермический однако со временем самопроизвольно некоторым для этого требуется большее количество энергии, и это напрямую влияет на температуру для достижения теплового равновесия.
читатьтакже:Какая температура?
скрытая теплота
Возможно, что во время теплообмена с окружающей средой тело представляет давление, температуру и объем, которые вызывают изменение его физического состояния. Эти изменения происходят в температурапостоянный (для тел, состоящих из одного вещества, без примесей), то есть, несмотря на получение или передачу тепла внешней среде, температура этих тел не изменяется.
Это возможно только потому, что в этом случае вся энергия, которой обмениваются, используется для изменения конформации ваших молекул. С того момента, как энергетический барьер «преодолен» и все содержимое тела находится в другом физическом состоянии, Тело продолжает обмениваться теплом с окружающей средой, если, конечно, его температура не равна температуре снаружи.
O скрытая теплота можно рассчитать по формуле, показанной на рисунке ниже, проверьте это:
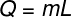
Q – скрытое тепло (лайм или Дж)
м – масса (г или кг)
L – удельная скрытая теплота (кал / г или Дж / кг)
Формула теплового равновесия
Если мы хотим узнать, что такое температуравостаток средств некоторой термодинамической системы, необходимо, чтобы мы рассматривали данную систему как системаизолированные, то есть мы должны предположить, что никакое количество тепла не обменивается с окрестностями этой системы.
Исходя из этого условия, мы можем сказать, что весь объем теплообмена передается только между телами, составляющими эту систему, без учета тепловых потерь для стенок емкости, например. В этом случае мы говорим, что контейнер имеет теплоемкость незначительна, т. е. не поглощает тепло.
Представьте себе такую ситуацию: в чашку горячего чая с незначительной теплоемкостью насыпьте несколько кубиков льда. Чтобы определить температуру теплового равновесия, помимо знания начальных условий системы, мы должны сделать некоторые соображения:
-
Все тепло, которое горячий чай отдает льду, будет им полностью поглощено, так как чашка имеет незначительную теплоемкость.
-
Мы не должны учитывать потери тепла в воздух и любую другую среду, чтобы эту чашку чая можно было понимать как замкнутую термодинамическую систему.
Таким образом, мы можем установить, что все количество тепла, полученного льдом, было отдано горячим чаем, с этим мы написали нашу формулу для расчета теплового баланса:
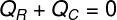
Qр – Получено тепло
QÇ – тепло отдано в
Теплота, указанная в (QÇ), относится к количеству тепла, которое горячий чай передал вставленным в него кубикам льда. Уже получено тепло (Qр) – количество тепла, полученного этими кубиками льда. Это количество тепла будет иметь две природы: тепло. чувствительный и горячо скрытый, поскольку для достижения теплового равновесия кубики льда, скорее всего, растают.
Определение температуры теплового равновесия
Определим температуру теплового равновесия из следующей ситуации:
В чашку с незначительной теплоемкостью, в которой содержится 200 мл (200 г) чая при начальной температуре 70 ° C, помещается 10 г льда при температуре -10 ° C. Определите температуру теплового равновесия системы (предположим, что удельная теплоемкость чая равна удельной теплоемкости воды):
Данные:
çВОДА = 1,0 кал / г ° C
çЛЕД = 0,5 кал / г ° C
LЛЕД = 80 кал / г
Во-первых, мы считаем, что все тепло, полученное льдом, отдано чаю:

Далее необходимо детализировать, какие формы тепла были отданы и получены:
-
Чай: Чай давал только ощутимое тепло (Qs), поскольку его физическое состояние не изменилось.
-
Лед: Изначально лед имел температуру -10 ° C, поэтому он получил явное тепло (Qs) до температуры 0 ºC, затем получали скрытое тепло (QL) разжижать. Став жидкостью, он получил скрытое тепло (Qs) до тех пор, пока он не войдет в тепловое равновесие (TF) с чаем.
Переводя то, что было проанализировано выше, в форму уравнения, нам нужно будет решить следующий расчет:
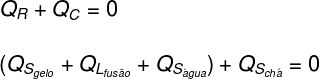
Заменив данные, предоставленные упражнением, на приведенное выше уравнение, нам нужно будет решить следующий расчет:
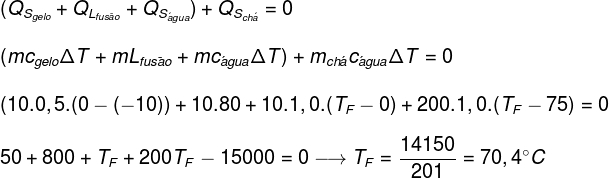
Согласно расчетам, сделанным выше, равновесная температура системы чай + лед должна составлять примерно 70,4 ° C.
Эксперимент по тепловому балансу
Чтобы проверить тепловой баланс между двумя телами, мы можем провести несколько экспериментов. Однако самый простой из них предполагает использование калориметр это термометр. Калориметр представляет собой адиабатический контейнер (не пропускающий тепло) с теплоемкостью онезначительныйНапример, горшок, облицованный пенополистиролом, который является хорошим теплоизолятором.

Калориметр используется для измерения изменения температуры внутри системы.
Тепловой баланс и жизнь на Земле
O остаток средствтермический он играет фундаментальную роль в земной жизни. Без присутствия парниковых газов в атмосфере Земли большая часть тепловое излучение планеты покинет его, распространяясь в космос. Со временем это вызовет массовое похолодание по всей планете, в результате чего океаны со временем замерзнут.
Кроме того, океаны играют ключевую роль в остаток средствтермический планеты. В силу своего большого макароны а также нагреватьконкретный, океаны наделены огромным вместимостьтермический то есть им нужно получать огромное количество тепла, чтобы изменить свою температуру. По этой причине они могут очень эффективно регулировать температуру планеты. В районах, удаленных от океанов и с небольшим количеством воды, обычно имеются большие площади. тепловые диапазоны, как и в случае с пустынями, где днем очень жарко, а ночью замерзает.
Следовательно остаток средствтермический это процесс фундаментальной важности для поддержания физических, химических и биологических процессов на планете и, следовательно, необходим для существования жизни на Земле.
Автор: Рафаэль Хелерброк
