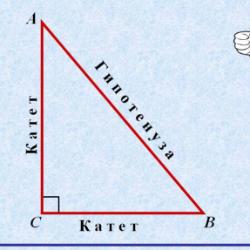
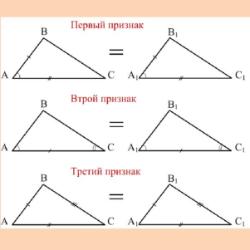
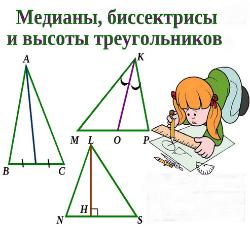
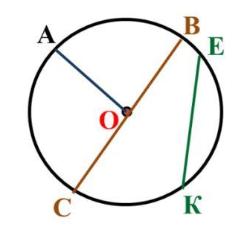
-
Геометрия. 7 класс. Итоговый тест по геометрии за 2019 – 2020 учебный год.
-
7 класс геометрия учебник Л.С.Атанасян. Данный тест предназначен для повторения теории по курсу геометрии 7 класса. В тесте 40 вопросов, которые выбираются случайным образом из общей базы заданий 80 вопросов. По завершении выставляется оценка. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%.
-
Итоговый тест по геометрии 7 класса за 2019/2020 учебный год по всем темам учебной программы
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Параллельные прямые.”.
-
Тест по теме “Прямоугольные треугольники” для 7 класса. Содержит 10 вопросов, расположенных в последовательности от простых к более сложным
-
7 класс геометрия учебник Л.С.Атанасян. Данный тест предназначен для повторения Главы 2 “Труегольники”. Вопросы двух типов – по теории и практические задания. В тест случайным образом выбираются 5 теоретических вопросов и 5 практических.
-
Годовая контрольная работа по геометрии состоит из 11 заданий.
с 1 по 5 – тестовые задания (от 1 до 4 правильных),
с 6 по 7 нужно установить соответствие (1-4:А-Д),
с 8 по 9 нужно вписать ответ (число),
с 10 по 11 – вписать ответ.Время на контрольную – 60 мин.
-
7 класс геометрия учебник Л.С.Атанасян.
-
Данный тест предназначен для закрепления материала по теме “Неравенство треугольника”. Очень внимательно читайте задание и инструкцию к работе. Желаю удачи!!!
-
Тест направлен на проверку знаний учащихся по теме “Смежные и вертикальные углы”
-
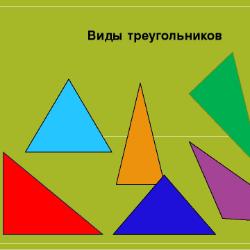
Ребята! Я предлагаю вам ответить на вопросы теста по теме “Виды треугольников”. Будьте внимательны!
-
Тест – тренинг на применение признаков равенства прямоугольных треугольников. Тест содержит 5 задач на готовых чертежах.
-
Тест по геометрии рассчитан на учащихся 7 классов для проверки знаний по теме: “Окружность”. Время прохождения теста ограничено 30 минутами.
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Сумма углов треугольника. Внешний угол треугольника.”
-
Тест предназначен для учащихся 8 классов при отработке навыков решения задач по теме “Прямоугольный треугольник. Углы и их свойства.”
-
Проверочный тест по теме “Равнобедренный треугольник”. Геометрия 7 класс.
-
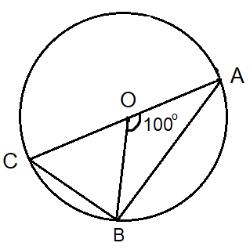
Тест предназначен для проверки знаний учащихся после изучения темы “Окружность”. Основные тестируемые понятия: окружность, радиус, хорда, касательная
-
Данный тест предназначен для проверки знаний учащихся по темам “Треугольники”, “Равнобедренный треугольник и его свойства”, “Прямоугольный треугольник”
-
Здравствуйте, ребята. Снгодня вам предстоит справится с заданиями Годовой контрольной работы по геометрии.
-
Данный тест предназначен для проверки знаний учащихся 7 класса по темам “Треугольники”, “Равнобедренный треугольник и его свойства”, “Прямоугольный треугольник”
-
Тест предназначен для закрепления изученного материала и его повторения. Удачи в прохождении!!!
-
Контрольная работа по теме “ОКружноть и круг. Геометрические построения”, вариант 1.
Всего вопросов 8. С выбором ответа – 4 вопроса; с кратким ответом – 3 вопроса; заполнить пропуски в тексте – 1 вопрос.
Максимальное количестко баллов – 22 балла. Пятибальная система оценивания. -
Тест предназначен для проверки усвоения учащимися 7 класса тем “Окружность”, “Элементы окружности”.
-
Тест по теме “Свойства прямоугольного треугольника” 7 класс, геометрия. Состоит из 6 задач с необходимостью вписать получившееся число. Пять заданий оцниваются в 1 балл, одно – в 2 балла.
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Смежные и вертикальные углы”.
-
Данный тест предназначен для проверки знаний по математике учащихся 7-х классов. Тест состоит из 16 заданий, рассчитан на 40 минут выполнения.
-
Тест по теме “Некоторые свойства прямоугольных треугольников”
-
Тест содержит 20 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: “3” 50-69%, “4” 70-90%, “5” 91-100%. Оценка выставляется сразу после прохождения теста.
-
Тест на знание теоретического материала по геометрии 7 класса
-
Тест на знание теоретического материала по теме “Треугольники” для 7 класса
-
Определение угла. Виды углов. Измерение углов. Сравнение углов.Построение углов.
-
Тест по теме “Прямоугольные треугольники” для 7 класса. Содержит 10 вопросов, расположенных в последовательности от простых к более сложным
-
Тест по геометрии для 7 класса по теме “Признаки равенства треугольников”
-
Проверочный тест по теме “Медианы биссектрисы и высоты треугольника”
-
Тест предназначен для проверки усвоения учащимися 7 класса темы “Окружностьи ее элементы”
-
Данный тест предназначен для определения знания предмета “Геометрия” за курс 7 класса.
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Равнобедренный и равносторонний треугольники.”
-
В этом тесте вы проверите свои знания по теме равенства треугольников. Перед прохождением теста необходимо повторить данную тему по учебнику.
-
В тесте 30 вопросов, которые выбираются случайным образом из общей базы заданий. По завершении выставляется оценка. Критерии: “3” 50-69%, “4” 70-90%, “5” 91-100%.
-
Тест предназначен для учащихся 7 класса средней школы для проверки уровня знаний по темам: “Сумма углов треугольника.”, “Свойства углов равнобедренного треугольника.”, “Внешний угол треугольника.”
-
Данный тест можно использовать на последних уроках геометрии. Обучающиеся выбирают верные ответы на каждый вопрос, по окончании тестирования получают оценку
-
С помощью этого теста можно проверить кругозор семиклассников
по теме: «Признаки параллельности прямых» -
Обобщающий тест по теме “Построение треугольника по трем элементам”. Состоит из 6 вопросов с выбором ответа и заполнением пропусков.
-
Тест предназначен для текущего опроса по теме признак параллельности прямых
-
Тест по теме “Сумма углов треугольника” предназначен для учащихся 7 класса , содержит 10 задний с чертежами, по которым надо решить и записать ответ в окно теста.
-
Тест содержит 25 вопросов с кратким ответом. Внимательно читайте каждый вопрос и комментарий к нему, каким образом должен быть записан ответ. Все ответы в именительном падеже, одним словом, без пробелов, с маленькой буквы. Ответы, в которых получается число, записываются без единиц измерения и других символов. Названия углов, сторон, точек пишутся английскими буквами согласно требований к их обозначению.
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Свойства углов, образованных при пересечении параллельных прямых секущей.”.
-
Контрольная работа по теме “ОКружноть и круг. Геометрические построения”, вариант 2.
Всего вопросов 8. С выбором ответа – 4 вопроса; с кратким ответом – 3 вопроса; заполнить пропуски в тексте – 1 вопрос.
Максимальное количестко баллов – 22 балла. Пятибальная система оценивания.
-
Тест по геометрии «Свойства параллельных прямых» состоит из десяти заданий с выбором правильного варианта ответа из числа предложенных. Он поможет семиклассникам вспомнить все изученное по этой важной теме, а старшеклассникам – повторить материал при подготовке к экзамену. Решить тест можно на нашем сайте онлайн.
-
Тест седержит несколько интересных теоретических и практических вопросов по теме “Первый признак равенства теругольников”.
-
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
вопросы содержат теоретический материал, служат проверкой первоначальных знаний по предмету
-
Теоретический тест по теме “Параллельные прямые” 7 класс.Для урока обобщения изученного материала.
-
Данный тест предназначен для повторения темы: “Прямая и отрезок. Луч и угол”
-
Тест состоит из 8 вопросов по теме “Треугольники”. Рассчитан на учащихся 7 класса. В каждом вопросе только один правильный вариант ответа.
-
Тестовая работа к ГЛАВЕ 1. Начальные геометрические сведения. Прямая. Отрезок. Измерение углов
-
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
7 класс геометрия учебник Л.С.Атанасян. Тест предназначени для повторения и закрепления теоретического материала по теме “Медианы, биссектрисы и высоты треугольника”. Содержит 17 заданий.
-
Тест для обучающихся 7 класса по теме : “Первый признак равенства треугольников”. Тест содержит 10 заданий, которые направлены на выявление уровня освоения обучающимися данного материала.
Составитель: Инютина Н.В. -
Тест состоит из пяти вопросов. В каждом вопросе один правильный ответ
-
Тест предназначен для проверки заний по 3 главе. Удачи в прохождении!!!
-
ест направлен на проверку первоначальных знаний по теме “Отрезок.Прямая.Луч”.Используется на уроках , а так-же как домашнее задание.
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Прямые на плоскости.”.
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Смежные углы.”
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Смежные и вертикальные углы.”
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Треугольники.”
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Признаки равенства треугольников.”
-
Тест предназначен для учащихся 7 классов при отработке навыков устного счёта при решении задач по теме “Смежные углы”.
-
Тест предназначен для учащихся 7 классов при отработке навыков устного счёта при решении задач по теме “Смежные углы”.
-
Тест предназначен для учащихся 7 классов при отработке навыков устного счёта при решении задач по теме “Смежные и вертикальные углы”.
-
Тест предназначен для учащихся 7 классов при отработке навыков устного счёта при решении задач по теме “Смежные и вертикальные углы”.
-
Тэст прызначаны для навучэнцаў 7 класаў пры адпрацоўцы навыкаў рашэня задач па тэме .
-
Тест по теме “Прямоугольный треугольник. Элементы, признаки равенства”
-
Итоговый тест по теме “Признаки равенства треугольников. Медиана, биссектриса и высота треугольника”
-
Входной тест по геометрии контролирующий освоение учениками темы измерение отрезков и углов.
-
Геометрия, 7 класс. Тест предназначен для закрепления материала “Сумма углов в треугольнике”.
-
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
Тест предназначен для проверки теоретических знаний по геометрии 7 класса. Ориентирован на учебник Л. С. Атанасяна и др. “Геометрия 7-9 классы”. Может быть использован для подготовки к ОГЭ по математике.
-
Тест составлен на основе учебника по геометрии за 7 класс авторы Мерзляк А.Г., Полонский В. Б., Якир М. С.
-
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме “Признаки равенства треугольников.”
-
Тест по теме “Прямая, луч, отрезок” проверяет умение находить длины отрезков, устанавливать пересекаются ли прямые, отрезки и лучи на рисунке.
-
Рефлексия ______________________________________________________________________________________________________
-
Тест по геометрии для 7 класса по темам “Первый признак равенства треугольников”, “Второй признак равенства треугольников”. Тест содержит задания с одиночным и множественным выборами правильных ответов, а также с вводом правильного ответа.
Составитель: Инютина Н.В. -
Тест по теме “Свойства параллельных прямых. Сумма внутренних углов треугольника.” (геометрии 7 класс)
-
Итоговый тест по теме “Параллельные прямые”. Уровень- базовый. Может быть использован для подготовки к ГИА (ОГЭ, ГВЭ).
-
Данный тест предназначен для оценки знаний учащихся 7 и 8 классов. Состоит из 25 вопросов базового уровня. Целесообразно тестировать учащихся в конце учебного года 7 класса или вначале 8 класса, при повторении изученного материала.
Государственное бюджетное образовательное учреждение
средняя общеобразовательная школа № 402
111538, г.Москва, ул. Косинская, дом 10 строение 1, Тел.375-71-31,тел/факс 375-59-11
Итоговое тестирование по геометрии
в 7 классе (предпрофильный).
Учитель: Рощина Елена Александровна
Москва 2012
Итоговая государственная аттестация учащихся проводится в форме тестирования, поэтому тестирование становится основной формой контроля знаний, умений и навыков учащихся и определения уровня их математической компетенции. Итоговая аттестация в 9 и 11 классах требует умения выстраивать логическую цепочку рассуждений, применять изученный материал при решении задач, распознавать на чертежах геометрические фигуры и их взаимное расположение. С целью формирования навыка работы с тестами итоговую контрольную работу можно заменить тестированием.
В тесты включены задания, которые встречаются в открытом банке задач ГИА и ЕГЭ. Привожу четыре вариантов тестов с ответами.
Тест состоит из двух частей А и В.
Часть А содержит восемь заданий, среди которых задания с выбором ответа или с кратким ответом. Задание №1,2,3,5,6 оцениваются в один балл; задания №4,7,8 оцениваются двумя баллами.
Часть В состоит из десяти задач. Все они выполняются с записью решения. Задания №1,2,4,5,7,9,10 оцениваются двумя баллами. Задания №3,6,8 оцениваются тремя баллами.
Работа рассчитана на два урока. По усмотрению учителя часть задания раздела В можно не предлагать.
Примечание: тест составлен для предпрофильного класса, в котором геометрия(как отдельный предмет) изучается с 5 класса. Тема «Параллелограмм, его свойства и признаки» было изучено в 7 классе. «Виды параллелограмма» в 7 классе не рассматривались. Предложенный тест можно использовать и в общеобразовательных классах, исключив задачи на параллелограмм.
Ответы на часть А учащиеся отмечают в бланках заданий. Решение задач части В учащиеся выполняют на предложенных листах.
Вариант №1
Часть А
1. Если угол АОС = 75 °, угол ВОС = 105°, то эти углы :
а) смежные в) определить невозможно
б) вертикальные
2. Сумма двух углов, полученных при пересечении двух прямых, равна 80°. Найдите один из двух других углов.
Ответ:______________________________
3. Какое наибольшее число лучей может выходить из одной точки, чтобы все углы, образованные соседними лучами, были тупыми?
Ответ:______________________________
4. Периметр равнобедренного треугольника равен 19 см. Одна из его сторон равна 7 см. Найдете длины двух других сторон.
Ответ______________________________
5. Сумма двух односторонних углов, образованных при пересечении прямых m и n секущей k, равна 148°. Определить взаимное расположение прямых m и n.
а) пересекаются б) параллельны в) такая ситуация невозможна
6. Определите вид треугольника, если сумма двух его углов равна третьему углу?
а) остроугольный в) прямоугольный
б) тупоугольный г) определить невозможно
7. Углы треугольника относятся как 1:1:7. Определите вид данного треугольника.
По углам: по сторонам:
- остроугольный 1. разносторонний
- прямоугольный 2. равносторонний
- тупоугольный 3.равнобедренный
8. Сколько различных треугольников можно составить из пяти отрезков, длины которых равны : 2см, 3см, 4 см, 5см, 6 см.
Ответ:_____________________________
Часть В
1.В треугольнике АВС, высота ВD является медианой. Найдите периметр треугольника АВС, если периметр треугольника АВD равен 15 см, высота ВD равна 4 см.
2.В треугольнике АВС на стороне АС отмечена точка D, такая, что АВ=ВD=DС. Отрезок DF медиана треугольника ВDС. Найдите угол FDС, если угол ВАС = 70°.
3.В треугольнике АВС внешний угол при вершине А на 64° больше внешнего угла при вершине В. Найдите угол В, если угол С равен 80°.
4.Внутри треугольника АВС отмечена точка О, такая, что ОА=ОВ=ОС. Известно, что угол ВОС =160°, угол СОА = 130°. Найдите угол ВСА треугольника АВС.
5.Биссектрисы АD и ВЕ треугольника АВС пересекаются в точке О. Угол АОВ =140°. Найдите угол С треугольника АВС.
6. В треугольнике АВС на высоте ВF отмечена точка О, такая, что АО=ОС. Расстояние от точки О до стороны АВ равно 4 см, а до стороны АС : 7см. Найдите расстояние от точки О до стороны ВС.
7.В треугольнике АВС проведены медиана АF и высота СD, найдите DF, если ВС = 10 см.
8.В прямоугольном треугольнике АСВ проведена высота СD. Гипотенуза АВ равна 10 см, угол СВА = 30°. Найдите ВD.
9.В параллелограмме АВСD высота ВН( Н принадлежит АD) в 2 раза меньше стороны СD. Найдите углы параллелограмма.
10.В параллелограмме АВСD биссектриса острого угла А пересекает сторону ВС в точке F. ВF: FС=2:3. Периметр параллелограмма равен 56 см. Найдите длины его сторон.
Вариант №2
Часть А
1.Один из смежных углов – острый. Каким будет второй угол?
а) острым б) прямым в) тупым
2.Найдите угол, если сумма двух смежных с ним углов равна 210°.
Ответ:_______________________________
3.Какое наименьшее число лучей может выходить из одной точки, чтобы все углы, образованные соседними лучами, были острыми?
Ответ:_______________________________
4.Периметр равнобедренного треугольника равен 18 см. Одна из его сторон равна 6см. Найдите длины двух других сторон.
Ответ:_______________________________
5. угол 1= 135°, угол 2=45°. Определите взаимное расположение прямых m и n.
а) пересекаются б) параллельны
в)такая ситуация невозможна
1
m
2
n
6.Определите вид треугольника, если сумма двух его углов меньше третьего угла.
а) остроугольный в) тупоугольный
б) прямоугольный г)определить невозможно
7. Углы треугольника относятся 1:1:2. Определите вид данного треугольника.
по углам: по сторонам:
1. остроугольный 1. разносторонний
2.прямоугольный 2.равносторонний
3.тупоугольный 3. равнобедренный
8. Сколько различных треугольников можно составить из пяти отрезков, длины которых равны 1см,2см,3см,4см,5см?
Ответ:__________________________________
Часть В
1.В треугольнике АВС медиана ВD является биссектрисой треугольника. Найдите периметр треугольника АВС, если периметр треугольника АВD равен 16 см, ВD=5см.
2.Медиана ВМ треугольника АВС перпендикулярна его биссектрисе АD. Найдите АВ, если АС=12см.
3.Дан прямоугольный треугольник АСВ. Найдите угол АОВ, где О – точка пересечения биссектрис острых углов треугольника.
4.Внутри равностороннего треугольника АВС отмечена точка D, такая, что угол ВАD равен углу ВСD=15°. Найдите угол АDС.
5.Биссектрисы АD и ВЕ треугольника АВС пересекаются в точке О. Найдите угол С треугольника, если угол АОЕ=50°.
6.В треугольнике АВС на медиане ВD отмечена точка О, такая, что угол САО равен углу ОСА. Расстояния от точки О до стороны АВ равно 8 см, а до стороны АС равно 5см. Найдите расстояние от точки О до стороны ВС.
7. Из вершины прямого угла к гипотенузе прямоугольного треугольника проведена медиана. Определите длину гипотенузы, если длина медианы равна 12 см.
8.Треугольник АСВ прямоугольный, СD высота. Найдите АD, если угол СВА равен 30°, гипотенуза АВ равна 8 см.
9.Высота ВН параллелограмма АВСD отсекает от него равнобедренный прямоугольный треугольник. Найдите углы параллелограмма.
10.В параллелограмма АВСD биссектриса острого угла А пересекает сторону ВС в точке М. ВМ:МС=3:4. Периметр параллелограмма равен 80 см. Найдите длины его сторон.
Вариант №3
Часть А
1.Если сумма двух углов равна 180°, то эти углы:
а) смежные б)вертикальный в) определить невозможно
2.Один из смежных углов в пять раз больше другого. Найдите эти углы.
Ответ:___________________________
3.Сколько лучей выходит из одной точки, если все углы, образованные соседними лучами, прямые?
Ответ:___________________________
4.В равнобедренном треугольнике стороны равны 8см и 5см. Найдите периметр треугольника.
Ответ:___________________________
5.Угол 1=30°, угол 2 на 120° больше угла 1. Определите взаимное расположение прямых m и n.
а) пересекаются б) параллельны
в) такая ситуация невозможна.
2
m
n 1
6.Определите вид треугольника, если сумма двух его углов больше третьего угла.
а) остроугольный в)тупоугольный
б) прямоугольный г) определить невозможно.
7. Углы треугольника относятся как 1:1:1. Определите вид данного треугольника.
по углам: по сторонам:
1.остроугольный 1.разносторонний
2.прямоугольный 2.равносторонний
3.тупоугольный 3.равнобедренный
8. Сколько различных треугольников можно составить из пяти отрезков, длины которых равны 1см,3см,4см,5см,6см?
Ответ:____________________________
Часть В
1.В треугольнике АВС биссектриса ВD является высотой треугольника. Найдите периметр треугольника АВС, если периметр треугольника АВD равен 14 см, а биссектриса ВD равна 3 см.
2.В треугольнике АВС на стороне АС отмечена точка D, такая, что АВ=ВD=DС. DF медиана треугольника ВDС. Найдите угол ВАС, если угол FDC равен 65°.
3.Высоты АМ и СN равностороннего треугольника АВС пересекаются в точке О. Найдите угол АОС.
4.Треугольник АВС равнобедренный с основанием АС. АР биссектриса угла треугольника, угол АВС=88°. Найдите угол АРВ.
5.Биссектрисы АD и ВЕ треугольника АВС пересекаются в точке О. Найдите угол С треугольника, если он в два раза меньше угла АОВ.
6.В треугольнике АВС биссектриса ВD делит сторону АС пополам. На биссектрисе ВD отмечена точка О, такая, что расстояние от точки О до стороны АВ равно 8 см, до стороны АС равно 5 см. Найдите расстояние от точки О до стороны ВС.
7.В треугольнике АВС проведена высота СD. Точка F – середина стороны ВС. Найдите ВС, если DF = 10см.
8.Треугольник АСВ прямоугольный. СD высота. Найдите гипотенузу АВ, если угол СВА равен 30°, АD=4 см.
9.В параллелограмме АВСD проведена высота ВН, Н€АD. Отрезок АН в 2 раза меньше стороны АВ. Найдите углы параллелограмма.
10.В параллелограмме АВСD проведена биссектриса А, которая пересекает сторону ВС в точке К. ВК:КС=2:3. Периметр параллелограмма равен 42 см. Найдите длины его сторон.
Вариант №4
Часть А
1.Если сумма двух углов равна 180°, то эти углы:
а)вертикальные б)определить невозможно в) смежные
2.Один из углов, полученных при пересечении двух прямых, больше другого на 40°. Найдите меньший угол.
Ответ:_________________________________
3.Какое наименьшее число лучей может выходить из одной точки, чтобы все углы, образованные соседними лучами, были не острыми?
Ответ:_________________________________
4.Периметр равнобедренного треугольника равен 19 см. Одна из его сторон равна 3 см. Найдите длины двух других сторон.
Ответ:_________________________________
5.Один из соответственных углов, образованных при пересечении прямых
n и m, секущей k, больше другого. Определите взаимное расположение прямых n и m.
а) пересекаются б) параллельны в)такая ситуация невозможна.
6.Определите вид треугольника, если разность двух его углов равна третьему углу.
а) остроугольный в)тупоугольный
б)прямоугольный г) определить невозможно
7.Углы треугольника относятся как 5:2:5. Определите вид данного треугольника.
по углам: по сторонам:
1.остроугольный 1.разностороний
2.прямоугольный 2.равносторонний
3.тупоугольный 3.равнобедренный
8.Сколько различных треугольников можно составить из пяти отрезков, длины которых равны 1см,2см,4см,5см,6см?
Ответ:_________________________________
Часть В
1.В треугольнике АВС высота ВD является биссектрисой треугольника. Найдите периметр треугольника АВС, если периметр треугольника АВD равен 17 см, а высота ВD равна 6 см.
2.ВМ – медиана треугольника АВС. Прямая АD перпендикулярна медиане и делит ее пополам. Сравните длины АВ и АС.
3.Треугольник АВС равнобедренный с основанием АС. Биссектрисы СD и АF пересекаются в точке О. Найдите угол АОС, если угол при основании равен 70°.
4.В треугольнике АВС угол А равен 64°. Биссектрисы углов В и С пересекаются в точке D. Найдите угол СDВ.
5.Биссектрисы АD и ВЕ треугольника АВС пересекаются в точке О. Найдите угол С треугольника, если он на 20° меньше угла АОВ.
6.В треугольнике АВС на высоте ВF отмечена точка О, такая, что угол АОF равен углу FОС. Расстояние от точки О до стороны АВ равно 3см, а до стороны АС равно 5 см. Найдите расстояние от точки О до стороны ВС.
7.Из вершины прямого угла к гипотенузе прямоугольного треугольника проведена медиана. Найдите длину медианы, если длина гипотенузы равна 18 см.
8.Треугольник АСВ прямоугольный, СD высота. Найдите гипотенузу АВ, если ВС=6см, ВD=3см.
9.Один из углов параллелограмма на 50° больше другого. Найдите углы параллелограмма.
10.В параллелограмме АВСD биссектриса угла А пересекает сторону ВС в точке Р. ВР:РС=4:3. Периметр параллелограмма равен 110 см. Найдите стороны параллелограмма.
Ответы к тестам.
Часть А.
|
вар. №зад. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
I |
a |
140° |
3 |
7см,5см; 6см,6см |
а |
в |
3;3 |
6 |
|
II |
в |
75° |
5 |
6см,6см |
б |
в |
2;3 |
3 |
|
III |
в |
30°;150° |
4 |
21см;18см |
б |
а |
1;2 |
4 |
|
IV |
б |
70° |
2 |
8см,8см |
ф |
б |
1;3 |
3 |
Часть В.
|
вар. №зад. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
I |
22см |
55° |
82° |
35° |
100° |
4см |
5см |
7,5см |
30°, 150° |
8см, 20см |
|
II |
22см |
6см |
135° |
90° |
80° |
8см |
24см |
2см |
45°, 135° |
12см, 28см |
|
III |
22см |
50° |
120° |
69° |
60° |
8см |
20см |
16см |
60°, 120° |
6см, 15см |
|
IV |
22см |
АВ= |
110° |
122° |
140° |
3см |
9см |
12см |
65°, 115° |
20см, 35см |
Используемая литература:
1.Н.С. Атаносян, Б.Ф. Бутузов, С.Б. Кадомцев и др. «Геометрия 7-9»,М.: Просвещение, 2009.
2.Т.М. Мищенко, А.Д. Блинков, Геометрия. Тематические тесты. 7 класс. М.: Просвещение, 2011.
Вопрос №
1
Через точку, не лежащую на прямой, можно провести …
две прямые, параллельные данной прямой
только одну прямую, параллельную данной
ни одной прямой, параллельной данной
множество параллельных прямых
Вопрос №
2
Точка М делит отрезок АВ на две части, одна из которой в 3 раза больше другой. Найдите длину большей части, если длина отрезка АВ равна
60 см.
45 см
30 см
15 см
другой ответ
Вопрос №
3
Через две любые точки А и В можно провести:
только две прямые
только одну прямую
ни одной прямой
множество прямых
Вопрос №
4
Выберите верное утверждение из предложенных:
Через любую точку можно провести только одну прямую
Сумма смежных углов равна 180 градусов
Если при пересечении двух прямых третьей прямой соответственные углы составляют в сумме 1800 градусов, то эти две прямые параллельны
Через любые две точки проходит более одной прямой
Вопрос №
5
Выберите верное утверждение из предложенных:
Градусная мера прямого угла равна 90 градусов
Градусная мера прямого угла больше 90 градусов
При параллельных прямых и секущей накрест лежащие углы в сумме образуют 180 градусов
Два треугольника равны, если соответствующие углы равны
Вопрос №
6
Выберите верное утверждение.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Каждая сторона треугольника меньше разности двух других сторон
Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны
Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны
Вопрос №
7
С какими из предложенных измерений сторон может существовать треугольник?
10 см, 6 см, 8 см
70 см, 30 см, 30 см
60 см, 30 см, 20 см
30 см, 30 см, 80 см
Вопрос №
8
Какое свойство имеет любой прямоугольник?
диагонали равные;
диагонали перпендикулярные;
диагонали есть биссектрисами его углов;
угол между диагоналями равен 30 гадусов
Вопрос №
9
Что есть центром описанной окружности любого треугольника?
точка пересечения высот;
точка пересечения медиан;
точка пересечения биссектрис;
точка пересечения серединных перпендикуляров его сторон.
Вопрос №
10
Какая фигура есть геометрическим местом точек плоскости, равноудаллёных от данной точки?
Луч;
Окружность;
Прямая;
Отрезок.
Проверьте свои знания по предмету геометрия за 7 класс при помощи нашего теста.
Ответьте на вопросы и нажмите “Узнать результат”
1. Как найти высоту в равностороннем треугольнике, если известна площадь и периметр
найти через периметр сторону треугольника и выразить высоту через площадь или воспользоваться формулой
требуются данные об угле
это невозможно
сразу воспользоваться формулой
2. Какая величина нужна, чтобы определить высоту равностороннего треугольника
площадь
два угла
угол
сторона
3. Можно ли в равностороннем треугольнике найти высоту через площадь
нельзя
только если он прямоугольный
можно
только если он равнобедренный
4. Тупой угол – это угол
менее 90 градусов
не менее 60 градусов
более 90 градусов
нет верного ответа
5. У угла EFH есть биссектриса FK. Найдите угол EFH, если угол EFK=50°
6. У угла EFH есть биссектриса FK. Найдите угол EFK, если угол KFH=36°
7. Две прямые, которые пересекаются под углом 90°, являются
вертикальными
смежными
перпендикулярными
параллельными
8. Сумма углов равна 180°, если они
являются смежными
являются развернутыми
являются вертикальными
равны смежным углам
9. Два угла называются вертикальными, если
их сумма равна 180°
они равны
стороны одного угла являются дополнительными полупрямыми сторон другого
у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми
10. Выберите правильное утверждение
если на протяжении всей длины двух прямых расстояние между ними не меняется, то прямые будут параллельными
если на протяжении всей длины двух прямых расстояние между ними не меняется, то прямые будут перпендикулярны
если на протяжении всей длины двух прямых расстояние между ними меняется, то прямые будут параллельными
если расстояние между прямыми в начале и в конце одинаково, то прямые будут параллельными
11. Если каждая из двух прямых перпендикулярны третьей, то эти прямые параллельны – гласит свойство перпендикулярности, так почему прямые параллельны
получившиеся односторонние углы будут в сумме давать 180 градусов
получившиеся равносторонние углы будут в сумме давать 180 градусов
получившиеся соответственные углы в сумме дадут 180 градусов
получившиеся соответственные углы в сумме дают 90 градусов
12. Чтобы отрезки назывались перпендикулярными, должно выполняться два условия
отрезки должны пересекаться, а угол пересечения между ними должен равняться 180 градусов
отрезки должны пересекаться, а угол пересечения между ними должен равняться 90 градусов
отрезки должны быть параллельными, а угол между ними должен равняться 90 градусов
отрезки должны быть параллельны, а односторонние углы между ними должны равняться 180 градусов
13. Сколько малых треугольников образуется, если провести в треугольнике 3 средние линии
14. Чему равна средняя линия треугольника
половине основания
четверти основания
трети основания
основанию
15. В прямоугольном треугольнике провели три средние линии. Какие малые треугольники образовались
все прямоугольные
все равносторонние
все равнобедренные
все произвольные
16. Правильный треугольник состоит из
двух углов
четырех сторон
трех отрезков
пяти углов
17. Для того чтобы найти площадь правильного треугольника необходимо
найти корень квадратный
подставить в формулу числовое значение угла этой фигуры
подставить в формулу числовое значение длины стороны
определить радиус окружности
18. В равностороннем треугольнике биссектриса, медиана и высота
совпадают
находятся на определенном расстоянии
перпендикулярны между собой
не лежат на одной линии
19. Выберите углы, которые не возникают при пересечении параллельных прямых секущей
равносторонние
накрест лежащие
односторонние
соответственные углы
20. Аксиома параллельных прямых звучит следующим образом
Через точку можно провести прямую, параллельную данной и при том не более трех
Через точку можно провести прямую, параллельную данной и при том только одну
Через две точки можно провести прямую, параллельную данной и при том только одну
Через точку можно провести прямую, параллельную данной, и сумма односторонних углов будет более 180 градусов
21. Углы при основании равнобедренного треугольника
нет верного ответа
пропорциональны
тупые
равны
22. Сколько сторон у равнобедренного треугольника
23. Сколько оснований у равнобедренного треугольника
24. В прямоугольном треугольнике катеты 5 см и 12 см. Найти радиус описанной окружности
6,5 см
2,7 см
11,8 см
3,6 см
25. Гипотенуза прямоугольного треугольника равна 12 см. Радиус описанной окружности
26. Из точки А к окружности с центром О проведена касательная АВ (В — точка касания). Угол АВО
развернутый
острый
тупой
прямой
27. Центр окружности, описанной около прямоугольного треугольника, лежит на середине
медианы
катета
биссектрисы
гипотенузы
28. Окружности радиусов 3 см и 7 см касаются внешним образом. Расстояние между их центрами равно
29. Ширина кольца, образованного двумя концентрическими окружностями с диаметрами 10 см и 16 см, равна
30. Из точки А к окружности проведены касательные АВ и АС (В и С — точки касания). Какое утверждение верно
АВ = АС
АВ < AC
AB > AC
определить невозможно
Самойлова Л.Н. МБОУ СОШ № 4, Серпухов, Московская область
Тест по геометрии за курс 7 класса
Фамилия, имя _____________________________________ класс _______
Вариант № 1
Продолжите предложения:
1. Два угла называются вертикальными, если…
а) стороны одного угла являются дополнительными полупрямыми сторон другого;
б) у них одна сторона общая, а другие стороны этих углов являются дополнительными
полупрямыми;
в) они равны;
г) их сумма равна 180
.
2. Сумма углов равна 180, если они…
а) являются смежными; б) являются вертикальными;
в) равны смежным углам; г) являются развернутыми.
3. Две прямые, которые пересекаются под углом 90, являются…
а) смежными; б) вертикальными;
в) параллельными; г) перпендикулярными.
4. В равных треугольниках:
а) против равных сторон лежат другие равные стороны;
б) все углы и стороны равны;
в) против соответственно равных сторон лежат равные углы.
5. Треугольник называется равнобедренным, если:
а) его стороны равны;
б) его углы равны;
в) у него есть боковые стороны и основание;
г) две его стороны равны.
6. Первый признак равенства треугольника гласит:
а) если две стороны и угол между ними одного треугольника соответственно равны двум
сторонам и углу между ними другого треугольника, то такие треугольники равны;
б) если две стороны и угол между ними одного треугольника соответственно равны двум
сторонам и углу другого треугольника, то такие треугольники равны;
в) если стороны и угол между ними одного треугольника соответственно равны сторонам
и углу между ними другого треугольника, то такие треугольники равны;
г) если две стороны и угол между ними одного треугольника равны двум сторонам и углу
другого треугольника, то такие треугольники равны.
7. Если прямые параллельны, то внутренние односторонние…
а) углы равны; б) углы в сумме дают 180
;
в) стороны равны; г) углы в сумме дают 90
.
8. Треугольник называется прямоугольным, если у него…
а) один угол острый; б) два угла прямые;
в) два угла острые; г) один угол прямой.
9. Сторона равнобедренного треугольника, отличная от двух других сторон
называется…
а) боковой стороной; б) гипотенузой;
в) основанием; г) катетом.
10. Сумма углов треугольника равна…
а) 90
; б) 180
; в) 360
; г) нет правильного ответа.
Самойлова Л.Н. МБОУ СОШ № 4, Серпухов, Московская область
11. MPK=PMN (см. рисунок) по …, если KMP=NPM.
а) гипотенузе и катету; б) катету и острому углу;
в) двум катетам; г) гипотенузе и острому углу.
12.Найдите третий угол треугольника, если два его угла 36 и 57.
а) 36
; б) 57
; в) 93
; г) 87
; д) нет правильного ответа.
13. Найдите углы при основании равнобедренного треугольника, если угол при
вершине равен 38.
а) 71
и 71
; б) 38
и 76
; в) 38
и 104
; г) нет правильного ответа.
14. Прямые параллельны, если равны…
а) вертикальные углы; б) внутренние накрест лежащие углы;
в) соответственные углы; г) внутренние односторонние углы.
15. Начертите две пересекающиеся прямые AB и CD в точке О. BOC и …
вертикальные углы.
а)
COA; б)
AOD; в)
DOB; г) нет правильного ответа.
16. Точка С принадлежит отрезку АВ. Чему равна длина отрезка АВ, если АС=3,4 см,
ВС=1,5 см .
а) 1,9 б) 7,2 в) 6,1 г) 4,9
17. Найдите острый угол прямоугольного треугольника, если другой острый угол
равен 69.
а) 21
; б) 69
; в) 90
; г) 180
; д) нет правильного ответа.
18. Известны стороны равнобедренного треугольника: 4 см и 1 см. Чему равен его
периметр?
а) 5 б) 6 в) 9 г) 14
19. На сколько частей делят плоскость две пересекающиеся прямые?
а) 2 б) 4 в) 6 г) 8
20. Сколько прямых можно провести через одну точку?
а) 1 б) 2 в) 3 г) бесконечно много
21. В прямоугольном треугольнике:
а) все углы прямые;
б) сумма острых углов равна 90 градусов
в) один из углов прямой, а другие могут быть как острыми, так и тупыми;
г) один из углов прямой, а два других острые и равны друг другу.
22. Каждая сторона треугольника:
а) равна сумме двух других его сторон;
б) больше суммы двух других его сторон;
в) меньше или равна сумме двух других его сторон;
г) меньше суммы двух других его сторон.
23. Угол – это геометрическая фигура, которая состоит:
а) из точки и пересекающихся лучей;
б) из точки и двух лучей, исходящих из этой точки;
в) из точки и двух прямых, проходящих через эту точку;
г) из двух пересекающихся прямых.
24. Отрезок – это:
а) часть прямой;
б) часть прямой, ограниченная двумя точками;
в) часть прямой, на которой отмечены две точки;
г) прямая, имеющая начало и конец.
25. Угол называют острым, если его градусная мера:
а) меньше 90 градусов; б) больше 90 градусов;
в) меньше развернутого угла; г) больше прямого угла.
Самойлова Л.Н. МБОУ СОШ № 4, Серпухов, Московская область
26. Биссектриса угла – это луч, который:
а) делит угол пополам;
б) исходит из вершины угла и проходит между его сторонами;
в) исходит из вершины угла и проходит во внутренней области угла;
г) исходит из вершины угла и делит его на два равных угла.
27. Две фигуры называются равными, если:
а) их можно совместить наложением;
б) все их стороны равны;
в) все их углы равны;
г) они имеют одинаковые формы.
28. Треугольник – это геометрическая фигура, состоящая:
а) из трех точек, не лежащих на одной прямой, и трех отрезков, их соединяющих;
б) из трех точек и трех отрезков, их соединяющих;
в) из трех отрезков;
г) из трех точек и трех отрезков.
29. Две прямые на плоскости называются параллельными, если они:
а) перпендикулярны одной прямой;
б) находятся на одинаковом расстоянии друг от друга;
в) не пересекаются на данном чертеже;
г) не пересекаются.
30. Один из признаков параллельности прямых двух прямых гласит:
а) если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые
параллельны;
б) если при пересечении двух прямых секущей сумма соответственных углов равна 180
градусов, то прямые параллельны;
в) если при пересечении двух прямых секущей односторонние углы равны, то прямые
параллельны;
г) если при пересечении двух прямых секущей вертикальные углы равны, то прямые
параллельны;
31. Внешний угол треугольника:
а) это угол, градусная мера которого равна сумме градусных мер двух углов
треугольника;
б) это угол, который расположен вне данного треугольника;
в) это угол, смежный с каким–нибудь углом этого треугольника;
г) это угол, который равен сумме двух других углов.
32. В треугольнике:
а) против большего угла лежит меньшая сторона;
б) против большей стороны лежит больший угол;
в) против меньшего угла лежит большая сторона;
г) против большей стороны лежит тупой угол.
33. В прямоугольном треугольнике:
а) если гипотенуза равна половине катета, то данная гипотенуза лежит против угла,
равного 30 градусов;
б) сумма любых двух углов равна 90 градусов;
в) катет, лежащий против угла, равного 30 градусов, составляет половину гипотенузы;
г) катет, прилежащий к углу, равному 30 градусов, составляет половину гипотенузы.
34. Расстоянием от точки до прямой называется:
а) длина отрезка, проведенного из данной точки к данной прямой;
б) длина перпендикуляра, проведенного из данной точки к данной прямой;
в) расстояние от данной точки до какой–нибудь точки данной прямой;
г) длина отрезка, соединяющего данную точку с какой–нибудь точкой данной прямой.
Самойлова Л.Н. МБОУ СОШ № 4, Серпухов, Московская область
35. Для доказательства равенства треугольников АВС и NКМ достаточно доказать,
что…
а) С = К;
б) С = М;
в) В = М.
36. Для доказательства равенства треугольников АВС и КМР достаточно
доказать, что…
а) ВС = МР;
б) ВС = РК;
в) МК = ВС.
37. В треугольнике АВС А = 40°, С = 41°. Тогда из сторон ВС и АВ больше…
38. Угол при вершине равнобедренного треугольника АВС равен 110°. СН –
высота.
39. Отрезки
пересекаются в их общей середине. Докажите, что прямые
Самойлова Л.Н. МБОУ СОШ № 4, Серпухов, Московская область
Тест по геометрии за курс 7 класса
Фамилия, имя _____________________________________ класс _______
Вариант № 2
Продолжите предложения:
1. Два угла называются смежными, если…
а) у них одна сторона общая, а две другие являются продолжениями одна другой;
б) их сумма равна 180
;
в) они равны;
г) стороны одного угла являются продолжениями сторон другого.
2. Отрезок – это;
а) часть прямой;
б) часть прямой, ограниченная двумя точками;
в) часть прямой, на которой отмечены две точки;
г) прямая, имеющая начало и конец.
3. Середина отрезка – это:
а) точка, которая принадлежит данному отрезку;
б) точка, которая делит данный отрезок на части;
в) точка отрезка, делящая его пополам;
г) точка, равноудаленная от концов отрезка.
4. Если сумма двух углов равна 180, то:
а) эти углы смежные; б) эти углы вертикальные;
в) эти углы перпендикулярные; г) нельзя определить.
5. Периметр треугольника – это:
а) длина всех его сторон; б) сумма длин всех его сторон;
в) сумма длин всех отрезков; г) произведение всех его сторон.
6. Второй признак равенства треугольника гласит:
а) если сторона и два прилежащих к ней угла одного треугольника равны стороне и двум
углам другого треугольника, то такие треугольники равны;
б) если сторона и два угла одного треугольника соответственно равны стороне и двум
углам другого треугольника, то такие треугольники равны;
в) если сторона и прилежащий к ней угол одного треугольника соответственно равны
стороне и прилежащему к ней углу другого треугольника, то такие треугольники равны;
г) если сторона и два прилежащих к ней угла одного треугольника соответственно равны
стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники
равны.
7. Диаметр окружности – это:
а) отрезок, равный двум радиусам;
б) отрезок, соединяющий две точки окружности;
в) хорда, проходящая через центр окружности;
г) отрезок, проходящий через центр окружности.
8. При пересечении двух прямых секущей образуются углы, имеющие специальные
названия:
а) смежные и вертикальные; б) острые, прямые и тупые;
в) параллельные и перпендикулярные;
г) накрест лежащие, соответственные и односторонние.
9. Расстоянием от точки до прямой называется:
а) длина отрезка, проведенного из данной точки к данной прямой;
б) длина перпендикуляра, проведенного из данной точки к прямой;
в) расстояние от данной точки до какой–нибудь точки данной прямой;
г) длина отрезка, соединяющего данную точку с какой–нибудь точкой данной прямой.
Самойлова Л.Н. МБОУ СОШ № 4, Серпухов, Московская область
10. . Вертикальные углы изображены на рисунке…
11. Для сторон данного треугольника справедливо равенство…
1) m = k; 2) k = 2n; 3) n = m.
12.Найдите третий угол треугольника, если два его угла 35 и 97.
а) 35
; б) 97
; в) 48
; г) 132
; д) нет правильного ответа.
13. Найдите угол при вершине равнобедренного треугольника, если угол при
основании равен 52.
а) 76
; б) 104; в) 100
; г) нет правильного ответа.
14. Аксиома – это:
а) положение геометрии, требующее обоснований;
б) положение геометрии, не требующее доказательства;
в) положение геометрии, имеющее следствие;
г) положение геометрии, обратное к которому верно.
15. Начертите две пересекающиеся прямые AB и CD в точке О. DОB и …
вертикальные углы.
а)
COA; б)
AOD; в)
DOB; г) нет правильного ответа.
16. Точка С принадлежит отрезку АВ. Чему равна длина отрезка АВ, если АС=4,4 см,
ВС=10,5 см .
а) 6,1 б) 7,2 в) 14,9 г) 4,9
17. Найдите острый угол прямоугольного треугольника, если другой острый угол
равен 52.
а) 38
; б) 52
; в) 90
; г) 180
; д) нет правильного ответа.
18. Известны стороны равнобедренного треугольника: 6 см и 3 см. Чему равен его
периметр?
а)15 б) 8 в) 15 г) 12
19. На сколько частей делят плоскость три пересекающиеся прямые?
а) 2 б) 4 в) 6 г) 8
20. Сколько прямых можно провести через две точки?
а) 1 б) 2 в) 3 г) бесконечно много
21. В треугольнике:
а) против большего угла лежит прямой угол;
б) против большей стороны лежит тупой или прямой угол;
в) против меньшего угла лежит большая сторона;
г) против меньшего угла лежит острый угол.
22. Каждая сторона треугольника:
а) равна сумме двух других его сторон;
б) больше суммы двух других сторон;
в) меньше или равна сумме двух других его сторон;
г) меньше суммы двух других его сторон.
Самойлова Л.Н. МБОУ СОШ № 4, Серпухов, Московская область
23. В остроугольном треугольнике:
а) все углы острые;
б) один угол острый, два других – любые;
в) менее трех острых углов;
г) сумма углов меньше суммы углов в прямоугольном или тупоугольном треугольнике.
24. Прямоугольные треугольники равны, если:
а) гипотенуза и угол одного треугольника равны гипотенузе и углу другого треугольника;
б) два угла одного треугольника равны двум углам другого треугольника;
в) гипотенуза и катет одного треугольника равны гипотенузе и катету другого
треугольника;
г) катет и угол одного треугольника равны катету и углу другого треугольника.
25. Угол называют тупым, если его градусная мера:
а) меньше 90 градусов; б) больше 90 градусов, но меньше 180;
в) меньше развернутого угла; г) больше прямого угла.
26. Треугольник – это геометрическая фигура, состоящая:
а) из трех точек, не лежащих на одной прямой, и трех отрезков, их соединяющих;
б) из трех точек и трех отрезков, их соединяющих;
в) из трех отрезков;
г) из трех точек и трех отрезков.
27. Два треугольника равны, если:
а) у них соответственные углы равны;
б) две стороны одного треугольника равны двум сторонам другого треугольника;
в) три стороны одного треугольника соответственно равны трем сторонам другого
треугольника;
г) два угла одного треугольника равны двум углам другого треугольника.
28. Если две параллельные прямые пересечены третьей, то:
а) сумма накрест лежащих углов равна 180
;
б) односторонние углы равны;
в) сумма односторонних углов равна 180
;
г) сумма соответственных углов равна 180
.
29. Выберите верное утверждение:
а) через точку, не лежащую на данной прямой, проходят по крайней мере две прямые,
параллельные данной;
б) если прямая пересекает одну из двух параллельных прямых, то она пересекает и
другую;
в) если две прямые параллельны третьей, то они пересекаются;
г) если прямая пересекает одну из двух прямых, то она пересекает и другую.
30. Один из признаков параллельности прямых двух прямых гласит:
а) если при пересечении двух прямых секущей сумма смежных углов равна 180
, то
прямые параллельны;
б) если при пересечении двух прямых секущей сумма накрест лежащих углов равна 180
,
то прямые параллельны;
в) если при пересечении двух прямых секущей односторонние углы равны, то прямые
параллельны;
г) если при пересечении двух прямых секущей соответственные углы равны, то прямые
параллельны.
31. Обратной данной, называется теорема, в которой:
а) условие и заключение являются обратными;
б) теорема доказывается методом от противного;
в) условие является заключение данной теоремы, а заключением – условие данной
теоремы;
г) доказывается, что такого быть не может.
Самойлова Л.Н. МБОУ СОШ № 4, Серпухов, Московская область
32. Внешний угол треугольника:
а) равен сумме двух углов треугольника, не смежных с ним;
б) это угол, смежный с каким–нибудь углом вне этого треугольника;
в) является тупым;
г) равен сумме углов треугольника
33. В прямоугольном треугольнике:
а) если гипотенуза равна половине катета, то данная гипотенуза лежит против угла,
равного 30 градусов;
б) сумма любых двух углов равна 90 градусов;
в) катет, лежащий против угла, равного 30 градусов, составляет половину гипотенузы;
г) катет, прилежащий к углу, равному 30 градусов, составляет половину гипотенузы.
34. Медианы треугольника:
а) попарно пересекаются;
б) пересекаются в одной точке;
в) соединяют середины сторон треугольника;
г) являются высотами и биссектрисами.
35. Для доказательства равенства треугольников АPK и DCE достаточно
доказать, что…
а) АР = CD; б) AP = DE; в) AP = CE.
36. Из равенства треугольников АРК и MFN следует, что…
а) АК = MF; б) AK = MN; в) A = M.
37. В треугольнике MNK MN = 17 см, NK = 15 см. Тогда из углов M и K
меньший…
38. Угол при вершине равнобедренного треугольника АВС равен 64°.
СК – высота.
39. В равнобедренном
Самойлова Л.Н. МБОУ СОШ № 4, Серпухов, Московская область
Критерии оценки знаний
Время написания теста 60 минут
Задания оцениваются 1 баллом.
«5» – 36-39 баллов
«4» – от 24 до 35 баллов
«3» – от 13 -23 баллов
«2» – меньше 12 баллов
Самойлова Л.Н. МБОУ СОШ № 4, Серпухов, Московская область
1) Рассмотрим треугольники AOC и
BOD: AO=ОВ, СО=OD по
условию, ∠АОС=∠BOD-
вертикальные. Значит,
треугольники равны по двум
сторонам и углу между ними;
2) Так как треугольники равны, то
∠А=∠В–накрест лежащие,
значит, АС ‖BD. Что требовалось
доказать.
1) Рассмотри треугольник ABC, так
как он равнобедренный, то
∠А=∠С–свойство
равнобедренного треугольника;
2) ∠ВАО=∠САО=∠ВСО=∠АСО так
как проведены биссектрисы
углов А и С;
3) Так как ∠САО=∠АСО, то
треугольник АОС–
равнобедренный–признак
равнобедренного треугольника.
Что требовалось доказать.
Список использованных материалов
1. Контрольно–измерительные материалы. Геометрия. 7 класс/ Н.Ф. Гаврилова. 2–е
изд., перераб. – М.: ВАКО, 2013. – 96 с. – (Контрольно–измерительные материалы).
2. Геометрия. 7–9 классы: учеб. для общеобразоват. организаций с прил. На
электрон. носителе / [Л. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 3-е изд. – М.:
Просвещение, 2014. – 383 с.: ил.
3. Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.–сост.
Г.И. Ковалева, Н.И. Мазурова. – Изд. 2–е. – Волгоград: Учитель, 2016. – 175 с.