Как составить трассировочную таблицу по информатике

Слайд 1

Линейные вычислительные алгоритмы. Операция п рисваивание. Трассировочная таблица.

Слайд 2

В линейных алгоритмах присваивание является важнейшей операцией в алгоритмах, работающих с величинами, поговорим о ней более подробно. Переменная величина получает значение в результате присваивания. Присваивание производится компьютером при выполнении одной из двух команд из представленной выше системы команд: команды присваивания или команды ввода. Рассмотрим последовательность выполнения четырех команд присваивания, в которых участвуют две переменные: а и b . В приведенной ниже таблице против каждой команды указываются значения переменных, которые устанавливаются после ее выполнения. Такая таблица называется трассировочной таблицей, а процесс ее заполнения называется трассировкой алгоритма.

Слайд 3

х:= 2 у:=х*х у:=у*у х:=у*х s:= x+y Шаг алгоритма Переменные x y s 1 2 3 4 5 2 2 4 2 32 32 16 16 48 16 – – – – – Вычисления по алгоритму Алгоритм Ответ : s = 48 Прочерк в таблице означает неопределенное значение переменной. Конечные значения, которые получают переменные а и b , соответственно равны 2 и 4 .

Слайд 4

Трассировочная таблица иллюстрирует три основных свойства присваивания. Вот эти свойства: 1) пока переменной не присвоено значение, она остается неопределенной; 2) значение, присвоенное переменной, сохраняется вплоть до выполнения следующего присваивания этой переменной нового значения; 3) новое значение, присвоенное переменной, заменяет ее предыдущее значение.

Слайд 5

Обмен значениями двух переменных Рассмотрим еще один очень полезный алгоритм, с которым при программировании часто приходится встречаться. Даны две переменные величины: X и Y . Требуется произвести между ними обмен значениями. Например, если первоначально было: X = 1; Y = 2 , то после обмена должно стать: X = 2, Y = 1 . Хорошим аналогом для решения такой задачи является следующая: даны два стакана, в первом — молоко, во втором — вода; требуется произвести обмен их содержимым. Всякому ясно, что в этом случае нужен дополнительный, третий, пустой стакан.

Слайд 6

Последовательность действий будет следующей: 1) перелить из 1-го стакана в 3-й; 2) перелить из 2-го стакана в 1-й; 3) перелить из 3-го стакана во 2-й. Цель достигнута! По аналогии для обмена значениями двух переменных нужна третья дополнительная переменная. Назовем ее Z. Тогда задача решается последовательным выполнением трех операторов присваивания (пусть начальные значения 1 и 2 для переменных X и Y задаются вводом):

Слайд 7

В трассировочной таблице выводимые значения выделены жирным шрифтом. Аналогия со стаканами не совсем точна в том смысле, что при переливании из одного стакана в другой первый становится пустым. В результате же присваивания ( Х:=Y ) переменная, стоящая справа ( Y ), сохраняет свое значение. Действительно, в итоге переменные X и Y поменялись значениями. На экран будут выведены значения X и Y: 2,1 .

Слайд 8

Описание линейного вычислительного алгоритма Алгоритмы, результатами выполнения которых являются числовые величины, будем называть вычислительными алгоритмами. Рассмотрим пример решения следующей математической задачи: даны две простые дроби; получить дробь, являющуюся результатом деления одной на другую. В школьном учебнике математики правила деления обыкновенных дробей описаны так: 1. Числитель первой дроби умножить на знаменатель второй. 2. Знаменатель первой дроби умножить на числитель второй. 3. Записать дробь, числителем которой является результат выполнения пункта 1, а знаменателем — результат выполнения пункта 2.

Слайд 9

В алгебраической форме это выглядит следующим образом: Теперь построим алгоритм деления дробей для компьютера. В этом алгоритме сохраним те же обозначения для переменных, которые использованы в записанной выше формуле. Исходными данными являются целочисленные переменные а, b , с, d . Результатом — также целые величины m и n . Ниже алгоритм представлен в двух формах: в виде блок-схемы и на Алгоритмическом языке (АЯ).

Слайд 10

Раньше прямоугольник в схемах алгоритмов управления мы называли блоком простой команды. Для вычислительных алгоритмов такой простой командой является команда присваивания. Прямоугольник будем называть блоком присваивания , или вычислительным блоком . В форме параллелограмма рисуется блок ввода/вывода . Полученный алгоритм имеет линейную структуру.

Слайд 11

В алгоритме на АЯ строка, стоящая после заголовка алгоритма, называется описанием переменных . Служебное слово цел означает целый тип. Величины этого типа могут иметь только целочисленные значения. Описание переменных имеет вид: <тип переменных> <список переменных> Список переменных включает все переменные величины данного типа, обрабатываемые в алгоритме. В блок-схемах типы переменных не указываются, но подразумеваются. Запись алгоритма на АЯ ближе по форме к языкам программирования, чем блок-схемы.

Слайд 12

Коротко о главном Трассировочная таблица пошаговое исполнение команд алгоритма с указанием значений переменных, которые устанавливаются после выполнения команд. Трассировка алгоритма – процесс заполнения трассировочной таблицы Основные свойства присваивания: • значение переменной не определено, если ей не присвоено никакого значения; • новое значение, присваиваемое переменной, заменяет ее старое значение; • присвоенное переменной значение сохраняется в ней вплоть до нового присваивания.

Слайд 13

Обмен значениями двух переменных можно производить через третью дополнительную переменную . Трассировочная таблица используется для «ручного» исполнения алгоритма с целью его проверки . В алгоритмах на АЯ указываются типы всех переменных . Такое указание называется описанием переменных . Числовые величины, принимающие только целочисленные значения, описываются с помощью служебного слова цел (целый).

Слайд 14

1) A : =1 B: =2 A: =A+B B: =2*A Задание. Постройте трассировочные таблицы для следующих алгоритмов: 2) A : =1 B: =2 C: =A A: =B B: =C 3) A: =1 B: =2 A: =A+B B: =A-B A: =A-B

Презентация на тему: ” 1 Правила заполнения трассировочной таблици. 2 1. Записать алгоритм в левой части. A:=2 B:=3 A:=A*A B:=3*B A:=B+10 B:=A-B.” — Транскрипт:

---

---

§ 7. Запись алгоритмов на языках программирования

Информатика. 11 класса. Босова Л.Л. Оглавление

---

Язык программирования

Язык программирования — формальная знаковая система, предназначенная для записи компьютерных программ.

Компьютерную программу можно считать последовательностью строк символов некоторого алфавита. Современные системы программирования допускают использование визуальных элементов (окон, иконок и др.) для построения программ, в частности для создания интерфейса пользователя. Такое программирование называют визуальным. Тем не менее основная, алгоритмическая часть любой программы строится с использованием символьных средств.

В основной школе вы познакомились со школьным алгоритмическим языком КуМир и языком программирования Pascal (Паскаль). В 11 классе мы продолжим работать с языком Pascal.

Желательно установить среду программирования на ваш домашний компьютер.

Все алгоритмы, представленные в этом учебнике на языке Pascal, вы можете записывать и на любом другом интересующем вас языке программирования.

7.1. Структурная организация данных

Информация, представленная в виде, пригодном для автоматизированной обработки, называется данными. Компьютер оперирует только одним видом данных — отдельными битами, или двоичными цифрами. Причём он работает с этими данными в соответствии с неизменным набором алгоритмов, которые определяются системой команд центрального процессора.

Задачи, которые решаются с помощью компьютера, редко выражаются на языке битов. Как правило, данные имеют форму чисел, символов, текстов и более сложных структур. Алгоритмы, создаваемые для обработки этих данных, учитывают их структуру.

Под структурой данных в общем случае понимают множество элементов данных и множество связей между ними.

Различают простые и сложные структуры данных.

Простые структуры данных не могут быть разделены на составные части больше, чем бит. К ним относятся числовые, символьные, логические и другие данные. Простые структуры данных служат основой для построения сложных структур данных — массивов, списков, графов, деревьев и др.

Некоторые простые типы данных языка Pascal приведены на рис. 2.10.

Рис. 2.10. Некоторые простые типы данных языка Pascal

7.2. Некоторые сведения о языке программирования Pascal

Таблица 2.2

Операции в языке Pascal

Выражение — это формула, по которой вычисляется значение. Выражение может состоять из операндов (констант, переменных, стандартных функций), знаков операций и круглых скобок. Выражения записываются в строку; знаки операций не пропускаются. Порядок выполнения операций определяется скобками и приоритетом операций (табл. 2.3). Операции одинакового приоритета выполняются слева направо, если порядок выполнения не задан явно круглыми скобками. Вычисление выражения с вложенными скобками начинается с внутренних скобок.

Таблица 2.3

Приоритет операций в языке Pascal

Программа на языке Pascal имеет следующую структуру:

Обязательными в ней являются два раздела: описания данных и описания действий, которые над этими данными необходимо выполнить.

Данные, обрабатываемые компьютером, хранятся в памяти. С точки зрения языка Pascal она разделена на секции, называемые переменными. Каждая переменная имеет имя, тип и значение; значения переменных могут меняться в ходе выполнения программы.

Блок описания действий начинается со слова begin, а заканчивается словом end и знаком точки. Действия представляются операторами (табл. 2.4). Операторы языка Pascal разделяются точкой с запятой. Операторы бывают простые и составные (заключённые в операторные скобки begin … end).

Таблица 2.4

Основные операторы языка Pascal

Пример 1. В начале этой главы мы обсуждали алгоритмы нахождения простых чисел. Напишем программу, проверяющую, является ли заданное натуральное число п простым.

Самый простой путь решения этой задачи — проверить, имеет ли данное число n (n >= 2) делители в интервале [2; n — 1].

Если делители есть, число n — составное, если — нет, то — простое.

В этой программе мы проверяли, нет ли у числа n делителей из интервала [2; n — 1]. Но если п = а • Ь, то меньшее из чисел а, b не больше

 (в противном случае оба числа были бы больше

, а следовательно, их произведение было бы больше n). Кроме того, из делимости числа n на а автоматически следует, что n делится и на n/а.

Усовершенствуйте приведённую выше программу с учётом этих соображений.

Проверку, является ли заданное натуральное число n >= 2 простым, мы осуществили методом перебора всех возможных его делителей. Метод перебора используется для решения достаточно широкого круга задач.

Пример 2. Применим метод перебора для поиска наибольшего общего делителя (НОД) двух натуральных чисел а и b.

Начнём перебор с d — наименьшего из чисел а и Ь. Это первый, очевидный кандидат на роль их наибольшего общего делителя. И далее, пока не найдём d, на которое оба числа делятся нацело, будем уменьшать его на единицу. Как только такое деление произойдёт, останавливаем уменьшение d. Полученное значение d и будет наибольшим общим делителем чисел а и Ь.

7.3. Анализ программ с помощью трассировочных таблиц.

Пример 3

Для анализа свойств алгоритма и проверки его соответствия решаемой задаче используются трассировочные таблицы. В них фиксируется пошаговое исполнение алгоритма (программы), что позволяет наглядно представлять значения переменных, изменяющиеся при его выполнении. Поэтому трассировочные таблицы иначе называют таблицами значений.

Пример 3. Определим значения переменных а и b, полученные в результате выполнения следующей программы:

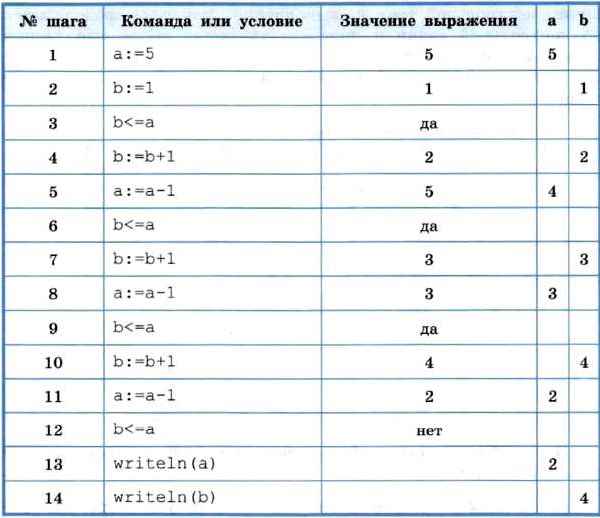
Составим трассировочную таблицу первого вида. В её заголовке поместим имена всех переменных, используемых в программе. В отдельном столбце будем записывать команды и условия, имеющиеся в программе. Каждая строка таблицы соответствует одному шагу алгоритма.

Чтобы не загромождать таблицу, будем записывать в каждой строке только то значение переменной, которое получено на соответствующем шаге.

Из таблицы видно, что в результате работы переменные приняли значения: а = 2 и b = 4.

Пример 4. Определим значение переменной s, полученное в результате выполнения следующей программы:

Построим трассировочную таблицу второго вида, отражая в каждой строке результат группы действий. Группу действий ограничим контрольной точкой: выполнение алгоритма продолжается до контрольной точки и приостанавливается после выполнения отмеченной ею строки.

Будем считать, что контрольная точка (КТ) поставлена на строке s := s + d.

Итак, в результате работы программы переменная приняла значение s = 60.

Каким должно быть значение d, чтобы в результате работы программы переменная приняла значение s = 186? Существует ли такое значение d, что в результате работы программы переменная примет значение s = 212?

Пример 5. Определим значение переменной s, полученное в результате выполнения следующей программы:

Трассировочная таблица может иметь вид:

Пример 6. Выясним, для чего предназначена следующая программа:

Прежде всего, обратим внимание на то, что в ней кроме переменной п целого типа используется строка nd, для которой символ « + » обозначает операцию сцепления строк. Начальное значение n вводится с клавиатуры, поэтому зададим его по своему усмотрению, например n = 12.

Выполните программу для n = 25. Какую задачу, по вашему мнению, решает эта программа?

Функциональный подход к анализу программ

Тесно взаимосвязанным с диалектическим подходом является функциональный подход. Его сущность состоит в рассмотрении исследуемой программы или ее составляющих элементов только с позиций внешней среды. При этом исследуемая программа представляется в виде «черного ящика». Это позволяет рассматривать отношения программы с другими системами и внешней средой абстрактно, не вникая в процессы, происходящие непосредственно в исследуемой программе.

Именно поэтому все то, что отражает поведение и отношения таким образом представленной функционирующей программы, называют функцией, а подход функциональным.

При изменении в изучаемой программе каких-либо параметров в связи с происходящим процессом в «черном ящике» меняется ее состояние, в том числе взаимосвязи с внешней средой. Зная принципы происходящих в программе процессов, можно исследовать саму программу и получить новые знания. Например, собрав информацию о сбоях и отказах компьютерной сети предприятия, не вникая в сущность происходящих в ней процессов, можно дать их прогноз.

Функциональный подход, подобно системному и ситуационному, не исключает использование при исследовании систем управления процессного подхода. На практике функциональный подход может широко применяться при изучении экономических явлений, в том числе планирования, тенденций экономического развития, оценке акционерного капитала, изменения цен и т.п.

Трассировка алгоритма

Рассмотрим последовательность выполнения четырех команд присваивания, в которых участвуют две переменные а и b. В приведенной ниже таблице против каждой команды указываются значения переменных, которые устанавливаются после ее выполнения. Такая таблица называется трассировочной таблицей, а процесс ее заполнения называется трассировкой алгоритма. Компьютер выполняет команды в порядке их записи в алгоритме.

Прочерк в таблице обозначает неопределенное значение переменной. Конечные значения, которые получают переменные а и b, соответственно равны 2 и 4.

7.4. Другие приёмы анализа программ.

Пример 7

Трассировочная таблица — наглядный, но не универсальный инструмент анализа программ. Например, её затруднительно строить, если в алгоритме много шагов.

Пример 7. Требуется выяснить, какое число будет напечатано в результате выполнения следующей программы:

Трассировочная таблица для этой программы будет содержать не одну сотню строк. Попробуем проанализировать программу иначе.

1. Выясним, какую функцию выполняет каждая из переменных, задействованных в программе. Начальное значение переменной s = 400. При каждом выполнении тела цикла к значению s прибавляется число 12. Начальное значение переменной n = 0. При каждом выполнении тела цикла значение переменной увеличивается на 2: n — 2, если тело цикла выполнено 1 раз; n = 4 — если 2 раза; n = 6 — если 3 раза и т. д. Таким образом, искомое значение n — это 2 • k, где k — число выполнений тела цикла.

2. Выясним, при каком условии произойдёт выход из цикла. Цикл выполняется, пока s < 2992. Следовательно, цикл завершится при достижении s значения, равного или большего 2992.

3. Выясним, сколько раз выполнится тело цикла, вычислив значение выражения: (2992 — 400)/12 = 216. После того как тело цикла выполнится 216 раз, значение переменной s будет равно 2992, что является условием выхода из цикла. При этом n = 2 • 216 = 432.

Выясните, каким будет результат работы программы, если в ней условие выхода из цикла будет изменено на:

1) s < 2990;

2) s <= 2992;

3) s <= 300.

Пример 8. Получив на вход некоторое натуральное число х, эта программа выводит два числа — m и n.

Известно, что при некотором значении х были выведены числа 5 и 25. Выясним, сколько существует разных значений х, при вводе которых может быть получен такой результат.

Выясним, какие именно данные накапливаются в переменных.

Начальное значение переменной х задаётся пользователем. Тип этой переменной integer, следовательно, она не может превышать 32 767. В цикле значение переменной х изменяется по правилу, заданному командой:

х:=х div 10

При таком преобразовании значение переменной х уменьшается в 10 раз и дробная часть результата отбрасывается. Можно сказать, что при каждом выполнении тела цикла от значения переменной х «отсекается» одна цифра справа.

Начальное значение переменной m = 0. При каждом выполнении цикла значение переменной m увеличивается на единицу. Можно сказать, что в m подсчитывается количество цифр, «отсечённых» от х.

Начальное значение переменной n = 1. В цикле значение переменной n изменяется по правилу, заданному командой:

n: =n*(х mod 10)

Здесь х mod 10 — не что иное, как последняя цифра числа х. Таким образом, в переменной n накапливается произведение цифр числа х, взятых справа налево.

Выход из цикла осуществляется при х <= 0, т. е. когда все значащие цифры этого числа будут рассмотрены.

Следовательно, если на экран первой выводится цифра 5, то исходное число пятизначное. Второе число указывает на то, что 25 — это произведение всех цифр исходного числа х.

Рассмотрим варианты пятизначных чисел, произведение цифр которых равно 25. Например, 11551, 51151 и т. д. Очевидно, в записи любого из таких чисел должны быть две пятёрки и три единицы. Применение известной вам формулы из комбинаторики позволяет вычислить количество разных чисел, удовлетворяющих такому условию, — это 10.

О какой формуле идёт речь? Приведите эту формулу и выполните соответствующие вычисления.

Укажите наибольшее и наименьшее числа, удовлетворяющие условию задачи.

Выпишите все числа, удовлетворяющие условию задачи.

---

САМОЕ ГЛАВНОЕ

Компьютерную программу можно считать последовательностью строк символов некоторого алфавита. Современные системы программирования и языки допускают использование визуальных элементов (окон, иконок и др.) для построения программ, в частности для создания интерфейса пользователя. Тем не менее основная, алгоритмическая, часть любой программы строится с использованием символьных средств.

В основной школе вы познакомились со школьным алгоритмическим языком КуМир и языком программирования Pascal (Паскаль). В 11 классе мы продолжаем работать с языком Pascal.

Компьютер оперирует только одним видом данных — отдельными битами, или двоичными цифрами. Задачи, решаемые с помощью компьютера, оперируют данными, имеющими форму чисел, символов, текстов и более сложных структур. Алгоритмы для обработки этих данных создаются с учётом их структуры — множества элементов данных и множества связей между ними.

Различают простые и сложные структуры данных. Простые структуры данных не могут быть разделены на составные части больше, чем бит. К ним относятся числовые, символьные, логические и другие данные. Простые структуры данных служат основой для построения сложных структур данных — массивов, списков, графов, деревьев и др.

---

Вопросы и задания

1. Что такое язык программирования? Опишите состав и интерфейс среды разработки программ на используемом вами языке программирования.

2. Приведите примеры структур данных, используемых в языке программирования Pascal.

3. Кратко охарактеризуйте основные элементы языка программирования Pascal.

4. Опишите структуру программы на языке Pascal.

5. Для чего предназначены трассировочные таблицы?

6. Вещественные числа х, у, z являются исходными данными для следующего алгоритма:

7. Определите значение переменной n, которое будет получено в результате выполнения следующей программы:

8. Определите значение переменной s, которое будет получено в результате выполнения следующей программы:

9. Требуется выяснить, какое число будет выведено в результате выполнения следующей программы:

10. Получив на вход число х, приведённая ниже программа выводит два числа — m и n.

11. Напишите программу, выводящую на экран все чётные трёхзначные числа.

12. Напишите программу, подсчитывающую сумму квадратов всех чисел от 1 до n.

13. Напишите программу, позволяющую определить, входит ли заданная цифра в некоторое целое неотрицательное число.

14. Разработайте программу перевода десятичного натурального числа n в троичную систему счисления.

15. Разработайте программу, которая выводит сообщение «Да», если точка с координатами (х, у) принадлежит закрашенной области, и «Нет» в противном случае.

16. Шифр кодового замка является двузначным числом. Буратино забыл код, но помнит, что сумма цифр этого числа, сложенная с их произведением, равна самому числу. Напишите все возможные варианты кода, чтобы Буратино смог быстрее открыть замок. Решите задачу методом перебора.

---

§ 6. Алгоритмические структуры
§ 7. Запись алгоритмов на языках программирования
§ 8. Структурированные типы данных. Массивы

---

Урок 10
§7(3). Анализ программ с помощью трассировочных таблиц

Для анализа свойств алгоритма и проверки его соответствия решаемой задаче используются трассировочные таблицы. В них фиксируется пошаговое исполнение алгоритма (программы), что позволяет наглядно представлять значения переменных, изменяющиеся при его выполнении. Поэтому трассировочные таблицы иначе называют таблицами значений.

Используются трассировочные таблицы двух видов:

1) таблицы, каждая строка которых отражает результат одного действия;
2) таблицы, каждая строка которых отражает результат выполнения группы действий.

Пример 3. Определим значения переменных а и b, полученные в результате выполнения следующей программы:

Составим трассировочную таблицу первого вида. В её заголовке поместим имена всех переменных, используемых в программе. В отдельном столбце будем записывать команды и условия, имеющиеся в программе. Каждая строка таблицы соответствует одному шагу алгоритма.

Чтобы не загромождать таблицу, будем записывать в каждой строке только то значение переменной, которое получено на соответствующем шаге.

Из таблицы видно, что в результате работы переменные приняли значения: а = 2 и b = 4.

Cкачать материалы урока

Тема 9. Таблицы трассировки

Ранее мы посмотрели, как загрузить исходные требования в проектную базу и работать уже с ними, как с самостоятельными элементами — оценивать наличие ошибок, некорректных формулировок, управлять приоритетами и статусами.

Однако кроме требований в проекте можно и нужно разрабатывать и управлять и другими данными. Например, структурой системы (в демо-проекте это SBS), рисками, верифи кациями, словарем, задачами.

Технически в Cradle для этого используются те же самые инструменты, что и для управления требованиями. Т.е. интерфейс унифицирован и если вы разобрались с требованиями, то значит вы освоили и работу с остальными типами проектных данных.

Самое важное — это то, что никакое требование не существует отдельно от других проектных данных. Оно обязательно должно быть связано напрямую или косвенно, например, с элементом структуры системы (в английской терминологии это называется allocation и является одной из задач проектирования).
Требования также могут быть связаны с конкретными заказчиками. С требованиями могут быть связаны риски.
И, конечно, требования часто взаимозависимы, а значит эти связи также должны быть отражены в проекте.
И так далее, в соответствии с выбранной моделью трассировки.

Назначение трассировки — отражение проектных связей, которые далее используются в качестве базы знаний проекта, для верификации проекта и управления изменениями.

Все известные мне международные стандарты, связанные с системной инженерией, говорят одно и то же: «требования должны быть трассируемы», т.е. должна быть возможность проследить все связи от исходных требований, до их реализации (через все промежуточные требования и проектные решения).

В Cradle можно настроить очень много удобных представлений для анализа проектных связей. Технически они делятся на три класса:

• Таблицы трассировки
• Матрицы трассировки
• Иерархические диаграммы трассировки

— это три разных способа показать связи между проектными данными.

Сегодня мы посмотрим подробнее на таблицы трассировки.
Они основаны на Представлениях, которые мы уже немного разбирали (в рамках отображения загруженных требований (8)).
Далее иллюстрации.

На этой иллюстрации представлена типичная структура таблицы трассировки. Слева отображается один тип элементов, справа — элементы другого типа, связанные с теми, что справа. В данном случае эта таблица отражает риски, связанные с требованиями, а заоднопоказывает вероятность этих рисков.

Что можно быстро увидеть по этой таблице? Например, Тр1 — какое-то подозрительно рискованное, с ним связано аж два риска, один из них с высокой вероятностью. Возможно стоит это требование исключить или наоборот, уделить ему больше внимания.

Теперь пример из Cradle. Это отчет, включающий таблицу трассировки, который показывает, как исходные требования, связаны с производными системными требованиями.

А вот еще одно представление (не из демо-проекта), с таблицей трассировки. В этот раз от бизнес-целей к бизнес-правилам. Это уже более сложное иерархическое представление, для его генерации используется рекурсия (представление вызывает само себя).
Здесь мы видим, какие накладываются ограничения на наши бизнес-цели. Это демо-проект, поэтому конкретные цели/требования не указаны, но если бы он был наполнен реальными данными, вся картина проблем, задач и ограничений была бы как на ладони.

Еще несколько примеров. Трассировка от Требований к «Фичам»

Трассировка от тестов к требованиями. Сразу можем видеть, по каким требованиям не прошли тесты. Обратите внимание, что некоторые тесты покрывают несколько требований.

И трассировка через три типа элементов — от результатов тестов, к тесткейсам и требованиям

Еще один пример совершенно иной таблицы трассировки через три типа элементов (Доска Scrum) Релизы-User Stories-Задачи, связанные с каждой пользовательской историей

Что такое трассировочная таблица

Трассировка

Для понимания чужой программы и для проверки правильности написания своей используют метод пошагового выполнения программы с отслеживанием значений всех переменных.

Пример 6.4.
Вычисление суммы чисел от 6 до 10

Program Test.4;
var
N: integer; будет счетчик цикла for >
S: integer;
begin
S:=0;
for N:=6 to 10 do
S:=S + N;
writeln(‘Сумма чисел=’, S:6);
readln
end.

Рис. 6.3. Блок-схема алгоритма вычисления суммы чисел от 6 до 10

Для проверки правильности работы программы рекомендуется пошагово отслеживать изменение всех переменных после выполнения каждого оператора программы.
Такой процесс называется трассирввкой. Продемонстрируем этот прием (табл. 6.1).
В результате работы программы на экране получим число 40.

Таблица 6.1. Трассировка программы из примера 6.4

Оператор	Условие	N	S	Примечание
S:=0	0
for N:= 6 to 10 do	Да	6
S:=S + N	6	0+6-6
For N:= 6 to 10 do	Да	7
S:= S + N	13	6 + 7 = 13
For N:= 6 to 10 do	Да	8
S:= S + N	21	13 + 8 = 21
For N:= 6 to 10 do	Да	9
S:= S + N	30	21 + 9 = 30
For N:= 6 to 10 do	Да	10
S:= S + N	40	30 + 10 = 40
For N:=6 to 10 do	Нет	11
writeln (‘Сумма чисел’,S:3)	.	На экране: Сумма чисел=40

Для операторов, выполняющих проверку условий (if, for и т. п.) в столбце «Условие» принято указывать результат проверки. В данном случае в цикле for проверяется условие продолжения цикла.
Символы «. » подчеркивают, что значение счетчика цикла по выходе из цикла считается неопределенным.

Метод трассировки очень помогает при отладке программы, когда программа выдает не тот результат, который должна выдать. Осуществляя пошаговую трассировку, мы вникаем в логику работы программы и на каждом шаге проверяем, правильны ли были наши рассуждения при ее написании.

Вычисление суммы ряда

Рассмотрим задачу вычисления суммы ряда:
1/(1*1) + 1/(2*2) + 1/(3*3) + 1/(4*4) + 1/(5*5)

Здесь мы имеем ряд дробей, у которых в знаменателях записаны квадраты чисел от 1 до 5.
Рассмотрим каждую дробь как произведение двух дробей, например:
1/(3*3) = 1/3 * 1/3

В общем виде это можно записать так:
1/(N * N) = 1/N * 1/N

Блок-схема алгоритма решения задачи представлена на рис. 6.4.

Задание 6.5.
Написать программу вычисления n! (факториал числа n), где n положительно. Определение факториала:

Другими словами, n! — это произведение первых n натуральных чисел.

Каждый следующий результат (обозначим его Р) получается путем умножения предыдущего результата (предыдущего Р) на счетчик, который пробегает значения от 1 до n.
Обозначим значение счетчика буквой k.

Получаем общий вид выражения: Р = Р * k (то есть воспользуемся рекуррентной формулой вычисления факториала: n! = (n — 1)! * n).

Программа должна быть организована так: с клавиатуры вводится число n (n— положительно), а затем на экран выдается таблица факториалов чисел до n включительно.

Задание 6.6.
Написать программу вычисления суммы ряда S=1 + 2 + 3 + 4 + 5 + 6. Нарисовать блок-схему и заполнить таблицу трассировки. Убедиться при трассировке, что сумма равна 21.

Таблица 6.2. Заготовка для таблицы трассировки алгоритма из задания 6.6

---

---

Что такое трассировка? Как она производится?

---

Трассировка – процесс заполнения таблицы последовательностью выполнения команд программы.
Она производится путем создания таблицы со столбцами (первый столбец с командами, а другие содержат имена переменных, которые есть в программе) и строками (в одной строке одна команда, а в других ячейках записываются значения, которые были присвоены или прочерк, если у переменной неопределенное значение).